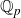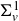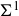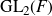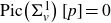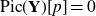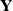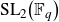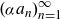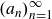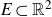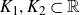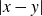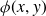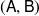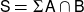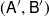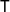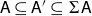Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
A characterisation of atomicity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 459-465
- Print publication:
- September 2023
-
- Article
- Export citation
Relatively hyperbolic groups with strongly shortcut parabolics are strongly shortcut
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 17 April 2023, pp. 367-380
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PSP volume 174 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 13 April 2023, pp. b1-b5
- Print publication:
- May 2023
-
- Article
-
- You have access
- Export citation
The Picard group of vertex affinoids in the first Drinfeld covering
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 13 April 2023, pp. 423-432
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PSP volume 174 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 13 April 2023, pp. f1-f2
- Print publication:
- May 2023
-
- Article
-
- You have access
- Export citation
Random amenable C*-algebras
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 345-366
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equations of mirrors to log Calabi–Yau pairs via the heart of canonical wall structures
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 381-421
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable finiteness does not imply linear soficity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 319-325
- Print publication:
- September 2023
-
- Article
- Export citation
Intermediate-scale statistics for real-valued lacunary sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 303-318
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Log Product Formula in Quantum K-theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 225-252
- Print publication:
- September 2023
-
- Article
- Export citation
Paucity problems and some relatives of Vinogradov’s mean value theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 05 April 2023, pp. 327-343
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite point configurations in products of thick Cantor sets and a robust nonlinear Newhouse Gap Lemma
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 285-301
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Co-t-structures, cotilting and cotorsion pairs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 10 March 2023, pp. 89-106
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motivic zeta functions of hyperplane arrangements
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 07 March 2023, pp. 187-215
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NAV volume 76 issue 2-3 Cover and Front matter
-
- Journal:
- The Journal of Navigation / Volume 76 / Issue 2-3 / March 2023
- Published online by Cambridge University Press:
- 15 August 2023, pp. f1-f2
- Print publication:
- March 2023
-
- Article
-
- You have access
- Export citation
Minimum required accuracy for HD maps
-
- Journal:
- The Journal of Navigation / Volume 76 / Issue 2-3 / March 2023
- Published online by Cambridge University Press:
- 22 June 2023, pp. 238-254
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ionospheric correction of S-band tracking radar data using NavIC S-band signals in missile test range applications
-
- Journal:
- The Journal of Navigation / Volume 76 / Issue 2-3 / March 2023
- Published online by Cambridge University Press:
- 05 April 2023, pp. 225-237
- Print publication:
- March 2023
-
- Article
- Export citation
Characterisation and position-aiding performance analysis of Doppler observation from android smartphones
-
- Journal:
- The Journal of Navigation / Volume 76 / Issue 2-3 / March 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 375-393
- Print publication:
- March 2023
-
- Article
- Export citation
A collaborative collision avoidance strategy for autonomous ships under mixed scenarios
-
- Journal:
- The Journal of Navigation / Volume 76 / Issue 2-3 / March 2023
- Published online by Cambridge University Press:
- 05 April 2023, pp. 200-224
- Print publication:
- March 2023
-
- Article
- Export citation
Collision risk quantification for pairs of recorded aircraft trajectories
-
- Journal:
- The Journal of Navigation / Volume 76 / Issue 2-3 / March 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 181-199
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation