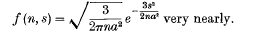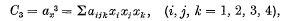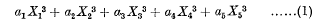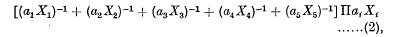Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
On the Penetration of Waves and their Rays into a Medium of Gradually Varying Properties
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 124-131
- Print publication:
- May 1924
-
- Article
- Export citation
On the Angle of Incidence in Soaring Flight
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 186-188
- Print publication:
- May 1924
-
- Article
- Export citation
The Electromagnetic Equations as Basis of Einstein's Quadratic Form
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 138-162
- Print publication:
- May 1924
-
- Article
- Export citation
On Graeffe's Method for Complex Roots of Algebraic Equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 83-87
- Print publication:
- May 1924
-
- Article
- Export citation
The Problems of Random Flight and Conduction of Heat
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-168
- Print publication:
- May 1924
-
- Article
- Export citation
PSP volume 22 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- May 1924
-
- Article
-
- You have access
- Export citation
On the Polygons Inscribed in one Conic and Circumscribed to Another
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 163-166
- Print publication:
- May 1924
-
- Article
- Export citation
The Integral Expansions of Arbitrary Functions connected with Integral Equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 169-185
- Print publication:
- May 1924
-
- Article
- Export citation
PSP volume 22 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- May 1924
-
- Article
-
- You have access
- Export citation
On Protecting and Sensitising Colloidal Sols
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 101-104
- Print publication:
- May 1924
-
- Article
- Export citation
The Equation of State of a Gas
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 105-112
- Print publication:
- May 1924
-
- Article
- Export citation
Dissociation under a Temperature Gradient
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 132-137
- Print publication:
- May 1924
-
- Article
- Export citation
Canonical Forms of the Quaternary Cubic associated with arbitrary Quadrics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 92-100
- Print publication:
- May 1924
-
- Article
- Export citation
On the Differential Invariants of the Laguerre Group
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 2 / May 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 113-123
- Print publication:
- May 1924
-
- Article
- Export citation
The conics through fives of six points
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 11-15
- Print publication:
- February 1924
-
- Article
- Export citation
On a modified electrostatic oscillograph
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 68-69
- Print publication:
- February 1924
-
- Article
- Export citation
An oscillographic study of the production of X-rays by a Coolidge tube
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 70-75
- Print publication:
- February 1924
-
- Article
- Export citation
On the generalisation of a theorem of Steiner
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 28-33
- Print publication:
- February 1924
-
- Article
- Export citation
PSP volume 22 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- February 1924
-
- Article
-
- You have access
- Export citation
PSP volume 22 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- February 1924
-
- Article
-
- You have access
- Export citation