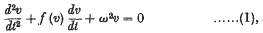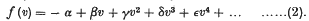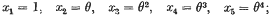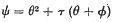Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
On the Stability of the Periodic States of the Triode Oscillator
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 16-23
- Print publication:
- February 1924
-
- Article
- Export citation
Angular Momentum and Electron Impact
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 56-66
- Print publication:
- February 1924
-
- Article
- Export citation
Involutions on a Normal Quartic Curve in Space of Four Dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 24-25
- Print publication:
- February 1924
-
- Article
- Export citation
Hankel Transforms*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, p. 67
- Print publication:
- February 1924
-
- Article
- Export citation
On the real twisted cubic curves which are geodesic upon a quadric surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 42-48
- Print publication:
- February 1924
-
- Article
- Export citation
On errors of observation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 26-27
- Print publication:
- February 1924
-
- Article
- Export citation
On the Number of Lines which meet Four Regions* in Hyper-Space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-53
- Print publication:
- February 1924
-
- Article
- Export citation
An early formulation by Stokes of the theories of the rotatory polarizations of light
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 76-81
- Print publication:
- February 1924
-
- Article
- Export citation
On certain nets of plane curves
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-10
- Print publication:
- February 1924
-
- Article
- Export citation
The Mechanism of the Rusting of Iron
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 54-55
- Print publication:
- February 1924
-
- Article
- Export citation
On an extension of Wallace's pedal property of the circumcircle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 1 / February 1924
- Published online by Cambridge University Press:
- 24 October 2008, pp. 34-41
- Print publication:
- February 1924
-
- Article
- Export citation
APPENDIX J - NOTE ON THE SIZE AND INERTIA OF ELECTRONS
-
- Book:
- Electromagnetic Theory
- Published online:
- 05 March 2012
- Print publication:
- 02 June 2011, pp 131-134
- First published in:
- 1912
-
- Chapter
- Export citation
Contents
-
- Book:
- Electromagnetic Theory
- Published online:
- 05 March 2012
- Print publication:
- 02 June 2011, pp v-x
- First published in:
- 1912
-
- Chapter
- Export citation
APPENDIX K - VECTOR ANALYSIS
-
- Book:
- Electromagnetic Theory
- Published online:
- 05 March 2012
- Print publication:
- 02 June 2011, pp 135-143
- First published in:
- 1912
-
- Chapter
- Export citation
PREFACE
-
- Book:
- Electromagnetic Theory
- Published online:
- 05 March 2012
- Print publication:
- 02 June 2011, pp iii-iii
- First published in:
- 1912
-
- Chapter
- Export citation
IN MEMORY OF GEORGE FRANCIS FITZGERALD, F.R.S.
-
- Book:
- Electromagnetic Theory
- Published online:
- 05 March 2012
- Print publication:
- 02 June 2011, pp iv-iv
- First published in:
- 1912
-
- Chapter
- Export citation
CHAPTER X - WAVES IN THE ETHER
-
- Book:
- Electromagnetic Theory
- Published online:
- 05 March 2012
- Print publication:
- 02 June 2011, pp 144-519
- First published in:
- 1912
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Electromagnetic Theory
- Published online:
- 05 March 2012
- Print publication:
- 02 June 2011, pp i-ii
- First published in:
- 1912
-
- Chapter
- Export citation
CHAPTER IX - WAVES FROM MOVING SOURCES
-
- Book:
- Electromagnetic Theory
- Published online:
- 05 March 2012
- Print publication:
- 02 June 2011, pp 1-130
- First published in:
- 1912
-
- Chapter
- Export citation
JAMES PRESCOTT JOULE
-
- Book:
- Memoir and Scientific Correspondence of the Late Sir George Gabriel Stokes, Bart.
- Published online:
- 05 October 2010
- Print publication:
- 24 June 2010, pp 46-51
- First published in:
- 1907
-
- Chapter
- Export citation