We prove that if u(x, t) is a solution of the one dimensional heat equation and if A u(x, t) is its Appell transform, then u(x, t) has the semi-group (Huygens) property in a domain D if and only if A u(x, t) has the semi-group property in a dual region. We apply this result to simplify and extend some results of Rosenbloom and Widder.

In Section 1 of this note we will construct an example of a subset of R × Rn such that the parabolic capacity with respect to the heat equation is zero although its orthogonal projection onto {0} × Rn is the whole space. Such examples were already given by R. Kaufman and J.-M. Wu in [5] and [6]. However, our probabilistic approach seems to be more transparent since it does not depend on explicit formulas for Green functions.

In this paper, we consider an extended model of a coupled nonlinear reaction-diffusion equations with Neumann-Neumann boundary conditions. We obtain upper linear growth bound for one of the components. We also find the corresponding bound for the case of Dirichlet-Dirichlet boundary conditions.

The Cauchy problem in the form of (1.11) with linear and constant coefficients is discussed. The solution (1.10) can be given in explicit form when the stochastic process is a multidimensional autoregression (AR) type, or Ornstein–Uhlenbeck process. Functionals of (1.10) form were studied by Kac in the Brownian motion case. The solutions are obtained with the help of the Radon–Nikodym transformation, proposed by Novikov [12].

We prove a priori estimates for the gradient and curvature of spacelike hypersurfaces moving by mean curvature in a Lorentzian manifold. These estimates are obtained under much weaker conditions than have been previously assumed. We also use mean curvature flow in the construction of maximal slices in asymptotically flat spacetimes. An essential tool is a maximum principle for sub-solutions of a parabolic operator on complete Riemannian manifolds with time-dependent metric.

A class of functional differential equations in some Hilbert space are studied. The results are applicable to many quasi-linear parabolic paratial differential equations with (possibly) countably many discrete delays and finitely many distributed delays in the highest order spatial derivatives. For the linear case, an evolution operator on the underline space H is introduced, via which a variation of constant formula for the solution of the equation in the underline space H is derived. Some spectral properties of the generator of the solution semigroup defined on some appropriate space are discussed as well.

Consider positive solutions of the one dimensional heat equation. The space variable x lies in (–a, a): the time variable t in (0,∞). When the solution u satisfies (i) u (±a, t) = 0, and (ii) u(·, 0) is logconcave, we give a new proof based on the Maximum Principle, that, for any fixed t > 0, u(·, t) remains logconcave. The same proof techniques are used to establish several new results related to this, including results concerning joint concavity in (x, t) similar to those considered in Kennington [15].

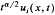Let ui(x, t) be the ith component of a nonnegative solution of a weakly coupled system of second-order, linear, parabolic partial differential equations, for x ∈ Rn and 0 < t < T. We obtain lower estimates, near t = 0, for the Lebesgue measure of the set of x for which exceeds 1. Related results for Poisson integrals on a half-space are also described, some applications are given, and interesting comparisons emerge.

Let u be a solution of the heat equation which can be written as the difference of two non-negative solutions, and let v be a non-negative solution. A study is made of the behaviour of u(x, t)/v(x, t) as t → 0+. The methods are based on the Gauss-Weierstrass integral representation of solutions on Rn × ]0, a[ and results on the relative differentiation of measures, which are employed in a novel way to obtain several domination, non-negativity, uniqueness and representation theorems.

In this paper an ill-posed problem for the heat equation is investigated. Solutions u to the equation ut – uxx = 0, which are approximately known on the positive half-axis t = 0 and on some vertical lines x = x1,…, x = xn, are considered and stability estimates of these solutions are presented. We assume an a priori bound, governing the heat flow across the boundary x = 0.

The aim of this article is to review the progress made in the last few years in the representation theory of solutions of parabolic systems in the sense of Petrowskii.

The Stefan problem is a particular free boundary problem for the heat equation which arises in the investigation of the melting of solids. In the case of one space dimension there are numerous results available concerning the existence, uniqueness, and stability of the solution [c.f. 6]. However the case of several space variables is considerably more difficult. This is due in large part to the fact that the geometry of the problem can become quite complicated, and smooth initial and boundary data do not necessarily lead to smooth solutions. In particular, under heating, a connected solid can melt into two (or more) disconnected solids, thus leading to a problem in which the free boundary varies in a discontinuous manner. These difficulties have motivated several researchers to look for “weak” solutions to the Stefan problem [c.f. 1, 3, 5]. Although this approach is quite general and leads to numerical schemes for solving the problem under consideration, there are several drawbacks to this method, among them being the fact that no information is obtained concerning the structure of the interphase boundary, nor is there much information on the regularity of these weak solutions.