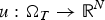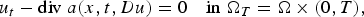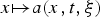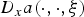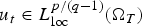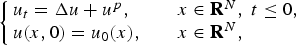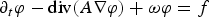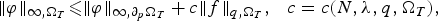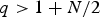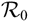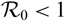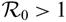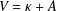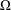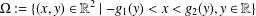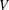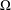Refine listing
Actions for selected content:
292 results in 35Kxx
On higher differentiability of solutions of parabolic systems with discontinuous coefficients and (p, q)-growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 419-451
- Print publication:
- February 2020
-
- Article
- Export citation
Asymptotically self-similar behaviour of global solutions for semilinear heat equations with algebraically decaying initial data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 789-811
- Print publication:
- April 2020
-
- Article
- Export citation
Existence of bistable waves for a nonlocal and nonmonotone reaction-diffusion equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 721-739
- Print publication:
- April 2020
-
- Article
- Export citation
Complete quenching phenomenon and instantaneous shrinking of support of solutions of degenerate parabolic equations with nonlinear singular absorption
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1323-1346
- Print publication:
- October 2019
-
- Article
- Export citation
Logarithmic upper bounds for weak solutions to a class of parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1481-1491
- Print publication:
- December 2019
-
- Article
- Export citation
Existence of travelling waves with the critical speed for an influenza model with treatment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 232-245
-
- Article
- Export citation
Lorentz Estimates for Weak Solutions of Quasi-linear Parabolic Equations with Singular Divergence-free Drifts
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 937-982
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Singular limits and properties of solutions of some degenerate elliptic and parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 353-385
- Print publication:
- April 2019
-
- Article
- Export citation
Autonomous and non-autonomous unbounded attractors under perturbations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 877-903
- Print publication:
- August 2019
-
- Article
- Export citation
EXISTENCE AND BLOW-UP OF SOLUTIONS TO A PARABOLIC EQUATION WITH NONSTANDARD GROWTH CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. 242-249
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Gradient Estimates for Spacelike Mean Curvature Flow with Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 459-469
-
- Article
- Export citation
Simulation of multiphase porous media flows with minimising movement and finite volume schemes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 1123-1152
-
- Article
- Export citation
Dynamics and asymptotic profiles of endemic equilibrium for two frequency-dependent SIS epidemic models with cross-diffusion
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 26-56
-
- Article
- Export citation
On the avascular ellipsoidal tumour growth model within a nutritive environment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 111-142
-
- Article
- Export citation
OPTION PRICING UNDER THE KOBOL MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 September 2018, pp. 175-190
-
- Article
-
- You have access
- Export citation
Time adaptive numerical solution of a highly non-linear degenerate cross-diffusion system arising in multi-species biofilm modelling
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 10 September 2018, pp. 1035-1061
-
- Article
-
- You have access
- Export citation
A Class of Parabolic Equations Driven by the Mean Curvature Flow
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 135-163
-
- Article
- Export citation
The effect of impurities on striped phases
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 August 2018, pp. 131-168
- Print publication:
- February 2019
-
- Article
- Export citation
ENTIRE SOLUTIONS OF A CURVATURE FLOW IN AN UNDULATING CYLINDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 137-147
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
MATHEMATICAL ANALYSIS OF COMBUSTION WAVES IN COMPETITIVE EXOTHERMIC REACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 339-342
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation