Refine search
Actions for selected content:
18 results
5 - Advanced Miscellany
-
- Book:
- ADE
- Published online:
- 01 August 2025
- Print publication:
- 07 August 2025, pp 122-164
-
- Chapter
- Export citation
RIGIDITY FOR VON NEUMANN ALGEBRAS OF GRAPH PRODUCT GROUPS II. SUPERRIGIDITY RESULTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 117-156
- Print publication:
- January 2025
-
- Article
- Export citation
Poisson boundaries of II1 factors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 October 2022, pp. 1746-1776
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noncommutative strong maximals and almost uniform convergence in several directions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e57
-
- Article
-
- You have access
- Open access
- Export citation
On the von Neumann algebras associated to Yang–Baxter operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 28 August 2020, pp. 1331-1354
- Print publication:
- August 2021
-
- Article
- Export citation
ON FUNDAMENTAL GROUPS OF TENSOR PRODUCT
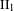 $\text{II}_{1}$ FACTORS
$\text{II}_{1}$ FACTORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 02 August 2018, pp. 1121-1139
- Print publication:
- July 2020
-
- Article
- Export citation
ORTHOMODULAR-VALUED MODELS FOR QUANTUM SET THEORY
-
- Journal:
- The Review of Symbolic Logic / Volume 10 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 05 June 2017, pp. 782-807
- Print publication:
- December 2017
-
- Article
- Export citation
Cloning in C *-Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 15 December 2016, pp. 689-705
-
- Article
- Export citation
Perturbations of Von Neumann Subalgebras With Finite Index
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 320-325
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
STRONG SKEW COMMUTATIVITY PRESERVING MAPS ON RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 25 November 2015, pp. 78-85
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Some Applications of the Perturbation Determinant in Finite von Neumann Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 133-156
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
A MEAN ERGODIC THEOREM FOR ACTIONS OF AMENABLE QUANTUM GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 87-95
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
Inner E 0-Semigroups on Infinite Factors
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 3 / 01 September 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 371-380
- Print publication:
- 01 September 2006
-
- Article
-
- You have access
- Export citation
A weak type inequality for non-commutative martingales and applications
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 91 / Issue 2 / September 2005
- Published online by Cambridge University Press:
- 23 August 2005, pp. 509-544
- Print publication:
- September 2005
-
- Article
- Export citation
QUANTUM GROUPOIDS OF COMPACT TYPE
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 4 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 10 February 2005, pp. 29-133
- Print publication:
- January 2005
-
- Article
- Export citation
Embeddings of ℓp into Non-commutative Spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-350
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Correspondences, von Neumann Algebras and Holomorphic L 2 Torsion
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 4 / 01 August 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 695-736
- Print publication:
- 01 August 2000
-
- Article
-
- You have access
- Export citation
Compact Derivations on Von Neumann Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 24 / Issue 1 / 01 March 1981
- Published online by Cambridge University Press:
- 20 November 2018, pp. 87-90
- Print publication:
- 01 March 1981
-
- Article
-
- You have access
- Export citation






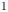
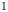
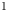
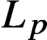
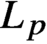
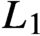
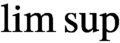
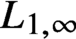
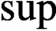
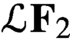
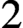
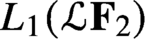
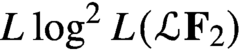
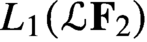
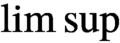
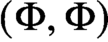
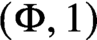
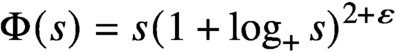
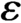
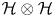
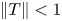
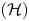
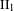
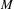
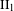
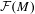
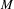
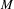
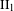
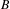
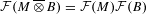
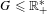
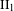
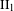
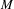
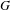
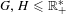
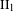
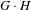
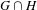
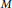
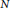
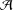
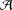

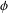
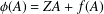
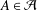
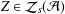
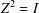
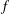
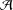
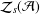
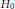
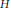
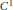
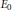
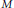
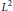
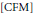
 is a von Neumann algebra that thas no nonzero finite discrete central projection, then there is no nontrivial compact derivation of
is a von Neumann algebra that thas no nonzero finite discrete central projection, then there is no nontrivial compact derivation of 