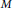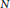Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bakshi, Keshab Chandra
and
Gupta, Ved Prakash
2021.
Lattice of intermediate subalgebras.
Journal of the London Mathematical Society,
Vol. 104,
Issue. 5,
p.
2082.