Refine search
Actions for selected content:
23 results
Generalized Airy operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-31
-
- Article
- Export citation
EVENTUAL POSITIVITY AND ASYMPTOTIC BEHAVIOUR FOR HIGHER-ORDER EVOLUTION EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 26 October 2023, pp. 165-167
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
A non-periodic indefinite variational problem in ℝN with critical exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 June 2023, pp. 579-612
-
- Article
- Export citation
On the spectral theory of groups of automorphisms of S-adic nilmanifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 705-726
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectra of infinite graphs via freeness with amalgamation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1633-1684
- Print publication:
- October 2023
-
- Article
- Export citation
A deep look into the dagum family of isotropic covariance functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 1026-1041
- Print publication:
- December 2022
-
- Article
- Export citation
Singular boundary conditions for Sturm–Liouville operators via perturbation theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 1110-1146
- Print publication:
- August 2023
-
- Article
- Export citation
Undecidability of the Spectral Gap
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 June 2022, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral alignment of correlated Gaussian matrices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 January 2022, pp. 279-310
- Print publication:
- March 2022
-
- Article
- Export citation
Self-adjoint extensions of bipartite Hamiltonians
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 22 June 2021, pp. 433-447
-
- Article
- Export citation
3 - Applications of Spectral Theory to Special Functions
-
-
- Book:
- Lectures on Orthogonal Polynomials and Special Functions
- Published online:
- 07 October 2020
- Print publication:
- 15 October 2020, pp 131-212
-
- Chapter
- Export citation
Spectral projections correlation structure for short-to-long range dependent processes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 31 January 2020, pp. 1-31
-
- Article
- Export citation
PACKING SUBORDINACY WITH APPLICATION TO SPECTRAL CONTINUITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 13 June 2019, pp. 226-244
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Borg's Periodicity Theorems for First-Order Self-Adjoint Systems with Complex Potentials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 19 December 2016, pp. 615-633
-
- Article
- Export citation
Constructive Proof of the Carpenter's Theorem
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-476
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
SOME INEQUALITIES OF JENSEN TYPE FOR ARG-SQUARE CONVEX FUNCTIONS OF UNITARY OPERATORS IN HILBERT SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 65-73
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Spectral Properties of Random and Deterministic CMVMatrices
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 5 / 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 270-281
- Print publication:
- 2014
-
- Article
- Export citation
Spectral and dynamical properties of sparse one-dimensional continuous Schrödinger and Dirac operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 667-700
-
- Article
-
- You have access
- Export citation
ON REPRESENTATIONS OF QUANTUM GROUPS Uq(fm(K,H))
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 261-284
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Geometry and Spectra of Closed Extensions of Elliptic Cone Operators
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 4 / 01 August 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 742-794
- Print publication:
- 01 August 2007
-
- Article
-
- You have access
- Export citation





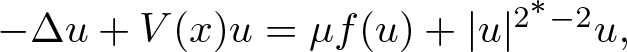
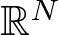
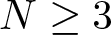
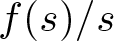


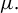
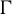
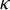
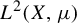
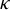
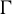
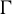
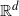
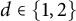
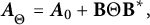
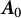

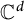
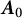
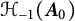


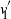
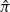
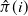
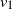
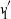
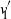
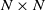
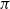
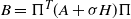
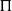
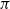
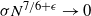
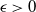
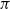
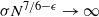
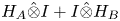
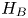
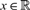
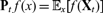

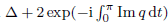 are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which
are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which 