Article contents
Singular boundary conditions for Sturm–Liouville operators via perturbation theory
Published online by Cambridge University Press: 23 June 2022
Abstract
We show that all self-adjoint extensions of semibounded Sturm–Liouville operators with limit-circle endpoint(s) can be obtained via an additive singular form-bounded self-adjoint perturbation of rank equal to the deficiency indices, say 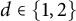 $d\in \{1,2\}$. This characterization generalizes the well-known analog for semibounded Sturm–Liouville operators with regular endpoints. Explicitly, every self-adjoint extension of the minimal operator can be written as
$d\in \{1,2\}$. This characterization generalizes the well-known analog for semibounded Sturm–Liouville operators with regular endpoints. Explicitly, every self-adjoint extension of the minimal operator can be written as 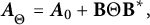 $$ \begin{align*} \boldsymbol{A}_{ {}_{\scriptstyle \Theta}}=\boldsymbol{A}_0+\mathbf{B}\Theta\mathbf{B}^*, \end{align*} $$
$$ \begin{align*} \boldsymbol{A}_{ {}_{\scriptstyle \Theta}}=\boldsymbol{A}_0+\mathbf{B}\Theta\mathbf{B}^*, \end{align*} $$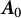 $\boldsymbol {A}_0$ is a distinguished self-adjoint extension and
$\boldsymbol {A}_0$ is a distinguished self-adjoint extension and  $\Theta $ is a self-adjoint linear relation in
$\Theta $ is a self-adjoint linear relation in 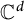 $\mathbb {C}^d$. The perturbation is singular in the sense that it does not belong to the underlying Hilbert space but is form-bounded with respect to
$\mathbb {C}^d$. The perturbation is singular in the sense that it does not belong to the underlying Hilbert space but is form-bounded with respect to 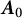 $\boldsymbol {A}_0$, i.e., it belongs to
$\boldsymbol {A}_0$, i.e., it belongs to 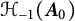 $\mathcal {H}_{-1}(\boldsymbol {A}_0)$, with possible “infinite coupling.” A boundary triple and compatible boundary pair for the symmetric operator are constructed to ensure that the perturbation is well defined and self-adjoint extensions are in a one-to-one correspondence with self-adjoint relations
$\mathcal {H}_{-1}(\boldsymbol {A}_0)$, with possible “infinite coupling.” A boundary triple and compatible boundary pair for the symmetric operator are constructed to ensure that the perturbation is well defined and self-adjoint extensions are in a one-to-one correspondence with self-adjoint relations  $\Theta $.
$\Theta $.
The merging of boundary triples with perturbation theory provides a more holistic view of the operator’s matrix-valued spectral measures: identifying not just the location of the spectrum, but also certain directional information.
As an example, self-adjoint extensions of the classical Jacobi differential equation (which has two limit-circle endpoints) are obtained, and their spectra are analyzed with tools both from the theory of boundary triples and perturbation theory.
Keywords
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
M. Bush and C. Liaw were partially supported by the National Science Foundation Grant No. DMS-1802682. D. Frymark was partially supported by the Swedish Foundation for Strategic Research under Grant No. AM13-0011. Since August 2020, C. Liaw has been serving as a Program Director in the Division of Mathematical Sciences at the National Science Foundation (NSF), USA, and as a component of this position, she received support from NSF for research, which included work on this paper. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the NSF.
References
- 3
- Cited by


