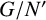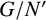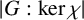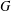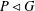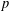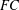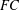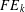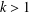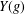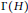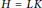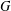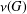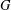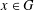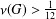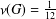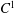Refine search
Actions for selected content:
26 results
9 - Gromov’s Theorem
- from Part II - Results and Applications
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 301-354
-
- Chapter
- Export citation
8 - The Milnor–Wolf Theorem
- from Part II - Results and Applications
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 273-300
-
- Chapter
- Export citation
1 - Background
- from Part I - Tools and Theory
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 3-49
-
- Chapter
- Export citation
7 - Choquet–Deny Groups
- from Part II - Results and Applications
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 246-272
-
- Chapter
- Export citation
A CHARACTERISATION OF SOLUBLE
 ${PST}$-GROUPS
${PST}$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 520-527
- Print publication:
- December 2024
-
- Article
- Export citation
HALL CLASSES OF GROUPS WITH A LOCALLY FINITE OBSTRUCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 16-43
- Print publication:
- August 2024
-
- Article
- Export citation
SOME CRITERIA FOR SOLVABILITY AND NILPOTENCY OF FINITE GROUPS BY STRONGLY MONOLITHIC CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 120-124
- Print publication:
- August 2023
-
- Article
- Export citation
BOUNDNESS OF INTERSECTION NUMBERS FOR ACTIONS BY TWO-DIMENSIONAL BIHOLOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 1677-1700
- Print publication:
- September 2022
-
- Article
- Export citation
ON UNRAMIFIED SOLVABLE EXTENSIONS OF SMALL NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 428-437
- Print publication:
- June 2021
-
- Article
- Export citation
Variations on results on orders of products in finite groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 12 October 2020, pp. 1443-1449
- Print publication:
- October 2021
-
- Article
- Export citation
AXIOMATISABILITY OF THE CLASS OF MONOLITHIC GROUPS IN A VARIETY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 67-76
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
5 - Nilpotent Groups, Commutators and Nilprogressions
-
- Book:
- Introduction to Approximate Groups
- Published online:
- 31 October 2019
- Print publication:
- 14 November 2019, pp 81-108
-
- Chapter
- Export citation
Global fixed points for nilpotent actions on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3339-3367
- Print publication:
- December 2020
-
- Article
- Export citation
SQUARES OF DEGREES OF BRAUER CHARACTERS AND MONOMIAL BRAUER CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 58-60
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
A NILPOTENCY-LIKE CONDITION FOR INFINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 24-33
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
ω-STABILITY AND MORLEY RANK OF BILINEAR MAPS, RINGS AND NILPOTENT GROUPS
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 19 June 2017, pp. 754-777
- Print publication:
- June 2017
-
- Article
- Export citation
Co-maximal Graphs of Subgroups of Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 12-25
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
NILPOTENCY IN UNCOUNTABLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 27 October 2016, pp. 59-69
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
ON THE PROBABILITY OF GENERATING NILPOTENT SUBGROUPS IN A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 447-453
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Sur les rapprochements par conjugaison en dimension 1 et classe
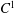 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^1$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 19 June 2014, pp. 1183-1195
- Print publication:
- July 2014
-
- Article
- Export citation