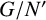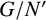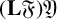1 Introduction
If N is a nilpotent normal subgroup of a group G, the structure of the factor group
![]() $G/N'$
has a strong influence on the whole group G. The first evidence of this phenomenon can be traced back to a classical theorem of Hall [Reference Hall11] which states that if
$G/N'$
has a strong influence on the whole group G. The first evidence of this phenomenon can be traced back to a classical theorem of Hall [Reference Hall11] which states that if
![]() $G/N'$
is nilpotent, then G itself is nilpotent. A few years later, Plotkin [Reference Plotkin15] gave a different proof of Hall’s nilpotency criterion and proved that if
$G/N'$
is nilpotent, then G itself is nilpotent. A few years later, Plotkin [Reference Plotkin15] gave a different proof of Hall’s nilpotency criterion and proved that if
![]() $G/N'$
is locally nilpotent, then G is locally nilpotent too, a fact that is not a direct consequence of the previous theorem. In 1968, Robinson [Reference Robinson16] showed that this kind of result is strictly connected to the behaviour of certain tensor products of G-modules; this approach makes it possible to obtain similar statements for many other relevant group properties.
$G/N'$
is locally nilpotent, then G is locally nilpotent too, a fact that is not a direct consequence of the previous theorem. In 1968, Robinson [Reference Robinson16] showed that this kind of result is strictly connected to the behaviour of certain tensor products of G-modules; this approach makes it possible to obtain similar statements for many other relevant group properties.
Along these lines, we say that a group class 𝔛 is a Hall class if it contains every group G admitting a nilpotent normal subgroup N such that
![]() $G/N'$
belongs to 𝔛. Clearly, finite groups and locally cyclic groups form Hall classes, and it is also easy to see that any class consisting only of groups with a locally cyclic Fitting subgroup is a Hall class.
$G/N'$
belongs to 𝔛. Clearly, finite groups and locally cyclic groups form Hall classes, and it is also easy to see that any class consisting only of groups with a locally cyclic Fitting subgroup is a Hall class.
In our terminology, the theorems of Hall and Plotkin just say that the class 𝔑 of nilpotent groups and the class L𝔑 of locally nilpotent groups are Hall classes. Moreover, it follows from the result of Robinson that hypercentral groups, hypercyclic groups, (locally) supersoluble groups and (locally) polycyclic groups form Hall classes; also, it turns out that a group class 𝔛 that is closed with respect to forming normal subgroups and extensions is a Hall class, provided that it contains all homomorphic images of the tensor product of any pair of abelian 𝔛-groups. More recently, it was proved that the class of paranilpotent groups is a Hall class (see [Reference Franciosi and de Giovanni10]), and also that
![]() $FC$
-nilpotent,
$FC$
-nilpotent,
![]() $FC$
-hypercentral and locally
$FC$
-hypercentral and locally
![]() $FC$
-nilpotent groups form Hall classes (see [Reference Amberg, Franciosi and de Giovanni1]).
$FC$
-nilpotent groups form Hall classes (see [Reference Amberg, Franciosi and de Giovanni1]).
Since any Hall class containing all abelian groups must contain 𝔑, it is clear that for every positive integer c, the class of nilpotent groups of class at most c is not a Hall class, so in particular abelian groups do not form a Hall class. We remark also that the class of torsion-free groups is not a Hall class, although the class of locally finite groups and the class of groups of finite exponent are Hall classes.
It is obvious that unions and intersections of collections of Hall classes are likewise Hall classes. However, if 𝔛 and 𝔜 are Hall classes, the class 𝔛𝔜, consisting of all groups G containing a normal 𝔛-subgroup N such that
![]() $G/N$
is in 𝔜, need not be a Hall class. For instance, the class 𝔉𝔑 of all finite-by-nilpotent groups is not a Hall class; actually, for many natural choices of the Hall class 𝔜, groups that are finite-by-𝔜 do not form a Hall class (see [Reference de Giovanni, Trombetti and Wehrfritz7], where many examples of this circumstance can be found).
$G/N$
is in 𝔜, need not be a Hall class. For instance, the class 𝔉𝔑 of all finite-by-nilpotent groups is not a Hall class; actually, for many natural choices of the Hall class 𝔜, groups that are finite-by-𝔜 do not form a Hall class (see [Reference de Giovanni, Trombetti and Wehrfritz7], where many examples of this circumstance can be found).
The aim of this paper is to prove that the situation is completely different if the finite obstruction at the bottom is replaced by a locally finite one. The following summarizes very briefly most of our main conclusions.
Theorem. The class of all (locally finite)-by-𝔜 groups and the class of all (locally finite of finite exponent)-by-𝔜 groups are Hall classes for the following 18 choices for 𝔜: nilpotent, Fitting, hypercentral, Engel, Baer, Gruenberg, locally nilpotent, paranilpotent, hypercyclic, locally supersoluble, FC-nilpotent, FC-hypercentral, locally (nilpotent-by-finite), soluble, hyperabelian, locally soluble, finite (Prüfer) rank, finite abelian section rank.
Note that (locally finite)-by-nilpotent groups and (locally finite of finite exponent)-by-nilpotent groups were already proved to form Hall classes in [Reference Endimioni and Traustason9, Reference Shumyatsky18], respectively, although with different proofs.
Our notation, which is mostly standard, can be found in [Reference Robinson17]; we refer to [Reference Wehrfritz20] for results and terminology concerning linear groups.
2 Nilpotency conditions
As mentioned in the introduction, nilpotent groups, locally nilpotent groups and hypercentral groups form Hall classes; in addition, it is known that Baer groups, Gruenberg groups, Fitting groups and Engel groups have the same behaviour (see [Reference de Giovanni, Trombetti and Wehrfritz7]). The goal of this section is to prove that if 𝔜 is any of these seven group classes, then
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{Y}$
is likewise a Hall class, where L𝔉 denotes the class of all locally finite groups.
$(\mathbf{L}\mathfrak{F})\mathfrak{Y}$
is likewise a Hall class, where L𝔉 denotes the class of all locally finite groups.
Let G be a group. If A and B are G-modules, the tensor product
![]() $A\otimes _{\mathbb{Z}}\! B$
can be made into a G-module via
$A\otimes _{\mathbb{Z}}\! B$
can be made into a G-module via
![]() $(a\otimes b)g=(ag)\otimes (bg)$
for all
$(a\otimes b)g=(ag)\otimes (bg)$
for all
![]() $a\in A$
,
$a\in A$
,
![]() $b\in B$
,
$b\in B$
,
![]() $g\in G$
. Recall that a class
$g\in G$
. Recall that a class
![]() $\cal M$
of G-modules is tensorial if, for all A and B in
$\cal M$
of G-modules is tensorial if, for all A and B in
![]() $\cal M$
, every G-homomorphic image of
$\cal M$
, every G-homomorphic image of
![]() $A\otimes _{\mathbb{Z}}\! B$
(and in particular
$A\otimes _{\mathbb{Z}}\! B$
(and in particular
![]() $A\otimes _{\mathbb{Z}}\! B$
itself) belongs to
$A\otimes _{\mathbb{Z}}\! B$
itself) belongs to
![]() $\cal M$
. It is well known that if N is a normal subgroup of G, for each positive integer i, there exists a G-epimorphism
$\cal M$
. It is well known that if N is a normal subgroup of G, for each positive integer i, there exists a G-epimorphism
where the factors of the lower central series of N are regarded as G-modules by conjugation. This is the reason for which tensorial classes play a relevant role in the context of Hall classes. For instance, Hall’s nilpotency criterion rests upon the fact that the class of polytrivial G-modules (that is, G-modules admitting a finite series of G-submodules whose factors are trivial G-modules) is tensorial (see for instance [Reference Wehrfritz21, page 10]).
If G is a group and if
![]() $\cal M$
,
$\cal M$
,
![]() $\cal N$
are classes of G-modules, we say that a G-module A is
$\cal N$
are classes of G-modules, we say that a G-module A is
![]() $\cal M$
-by-
$\cal M$
-by-
![]() $\cal N$
if it has a G-submodule
$\cal N$
if it has a G-submodule
![]() $B\in {\cal M}$
such that
$B\in {\cal M}$
such that
![]() $A/B$
is in
$A/B$
is in
![]() $\cal N$
. Moreover, in the following, we denote by
$\cal N$
. Moreover, in the following, we denote by
![]() ${\cal T}_G$
the class of all G-modules whose underlying abelian groups are periodic.
${\cal T}_G$
the class of all G-modules whose underlying abelian groups are periodic.
Lemma 2.1. Let G be a group and let
![]() $\cal M$
be a tensorial class of G-modules that is quotient-closed. Then the class of all G-modules that are
$\cal M$
be a tensorial class of G-modules that is quotient-closed. Then the class of all G-modules that are
![]() ${\cal T}_G$
-by-
${\cal T}_G$
-by-
![]() $\cal M$
is tensorial.
$\cal M$
is tensorial.
Proof. Clearly, the class
![]() ${\cal T}_G$
-by-
${\cal T}_G$
-by-
![]() $\cal M$
is quotient-closed. Let A and B be two arbitrary G-modules that are
$\cal M$
is quotient-closed. Let A and B be two arbitrary G-modules that are
![]() ${\cal T}_G$
-by-
${\cal T}_G$
-by-
![]() $\cal M$
, and let
$\cal M$
, and let
![]() $T_A$
and
$T_A$
and
![]() $T_B$
be the periodic parts of A and B (as abelian groups), respectively. The natural sequence
$T_B$
be the periodic parts of A and B (as abelian groups), respectively. The natural sequence
is exact, where the G-submodule
is easily seen to be in
![]() ${\cal T}_G$
and
${\cal T}_G$
and
is in
![]() $\cal M$
since
$\cal M$
since
![]() $A/T_A$
and
$A/T_A$
and
![]() $B/T_B$
are. Therefore, the G-module
$B/T_B$
are. Therefore, the G-module
![]() $A\otimes _{\mathbb{Z}}\! B$
is
$A\otimes _{\mathbb{Z}}\! B$
is
![]() ${\cal T}_G$
-by-
${\cal T}_G$
-by-
![]() $\cal M$
and the statement is proved.
$\cal M$
and the statement is proved.
Corollary 2.2. If G is a group, the class of all G-modules that are
![]() ${\cal T}_G$
-by- polytrivial is tensorial.
${\cal T}_G$
-by- polytrivial is tensorial.
A classical theorem of Issai Schur states that if a group G is (locally) finite over its centre
![]() $\zeta _1(G)$
, then
$\zeta _1(G)$
, then
![]() $G'$
is (locally) finite (see [Reference Robinson17, Part 1, Theorem 4.12 and its Corollary]). For our purposes, we need the following application of Schur’s theorem.
$G'$
is (locally) finite (see [Reference Robinson17, Part 1, Theorem 4.12 and its Corollary]). For our purposes, we need the following application of Schur’s theorem.
Lemma 2.3. Let G be a group and let N be a normal subgroup of G. If N has a finite G-invariant series whose factors are either locally finite or central in G, then the subgroup
![]() $[N,_kG]$
is locally finite, where k is the number of factors of this series that are not locally finite.
$[N,_kG]$
is locally finite, where k is the number of factors of this series that are not locally finite.
Proof. Let
be a finite G-invariant series of minimal length t such that each
![]() $N_{i+1}/N_i$
is either locally finite or central in G and at most k factors are not locally finite. Of course, we may suppose that G has no nontrivial locally finite normal subgroups and
$N_{i+1}/N_i$
is either locally finite or central in G and at most k factors are not locally finite. Of course, we may suppose that G has no nontrivial locally finite normal subgroups and
![]() $k>0$
, so that in particular
$k>0$
, so that in particular
![]() $N_1\leq \zeta _1(G)$
. By induction, we have that
$N_1\leq \zeta _1(G)$
. By induction, we have that
is locally finite. Then
![]() $M/\zeta _1(M)$
is locally finite, so
$M/\zeta _1(M)$
is locally finite, so
![]() $M'$
is locally finite by Schur’s theorem and hence M is torsion-free abelian. Since
$M'$
is locally finite by Schur’s theorem and hence M is torsion-free abelian. Since
![]() $N_1\leq \zeta _1(G)$
and
$N_1\leq \zeta _1(G)$
and
![]() $M/N_1$
is locally finite, it follows that M is central in G and hence
$M/N_1$
is locally finite, it follows that M is central in G and hence
![]() $[N,_kG]\leq [M,G]=\{1\}$
.
$[N,_kG]\leq [M,G]=\{1\}$
.
The choice
![]() $N=G$
in the above statement gives the following characterization of (locally finite)-by-nilpotent groups.
$N=G$
in the above statement gives the following characterization of (locally finite)-by-nilpotent groups.
Corollary 2.4. A group G is (locally finite)-by-nilpotent if and only it has a normal series of finite length whose factors are either locally finite or central in G.
We are now in a position to prove the first main theorem of this section.
Theorem 2.5. The class
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{N}$
of all (locally finite)-by-nilpotent groups is a Hall class.
$(\mathbf{L}\mathfrak{F})\mathfrak{N}$
of all (locally finite)-by-nilpotent groups is a Hall class.
Proof. Let N be a nilpotent normal subgroup of a group G such that
![]() $G/N'$
is in
$G/N'$
is in
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{N}$
. If
$(\mathbf{L}\mathfrak{F})\mathfrak{N}$
. If
![]() $T/N'$
is the periodic part of
$T/N'$
is the periodic part of
![]() $N/N'$
, then
$N/N'$
, then
![]() $N/T$
has a finite G-invariant series whose factors are central in G and hence
$N/T$
has a finite G-invariant series whose factors are central in G and hence
![]() $N/N'$
is
$N/N'$
is
![]() ${\cal T}_G$
-by-polytrivial as a G-module (by conjugation). Application of Corollary 2.2 yields that N has a finite G-invariant series whose nonperiodic factors are central in G. It follows that G has a normal series of finite length whose factors are either locally finite or central, and hence it is (locally finite)-by-nilpotent by Corollary 2.4.
${\cal T}_G$
-by-polytrivial as a G-module (by conjugation). Application of Corollary 2.2 yields that N has a finite G-invariant series whose nonperiodic factors are central in G. It follows that G has a normal series of finite length whose factors are either locally finite or central, and hence it is (locally finite)-by-nilpotent by Corollary 2.4.
Philip Hall proved that if N is a nilpotent normal subgroup of a group G and
![]() $G/N'$
is nilpotent, then the nilpotency class of G can be bounded in terms of the nilpotency classes of N and
$G/N'$
is nilpotent, then the nilpotency class of G can be bounded in terms of the nilpotency classes of N and
![]() $G/N'$
. Note here that the above proof allows us to give a quantitative version of Theorem 2.5 too.
$G/N'$
. Note here that the above proof allows us to give a quantitative version of Theorem 2.5 too.
Theorem 2.6. There exists an integer-valued function
![]() $f=f(c,d)$
such that, if G is any group containing a nilpotent normal subgroup N of class c such that
$f=f(c,d)$
such that, if G is any group containing a nilpotent normal subgroup N of class c such that
![]() $\gamma _{d+1}(G/N')$
is locally finite, then
$\gamma _{d+1}(G/N')$
is locally finite, then
![]() $\gamma _{f(c,d)}(G)$
is locally finite.
$\gamma _{f(c,d)}(G)$
is locally finite.
Recall that a group G is a Fitting group if it is generated by its nilpotent normal subgroups. Of course, Fitting groups are locally nilpotent and it follows easily from Hall’s theorem that they form a Hall class (see [Reference de Giovanni, Trombetti and Wehrfritz7] for details).
Corollary 2.7. The class of all (locally finite)-by-Fitting groups is a Hall class.
Proof. Let G be a group containing a nilpotent normal subgroup N such that
![]() $G/N'$
is (locally finite)-by-Fitting and let T be the unique maximal locally finite normal subgroup of G. If
$G/N'$
is (locally finite)-by-Fitting and let T be the unique maximal locally finite normal subgroup of G. If
![]() $L/N'$
is the subgroup of all elements of finite order of
$L/N'$
is the subgroup of all elements of finite order of
![]() $G/N'$
and
$G/N'$
and
![]() $K/L$
is any nilpotent normal subgroup of
$K/L$
is any nilpotent normal subgroup of
![]() $G/L$
, we have that
$G/L$
, we have that
![]() $KN/N'$
is (locally finite)-by-nilpotent and hence also the normal subgroup
$KN/N'$
is (locally finite)-by-nilpotent and hence also the normal subgroup
![]() $KN$
of G is (locally finite)-by-nilpotent by Theorem 2.5. Thus,
$KN$
of G is (locally finite)-by-nilpotent by Theorem 2.5. Thus,
![]() $KN/T$
is nilpotent, so that
$KN/T$
is nilpotent, so that
![]() $G/T$
is a Fitting group and G is (locally finite)-by-Fitting.
$G/T$
is a Fitting group and G is (locally finite)-by-Fitting.
The main ingredients of the proof of Theorem 2.5 are essentially the tensoriality of
![]() ${\cal T}_G$
-by-polytrivial G-modules (Corollary 2.2) and the sufficient part of the characterization of (locally finite)-by-nilpotent groups given in Corollary 2.4. Actually, many of the most relevant classes of groups with a locally finite obstruction at the bottom can be proved to be Hall classes, provided that results corresponding to Corollaries 2.2 and 2.4 are obtained (it is then enough to repeat the argument of the above proof).
${\cal T}_G$
-by-polytrivial G-modules (Corollary 2.2) and the sufficient part of the characterization of (locally finite)-by-nilpotent groups given in Corollary 2.4. Actually, many of the most relevant classes of groups with a locally finite obstruction at the bottom can be proved to be Hall classes, provided that results corresponding to Corollaries 2.2 and 2.4 are obtained (it is then enough to repeat the argument of the above proof).
If G is a group and
![]() $\tau $
is an ordinal number, a G-module A is called hypertrivial (of height
$\tau $
is an ordinal number, a G-module A is called hypertrivial (of height
![]() $\tau $
) if it has an ascending series of G-submodules
$\tau $
) if it has an ascending series of G-submodules
such that
![]() $A_{\alpha +1}/A_\alpha $
is a trivial G-module for each ordinal
$A_{\alpha +1}/A_\alpha $
is a trivial G-module for each ordinal
![]() $\alpha <\tau $
. Since the class of hypertrivial G-modules is tensorial (see [Reference Robinson16, Lemma 1]), Lemma 2.1 has the following consequence, which corresponds to Corollary 2.2.
$\alpha <\tau $
. Since the class of hypertrivial G-modules is tensorial (see [Reference Robinson16, Lemma 1]), Lemma 2.1 has the following consequence, which corresponds to Corollary 2.2.
Corollary 2.8. If G is a group, the class of all G-modules that are
![]() ${\cal T}_G$
-by- hypertrivial is tensorial.
${\cal T}_G$
-by- hypertrivial is tensorial.
In the following, if G is a group,
![]() $\overline \zeta (G)$
denotes the hypercentre of G, and we say that a normal section
$\overline \zeta (G)$
denotes the hypercentre of G, and we say that a normal section
![]() $X/Y$
of G is hypercentrally embedded in G if
$X/Y$
of G is hypercentrally embedded in G if
![]() $X/Y\leq \overline \zeta (G/Y)$
.
$X/Y\leq \overline \zeta (G/Y)$
.
Lemma 2.9. Let G be a group and let N be a torsion-free normal subgroup of G such that
![]() $N\overline \zeta (G)/\overline \zeta (G)$
is locally finite. Then N is contained in
$N\overline \zeta (G)/\overline \zeta (G)$
is locally finite. Then N is contained in
![]() $\overline \zeta (G)$
.
$\overline \zeta (G)$
.
Proof. Since
![]() $N/\overline \zeta (N)$
is obviously locally finite, N contains a locally finite normal subgroup M such that
$N/\overline \zeta (N)$
is obviously locally finite, N contains a locally finite normal subgroup M such that
![]() $N/M$
is hypercentral (see [Reference De Falco, de Giovanni, Musella and Sysak3, Lemma 2]). However, N is torsion-free and hence it is hypercentral. Assume for a contradiction that the statement is false and let
$N/M$
is hypercentral (see [Reference De Falco, de Giovanni, Musella and Sysak3, Lemma 2]). However, N is torsion-free and hence it is hypercentral. Assume for a contradiction that the statement is false and let
![]() $\mu $
be the least ordinal number such that
$\mu $
be the least ordinal number such that
![]() $\zeta _\mu (N)$
is not contained in
$\zeta _\mu (N)$
is not contained in
![]() $\overline \zeta (G)$
. Then
$\overline \zeta (G)$
. Then
![]() $\mu>0$
is not a limit and
$\mu>0$
is not a limit and
![]() $\zeta _{\mu -1}(N)\leq \overline \zeta (G)$
. Since
$\zeta _{\mu -1}(N)\leq \overline \zeta (G)$
. Since
![]() $N/\zeta _{\mu -1}(N)$
is torsion-free (see [Reference Robinson17, Part 1, Theorem 2.25]), we may replace G by
$N/\zeta _{\mu -1}(N)$
is torsion-free (see [Reference Robinson17, Part 1, Theorem 2.25]), we may replace G by
![]() $G/\zeta _{\mu -1}(N)$
and N by
$G/\zeta _{\mu -1}(N)$
and N by
![]() $\zeta _\mu (N)/\zeta _{\mu -1}(N)$
, and so assume without loss of generality that N is abelian.
$\zeta _\mu (N)/\zeta _{\mu -1}(N)$
, and so assume without loss of generality that N is abelian.
Since
![]() $N/(N\cap \overline \zeta (G))$
is locally finite, we may consider the least ordinal number
$N/(N\cap \overline \zeta (G))$
is locally finite, we may consider the least ordinal number
![]() $\sigma $
such that
$\sigma $
such that
![]() $N/(N\cap \zeta _\sigma (G))$
is not torsion-free. Clearly,
$N/(N\cap \zeta _\sigma (G))$
is not torsion-free. Clearly,
![]() $\sigma>0$
is not a limit and
$\sigma>0$
is not a limit and
![]() $N/(N\cap \zeta _{\sigma -1}(G))$
is torsion-free. Thus, a further replacement of G by the factor group
$N/(N\cap \zeta _{\sigma -1}(G))$
is torsion-free. Thus, a further replacement of G by the factor group
![]() $G/\zeta _{\sigma -1}(G)$
allows us to assume that
$G/\zeta _{\sigma -1}(G)$
allows us to assume that
![]() $N/(N\cap \zeta _1(G))$
is not torsion-free. Then there is an element x of
$N/(N\cap \zeta _1(G))$
is not torsion-free. Then there is an element x of
![]() $N\setminus \zeta _1(G)$
such that
$N\setminus \zeta _1(G)$
such that
![]() $x^k\in \zeta _1(G)$
for some positive integer k. If g is any element of G,
$x^k\in \zeta _1(G)$
for some positive integer k. If g is any element of G,
so
![]() $[x,g]=1$
because N is torsion-free and hence
$[x,g]=1$
because N is torsion-free and hence
![]() $x\in \zeta _1(G)$
. This contradiction completes the proof of the statement.
$x\in \zeta _1(G)$
. This contradiction completes the proof of the statement.
Lemma 2.10. Let G be a group and let N be a normal subgroup of G. If N has a G-invariant series of finite length each of whose factors is either locally finite or hypercentrally embedded in G, then N contains a locally finite G-invariant subgroup T such that
![]() $N/T$
is hypercentrally embedded in G.
$N/T$
is hypercentrally embedded in G.
Proof. Let
be a G-invariant series of finite length whose factors are either locally finite or hypercentrally embedded in G. Without loss of generality, we may assume that N has no nontrivial locally finite normal subgroups, so in particular
![]() $N_1\leq \overline \zeta (G)$
, and also that
$N_1\leq \overline \zeta (G)$
, and also that
![]() $N_2/N_1$
is locally finite. Then
$N_2/N_1$
is locally finite. Then
![]() $N_2/\overline \zeta (N_2)$
is locally finite and hence it follows from [Reference De Falco, de Giovanni, Musella and Sysak3, Lemma 2] that
$N_2/\overline \zeta (N_2)$
is locally finite and hence it follows from [Reference De Falco, de Giovanni, Musella and Sysak3, Lemma 2] that
![]() $N_2$
is hypercentral, and so also torsion-free. Application of Lemma 2.9 yields now that
$N_2$
is hypercentral, and so also torsion-free. Application of Lemma 2.9 yields now that
![]() $N_2\leq \overline \zeta (G)$
. It follows that N has a G-invariant series of the above type whose length is strictly smaller than t and hence the statement is proved by induction.
$N_2\leq \overline \zeta (G)$
. It follows that N has a G-invariant series of the above type whose length is strictly smaller than t and hence the statement is proved by induction.
The above result allows us to characterize (locally finite)-by-hypercentral groups in a way similar to that in which (locally finite)-by-nilpotent groups are described in Corollary 2.4.
Corollary 2.11. A group G is (locally finite)-by-hypercentral if and only if it has a normal series of finite length whose factors are either locally finite or hypercentrally embedded in G.
It is now possible to state the following result, whose proof runs along the same lines of that of Theorem 2.5.
Theorem 2.12. The class of all (locally finite)-by-hypercentral groups is a Hall class.
We turn now to the case in which 𝔜 is the class of Engel groups. Recall here that an element x of a group G is right Engel if for each
![]() $g\in G$
, there is a positive integer
$g\in G$
, there is a positive integer
![]() $m=m(x,g)$
such that
$m=m(x,g)$
such that
![]() $[x,_mg]=1$
, and G is called an Engel group if all its elements are right Engel.
$[x,_mg]=1$
, and G is called an Engel group if all its elements are right Engel.
Let G be a group and let A be a G-module. We say that A is an Engel G-module if for all elements a of A and g of G, there exists a positive integer
![]() $m=m(a,g)$
such that
$m=m(a,g)$
such that
![]() $a(g-1)^m=0$
. Clearly, if A is an abelian normal subgroup of a group G that is an Engel G-module by conjugation, then all elements of A are right Engel in G.
$a(g-1)^m=0$
. Clearly, if A is an abelian normal subgroup of a group G that is an Engel G-module by conjugation, then all elements of A are right Engel in G.
The class of all Engel G-modules is closed with respect to forming submodules, quotient modules and extensions, and it is easy to show that this class of modules is tensorial (see [Reference de Giovanni, Trombetti and Wehrfritz7]). Thus, Lemma 2.1 above has the following further consequence.
Corollary 2.13. If G is a group, the class of all G-modules which are
![]() ${\cal T}_G$
-by-Engel is tensorial.
${\cal T}_G$
-by-Engel is tensorial.
Lemma 2.14. Let G be a group and let A be a G-module that is torsion-free as an abelian group. If A contains an Engel G-submodule B such that
![]() $A/B\in {\cal T}_G$
, then A is an Engel G-module.
$A/B\in {\cal T}_G$
, then A is an Engel G-module.
Proof. Let a and g be arbitrary elements of A and G, respectively, and let
![]() $k=k(a)$
be a positive integer such that
$k=k(a)$
be a positive integer such that
![]() $ka\in B$
. Then there exists a positive integer
$ka\in B$
. Then there exists a positive integer
![]() $m\!=\!m(a,g)$
such that
$m\!=\!m(a,g)$
such that
![]() $(ka)(g-1)^m=0$
, so
$(ka)(g-1)^m=0$
, so
![]() $k(a(g-1)^m)=0$
and hence
$k(a(g-1)^m)=0$
and hence
![]() $a(g-1)^m=0$
. Therefore, A is an Engel G-module.
$a(g-1)^m=0$
. Therefore, A is an Engel G-module.
Lemma 2.15. Let G be a group and let N be a normal subgroup of G. If N has a G-invariant series of finite length each of whose factors is either locally finite or an Engel G-module (by conjugation), then N contains a locally finite G-invariant subgroup T such that
![]() $N/T$
consists of right Engel elements of
$N/T$
consists of right Engel elements of
![]() $G/T$
.
$G/T$
.
Proof. Let
be a G-invariant series of finite length whose factors are either locally finite or Engel G-modules. Without loss of generality, it can be assumed that N has no locally finite nontrivial normal subgroups, so in particular
![]() $N_1$
is an Engel G-module that is torsion-free as an abelian group. Moreover, by induction on t, we may also suppose that
$N_1$
is an Engel G-module that is torsion-free as an abelian group. Moreover, by induction on t, we may also suppose that
![]() $N/N_1$
contains a locally finite G-invariant subgroup
$N/N_1$
contains a locally finite G-invariant subgroup
![]() $M/N_1$
such that
$M/N_1$
such that
![]() $N/M$
consists of right Engel elements of
$N/M$
consists of right Engel elements of
![]() $G/M$
. Let E be an arbitrary finitely generated subgroup of M and put
$G/M$
. Let E be an arbitrary finitely generated subgroup of M and put
![]() $A=E\cap N_1$
. Then
$A=E\cap N_1$
. Then
![]() $E/A$
is finite and hence A is finitely generated. Since
$E/A$
is finite and hence A is finitely generated. Since
![]() $N_1$
is an Engel G-module, for each element x of E, there exists a positive integer k such that
$N_1$
is an Engel G-module, for each element x of E, there exists a positive integer k such that
![]() $[A,_kx]=\{1\}$
. It follows that the subgroup
$[A,_kx]=\{1\}$
. It follows that the subgroup
![]() $\langle x,A\rangle $
is nilpotent and so even abelian (see for instance [Reference Robinson17, Part 2, Lemma 6.37] or [Reference Casolo2, Proposition 2.1.3]). Therefore,
$\langle x,A\rangle $
is nilpotent and so even abelian (see for instance [Reference Robinson17, Part 2, Lemma 6.37] or [Reference Casolo2, Proposition 2.1.3]). Therefore,
![]() $A\leq \zeta _1(E)$
and so
$A\leq \zeta _1(E)$
and so
![]() $N_1\leq \zeta _1(M)$
. In particular,
$N_1\leq \zeta _1(M)$
. In particular,
![]() $M/\zeta _1(M)$
is locally finite and hence M is torsion-free abelian by Schur’s theorem. Application of Lemma 2.14 yields now that M is an Engel G-module. However, each element of
$M/\zeta _1(M)$
is locally finite and hence M is torsion-free abelian by Schur’s theorem. Application of Lemma 2.14 yields now that M is an Engel G-module. However, each element of
![]() $N/M$
is right Engel in
$N/M$
is right Engel in
![]() $G/M$
and so all elements of N are right Engel in G. The statement is proved.
$G/M$
and so all elements of N are right Engel in G. The statement is proved.
Corollary 2.16. Let G be a group admitting a normal series of finite length each of whose factors is either locally finite or an Engel G-module. Then G is (locally finite)-by-Engel.
Theorem 2.17. The class of all (locally finite)-by-Engel groups is a Hall class.
Proof. Let G be a group and let N be a nilpotent normal subgroup of G such that
![]() $G/N'$
is (locally finite)-by-Engel. Then
$G/N'$
is (locally finite)-by-Engel. Then
![]() $N/N'$
is
$N/N'$
is
![]() ${\cal T}_G$
-by-Engel as a G-module and so by Corollary 2.13, we have that N has a finite G-invariant series whose nonperiodic subgroups are Engel G-modules. If
${\cal T}_G$
-by-Engel as a G-module and so by Corollary 2.13, we have that N has a finite G-invariant series whose nonperiodic subgroups are Engel G-modules. If
![]() $L/N'$
is the unique maximal locally finite normal subgroup of
$L/N'$
is the unique maximal locally finite normal subgroup of
![]() $G/N'$
, it follows that L has a G-invariant series of finite length each of whose factors is either locally finite or an Engel G-module. Application of Lemma 2.15 yields that L contains a locally finite G-invariant subgroup T such that
$G/N'$
, it follows that L has a G-invariant series of finite length each of whose factors is either locally finite or an Engel G-module. Application of Lemma 2.15 yields that L contains a locally finite G-invariant subgroup T such that
![]() $L/T$
consists of right Engel elements of
$L/T$
consists of right Engel elements of
![]() $G/T$
. Therefore, G is (locally finite)-by-Engel and the statement is proved.
$G/T$
. Therefore, G is (locally finite)-by-Engel and the statement is proved.
A closer look at the above arguments allows us to state the following result concerning bounded Engel groups; recall here that a group G is bounded Engel if there exists a positive integer m such that
![]() $[x,_my]=1$
for all
$[x,_my]=1$
for all
![]() $x,y$
in G.
$x,y$
in G.
Theorem 2.18. The class of all (locally finite)-by-(bounded Engel) groups is a Hall class.
Let G be a group. Recall that G is a Baer group if all its cyclic subgroups are subnormal, while G is a Gruenberg group if every cyclic subgroup of G is ascendant. It is known that G is a Baer group (respectively a Gruenberg group) if it is generated by abelian subnormal (respectively abelian ascendant) subgroups. Of course, Baer groups are Gruenberg and every Gruenberg group is locally nilpotent. Notice also that a soluble group is Baer (respectively Gruenberg) if and only if it is bounded Engel (respectively Engel); for these results, see [Reference Robinson17, Part 2, Theorems 7.34 and 7.35]. Thus it follows from Theorems 2.18 and 2.17 that soluble groups that are (locally finite)-by-Baer and soluble groups that are (locally finite)-by-Gruenberg form Hall classes. Actually, we can prove that the solubility assumption can be dropped.
Let 𝔛 be a group class. As usual, we denote by
![]() $\mathbf{S}_n\mathfrak{X}$
(respectively, Q𝔛) the class of all groups that are isomorphic to subnormal subgroups (respectively to factor groups) of 𝔛-groups. Of course,
$\mathbf{S}_n\mathfrak{X}$
(respectively, Q𝔛) the class of all groups that are isomorphic to subnormal subgroups (respectively to factor groups) of 𝔛-groups. Of course,
![]() $\mathbf{S}_n\mathfrak{X}=\mathfrak{X}$
if and only if 𝔛 is closed with respect to forming normal subgroups and
$\mathbf{S}_n\mathfrak{X}=\mathfrak{X}$
if and only if 𝔛 is closed with respect to forming normal subgroups and
![]() $\mathbf{Q}\mathfrak{X}=\mathfrak{X}$
if and only if all homomorphic images of 𝔛-groups belong to 𝔛.
$\mathbf{Q}\mathfrak{X}=\mathfrak{X}$
if and only if all homomorphic images of 𝔛-groups belong to 𝔛.
Lemma 2.19. Let 𝔛 and 𝔜 be group classes such that
![]() $\mathbf{S}_n\mathfrak{X}=\mathfrak{X}$
,
$\mathbf{S}_n\mathfrak{X}=\mathfrak{X}$
,
![]() $\mathbf{Q}\mathfrak{Y}=\mathfrak{Y}$
and 𝔛𝔑 is a Hall class. If G is a group containing a nilpotent normal subgroup N with
$\mathbf{Q}\mathfrak{Y}=\mathfrak{Y}$
and 𝔛𝔑 is a Hall class. If G is a group containing a nilpotent normal subgroup N with
![]() $G/N'\in \mathfrak{XY}$
, then N is contained in a normal subgroup M of G such that
$G/N'\in \mathfrak{XY}$
, then N is contained in a normal subgroup M of G such that
![]() $G/M\in \mathfrak{Y}$
and
$G/M\in \mathfrak{Y}$
and
![]() $\gamma _k(M)\in \mathfrak{X}$
for some positive integer k.
$\gamma _k(M)\in \mathfrak{X}$
for some positive integer k.
Proof. Let
![]() $X/N'$
be a normal 𝔛-subgroup of
$X/N'$
be a normal 𝔛-subgroup of
![]() $G/N'$
such that
$G/N'$
such that
![]() $G/X\in \mathfrak{Y}$
. Clearly, the group
$G/X\in \mathfrak{Y}$
. Clearly, the group
![]() $XN/N'$
is 𝔛-by-abelian, so the normal subgroup
$XN/N'$
is 𝔛-by-abelian, so the normal subgroup
![]() $M=XN$
is 𝔛-by-nilpotent since 𝔛𝔑 is a Hall class. Thus, there is a positive integer k such that the subgroup
$M=XN$
is 𝔛-by-nilpotent since 𝔛𝔑 is a Hall class. Thus, there is a positive integer k such that the subgroup
![]() $\gamma _k(M)$
belongs to
$\gamma _k(M)$
belongs to
![]() $\mathbf{S}_n\mathfrak{X}=\mathfrak{X}$
. Moreover,
$\mathbf{S}_n\mathfrak{X}=\mathfrak{X}$
. Moreover,
![]() $G/M$
belongs to
$G/M$
belongs to
![]() $\mathbf{Q}\mathfrak{Y}=\mathfrak{Y}$
and the statement is proved.
$\mathbf{Q}\mathfrak{Y}=\mathfrak{Y}$
and the statement is proved.
Theorem 2.20. The class of all (locally finite)-by-Baer groups and the class of all (locally finite)-by-Gruenberg groups are Hall classes.
Proof. Let G be a group and let N be a nilpotent normal subgroup of G such that
![]() $G/N'$
is (locally finite)-by-Baer. To prove that G itself is (locally finite)-by-Baer, we may suppose that G has no nontrivial locally finite normal subgroups. Thus, a combination of Theorem 2.5 and Lemma 2.19 with
$G/N'$
is (locally finite)-by-Baer. To prove that G itself is (locally finite)-by-Baer, we may suppose that G has no nontrivial locally finite normal subgroups. Thus, a combination of Theorem 2.5 and Lemma 2.19 with
![]() $\mathfrak{X}=\mathbf{L}\mathfrak{F}$
shows that there exists a nilpotent normal subgroup M of G such that
$\mathfrak{X}=\mathbf{L}\mathfrak{F}$
shows that there exists a nilpotent normal subgroup M of G such that
![]() $G/M'$
is (locally finite)-by-Baer and
$G/M'$
is (locally finite)-by-Baer and
![]() $G/M$
is a Baer group. If g is an arbitrary element of G, the subgroup
$G/M$
is a Baer group. If g is an arbitrary element of G, the subgroup
![]() $\langle g,M\rangle $
is subnormal in G and
$\langle g,M\rangle $
is subnormal in G and
![]() $\langle g,M\rangle /M'$
is (locally finite)-by-nilpotent. Thus,
$\langle g,M\rangle /M'$
is (locally finite)-by-nilpotent. Thus,
![]() $\langle g,M\rangle $
is (locally finite)-by-nilpotent by Theorem 2.5, and so even nilpotent because G has no nontrivial locally finite normal subgroups. It follows that
$\langle g,M\rangle $
is (locally finite)-by-nilpotent by Theorem 2.5, and so even nilpotent because G has no nontrivial locally finite normal subgroups. It follows that
![]() $\langle g\rangle $
is subnormal in G and hence G is a Baer group.
$\langle g\rangle $
is subnormal in G and hence G is a Baer group.
To prove that (locally finite)-by-Gruenberg groups form a Hall class, we can use a similar argument, replacing subnormality by ascendancy and Theorem 2.5 by Theorem 2.12.
To accomplish what we promised at the beginning of this section, it only remains to show that
![]() $(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
is a Hall class.
$(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
is a Hall class.
If G is a group and
![]() $\cal M$
is a class of G-modules, we denote by
$\cal M$
is a class of G-modules, we denote by
![]() $\mathbf{L}\cal M$
the class of all G-modules A such that for each finite subset X of A, there is an
$\mathbf{L}\cal M$
the class of all G-modules A such that for each finite subset X of A, there is an
![]() $\cal M$
-submodule of A containing X. The G-modules in the class
$\cal M$
-submodule of A containing X. The G-modules in the class
![]() $\mathbf{L}{\cal M}$
are called locally
$\mathbf{L}{\cal M}$
are called locally
![]() ${\cal M}$
.
${\cal M}$
.
Lemma 2.21. Let G be a group and let
![]() $\cal M$
be a tensorial class of G-modules. If
$\cal M$
be a tensorial class of G-modules. If
![]() $\cal M$
is closed with respect to forming G-sections, then the class
$\cal M$
is closed with respect to forming G-sections, then the class
![]() $\mathbf{L}\cal M$
is tensorial.
$\mathbf{L}\cal M$
is tensorial.
Proof. Suppose that A and B are G-modules in the class
![]() $\mathbf{L}\cal M$
, and let E be a finitely generated G-submodule of
$\mathbf{L}\cal M$
, and let E be a finitely generated G-submodule of
![]() $A\otimes _{\mathbb{Z}}B$
. Clearly, there exist finitely generated submodules
$A\otimes _{\mathbb{Z}}B$
. Clearly, there exist finitely generated submodules
![]() $A_0$
of A and
$A_0$
of A and
![]() $B_0$
of B such that E is G-isomorphic to a G-section of
$B_0$
of B such that E is G-isomorphic to a G-section of
![]() $A_0\otimes _{\mathbb{Z}}B_0$
. Since
$A_0\otimes _{\mathbb{Z}}B_0$
. Since
![]() $A_0$
and
$A_0$
and
![]() $B_0$
belong to the tensorial class
$B_0$
belong to the tensorial class
![]() $\cal M$
, also E is in
$\cal M$
, also E is in
![]() $\cal M$
. Therefore,
$\cal M$
. Therefore,
![]() $A\otimes _{\mathbb{Z}}B$
belongs to
$A\otimes _{\mathbb{Z}}B$
belongs to
![]() $\mathbf{L}\cal M$
and hence
$\mathbf{L}\cal M$
and hence
![]() $\mathbf{L}\cal M$
is tensorial.
$\mathbf{L}\cal M$
is tensorial.
Since the class of polytrivial G-modules is tensorial, it follows from Lemma 2.21 that also locally polytrivial G-modules form a tensorial class and therefore Lemma 2.1 has the following consequence.
Corollary 2.22. If G is a group, the class of all G-modules that are
![]() ${\cal T}_G$
-by-(locally polytrivial) is tensorial.
${\cal T}_G$
-by-(locally polytrivial) is tensorial.
The following statement and the subsequent remark describe the relation between locally polytrivial and hypertrivial modules; this is employed in the proof of our next main result.
Lemma 2.23. Let G be a group and let A be a G-module. Then A is locally polytrivial if and only if A is hypertrivial of height at most
![]() $\omega $
.
$\omega $
.
Proof. Assume first that A is locally polytrivial and let
![]() $\cal E$
be the collection of all finitely generated G-submodules of A. Each
$\cal E$
be the collection of all finitely generated G-submodules of A. Each
![]() $E\in {\cal E}$
admits a finite series of G-submodules
$E\in {\cal E}$
admits a finite series of G-submodules
whose factors are trivial G-modules. For each nonnegative integer n, let
![]() $A_n$
be the G-submodule of A generated by all
$A_n$
be the G-submodule of A generated by all
![]() $F_n$
, where
$F_n$
, where
![]() $F\in {\cal E}$
and
$F\in {\cal E}$
and
![]() $k(F)\geq n$
. Then,
$k(F)\geq n$
. Then,
is an ascending series of G-submodules of A whose factors are trivial G-modules. Therefore, A is hypertrivial of height at most
![]() $\omega $
.
$\omega $
.
Conversely, let
be an ascending series of G-submodules of A such that every
![]() $A_{n+1}/A_n$
is a trivial G-module. If E is any finitely generated G-submodule of A, there is a nonnegative integer n such that
$A_{n+1}/A_n$
is a trivial G-module. If E is any finitely generated G-submodule of A, there is a nonnegative integer n such that
![]() $A_n$
contains E. Then E is a polytrivial G-module and the statement is proved.
$A_n$
contains E. Then E is a polytrivial G-module and the statement is proved.
Lemma 2.23 shows that the class of locally polytrivial G-modules is contained in that of hypertrivial G-modules, and this inclusion is strict, a property which is in contrast to the well-known fact that hypercentral groups form a proper subclass of L𝔑. This can be seen from the following example. Let p be a prime and let
be the direct product of infinitely many groups of order p; consider the automorphisms x and
![]() $y_k$
(for each
$y_k$
(for each
![]() $k>1$
) of A defined by the positions
$k>1$
) of A defined by the positions
and
If
![]() $G=\langle x,y_k\;|\; k\geq 1\rangle $
, we have that
$G=\langle x,y_k\;|\; k\geq 1\rangle $
, we have that
![]() $A=\langle a\rangle ^G$
is a cyclic G-module, which is hypertrivial of height
$A=\langle a\rangle ^G$
is a cyclic G-module, which is hypertrivial of height
![]() $\omega +1$
but not polytrivial.
$\omega +1$
but not polytrivial.
Theorem 2.24. The class
![]() $(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
of all (locally finite)-by-(locally nilpotent) groups is a Hall class.
$(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
of all (locally finite)-by-(locally nilpotent) groups is a Hall class.
Proof. Let N be a nilpotent normal subgroup of the group G such that
![]() $G/N'$
belongs to
$G/N'$
belongs to
![]() $(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
. To prove that
$(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
. To prove that
![]() $G\in (\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
, we may assume that G has no nontrivial locally finite normal subgroups, so in particular N is torsion-free. Consider any finitely generated subgroup E of G and let
$G\in (\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
, we may assume that G has no nontrivial locally finite normal subgroups, so in particular N is torsion-free. Consider any finitely generated subgroup E of G and let
![]() $T/N$
be the subgroup of all elements of finite order of
$T/N$
be the subgroup of all elements of finite order of
![]() $EN/N$
, so that
$EN/N$
, so that
![]() $EN/T$
is nilpotent. Since
$EN/T$
is nilpotent. Since
![]() $N/N'$
is
$N/N'$
is
![]() ${\cal T}_G$
-by-(locally polytrivial) as an E-module, it follows from Corollary 2.22 that N (and so also T) has an E-invariant series of finite length whose factors are either locally finite or locally polytrivial E-modules. However, locally polytrivial E-modules are hypertrivial by Lemma 2.23 and hence an application of Lemma 2.10 yields that T is hypercentrally embedded in
${\cal T}_G$
-by-(locally polytrivial) as an E-module, it follows from Corollary 2.22 that N (and so also T) has an E-invariant series of finite length whose factors are either locally finite or locally polytrivial E-modules. However, locally polytrivial E-modules are hypertrivial by Lemma 2.23 and hence an application of Lemma 2.10 yields that T is hypercentrally embedded in
![]() $EN$
. Thus,
$EN$
. Thus,
![]() $EN$
is hypercentral and so G is locally nilpotent.
$EN$
is hypercentral and so G is locally nilpotent.
If 𝔛 is any group class, L𝔛 denotes the class of all locally 𝔛-groups, that is, groups each of whose finite subsets lies in an 𝔛-subgroup; of course, if 𝔛 is subgroup-closed, a group G is locally 𝔛 if and only if all its finitely generated subgroups belong to 𝔛.
It is known that
![]() $\mathbf{L}(\mathfrak{NF})$
is a Hall class (see for instance [Reference Amberg, Franciosi and de Giovanni1, Proposition 3.1]) and it has been recently proved that also
$\mathbf{L}(\mathfrak{NF})$
is a Hall class (see for instance [Reference Amberg, Franciosi and de Giovanni1, Proposition 3.1]) and it has been recently proved that also
![]() $\mathbf{L}(\mathfrak{FN})$
is a Hall class (see [Reference de Giovanni, Trombetti and Wehrfritz7]). Since the intersection of Hall classes is likewise a Hall class, a combination of Theorem 2.24 and our next lemma provides a different proof of this latter fact.
$\mathbf{L}(\mathfrak{FN})$
is a Hall class (see [Reference de Giovanni, Trombetti and Wehrfritz7]). Since the intersection of Hall classes is likewise a Hall class, a combination of Theorem 2.24 and our next lemma provides a different proof of this latter fact.
Lemma 2.25.
![]() $(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})=\mathbf{L}((\mathbf{L}\mathfrak{F})\mathfrak{N})$
and
$(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})=\mathbf{L}((\mathbf{L}\mathfrak{F})\mathfrak{N})$
and
![]() $\mathbf{L}(\mathfrak{FN})=((\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N}))\cap \mathbf{L}(\mathfrak{NF})$
.
$\mathbf{L}(\mathfrak{FN})=((\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N}))\cap \mathbf{L}(\mathfrak{NF})$
.
Proof. It is obvious that
![]() $(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})\leq \mathbf{L}((\mathbf{L}\mathfrak{F})\mathfrak{N})$
. Conversely, if G is any group in
$(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})\leq \mathbf{L}((\mathbf{L}\mathfrak{F})\mathfrak{N})$
. Conversely, if G is any group in
![]() $\mathbf{L}((\mathbf{L}\mathfrak{F})\mathfrak{N})$
, the elements of finite order of G form a locally finite subgroup T and
$\mathbf{L}((\mathbf{L}\mathfrak{F})\mathfrak{N})$
, the elements of finite order of G form a locally finite subgroup T and
![]() $G/T$
is locally nilpotent. Thus,
$G/T$
is locally nilpotent. Thus,
![]() $\mathbf{L}((\mathbf{L}\mathfrak{F})\mathfrak{N})\leq (\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
and the first equality is proved.
$\mathbf{L}((\mathbf{L}\mathfrak{F})\mathfrak{N})\leq (\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
and the first equality is proved.
To prove the second equality, note that
by the first part of the proof. Since every finite-by-nilpotent group is obviously nilpotent-by-finite, we have also
![]() $\mathbf{L}(\mathfrak{FN})\leq \mathbf{L}(\mathfrak{NF})$
and hence
$\mathbf{L}(\mathfrak{FN})\leq \mathbf{L}(\mathfrak{NF})$
and hence
Suppose now that G is a group in
![]() $((\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N}))\cap \mathbf{L}(\mathfrak{NF})$
and let E be any finitely generated subgroup of G. Since E is nilpotent-by-finite, it satisfies the maximal condition; then E is finite-by-nilpotent because it belongs to
$((\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N}))\cap \mathbf{L}(\mathfrak{NF})$
and let E be any finitely generated subgroup of G. Since E is nilpotent-by-finite, it satisfies the maximal condition; then E is finite-by-nilpotent because it belongs to
![]() $(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
. The proof is complete.
$(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
. The proof is complete.
We give now an example which shows in particular that (locally finite)-by-(finitely generated nilpotent) groups do not form a Hall class.
Theorem 2.26. There exists a torsion-free nilpotent linear group G over a field of characteristic
![]() $0$
that is not finitely generated, but
$0$
that is not finitely generated, but
![]() $G/G'$
is periodic-by-(finitely generated abelian).
$G/G'$
is periodic-by-(finitely generated abelian).
Proof. Let
![]() $\mathrm{Tr}_1(3,\mathbb{Q})$
be the group of all unitriangular matrices of order
$\mathrm{Tr}_1(3,\mathbb{Q})$
be the group of all unitriangular matrices of order
![]() $3$
over the rationals, and let
$3$
over the rationals, and let
![]() $G\leq \mathrm{Tr}_1(3,\mathbb{Q})$
be the group generated by the matrices
$G\leq \mathrm{Tr}_1(3,\mathbb{Q})$
be the group generated by the matrices
 $$ \begin{align*}x=\begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}, \quad y=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix}\quad \mathrm{and} \quad z(a)=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ a & 0 & 1 \end{pmatrix},\end{align*} $$
$$ \begin{align*}x=\begin{pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}, \quad y=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix}\quad \mathrm{and} \quad z(a)=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ a & 0 & 1 \end{pmatrix},\end{align*} $$
where a ranges over all rational numbers. Clearly
![]() $[y,x]=z(1)$
, so
$[y,x]=z(1)$
, so
is periodic-by-(finitely generated abelian). However, G is a torsion-free nilpotent group that is not finitely generated.
Although the above example is linear, it turns out that the situation is completely different in the case of a positive characteristic; this is essentially due to an intrinsic property of linear groups of positive characteristic. If G is a linear group, we denote by
![]() $u(G)$
the unipotent radical of G, that is, its unique maximal unipotent normal subgroup.
$u(G)$
the unipotent radical of G, that is, its unique maximal unipotent normal subgroup.
Lemma 2.27. Let G be a linear group over a field of positive characteristic and let N be a nilpotent normal subgroup of G. Then
![]() $N'$
is locally finite.
$N'$
is locally finite.
Proof. Put
![]() $U=u(G)$
. Since G has positive characteristic, U is locally finite and
$U=u(G)$
. Since G has positive characteristic, U is locally finite and
![]() $G/U$
is isomorphic to a completely reducible linear group (see for instance [Reference de Giovanni, Trombetti and Wehrfritz6, Lemma 2.13]). Then also
$G/U$
is isomorphic to a completely reducible linear group (see for instance [Reference de Giovanni, Trombetti and Wehrfritz6, Lemma 2.13]). Then also
![]() $NU/U$
is completely reducible (see [Reference Wehrfritz20, Corollary 1.8]) and hence, being nilpotent, it is central-by-finite (see [Reference Wehrfritz20]). It follows from Schur’s theorem that
$NU/U$
is completely reducible (see [Reference Wehrfritz20, Corollary 1.8]) and hence, being nilpotent, it is central-by-finite (see [Reference Wehrfritz20]). It follows from Schur’s theorem that
![]() $N'U/U$
is finite and hence
$N'U/U$
is finite and hence
![]() $N'$
is locally finite.
$N'$
is locally finite.
The above lemma suggests that certain classes of groups with a locally finite obstruction at the bottom can behave as Hall classes in suitable universes, even if they are not Hall classes. This idea can be formalized as follows.
If 𝔘 is a fixed class of groups, we say that a group class 𝔛 is a 𝔘-Hall class (or also a Hall class within the universe 𝔘) if it contains every 𝔘-group G admitting a nilpotent normal subgroup N such that
![]() $G/N'\in \mathfrak{X}$
. Of course, if 𝔘 is the class of all groups, 𝔘-Hall classes are just the usual Hall classes.
$G/N'\in \mathfrak{X}$
. Of course, if 𝔘 is the class of all groups, 𝔘-Hall classes are just the usual Hall classes.
Theorem 2.28. Let 𝔛 be any class of groups. Then
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{X}$
is a Hall class within the universe of linear groups of positive characteristic.
$(\mathbf{L}\mathfrak{F})\mathfrak{X}$
is a Hall class within the universe of linear groups of positive characteristic.
Notice that the concept of a 𝔘-Hall class is further generalized in Section 5, by imposing a restriction also to the nilpotent normal subgroup N in the above definition.
3 Supersolubility conditions
The aim of this section is to prove that
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{Y}$
is a Hall class, when 𝔜 is one of the most natural generalizations of the class of supersoluble groups, like those of paranilpotent groups, of hypercyclic groups and of locally supersoluble groups.
$(\mathbf{L}\mathfrak{F})\mathfrak{Y}$
is a Hall class, when 𝔜 is one of the most natural generalizations of the class of supersoluble groups, like those of paranilpotent groups, of hypercyclic groups and of locally supersoluble groups.
Note preliminarily that (locally finite)-by-supersoluble groups do not form a Hall class (see Theorem 2.26). This is essentially due to the fact that (locally finite)-by-supersoluble groups cannot be characterized in a way similar to that of Corollary 2.4, replacing centrality by the property of being cyclic, an obvious example being the additive group of rational numbers.
We first deal with the class of (locally finite)-by-paranilpotent groups. Recall that a normal subgroup N of a group G is said to be paranilpotently embedded in G if there exists a finite series
of normal subgroups of G such that, for
![]() $i=0,\ldots ,t-1$
, the factor group
$i=0,\ldots ,t-1$
, the factor group
![]() $N_{i+1}/N_i$
is paracentral in G, that is, it is abelian and all its subgroups are normal in
$N_{i+1}/N_i$
is paracentral in G, that is, it is abelian and all its subgroups are normal in
![]() $G/N_i$
. A group G is paranilpotent if it is paranilpotently embedded in itself. Paranilpotent groups were introduced in [Reference Wehrfritz19] under the name of parasoluble groups, while the term paranilpotent group has recently been employed (see for instance [Reference de Giovanni and Trombetti4, Reference de Giovanni, Trombetti and Wehrfritz5]). Of course, every nilpotent group is paranilpotent, while paranilpotent groups are locally supersoluble.
$G/N_i$
. A group G is paranilpotent if it is paranilpotently embedded in itself. Paranilpotent groups were introduced in [Reference Wehrfritz19] under the name of parasoluble groups, while the term paranilpotent group has recently been employed (see for instance [Reference de Giovanni and Trombetti4, Reference de Giovanni, Trombetti and Wehrfritz5]). Of course, every nilpotent group is paranilpotent, while paranilpotent groups are locally supersoluble.
As in the previous section, we obtain results corresponding to Corollaries 2.2 and 2.4 for the class of (locally finite)-by-paranilpotent groups.
If G is any group, a G-module A is called paranilpotent if it has a finite series of G-submodules
such that every subgroup of
![]() $A_{i+1}/A_i$
is a G-submodule for all
$A_{i+1}/A_i$
is a G-submodule for all
![]() $i=0,1,\ldots ,t-1$
. Of course, any abelian normal subgroup of a paranilpotent group G is a paranilpotent G-module by conjugation.
$i=0,1,\ldots ,t-1$
. Of course, any abelian normal subgroup of a paranilpotent group G is a paranilpotent G-module by conjugation.
The class of all paranilpotent G-modules is easily seen to be tensorial and quotient-closed (see for instance [Reference Franciosi and de Giovanni10]), so that Lemma 2.1 has the following consequence.
Corollary 3.1. If G is a group, the class of all G-modules that are
![]() ${\cal T}_G$
-by- paranilpotent is tensorial.
${\cal T}_G$
-by- paranilpotent is tensorial.
The following result corresponds to Lemma 2.14, bearing in mind that the only nontrivial automorphism fixing all subgroups of a nonperiodic abelian group is the inversion.
Lemma 3.2. Let G be a group, A a G-module that is torsion-free as an abelian group and B a G-submodule of A such that
![]() $A/B\in {\cal T}_G$
. If g is an element of G centralizing B (respectively inverting B), then g centralizes A (respectively inverts A).
$A/B\in {\cal T}_G$
. If g is an element of G centralizing B (respectively inverting B), then g centralizes A (respectively inverts A).
Proof. Let a be any element of A and let k be a positive integer such that
![]() $ka\in B$
. Then,
$ka\in B$
. Then,
![]() $(ka)g=\varepsilon (ka)$
, where
$(ka)g=\varepsilon (ka)$
, where
![]() $\varepsilon \in \{1,-1\}$
, so that
$\varepsilon \in \{1,-1\}$
, so that
![]() $k(ag-\varepsilon a)=0$
and hence
$k(ag-\varepsilon a)=0$
and hence
![]() $ag=\varepsilon a$
since A is torsion-free as an abelian group.
$ag=\varepsilon a$
since A is torsion-free as an abelian group.
Lemma 3.3. Let G be a group and let N be a normal subgroup of G. If N has a G-invariant series of finite length whose factors are either locally finite or paracentral in G, then N contains a locally finite G-invariant subgroup T such that
![]() $N/T$
is paranilpotently embedded in G.
$N/T$
is paranilpotently embedded in G.
Proof. Let
be a G-invariant series of finite length whose factors are either locally finite or paracentral in G. Without loss of generality, we may assume that N has no locally finite nontrivial normal subgroups, so in particular
![]() $N_1$
is torsion-free and paracentral in G. Moreover, we may suppose by induction on t that
$N_1$
is torsion-free and paracentral in G. Moreover, we may suppose by induction on t that
![]() $N/N_1$
contains a locally finite G-invariant subgrup
$N/N_1$
contains a locally finite G-invariant subgrup
![]() $M/N_1$
such that
$M/N_1$
such that
![]() $N/M$
is paranilpotently embedded in G. Put
$N/M$
is paranilpotently embedded in G. Put
![]() $C=C_M(N_1)$
, so that
$C=C_M(N_1)$
, so that
![]() $M/C$
has order at most
$M/C$
has order at most
![]() $2$
and
$2$
and
![]() $N/C$
is paranilpotently embedded in G. Clearly,
$N/C$
is paranilpotently embedded in G. Clearly,
![]() $N_1\leq \zeta _1(C)$
, so
$N_1\leq \zeta _1(C)$
, so
![]() $C/\zeta _1(C)$
is locally finite and hence C is abelian by Schur’s theorem. An application of Lemma 3.2 yields that C is paracentral in G and hence G is paranilpotent.
$C/\zeta _1(C)$
is locally finite and hence C is abelian by Schur’s theorem. An application of Lemma 3.2 yields that C is paracentral in G and hence G is paranilpotent.
Corollary 3.4. A group G is (locally finite)-by-paranilpotent if and only if it has a normal series of finite length whose factors are either locally finite or paranilpotently embedded in G.
The first main result of this section is a consequence of Corollaries 3.1 and 3.4.
Theorem 3.5. The class of all (locally finite)-by-paranilpotent groups is a Hall class.
We move now from paranilpotent groups to hypercyclic groups, that is, groups having an ascending normal series with cyclic factors. In general, a normal section
![]() $X/Y$
of a group G is hypercyclically embedded in G if it has an ascending G-invariant series with cyclic factors. Notice that if N is a hypercyclically embedded normal subgroup of G, then
$X/Y$
of a group G is hypercyclically embedded in G if it has an ascending G-invariant series with cyclic factors. Notice that if N is a hypercyclically embedded normal subgroup of G, then
![]() $N\cap G'$
is contained in the hypercentre of
$N\cap G'$
is contained in the hypercentre of
![]() $G'$
; in particular, the commutator subgroup of any hypercyclic group is hypercentral. Moreover, it is easy to see that paranilpotent groups are hypercyclic and that hypercyclic groups are locally supersoluble.
$G'$
; in particular, the commutator subgroup of any hypercyclic group is hypercentral. Moreover, it is easy to see that paranilpotent groups are hypercyclic and that hypercyclic groups are locally supersoluble.
Let G be a group. We say that a G-module A is hypercyclic if it has an ascending series of G-submodules
each of whose factors is cyclic as an abelian group; the least ordinal
![]() $\tau $
for which such a series exists is called the height of A. It is known that the class of all hypercyclic G-modules is tensorial (see [Reference Robinson16]), so that Lemma 2.1 has the following consequence.
$\tau $
for which such a series exists is called the height of A. It is known that the class of all hypercyclic G-modules is tensorial (see [Reference Robinson16]), so that Lemma 2.1 has the following consequence.
Corollary 3.6. If G is a group, the class of all G-modules that are
![]() ${\cal T}_G$
-by- hypercyclic is tensorial.
${\cal T}_G$
-by- hypercyclic is tensorial.
Lemma 3.7. Let G be a group and let N be a normal subgroup of G. If N has a G-invariant series of finite length each of whose factors is either locally finite or hypercyclically embedded in G, then N contains a locally finite G-invariant subgroup T such that
![]() $N/T$
is hypercyclically embedded in G.
$N/T$
is hypercyclically embedded in G.
Proof. As in the proofs of Lemmas 2.10 and 3.3, we may suppose that N has no nontrivial locally finite normal subgroups and contains a G-invariant subgroup M such that M is hypercyclically embedded in G and
![]() $N/M$
is locally finite. Then
$N/M$
is locally finite. Then
![]() $M\cap G'\leq \overline \zeta (N\cap G')$
, so that
$M\cap G'\leq \overline \zeta (N\cap G')$
, so that
![]() $(N\cap G')/\overline \zeta (N\cap G')$
is locally finite and hence
$(N\cap G')/\overline \zeta (N\cap G')$
is locally finite and hence
![]() $N\cap G'$
is hypercentral and torsion-free by Lemma 2.10. Put
$N\cap G'$
is hypercentral and torsion-free by Lemma 2.10. Put
![]() $Z=\zeta _1(N\cap G')$
. By hypothesis, Z contains a nontrivial cyclic G-invariant subgroup and we may consider a subgroup A of Z that is maximal with respect to the condition that all its subgroups are normal in G; obviously A is hypercyclically embedded in G. If
$Z=\zeta _1(N\cap G')$
. By hypothesis, Z contains a nontrivial cyclic G-invariant subgroup and we may consider a subgroup A of Z that is maximal with respect to the condition that all its subgroups are normal in G; obviously A is hypercyclically embedded in G. If
![]() $B/A$
is the subgroup of all elements of finite order of
$B/A$
is the subgroup of all elements of finite order of
![]() $Z/A$
, it follows from Lemma 3.2 that all subgroups of B are normal in G. Thus,
$Z/A$
, it follows from Lemma 3.2 that all subgroups of B are normal in G. Thus,
![]() $A=B$
, so
$A=B$
, so
![]() $Z/A$
is torsion-free and hence either
$Z/A$
is torsion-free and hence either
![]() $Z=A$
or
$Z=A$
or
![]() $Z/A$
contains a nontrivial cyclic G-invariant subgroup. This procedure shows that Z is hypercyclically embedded in G. Since all factors of the upper central series of
$Z/A$
contains a nontrivial cyclic G-invariant subgroup. This procedure shows that Z is hypercyclically embedded in G. Since all factors of the upper central series of
![]() $N\cap G'$
are torsion-free, we may employ the same argument to prove that all such factors are hypercyclically embedded in G. Therefore,
$N\cap G'$
are torsion-free, we may employ the same argument to prove that all such factors are hypercyclically embedded in G. Therefore,
![]() $N\cap G'$
is hypercyclically embedded in G. Since
$N\cap G'$
is hypercyclically embedded in G. Since
![]() $[N,G]\leq N\cap G'$
, it follows that also N is hypercyclically embedded in G.
$[N,G]\leq N\cap G'$
, it follows that also N is hypercyclically embedded in G.
Corollary 3.8. A group G is (locally finite)-by-hypercyclic if and only if it has a normal series of finite length whose factors are either locally finite or hypercyclically embedded in G.
As in the previous cases, the following can be deduced.
Theorem 3.9. The class of all (locally finite)-by-hypercyclic groups is a Hall class.
Finally, we consider the class of (locally finite)-by-(locally supersoluble) groups; we need the following easy lemma.
Lemma 3.10. Let G be a group whose finitely generated subgroups are (locally finite)-by-supersoluble. Then G is (locally finite)-by-(locally supersoluble).
Proof. We may obviously assume that G has no nontrivial locally finite normal subgroups. Since the commutator subgroup of any finitely generated subgroup of G is (locally finite)-by-nilpotent,
![]() $G'$
belongs to
$G'$
belongs to
![]() $(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
by Lemma 2.25 and hence
$(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{N})$
by Lemma 2.25 and hence
![]() $G'$
is torsion-free and locally nilpotent. Let E be any finitely generated subgroup of G and let T be the unique maximal locally finite normal subgroup of E. Then
$G'$
is torsion-free and locally nilpotent. Let E be any finitely generated subgroup of G and let T be the unique maximal locally finite normal subgroup of E. Then
![]() $E/T$
is supersoluble and
$E/T$
is supersoluble and
![]() $T\leq \zeta _1(E)$
, because
$T\leq \zeta _1(E)$
, because
![]() $T\cap E'=\{1\}$
. Therefore, E is supersoluble and G is locally supersoluble.
$T\cap E'=\{1\}$
. Therefore, E is supersoluble and G is locally supersoluble.
In the proof of Theorem 2.24, a major role is played by locally polytrivial modules and hypertrivial modules. Here, this role is taken by locally paranilpotent modules and their relations with hypercyclic modules.
The example just before Theorem 2.24 shows that hypercyclic modules need not be locally paranilpotent, and in contrast to Lemma 2.23, we prove that locally paranilpotent modules are not in general hypercyclic of height at most
![]() $\omega $
. To see this, consider an uncountable free abelian group
$\omega $
. To see this, consider an uncountable free abelian group
and let
be an elementary abelian
![]() $2$
-group acting on A according to the rules
$2$
-group acting on A according to the rules
Then A is a locally paranilpotent G-module which is hypercyclic of height strictly larger than
![]() $\omega $
. However, it is straightforward to show that any locally paranilpotent module is at least hypercyclic, and this is enough to prove that (locally finite)-by-(locally supersoluble) groups form a Hall class.
$\omega $
. However, it is straightforward to show that any locally paranilpotent module is at least hypercyclic, and this is enough to prove that (locally finite)-by-(locally supersoluble) groups form a Hall class.
Theorem 3.11. The class of all (locally finite)-by-(locally supersoluble) groups is a Hall class.
Proof. Let G be a group and let N be a nilpotent normal subgroup of G such that
![]() $G/N'$
is (locally finite)-by-(locally supersoluble). Consider any finitely generated subgroup E of G, so in particular
$G/N'$
is (locally finite)-by-(locally supersoluble). Consider any finitely generated subgroup E of G, so in particular
![]() $EN/N$
is (locally finite)-by-supersoluble. Since
$EN/N$
is (locally finite)-by-supersoluble. Since
![]() $N/N'$
is
$N/N'$
is
![]() ${\cal T}_G$
-by-(locally paranilpotent) as an E-module, it is also
${\cal T}_G$
-by-(locally paranilpotent) as an E-module, it is also
![]() ${\cal T}_G$
-by-hypercyclic. The nilpotency of N and Corollary 3.6 yield that N (and so also
${\cal T}_G$
-by-hypercyclic. The nilpotency of N and Corollary 3.6 yield that N (and so also
![]() $EN$
) has an
$EN$
) has an
![]() $EN$
-invariant series of finite length whose factors are either locally finite, or abelian and hypercyclic as
$EN$
-invariant series of finite length whose factors are either locally finite, or abelian and hypercyclic as
![]() $EN$
-modules. It follows now from Lemma 3.7 that
$EN$
-modules. It follows now from Lemma 3.7 that
![]() $EN$
is (locally finite)-by-hypercyclic and so E is (locally finite)-by-supersoluble. Therefore, G is (locally finite)-by-(locally supersoluble) by Lemma 3.10.
$EN$
is (locally finite)-by-hypercyclic and so E is (locally finite)-by-supersoluble. Therefore, G is (locally finite)-by-(locally supersoluble) by Lemma 3.10.
A similar proof to that of Lemma 2.25 shows that the class of locally (finite-by-supersoluble) groups is the intersection of the class of (locally finite)-by-(locally supersoluble) groups with the class of locally (nilpotent-by-finite) groups. Thus, locally (finite-by-supersoluble) groups form a Hall class by Theorem 3.11; a different proof of this result is given in [Reference de Giovanni, Trombetti and Wehrfritz7].
4
 $FC$
-nilpotency conditions
$FC$
-nilpotency conditions
Let G be a group. The
![]() $FC$
-centre of G is the characteristic subgroup
$FC$
-centre of G is the characteristic subgroup
![]() $FC_1(G)$
consisting of all elements of G with only finitely many conjugates, or equivalently of those elements
$FC_1(G)$
consisting of all elements of G with only finitely many conjugates, or equivalently of those elements
![]() $g\in G$
for which the centralizer
$g\in G$
for which the centralizer
![]() $C_G(g)$
has finite index in G. The upper
$C_G(g)$
has finite index in G. The upper
![]() $FC$
-central series of G is the ascending characteristic series
$FC$
-central series of G is the ascending characteristic series
![]() $\{ FC_\alpha (G)\}_\alpha $
recursively defined by setting
$\{ FC_\alpha (G)\}_\alpha $
recursively defined by setting
![]() $FC_0(G)=\{1\}$
,
$FC_0(G)=\{1\}$
,
for each ordinal
![]() $\alpha $
and
$\alpha $
and
 $$ \begin{align*}FC_\lambda(G)=\bigcup_{\beta<\lambda}FC_\beta(G)\end{align*} $$
$$ \begin{align*}FC_\lambda(G)=\bigcup_{\beta<\lambda}FC_\beta(G)\end{align*} $$
if
![]() $\lambda $
is a limit ordinal. The last term of the upper
$\lambda $
is a limit ordinal. The last term of the upper
![]() $FC$
-central series of G is called the
$FC$
-central series of G is called the
![]() $FC$
-hypercentre of G, and G is said to be
$FC$
-hypercentre of G, and G is said to be
![]() $FC$
-hypercentral if it coincides with its
$FC$
-hypercentral if it coincides with its
![]() $FC$
-hypercentre. Moreover, G is called
$FC$
-hypercentre. Moreover, G is called
![]() $FC$
-nilpotent if
$FC$
-nilpotent if
![]() $FC_k(G)=G$
for some nonnegative integer k. Of course, nilpotent-by-finite groups are
$FC_k(G)=G$
for some nonnegative integer k. Of course, nilpotent-by-finite groups are
![]() $FC$
-nilpotent and it is known that any finitely generated
$FC$
-nilpotent and it is known that any finitely generated
![]() $FC$
-nilpotent group is nilpotent-by-finite (see [Reference McLain13]). It follows that every
$FC$
-nilpotent group is nilpotent-by-finite (see [Reference McLain13]). It follows that every
![]() $FC$
-hypercentral group is locally
$FC$
-hypercentral group is locally
![]() $FC$
-nilpotent and that the class of locally
$FC$
-nilpotent and that the class of locally
![]() $FC$
-nilpotent groups coincides with that of locally (nilpotent-by-finite) groups.
$FC$
-nilpotent groups coincides with that of locally (nilpotent-by-finite) groups.
In this section, we prove that
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{Y}$
is a Hall class, when 𝔜 is chosen to be one of the classes of
$(\mathbf{L}\mathfrak{F})\mathfrak{Y}$
is a Hall class, when 𝔜 is chosen to be one of the classes of
![]() $FC$
-nilpotent,
$FC$
-nilpotent,
![]() $FC$
-hypercentral or locally
$FC$
-hypercentral or locally
![]() $FC$
-nilpotent groups.
$FC$
-nilpotent groups.
Let G be a group. If A is a G-module and a is any element of A, we denote by
![]() $G_a$
the stabilizer of a in G, that is, the subgroup formed by all elements
$G_a$
the stabilizer of a in G, that is, the subgroup formed by all elements
![]() $g\in G$
such that
$g\in G$
such that
![]() $ag=a$
. It is easy to see that the set
$ag=a$
. It is easy to see that the set
![]() $FC_1^G(A)$
, consisting of all elements a of A such that the index
$FC_1^G(A)$
, consisting of all elements a of A such that the index
![]() $|G:G_a|$
is finite, is a G-submodule of A. We can now define recursively the upper
$|G:G_a|$
is finite, is a G-submodule of A. We can now define recursively the upper
![]() $FC$
-series
$FC$
-series
![]() $\{FC_\alpha ^G(A)\}$
of A by
$\{FC_\alpha ^G(A)\}$
of A by
for each ordinal
![]() $\alpha $
and
$\alpha $
and
 $$ \begin{align*}FC_\lambda^G(A)=\bigcup_{\beta<\lambda}FC_\beta^G(A)\end{align*} $$
$$ \begin{align*}FC_\lambda^G(A)=\bigcup_{\beta<\lambda}FC_\beta^G(A)\end{align*} $$
if
![]() $\lambda $
is a limit ordinal. The last term of this series is called the
$\lambda $
is a limit ordinal. The last term of this series is called the
![]() $FC^G$
-hypercentre of A, and A is called hyper-
$FC^G$
-hypercentre of A, and A is called hyper-
![]() ${\cal FC}$
if coincides with its
${\cal FC}$
if coincides with its
![]() $FC^G$
-hypercentre. Moreover, the G-module A is said to be poly-
$FC^G$
-hypercentre. Moreover, the G-module A is said to be poly-
![]() ${\cal FC}$
if
${\cal FC}$
if
![]() $A=FC_k^G(A)$
for some nonnegative integer k.
$A=FC_k^G(A)$
for some nonnegative integer k.
Since G-modules that are poly-
![]() ${\cal FC}$
and G-modules that are hyper-
${\cal FC}$
and G-modules that are hyper-
![]() ${\cal FC}$
form tensorial classes (see for instance [Reference Amberg, Franciosi and de Giovanni1]), an application of Lemma 2.1 yields the following result.
${\cal FC}$
form tensorial classes (see for instance [Reference Amberg, Franciosi and de Giovanni1]), an application of Lemma 2.1 yields the following result.
Corollary 4.1. If G is a group, the class of all G-modules that are
![]() ${\cal T}_G$
-by-(poly-
${\cal T}_G$
-by-(poly-
![]() $\cal {FC}$
) and the class of all G-modules that are
$\cal {FC}$
) and the class of all G-modules that are
![]() ${\cal T}_G$
-by-(hyper-
${\cal T}_G$
-by-(hyper-
![]() $\cal {FC}$
) are tensorial.
$\cal {FC}$
) are tensorial.
To prove that (locally finite)-by-(
![]() $FC$
-nilpotent) groups form a Hall class, it is not possible to emulate the proof of Theorem 2.5 since there is no analogue of Corollary 2.4 in this case. In fact, we now construct a group that is not (locally finite)-by-(
$FC$
-nilpotent) groups form a Hall class, it is not possible to emulate the proof of Theorem 2.5 since there is no analogue of Corollary 2.4 in this case. In fact, we now construct a group that is not (locally finite)-by-(
![]() $FC$
-hypercentral), although it is locally finite over its
$FC$
-hypercentral), although it is locally finite over its
![]() $FC$
-centre.
$FC$
-centre.
Let H and K be groups and let N be a normal subgroup of K. Then
![]() $H\wr _N\! K$
denotes the split extension of the direct product B of copies
$H\wr _N\! K$
denotes the split extension of the direct product B of copies
![]() $H_{Nk}$
of H, where
$H_{Nk}$
of H, where
![]() $Nk$
runs over
$Nk$
runs over
![]() $K/N$
, and K permutes the copies
$K/N$
, and K permutes the copies
![]() $H_{Nk}$
in the obvious way. In particular, N centralizes the base group of
$H_{Nk}$
in the obvious way. In particular, N centralizes the base group of
![]() $H\wr _N\! K$
, which is B.
$H\wr _N\! K$
, which is B.
Let
![]() $C_1,C_2,\ldots ,C_n,\ldots $
be a countably infinite sequence of groups of order
$C_1,C_2,\ldots ,C_n,\ldots $
be a countably infinite sequence of groups of order
![]() $2$
, and set by induction
$2$
, and set by induction
![]() $W_{n+1}=C_{n+1}\wr W_n$
for each nonnegative integer n, where
$W_{n+1}=C_{n+1}\wr W_n$
for each nonnegative integer n, where
![]() $W_0=\{1\}$
; moreover, let W be the direct limit of the groups
$W_0=\{1\}$
; moreover, let W be the direct limit of the groups
![]() $W_n$
with the obvious inclusions. Consider now an infinite dihedral group
$W_n$
with the obvious inclusions. Consider now an infinite dihedral group
![]() $X=\langle x,y\rangle $
, where x has infinite order and
$X=\langle x,y\rangle $
, where x has infinite order and
![]() $y^2=1$
, and set
$y^2=1$
, and set
![]() $G_1=X$
and
$G_1=X$
and
![]() $A_1=\langle x\rangle $
. Suppose that we have constructed, for some
$A_1=\langle x\rangle $
. Suppose that we have constructed, for some
![]() $n\geq 1$
, a group
$n\geq 1$
, a group
![]() $G_n$
containing a free abelian normal subgroup
$G_n$
containing a free abelian normal subgroup
![]() $A_n$
of finite rank such that
$A_n$
of finite rank such that
![]() $G_n/A_n\simeq W_n$
. Put
$G_n/A_n\simeq W_n$
. Put
![]() $G_{n+1}=X\wr _{A_n}\!\! G_n$
and let
$G_{n+1}=X\wr _{A_n}\!\! G_n$
and let
![]() $A_{n+1}=A_n\times B_{n+1}$
, where
$A_{n+1}=A_n\times B_{n+1}$
, where
![]() $B_{n+1}$
denotes the normal closure of
$B_{n+1}$
denotes the normal closure of
![]() $\langle x\rangle $
in
$\langle x\rangle $
in
![]() $G_{n+1}$
. Then
$G_{n+1}$
. Then
![]() $A_{n+1}$
is a free abelian normal subgroup of finite rank of
$A_{n+1}$
is a free abelian normal subgroup of finite rank of
![]() $G_{n+1}$
and
$G_{n+1}$
and
![]() $G_{n+1}/A_{n+1}\simeq W_{n+1}$
.
$G_{n+1}/A_{n+1}\simeq W_{n+1}$
.
Let
![]() $G=\bigcup _nG_n$
be the direct limit of the
$G=\bigcup _nG_n$
be the direct limit of the
![]() $G_n$
, so
$G_n$
, so
![]() $A=\bigcup _nA_n$
is a free abelian normal subgroup of G and
$A=\bigcup _nA_n$
is a free abelian normal subgroup of G and
![]() $G/A\simeq W$
is locally finite. For each positive integer k, the subgroup
$G/A\simeq W$
is locally finite. For each positive integer k, the subgroup
![]() $A_k$
centralizes the base group of
$A_k$
centralizes the base group of
![]() $G_h$
for all
$G_h$
for all
![]() $h>k$
, and so every element of
$h>k$
, and so every element of
![]() $A_k$
has at most
$A_k$
has at most
![]() $|W_k|$
conjugates in
$|W_k|$
conjugates in
![]() $G_h$
. It follows that A is contained in the
$G_h$
. It follows that A is contained in the
![]() $FC$
-centre of G. If g is any element of
$FC$
-centre of G. If g is any element of
![]() $G\setminus A$
, there is a positive integer m such that
$G\setminus A$
, there is a positive integer m such that
![]() $g\in G_m\setminus A_m$
and hence there exists a in
$g\in G_m\setminus A_m$
and hence there exists a in
![]() $A_{m+1}$
with
$A_{m+1}$
with
![]() $[a,g]\neq 1$
. Thus,
$[a,g]\neq 1$
. Thus,
![]() $C_G(A)=A$
and so G has no nontrivial periodic normal subgroups. Since
$C_G(A)=A$
and so G has no nontrivial periodic normal subgroups. Since
![]() $G/A\simeq W$
has no nontrivial finite normal subgroups (see for instance [Reference Robinson17, Part 2, Theorem 6.23]), A coincides with the
$G/A\simeq W$
has no nontrivial finite normal subgroups (see for instance [Reference Robinson17, Part 2, Theorem 6.23]), A coincides with the
![]() $FC$
-hypercentre of G. Consequently, G is locally finite over the
$FC$
-hypercentre of G. Consequently, G is locally finite over the
![]() $FC$
-centre, but it is not (locally finite)-by-(
$FC$
-centre, but it is not (locally finite)-by-(
![]() $FC$
-hypercentral).
$FC$
-hypercentral).
In contrast to the above example, we can at least prove that a result corresponding to Corollary 2.4 holds in the case of modules. To this aim, we need the following result that should be seen in relation with a well-known theorem of Mal’cev on the upper central series of torsion-free groups (see for instance [Reference Robinson17, Part 1, Theorem 2.25]).
Lemma 4.2. Let G be a group and let A be a G-module that is torsion-free as an abelian group. Then
![]() $A/FC_\alpha ^G(A)$
is torsion-free as an abelian group for each ordinal
$A/FC_\alpha ^G(A)$
is torsion-free as an abelian group for each ordinal
![]() $\alpha $
.
$\alpha $
.
Proof. It is clearly enough to prove the statement when
![]() $\alpha =1$
. Let a be any element of A such that
$\alpha =1$
. Let a be any element of A such that
![]() $b=ka\in FC_1^G(A)$
for some positive integer k. If g belongs to the stabilizer
$b=ka\in FC_1^G(A)$
for some positive integer k. If g belongs to the stabilizer
![]() $G_b$
, we have
$G_b$
, we have
![]() $k(a(g-1))=b(g-1)=0$
and hence
$k(a(g-1))=b(g-1)=0$
and hence
![]() $a(g-1)=0$
because A is torsion-free as an abelian group. Thus,
$a(g-1)=0$
because A is torsion-free as an abelian group. Thus,
![]() $G_a=G_b$
has finite index in G, so
$G_a=G_b$
has finite index in G, so
![]() $a\in FC_1^G(A)$
and hence
$a\in FC_1^G(A)$
and hence
![]() $A/FC_1^G(A)$
is torsion-free as an abelian group.
$A/FC_1^G(A)$
is torsion-free as an abelian group.
Corollary 4.3. Let G be a group and let A be a G-module that is torsion-free as an abelian group.
-
(a) If A has a finite series of G-submodules each of whose factors either belongs to
 ${\cal T}_G$
or is poly-
${\cal T}_G$
or is poly-
 ${\cal FC}$
, then A is poly-
${\cal FC}$
, then A is poly-
 ${\cal FC}$
.
${\cal FC}$
. -
(b) If A has a finite series of G-submodules each of whose factors either belongs to
 ${\cal T}_G$
or is hyper-
${\cal T}_G$
or is hyper-
 ${\cal FC}$
, then A is hyper-
${\cal FC}$
, then A is hyper-
 ${\cal FC}$
.
${\cal FC}$
.
Proof. We only prove part (a) because the same argument works also for part (b). Let
be a finite series of G-submodules of A such that, for each
![]() $i=0,1,\ldots ,t-1$
, the G-module
$i=0,1,\ldots ,t-1$
, the G-module
![]() $A_{i+1}/A_i$
either belongs to
$A_{i+1}/A_i$
either belongs to
![]() ${\cal T}_G$
or is poly-
${\cal T}_G$
or is poly-
![]() ${\cal FC}$
. Clearly,
${\cal FC}$
. Clearly,
![]() $A_1$
is poly-
$A_1$
is poly-
![]() $\cal {FC}$
and if
$\cal {FC}$
and if
![]() $T/A_1$
is the subgroup consisting of all elements of finite order of
$T/A_1$
is the subgroup consisting of all elements of finite order of
![]() $A/A_1$
, it follows from Lemma 4.2 that T is also poly-
$A/A_1$
, it follows from Lemma 4.2 that T is also poly-
![]() ${\cal FC}$
. Moreover, the G-module
${\cal FC}$
. Moreover, the G-module
![]() $A/T$
is torsion-free as an abelian group and so it is poly-
$A/T$
is torsion-free as an abelian group and so it is poly-
![]() ${\cal FC}$
by induction on t. Therefore, A is poly-
${\cal FC}$
by induction on t. Therefore, A is poly-
![]() ${\cal FC}$
and the statement is proved.
${\cal FC}$
and the statement is proved.
Theorem 4.4. The class of all (locally finite)-by-(
![]() $FC$
-nilpotent) groups is a Hall class.
$FC$
-nilpotent) groups is a Hall class.
Proof. Let G be a group and let N be a nilpotent normal subgroup of G such that
![]() $G/N'$
is (locally finite)-by-(
$G/N'$
is (locally finite)-by-(
![]() $FC$
-nilpotent). To prove that G itself is (locally finite)-by-(
$FC$
-nilpotent). To prove that G itself is (locally finite)-by-(
![]() $FC$
-nilpotent), we may suppose that G has no nontrivial locally finite normal subgroups. Then it follows from Theorem 2.5 and Lemma 2.19 that G contains a nilpotent normal subgroup M such that
$FC$
-nilpotent), we may suppose that G has no nontrivial locally finite normal subgroups. Then it follows from Theorem 2.5 and Lemma 2.19 that G contains a nilpotent normal subgroup M such that
![]() $G/M'$
is (locally finite)-by-(
$G/M'$
is (locally finite)-by-(
![]() $FC$
-nilpotent) and
$FC$
-nilpotent) and
![]() $G/M$
is
$G/M$
is
![]() $FC$
-nilpotent, and of course M is torsion-free.
$FC$
-nilpotent, and of course M is torsion-free.
We claim that M is contained in
![]() $FC_k(G)$
for some nonnegative integer k. Consider
$FC_k(G)$
for some nonnegative integer k. Consider
![]() $A=\zeta _1(M)$
as a G-module by conjugation. Since
$A=\zeta _1(M)$
as a G-module by conjugation. Since
![]() $M/A$
is torsion-free (see for instance [Reference Robinson17, Part 1, Theorem 2.25]), induction on the nilpotency class of M yields that
$M/A$
is torsion-free (see for instance [Reference Robinson17, Part 1, Theorem 2.25]), induction on the nilpotency class of M yields that
![]() $M/A$
is contained in some term with finite ordinal type of the upper
$M/A$
is contained in some term with finite ordinal type of the upper
![]() $FC$
-central series of
$FC$
-central series of
![]() $G/A$
. Moreover,
$G/A$
. Moreover,
![]() $M/M'$
is
$M/M'$
is
![]() ${\cal T}_G$
-by-(poly-
${\cal T}_G$
-by-(poly-
![]() ${\cal FC}$
) as a G-module, and so it follows from Corollary 4.1 that A has a finite series of G-submodules each of whose factors is either in
${\cal FC}$
) as a G-module, and so it follows from Corollary 4.1 that A has a finite series of G-submodules each of whose factors is either in
![]() ${\cal T}_G$
or poly-
${\cal T}_G$
or poly-
![]() ${\cal FC}$
. Thus, A is poly-
${\cal FC}$
. Thus, A is poly-
![]() ${\cal FC}$
by Corollary 4.3(a), so that
${\cal FC}$
by Corollary 4.3(a), so that
![]() $A\leq FC_h(G)$
for some integer
$A\leq FC_h(G)$
for some integer
![]() $h>0$
and hence the claim is proved.
$h>0$
and hence the claim is proved.
Since
![]() $M\leq FC_k(G)$
and
$M\leq FC_k(G)$
and
![]() $G/M$
is
$G/M$
is
![]() $FC$
-nilpotent, it follows that G is
$FC$
-nilpotent, it follows that G is
![]() $FC$
-nilpotent and the proof is complete.
$FC$
-nilpotent and the proof is complete.
The same argument, essentially replacing poly-
![]() ${\cal FC}$
by hyper-
${\cal FC}$
by hyper-
![]() ${\cal FC}$
and part (a) of Corollary 4.3 by part (b), allows us to prove the following.
${\cal FC}$
and part (a) of Corollary 4.3 by part (b), allows us to prove the following.
Theorem 4.5. The class of all (locally finite)-by-(
![]() $FC$
-hypercentral) groups is a Hall class.
$FC$
-hypercentral) groups is a Hall class.
The final result of this section shows that
![]() $(\mathbf{L}\mathfrak{F})(\mathbf{L}(\mathfrak{NF}))$
is a Hall class. Notice that obviously, if G is a group and A is a G-module that is locally poly-
$(\mathbf{L}\mathfrak{F})(\mathbf{L}(\mathfrak{NF}))$
is a Hall class. Notice that obviously, if G is a group and A is a G-module that is locally poly-
![]() ${\cal FC}$
, then A is also hyper-
${\cal FC}$
, then A is also hyper-
![]() ${\cal FC}$
(although, as in the case of locally paranilpotent modules, it is not difficult to see that hyper-
${\cal FC}$
(although, as in the case of locally paranilpotent modules, it is not difficult to see that hyper-
![]() ${\cal FC}$
modules are not in general locally poly-
${\cal FC}$
modules are not in general locally poly-
![]() ${\cal FC}$
).
${\cal FC}$
).
Theorem 4.6. The class of all (locally finite)-by-(locally
![]() $FC$
-nilpotent) groups is a Hall class.
$FC$
-nilpotent) groups is a Hall class.
Proof. Let G be a group and let N be a nilpotent normal subgroup of G such that
![]() $G/N'$
is (locally finite)-by-(locally
$G/N'$
is (locally finite)-by-(locally
![]() $FC$
-nilpotent). To prove that G itself is (locally finite)-by-(locally
$FC$
-nilpotent). To prove that G itself is (locally finite)-by-(locally
![]() $FC$
-nilpotent), we may obviously suppose that G has no nontrivial locally finite normal subgroups. Thus, Theorem 2.5 and Lemma 2.19 yield that G contains a nilpotent normal subgroup M such that
$FC$
-nilpotent), we may obviously suppose that G has no nontrivial locally finite normal subgroups. Thus, Theorem 2.5 and Lemma 2.19 yield that G contains a nilpotent normal subgroup M such that
![]() $G/M'$
is (locally finite)-by-(locally
$G/M'$
is (locally finite)-by-(locally
![]() $FC$
-nilpotent) and
$FC$
-nilpotent) and
![]() $G/M$
is locally
$G/M$
is locally
![]() $FC$
-nilpotent; of course, M is torsion-free.
$FC$
-nilpotent; of course, M is torsion-free.
Consider now any finitely generated subgroup E of G, so in particular the group
![]() $EM/M$
is
$EM/M$
is
![]() $FC$
-nilpotent. Since
$FC$
-nilpotent. Since
![]() $M/M'$
is
$M/M'$
is
![]() ${\cal T}_E$
-by-(locally poly-
${\cal T}_E$
-by-(locally poly-
![]() ${\cal FC}$
) as an E-module, it is also
${\cal FC}$
) as an E-module, it is also
![]() ${\cal T}_E$
-by-(hyper-
${\cal T}_E$
-by-(hyper-
![]() ${\cal FC}$
). The nilpotency of M and Corollary 4.1 yield that M has an
${\cal FC}$
). The nilpotency of M and Corollary 4.1 yield that M has an
![]() $EM$
-invariant series of finite length whose factors are either locally finite, or torsion-free abelian and hyper-
$EM$
-invariant series of finite length whose factors are either locally finite, or torsion-free abelian and hyper-
![]() ${\cal FC}$
as
${\cal FC}$
as
![]() $EM$
-modules.
$EM$
-modules.
It follows now from Corollary 4.3 that each factor of the upper central series of M is hyper-
![]() ${\cal FC}$
as an
${\cal FC}$
as an
![]() $EM$
-module. Thus, M is contained in the
$EM$
-module. Thus, M is contained in the
![]() $FC$
-hypercentre of
$FC$
-hypercentre of
![]() $EM$
and so
$EM$
and so
![]() $EM$
is
$EM$
is
![]() $FC$
-hypercentral. In particular, E is nilpotent-by-finite and hence G is locally
$FC$
-hypercentral. In particular, E is nilpotent-by-finite and hence G is locally
![]() $FC$
-nilpotent.
$FC$
-nilpotent.
5 Solubility and rank conditions
In this short section, we deal with group classes of the form
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{Y}$
, where 𝔜 is either a class of generalized soluble groups or a class of groups satisfying suitable rank conditions. To avoid the repetition of the same argument, we prove the following general lemma, which is of independent interest.
$(\mathbf{L}\mathfrak{F})\mathfrak{Y}$
, where 𝔜 is either a class of generalized soluble groups or a class of groups satisfying suitable rank conditions. To avoid the repetition of the same argument, we prove the following general lemma, which is of independent interest.
Lemma 5.1. Let 𝔛 and 𝔜 be group classes such that
![]() $\mathfrak{X}=\mathbf{S}_n\mathfrak{X}$
and
$\mathfrak{X}=\mathbf{S}_n\mathfrak{X}$
and
![]() $\mathfrak{NY}=\mathfrak{Y}$
. If 𝔛𝔑 is a Hall class, then 𝔛𝔜 is also a Hall class.
$\mathfrak{NY}=\mathfrak{Y}$
. If 𝔛𝔑 is a Hall class, then 𝔛𝔜 is also a Hall class.
Proof. Let G be a group and let N be a nilpotent normal subgroup of G such that
![]() $G/N'$
belongs to 𝔛𝔜, so G has a normal subgroup M with
$G/N'$
belongs to 𝔛𝔜, so G has a normal subgroup M with
![]() $N'\leq M$
,
$N'\leq M$
,
![]() ${M/N'\in \mathfrak{X}}$
and
${M/N'\in \mathfrak{X}}$
and
![]() $G/M\in \mathfrak{Y}$
. Thus,
$G/M\in \mathfrak{Y}$
. Thus,
![]() $MN/N'\in \mathfrak{XA}$
and hence
$MN/N'\in \mathfrak{XA}$
and hence
![]() $MN$
belongs to the Hall class 𝔛𝔑. Let L be a normal 𝔛-subgroup of
$MN$
belongs to the Hall class 𝔛𝔑. Let L be a normal 𝔛-subgroup of
![]() $MN$
such that
$MN$
such that
![]() $MN/L$
is nilpotent and let c be a positive integer with
$MN/L$
is nilpotent and let c be a positive integer with
![]() $\gamma _c(MN)\leq L$
. Then
$\gamma _c(MN)\leq L$
. Then
![]() $X=\gamma _c(MN)\cap M$
is a normal subgroup of G that belongs to
$X=\gamma _c(MN)\cap M$
is a normal subgroup of G that belongs to
![]() $\mathfrak{X}=\mathbf{S}_n\mathfrak{X}$
. Moreover,
$\mathfrak{X}=\mathbf{S}_n\mathfrak{X}$
. Moreover,
![]() $G/X$
belongs to
$G/X$
belongs to
![]() $\mathfrak{NY}=\mathfrak{Y}$
and hence G is in 𝔛𝔜. Therefore, 𝔛𝔜 is a Hall class.
$\mathfrak{NY}=\mathfrak{Y}$
and hence G is in 𝔛𝔜. Therefore, 𝔛𝔜 is a Hall class.
By Theorem 2.5, the above lemma applies in particular to
![]() $\mathfrak{X}=\mathbf{L}\mathfrak{F}$
when either
$\mathfrak{X}=\mathbf{L}\mathfrak{F}$
when either
![]() $\mathfrak{Y}=\mathfrak{S}$
or
$\mathfrak{Y}=\mathfrak{S}$
or
![]() $\mathfrak{Y}=\mathbf{L}\mathfrak{S}$
, but also if 𝔜 is the class
$\mathfrak{Y}=\mathbf{L}\mathfrak{S}$
, but also if 𝔜 is the class
![]() $\acute {\mathbf{P}}_n\mathfrak{A}$
consisting of all hyperabelian groups.
$\acute {\mathbf{P}}_n\mathfrak{A}$
consisting of all hyperabelian groups.
Theorem 5.2. The group classes
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{S}$
,
$(\mathbf{L}\mathfrak{F})\mathfrak{S}$
,
![]() $(\mathbf{L}\mathfrak{F})(\acute {\mathbf{P}}_n\mathfrak{A})$
and
$(\mathbf{L}\mathfrak{F})(\acute {\mathbf{P}}_n\mathfrak{A})$
and
![]() $(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{S})$
are Hall classes.
$(\mathbf{L}\mathfrak{F})(\mathbf{L}\mathfrak{S})$
are Hall classes.
The fact that
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{S}$
is a Hall class can be stated in a quantitative way, by using Theorem 2.6 in the proof of Lemma 5.1.
$(\mathbf{L}\mathfrak{F})\mathfrak{S}$
is a Hall class can be stated in a quantitative way, by using Theorem 2.6 in the proof of Lemma 5.1.
As a further consequence of Theorem 2.5, we have the following easy result concerning the class
![]() $\mathfrak{N}^k$
of soluble groups admitting a finite normal series with nilpotent factors of length at most k.
$\mathfrak{N}^k$
of soluble groups admitting a finite normal series with nilpotent factors of length at most k.
Theorem 5.3. The class
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{N}^k$
is a Hall class for each positive integer k.
$(\mathbf{L}\mathfrak{F})\mathfrak{N}^k$
is a Hall class for each positive integer k.
Proof. By Theorem 2.5, the statement is true if
![]() $k=1$
. Suppose
$k=1$
. Suppose
![]() $k>1$
and let G be a group containing a nilpotent normal subgroup N such that
$k>1$
and let G be a group containing a nilpotent normal subgroup N such that
![]() $G/N'\in (\mathbf{L}\mathfrak{F})\mathfrak{N}^k$
. Then
$G/N'\in (\mathbf{L}\mathfrak{F})\mathfrak{N}^k$
. Then
![]() $G/N'$
has a normal subgroup
$G/N'$
has a normal subgroup
![]() $M/N'\in (\mathbf{L}\mathfrak{F})\mathfrak{N}^{k-1}$
such that
$M/N'\in (\mathbf{L}\mathfrak{F})\mathfrak{N}^{k-1}$
such that
![]() $G/M$
is nilpotent. Since
$G/M$
is nilpotent. Since
![]() $k>1$
, the group
$k>1$
, the group
![]() $MN/N'$
belongs to the class
$MN/N'$
belongs to the class
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{N}^{k-1}$
by Fitting’s theorem; whence
$(\mathbf{L}\mathfrak{F})\mathfrak{N}^{k-1}$
by Fitting’s theorem; whence
![]() $MN$
lies in
$MN$
lies in
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{N}^{k-1}$
by induction on k. Therefore,
$(\mathbf{L}\mathfrak{F})\mathfrak{N}^{k-1}$
by induction on k. Therefore,
![]() $G\in (\mathbf{L}\mathfrak{F})\mathfrak{N}^k$
and the statement is proved.
$G\in (\mathbf{L}\mathfrak{F})\mathfrak{N}^k$
and the statement is proved.
In the second half of this section, we deal with group classes defined by the imposition of a rank condition. We start by recalling the necessary definitions.
Recall that a group G is said to have finite (Prüfer) rank if there is a positive integer r such that every finitely generated subgroup of G can be generated by r elements. Of course, the tensor product of two abelian groups of finite rank has finite rank (see for instance [Reference Wehrfritz22, Lemma 10]) and hence the class of groups of finite rank is easily seen to be a Hall class.
Let A be an abelian group. The
![]() $0$
-rank
$0$
-rank
![]() $r_0(A)$
of A is defined as the rank of the torsion-free group
$r_0(A)$
of A is defined as the rank of the torsion-free group
![]() $A/T$
, where T is the periodic part of A; moreover, for each prime p, the p-rank
$A/T$
, where T is the periodic part of A; moreover, for each prime p, the p-rank
![]() $r_p(A)$
of A is the rank of the p-component of A. Of course, A has finite rank if and only if
$r_p(A)$
of A is the rank of the p-component of A. Of course, A has finite rank if and only if
We say that A has finite total rank if
 $$ \begin{align*}r_0(A)+\sum_pr_p(A)<\infty.\end{align*} $$
$$ \begin{align*}r_0(A)+\sum_pr_p(A)<\infty.\end{align*} $$
A group G is said to have finite abelian section rank if every abelian section of G has finite
![]() $0$
-rank and finite p-rank for all primes p. Moreover, G has finite abelian total rank if it admits a series of finite length each of whose infinite factors is an abelian group of finite total rank; of course, every group of finite abelian total rank is soluble-by-finite and has finite rank, while any torsion-free nilpotent group of finite rank has finite abelian total rank, because all factors of its upper central series are torsion-free. Notice that the class of groups with finite abelian total rank is not quotient-closed, since
$0$
-rank and finite p-rank for all primes p. Moreover, G has finite abelian total rank if it admits a series of finite length each of whose infinite factors is an abelian group of finite total rank; of course, every group of finite abelian total rank is soluble-by-finite and has finite rank, while any torsion-free nilpotent group of finite rank has finite abelian total rank, because all factors of its upper central series are torsion-free. Notice that the class of groups with finite abelian total rank is not quotient-closed, since
![]() $\mathbb{Q}/\mathbb{Z}$
is the direct product of infinitely many Prüfer groups; however, if G is a group with finite abelian total rank and N is a periodic normal subgroup of G, it is easy to see that
$\mathbb{Q}/\mathbb{Z}$
is the direct product of infinitely many Prüfer groups; however, if G is a group with finite abelian total rank and N is a periodic normal subgroup of G, it is easy to see that
![]() $G/N$
also has finite abelian total rank.
$G/N$
also has finite abelian total rank.
If G is a group, in the following, we denote by
![]() ${\cal R}_G$
the class of all G-modules that have finite rank as abelian groups. Our next result is an application of Lemma 2.1.
${\cal R}_G$
the class of all G-modules that have finite rank as abelian groups. Our next result is an application of Lemma 2.1.
Corollary 5.4. If G is a group, the class of all G-modules that are
![]() ${\cal T}_G$
-by-
${\cal T}_G$
-by-
![]() ${\cal R}_G$
is tensorial.
${\cal R}_G$
is tensorial.
The following result is well known (and even trivial in the abelian case), so for completeness, we only sketch its proof.
Lemma 5.5. Let G be a group admitting a normal series of finite length whose factors are either locally finite or abelian of finite rank. Then G contains a locally finite normal subgroup T such that
![]() $G/T$
has finite rank.
$G/T$
has finite rank.
Proof. By induction, it is enough to prove the statement when G contains a torsion-free abelian normal subgroup A of finite rank such that
![]() $G/A$
is locally finite. Then
$G/A$
is locally finite. Then
![]() $C=C_G(A)$
has finite index in G because periodic linear groups over the field of rational numbers are finite (see for instance [Reference Wehrfritz20, Theorem 9.33]). Moreover,
$C=C_G(A)$
has finite index in G because periodic linear groups over the field of rational numbers are finite (see for instance [Reference Wehrfritz20, Theorem 9.33]). Moreover,
![]() $C'$
is locally finite by Schur’s theorem and the abelian group
$C'$
is locally finite by Schur’s theorem and the abelian group
![]() $C/C'$
is periodic-by-(finite rank), which completes the proof.
$C/C'$
is periodic-by-(finite rank), which completes the proof.
Theorem 5.6. The class of all (locally finite)-by-(finite rank) groups is a Hall class.
Proof. The proof runs along the same lines as that of Theorem 2.17, just replacing Engel modules by modules whose underlying group has finite rank, and using Corollary 5.4 and Lemma 5.5.
We point out that since periodic subgroups of
![]() $\mathrm {GL}(n,\mathbb{Q})$
are finite and their order is bounded in terms of n, a slight modification of Lemma 5.5 allows us to obtain a quantitative version of Theorem 5.6.
$\mathrm {GL}(n,\mathbb{Q})$
are finite and their order is bounded in terms of n, a slight modification of Lemma 5.5 allows us to obtain a quantitative version of Theorem 5.6.
Theorem 5.7. The class of all (locally finite)-by-(finite abelian total rank) groups is a Hall class.
Proof. Let G be a group and let N be a nilpotent normal subgroup of G such that
![]() $G/N'$
contains a locally finite normal subgroup
$G/N'$
contains a locally finite normal subgroup
![]() $L/N'$
with
$L/N'$
with
![]() $G/L$
of finite abelian total rank. We may obviously assume that G has no nontrivial locally finite normal subgroups, so in particular G has finite rank by Theorem 5.6. Let c be the nilpotency class of the torsion-free nilpotent group
$G/L$
of finite abelian total rank. We may obviously assume that G has no nontrivial locally finite normal subgroups, so in particular G has finite rank by Theorem 5.6. Let c be the nilpotency class of the torsion-free nilpotent group
![]() $N'$
. For each nonnegative integer
$N'$
. For each nonnegative integer
![]() $i<c$
, we have that
$i<c$
, we have that
![]() $\zeta _{i+1}(N')/\zeta _i(N')$
is torsion-free abelian of finite rank and hence
$\zeta _{i+1}(N')/\zeta _i(N')$
is torsion-free abelian of finite rank and hence
![]() $L/C_L(\zeta _{i+1}(N')/\zeta _i(N'))$
is finite (see [Reference Wehrfritz20, Theorem 9.33]). Thus, the normal subgroup
$L/C_L(\zeta _{i+1}(N')/\zeta _i(N'))$
is finite (see [Reference Wehrfritz20, Theorem 9.33]). Thus, the normal subgroup
 $$ \begin{align*}C=\bigcap_{i=0}^{c-1}C_L(\zeta_{i+1}(N')/\zeta_i(N'))\end{align*} $$
$$ \begin{align*}C=\bigcap_{i=0}^{c-1}C_L(\zeta_{i+1}(N')/\zeta_i(N'))\end{align*} $$
has finite index in L, so
![]() $G/C$
has finite abelian total rank. Since
$G/C$
has finite abelian total rank. Since
![]() $N'\leq \zeta _c(C)$
, the group
$N'\leq \zeta _c(C)$
, the group
![]() $C/\zeta _c(C)$
is locally finite and hence C is torsion-free nilpotent (see [Reference Robinson17, Part 1, Corollary 2 to Theorem 4.21]). It follows that C has finite abelian total rank and hence G also has finite abelian total rank. The statement is proved.
$C/\zeta _c(C)$
is locally finite and hence C is torsion-free nilpotent (see [Reference Robinson17, Part 1, Corollary 2 to Theorem 4.21]). It follows that C has finite abelian total rank and hence G also has finite abelian total rank. The statement is proved.
Theorem 5.8. The class of all (locally finite)-by-(finite abelian section rank) groups is a Hall class.
Proof. Let G be a group containing a nilpotent normal subgroup N such that
![]() $G/N'$
is (locally finite)-by-(finite abelian section rank). We may suppose by Lemma 2.19 that
$G/N'$
is (locally finite)-by-(finite abelian section rank). We may suppose by Lemma 2.19 that
![]() $G/N$
has finite abelian section rank. Of course, it can also be assumed that N is torsion-free. Since
$G/N$
has finite abelian section rank. Of course, it can also be assumed that N is torsion-free. Since
![]() $N/N'$
is (locally finite)-by-(finite abelian total rank), it follows from Theorem 5.7 that N has finite abelian total rank. Therefore, G has finite abelian section rank and the statement is proved.
$N/N'$
is (locally finite)-by-(finite abelian total rank), it follows from Theorem 5.7 that N has finite abelian total rank. Therefore, G has finite abelian section rank and the statement is proved.
6 Obstructions of finite exponent
In the previous sections, we proved that
![]() $(\mathbf{L}\mathfrak{F})\mathfrak{X}$
is a Hall class for several natural choices of the group class 𝔛. It is therefore natural to ask what happens when
$(\mathbf{L}\mathfrak{F})\mathfrak{X}$
is a Hall class for several natural choices of the group class 𝔛. It is therefore natural to ask what happens when
![]() $\mathbf{L}\mathfrak{F}$
is replaced by its subclass 𝔅 consisting of all locally finite groups of finite exponent. In dealing with this problem, the role played by Schur’s theorem in the case of locally finite obstructions is taken by the following result of Mann [Reference Mann12].
$\mathbf{L}\mathfrak{F}$
is replaced by its subclass 𝔅 consisting of all locally finite groups of finite exponent. In dealing with this problem, the role played by Schur’s theorem in the case of locally finite obstructions is taken by the following result of Mann [Reference Mann12].
Lemma 6.1. Let G be a group such that
![]() $G/\zeta _1(G)$
is locally finite of finite exponent e. Then
$G/\zeta _1(G)$
is locally finite of finite exponent e. Then
![]() $G'$
has finite exponent bounded by a function of e.
$G'$
has finite exponent bounded by a function of e.
If k is any positive integer and A is an abelian group of exponent k, the tensor product
![]() $A\otimes _{\mathbb{Z}}B$
has exponent dividing k for every abelian group B. Thus, the proof of Lemma 2.1 can be used to prove the following result, where
$A\otimes _{\mathbb{Z}}B$
has exponent dividing k for every abelian group B. Thus, the proof of Lemma 2.1 can be used to prove the following result, where
![]() ${\cal B}_G^{(k)}$
denotes the class of all G-modules whose underlying group has finite exponent dividing k.
${\cal B}_G^{(k)}$
denotes the class of all G-modules whose underlying group has finite exponent dividing k.
Lemma 6.2. Let G be a group and let
![]() $\cal M$
be a quotient-closed, tensorial class of G-modules. Then for each positive integer k, the class of all G-modules that are
$\cal M$
be a quotient-closed, tensorial class of G-modules. Then for each positive integer k, the class of all G-modules that are
![]() ${\cal B}_G^{(k)}$
-by-
${\cal B}_G^{(k)}$
-by-
![]() $\cal M$
is tensorial.
$\cal M$
is tensorial.
If G is a group and
![]() $\cal M$
is a class of G-modules, we denote by
$\cal M$
is a class of G-modules, we denote by
![]() $\mathbf{P}\cal M$
the class of all G-modules A admitting a finite series of G-submodules
$\mathbf{P}\cal M$
the class of all G-modules A admitting a finite series of G-submodules
such that
![]() $A_{i+1}/A_i$
belongs to
$A_{i+1}/A_i$
belongs to
![]() ${\cal M}$
for each
${\cal M}$
for each
![]() $i=0,1,\ldots ,t-1$
. The G-modules in the class
$i=0,1,\ldots ,t-1$
. The G-modules in the class
![]() $\mathbf{P}{\cal M}$
are called poly-
$\mathbf{P}{\cal M}$
are called poly-
![]() ${\cal M}$
.
${\cal M}$
.
Lemma 6.3. Let G be a group and let
![]() $\cal M$
be a class of G-modules that is closed with respect to forming G-submodules. If A is a G-module and B is a G-submodule of A such that
$\cal M$
be a class of G-modules that is closed with respect to forming G-submodules. If A is a G-module and B is a G-submodule of A such that
![]() $B\in {\cal M}$
and
$B\in {\cal M}$
and
![]() $A/B\in {\cal B}_G^{(k)}$
for some positive integer k, then there exists a G-submodule C of A with
$A/B\in {\cal B}_G^{(k)}$
for some positive integer k, then there exists a G-submodule C of A with
![]() $C\in {\cal B}_G^{(k)}$
and
$C\in {\cal B}_G^{(k)}$
and
![]() $A/C\in {\cal M}$
.
$A/C\in {\cal M}$
.
Proof. Clearly,
![]() $kA\leq B$
and so
$kA\leq B$
and so
![]() $kA\in {\cal M}$
. Since the map
$kA\in {\cal M}$
. Since the map
![]() $\varphi :a\mapsto ka$
is a G- homomorphism of A onto
$\varphi :a\mapsto ka$
is a G- homomorphism of A onto
![]() $kA$
, it follows that the kernel C of
$kA$
, it follows that the kernel C of
![]() $\varphi $
is a G-submodule of A whose exponent as an abelian group divides k and the G-module
$\varphi $
is a G-submodule of A whose exponent as an abelian group divides k and the G-module
![]() $A/C$
is in
$A/C$
is in
![]() $\cal M$
.
$\cal M$
.
The above lemma and a simple induction argument prove the following result.
Corollary 6.4. Let G be a group and let
![]() $\cal M$
be a class of G-modules that is closed with respect to forming G-submodules. If k is a positive integer and A is a G-module admitting a series of G-submodules of finite length t each of whose factors belongs to
$\cal M$
be a class of G-modules that is closed with respect to forming G-submodules. If k is a positive integer and A is a G-module admitting a series of G-submodules of finite length t each of whose factors belongs to
![]() ${\cal B}_G^{(k)}\cup \cal M$
, then there exists a G-submodule C of A such that
${\cal B}_G^{(k)}\cup \cal M$
, then there exists a G-submodule C of A such that
![]() $C\in {\cal B}_G^{({k^t})}$
and
$C\in {\cal B}_G^{({k^t})}$
and
![]() $A/C$
is poly-
$A/C$
is poly-
![]() $\cal M$
.
$\cal M$
.
A crucial point in our considerations is to prove that 𝔅𝔑 is a Hall class.
Lemma 6.5. Let G be a group and let N be a normal subgroup of G. If N has a finite G-invariant series each of whose factors is either in 𝔅 or central in G, then there is a positive integer k such that
![]() $[N,_kG]$
belongs to 𝔅.
$[N,_kG]$
belongs to 𝔅.
Proof. Let
be a finite G-invariant series of minimal length t such that for each nonnegative integer
![]() $i<t$
,
$i<t$
,
![]() $N_{i+1}/N_i$
either belongs to 𝔅 or is central in G. By induction, there is a positive integer h such that
$N_{i+1}/N_i$
either belongs to 𝔅 or is central in G. By induction, there is a positive integer h such that
![]() $M/N_1=[N,_hG]N_1/N_1\in \mathfrak{B}$
, and without loss of generality we may suppose that
$M/N_1=[N,_hG]N_1/N_1\in \mathfrak{B}$
, and without loss of generality we may suppose that
![]() $N_1\leq \zeta _1(G)$
. Then the group
$N_1\leq \zeta _1(G)$
. Then the group
![]() $M/\zeta _1(M)$
is locally finite of finite exponent and so by Lemma 6.1,
$M/\zeta _1(M)$
is locally finite of finite exponent and so by Lemma 6.1,
![]() $M'$
also lies in 𝔅. Application of Lemma 6.3 to the G-module
$M'$
also lies in 𝔅. Application of Lemma 6.3 to the G-module
![]() $M/M'$
when
$M/M'$
when
![]() $\cal M$
is the class of all trivial G-modules yields that M contains a G-invariant subgroup
$\cal M$
is the class of all trivial G-modules yields that M contains a G-invariant subgroup
![]() $L\geq M'$
of finite exponent such that
$L\geq M'$
of finite exponent such that
![]() $M/L\leq \zeta _1(G/L)$
. Thus,
$M/L\leq \zeta _1(G/L)$
. Thus,
![]() $[N,_{h+1}G]\leq [M,G]\leq L$
has finite exponent and the statement is proved.
$[N,_{h+1}G]\leq [M,G]\leq L$
has finite exponent and the statement is proved.
Corollary 6.6. A group G is 𝔅-by-nilpotent if and only if it has a normal series of finite length each of whose factors either belongs to 𝔅 or is central in G.
Theorem 6.7. The class 𝔅𝔑 is a Hall class.
Proof. It is enough to reproduce the proof of Theorem 2.5, replacing Lemma 2.1 by Lemma 6.2 and Corollary 2.4 by Corollary 6.6.
Corollary 6.8. The group classes
![]() $\mathfrak{B}\mathfrak{S}$
,
$\mathfrak{B}\mathfrak{S}$
,
![]() $\mathfrak{B}(\acute {\mathbf{P}}_n\mathfrak{A})$
and
$\mathfrak{B}(\acute {\mathbf{P}}_n\mathfrak{A})$
and
![]() $\mathfrak{B}(\mathbf{L}\mathfrak{S})$
are Hall classes.
$\mathfrak{B}(\mathbf{L}\mathfrak{S})$
are Hall classes.
Proof. Since 𝔅𝔑 is a Hall class by Theorem 6.7, the statement follows directly from Lemma 5.1 by choosing
![]() $\mathfrak{X}=\mathfrak{B}$
and 𝔜 as one of the classes 𝔖,
$\mathfrak{X}=\mathfrak{B}$
and 𝔜 as one of the classes 𝔖,
![]() $\acute {\mathbf{P}}_n\mathfrak{A}$
,
$\acute {\mathbf{P}}_n\mathfrak{A}$
,
![]() $\mathbf{L}\mathfrak{S}$
.
$\mathbf{L}\mathfrak{S}$
.
Corollary 6.9. The class
![]() $\mathfrak{B}\mathfrak{N}^k$
is a Hall class for each positive integer k.
$\mathfrak{B}\mathfrak{N}^k$
is a Hall class for each positive integer k.
Proof. The case
![]() $k=1$
is just Theorem 6.7. Suppose
$k=1$
is just Theorem 6.7. Suppose
![]() $k>1$
and let G be a group containing a nilpotent normal subgroup N such that
$k>1$
and let G be a group containing a nilpotent normal subgroup N such that
![]() $G/N'\in \mathfrak{B}\mathfrak{N}^k$
. Then there is a normal subgroup
$G/N'\in \mathfrak{B}\mathfrak{N}^k$
. Then there is a normal subgroup
![]() $M/N'$
of
$M/N'$
of
![]() $G/N'$
such that
$G/N'$
such that
![]() $G/M\in \mathfrak{N}$
and
$G/M\in \mathfrak{N}$
and
![]() $M/N'\in \mathfrak{B}\mathfrak{N}^{k-1}$
. Since
$M/N'\in \mathfrak{B}\mathfrak{N}^{k-1}$
. Since
![]() $k>1$
, Fitting’s theorem yields that
$k>1$
, Fitting’s theorem yields that
![]() $MN/N'$
belongs to
$MN/N'$
belongs to
![]() $\mathfrak{B}\mathfrak{N}^{k-1}\!$
, so
$\mathfrak{B}\mathfrak{N}^{k-1}\!$
, so
![]() $MN$
lies in
$MN$
lies in
![]() $\mathfrak{B}\mathfrak{N}^{k-1}$
by induction. It follows that
$\mathfrak{B}\mathfrak{N}^{k-1}$
by induction. It follows that
![]() $G\in \mathfrak{B}\mathfrak{N}^k$
and so the statement is proved.
$G\in \mathfrak{B}\mathfrak{N}^k$
and so the statement is proved.
Our next theorem shows that the class 𝔅 behaves better that 𝔉 and L𝔉, at least in our context. If e is any positive integer, we denote by
![]() $\mathfrak{B}_e$
the class of all groups of finite exponent dividing e, so
$\mathfrak{B}_e$
the class of all groups of finite exponent dividing e, so
![]() $\mathfrak{B}=\bigcup _e\mathfrak{B}_e.$
$\mathfrak{B}=\bigcup _e\mathfrak{B}_e.$
Theorem 6.10. The class 𝔅𝔜 is a Hall class, where 𝔜 is any of the following classes of groups:
-
(a) the class of finitely generated nilpotent groups;
-
(b) the class of hypercentral groups;
-
(c) the class of locally nilpotent groups;
-
(d) the class of Engel groups;
-
(e) the class of supersoluble groups;
-
(f) the class of paranilpotent groups;
-
(g) the class of hypercyclic groups;
-
(h) the class of locally supersoluble groups;
-
(i) the class of
 $FC$
-nilpotent groups;
$FC$
-nilpotent groups; -
(j) the class of
 $FC$
-hypercentral groups;
$FC$
-hypercentral groups; -
(k) the class of locally
 $FC$
-nilpotent groups.
$FC$
-nilpotent groups.
Proof. Let 𝔜 be any of the classes considered in the statement and let N be a nilpotent normal subgroup of a group G such that
![]() $G/N'$
belongs to 𝔅𝔜. It follows from Theorem 6.7 and Lemma 2.19 that G contains a normal subgroup M such that
$G/N'$
belongs to 𝔅𝔜. It follows from Theorem 6.7 and Lemma 2.19 that G contains a normal subgroup M such that
![]() $G/M'$
is in 𝔅𝔜,
$G/M'$
is in 𝔅𝔜,
![]() $G/M$
is in 𝔜 and
$G/M$
is in 𝔜 and
![]() $\gamma _k(M)$
has finite exponent for some positive integer k. To prove that G itself is in 𝔅𝔜, we may factor out
$\gamma _k(M)$
has finite exponent for some positive integer k. To prove that G itself is in 𝔅𝔜, we may factor out
![]() $\gamma _k(M)$
and so assume that M is nilpotent.
$\gamma _k(M)$
and so assume that M is nilpotent.
Put
![]() $A=\zeta _1(M)$
, so
$A=\zeta _1(M)$
, so
![]() $G/A\in \mathfrak{BY}$
by induction on the nilpotency class of M. If
$G/A\in \mathfrak{BY}$
by induction on the nilpotency class of M. If
![]() $K/A$
is a normal 𝔅-subgroup of
$K/A$
is a normal 𝔅-subgroup of
![]() $G/A$
such that
$G/A$
such that
![]() $G/K\in \mathfrak{Y}$
, we have that
$G/K\in \mathfrak{Y}$
, we have that
![]() $G/B$
is also a 𝔜-group, where
$G/B$
is also a 𝔜-group, where
![]() $B=M\cap K$
. Since
$B=M\cap K$
. Since
![]() $A\leq \zeta _1(B)$
, it follows from Lemma 6.1 that
$A\leq \zeta _1(B)$
, it follows from Lemma 6.1 that
![]() $B'$
belongs to 𝔅, so the replacement of G by
$B'$
belongs to 𝔅, so the replacement of G by
![]() $G/B'$
allows us to assume that B is abelian.
$G/B'$
allows us to assume that B is abelian.
We complete the proof only for parts (b), (c) and (h) since all other statements can be proved in similar ways.
Let 𝔜 be the class of hypercentral groups. Since
![]() $M/M'$
is
$M/M'$
is
![]() ${\cal B}_G$
-by-hypertrivial as a G-module, it follows from Lemma 6.2 that M has a finite G-invariant series each of whose factors is either in 𝔅 or hypercentrally embedded in G. Thus, the G-module B has a finite series of G-submodules each of whose factors either belongs to
${\cal B}_G$
-by-hypertrivial as a G-module, it follows from Lemma 6.2 that M has a finite G-invariant series each of whose factors is either in 𝔅 or hypercentrally embedded in G. Thus, the G-module B has a finite series of G-submodules each of whose factors either belongs to
![]() ${\cal B}_G$
or is hypertrivial and hence it contains a G-submodule C such that
${\cal B}_G$
or is hypertrivial and hence it contains a G-submodule C such that
![]() $C\in {\cal B}_G$
and
$C\in {\cal B}_G$
and
![]() $B/C$
is hypertrivial by Corollary 6.4. Of course, C is a normal subgroup of finite exponent of G and
$B/C$
is hypertrivial by Corollary 6.4. Of course, C is a normal subgroup of finite exponent of G and
![]() $G/C$
is hypercentral. This completes the proof of part (b).
$G/C$
is hypercentral. This completes the proof of part (b).
Suppose now that
![]() $\mathfrak{Y}=\mathbf{L}\mathfrak{N}$
and let e be a positive integer such that
$\mathfrak{Y}=\mathbf{L}\mathfrak{N}$
and let e be a positive integer such that
![]() $G/M'$
belongs to
$G/M'$
belongs to
![]() $\mathfrak{B}_e(\mathbf{L}\mathfrak{N})$
. Consider any finitely generated subgroup E of G. Since
$\mathfrak{B}_e(\mathbf{L}\mathfrak{N})$
. Consider any finitely generated subgroup E of G. Since
![]() $M/M'$
is
$M/M'$
is
![]() ${\cal B}_E^{(e)}$
-by-(locally polytrivial) as an E-module, it follows from Lemma 6.2 that the lower central factor
${\cal B}_E^{(e)}$
-by-(locally polytrivial) as an E-module, it follows from Lemma 6.2 that the lower central factor
![]() $\gamma _i(M)/\gamma _{i+1}(M)$
likewise is a
$\gamma _i(M)/\gamma _{i+1}(M)$
likewise is a
![]() ${\cal B}_E^{(e)}$
-by-(locally polytrivial) E-module for each positive integer
${\cal B}_E^{(e)}$
-by-(locally polytrivial) E-module for each positive integer
![]() $i\leq c$
, where c is the nilpotency class of M. Thus, the E-module B has a series of E-submodules of length at most c each of whose factors is
$i\leq c$
, where c is the nilpotency class of M. Thus, the E-module B has a series of E-submodules of length at most c each of whose factors is
![]() ${\cal B}_E^{(e)}$
-by-(locally polytrivial). Since locally polytrivial E-modules are hypertrivial by Lemma 2.23, an application of Corollary 6.4 yields that B contains an E-invariant subgroup C such that
${\cal B}_E^{(e)}$
-by-(locally polytrivial). Since locally polytrivial E-modules are hypertrivial by Lemma 2.23, an application of Corollary 6.4 yields that B contains an E-invariant subgroup C such that
![]() $B/C$
is hypercentrally embedded in
$B/C$
is hypercentrally embedded in
![]() $EB/C$
and C has finite exponent dividing
$EB/C$
and C has finite exponent dividing
![]() $h=e^{2c}$
. Of course,
$h=e^{2c}$
. Of course,
![]() $EB/C$
is locally nilpotent and we also have
$EB/C$
is locally nilpotent and we also have
![]() $C\leq B[h]=\{ b\in B\;|\; b^h=1\}$
, so that
$C\leq B[h]=\{ b\in B\;|\; b^h=1\}$
, so that
![]() $EB[h]/B[h]$
is nilpotent and
$EB[h]/B[h]$
is nilpotent and
![]() $G/B[h]$
is locally nilpotent. Therefore,
$G/B[h]$
is locally nilpotent. Therefore,
![]() $G\in \mathfrak{B}(\mathbf{L}\mathfrak{N})$
.
$G\in \mathfrak{B}(\mathbf{L}\mathfrak{N})$
.
Finally, if 𝔜 is the class of locally supersoluble groups, the proof runs along the same lines as part (c), just replacing locally polytrivial G-modules and hypertrivial G-modules by locally paranilpotent G-modules and hypercyclic G-modules, respectively; note that a group is locally supersoluble if and only if it is locally hypercyclic.
To complete our analysis of classes of the form 𝔅𝔜, where 𝔜 is a class of generalized nilpotent groups, we need some additional definitions.
Let G be a group and let A be a G-module. We say that A is a Baer G-module if A is a polytrivial
![]() $\langle g\rangle $
-module for each element g of G. Similarly, A is called a Gruenberg G-module if it is hypertrivial as a
$\langle g\rangle $
-module for each element g of G. Similarly, A is called a Gruenberg G-module if it is hypertrivial as a
![]() $\langle g\rangle $
-module for every
$\langle g\rangle $
-module for every
![]() $g\in G$
. Finally, A is said to be a Fitting G-module if it is polytrivial as a
$g\in G$
. Finally, A is said to be a Fitting G-module if it is polytrivial as a
![]() $\langle g\rangle ^G$
-module for each
$\langle g\rangle ^G$
-module for each
![]() $g\in G$
. Of course, the classes of Fitting, Baer and Gruenberg G-modules are closed with respect to forming submodules, quotient modules and extensions; our next lemma shows that these classes are also tensorial.
$g\in G$
. Of course, the classes of Fitting, Baer and Gruenberg G-modules are closed with respect to forming submodules, quotient modules and extensions; our next lemma shows that these classes are also tensorial.
Lemma 6.11. If G is any group, the class of Fitting G-modules, the class of Baer G-modules and the class of Gruenberg G-modules are tensorial.
Proof. Let A and B be Fitting (respectively Baer or Gruenberg) G-modules, and consider an arbitrary element g of G. Since A and B are polytrivial
![]() $\langle g\rangle ^G$
-modules (respectively polytrivial
$\langle g\rangle ^G$
-modules (respectively polytrivial
![]() $\langle g\rangle $
-modules or hypertrivial
$\langle g\rangle $
-modules or hypertrivial
![]() $\langle g\rangle $
-modules), also the tensor product
$\langle g\rangle $
-modules), also the tensor product
![]() $A\otimes _{\mathbb{Z}}B$
is a polytrivial
$A\otimes _{\mathbb{Z}}B$
is a polytrivial
![]() $\langle g\rangle ^G$
-module (respectively polytrivial
$\langle g\rangle ^G$
-module (respectively polytrivial
![]() $\langle g\rangle $
-module or hypertrivial
$\langle g\rangle $
-module or hypertrivial
![]() $\langle g\rangle $
-module). Therefore,
$\langle g\rangle $
-module). Therefore,
![]() $A\otimes _{\mathbb{Z}}B$
is a Fitting (respectively Baer or Gruenberg) G-module and the statement is proved.
$A\otimes _{\mathbb{Z}}B$
is a Fitting (respectively Baer or Gruenberg) G-module and the statement is proved.
The following results add some further Hall classes to the list given in Theorem 6.10.
Theorem 6.12. The class 𝔅𝔜 is a Hall class, where 𝔜 is one of the following classes of groups:
-
(l) the class of Fitting groups;
-
(m) the class of Baer groups;
-
(n) the class of Gruenberg groups.
Proof. We only prove the statement for Fitting groups, since the other cases can be proved in a similar fashion. Let G be a group containing a nilpotent normal subgroup N such that
![]() $G/N'$
is 𝔅-by-Fitting. As in the first part of the proof of Theorem 6.10, we may reduce to the case in which N contains an abelian G-invariant subgroup B such that
$G/N'$
is 𝔅-by-Fitting. As in the first part of the proof of Theorem 6.10, we may reduce to the case in which N contains an abelian G-invariant subgroup B such that
![]() $G/B$
is a Fitting group. Since
$G/B$
is a Fitting group. Since
![]() $N/N'$
is
$N/N'$
is
![]() ${\cal B}_G$
-by-Fitting as a G-module, it follows from Lemma 6.2 that N has a finite G-invariant series each of whose factors either is in 𝔅 or is an abelian group that is a Fitting G-module by conjugation. Thus, the G-module B has a finite series of G-submodules each of whose factors either belongs to
${\cal B}_G$
-by-Fitting as a G-module, it follows from Lemma 6.2 that N has a finite G-invariant series each of whose factors either is in 𝔅 or is an abelian group that is a Fitting G-module by conjugation. Thus, the G-module B has a finite series of G-submodules each of whose factors either belongs to
![]() ${\cal B}_G$
or is a Fitting G-module. It follows from Corollary 6.4 that B contains a G-submodule C such that
${\cal B}_G$
or is a Fitting G-module. It follows from Corollary 6.4 that B contains a G-submodule C such that
![]() $C\in {\cal B}_G$
and
$C\in {\cal B}_G$
and
![]() $B/C$
is a Fitting G-module.
$B/C$
is a Fitting G-module.
If g is any element of G, we have that
![]() $B/C$
is a polytrivial
$B/C$
is a polytrivial
![]() $\langle g\rangle ^G$
-module, while
$\langle g\rangle ^G$
-module, while
![]() $\langle g\rangle ^GB/B$
is nilpotent because
$\langle g\rangle ^GB/B$
is nilpotent because
![]() $G/B$
is a Fitting group; thus,
$G/B$
is a Fitting group; thus,
![]() $\langle g\rangle ^GC/C$
is nilpotent. It follows that
$\langle g\rangle ^GC/C$
is nilpotent. It follows that
![]() $G/C$
is a Fitting group and hence G is 𝔅-by-Fitting.
$G/C$
is a Fitting group and hence G is 𝔅-by-Fitting.
Theorem 6.13. The class 𝔅𝔜 is a Hall class, where 𝔜 is one of the following classes of groups:
-
(o) the class of groups of finite rank;
-
(p) the class of groups with finite abelian section rank.
Proof. The proof is similar to that of part (b) of Theorem 6.10.
Our results seem to show that obstructions of finite exponent can be treated more easily than locally finite ones. However, this is not always true, as proved by the class of groups with finite abelian total rank. In fact, let
![]() $T=\mathrm {Tr}(2,\mathbb{Q})$
be the group of all lower triangular matrices of degree
$T=\mathrm {Tr}(2,\mathbb{Q})$
be the group of all lower triangular matrices of degree
![]() $2$
over the rationals and consider its central subgroup Z generated by the matrix
$2$
over the rationals and consider its central subgroup Z generated by the matrix
 $$ \begin{align*}\begin{pmatrix}1&0\\ 1&1\end{pmatrix}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix}1&0\\ 1&1\end{pmatrix}.\end{align*} $$
Then
![]() $G=T/Z$
is a nilpotent group such that
$G=T/Z$
is a nilpotent group such that
![]() $G/G'\simeq \mathbb{Q}\times \mathbb{Q}$
and
$G/G'\simeq \mathbb{Q}\times \mathbb{Q}$
and
![]() $G'$
is the direct product of infinitely many Prüfer groups. It follows that 𝔅-by-(finite abelian total rank) groups do not form a Hall class. This anomaly depends essentially on the fact that the class of groups with finite abelian total rank is not quotient-closed.
$G'$
is the direct product of infinitely many Prüfer groups. It follows that 𝔅-by-(finite abelian total rank) groups do not form a Hall class. This anomaly depends essentially on the fact that the class of groups with finite abelian total rank is not quotient-closed.
The results of this section fail to be true if the class 𝔅 is replaced by the class
![]() $\overline {\mathfrak{B}}$
consisting of all groups of finite exponent. Actually, it was proved by Endimioni and Traustason [Reference Endimioni and Traustason9] that there exists a group G having a nilpotent normal subgroup N such that
$\overline {\mathfrak{B}}$
consisting of all groups of finite exponent. Actually, it was proved by Endimioni and Traustason [Reference Endimioni and Traustason9] that there exists a group G having a nilpotent normal subgroup N such that
![]() $G/N'\in \overline {\mathfrak{B}}\mathfrak{A}$
, but G is not even in
$G/N'\in \overline {\mathfrak{B}}\mathfrak{A}$
, but G is not even in
![]() $\overline {\mathfrak{B}}(\mathbf{L}\mathfrak{S})$
; in particular,
$\overline {\mathfrak{B}}(\mathbf{L}\mathfrak{S})$
; in particular,
![]() $\overline {\mathfrak{B}}\mathfrak{N}$
is not a Hall class. Moreover, the replacement in their example of the Adjan group by the group constructed in [Reference Ol’shanskiĭ14, Theorem 31.4] shows that in Theorem 6.13, the class 𝔅 cannot be replaced by the class
$\overline {\mathfrak{B}}\mathfrak{N}$
is not a Hall class. Moreover, the replacement in their example of the Adjan group by the group constructed in [Reference Ol’shanskiĭ14, Theorem 31.4] shows that in Theorem 6.13, the class 𝔅 cannot be replaced by the class
![]() $\overline {\mathfrak{B}}$
.
$\overline {\mathfrak{B}}$
.
As we did in the case of a locally finite obstruction at the bottom, one can slightly modify the proofs to obtain quantitative versions of Theorems 6.7, 6.13(o) and Corollary 6.8 (for the class 𝔅𝔖). For instance, we have the following result.
Theorem 6.14. Let G be a group and let N be a normal subgroup of G. If N is nilpotent of class c and
![]() $G/N'$
is (of finite exponent e)-by-(nilpotent of class d), then there exist positive integers h and k, depending only on c, d and e, such that G is (of exponent at most h)-by-(nilpotent of class at most k).
$G/N'$
is (of finite exponent e)-by-(nilpotent of class d), then there exist positive integers h and k, depending only on c, d and e, such that G is (of exponent at most h)-by-(nilpotent of class at most k).
It is reasonable to ask whether analogues of Corollary 6.6 can be proved for other group classes of the form 𝔅𝔜, since results of this type would provide alternative proofs for some of the theorems in this section. Our final result shows that, for instance, this is the case when 𝔜 is the class of paranilpotent groups.
Lemma 6.15. Let G be a group and let
![]() $\cal M$
be a class of G-modules that is closed with respect to forming G-submodules and G-homomorphic images, contains all trivial G-modules and satisfies the condition
$\cal M$
be a class of G-modules that is closed with respect to forming G-submodules and G-homomorphic images, contains all trivial G-modules and satisfies the condition
![]() $M(g-1)=\{0\}$
for each
$M(g-1)=\{0\}$
for each
![]() $M\in {\cal M}$
and
$M\in {\cal M}$
and
![]() $g\in G'$
. If N is a normal subgroup of G admitting a finite G-invariant series whose factors are either in 𝔅 or G-modules in
$g\in G'$
. If N is a normal subgroup of G admitting a finite G-invariant series whose factors are either in 𝔅 or G-modules in
![]() $\cal M$
, then there exists a G-invariant subgroup B of N of finite exponent such that
$\cal M$
, then there exists a G-invariant subgroup B of N of finite exponent such that
![]() $N/B$
has a finite G-invariant series whose factors are G-modules in
$N/B$
has a finite G-invariant series whose factors are G-modules in
![]() $\cal M$
.
$\cal M$
.
Proof. Let
be a finite G-invariant series of minimal length t such that each
![]() $N_{i+1}/N_i$
is either in 𝔅 or a G-module in
$N_{i+1}/N_i$
is either in 𝔅 or a G-module in
![]() $\cal M$
. By induction, there exists a G-invariant subgroup
$\cal M$
. By induction, there exists a G-invariant subgroup
![]() $M\geq N_1$
of N such that
$M\geq N_1$
of N such that
![]() $M/N_1$
is in 𝔅 and
$M/N_1$
is in 𝔅 and
![]() $N/M$
has a finite G-invariant series whose factors are G-modules in
$N/M$
has a finite G-invariant series whose factors are G-modules in
![]() $\cal M$
. Thus, we may suppose that
$\cal M$
. Thus, we may suppose that
![]() $N_1$
is a G-module in
$N_1$
is a G-module in
![]() $\cal M$
, and in particular that
$\cal M$
, and in particular that
![]() $G'$
centralizes
$G'$
centralizes
![]() $N_1$
. Consider the normal subgroup
$N_1$
. Consider the normal subgroup
![]() $X=(M\cap G')N_1$
of G. Clearly,
$X=(M\cap G')N_1$
of G. Clearly,
![]() $N_1\leq \zeta _1(X)$
, so
$N_1\leq \zeta _1(X)$
, so
![]() $X/\zeta _1(X)\in \mathfrak{B}$
and hence also
$X/\zeta _1(X)\in \mathfrak{B}$
and hence also
![]() $X'$
belongs to 𝔅 by Lemma 6.1. Application of Lemma 6.3 to the G-module
$X'$
belongs to 𝔅 by Lemma 6.1. Application of Lemma 6.3 to the G-module
![]() $X/X'$
and to the class
$X/X'$
and to the class
![]() $\cal M$
yields that
$\cal M$
yields that
![]() $X/X'$
contains a 𝔅-subgroup
$X/X'$
contains a 𝔅-subgroup
![]() $B/X'$
that is normal in G and such that
$B/X'$
that is normal in G and such that
![]() $X/B$
belongs to
$X/B$
belongs to
![]() $\cal M$
. Since
$\cal M$
. Since
![]() $M/X$
is a central factor of G, it follows that
$M/X$
is a central factor of G, it follows that
![]() $N/B$
has a finite G-invariant series whose factors are either in 𝔅 or G-modules in
$N/B$
has a finite G-invariant series whose factors are either in 𝔅 or G-modules in
![]() $\cal M$
. Of course,
$\cal M$
. Of course,
![]() $B\in \mathfrak{B}$
and so the proof is complete.
$B\in \mathfrak{B}$
and so the proof is complete.
Corollary 6.16. A group G is 𝔅-by-paranilpotent if and only if it has a normal series of finite length whose factors are either in 𝔅 or paracentral in G.