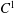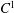Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
RIBÓN, JAVIER
2016.
Fixed points of nilpotent actions on.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 1,
p.
173.
Bonatti, C.
Monteverde, I.
Navas, A.
and
Rivas, C.
2017.
Rigidity for $$C^1$$ C 1 actions on the interval arising from hyperbolicity I: solvable groups.
Mathematische Zeitschrift,
Vol. 286,
Issue. 3-4,
p.
919.
Bonatti, Christian
Kim, Sang-hyun
Koberda, Thomas
and
Triestino, Michele
2020.
Small C1 actions of semidirect products on
compact manifolds.
Algebraic & Geometric Topology,
Vol. 20,
Issue. 6,
p.
3183.
Navas, Andrés
2021.
(Un)distorted diffeomorphisms in different regularities.
Israel Journal of Mathematics,
Vol. 244,
Issue. 2,
p.
727.
Eynard-Bontemps, Hélène
and
Navas, Andrés
2021.
Mather invariant, distortion, and conjugates for diffeomorphisms of the interval.
Journal of Functional Analysis,
Vol. 281,
Issue. 9,
p.
109149.
Navas, Andrés
2023.
On Conjugates and the Asymptotic Distortion of One-Dimensional C1+bv Diffeomorphisms.
International Mathematics Research Notices,
Vol. 2023,
Issue. 1,
p.
372.
Hamenstädt, Ursula
2024.
Actions of finitely generated groups on compact metric spaces.
Proceedings of the American Mathematical Society,
Vol. 152,
Issue. 8,
p.
3599.
Eynard-Bontemps, Hélène
and
Navas, Andrés
2025.
The space of C1+ actions of Zd on a one-dimensional manifold is path-connected.
Advances in Mathematics,
Vol. 478,
Issue. ,
p.
110395.
Kim, Sang-hyun
de la Salle, Mikael
Matte Bon, Nicolás
and
Triestino, Michele
2025.
Subexponential Growth and C1 Actions on One-Manifolds.
International Mathematics Research Notices,
Vol. 2025,
Issue. 13,