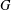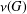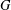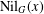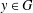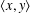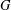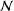Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wei, Huaquan
Gu, Huilong
Li, Jiao
and
Yang, Liying
2021.
On the nilpotent probability and supersolvability of finite groups.
Monatshefte für Mathematik,
Vol. 194,
Issue. 2,
p.
371.
Wei, Huaquan
Hou, Xuanyou
Sun, Changman
Diao, Xixi
Wu, Hui
and
Yang, Liying
2025.
The Nilpotent Probability of Finite Groups.
Acta Mathematica Sinica, English Series,
Vol. 41,
Issue. 4,
p.
1238.