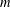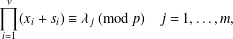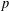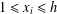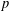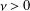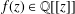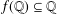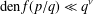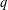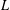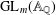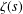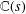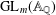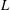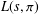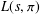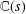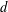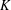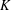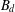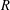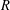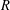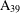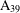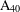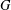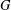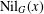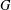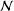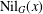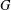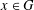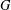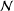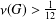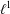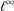Contents
Research Article
CAYLEY GRAPHS OVER A FINITE CHAIN RING AND GCD-GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 353-363
-
- Article
-
- You have access
- Export citation
SYSTEMS OF CONGRUENCES WITH PRODUCTS OF VARIABLES FROM SHORT INTERVALS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 364-371
-
- Article
-
- You have access
- Export citation
A NOTE ON LACUNARY POWER SERIES WITH RATIONAL COEFFICIENTS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 372-374
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROPERTIES OF INFINITE PRODUCTS OF CYCLOTOMIC POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2016, pp. 375-387
-
- Article
-
- You have access
- Export citation
HYPERTRANSCENDENCE OF
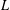 $L$-FUNCTIONS FOR
$L$-FUNCTIONS FOR 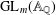 $\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
$\text{GL}_{m}(\mathbb{A}_{\mathbb{Q}})$
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 388-399
-
- Article
-
- You have access
- Export citation
CONGRUENCES MODULO 2 FOR CERTAIN PARTITION FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 400-409
-
- Article
-
- You have access
- Export citation
THE 7-REGULAR AND 13-REGULAR PARTITION FUNCTIONS MODULO 3
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 410-419
-
- Article
-
- You have access
- Export citation
ON NUMBER FIELDS WITHOUT A UNIT PRIMITIVE ELEMENT
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 420-432
-
- Article
-
- You have access
- Export citation
PROGRESS ON THE AUSLANDER–REITEN CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 16 March 2016, pp. 433-440
-
- Article
-
- You have access
- Export citation
A 2-ARC TRANSITIVE PENTAVALENT CAYLEY GRAPH OF
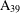 $\text{A}_{39}$
$\text{A}_{39}$
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2016, pp. 441-446
-
- Article
-
- You have access
- Export citation
ON THE PROBABILITY OF GENERATING NILPOTENT SUBGROUPS IN A FINITE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 20 November 2015, pp. 447-453
-
- Article
-
- You have access
- Export citation
A SUFFICIENT CONDITION UNDER WHICH A SEMIGROUP IS NONFINITELY BASED
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 454-466
-
- Article
-
- You have access
- Export citation
CHARACTERISATION OF THE FOURIER TRANSFORM ON COMPACT GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2015, pp. 467-472
-
- Article
-
- You have access
- Export citation
MAZUR–ULAM PROPERTY OF THE SUM OF TWO STRICTLY CONVEX BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 473-485
-
- Article
-
- You have access
- Export citation
ON ISOMETRIC REPRESENTATION SUBSETS OF BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2015, pp. 486-496
-
- Article
-
- You have access
- Export citation
ORBITALLY NONEXPANSIVE MAPPINGS
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 497-503
-
- Article
-
- You have access
- Open access
- Export citation
BUZANO’S INEQUALITY HOLDS FOR ANY PROJECTION
- Part of:
-
- Published online by Cambridge University Press:
- 20 January 2016, pp. 504-510
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
SELECTED TOPICS IN SPECTRAL GRAPH THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 511-512
-
- Article
-
- You have access
- Export citation
ALGORITHMS FOR GALOIS EXTENSIONS OF GLOBAL FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 513-515
-
- Article
-
- You have access
- Export citation
SYNTHETIC LIE THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 10 February 2016, pp. 516-517
-
- Article
-
- You have access
- Export citation