This thesis presents my contributions to various aspects of the theory of universally Baire sets. One of these aspects is the smallest inner model containing all reals whose all sets of reals are universally Baire (viz., $L(\mathbb {R})$) and its relation to its inner model $\mathsf {HOD}$. We verify here that $\mathsf {HOD}^{L(\mathbb {R})}$ enjoys a form of local definability inside $L(\mathbb {R})$, further justifying its characterization as a “core model” in $L(\mathbb {R})$. We then study a “bottom-up” construction of more complicated universally Baire sets (more generally, determined sets). This construction allows us to give an “L-like” description of the minimum model of $\mathsf {AD}_{\mathbb {R}} + \mathsf {Cof}(\Theta ) = \Theta $. A consequence of this description is that this minimum model is contained in the Chang-plus model. Our construction, together with Woodin’s work on the Chang-plus model, shows that a proper class of Woodin cardinals which are limits of Woodin cardinals implies the existence of a hod mouse with a measurable limit of Woodin cardinals whose strategy is universally Baire.

Another aspect of the theory of universally Baire sets is the generic absoluteness and maximality associated with them. We include some results concerning generic $\Sigma _1^{H(\omega _2)}$-absoluteness with universally Baire sets as predicates or parameters, as well as generic $\Pi _2^{H(\omega _2)}$-maximality with universally Baire sets as predicates. In the second case, we are led to consider the general question of when a model of an infinitary propositional formula can be added by a stationary-set-preserving poset. We characterize when this happens in terms of a game which is a variant of the Model Existence Game. We then give a sufficient condition for this in terms of generic embeddings.

Abstract taken directly from the thesis

E-mail: obrad@math.ucla.edu

URL: https://hal.science/view/index/docid/5273407

I investigate the relationships between three hierarchies of reflection principles for a forcing class $\Gamma $: the hierarchy of bounded forcing axioms, of $\Sigma ^1_1$-absoluteness, and of Aronszajn tree preservation principles. The latter principle at level $\kappa $ says that whenever T is a tree of height $\omega _1$ and width $\kappa $ that does not have a branch of order type $\omega _1$, and whenever ${\mathord {\mathbb P}}$ is a forcing notion in $\Gamma $, then it is not the case that ${\mathord {\mathbb P}}$ forces that T has such a branch. $\Sigma ^1_1$-absoluteness serves as an intermediary between these principles and the bounded forcing axioms. A special case of the main result is that for forcing classes that don’t add reals, the three principles at level $2^\omega $ are equivalent. Special attention is paid to certain subclasses of subcomplete forcing, since these are natural forcing classes that don’t add reals.

We show that Dependent Choice is a sufficient choice principle for developing the basic theory of proper forcing, and for deriving generic absoluteness for the Chang model in the presence of large cardinals, even with respect to$\mathsf {DC}$-preserving symmetric submodels of forcing extensions. Hence,$\mathsf {ZF}+\mathsf {DC}$ not only provides the right framework for developing classical analysis, but is also the right base theory over which to safeguard truth in analysis from the independence phenomenon in the presence of large cardinals. We also investigate some basic consequences of the Proper Forcing Axiom in$\mathsf {ZF}$, and formulate a natural question about the generic absoluteness of the Proper Forcing Axiom in$\mathsf {ZF}+\mathsf {DC}$ and$\mathsf {ZFC}$. Our results confirm$\mathsf {ZF} + \mathsf {DC}$ as a natural foundation for a significant portion of “classical mathematics” and provide support to the idea of this theory being also a natural foundation for a large part of set theory.

We investigate the effects of various forcings on several forms of the Halpern– Läuchli theorem. For inaccessible κ, we show they are preserved by forcings of size less than κ. Combining this with work of Zhang in [17] yields that the polarized partition relations associated with finite products of the κ-rationals are preserved by all forcings of size less than κ over models satisfying the Halpern– Läuchli theorem at κ. We also show that the Halpern–Läuchli theorem is preserved by <κ-closed forcings assuming κ is measurable, following some observed reflection properties.

We investigate properties of trees of height ω1 and their preservation under subcomplete forcing. We show that subcomplete forcing cannot add a new branch to an ω1-tree. We introduce fragments of subcompleteness which are preserved by subcomplete forcing, and use these in order to show that certain strong forms of rigidity of Suslin trees are preserved by subcomplete forcing. Finally, we explore under what circumstances subcomplete forcing preserves Aronszajn trees of height and width ω1. We show that this is the case if CH fails, and if CH holds, then this is the case iff the bounded subcomplete forcing axiom holds. Finally, we explore the relationships between bounded forcing axioms, preservation of Aronszajn trees of height and width ω1 and generic absoluteness of ${\rm{\Sigma }}_1^1$-statements over first order structures of size ω1, also for other canonical classes of forcing.

We prove several equivalences and relative consistency results regarding generic absoluteness beyond Woodin’s ${\left( {{\bf{\Sigma }}_1^2} \right)^{{\rm{u}}{{\rm{B}}_\lambda }}}$ generic absoluteness result for a limit of Woodin cardinals λ. In particular, we prove that two-step $\exists ^ℝ \left( {{\rm{\Pi }}_1^2 } \right)^{{\rm{uB}}_\lambda} $ generic absoluteness below a measurable limit of Woodin cardinals has high consistency strength and is equivalent, modulo small forcing, to the existence of trees for ${\left( {{\bf{\Pi }}_1^2} \right)^{{\rm{u}}{{\rm{B}}_\lambda }}}$ formulas. The construction of these trees uses a general method for building an absolute complement for a given tree T assuming many “failures of covering” for the models $L\left( {T,{V_\alpha }} \right)$ for α below a measurable cardinal.

In this paper, we analyze structures of Zermelo degrees via a list of four degree theoretic questions (see §2) in various fine structure extender models, or under large cardinal assumptions. In particular we give a detailed analysis of the structures of Zermelo degrees in the Mitchell model for ω many measurable cardinals. It turns out that there is a profound correlation between the complexity of the degree structures at countable cofinality singular cardinals and the large cardinal strength of the relevant cardinals. The analysis applies to general degree notions, Zermelo degree is merely the author’s choice for illustrating the idea.

I0(λ) is the assertion that there is an elementary embedding j : L(Vλ+1) → L(Vλ+1) with critical point < λ. We show that under I0(λ), the structure of Zermelo degrees at λ is very complicated: it has incomparable degrees, is not dense, satisfies Posner–Robinson theorem etc. In addition, we show that I0 together with a mild condition on the critical point of the embedding implies that the degree determinacy for Zermelo degrees at λ is false in L(Vλ+1). The key tool in this paper is a generic absoluteness theorem in the theory of I0, from which we obtain an analogue of Perfect Set Theorem for “projective” subsets of Vλ+1, and the Posner–Robinson follows as a corollary. Perfect Set Theorem and Posner–Robinson provide evidences supporting the analogy between $$AD$$ over L(ℝ) and I0 over L(Vλ+1), while the failure of degree determinacy is one for disanalogy. Furthermore, we conjecture that the failure of degree determinacy for Zermelo degrees at any uncountable cardinal is a theorem of $$ZFC$$.

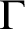
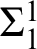
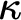
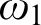
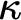
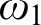
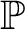
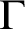
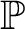
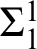
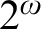
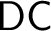
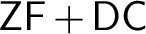
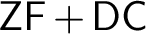
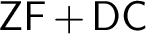
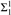
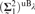
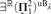
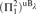
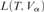
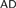
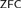
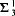We study the preservation under projective ccc forcing extensions of the property of L(ℝ) being a Solovay model. We prove that this property is preserved by every strongly- absolutely-ccc forcing extension, and that this is essentially the optimal preservation result, i.e., it does not hold for 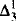absolutely-ccc forcing notions. We extend these results to the higher projective classes of ccc posets, and to the class of all projective ccc posets, using definably-Mahlo cardinals. As a consequence we obtain an exact equiconsistency result for generic absoluteness under projective absolutely-ccc forcing notions.