Article contents
SUBCOMPLETE FORCING, TREES, AND GENERIC ABSOLUTENESS
Published online by Cambridge University Press: 23 October 2018
Abstract
We investigate properties of trees of height ω1 and their preservation under subcomplete forcing. We show that subcomplete forcing cannot add a new branch to an ω1-tree. We introduce fragments of subcompleteness which are preserved by subcomplete forcing, and use these in order to show that certain strong forms of rigidity of Suslin trees are preserved by subcomplete forcing. Finally, we explore under what circumstances subcomplete forcing preserves Aronszajn trees of height and width ω1. We show that this is the case if CH fails, and if CH holds, then this is the case iff the bounded subcomplete forcing axiom holds. Finally, we explore the relationships between bounded forcing axioms, preservation of Aronszajn trees of height and width ω1 and generic absoluteness of 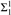 ${\rm{\Sigma }}_1^1$-statements over first order structures of size ω1, also for other canonical classes of forcing.
${\rm{\Sigma }}_1^1$-statements over first order structures of size ω1, also for other canonical classes of forcing.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
- 3
- Cited by

