Article contents
UNIVERSALLY BAIRE SETS AND GENERIC ABSOLUTENESS
Published online by Cambridge University Press: 09 January 2018
Abstract
We prove several equivalences and relative consistency results regarding generic absoluteness beyond Woodin’s 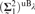 ${\left( {{\bf{\Sigma }}_1^2} \right)^{{\rm{u}}{{\rm{B}}_\lambda }}}$ generic absoluteness result for a limit of Woodin cardinals λ. In particular, we prove that two-step
${\left( {{\bf{\Sigma }}_1^2} \right)^{{\rm{u}}{{\rm{B}}_\lambda }}}$ generic absoluteness result for a limit of Woodin cardinals λ. In particular, we prove that two-step 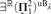 $\exists ^ℝ \left( {{\rm{\Pi }}_1^2 } \right)^{{\rm{uB}}_\lambda} $ generic absoluteness below a measurable limit of Woodin cardinals has high consistency strength and is equivalent, modulo small forcing, to the existence of trees for
$\exists ^ℝ \left( {{\rm{\Pi }}_1^2 } \right)^{{\rm{uB}}_\lambda} $ generic absoluteness below a measurable limit of Woodin cardinals has high consistency strength and is equivalent, modulo small forcing, to the existence of trees for 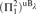 ${\left( {{\bf{\Pi }}_1^2} \right)^{{\rm{u}}{{\rm{B}}_\lambda }}}$ formulas. The construction of these trees uses a general method for building an absolute complement for a given tree T assuming many “failures of covering” for the models
${\left( {{\bf{\Pi }}_1^2} \right)^{{\rm{u}}{{\rm{B}}_\lambda }}}$ formulas. The construction of these trees uses a general method for building an absolute complement for a given tree T assuming many “failures of covering” for the models 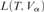 $L\left( {T,{V_\alpha }} \right)$ for α below a measurable cardinal.
$L\left( {T,{V_\alpha }} \right)$ for α below a measurable cardinal.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 2
- Cited by

