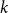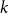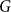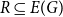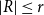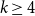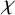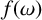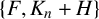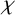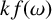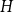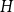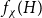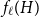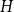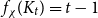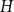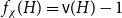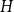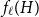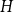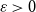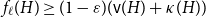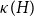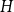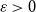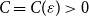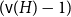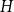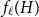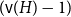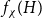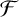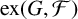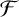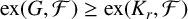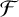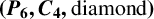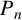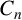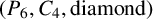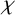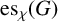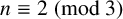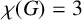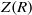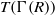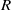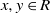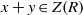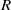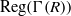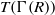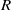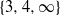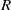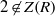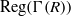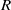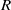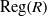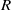Refine search
Actions for selected content:
16 results
COLORING EQUILATERAL TRIANGLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-14
-
- Article
- Export citation
Common graphs with arbitrary chromatic number
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 03 July 2025, pp. 594-634
- Print publication:
- March 2025
-
- Article
- Export citation
Vertex-critical graphs far from edge-criticality
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 151-157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON
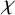 $\chi $-BINDING FUNCTIONS AND LINEAR FORESTS
$\chi $-BINDING FUNCTIONS AND LINEAR FORESTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 23-29
- Print publication:
- August 2025
-
- Article
- Export citation
On the choosability of
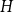 $H$-minor-free graphs
$H$-minor-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 129-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - Extreme Characteristics
- from Part II - Erdős–Rényi–Gilbert Model
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 111-124
-
- Chapter
- Export citation
LARGE
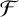 $\mathcal {F}$-FREE SUBGRAPHS IN
$\mathcal {F}$-FREE SUBGRAPHS IN 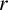 $r$-CHROMATIC GRAPHS
$r$-CHROMATIC GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 02 December 2022, pp. 200-204
- Print publication:
- October 2023
-
- Article
- Export citation
THE CHROMATIC NUMBER OF
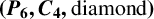 $\boldsymbol {(P_6,C_4,\mbox {diamond})}$-FREE GRAPHS
$\boldsymbol {(P_6,C_4,\mbox {diamond})}$-FREE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1-10
- Print publication:
- August 2023
-
- Article
- Export citation
SOME EXTREMAL RESULTS ON THE CHROMATIC STABILITY INDEX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 185-194
- Print publication:
- October 2022
-
- Article
- Export citation
10 - Individual graph descriptions
-
- Book:
- Strongly Regular Graphs
- Published online:
- 06 January 2022
- Print publication:
- 13 January 2022, pp 260-381
-
- Chapter
- Export citation
Triangle-free subgraphs with large fractional chromatic number
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 136-143
-
- Article
- Export citation
INFINITE COMBINATORICS PLAIN AND SIMPLE
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 23 October 2018, pp. 1247-1281
- Print publication:
- September 2018
-
- Article
- Export citation
DECIDING THE CHROMATIC NUMBERS OF ALGEBRAIC HYPERGRAPHS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 01 May 2018, pp. 128-145
- Print publication:
- March 2018
-
- Article
- Export citation
A Note on Conjectures of F. Galvin and R. Rado
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 317-325
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
THE REGULAR GRAPH OF A NONCOMMUTATIVE RING
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 13 February 2013, pp. 132-140
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Wild edge colourings of graphs
-
- Journal:
- The Journal of Symbolic Logic / Volume 69 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 12 March 2014, pp. 255-264
- Print publication:
- March 2004
-
- Article
- Export citation