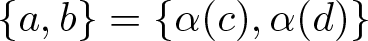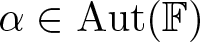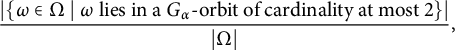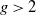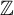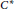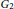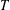Refine search
Actions for selected content:
38 results
3 - Groups Related to Chiral Polytopes
-
- Book:
- Abstract Chiral Polytopes
- Published online:
- 23 March 2025
- Print publication:
- 03 April 2025, pp 101-207
-
- Chapter
- Export citation

Abstract Chiral Polytopes
-
- Published online:
- 23 March 2025
- Print publication:
- 03 April 2025
4 - Symbolic dynamics and the stable algebra of matrices
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 266-422
-
- Chapter
- Export citation
CORRECTION TO ‘AUTOMORPHISM AND OUTER AUTOMORPHISM GROUPS OF RIGHT-ANGLED ARTIN GROUPS ARE NOT RELATIVELY HYPERBOLIC’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 30 April 2024, pp. 171-176
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - Künneth Structures
-
- Book:
- Künneth Geometry
- Published online:
- 07 December 2023
- Print publication:
- 21 December 2023, pp 57-72
-
- Chapter
- Export citation
Isomorphisms of quadratic quasigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 24 November 2023, pp. 1085-1109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TESTING DEFINITIONAL EQUIVALENCE OF THEORIES VIA AUTOMORPHISM GROUPS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1097-1118
- Print publication:
- December 2024
-
- Article
- Export citation
Finite transitive groups having many suborbits of cardinality at most 2 and an application to the enumeration of Cayley graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 30 January 2023, pp. 345-366
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CAYLEYNESS OF PRAEGER–XU GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 11 May 2022, pp. 353-356
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AUTOMORPHISM AND OUTER AUTOMORPHISM GROUPS OF RIGHT-ANGLED ARTIN GROUPS ARE NOT RELATIVELY HYPERBOLIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 102-112
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian actions on compact nonorientable Riemann surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 634-648
- Print publication:
- September 2022
-
- Article
- Export citation
On the automorphism group of minimal
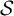 $\mathcal {S}$-adic subshifts of finite alphabet rank
$\mathcal {S}$-adic subshifts of finite alphabet rank
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 30 June 2021, pp. 2800-2822
- Print publication:
- September 2022
-
- Article
- Export citation
DECOMPOSITION THEOREMS FOR AUTOMORPHISM GROUPS OF TREES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 104-112
- Print publication:
- February 2021
-
- Article
- Export citation
On the virtual automorphism group of a minimal flow
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1281-1295
- Print publication:
- May 2021
-
- Article
- Export citation
Quantum Symmetries of Graph C *-algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 4 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 848-864
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
Order 3 Elements in G2 and Idempotents in Symmetric Composition Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 5 / 01 October 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1038-1075
- Print publication:
- 01 October 2018
-
- Article
-
- You have access
- Export citation
RETRACTIONS OF REVERSIBLE STRUCTURES
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1422-1437
- Print publication:
- December 2017
-
- Article
- Export citation
THE TWO-ARC-TRANSITIVE GRAPHS OF SQUARE-FREE ORDER ADMITTING ALTERNATING OR SYMMETRIC GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 29 March 2017, pp. 127-144
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
FINITE NORMAL 2-GEODESIC TRANSITIVE CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 338-348
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
RECONSTRUCTION OF SEPARABLY CATEGORICAL METRIC STRUCTURES
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 26 January 2016, pp. 216-224
- Print publication:
- March 2016
-
- Article
- Export citation