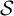 $\mathcal {S}$-adic subshifts of finite alphabet rank
$\mathcal {S}$-adic subshifts of finite alphabet rankPublished online by Cambridge University Press: 30 June 2021
It has been recently proved that the automorphism group of a minimal subshift with non-superlinear word complexity is virtually 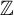 $\mathbb {Z}$
[Cyr and Kra. The automorphism group of a shift of linear growth: beyond transitivity. Forum Math. Sigma3 (2015), e5; Donoso et al. On automorphism groups of low complexity subshifts. Ergod. Th. & Dynam. Sys.36(1) (2016), 64–95]. In this article we extend this result to a broader class proving that the automorphism group of a minimal
$\mathbb {Z}$
[Cyr and Kra. The automorphism group of a shift of linear growth: beyond transitivity. Forum Math. Sigma3 (2015), e5; Donoso et al. On automorphism groups of low complexity subshifts. Ergod. Th. & Dynam. Sys.36(1) (2016), 64–95]. In this article we extend this result to a broader class proving that the automorphism group of a minimal 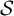 $\mathcal {S}$
-adic subshift of finite alphabet rank is virtually
$\mathcal {S}$
-adic subshift of finite alphabet rank is virtually 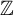 $\mathbb {Z}$
. The proof is based on a fine combinatorial analysis of the asymptotic classes in this type of subshifts, which we prove are a finite number.
$\mathbb {Z}$
. The proof is based on a fine combinatorial analysis of the asymptotic classes in this type of subshifts, which we prove are a finite number.