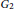Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Elduque, Alberto
and
Kochetov, Mikhail
2018.
Gradings on the simple real Lie algebras of types G2 and D4.
Journal of Algebra,
Vol. 512,
Issue. ,
p.
382.
Elduque, Alberto
2023.
Non-Associative Algebras and Related Topics.
Vol. 427,
Issue. ,
p.
287.
Guterman, A.E.
and
Zhilina, S.A.
2024.
On the lengths of Okubo algebras.
Journal of Algebra,
Vol. 653,
Issue. ,
p.
257.
Guterman, A.E.
and
Zhilina, S.A.
2024.
On the lengths of descendingly flexible and descendingly alternative algebras.
Journal of Algebra,
Vol. 651,
Issue. ,
p.
187.