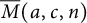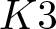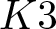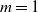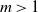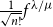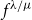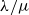Refine search
Actions for selected content:
97 results
Asymptotics for a multidimensional risk model with a random number of delayed claims and multivariate regularly varying distribution
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-30
-
- Article
- Export citation
A remark on the long-time asymptotics of global-in-time solutions for semilinear parabolic equations in
 ${\mathbb {R}^N}$
${\mathbb {R}^N}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 October 2025, pp. 1-21
-
- Article
- Export citation
Asymptotics for crank of overpartitions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-34
-
- Article
- Export citation
Modified Distribution-Free Goodness-of-Fit Test Statistic
-
- Journal:
- Psychometrika / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 01 January 2025, pp. 48-66
-
- Article
- Export citation
On Muthén’s Maximum Likelihood for Two-Level Covariance Structure Models
-
- Journal:
- Psychometrika / Volume 70 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 January 2025, pp. 147-167
-
- Article
- Export citation
On the Asymptotic Distributions of Two Statistics for Two-Level Covariance Structure Models within the Class of Elliptical Distributions
-
- Journal:
- Psychometrika / Volume 69 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 January 2025, pp. 437-457
-
- Article
- Export citation
Biases and Standard Errors of Standardized Regression Coefficients
-
- Journal:
- Psychometrika / Volume 76 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 01 January 2025, pp. 670-690
-
- Article
- Export citation
Comment on the Asymptotics of a Distribution-Free Goodness of Fit Test Statistic
-
- Journal:
- Psychometrika / Volume 80 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 01 January 2025, pp. 196-199
-
- Article
- Export citation
Asymptotically Corrected Person Fit Statistics for Multidimensional Constructs with Simple Structure and Mixed Item Types
-
- Journal:
- Psychometrika / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 January 2025, pp. 464-488
-
- Article
- Export citation
Rough multi-factor volatility for SPX and VIX options
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 16 December 2024, pp. 524-565
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tail variance and confidence of using tail conditional expectation: Analytical representation, capital adequacy, and asymptotics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 31 July 2024, pp. 346-369
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multivariate regularly varying insurance and financial risks in multidimensional risk models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1319-1342
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Toeplitz determinants with a one-cut regular potential and Fisher–Hartwig singularities I. Equilibrium measure supported on the unit circle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1431-1472
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact formulae and Turán inequalities for Vafa–Witten invariants of
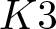 $K3$ surfaces
$K3$ surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. 845-861
-
- Article
- Export citation
2 - Basic Tools
- from Part I - Preliminaries
-
- Book:
- Random Graphs and Networks: A First Course
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 8-26
-
- Chapter
- Export citation
Giant descendant trees, matchings, and independent sets in age-biased attachment graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 299-324
- Print publication:
- June 2022
-
- Article
- Export citation
1 - Introduction
-
- Book:
- The Christoffel–Darboux Kernel for Data Analysis
- Published online:
- 31 March 2022
- Print publication:
- 07 April 2022, pp 1-6
-
- Chapter
- Export citation
Asymptotics for the number of standard tableaux of skew shape and for weighted lozenge tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 550-573
-
- Article
- Export citation
Pathwise large deviations for the rough Bergomi model: Corrigendum
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 849-850
- Print publication:
- September 2021
-
- Article
-
- You have access
- HTML
- Export citation
ASYMPTOTICS FOR SYSTEMIC RISK WITH DEPENDENT HEAVY-TAILED LOSSES
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 51 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 571-605
- Print publication:
- May 2021
-
- Article
- Export citation