Refine search
Actions for selected content:
10 results
Relations and trails in lattices of projections in W*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 23 August 2019, pp. 1189-1215
-
- Article
- Export citation
An Equivariant Theory for the Bivariant Cuntz Semigroup
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 573-598
-
- Article
- Export citation
Numerical Ranges in II1 Factors
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 16 March 2017, pp. 31-55
-
- Article
- Export citation
Von Neumann Algebras and Extensions of Inverse Semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 57-97
-
- Article
- Export citation
Schur Multipliers of Cartan Pairs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 413-440
-
- Article
- Export citation
THE LOGARITHMIC FUNCTION AND TRACE ZERO ELEMENTS IN FINITE VON NEUMANN FACTORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 290-295
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Structural results for free Araki–Woods factors and their continuous cores
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 4 / October 2010
- Published online by Cambridge University Press:
- 18 February 2010, pp. 741-767
- Print publication:
- October 2010
-
- Article
- Export citation
On completely singular von Neumann subalgebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 607-618
-
- Article
-
- You have access
- Export citation
Hochschild cohomology of II1 factors with Cartan maximal abelian subalgebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 287-295
-
- Article
-
- You have access
- Export citation
ON SOME NORMING PROPERTIES OF SUBFACTORS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 48 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 23 May 2005, pp. 499-506
-
- Article
-
- You have access
- Export citation
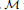 with Cartan maximal abelian self-adjoint algebra
with Cartan maximal abelian self-adjoint algebra 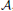 , generalizing the classical Schur multipliers of
, generalizing the classical Schur multipliers of 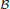 (
(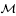 =
= 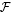 (
( and let
and let 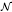 be a von Neumann subalgebra of ℳ. If
be a von Neumann subalgebra of ℳ. If 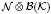 is singular in
is singular in 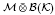 for every Hilbert space
for every Hilbert space 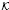 ,
, 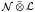 is completely singular in
is completely singular in 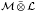 for every separable von Neumann algebra
for every separable von Neumann algebra 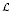 . As the second application, we prove that if
. As the second application, we prove that if 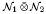 is completely singular in
is completely singular in 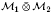 .
.