Article contents
On completely singular von Neumann subalgebras
Published online by Cambridge University Press: 23 September 2009
Abstract
Let ℳ be a von Neumann algebra acting on a Hilbert space  and let
and let 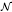 be a von Neumann subalgebra of ℳ. If
be a von Neumann subalgebra of ℳ. If 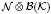 is singular in
is singular in 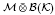 for every Hilbert space
for every Hilbert space 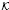 ,
, 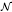 is said to be completely singular in ℳ. We prove that if
is said to be completely singular in ℳ. We prove that if 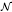 is a singular abelian von Neumann subalgebra or if
is a singular abelian von Neumann subalgebra or if 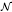 is a singular subfactor of a type-II1 factor ℳ, then
is a singular subfactor of a type-II1 factor ℳ, then 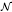 is completely singular in ℳ.
is completely singular in ℳ.  is separable, we prove that
is separable, we prove that 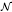 is completely singular in ℳ if and only if, for every θ∈Aut(
is completely singular in ℳ if and only if, for every θ∈Aut(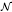 ′) such that θ(X)=X for all X ∈ ℳ′, θ(Y)=Y for all Y∈
′) such that θ(X)=X for all X ∈ ℳ′, θ(Y)=Y for all Y∈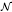 ′. As the first application, we prove that if ℳ is separable (with separable predual) and
′. As the first application, we prove that if ℳ is separable (with separable predual) and 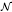 is completely singular in ℳ, then
is completely singular in ℳ, then 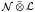 is completely singular in
is completely singular in 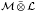 for every separable von Neumann algebra
for every separable von Neumann algebra 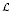 . As the second application, we prove that if
. As the second application, we prove that if 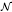 1 is a singular subfactor of a type-II1 factor ℳ1 and
1 is a singular subfactor of a type-II1 factor ℳ1 and 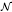 2 is a completely singular von Neumann subalgebra of ℳ2, then
2 is a completely singular von Neumann subalgebra of ℳ2, then 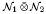 is completely singular in
is completely singular in 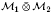 .
.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 52 , Issue 3 , October 2009 , pp. 607 - 618
- Copyright
- Copyright © Edinburgh Mathematical Society 2009
- 2
- Cited by

