Refine search
Actions for selected content:
5 results
The stack of G-zips is a Mori dream space
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-36
-
- Article
- Export citation
Examples of Non-finitely Generated Cox Rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 267-285
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
On Intrinsic Quadrics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 145-181
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
A Remark on Rationally Connected Varieties and Mori Dream Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 26 September 2018, pp. 259-263
-
- Article
- Export citation
Mori's Program for
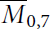 with Symmetric Divisors
with Symmetric Divisors
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 3 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 613-649
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation

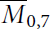 with Symmetric Divisors
with Symmetric Divisors
