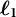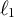Refine search
Actions for selected content:
272 results
A “broken egg” of U.S. Political Beliefs: Using response-item networks (ResIN) to measure ideological polarization
- Part of
-
- Journal:
- Network Science / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 December 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linking traditional and technological activities of daily living: Building modern, adaptable measures of daily functioning
-
- Journal:
- Journal of the International Neuropsychological Society / Volume 31 / Issue 9-10 / November 2025
- Published online by Cambridge University Press:
- 25 November 2025, pp. 721-730
-
- Article
- Export citation
Chapter 8 - Principles of Psychological Assessment
- from Section 2 - Tools and Methodologies
-
-
- Book:
- Research Methods in Mental Health
- Published online:
- 31 October 2025
- Print publication:
- 20 November 2025, pp 111-134
-
- Chapter
- Export citation
How to distinguish promotion, prevention, and treatment trials in public mental health: development and validation of the VErona-LUgano Tool (VELUT)
-
- Journal:
- Epidemiology and Psychiatric Sciences / Volume 34 / 2025
- Published online by Cambridge University Press:
- 12 November 2025, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generative Adversarial Networks for High-Dimensional Item Factor Analysis: A Deep Adversarial Learning Algorithm
-
- Journal:
- Psychometrika ,
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moving beyond symptom subtypes: testing a common dimension of lifetime OCD symptoms
-
- Journal:
- CNS Spectrums / Volume 30 / Issue 1 / 2025
- Published online by Cambridge University Press:
- 03 November 2025, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An Extended Two-Parameter Logistic Item Response Model to Handle Continuous Responses and Sparse Polytomous Responses
-
- Journal:
- Psychometrika ,
- Published online by Cambridge University Press:
- 02 September 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hamilton Rating Scale for Anxiety: exploring validity with robust measures of classical theory parameters and a rating scale model in university students
-
- Journal:
- BJPsych Open / Volume 11 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 12 August 2025, e176
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Accounting for Persistence in Tests with Linear Ballistic Accumulator Models
-
- Journal:
- Psychometrika / Volume 90 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1111-1135
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Factors associated with meal quality among schoolchildren in three Brazilian cities
-
- Journal:
- British Journal of Nutrition / Volume 133 / Issue 10 / 28 May 2025
- Published online by Cambridge University Press:
- 02 June 2025, pp. 1374-1384
- Print publication:
- 28 May 2025
-
- Article
- Export citation
Random Item Response Data Generation Using a Limited-Information Approach: Applications to Assessing Model Complexity
-
- Journal:
- Psychometrika / Volume 90 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1039-1066
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Identification and Interpretation of the Completely Oblique Rasch Bifactor Model
-
- Journal:
- Psychometrika / Volume 90 / Issue 4 / September 2025
- Published online by Cambridge University Press:
- 24 April 2025, pp. 1284-1318
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

The Hidden Measurement Crisis in Criminology
- Procedural Justice as a Case Study
-
- Published online:
- 03 March 2025
- Print publication:
- 27 March 2025
-
- Element
- Export citation
Multidimensional Latent Space Item Response Models: A Note on the Relativity of Conditional Dependence
-
- Journal:
- Psychometrika / Volume 90 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 799-826
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODGIRT: Multidimensional Dynamic Scaling of Aggregate Survey Data
-
- Journal:
- Political Analysis / Volume 33 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 17 January 2025, pp. 91-106
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adding Regularized Horseshoes to the Dynamics of Latent Variable Models
-
- Journal:
- Political Analysis / Volume 33 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 17 January 2025, pp. 171-177
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Every Trait Counts: Marginal Maximum Likelihood Estimation for Novel Multidimensional Count Data Item Response Models with Rotation or
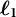 $\boldsymbol{\ell}_{\mathbf{1}}$–Regularization for Simple Structure
$\boldsymbol{\ell}_{\mathbf{1}}$–Regularization for Simple Structure
-
- Journal:
- Psychometrika / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 January 2025, pp. 304-330
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adjusting for Information Inflation Due to Local Dependency in Moderately Large Item Clusters
-
- Journal:
- Psychometrika / Volume 65 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 02 January 2025, pp. 73-91
-
- Article
- Export citation
A Note on the Identifiability of Fixed-Effect 3PL Models
-
- Journal:
- Psychometrika / Volume 81 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 01 January 2025, pp. 1093-1097
-
- Article
- Export citation
A New Concurrent Calibration Method for Nonequivalent Group Design under Nonrandom Assignment
-
- Journal:
- Psychometrika / Volume 74 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 January 2025, pp. 1-19
-
- Article
- Export citation