Refine search
Actions for selected content:
20 results
On
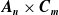 $\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
$\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 119-125
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From the Ideal Theorem to the class number
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1368-1375
- Print publication:
- December 2023
-
- Article
- Export citation
A NEW CHARACTERISATION FOR QUARTIC RESIDUACITY OF
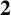 $\mathbf {2}$
$\mathbf {2}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1-6
- Print publication:
- August 2022
-
- Article
- Export citation
Distribution of Class Numbers in Continued Fraction Families of Real Quadratic Fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 20 August 2018, pp. 1193-1212
-
- Article
- Export citation
Regulators of an Infinite Family of theSimplest Quartic Function Fields
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 3 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 579-594
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
Application of the Strong Artin Conjecture to the Class Number Problem
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 6 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1201-1216
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
ON THE CLASS NUMBER AND THE FUNDAMENTAL UNIT OF THE REAL QUADRATIC FIELD

- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 359-370
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
An Explicit Treatment of Cubic Function Fields with Applications
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 4 / 01 August 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 787-807
- Print publication:
- 01 August 2010
-
- Article
-
- You have access
- Export citation
Class number formulae in the form of a product of determinants in function fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 227-238
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
AN ANALOGUE OF CIRCULAR UNITS FOR PRODUCTS OF ELLIPTIC CURVES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 47 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 27 May 2004, pp. 35-51
-
- Article
-
- You have access
- Export citation
Extreme Values of Artin L-Functions and Class Numbers
-
- Journal:
- Compositio Mathematica / Volume 136 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 04 December 2007, pp. 103-115
- Print publication:
- March 2003
-
- Article
-
- You have access
- Export citation
On the Rank of Picard Groups of Modular Varieties Attached to Orthogonal Groups
-
- Journal:
- Compositio Mathematica / Volume 133 / Issue 1 / August 2002
- Published online by Cambridge University Press:
- 04 December 2007, pp. 49-63
- Print publication:
- August 2002
-
- Article
-
- You have access
- Export citation
Exponents of Class Groups of Quadratic Function Fields over Finite Fields
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 4 / 01 December 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 398-407
- Print publication:
- 01 December 2001
-
- Article
-
- You have access
- Export citation
Class Numbers of CM-Fields with Solvable Normal Closure
-
- Journal:
- Compositio Mathematica / Volume 127 / Issue 3 / July 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 273-288
- Print publication:
- July 2001
-
- Article
-
- You have access
- Export citation
Merit Factors of Polynomials Formed by Jacobi Symbols
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 1 / 01 February 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-50
- Print publication:
- 01 February 2001
-
- Article
-
- You have access
- Export citation
The class number one problem for some non-abeliannormal CM-fields of 2-power degrees
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 76 / Issue 3 / May 1998
- Published online by Cambridge University Press:
- 01 May 1998, pp. 523-548
- Print publication:
- May 1998
-
- Article
- Export citation
Hodge cycles on the jacobian variety of the Catalan curve
-
- Journal:
- Compositio Mathematica / Volume 107 / Issue 3 / July 1997
- Published online by Cambridge University Press:
- 04 December 2007, pp. 339-353
- Print publication:
- July 1997
-
- Article
-
- You have access
- Export citation
A Completely General Rabinowi1sch Criterion for Complex Quadratic Fields
-
- Journal:
- Canadian Mathematical Bulletin / Volume 39 / Issue 1 / 01 March 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 106-110
- Print publication:
- 01 March 1996
-
- Article
-
- You have access
- Export citation
A Lower Bound for the Class Number of a Real Quadratic Field of ERD-Type
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 1 / 01 March 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 90-96
- Print publication:
- 01 March 1994
-
- Article
-
- You have access
- Export citation
On the Divisibility of the Class Numbers of Q(√−p) and Q(√−2p) by 16.
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 2 / 01 June 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 200-206
- Print publication:
- 01 June 1982
-
- Article
-
- You have access
- Export citation
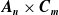

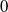
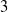
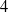

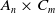
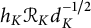
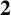
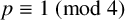
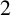
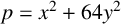
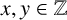
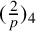
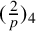
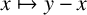
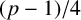
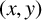
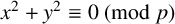
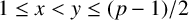
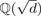
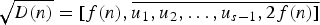
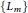

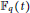
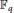

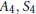
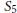
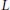
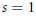

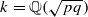 , let
, let 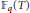
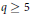
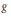
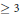
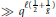
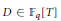
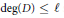
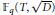
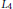
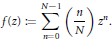
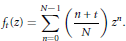
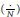
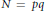
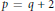
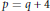
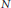
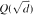 in general, but applied to greatest advantage when
in general, but applied to greatest advantage when 