
Published online by Cambridge University Press: 25 January 2012
For a real quadratic field 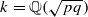 , let tk be the exact power of 2 dividing the class number hk of k and ηk the fundamental unit of k. The aim of this paper is to study tk and the value of Nk/ℚ(ηk). Various methods have been successfully applied to obtain results related to this topic. The idea of our work is to select a special circular unit ℰk of k and investigate C(k)=〈±ℰk 〉. We examine the indices [E(k):C(k)]and [C(k):CS (k)] , where E(k)is the group of units of k, and CS (k)is that of circular units of k defined by Sinnott. Then by using the Sinnott’s index formula [E(k):CS (k)]=hk, we obtain as much information about tk and Nk/ℚ (ηk)as possible.
, let tk be the exact power of 2 dividing the class number hk of k and ηk the fundamental unit of k. The aim of this paper is to study tk and the value of Nk/ℚ(ηk). Various methods have been successfully applied to obtain results related to this topic. The idea of our work is to select a special circular unit ℰk of k and investigate C(k)=〈±ℰk 〉. We examine the indices [E(k):C(k)]and [C(k):CS (k)] , where E(k)is the group of units of k, and CS (k)is that of circular units of k defined by Sinnott. Then by using the Sinnott’s index formula [E(k):CS (k)]=hk, we obtain as much information about tk and Nk/ℚ (ηk)as possible.
This work was supported by INHA UNIVERSITY Research Grant.