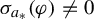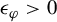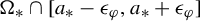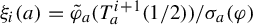Refine search
Actions for selected content:
221 results
Comparison on the criticality parameters for two supercritical branching processes with immigration in random environments
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A central limit theorem for partial transposes of multipartite Wishart matrices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-38
-
- Article
-
- You have access
- HTML
- Export citation
On the variance reduction of Hamiltonian Monte Carlo via an approximation scheme
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 19 August 2025, pp. 1-27
-
- Article
-
- You have access
- HTML
- Export citation
Limit theorems for a class of unbounded observables with an application to ‘Sampling the Lindelöf hypothesis’
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 12 August 2025, pp. 1-59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - Estimation of Population Parameters
-
- Book:
- Probability and Statistics for Data Science
- Published online:
- 19 June 2025
- Print publication:
- 03 July 2025, pp 325-389
-
- Chapter
- Export citation
Random walks and contracting elements I: deviation inequality and limit laws
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 1512-1575
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - “Fluctuation” of Intracellular Dynamics
-
- Book:
- Theoretical Biology of the Cell
- Published online:
- 05 June 2025
- Print publication:
- 19 June 2025, pp 135-175
-
- Chapter
- Export citation
3 - Moments and Measure Changes
- from Part I - Probability Theory
-
- Book:
- Derivatives Pricing
- Published online:
- 08 July 2025
- Print publication:
- 20 March 2025, pp 77-113
-
- Chapter
- Export citation
Interacting urns on directed networks with node-dependent sampling and reinforcement
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 972-996
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - Inference under Heterogeneity and Weak Dependence
-
- Book:
- Time Series for Economics and Finance
- Published online:
- 19 December 2024
- Print publication:
- 19 December 2024, pp 129-150
-
- Chapter
- Export citation
Central Limit Theorem for tensor products of free variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-33
-
- Article
- Export citation
5 - The Normal Curve
-
- Book:
- Social Behavioral Statistics
- Published online:
- 13 January 2025
- Print publication:
- 28 November 2024, pp 81-115
-
- Chapter
- Export citation
Random walks on groups and superlinear-divergent geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1403-1443
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A parameter ASIP for the quadratic family
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 663-703
- Print publication:
- March 2025
-
- Article
- Export citation
Limit theorems of occupation times of normalized binary contact path processes on lattices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 27 August 2024, pp. 44-66
- Print publication:
- March 2025
-
- Article
- Export citation
2 - Quantum probability approach to spectral analysis of growing graphs
-
-
- Book:
- Groups and Graphs, Designs and Dynamics
- Published online:
- 11 May 2024
- Print publication:
- 30 May 2024, pp 87-175
-
- Chapter
- Export citation
Depths in random recursive metric spaces
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1448-1462
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Central limit theorem for components in meandric systems through high moments
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 29 April 2024, pp. 597-610
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - Stochastic Modeling
-
- Book:
- Risk Revealed
- Published online:
- 05 April 2024
- Print publication:
- 11 April 2024, pp 94-218
-
- Chapter
- Export citation
Rigidity of pressures of Hölder potentials and the fitting of analytic functions through them
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 18 March 2024, pp. 3530-3564
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation