No CrossRef data available.
Article contents
A parameter ASIP for the quadratic family
Published online by Cambridge University Press: 24 September 2024
Abstract
Consider the quadratic family 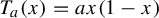 $T_a(x) = a x (1 - x)$ for
$T_a(x) = a x (1 - x)$ for 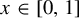 $x \in [0, 1]$ and mixing Collet–Eckmann (CE) parameters
$x \in [0, 1]$ and mixing Collet–Eckmann (CE) parameters 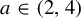 $a \in (2,4)$. For bounded
$a \in (2,4)$. For bounded 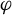 $\varphi $, set
$\varphi $, set  $\tilde \varphi _{a} := \varphi - \int \varphi \, d\mu _a$, with
$\tilde \varphi _{a} := \varphi - \int \varphi \, d\mu _a$, with 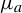 $\mu _a$ the unique acim of
$\mu _a$ the unique acim of 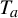 $T_a$, and put
$T_a$, and put 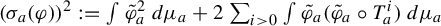 $(\sigma _a (\varphi ))^2 := \int \tilde \varphi _{a}^2 \, d\mu _a + 2 \sum _{i>0} \int \tilde \varphi _{a} (\tilde \varphi _{a} \circ T^i_{a}) \, d\mu _a$. For any mixing Misiurewicz parameter
$(\sigma _a (\varphi ))^2 := \int \tilde \varphi _{a}^2 \, d\mu _a + 2 \sum _{i>0} \int \tilde \varphi _{a} (\tilde \varphi _{a} \circ T^i_{a}) \, d\mu _a$. For any mixing Misiurewicz parameter 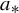 $a_{*}$, we find a positive measure set
$a_{*}$, we find a positive measure set  $\Omega _{*}$ of mixing CE parameters, containing
$\Omega _{*}$ of mixing CE parameters, containing 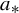 $a_{*}$ as a Lebesgue density point, such that for any Hölder
$a_{*}$ as a Lebesgue density point, such that for any Hölder  $\varphi $ with
$\varphi $ with 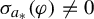 $\sigma _{a_{*}}(\varphi )\ne 0$, there exists
$\sigma _{a_{*}}(\varphi )\ne 0$, there exists 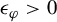 $\epsilon _\varphi>0$ such that, for normalized Lebesgue measure on
$\epsilon _\varphi>0$ such that, for normalized Lebesgue measure on 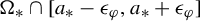 $\Omega _{*}\cap [a_{*}-\epsilon _\varphi , a_{*}+\epsilon _\varphi ]$, the functions
$\Omega _{*}\cap [a_{*}-\epsilon _\varphi , a_{*}+\epsilon _\varphi ]$, the functions 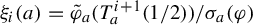 $\xi _i(a)=\tilde \varphi _a(T_a^{i+1}(1/2))/\sigma _a (\varphi )$ satisfy an almost sure invariance principle (ASIP) for any error exponent
$\xi _i(a)=\tilde \varphi _a(T_a^{i+1}(1/2))/\sigma _a (\varphi )$ satisfy an almost sure invariance principle (ASIP) for any error exponent 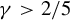 $\gamma>2/5$. (In particular, the Birkhoff sums satisfy this ASIP.) Our argument goes along the lines of Schnellmann’s proof for piecewise expanding maps. We need to introduce a variant of Benedicks–Carleson parameter exclusion and to exploit fractional response and uniform exponential decay of correlations from Baladi et al [Whitney–Hölder continuity of the SRB measure for transversal families of smooth unimodal maps. Invent. Math. 201 (2015), 773–844].
$\gamma>2/5$. (In particular, the Birkhoff sums satisfy this ASIP.) Our argument goes along the lines of Schnellmann’s proof for piecewise expanding maps. We need to introduce a variant of Benedicks–Carleson parameter exclusion and to exploit fractional response and uniform exponential decay of correlations from Baladi et al [Whitney–Hölder continuity of the SRB measure for transversal families of smooth unimodal maps. Invent. Math. 201 (2015), 773–844].
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press


