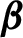 $\boldsymbol{\beta} $
-transformation with a hole at
$\boldsymbol{\beta} $
-transformation with a hole at
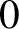 $0$
$0$
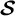 $\mathcal{\textbf{S}}$
-adic characterization of minimal ternary dendric shifts
$\mathcal{\textbf{S}}$
-adic characterization of minimal ternary dendric shifts
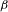 $\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
$\unicode[STIX]{x1D6FD}$-transformation with a hole at 0