Article contents
GAPS IN THE THUE–MORSE WORD
Published online by Cambridge University Press: 25 January 2022
Abstract
The Thue–Morse sequence is a prototypical automatic sequence found in diverse areas of mathematics, and in computer science. We study occurrences of factors w within this sequence, or more precisely, the sequence of gaps between consecutive occurrences. This gap sequence is morphic; we prove that it is not automatic as soon as the length of w is at least 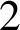 $2$, thereby answering a question by J. Shallit in the affirmative. We give an explicit method to compute the discrepancy of the number of occurrences of the block
$2$, thereby answering a question by J. Shallit in the affirmative. We give an explicit method to compute the discrepancy of the number of occurrences of the block 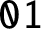 $\mathtt {01}$ in the Thue–Morse sequence. We prove that the sequence of discrepancies is the sequence of output sums of a certain base-
$\mathtt {01}$ in the Thue–Morse sequence. We prove that the sequence of discrepancies is the sequence of output sums of a certain base-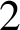 $2$ transducer.
$2$ transducer.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 114 , Issue 1 , February 2023 , pp. 110 - 144
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Michael Coons
The author was supported by the Austrian Science Fund (FWF), project F5502-N26, which is a part of the Special Research Program ‘Quasi Monte Carlo methods: Theory and Applications’, and by the FWF-ANR project ArithRand, grant numbers I4945-N and ANR-20-CE91-0006.
References
- 1
- Cited by


