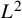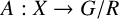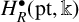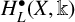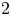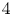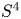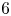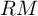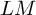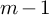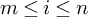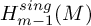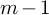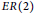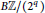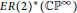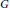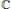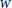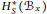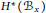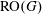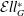Refine search
Actions for selected content:
28 results
VORONOI COMPLEXES IN HIGHER DIMENSIONS, COHOMOLOGY OF
 $GL_N(\mathbb{Z} )$ FOR
$GL_N(\mathbb{Z} )$ FOR  $N\geqslant 8$ AND THE TRIVIALITY OF
$N\geqslant 8$ AND THE TRIVIALITY OF  $K_8(\mathbb{Z} )$
$K_8(\mathbb{Z} )$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-26
-
- Article
- Export citation
Reflexive homology and involutive Hochschild homology as equivariant Loday constructions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant Segre and Verlinde invariants for Quot schemes
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Infinite flags and Schubert polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological structures of large-scale interacting systems via uniform functions and forms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e107
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED ACTIONS ON COHOMOLOGIES AND BIMODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 187-238
- Print publication:
- October 2024
-
- Article
- Export citation
Chern classes in equivariant bordism
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Realization of GKM fibrations and new examples of Hamiltonian non-Kähler actions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 24 August 2023, pp. 2149-2190
- Print publication:
- October 2023
-
- Article
- Export citation
ON MORPHISMS KILLING WEIGHTS AND STABLE HUREWICZ-TYPE THEOREMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 24 October 2022, pp. 521-556
- Print publication:
- March 2024
-
- Article
- Export citation
Equivariant cohomology of torus orbifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 299-328
- Print publication:
- April 2022
-
- Article
- Export citation
Symmetric Products of Equivariantly Formal Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 272-281
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
The ER(z)-cohomology of Bℤ/(2q ) and ℂℙn
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 1 / 01 February 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 191-217
- Print publication:
- 01 February 2018
-
- Article
-
- You have access
- Export citation
Segal's Spectral Sequence in Twisted Equivariant K-theory for Proper and Discrete Actions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 January 2018, pp. 121-150
-
- Article
- Export citation
Springer's Weyl Group Representation via Localization
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 3 / 01 September 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 478-483
- Print publication:
- 01 September 2017
-
- Article
-
- You have access
- Export citation
Generalized Equivariant Cohomology and Stratifications
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 3 / 01 September 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 483-496
- Print publication:
- 01 September 2016
-
- Article
-
- You have access
- Export citation
On the homotopy groups of the self-equivalences of linear spheres
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 26 October 2015, pp. 445-462
-
- Article
- Export citation
EQUIVARIANT ANDERSON DUALITY AND MACKEY FUNCTOR DUALITY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 649-676
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
The Equivariant Cohomology Rings of Peterson Varieties in All Lie Types
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 1 / 01 March 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 80-90
- Print publication:
- 01 March 2015
-
- Article
-
- You have access
- Export citation
THE GROMOV-LAWSON-ROSENBERG CONJECTURE FOR THE SEMI-DIHEDRAL GROUP OF ORDER 16
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 365-386
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
The elliptic Weyl character formula
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 1196-1234
- Print publication:
- July 2014
-
- Article
- Export citation