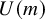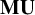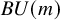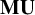Introduction
Complex cobordism
![]() $\mathbf {MU}$
is arguably the most important cohomology theory in algebraic topology. It represents the bordism theory of stably almost complex manifolds, and it is the universal complex oriented cohomology theory; via Quillen’s celebrated theorem [Reference Quillen13],
$\mathbf {MU}$
is arguably the most important cohomology theory in algebraic topology. It represents the bordism theory of stably almost complex manifolds, and it is the universal complex oriented cohomology theory; via Quillen’s celebrated theorem [Reference Quillen13],
![]() $\mathbf {MU}$
is the entry gate for the theory of formal group laws into stable homotopy theory and thus the cornerstone of chromatic stable homotopy theory.
$\mathbf {MU}$
is the entry gate for the theory of formal group laws into stable homotopy theory and thus the cornerstone of chromatic stable homotopy theory.
Tom Dieck’s homotopical equivariant bordism
![]() $\mathbf {MU}_G$
[Reference tom Dieck17], defined with the help of equivariant Thom spaces, strives to be the legitimate equivariant refinement of complex cobordism, for compact Lie groups G. The theory
$\mathbf {MU}_G$
[Reference tom Dieck17], defined with the help of equivariant Thom spaces, strives to be the legitimate equivariant refinement of complex cobordism, for compact Lie groups G. The theory
![]() $\mathbf {MU}_G$
is the universal equivariantly complex oriented theory, and for abelian compact Lie groups, the coefficient ring
$\mathbf {MU}_G$
is the universal equivariantly complex oriented theory, and for abelian compact Lie groups, the coefficient ring
![]() $\mathbf {MU}_G^*$
carries the universal G-equivariant formal group law [Reference Hausmann7]. Homotopical equivariant bordism receives a homomorphism from the geometrically defined equivariant bordism theory; due to the lack of equivariant transversality, this homomorphism is not an isomorphism for nontrivial groups. In general, the equivariant bordism ring
$\mathbf {MU}_G^*$
carries the universal G-equivariant formal group law [Reference Hausmann7]. Homotopical equivariant bordism receives a homomorphism from the geometrically defined equivariant bordism theory; due to the lack of equivariant transversality, this homomorphism is not an isomorphism for nontrivial groups. In general, the equivariant bordism ring
![]() $\mathbf {MU}^*_G$
is still largely mysterious; the purpose of this paper is to elucidate its structure for unitary groups and for products of unitary groups.
$\mathbf {MU}^*_G$
is still largely mysterious; the purpose of this paper is to elucidate its structure for unitary groups and for products of unitary groups.
Chern classes are important characteristic classes for complex vector bundles that were originally introduced in singular cohomology. Conner and Floyd [Reference Conner and Floyd4, Corollary 8.3] constructed Chern classes for complex vector bundles in complex cobordism; in the universal cases, these yield classes
![]() $c_k\in \mathbf {MU}^{2 k}(B U(m))$
that are nowadays referred to as Conner–Floyd–Chern classes. Conner and Floyd’s construction works in much the same way for any complex oriented cohomology theory (see [Reference Adams1, Part II, Lemma 4.3]); in singular cohomology, it reduces to the classical Chern classes. The purpose of this note is to define and study Chern classes in
$c_k\in \mathbf {MU}^{2 k}(B U(m))$
that are nowadays referred to as Conner–Floyd–Chern classes. Conner and Floyd’s construction works in much the same way for any complex oriented cohomology theory (see [Reference Adams1, Part II, Lemma 4.3]); in singular cohomology, it reduces to the classical Chern classes. The purpose of this note is to define and study Chern classes in
![]() $U(m)$
-equivariant homotopical bordism
$U(m)$
-equivariant homotopical bordism
![]() $\mathbf {MU}^*_{U(m)}$
that map to the Conner–Floyd–Chern classes under tom Dieck’s bundling homomorphism [Reference tom Dieck17, Proposition 1.2]. Our classes satisfy the analogous formal properties as their classical counterparts, including the equivariant refinement of the Whitney sum formula; see Theorem 1.4. Despite the many formal similarities, there are crucial qualitative differences compared to Chern classes in complex oriented cohomology theories: Our Chern classes are not characterized by their restriction to the maximal torus, and some of our Chern classes are zero-divisors; see Remark 1.2.
$\mathbf {MU}^*_{U(m)}$
that map to the Conner–Floyd–Chern classes under tom Dieck’s bundling homomorphism [Reference tom Dieck17, Proposition 1.2]. Our classes satisfy the analogous formal properties as their classical counterparts, including the equivariant refinement of the Whitney sum formula; see Theorem 1.4. Despite the many formal similarities, there are crucial qualitative differences compared to Chern classes in complex oriented cohomology theories: Our Chern classes are not characterized by their restriction to the maximal torus, and some of our Chern classes are zero-divisors; see Remark 1.2.
We will use our Chern classes and the splitting of [Reference Schwede15] to prove new structure results about the equivariant bordism rings
![]() $\mathbf {MU}^*_{U(m)}$
for unitary groups or more generally for products of unitary groups. To put this into context, we recall that in the special case when G is an abelian compact Lie group, the graded ring
$\mathbf {MU}^*_{U(m)}$
for unitary groups or more generally for products of unitary groups. To put this into context, we recall that in the special case when G is an abelian compact Lie group, the graded ring
![]() $\mathbf {MU}^*_G$
is concentrated in even degrees and free as a module over the nonequivariant cobordism ring
$\mathbf {MU}^*_G$
is concentrated in even degrees and free as a module over the nonequivariant cobordism ring
![]() $\mathbf {MU}^*$
[Reference Comezaña and May3, Theorem 5.3], [Reference Löffler10], and the bundling homomorphism
$\mathbf {MU}^*$
[Reference Comezaña and May3, Theorem 5.3], [Reference Löffler10], and the bundling homomorphism
![]() $\mathbf {MU}^*_G\to \mathbf {MU}^*(B G)$
is completion at the augmentation ideal of
$\mathbf {MU}^*_G\to \mathbf {MU}^*(B G)$
is completion at the augmentation ideal of
![]() $\mathbf {MU}^*_G$
[Reference Comezaña, May and May2, Theorem 1.1], [Reference Löffler11]. For nonabelian compact Lie groups G, however, the equivariant bordism rings
$\mathbf {MU}^*_G$
[Reference Comezaña, May and May2, Theorem 1.1], [Reference Löffler11]. For nonabelian compact Lie groups G, however, the equivariant bordism rings
![]() $\mathbf {MU}^*_G$
are still largely mysterious.
$\mathbf {MU}^*_G$
are still largely mysterious.
The main result of this note is the following:
Theorem. Let
![]() $m\geq 1$
be a natural number.
$m\geq 1$
be a natural number.
-
(i) The sequence of Chern classes
 $c_m^{(m)},c_{m-1}^{(m)},\dots ,c_1^{(m)}$
is a regular sequence that generates the augmentation ideal of the graded-commutative ring
$c_m^{(m)},c_{m-1}^{(m)},\dots ,c_1^{(m)}$
is a regular sequence that generates the augmentation ideal of the graded-commutative ring
 $\mathbf {MU}^*_{U(m)}$
.
$\mathbf {MU}^*_{U(m)}$
. -
(ii) The completion of
 $\mathbf {MU}_{U(m)}^*$
at the augmentation ideal is a graded
$\mathbf {MU}_{U(m)}^*$
at the augmentation ideal is a graded
 $\mathbf {MU}^*$
-power series algebra in the above Chern classes.
$\mathbf {MU}^*$
-power series algebra in the above Chern classes. -
(iii) The bundling homomorphism
 $\mathbf {MU}_{U(m)}^*\to \mathbf {MU}^*(B U(m))$
extends to an isomorphism from the completion at the augmentation ideal.
$\mathbf {MU}_{U(m)}^*\to \mathbf {MU}^*(B U(m))$
extends to an isomorphism from the completion at the augmentation ideal. $$\begin{align*}( \mathbf{MU}_{U(m)}^*)^\wedge_I \ \to \ \mathbf{MU}^*(BU(m)) \end{align*}$$
$$\begin{align*}( \mathbf{MU}_{U(m)}^*)^\wedge_I \ \to \ \mathbf{MU}^*(BU(m)) \end{align*}$$
We prove this result as a special case of Theorem 2.2 below; the more general version applies to products of unitary groups. As we explain in Remark 2.4, the regularity of the Chern classes also implies that the Greenlees–May local homology spectral sequence converging to
![]() $\mathbf {MU}^*(BU(m))$
degenerates because the relevant local homology groups vanish in positive degrees. As another application we use the Chern classes in equivariant bordism to give a reformulation and self-contained proof of work of Greenlees–May [Reference Greenlees and May6] and La Vecchia [Reference La Vecchia8] on the completion theorem for
$\mathbf {MU}^*(BU(m))$
degenerates because the relevant local homology groups vanish in positive degrees. As another application we use the Chern classes in equivariant bordism to give a reformulation and self-contained proof of work of Greenlees–May [Reference Greenlees and May6] and La Vecchia [Reference La Vecchia8] on the completion theorem for
![]() $\mathbf {MU}_G$
; see Theorem 3.5.
$\mathbf {MU}_G$
; see Theorem 3.5.
1 Equivariant
 $\mathbf {MU}$
-Chern classes
$\mathbf {MU}$
-Chern classes
In this section, we introduce the Chern classes in
![]() $U(m)$
-equivariant homotopical bordism; see Definition 1.1. We establish their basic properties in Theorem 1.4, including a Whitney sum formula and the fact that the bundling homomorphism takes our Chern classes to the Conner–Floyd–Chern classes in
$U(m)$
-equivariant homotopical bordism; see Definition 1.1. We establish their basic properties in Theorem 1.4, including a Whitney sum formula and the fact that the bundling homomorphism takes our Chern classes to the Conner–Floyd–Chern classes in
![]() $\mathbf {MU}$
-cohomology.
$\mathbf {MU}$
-cohomology.
We begin by fixing our notation. For a compact Lie group G, we write
![]() $\mathbf {MU}_G$
for the G-equivariant homotopical bordism spectrum introduced by tom Dieck [Reference tom Dieck17]. For our purposes, it is highly relevant that the theories
$\mathbf {MU}_G$
for the G-equivariant homotopical bordism spectrum introduced by tom Dieck [Reference tom Dieck17]. For our purposes, it is highly relevant that the theories
![]() $\mathbf {MU}_G$
for varying compact Lie groups G assemble into a global stable homotopy type; see [Reference Schwede14, Example 6.1.53]. For an integer n, we write
$\mathbf {MU}_G$
for varying compact Lie groups G assemble into a global stable homotopy type; see [Reference Schwede14, Example 6.1.53]. For an integer n, we write
![]() $\mathbf {MU}_G^n=\pi _{-n}^G(\mathbf {MU})$
for the G-equivariant coefficient group in cohomological degree n.
$\mathbf {MU}_G^n=\pi _{-n}^G(\mathbf {MU})$
for the G-equivariant coefficient group in cohomological degree n.
Since
![]() $\mathbf {MU}$
comes with the structure of a global ring spectrum, it supports graded-commutative multiplications on
$\mathbf {MU}$
comes with the structure of a global ring spectrum, it supports graded-commutative multiplications on
![]() $\mathbf {MU}_G^*$
, as well as external multiplication pairings
$\mathbf {MU}_G^*$
, as well as external multiplication pairings
for all pairs of compact Lie groups G and K. We write
![]() $\nu _k$
for the tautological representation of the unitary group
$\nu _k$
for the tautological representation of the unitary group
![]() $U(k)$
on
$U(k)$
on
![]() $\mathbb C^k$
; we denote its Euler class by
$\mathbb C^k$
; we denote its Euler class by
compare [Reference tom Dieck17, page 347]. We write
![]() $U(k,m-k)$
for the block subgroup of
$U(k,m-k)$
for the block subgroup of
![]() $U(m)$
consisting of matrices of the form
$U(m)$
consisting of matrices of the form
![]() $(\begin {smallmatrix}A & 0 \\ 0 & B \end {smallmatrix})$
for
$(\begin {smallmatrix}A & 0 \\ 0 & B \end {smallmatrix})$
for
![]() $(A,B)\in U(k)\times U(m-k)$
. We write
$(A,B)\in U(k)\times U(m-k)$
. We write
![]() $\operatorname {\mathrm {tr}}_{U(k,m-k)}^{U(m)}:\mathbf {MU}_{U(k,m-k)}^*\to \mathbf {MU}_{U(m)}^*$
for the transfer associated to the inclusion
$\operatorname {\mathrm {tr}}_{U(k,m-k)}^{U(m)}:\mathbf {MU}_{U(k,m-k)}^*\to \mathbf {MU}_{U(m)}^*$
for the transfer associated to the inclusion
![]() $U(k,m-k)\to U(m)$
; see, for example, [Reference Schwede14, Construction 3.2.22].
$U(k,m-k)\to U(m)$
; see, for example, [Reference Schwede14, Construction 3.2.22].
Definition 1.1. For
![]() $0\leq k\leq m$
, the k-th Chern class in equivariant complex bordism is the class
$0\leq k\leq m$
, the k-th Chern class in equivariant complex bordism is the class
where
![]() $1_{m-k}\in \mathbf {MU}_{U(m-k)}^0$
is the multiplicative unit. We also set
$1_{m-k}\in \mathbf {MU}_{U(m-k)}^0$
is the multiplicative unit. We also set
![]() $c_k^{(m)} =0$
for
$c_k^{(m)} =0$
for
![]() $k>m$
.
$k>m$
.
In the extreme cases
![]() $k=0$
and
$k=0$
and
![]() $k=m$
, we recover familiar classes: Since
$k=m$
, we recover familiar classes: Since
![]() $e_0$
is the multiplicative unit in the nonequivariant cobordism ring
$e_0$
is the multiplicative unit in the nonequivariant cobordism ring
![]() $\mathbf {MU}^*$
, the class
$\mathbf {MU}^*$
, the class
![]() $c_0^{(m)}=1_m$
is the multiplicative unit in
$c_0^{(m)}=1_m$
is the multiplicative unit in
![]() $\mathbf {MU}_{U(m)}^0$
. In the other extreme,
$\mathbf {MU}_{U(m)}^0$
. In the other extreme,
![]() $c_m^{(m)}=e_m=e(\nu _m)$
is the Euler class of the tautological
$c_m^{(m)}=e_m=e(\nu _m)$
is the Euler class of the tautological
![]() $U(m)$
-representation. As we will show in Theorem 1.4 (ii), the classes
$U(m)$
-representation. As we will show in Theorem 1.4 (ii), the classes
![]() $c_k^{(m)}$
are compatible in m under restriction to smaller unitary groups.
$c_k^{(m)}$
are compatible in m under restriction to smaller unitary groups.
Remark 1.2. We alert the reader that the restriction homomorphism
is not injective for
![]() $m\geq 2$
, where
$m\geq 2$
, where
![]() $T^m$
denotes a maximal torus in
$T^m$
denotes a maximal torus in
![]() $U(m)$
. So the Chern classes in
$U(m)$
. So the Chern classes in
![]() $\mathbf {MU}^*_{U(m)}$
are not characterized by their restrictions to the maximal torus – in contrast to the nonequivariant situation for complex oriented cohomology theories. To show this we let N denote the maximal torus normalizer inside
$\mathbf {MU}^*_{U(m)}$
are not characterized by their restrictions to the maximal torus – in contrast to the nonequivariant situation for complex oriented cohomology theories. To show this we let N denote the maximal torus normalizer inside
![]() $U(m)$
. The class
$U(m)$
. The class
has infinite order because the
![]() $U(m)$
-geometric fixed point map takes it to the multiplicative unit; in particular, this class is nonzero. The double coset formula [Reference Lewis, May and Steinberger9, IV Corollary 6.7 (i)]
$U(m)$
-geometric fixed point map takes it to the multiplicative unit; in particular, this class is nonzero. The double coset formula [Reference Lewis, May and Steinberger9, IV Corollary 6.7 (i)]
implies that the class
![]() $ 1- \operatorname {\mathrm {tr}}_N^{U(m)}(1)$
lies in the kernel of the restriction homomorphism
$ 1- \operatorname {\mathrm {tr}}_N^{U(m)}(1)$
lies in the kernel of the restriction homomorphism
![]() $\operatorname {\mathrm {res}}^{U(m)}_{T^m}:\mathbf {MU}^0_{U(m)}\to \mathbf {MU}^0_{T^m}$
.
$\operatorname {\mathrm {res}}^{U(m)}_{T^m}:\mathbf {MU}^0_{U(m)}\to \mathbf {MU}^0_{T^m}$
.
Moreover, the Chern class
![]() $c_1^{(2)}$
is a zero-divisor in the ring
$c_1^{(2)}$
is a zero-divisor in the ring
![]() $\mathbf {MU}^*_{U(2)}$
, also in stark contrast to Chern classes in complex oriented cohomology theories. Indeed, reciprocity for restriction and transfers [Reference Schwede14, Corollary 3.5.17 (v)] yields the relation
$\mathbf {MU}^*_{U(2)}$
, also in stark contrast to Chern classes in complex oriented cohomology theories. Indeed, reciprocity for restriction and transfers [Reference Schwede14, Corollary 3.5.17 (v)] yields the relation
 $$ \begin{align*} c_1^{(2)}\cdot (1-\operatorname{\mathrm{tr}}_N^{U(2)}(1)) \ &= \ \operatorname{\mathrm{tr}}_{U(1,1)}^{U(2)}(e_1\times 1)\cdot (1-\operatorname{\mathrm{tr}}_N^{U(2)}(1)) \\ &= \ \operatorname{\mathrm{tr}}_{U(1,1)}^{U(2)}((e_1\times 1)\cdot \operatorname{\mathrm{res}}^{U(2)}_{U(1,1)}(1-\operatorname{\mathrm{tr}}_N^{U(2)}(1))) \ = \ 0 . \end{align*} $$
$$ \begin{align*} c_1^{(2)}\cdot (1-\operatorname{\mathrm{tr}}_N^{U(2)}(1)) \ &= \ \operatorname{\mathrm{tr}}_{U(1,1)}^{U(2)}(e_1\times 1)\cdot (1-\operatorname{\mathrm{tr}}_N^{U(2)}(1)) \\ &= \ \operatorname{\mathrm{tr}}_{U(1,1)}^{U(2)}((e_1\times 1)\cdot \operatorname{\mathrm{res}}^{U(2)}_{U(1,1)}(1-\operatorname{\mathrm{tr}}_N^{U(2)}(1))) \ = \ 0 . \end{align*} $$
One can also show that the class
![]() $1-\operatorname {\mathrm {tr}}_N^{U(2)}(1)$
is infinitely divisible by the Euler class
$1-\operatorname {\mathrm {tr}}_N^{U(2)}(1)$
is infinitely divisible by the Euler class
![]() $e_2=c_2^{(2)}$
; so it is also in the kernel of the completion map at the ideal
$e_2=c_2^{(2)}$
; so it is also in the kernel of the completion map at the ideal
![]() $(e_2)$
.
$(e_2)$
.
The Chern class
![]() $c_k^{(m)}$
is defined as a transfer; so identifying its restriction to a subgroup of
$c_k^{(m)}$
is defined as a transfer; so identifying its restriction to a subgroup of
![]() $U(m)$
involves a double coset formula. The following double coset formula will take care of all cases we need in this paper; it ought to be well-known to experts, but I do not know a reference. The case
$U(m)$
involves a double coset formula. The following double coset formula will take care of all cases we need in this paper; it ought to be well-known to experts, but I do not know a reference. The case
![]() $l=1$
is established in [Reference Symonds16, Lemma 4.2]; see also [Reference Schwede14, Example 3.4.13]. The double coset space
$l=1$
is established in [Reference Symonds16, Lemma 4.2]; see also [Reference Schwede14, Example 3.4.13]. The double coset space
![]() $U(i,j)\backslash U(m)/ U(k,l)$
is discussed at various places in the literature, for example, [Reference Matsuki12, Example 3], but I have not seen the resulting double coset formula spelled out.
$U(i,j)\backslash U(m)/ U(k,l)$
is discussed at various places in the literature, for example, [Reference Matsuki12, Example 3], but I have not seen the resulting double coset formula spelled out.
Proposition 1.3 (Double coset formula).
Let
![]() $i,j,k,l$
be positive natural numbers such that
$i,j,k,l$
be positive natural numbers such that
![]() $i+j=k+l$
. Then
$i+j=k+l$
. Then
 $$\begin{align*}\operatorname{\mathrm{res}}^{U(i+j)}_{U(i,j)}\circ\operatorname{\mathrm{tr}}_{U(k,l)}^{U(k+l)} \ = \sum_{0,k-j\leq d\leq i,k}\, \operatorname{\mathrm{tr}}_{U(d,i-d,k-d,j-k+d)}^{U(i,j)}\circ\gamma_d^*\circ \operatorname{\mathrm{res}}^{U(k,l)}_{U(d,k-d,i-d,l-i+d)}\ ,\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{res}}^{U(i+j)}_{U(i,j)}\circ\operatorname{\mathrm{tr}}_{U(k,l)}^{U(k+l)} \ = \sum_{0,k-j\leq d\leq i,k}\, \operatorname{\mathrm{tr}}_{U(d,i-d,k-d,j-k+d)}^{U(i,j)}\circ\gamma_d^*\circ \operatorname{\mathrm{res}}^{U(k,l)}_{U(d,k-d,i-d,l-i+d)}\ ,\end{align*}$$
where
![]() $\gamma _d\in U(i+j)$
is the permutation matrix of the shuffle permutation
$\gamma _d\in U(i+j)$
is the permutation matrix of the shuffle permutation
![]() $\chi _d\in \Sigma _{i+j}$
given by
$\chi _d\in \Sigma _{i+j}$
given by
 $$ \begin{align*} \chi_d(a) \ = \ \begin{cases} a & \text{ for } 1\leq a\leq d,\\a-d+i& \textit{ for } d+1\leq a\leq k,\\a+d-k& \textit{ for } k+1\leq a\leq k+i-d \textit{ and}\\a & \textit{ for } a> k+i-d. \end{cases} \end{align*} $$
$$ \begin{align*} \chi_d(a) \ = \ \begin{cases} a & \text{ for } 1\leq a\leq d,\\a-d+i& \textit{ for } d+1\leq a\leq k,\\a+d-k& \textit{ for } k+1\leq a\leq k+i-d \textit{ and}\\a & \textit{ for } a> k+i-d. \end{cases} \end{align*} $$
Proof. We refer to [Reference Lewis, May and Steinberger9, IV Theorem 6.3] or [Reference Schwede14, Theorem 3.4.9] for the general double coset formula for
![]() $\operatorname {\mathrm {res}}^G_K\circ \operatorname {\mathrm {tr}}_H^G$
for two closed subgroups H and K of a compact Lie group G; we need to specialize it to the situation at hand. We first consider a matrix
$\operatorname {\mathrm {res}}^G_K\circ \operatorname {\mathrm {tr}}_H^G$
for two closed subgroups H and K of a compact Lie group G; we need to specialize it to the situation at hand. We first consider a matrix
![]() $A\in U(m)$
such that the center Z of
$A\in U(m)$
such that the center Z of
![]() $U(i,j)$
is not contained in the
$U(i,j)$
is not contained in the
![]() $U(i,j)$
-stabilizer
$U(i,j)$
-stabilizer
of the coset
![]() $A\cdot U(k,l)$
. Then
$A\cdot U(k,l)$
. Then
![]() $S_A\cap Z$
is a proper subgroup of the center Z of
$S_A\cap Z$
is a proper subgroup of the center Z of
![]() $U(i,j)$
, which is isomorphic to
$U(i,j)$
, which is isomorphic to
![]() $U(1)\times U(1)$
. So
$U(1)\times U(1)$
. So
![]() $S_A\cap Z$
has strictly smaller dimension than Z. Since the center of
$S_A\cap Z$
has strictly smaller dimension than Z. Since the center of
![]() $U(i,j)$
is contained in the normalizer of
$U(i,j)$
is contained in the normalizer of
![]() $S_A$
, we conclude that the group
$S_A$
, we conclude that the group
![]() $S_A$
has an infinite Weyl group inside
$S_A$
has an infinite Weyl group inside
![]() $U(i,j)$
. All summands in the double coset formula indexed by such points then involve transfers with infinite Weyl groups, and hence they vanish.
$U(i,j)$
. All summands in the double coset formula indexed by such points then involve transfers with infinite Weyl groups, and hence they vanish.
So all nontrivial contributions to the double coset formula stem from double cosets
![]() $U(i,j)\cdot A\cdot U(k,l)$
such that
$U(i,j)\cdot A\cdot U(k,l)$
such that
![]() $S_A$
contains the center of
$S_A$
contains the center of
![]() $U(i,j)$
. In particular, the matrix
$U(i,j)$
. In particular, the matrix
![]() $ \left ( \begin {smallmatrix} - E_i & 0 \\ 0 & E_j \end {smallmatrix} \right )$
then belongs to
$ \left ( \begin {smallmatrix} - E_i & 0 \\ 0 & E_j \end {smallmatrix} \right )$
then belongs to
![]() $S_A$
. We write
$S_A$
. We write
![]() $L=A\cdot (\mathbb C^k\oplus 0^l)$
, a complex k-plane in
$L=A\cdot (\mathbb C^k\oplus 0^l)$
, a complex k-plane in
![]() $\mathbb C^{k+l}$
; we consider
$\mathbb C^{k+l}$
; we consider
![]() $x\in \mathbb C^i$
and
$x\in \mathbb C^i$
and
![]() $y\in \mathbb C^j$
such that
$y\in \mathbb C^j$
such that
![]() $(x,y)\in L$
. Because
$(x,y)\in L$
. Because
![]() $ \left ( \begin {smallmatrix} - E_i & 0 \\ 0 & E_j \end {smallmatrix} \right )\cdot L=L$
, we deduce that
$ \left ( \begin {smallmatrix} - E_i & 0 \\ 0 & E_j \end {smallmatrix} \right )\cdot L=L$
, we deduce that
![]() $(-x,y)\in L$
. Since
$(-x,y)\in L$
. Since
![]() $(x,y)$
and
$(x,y)$
and
![]() $(-x,y)$
belong to L, so do the vectors
$(-x,y)$
belong to L, so do the vectors
![]() $(x,0)$
and
$(x,0)$
and
![]() $(y,0)$
. We have thus shown that the k-plane
$(y,0)$
. We have thus shown that the k-plane
![]() $L=A\cdot (\mathbb C^k\oplus 0^l)$
is spanned by the intersections
$L=A\cdot (\mathbb C^k\oplus 0^l)$
is spanned by the intersections
We organize the cosets with this property by the dimension of the first intersection: we define
![]() $M_d$
as the closed subspace of
$M_d$
as the closed subspace of
![]() $U(m)/U(k,l)$
consisting of those cosets
$U(m)/U(k,l)$
consisting of those cosets
![]() $A\cdot U(k,l)$
such that
$A\cdot U(k,l)$
such that
If
![]() $M_d$
is nonempty, we must have
$M_d$
is nonempty, we must have
![]() $0, k-j\leq d\leq i,k$
. The group
$0, k-j\leq d\leq i,k$
. The group
![]() $U(i,j)$
acts transitively on
$U(i,j)$
acts transitively on
![]() $M_d$
, and the coset
$M_d$
, and the coset
![]() $\gamma _d\cdot U(k,l)$
belongs to
$\gamma _d\cdot U(k,l)$
belongs to
![]() $M_d$
; so
$M_d$
; so
![]() $M_d$
is the
$M_d$
is the
![]() $U(i,j)$
-orbit type manifold of
$U(i,j)$
-orbit type manifold of
![]() $U(m)/U(k,l)$
for the conjugacy class of
$U(m)/U(k,l)$
for the conjugacy class of
The corresponding orbit space
![]() $U(i,j)\backslash M_d=U(i,j)\cdot \gamma _d\cdot U(k,l)$
is a single point inside the double coset space, so its internal Euler characteristic is 1. This orbit type thus contributes the summand
$U(i,j)\backslash M_d=U(i,j)\cdot \gamma _d\cdot U(k,l)$
is a single point inside the double coset space, so its internal Euler characteristic is 1. This orbit type thus contributes the summand
to the double coset formula.
In [Reference Conner and Floyd4, Corollary 8.3], Conner and Floyd define Chern classes for complex vector bundles in the nonequivariant
![]() $\mathbf {MU}$
-cohomology rings. In the universal cases, these yield classes
$\mathbf {MU}$
-cohomology rings. In the universal cases, these yield classes
![]() $c_k\in \mathbf {MU}^{2 k}(B U(m))$
that are nowadays referred to as Conner–Floyd–Chern classes. The next theorem spells out the key properties of our Chern classes
$c_k\in \mathbf {MU}^{2 k}(B U(m))$
that are nowadays referred to as Conner–Floyd–Chern classes. The next theorem spells out the key properties of our Chern classes
![]() $c_k^{(m)}$
; parts (i), (ii) and (iii) roughly say that all the familiar structural properties of the Conner–Floyd–Chern classes in
$c_k^{(m)}$
; parts (i), (ii) and (iii) roughly say that all the familiar structural properties of the Conner–Floyd–Chern classes in
![]() $\mathbf {MU}^*(B U(m))$
already hold for our Chern classes in
$\mathbf {MU}^*(B U(m))$
already hold for our Chern classes in
![]() $U(m)$
-equivariant
$U(m)$
-equivariant
![]() $\mathbf {MU}$
-theory. Part (iv) of the theorem refers to the bundling maps
$\mathbf {MU}$
-theory. Part (iv) of the theorem refers to the bundling maps
![]() $\mathbf {MU}_G^*\to \mathbf {MU}^*(B G)$
defined by tom Dieck in [Reference tom Dieck17, Proposition 1.2].
$\mathbf {MU}_G^*\to \mathbf {MU}^*(B G)$
defined by tom Dieck in [Reference tom Dieck17, Proposition 1.2].
Theorem 1.4. The Chern classes in homotopical equivariant bordism enjoy the following properties.
-
(i) For all
 $0\leq k\leq m=i+j$
, the relation holds in the group
$0\leq k\leq m=i+j$
, the relation holds in the group $$\begin{align*}\operatorname{\mathrm{res}}^{U(m)}_{U(i,j)}(c_k^{(m)})\ = \ \sum_{d=0,\dots,k} c_d^{(i)}\times c_{k-d}^{(j)}\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{res}}^{U(m)}_{U(i,j)}(c_k^{(m)})\ = \ \sum_{d=0,\dots,k} c_d^{(i)}\times c_{k-d}^{(j)}\end{align*}$$
 $\mathbf {MU}_{U(i,j)}^{2 k}$
.
$\mathbf {MU}_{U(i,j)}^{2 k}$
.
-
(ii) The relation
holds in the group $$ \begin{align*} \operatorname{\mathrm{res}}^{U(m)}_{U(m-1)}(c_k^{(m)})\ = \ \begin{cases} c_k^{(m-1)} & { for\ 0\leq k\leq m-1, and}\\ \ 0 & { for\ k=m} \end{cases} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{res}}^{U(m)}_{U(m-1)}(c_k^{(m)})\ = \ \begin{cases} c_k^{(m-1)} & { for\ 0\leq k\leq m-1, and}\\ \ 0 & { for\ k=m} \end{cases} \end{align*} $$
 $\mathbf {MU}_{U(m-1)}^{2 k}$
.
$\mathbf {MU}_{U(m-1)}^{2 k}$
.
-
(iii) Let
 $T^m$
denote the diagonal maximal torus of
$T^m$
denote the diagonal maximal torus of
 $U(m)$
. Then the restriction homomorphism takes the class
$U(m)$
. Then the restriction homomorphism takes the class $$\begin{align*}\operatorname{\mathrm{res}}^{U(m)}_{T^m} \ : \ \mathbf{MU}_{U(m)}^{2 k} \ \to \ \mathbf{MU}^{2 k}_{T^m} \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{res}}^{U(m)}_{T^m} \ : \ \mathbf{MU}_{U(m)}^{2 k} \ \to \ \mathbf{MU}^{2 k}_{T^m} \end{align*}$$
 $c_k^{(m)}$
to the k-th elementary symmetric polynomial in the classes
$c_k^{(m)}$
to the k-th elementary symmetric polynomial in the classes
 $p_1^*(e_1)$
, …,
$p_1^*(e_1)$
, …,
 $p_m^*(e_1)$
, where
$p_m^*(e_1)$
, where
 $p_i:T^m\to T=U(1)$
is the projection to the i-th factor.
$p_i:T^m\to T=U(1)$
is the projection to the i-th factor.
-
(iv) The bundling map
takes the class $$\begin{align*}\mathbf{MU}_{U(m)}^* \ \to \ \mathbf{MU}^*(BU(m)) \end{align*}$$
$$\begin{align*}\mathbf{MU}_{U(m)}^* \ \to \ \mathbf{MU}^*(BU(m)) \end{align*}$$
 $c_k^{(m)}$
to the k-th Conner–Floyd–Chern class.
$c_k^{(m)}$
to the k-th Conner–Floyd–Chern class.
Proof. (i) This property exploits the double coset formula for
![]() $\operatorname {\mathrm {res}}^{U(m)}_{U(i,j)}\circ \operatorname {\mathrm {tr}}_{U(k,m-k)}^{U(m)}$
recorded in Proposition 1.3, which is the second equation in the following list:
$\operatorname {\mathrm {res}}^{U(m)}_{U(i,j)}\circ \operatorname {\mathrm {tr}}_{U(k,m-k)}^{U(m)}$
recorded in Proposition 1.3, which is the second equation in the following list:
 $$ \begin{align*} \operatorname{\mathrm{res}}^{U(m)}_{U(i,j)}(c_k^{(m)})\ &= \ \operatorname{\mathrm{res}}^{U(m)}_{U(i,j)}(\operatorname{\mathrm{tr}}_{U(k,m-k)}^{U(m)}(e_k\times 1_{m-k})) \\ &= \ \sum_{d=0,\dots,k} \operatorname{\mathrm{tr}}_{U(d,i-d,k-d,j-k+d)}^{U(i,j)}(\gamma_d^*(\operatorname{\mathrm{res}}^{U(k,m-k)}_{U(d,k-d,i-d,j-k+d)}(e_k\times 1_{m-k})))\\ &= \ \sum_{d=0,\dots,k} \operatorname{\mathrm{tr}}_{U(d,i-d,k-d,j-k+d)}^{U(i,j)}(\gamma_d^*(e_d\times e_{k-d}\times 1_{i-d}\times 1_{j-k+d}))\\ &= \ \sum_{d=0,\dots,k} \operatorname{\mathrm{tr}}_{U(d,i-d,k-d,j-k+d)}^{U(i,j)}(e_d\times 1_{i-d}\times e_{k-d}\times 1_{j-k+d})\\ &= \ \sum_{d=0,\dots,k} \operatorname{\mathrm{tr}}_{U(d,i-d)}^{U(i)}(e_d\times 1_{i-d})\times \operatorname{\mathrm{tr}}_{U(k-d,j-k+d)}^{U(j)}(e_{k-d}\times 1_{j-k+d})\\ &= \ \sum_{d=0,\dots,k} c_d^{(i)}\times c_{k-d}^{(j)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{res}}^{U(m)}_{U(i,j)}(c_k^{(m)})\ &= \ \operatorname{\mathrm{res}}^{U(m)}_{U(i,j)}(\operatorname{\mathrm{tr}}_{U(k,m-k)}^{U(m)}(e_k\times 1_{m-k})) \\ &= \ \sum_{d=0,\dots,k} \operatorname{\mathrm{tr}}_{U(d,i-d,k-d,j-k+d)}^{U(i,j)}(\gamma_d^*(\operatorname{\mathrm{res}}^{U(k,m-k)}_{U(d,k-d,i-d,j-k+d)}(e_k\times 1_{m-k})))\\ &= \ \sum_{d=0,\dots,k} \operatorname{\mathrm{tr}}_{U(d,i-d,k-d,j-k+d)}^{U(i,j)}(\gamma_d^*(e_d\times e_{k-d}\times 1_{i-d}\times 1_{j-k+d}))\\ &= \ \sum_{d=0,\dots,k} \operatorname{\mathrm{tr}}_{U(d,i-d,k-d,j-k+d)}^{U(i,j)}(e_d\times 1_{i-d}\times e_{k-d}\times 1_{j-k+d})\\ &= \ \sum_{d=0,\dots,k} \operatorname{\mathrm{tr}}_{U(d,i-d)}^{U(i)}(e_d\times 1_{i-d})\times \operatorname{\mathrm{tr}}_{U(k-d,j-k+d)}^{U(j)}(e_{k-d}\times 1_{j-k+d})\\ &= \ \sum_{d=0,\dots,k} c_d^{(i)}\times c_{k-d}^{(j)}. \end{align*} $$
Part (ii) for
![]() $k<m$
follows from part (i) by restriction from
$k<m$
follows from part (i) by restriction from
![]() $U(m-1,1)$
to
$U(m-1,1)$
to
![]() $U(m-1)$
:
$U(m-1)$
:
 $$ \begin{align*} \operatorname{\mathrm{res}}^{U(m)}_{U(m-1)}(c_k^{(m)})\ &= \ \operatorname{\mathrm{res}}^{U(m-1,1)}_{U(m-1)}(\operatorname{\mathrm{res}}^{U(m)}_{U(m-1,1)}(c_k^{(m)}))\\[3pt]&= \ \operatorname{\mathrm{res}}^{U(m-1,1)}_{U(m-1)}(c_{k-1}^{(m-1)}\times c_1^{(1)}\ + \ c_k^{(m-1)}\times c_0^{(1)})\\[3pt]&= \ c_{k-1}^{(m-1)}\times \operatorname{\mathrm{res}}^{U(1)}_1(c_1^{(1)})\ +\ c_k^{(m-1)}\times \operatorname{\mathrm{res}}^{U(1)}_1(c_0^{(1)})\ = \ c_k^{(m-1)}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{res}}^{U(m)}_{U(m-1)}(c_k^{(m)})\ &= \ \operatorname{\mathrm{res}}^{U(m-1,1)}_{U(m-1)}(\operatorname{\mathrm{res}}^{U(m)}_{U(m-1,1)}(c_k^{(m)}))\\[3pt]&= \ \operatorname{\mathrm{res}}^{U(m-1,1)}_{U(m-1)}(c_{k-1}^{(m-1)}\times c_1^{(1)}\ + \ c_k^{(m-1)}\times c_0^{(1)})\\[3pt]&= \ c_{k-1}^{(m-1)}\times \operatorname{\mathrm{res}}^{U(1)}_1(c_1^{(1)})\ +\ c_k^{(m-1)}\times \operatorname{\mathrm{res}}^{U(1)}_1(c_0^{(1)})\ = \ c_k^{(m-1)}. \end{align*} $$
We have used that the class
![]() $c_1^{(1)}=e_1$
is in the kernel of the augmentation
$c_1^{(1)}=e_1$
is in the kernel of the augmentation
![]() $\operatorname {\mathrm {res}}^{U(1)}_1:\mathbf {MU}_{U(1)}^*\to \mathbf {MU}^*$
. The Euler class
$\operatorname {\mathrm {res}}^{U(1)}_1:\mathbf {MU}_{U(1)}^*\to \mathbf {MU}^*$
. The Euler class
![]() $c_m^{(m)}=e(\nu _m)$
restricts to 0 in
$c_m^{(m)}=e(\nu _m)$
restricts to 0 in
![]() $\mathbf {MU}^*_{U(m-1)}$
because the restriction of the tautological
$\mathbf {MU}^*_{U(m-1)}$
because the restriction of the tautological
![]() $U(m)$
-representation to
$U(m)$
-representation to
![]() $U(m-1)$
splits off a trivial one-dimensional summand.
$U(m-1)$
splits off a trivial one-dimensional summand.
(iii) An inductive argument based on property (i) shows the desired relation:
 $$ \begin{align*} \operatorname{\mathrm{res}}^{U(m)}_{T^m}(c_k^{(m)}) \ &= \ \operatorname{\mathrm{res}}^{U(m)}_{U(1,\dots,1)}(c_k^{(m)}) \\ &= \ \sum_{A\subset\{1,\dots,m\}, |A|=k}\quad \prod_{a\in A} p_a^*(c_1^{(1)})\cdot\prod_{b\not\in A}p_b^*(c_0^{(1)}) \\ &= \ \sum_{A\subset\{1,\dots,m\}, |A|=k} \quad \prod_{a\in A} p_a^*(e_1). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{res}}^{U(m)}_{T^m}(c_k^{(m)}) \ &= \ \operatorname{\mathrm{res}}^{U(m)}_{U(1,\dots,1)}(c_k^{(m)}) \\ &= \ \sum_{A\subset\{1,\dots,m\}, |A|=k}\quad \prod_{a\in A} p_a^*(c_1^{(1)})\cdot\prod_{b\not\in A}p_b^*(c_0^{(1)}) \\ &= \ \sum_{A\subset\{1,\dots,m\}, |A|=k} \quad \prod_{a\in A} p_a^*(e_1). \end{align*} $$
(iv) As before, we let
![]() $T^m$
denote the diagonal maximal torus in
$T^m$
denote the diagonal maximal torus in
![]() $U(m)$
. The splitting principle holds for nonequivariant complex oriented cohomology theories; see, for example, [Reference Dold5, Proposition 8.10]. In other words, the right vertical map in the commutative square of graded rings is injective:
$U(m)$
. The splitting principle holds for nonequivariant complex oriented cohomology theories; see, for example, [Reference Dold5, Proposition 8.10]. In other words, the right vertical map in the commutative square of graded rings is injective:

The k-th Conner–Floyd–Chern class is characterized as the unique element of
![]() $\mathbf {MU}^{2 k}(B U(m))$
that maps to the k-th elementary symmetric polynomial in the classes
$\mathbf {MU}^{2 k}(B U(m))$
that maps to the k-th elementary symmetric polynomial in the classes
![]() $p_1^*(e_1),\dots ,p_m^*(e_1)$
. Together with part (iii), this proves the claim.
$p_1^*(e_1),\dots ,p_m^*(e_1)$
. Together with part (iii), this proves the claim.
2 Regularity results
In this section, we use the Chern classes to formulate new structural properties of the equivariant bordism ring
![]() $\mathbf {MU}_{U(m)}^*$
. In particular, we can say what
$\mathbf {MU}_{U(m)}^*$
. In particular, we can say what
![]() $\mathbf {MU}_{U(m)}^*$
looks like after dividing out some of the Chern classes, and after completing at the Chern classes. The following theorem states these facts more generally for
$\mathbf {MU}_{U(m)}^*$
looks like after dividing out some of the Chern classes, and after completing at the Chern classes. The following theorem states these facts more generally for
![]() $U(m)\times G$
instead of
$U(m)\times G$
instead of
![]() $U(m)$
; by induction on the number of factors, we can then deduce corresponding results for products of unitary groups, see Theorem 2.2. The results in this section make crucial use of the splitting theorem for global functors established in [Reference Schwede15].
$U(m)$
; by induction on the number of factors, we can then deduce corresponding results for products of unitary groups, see Theorem 2.2. The results in this section make crucial use of the splitting theorem for global functors established in [Reference Schwede15].
Theorem 2.1. For every compact Lie group G and all
![]() $0\leq k\leq m$
, the sequence of Chern classes
$0\leq k\leq m$
, the sequence of Chern classes
is a regular sequence in the graded-commutative ring
![]() $\mathbf {MU}^*_{U(m)\times G}$
that generates the kernel of the surjective restriction homomorphism
$\mathbf {MU}^*_{U(m)\times G}$
that generates the kernel of the surjective restriction homomorphism
In particular, the sequence of Chern classes
![]() $(c_m^{(m)},c_{m-1}^{(m)},\dots ,c_1^{(m)})$
is a regular sequence that generates the augmentation ideal of the graded-commutative ring
$(c_m^{(m)},c_{m-1}^{(m)},\dots ,c_1^{(m)})$
is a regular sequence that generates the augmentation ideal of the graded-commutative ring
![]() $\mathbf {MU}^*_{U(m)}$
.
$\mathbf {MU}^*_{U(m)}$
.
Proof. We argue by downward induction on k. The induction starts with
![]() $k=m$
, where there is nothing to show. Now, we assume the claim for some
$k=m$
, where there is nothing to show. Now, we assume the claim for some
![]() $k\leq m$
, and we deduce it for
$k\leq m$
, and we deduce it for
![]() $k-1$
. The inductive hypothesis shows that
$k-1$
. The inductive hypothesis shows that
![]() $c_m^{(m)}\times 1_G,\dots ,c_{k+1}^{(m)}\times 1_G$
is a regular sequence in the graded-commutative ring
$c_m^{(m)}\times 1_G,\dots ,c_{k+1}^{(m)}\times 1_G$
is a regular sequence in the graded-commutative ring
![]() $\mathbf {MU}^*_{U(m)\times G}$
, and that the restriction homomorphism
$\mathbf {MU}^*_{U(m)\times G}$
, and that the restriction homomorphism
![]() $\operatorname {\mathrm {res}}^{U(m)\times G}_{U(k)\times G}$
factors through an isomorphism
$\operatorname {\mathrm {res}}^{U(m)\times G}_{U(k)\times G}$
factors through an isomorphism
We exploit that the various equivariant bordism spectra
![]() $\mathbf {MU}_G$
underlie a global spectrum; see [Reference Schwede14, Example 6.1.53]; thus the restriction homomorphism
$\mathbf {MU}_G$
underlie a global spectrum; see [Reference Schwede14, Example 6.1.53]; thus the restriction homomorphism
![]() $\operatorname {\mathrm {res}}^{U(k)\times G}_{U(k-1)\times G}$
is surjective by Theorem 1.4 and Proposition 2.2 of [Reference Schwede15]. Hence, the standard long exact sequence unsplices into a short exact sequence of graded
$\operatorname {\mathrm {res}}^{U(k)\times G}_{U(k-1)\times G}$
is surjective by Theorem 1.4 and Proposition 2.2 of [Reference Schwede15]. Hence, the standard long exact sequence unsplices into a short exact sequence of graded
![]() $\mathbf {MU}^*$
-modules:
$\mathbf {MU}^*$
-modules:
Because
we conclude that
![]() $c_k^{(m)}\times 1_G$
is a non zero-divisor in
$c_k^{(m)}\times 1_G$
is a non zero-divisor in
![]() $\mathbf {MU}_{U(m)\times G}^*/(c_m^{(m)}\times 1_G,c_{m-1}^{(m)}\times 1_G,\dots ,c_{k+1}^{(m)}\times 1_G)$
and that additionally dividing out
$\mathbf {MU}_{U(m)\times G}^*/(c_m^{(m)}\times 1_G,c_{m-1}^{(m)}\times 1_G,\dots ,c_{k+1}^{(m)}\times 1_G)$
and that additionally dividing out
![]() $c_k^{(m)}\times 1_G$
yields
$c_k^{(m)}\times 1_G$
yields
![]() $\mathbf {MU}_{U(k-1)\times G}^*$
. This completes the inductive step.
$\mathbf {MU}_{U(k-1)\times G}^*$
. This completes the inductive step.
We can now identify the completion of
![]() $\mathbf {MU}^*_{U(m)}$
at the augmentation ideal as an
$\mathbf {MU}^*_{U(m)}$
at the augmentation ideal as an
![]() $\mathbf {MU}^*$
-power series algebra on the Chern classes. We state this somewhat more generally for products of unitary groups, which we write as
$\mathbf {MU}^*$
-power series algebra on the Chern classes. We state this somewhat more generally for products of unitary groups, which we write as
for natural numbers
![]() $m_1,\dots ,m_l\geq 1$
. For
$m_1,\dots ,m_l\geq 1$
. For
![]() $1\leq i\leq l$
, we write
$1\leq i\leq l$
, we write
for the projection to the i-th factor, and we set
The following theorem was previously known for tori, that is, for
![]() $m_1=\dots =m_l=1$
.
$m_1=\dots =m_l=1$
.
Theorem 2.2. Let
![]() $m_1,\dots ,m_l\geq 1$
be positive integers.
$m_1,\dots ,m_l\geq 1$
be positive integers.
-
(i) The sequence of Chern classes
(2.3)is a regular sequence that generates the augmentation ideal of the graded-commutative ring $$ \begin{align} c_{m_1}^{[1]},\dots,c_1^{[1]},c_{m_2}^{[2]},\dots,c_1^{[2]},\dots, c_{m_l}^{[l]},\dots,c_1^{[l]} \end{align} $$
$$ \begin{align} c_{m_1}^{[1]},\dots,c_1^{[1]},c_{m_2}^{[2]},\dots,c_1^{[2]},\dots, c_{m_l}^{[l]},\dots,c_1^{[l]} \end{align} $$
 $\mathbf {MU}^*_{U(m_1,\dots ,m_l)}$
.
$\mathbf {MU}^*_{U(m_1,\dots ,m_l)}$
.
-
(ii) The completion of
 $\mathbf {MU}_{U(m_1,\dots ,m_l)}^*$
at the augmentation ideal is a graded
$\mathbf {MU}_{U(m_1,\dots ,m_l)}^*$
at the augmentation ideal is a graded
 $\mathbf {MU}^*$
-power series algebra in the Chern classes (2.3).
$\mathbf {MU}^*$
-power series algebra in the Chern classes (2.3). -
(iii) The bundling map
 $\mathbf {MU}_{U(m_1,\dots ,m_l)}^*\to \mathbf {MU}^*(B U(m_1,\dots ,m_l))$
extends to an isomorphism from the completion at the augmentation ideal.
$\mathbf {MU}_{U(m_1,\dots ,m_l)}^*\to \mathbf {MU}^*(B U(m_1,\dots ,m_l))$
extends to an isomorphism from the completion at the augmentation ideal. $$\begin{align*}( \mathbf{MU}_{U(m_1,\dots,m_l)}^*)^\wedge_I \ \to \ \mathbf{MU}^*(BU(m_1,\dots,m_l)) \end{align*}$$
$$\begin{align*}( \mathbf{MU}_{U(m_1,\dots,m_l)}^*)^\wedge_I \ \to \ \mathbf{MU}^*(BU(m_1,\dots,m_l)) \end{align*}$$
Proof. Part (i) follows from Theorem 2.1 by induction on the number l of factors.
We prove parts (ii) and (iii) together. We must show that for every
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $\mathbf {MU}_{U(m_1,\dots ,m_l)}^*/I^n$
is free as an
$\mathbf {MU}_{U(m_1,\dots ,m_l)}^*/I^n$
is free as an
![]() $\mathbf {MU}^*$
-module on the monomials of degree less than n in the Chern classes (2.3). There is nothing to show for
$\mathbf {MU}^*$
-module on the monomials of degree less than n in the Chern classes (2.3). There is nothing to show for
![]() $n=1$
. The short exact sequence
$n=1$
. The short exact sequence
and the inductive hypothesis reduce the claim to showing that
![]() $I^n/I^{n+1}$
is free as an
$I^n/I^{n+1}$
is free as an
![]() $\mathbf {MU}^*$
-module on the monomials of degree exactly n in the Chern classes (2.3). Since the augmentation ideal I is generated by these Chern classes, the n-th power
$\mathbf {MU}^*$
-module on the monomials of degree exactly n in the Chern classes (2.3). Since the augmentation ideal I is generated by these Chern classes, the n-th power
![]() $I^n$
is generated, as a module over
$I^n$
is generated, as a module over
![]() $\mathbf {MU}_{U(m_1,\dots ,m_l)}^*$
, by the monomials of degree n. So
$\mathbf {MU}_{U(m_1,\dots ,m_l)}^*$
, by the monomials of degree n. So
![]() $I^n/I^{n+1}$
is generated by these monomials as a module over
$I^n/I^{n+1}$
is generated by these monomials as a module over
![]() $\mathbf {MU}^*$
.
$\mathbf {MU}^*$
.
The bundling map
![]() $\mathbf {MU}_{U(m_1,\dots ,m_l)}^*\to \mathbf {MU}^*(B U(m_1,\dots ,m_l))$
is a homomorphism of augmented
$\mathbf {MU}_{U(m_1,\dots ,m_l)}^*\to \mathbf {MU}^*(B U(m_1,\dots ,m_l))$
is a homomorphism of augmented
![]() $\mathbf {MU}^*$
-algebras, and it takes the Chern class
$\mathbf {MU}^*$
-algebras, and it takes the Chern class
![]() $c_k^{[i]}$
to the inflation of the k-th Conner–Floyd–Chern class along the projection to the i-th factor. By the theory of complex orientations, the collection of these Conner–Floyd–Chern classes are
$c_k^{[i]}$
to the inflation of the k-th Conner–Floyd–Chern class along the projection to the i-th factor. By the theory of complex orientations, the collection of these Conner–Floyd–Chern classes are
![]() $\mathbf {MU}^*$
-power series generators of
$\mathbf {MU}^*$
-power series generators of
![]() $\mathbf {MU}^*(B U(m_1,\dots ,m_l))$
; in particular, the images of the Chern class monomials are
$\mathbf {MU}^*(B U(m_1,\dots ,m_l))$
; in particular, the images of the Chern class monomials are
![]() $\mathbf {MU}^*$
-linearly independent in
$\mathbf {MU}^*$
-linearly independent in
![]() $\mathbf {MU}^*(B U(m_1,\dots ,m_l))$
. Hence, these classes are themselves linearly independent in
$\mathbf {MU}^*(B U(m_1,\dots ,m_l))$
. Hence, these classes are themselves linearly independent in
![]() $I^n/I^{n+1}$
.
$I^n/I^{n+1}$
.
Remark 2.4. Greenlees and May [Reference Greenlees and May6, Corollary 1.6] construct a local homology spectral sequence
The regularity results about Chern classes from Theorem 2.2 imply that, whenever
![]() $G=U(m_1,\dots ,m_l)$
is a product of unitary groups, the
$G=U(m_1,\dots ,m_l)$
is a product of unitary groups, the
![]() $E_2^{p,q}$
-term vanishes for all
$E_2^{p,q}$
-term vanishes for all
![]() $p\ne 0$
, and the spectral sequence degenerates into the isomorphism
$p\ne 0$
, and the spectral sequence degenerates into the isomorphism
of Theorem 2.2 (iii).
Remark 2.5. The previous regularity theorems are special cases of the following more general results that hold for every global
![]() $\mathbf {MU}$
-module E:
$\mathbf {MU}$
-module E:
-
• For every compact Lie group G, the sequence of Chern classes
 $c_m^{(m)}\times 1_G,\dots ,c_1^{(m)}\times 1_G$
acts regularly on the graded
$c_m^{(m)}\times 1_G,\dots ,c_1^{(m)}\times 1_G$
acts regularly on the graded
 $\mathbf {MU}^*_{U(m)\times G}$
-module
$\mathbf {MU}^*_{U(m)\times G}$
-module
 $E^*_{U(m)\times G}$
.
$E^*_{U(m)\times G}$
. -
• The restriction homomorphism
factors through an isomorphism $$\begin{align*}\operatorname{\mathrm{res}}^{ U(m)\times G}_ G\ :\ E_{U(m)\times G}^*\ \to \ E_G^*\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{res}}^{ U(m)\times G}_ G\ :\ E_{U(m)\times G}^*\ \to \ E_G^*\end{align*}$$
 $$\begin{align*}E_{U(m)\times G}^*/(c_m^{(m)}\times 1_G,\dots, c_1^{(m)}\times 1_G)\ \cong \ E_G^* \ .\end{align*}$$
$$\begin{align*}E_{U(m)\times G}^*/(c_m^{(m)}\times 1_G,\dots, c_1^{(m)}\times 1_G)\ \cong \ E_G^* \ .\end{align*}$$
-
• For all
 $m_1,\dots ,m_l\geq 1$
, the sequence of Chern classes (2.3) acts regularly on the graded
$m_1,\dots ,m_l\geq 1$
, the sequence of Chern classes (2.3) acts regularly on the graded
 $\mathbf {MU}^*_{U(m_1,\dots ,m_l)}$
-module
$\mathbf {MU}^*_{U(m_1,\dots ,m_l)}$
-module
 $E^*_{U(m_1,\dots ,m_l)}$
.
$E^*_{U(m_1,\dots ,m_l)}$
.
As in Remark 2.4, the regularity properties also imply the degeneracy of the Greenlees–May local homology spectral sequence converging to
![]() $E^*(B U(m_1,\dots ,m_l))$
.
$E^*(B U(m_1,\dots ,m_l))$
.
3 The
 $\mathbf {MU}$
-completion theorem via Chern classes
$\mathbf {MU}$
-completion theorem via Chern classes
In this section, we use the Chern classes to reformulate the
![]() $\mathbf {MU}_G$
-completion theorem of Greenlees–May [Reference Greenlees and May6] and La Vecchia [Reference La Vecchia8], for any compact Lie group G, and we give a short and self-contained proof. We emphasize that the essential arguments of this section are all contained in [Reference Greenlees and May6] and [Reference La Vecchia8]; the Chern classes let us arrange them in a more conceptual and concise way. The references [Reference Greenlees and May6, Reference La Vecchia8] ask for a finitely generated ideal of
$\mathbf {MU}_G$
-completion theorem of Greenlees–May [Reference Greenlees and May6] and La Vecchia [Reference La Vecchia8], for any compact Lie group G, and we give a short and self-contained proof. We emphasize that the essential arguments of this section are all contained in [Reference Greenlees and May6] and [Reference La Vecchia8]; the Chern classes let us arrange them in a more conceptual and concise way. The references [Reference Greenlees and May6, Reference La Vecchia8] ask for a finitely generated ideal of
![]() $\mathbf {MU}_G^*$
that is ‘sufficiently large’ in the sense of [Reference Greenlees and May6, Definition 2.4]. While we have no need to explicitly mention sufficiently large ideals, the new insight is that the ideal generated by the Chern classes of any faithful G-representation is ‘sufficiently large’.
$\mathbf {MU}_G^*$
that is ‘sufficiently large’ in the sense of [Reference Greenlees and May6, Definition 2.4]. While we have no need to explicitly mention sufficiently large ideals, the new insight is that the ideal generated by the Chern classes of any faithful G-representation is ‘sufficiently large’.
Construction 3.1 (Chern classes of representations).
We let V be a complex representation of a compact Lie group G. We let
![]() $\rho :G\to U(m)$
be a continuous homomorphism that classifies V, that is, such that
$\rho :G\to U(m)$
be a continuous homomorphism that classifies V, that is, such that
![]() $\rho ^*(\nu _m)$
is isomorphic to V; here,
$\rho ^*(\nu _m)$
is isomorphic to V; here,
![]() $m=\dim _{\mathbb C}(V)$
. The k-th Chern class of V is
$m=\dim _{\mathbb C}(V)$
. The k-th Chern class of V is
In particular,
![]() $c_0(V)=1$
,
$c_0(V)=1$
,
![]() $c_m(V)=e(V)$
is the Euler class, and
$c_m(V)=e(V)$
is the Euler class, and
![]() $c_k(V)=0$
for
$c_k(V)=0$
for
![]() $k>m$
.
$k>m$
.
Example 3.2. As an example, we consider the tautological representation
![]() $\nu _2$
of
$\nu _2$
of
![]() $S U(2)$
on
$S U(2)$
on
![]() $\mathbb C^2$
. By the general properties of Chern classes, we have
$\mathbb C^2$
. By the general properties of Chern classes, we have
![]() $c_0(\nu _2)=1$
,
$c_0(\nu _2)=1$
,
![]() $c_2(\nu _2)=e(\nu _2)$
is the Euler class, and
$c_2(\nu _2)=e(\nu _2)$
is the Euler class, and
![]() $c_k(\nu _2)=0$
for
$c_k(\nu _2)=0$
for
![]() $k\geq 3$
. The first Chern class of
$k\geq 3$
. The first Chern class of
![]() $\nu _2$
can be rewritten by using a double coset formula as follows:
$\nu _2$
can be rewritten by using a double coset formula as follows:
 $$ \begin{align*} c_1(\nu_2)\ &= \ \operatorname{\mathrm{res}}^{U(2)}_{S U(2)}(c_1^{(2)}) \ = \ \operatorname{\mathrm{res}}^{U(2)}_{S U(2)}(\operatorname{\mathrm{tr}}_{U(1,1)}^{U(2)}(e_1\times 1)) \\ &= \ \operatorname{\mathrm{tr}}_T^{S U(2)}(\operatorname{\mathrm{res}}^{U(1,1)}_T(e_1\times 1)) \ = \ \operatorname{\mathrm{tr}}_T^{S U(2)}(e(\chi)) . \end{align*} $$
$$ \begin{align*} c_1(\nu_2)\ &= \ \operatorname{\mathrm{res}}^{U(2)}_{S U(2)}(c_1^{(2)}) \ = \ \operatorname{\mathrm{res}}^{U(2)}_{S U(2)}(\operatorname{\mathrm{tr}}_{U(1,1)}^{U(2)}(e_1\times 1)) \\ &= \ \operatorname{\mathrm{tr}}_T^{S U(2)}(\operatorname{\mathrm{res}}^{U(1,1)}_T(e_1\times 1)) \ = \ \operatorname{\mathrm{tr}}_T^{S U(2)}(e(\chi)) . \end{align*} $$
Here,
![]() $T=\{ (\begin {smallmatrix} \lambda & 0 \\ 0 & \lambda ^{-1} \end {smallmatrix}) \ : \ \lambda \in U(1) \}$
is the diagonal maximal torus of
$T=\{ (\begin {smallmatrix} \lambda & 0 \\ 0 & \lambda ^{-1} \end {smallmatrix}) \ : \ \lambda \in U(1) \}$
is the diagonal maximal torus of
![]() $S U(2)$
,
$S U(2)$
,
![]() $\chi :T\cong U(1)$
is the character that projects onto the upper left diagonal entry, and
$\chi :T\cong U(1)$
is the character that projects onto the upper left diagonal entry, and
![]() $e(\chi )\in \mathbf {MU}^2_T$
is its Euler class.
$e(\chi )\in \mathbf {MU}^2_T$
is its Euler class.
Construction 3.3. We recall a specific G-equivariant
![]() $\mathbf {MU}_G$
-module associated to a complex representation V of a compact Lie group G. The construction is known as the stable Koszul complex for the Chern classes
$\mathbf {MU}_G$
-module associated to a complex representation V of a compact Lie group G. The construction is known as the stable Koszul complex for the Chern classes
![]() $c_1(V),\dots ,c_m(V)$
, where
$c_1(V),\dots ,c_m(V)$
, where
![]() $m=\dim _{\mathbb C}(V)$
; in the notation of Greenlees–May [Reference Greenlees and May6] and La Vecchia [Reference La Vecchia8], our
$m=\dim _{\mathbb C}(V)$
; in the notation of Greenlees–May [Reference Greenlees and May6] and La Vecchia [Reference La Vecchia8], our
![]() $K(G,V)$
would appear as
$K(G,V)$
would appear as
![]() $\Gamma _I(\mathbf {MU}_G)$
, where
$\Gamma _I(\mathbf {MU}_G)$
, where
![]() $I=(c_1(V),\dots ,c_m(V))$
is the ideal generated by the Chern classes.
$I=(c_1(V),\dots ,c_m(V))$
is the ideal generated by the Chern classes.
For any equivariant homotopy class
![]() $x\in \mathbf {MU}_G^l$
, we write
$x\in \mathbf {MU}_G^l$
, we write
![]() $\mathbf {MU}_G[1/x]$
for the
$\mathbf {MU}_G[1/x]$
for the
![]() $\mathbf {MU}_G$
-module localization of
$\mathbf {MU}_G$
-module localization of
![]() $\mathbf {MU}_G$
with x inverted; in other words,
$\mathbf {MU}_G$
with x inverted; in other words,
![]() $\mathbf {MU}_G[1/x]$
is a homotopy colimit (mapping telescope) in the triangulated category of the sequence
$\mathbf {MU}_G[1/x]$
is a homotopy colimit (mapping telescope) in the triangulated category of the sequence
We write
![]() $K(x)$
for the fiber of the morphism
$K(x)$
for the fiber of the morphism
![]() $\mathbf {MU}_G\to \mathbf {MU}_G[1/x]$
. Then we define
$\mathbf {MU}_G\to \mathbf {MU}_G[1/x]$
. Then we define
The smash product of the morphisms
![]() $K(c_i(V))\to \mathbf {MU}_G$
provides a morphism of G-equivariant
$K(c_i(V))\to \mathbf {MU}_G$
provides a morphism of G-equivariant
![]() $\mathbf {MU}_G$
-module spectra
$\mathbf {MU}_G$
-module spectra
By general principles, the module
![]() $K(G,V)$
only depends on the radical of the ideal generated by the classes
$K(G,V)$
only depends on the radical of the ideal generated by the classes
![]() $c_1(V),\dots ,c_m(V)$
. But more is true: As a consequence of Theorem 3.5 below,
$c_1(V),\dots ,c_m(V)$
. But more is true: As a consequence of Theorem 3.5 below,
![]() $K(G,V)$
is entirely independent, as a G-equivariant
$K(G,V)$
is entirely independent, as a G-equivariant
![]() $\mathbf {MU}_G$
-module, of the faithful representation V.
$\mathbf {MU}_G$
-module, of the faithful representation V.
Proposition 3.4. Let V be a faithful complex representation of a compact Lie group G.
-
(i) The morphism
 $\epsilon _V:K(G,V)\to \mathbf {MU}_G$
is an equivalence of underlying nonequivariant spectra.
$\epsilon _V:K(G,V)\to \mathbf {MU}_G$
is an equivalence of underlying nonequivariant spectra. -
(ii) For every nontrivial closed subgroup H of G, the H-geometric fixed point spectrum
 $\Phi ^H(K(G,V))$
is trivial.
$\Phi ^H(K(G,V))$
is trivial.
Proof. (i) We set
![]() $m=\dim _{\mathbb C}(V)$
. The Chern classes
$m=\dim _{\mathbb C}(V)$
. The Chern classes
![]() $c_1(V),\dots ,c_m(V)$
belong to the augmentation ideal of
$c_1(V),\dots ,c_m(V)$
belong to the augmentation ideal of
![]() $\mathbf {MU}_G^*$
, so they restrict to 0 in
$\mathbf {MU}_G^*$
, so they restrict to 0 in
![]() $\mathbf {MU}_{\{1\}}^*$
, and hence the underlying nonequivariant spectrum of
$\mathbf {MU}_{\{1\}}^*$
, and hence the underlying nonequivariant spectrum of
![]() $\mathbf {MU}_G[1/c_i(V)]$
is trivial for each
$\mathbf {MU}_G[1/c_i(V)]$
is trivial for each
![]() $i=1,\dots ,m$
. Hence, the morphisms
$i=1,\dots ,m$
. Hence, the morphisms
![]() $K(c_i(V))\to \mathbf {MU}_G$
are underlying nonequivariant equivalences for
$K(c_i(V))\to \mathbf {MU}_G$
are underlying nonequivariant equivalences for
![]() $i=1,\dots ,m$
. So also the morphism
$i=1,\dots ,m$
. So also the morphism
![]() $\epsilon _V$
is an underlying nonequivariant equivalence.
$\epsilon _V$
is an underlying nonequivariant equivalence.
(ii) We let H be a nontrivial closed subgroup of G. We set
![]() $W=V-V^H$
, the orthogonal complement of the H-fixed points. This is a complex H-representation with
$W=V-V^H$
, the orthogonal complement of the H-fixed points. This is a complex H-representation with
![]() $W^H=0$
; moreover, W is nonzero because H acts faithfully on V and
$W^H=0$
; moreover, W is nonzero because H acts faithfully on V and
![]() $H\ne \{1\}$
. For
$H\ne \{1\}$
. For
![]() $k=\dim _{\mathbb C}(W)$
, we then have
$k=\dim _{\mathbb C}(W)$
, we then have
the second equation uses the fact that adding a trivial representation leaves Chern classes unchanged, by part (ii) of Theorem 1.4.
Since
![]() $W^H=0$
, the geometric fixed point homomorphism
$W^H=0$
, the geometric fixed point homomorphism
![]() $\Phi ^H:\mathbf {MU}_H^*\to \Phi _H^*(\mathbf {MU})$
sends the Euler class
$\Phi ^H:\mathbf {MU}_H^*\to \Phi _H^*(\mathbf {MU})$
sends the Euler class
![]() $e(W) = \operatorname {\mathrm {res}}^G_H( c_k(V))$
to an invertible element. The functor
$e(W) = \operatorname {\mathrm {res}}^G_H( c_k(V))$
to an invertible element. The functor
![]() $\Phi ^H\circ \operatorname {\mathrm {res}}^G_H$
commutes with inverting elements. Since the class
$\Phi ^H\circ \operatorname {\mathrm {res}}^G_H$
commutes with inverting elements. Since the class
![]() $\Phi ^H(\operatorname {\mathrm {res}}^G_H(c_k(V)))$
is already invertible, the localization morphism
$\Phi ^H(\operatorname {\mathrm {res}}^G_H(c_k(V)))$
is already invertible, the localization morphism
![]() $\mathbf {MU}_G\to \mathbf {MU}_G[1/c_k(V)]$
induces an equivalence on H-geometric fixed points. Since the functor
$\mathbf {MU}_G\to \mathbf {MU}_G[1/c_k(V)]$
induces an equivalence on H-geometric fixed points. Since the functor
![]() $\Phi ^H\circ \operatorname {\mathrm {res}}^G_H$
is exact, it annihilates the fiber
$\Phi ^H\circ \operatorname {\mathrm {res}}^G_H$
is exact, it annihilates the fiber
![]() $K(c_k(V))$
of the localization
$K(c_k(V))$
of the localization
![]() $\mathbf {MU}_G\to \mathbf {MU}_G[1/c_k(V)]$
. The functor
$\mathbf {MU}_G\to \mathbf {MU}_G[1/c_k(V)]$
. The functor
![]() $\Phi ^H\circ \operatorname {\mathrm {res}}^G_H$
is also strong monoidal in the sense of a natural equivalence of nonequivariant spectra
$\Phi ^H\circ \operatorname {\mathrm {res}}^G_H$
is also strong monoidal in the sense of a natural equivalence of nonequivariant spectra
for all G-equivariant
![]() $\mathbf {MU}_G$
-modules X and Y. Since
$\mathbf {MU}_G$
-modules X and Y. Since
![]() $K(G,V)$
contains
$K(G,V)$
contains
![]() $K(c_k(V))$
as a factor (with respect to
$K(c_k(V))$
as a factor (with respect to
![]() $\wedge _{\mathbf {MU}_G}$
), we conclude that the spectrum
$\wedge _{\mathbf {MU}_G}$
), we conclude that the spectrum
![]() $\Phi ^H(K(G,V))$
is trivial.
$\Phi ^H(K(G,V))$
is trivial.
The following ‘completion theorem’ is a reformulation of the combined work of Greenlees–May [Reference Greenlees and May6, Theorem 1.3] and La Vecchia [Reference La Vecchia8]. It is somewhat more precise in that an unspecified ‘sufficiently large’ finitely generated ideal of
![]() $\mathbf {MU}_G^*$
is replaced by the ideal generated by the Chern classes of a faithful G-representation. The proof is immediate from the properties of
$\mathbf {MU}_G^*$
is replaced by the ideal generated by the Chern classes of a faithful G-representation. The proof is immediate from the properties of
![]() $K(G,V)$
listed in Proposition 3.4. We emphasize, however, that our proof is just a different way of arranging some arguments from [Reference Greenlees and May6] and [Reference La Vecchia8] while taking advantage of the Chern class formalism.
$K(G,V)$
listed in Proposition 3.4. We emphasize, however, that our proof is just a different way of arranging some arguments from [Reference Greenlees and May6] and [Reference La Vecchia8] while taking advantage of the Chern class formalism.
Since the morphism
![]() $\epsilon _V:K(G,V)\to \mathbf {MU}_G$
is a nonequivariant equivalence of underlying spectra, the morphism
$\epsilon _V:K(G,V)\to \mathbf {MU}_G$
is a nonequivariant equivalence of underlying spectra, the morphism
![]() $E G_+\wedge \mathbf {MU}_G\to \mathbf {MU}_G$
that collapses the universal space
$E G_+\wedge \mathbf {MU}_G\to \mathbf {MU}_G$
that collapses the universal space
![]() $E G$
to a point admits a unique lift to a morphism of G-equivariant
$E G$
to a point admits a unique lift to a morphism of G-equivariant
![]() $\mathbf {MU}_G$
-modules
$\mathbf {MU}_G$
-modules
![]() $\psi : E G_+\wedge \mathbf {MU}_G\to K(G,V)$
across
$\psi : E G_+\wedge \mathbf {MU}_G\to K(G,V)$
across
![]() $\epsilon _V$
.
$\epsilon _V$
.
Theorem 3.5. Let V be a faithful complex representation of a compact Lie group G. Then the morphism
is an equivalence of G-equivariant
![]() $\mathbf {MU}_G$
-module spectra.
$\mathbf {MU}_G$
-module spectra.
Proof. Because the underlying space of
![]() $E G$
is contractible, the composite
$E G$
is contractible, the composite
is an equivariant equivalence of underlying nonequivariant spectra. Since
![]() $\epsilon _V$
is an equivariant equivalence of underlying nonequivariant spectra by Proposition 3.4, so is
$\epsilon _V$
is an equivariant equivalence of underlying nonequivariant spectra by Proposition 3.4, so is
![]() $\psi $
. For all nontrivial closed subgroups H of G, source and target of
$\psi $
. For all nontrivial closed subgroups H of G, source and target of
![]() $\psi $
have trivial H-geometric fixed points spectra, again by Proposition 3.4. So the morphism
$\psi $
have trivial H-geometric fixed points spectra, again by Proposition 3.4. So the morphism
![]() $\psi $
induces an equivalence on geometric fixed point spectra for all closed subgroup of G, and it is thus an equivariant equivalence.
$\psi $
induces an equivalence on geometric fixed point spectra for all closed subgroup of G, and it is thus an equivariant equivalence.
Competing interest
The author has no competing interest to declare.
Financial support
The author is a member of the Hausdorff Center for Mathematics at the University of Bonn (DFG GZ 2047/1, project ID 390685813).