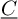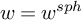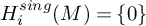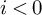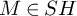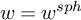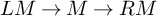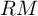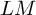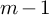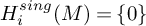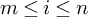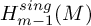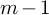Introduction
Let us recall that, for any object M of a triangulated category
![]() $\underline {C}$
and any integer n, a weight structure w on
$\underline {C}$
and any integer n, a weight structure w on
![]() $\underline {C}$
gives (essentially by definition) an n-weight decomposition triangle
$\underline {C}$
gives (essentially by definition) an n-weight decomposition triangle
![]() $LM\to M\to RM\to LM[1]$
, where
$LM\to M\to RM\to LM[1]$
, where
![]() $LM$
is of weights at most n and
$LM$
is of weights at most n and
![]() $RM$
is of weights at least
$RM$
is of weights at least
![]() $n+1$
;Footnote
1
however, this triangle is not canonical. In particular, for the spherical weight structure
$n+1$
;Footnote
1
however, this triangle is not canonical. In particular, for the spherical weight structure
![]() $w^{sph}$
on the stable homotopy category
$w^{sph}$
on the stable homotopy category
![]() $SH$
(see §4.2 of [Reference Bondarko7], Theorem 4.2.4 and Theorem 4.2.5(1) below) one can take
$SH$
(see §4.2 of [Reference Bondarko7], Theorem 4.2.4 and Theorem 4.2.5(1) below) one can take
![]() $LM$
to be an arbitrary choice of an n-skeleton for the spectrum M in the sense of §6.3 of [Reference Margolis20]; thus,
$LM$
to be an arbitrary choice of an n-skeleton for the spectrum M in the sense of §6.3 of [Reference Margolis20]; thus,
![]() $LM$
is not determined by M uniquely. However, it was noticed by J. Wildeshaus that if one can choose an n-weight decomposition such that
$LM$
is not determined by M uniquely. However, it was noticed by J. Wildeshaus that if one can choose an n-weight decomposition such that
![]() $LM$
is of weights at most
$LM$
is of weights at most
![]() $m-1$
for some
$m-1$
for some
![]() $m\le n$
, then this stronger assumption makes the decomposition canonical. In this case, M is said to be without weights
$m\le n$
, then this stronger assumption makes the decomposition canonical. In this case, M is said to be without weights
![]() $m,\dots , n$
. In this paper, we prove that M satisfies this condition if and only if its weight complex
$m,\dots , n$
. In this paper, we prove that M satisfies this condition if and only if its weight complex
![]() $t(M)$
is homotopy equivalent to a complex with zero terms in degrees
$t(M)$
is homotopy equivalent to a complex with zero terms in degrees
![]() $-n,\dots , -m$
;Footnote
2
recall here that t is a ‘weakly exact’ functor from
$-n,\dots , -m$
;Footnote
2
recall here that t is a ‘weakly exact’ functor from
![]() $\underline {C}$
into a certain quotient
$\underline {C}$
into a certain quotient
![]() $K_{\mathfrak {w}}({\underline {Hw}})$
of the homotopy category of complexes in the heart
$K_{\mathfrak {w}}({\underline {Hw}})$
of the homotopy category of complexes in the heart
![]() ${\underline {Hw}}$
of w. It easily follows that one can find out whether M is without weights
${\underline {Hw}}$
of w. It easily follows that one can find out whether M is without weights
![]() $m,\dots , n$
by applying functors that are pure (in the sense of Definition 2.4.1 below) to M. Moreover, one can put
$m,\dots , n$
by applying functors that are pure (in the sense of Definition 2.4.1 below) to M. Moreover, one can put
![]() $m=-\infty $
or
$m=-\infty $
or
![]() $n=+\infty $
in these statements to obtain that t is ‘conservative up to weight-degenerate objects’. One may say that t is conservative up to objects of infinitely small and infinitely large weights. This is a significant improvement over previously known bounded conservativity results. One may say that objects of
$n=+\infty $
in these statements to obtain that t is ‘conservative up to weight-degenerate objects’. One may say that t is conservative up to objects of infinitely small and infinitely large weights. This is a significant improvement over previously known bounded conservativity results. One may say that objects of
![]() $\underline {C}$
may be ‘detected’ by means of objects of a much simpler category
$\underline {C}$
may be ‘detected’ by means of objects of a much simpler category
![]() $K_{\mathfrak {w}}({\underline {Hw}})$
. We apply our conservativity of weight complexes result to calculate certain intersections of purely generated subcategories (this result was applied in [Reference Bondarko5]) and to prove that certain weight-exact functors are conservative. The latter statement generalizes Theorems 2.5 and 2.8 of [Reference Wildeshaus29]; in particular, we treat not necessarily bounded weight structures.
$K_{\mathfrak {w}}({\underline {Hw}})$
. We apply our conservativity of weight complexes result to calculate certain intersections of purely generated subcategories (this result was applied in [Reference Bondarko5]) and to prove that certain weight-exact functors are conservative. The latter statement generalizes Theorems 2.5 and 2.8 of [Reference Wildeshaus29]; in particular, we treat not necessarily bounded weight structures.
Moreover, we apply our general results to equivariant stable homotopy categories and spherical weight structures on them (as introduced in §4 of [Reference Bondarko7]). The aforementioned conservativity of weight complexes results yield a certain converse to the equivariant stable Hurewicz theorem. In particular, in the case of a trivial group the weight complex functor essentially calculates singular homology; thus, we obtain that the singular homology of a spectrum
![]() $E\in \operatorname {Obj} SH$
vanishes in negative degrees if and only if E is an extension of a connective spectrum by an acyclic one. This statement appears to be completely new since in all the previously existing formulations only the case where E is bounded below was considered; see Theorem 2.1(i) of [Reference Lewis18], Proposition 7.1.2(f) of [Reference Hovey, Palmieri and Strickland15] and Theorem 6.9 of [Reference Margolis20]. Moreover, the vanishing of
$E\in \operatorname {Obj} SH$
vanishes in negative degrees if and only if E is an extension of a connective spectrum by an acyclic one. This statement appears to be completely new since in all the previously existing formulations only the case where E is bounded below was considered; see Theorem 2.1(i) of [Reference Lewis18], Proposition 7.1.2(f) of [Reference Hovey, Palmieri and Strickland15] and Theorem 6.9 of [Reference Margolis20]. Moreover, the vanishing of
![]() $H^{sing}_i(E)$
for two subsequent values of i gives a canonical ‘decomposition’ of E into a distinguished triangle. This result is new as well. Our main definitions and statements are nicely illustrated by Theorems 4.2.4 and 4.2.5. In particular, we prove that
$H^{sing}_i(E)$
for two subsequent values of i gives a canonical ‘decomposition’ of E into a distinguished triangle. This result is new as well. Our main definitions and statements are nicely illustrated by Theorems 4.2.4 and 4.2.5. In particular, we prove that
![]() $w^{sph}$
-Postnikov towers are the cellular ones in the sense of [Reference Margolis20] (thus completing the proof of [Reference Bondarko7, Theorem 4.2.1]). Our central statements can also be applied to Tate motives; see Remark 4.1.8(1) below.
$w^{sph}$
-Postnikov towers are the cellular ones in the sense of [Reference Margolis20] (thus completing the proof of [Reference Bondarko7, Theorem 4.2.1]). Our central statements can also be applied to Tate motives; see Remark 4.1.8(1) below.
The main tool for obtaining these results is the new interesting notion of morphisms killing weights
![]() $m,\dots , n$
; for a morphism
$m,\dots , n$
; for a morphism
![]() $g:M\to N$
this means that g is ‘compatible with’ some morphism
$g:M\to N$
this means that g is ‘compatible with’ some morphism
![]() $w_{\le n}M\to w_{\le m-1}N$
. This definition is equivalent to several other ones. In particular, if
$w_{\le n}M\to w_{\le m-1}N$
. This definition is equivalent to several other ones. In particular, if
![]() $m=n$
, then one can easily reformulate this condition in terms of
$m=n$
, then one can easily reformulate this condition in terms of
![]() $t(g)$
. Thus, an
$t(g)$
. Thus, an
![]() $SH$
-morphism g kills weight m if and only if
$SH$
-morphism g kills weight m if and only if
![]() $H_{sing}^m(g,\Gamma )=0$
for every abelian group
$H_{sing}^m(g,\Gamma )=0$
for every abelian group
![]() $\Gamma $
. More generally, an
$\Gamma $
. More generally, an
![]() $SH$
-morphism g kills weights
$SH$
-morphism g kills weights
![]() $m,\dots , n$
whenever it ‘sends n-skeleta into
$m,\dots , n$
whenever it ‘sends n-skeleta into
![]() $m-1$
-skeleta’; see Proposition 2.1.1(4) and Theorem 4.2.5.
$m-1$
-skeleta’; see Proposition 2.1.1(4) and Theorem 4.2.5.
Let us now describe the contents of the paper.
§1 contains some preliminaries, mostly on weight structures.
In §2, we define morphisms killing weights
![]() $m,\dots , n$
and objects without these weights and study these notions in detail. In particular, we relate killing weights to weight complexes and pure functors. This gives a new conservativity of the weight complex functor result.
$m,\dots , n$
and objects without these weights and study these notions in detail. In particular, we relate killing weights to weight complexes and pure functors. This gives a new conservativity of the weight complex functor result.
In §3, we extend some of the results of the previous section to the case where
![]() ${\underline {Hw}}$
is not Karoubian (thus,
${\underline {Hw}}$
is not Karoubian (thus,
![]() ${\underline {Hw}}$
-idempotents do not yield direct summands in
${\underline {Hw}}$
-idempotents do not yield direct summands in
![]() $\underline {C}$
), so we formulate Theorem 3.1.3 that is central for this paper. We also give applications to intersections of purely generated subcategories and prove that certain weight-exact functors are ‘conservative up to weight-degenerate objects’.
$\underline {C}$
), so we formulate Theorem 3.1.3 that is central for this paper. We also give applications to intersections of purely generated subcategories and prove that certain weight-exact functors are ‘conservative up to weight-degenerate objects’.
In §4, we study purely compactly generated categories. We also consider equivariant stable homotopy examples to obtain certain converse stable Hurewicz theorems (see Theorems 4.2.2 and 4.2.4) and several related statements (including the aforementioned Theorem 4.2.5).
The author is deeply grateful to the referees for really actual comments.
An alternative version of this paper can be found at [Reference Bondarko6]. Another closely related text is the new [Reference Bondarko and Vostokov12]; see Remark 2.3.2(2) below.
1 Weight structures: reminder
In §1.1, we introduce some notation and conventions. In §1.2, we recall some basics on weight structures. The only new statement of this section is the technical (yet important) Lemma 1.2.7(2).
In §1.3, we recall some properties of weight complex functors and of the weak homotopy equivalence relation for morphisms between complexes.
1.1 Some (categorical) notation
-
• Let C be a category and
 $X,Y\in \operatorname {Obj} C$
. Then we will write
$X,Y\in \operatorname {Obj} C$
. Then we will write
 $C(X,Y)$
for the set of morphisms from X to Y in C.
$C(X,Y)$
for the set of morphisms from X to Y in C. -
• We say that X is a retract of Y if
 $\operatorname {id}_X$
can be factored through Y.
$\operatorname {id}_X$
can be factored through Y. -
• A subcategory
 $\mathcal {P}$
of an additive category C is said to be retraction-closed in C if it contains all retracts of its objects in C.
$\mathcal {P}$
of an additive category C is said to be retraction-closed in C if it contains all retracts of its objects in C. -
• For any
 $(C,\mathcal {P})$
as above the full subcategory
$(C,\mathcal {P})$
as above the full subcategory
 $\operatorname {\mathrm {\operatorname {Kar}}}_{C}(\mathcal {P})$
of C whose objects are all retracts of finite direct sums of objects
$\operatorname {\mathrm {\operatorname {Kar}}}_{C}(\mathcal {P})$
of C whose objects are all retracts of finite direct sums of objects
 $\mathcal {P}$
in C will be called the retraction-closure of
$\mathcal {P}$
in C will be called the retraction-closure of
 $\mathcal {P}$
in C. Note that this subcategory is obviously additive and retraction-closed in C.
$\mathcal {P}$
in C. Note that this subcategory is obviously additive and retraction-closed in C. -
• Below
 $\underline {A}$
will always denote some abelian category;
$\underline {A}$
will always denote some abelian category;
 $\underline {B}$
is an additive category.
$\underline {B}$
is an additive category. -
• We will write
 $\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
(no lower index) for the idempotent completion
$\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
(no lower index) for the idempotent completion
 $\underline {B}$
; see Definition 1.2 of [Reference Balmer and Schlichting1]. Recall that its objects are the pairs
$\underline {B}$
; see Definition 1.2 of [Reference Balmer and Schlichting1]. Recall that its objects are the pairs
 $(A,p)$
for
$(A,p)$
for
 $A\in \operatorname {Obj} \underline {B},\ p\in \underline {B}(A,A),\ p^2=p$
; the correspondence
$A\in \operatorname {Obj} \underline {B},\ p\in \underline {B}(A,A),\ p^2=p$
; the correspondence
 $A\mapsto (A,\operatorname {id}_A)$
(for
$A\mapsto (A,\operatorname {id}_A)$
(for
 $A\in \operatorname {Obj} \underline {B}$
) fully embeds
$A\in \operatorname {Obj} \underline {B}$
) fully embeds
 $\underline {B}$
into
$\underline {B}$
into
 $\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
; see Proposition 1.3 and Remark 1.4 of loc. cit. Moreover,
$\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
; see Proposition 1.3 and Remark 1.4 of loc. cit. Moreover,
 $\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
is Karoubian, that is, every idempotent morphism gives a direct sum decomposition in
$\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
is Karoubian, that is, every idempotent morphism gives a direct sum decomposition in
 $\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
, and
$\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
, and
 $\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
is triangulated if
$\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
is triangulated if
 $\underline {B}$
is; see Theorem 1.5 of loc. cit.
$\underline {B}$
is; see Theorem 1.5 of loc. cit. -
• The symbol
 $\underline {C}$
below will always denote some triangulated category. Usually it is endowed with a weight structure w. The symbols
$\underline {C}$
below will always denote some triangulated category. Usually it is endowed with a weight structure w. The symbols
 $\underline {C}'$
and
$\underline {C}'$
and
 $\underline {D}$
will also be used for triangulated categories only.
$\underline {D}$
will also be used for triangulated categories only. -
• For any
 $A,B,C \in \operatorname {Obj}\underline {C}$
we say that C is an extension of B by A if there exists a distinguished triangle
$A,B,C \in \operatorname {Obj}\underline {C}$
we say that C is an extension of B by A if there exists a distinguished triangle
 $A \stackrel {f}{\to } C \to B \to A[1]$
.
$A \stackrel {f}{\to } C \to B \to A[1]$
.Moreover, we will write
 $B=\operatorname {\mathrm {\operatorname {Cone}}}(f)$
. Recall here that different choices of cones are connected by nonunique isomorphisms.
$B=\operatorname {\mathrm {\operatorname {Cone}}}(f)$
. Recall here that different choices of cones are connected by nonunique isomorphisms. -
• For
 $X,Y\in \operatorname {Obj} \underline {C}$
we write
$X,Y\in \operatorname {Obj} \underline {C}$
we write
 $X\perp Y$
if
$X\perp Y$
if
 $\underline {C}(X,Y)=\{0\}$
. If D and E are classes of objects or subcategories of
$\underline {C}(X,Y)=\{0\}$
. If D and E are classes of objects or subcategories of
 $\underline {C}$
, then we will write
$\underline {C}$
, then we will write
 $D\perp E$
if
$D\perp E$
if
 $X\perp Y$
for all
$X\perp Y$
for all
 $X\in D,\ Y\in E$
. Moreover, we write
$X\in D,\ Y\in E$
. Moreover, we write
 $D^\perp $
for the class dually,
$D^\perp $
for the class dually, $$ \begin{align*}\{Y\in \operatorname{Obj} \underline{C}:\ X\perp Y\ \forall X\in D\};\end{align*} $$
$$ \begin{align*}\{Y\in \operatorname{Obj} \underline{C}:\ X\perp Y\ \forall X\in D\};\end{align*} $$
 ${}^\perp {}D$
is the class
${}^\perp {}D$
is the class
 $ \{Y\in \operatorname {Obj} \underline {C}:\ Y\perp X\ \forall X\in D\}$
.
$ \{Y\in \operatorname {Obj} \underline {C}:\ Y\perp X\ \forall X\in D\}$
.
-
• We write
 $C(\underline {B})$
for the category of cohomological complexes in
$C(\underline {B})$
for the category of cohomological complexes in
 $\underline {B}$
, and the corresponding homotopy category will be denoted by
$\underline {B}$
, and the corresponding homotopy category will be denoted by
 $K(\underline {B})$
. We will write
$K(\underline {B})$
. We will write
 $M=(M^i)$
if
$M=(M^i)$
if
 $M^i$
are the terms of the complex M.
$M^i$
are the terms of the complex M. -
• We say that an additive covariant (resp. contravariant) functor H from
 $\underline {C}$
into
$\underline {C}$
into
 $\underline {A}$
is homological (resp. cohomological) if it converts distinguished triangles into long exact sequences. We will write
$\underline {A}$
is homological (resp. cohomological) if it converts distinguished triangles into long exact sequences. We will write
 $H_i$
(resp.
$H_i$
(resp.
 $H^i$
) for the composition
$H^i$
) for the composition
 $H\circ [-i]$
.
$H\circ [-i]$
.
1.2 Weight structures: basics
Definition 1.2.1. We say that subclasses
![]() $\underline {C}_{w\le 0}$
and
$\underline {C}_{w\le 0}$
and
![]() $\underline {C}_{w\ge 0}\subset \operatorname {Obj} \underline {C}$
give a weight structure w or
$\underline {C}_{w\ge 0}\subset \operatorname {Obj} \underline {C}$
give a weight structure w or
![]() $(\underline {C},w)$
on a triangulated category
$(\underline {C},w)$
on a triangulated category
![]() $\underline {C}$
and that
$\underline {C}$
and that
![]() $\underline {C}$
is weighted if the following conditions are fulfilled.
$\underline {C}$
is weighted if the following conditions are fulfilled.
(i)
![]() $\underline {C}_{w\ge 0}$
and
$\underline {C}_{w\ge 0}$
and
![]() $\underline {C}_{w\le 0}$
are retraction-closed in
$\underline {C}_{w\le 0}$
are retraction-closed in
![]() $\underline {C}$
, that is, they contain all
$\underline {C}$
, that is, they contain all
![]() $\underline {C}$
-retracts of their objects).
$\underline {C}$
-retracts of their objects).
(ii)
![]() $\underline {C}_{w\le 0}\subset \underline {C}_{w\le 0}[1]$
and
$\underline {C}_{w\le 0}\subset \underline {C}_{w\le 0}[1]$
and
![]() $\underline {C}_{w\ge 0}[1]\subset \underline {C}_{w\ge 0}$
.
$\underline {C}_{w\ge 0}[1]\subset \underline {C}_{w\ge 0}$
.
(iii) Orthogonality:
![]() $\underline {C}_{w\le 0}\perp \underline {C}_{w\ge 0}[1]$
.
$\underline {C}_{w\le 0}\perp \underline {C}_{w\ge 0}[1]$
.
(iv) For any
![]() $M\in \operatorname {Obj} \underline {C}$
there exists a distinguished triangle
$M\in \operatorname {Obj} \underline {C}$
there exists a distinguished triangle
such that
![]() $LM\in \underline {C}_{w\le 0} $
and
$LM\in \underline {C}_{w\le 0} $
and
![]() $ RM\in \underline {C}_{w\ge 0}[1]$
.
$ RM\in \underline {C}_{w\ge 0}[1]$
.
We also need the following definitions.
Definition 1.2.2. Assume that
![]() $i,j\in {\mathbb {Z}}$
and
$i,j\in {\mathbb {Z}}$
and
![]() $(\underline {C},w)$
is a weight structure.
$(\underline {C},w)$
is a weight structure.
-
1. The full subcategory
 ${\underline {Hw}}$
of
${\underline {Hw}}$
of
 $ \underline {C}$
whose objects are
$ \underline {C}$
whose objects are
 $\underline {C}_{w=0}=\underline {C}_{w\ge 0}\cap \underline {C}_{w\le 0}$
is called the heart of w.
$\underline {C}_{w=0}=\underline {C}_{w\ge 0}\cap \underline {C}_{w\le 0}$
is called the heart of w. -
2.
 $\underline {C}_{w\ge i}$
(resp.
$\underline {C}_{w\ge i}$
(resp.
 $\underline {C}_{w\le i}$
, resp.
$\underline {C}_{w\le i}$
, resp.
 $\underline {C}_{w= i}$
) will denote the class
$\underline {C}_{w= i}$
) will denote the class
 $\underline {C}_{w\ge 0}[i]$
(resp.
$\underline {C}_{w\ge 0}[i]$
(resp.
 $\underline {C}_{w\le 0}[i]$
, resp.
$\underline {C}_{w\le 0}[i]$
, resp.
 $\underline {C}_{w= 0}[i]$
).
$\underline {C}_{w= 0}[i]$
). -
3.
 $\underline {C}_{[i,j]}$
denotes
$\underline {C}_{[i,j]}$
denotes
 $\underline {C}_{w\ge i}\cap \underline {C}_{w\le j}$
, so, this class equals
$\underline {C}_{w\ge i}\cap \underline {C}_{w\le j}$
, so, this class equals
 $\{0\}$
if
$\{0\}$
if
 $i>j$
.
$i>j$
. -
4. We will say that
 $\underline {C}$
(or
$\underline {C}$
(or
 $(\underline {C},w)$
) is weight-Karoubian if
$(\underline {C},w)$
) is weight-Karoubian if
 ${\underline {Hw}}$
is Karoubian.
${\underline {Hw}}$
is Karoubian. -
5. Let
 $\underline {C}'$
be a triangulated category endowed with a weight structure
$\underline {C}'$
be a triangulated category endowed with a weight structure
 $w'$
; let
$w'$
; let
 $F:\underline {C}\to \underline {C}'$
be an exact functor.
$F:\underline {C}\to \underline {C}'$
be an exact functor.Then F is said to be weight-exact with respect to
 $w,w'$
if it maps
$w,w'$
if it maps
 $\underline {C}_{w\le 0}$
into
$\underline {C}_{w\le 0}$
into
 $\underline {C}^{\prime }_{w'\le 0}$
and sends
$\underline {C}^{\prime }_{w'\le 0}$
and sends
 $\underline {C}_{w\ge 0}$
into
$\underline {C}_{w\ge 0}$
into
 $\underline {C}^{\prime }_{w'\ge 0}$
.
$\underline {C}^{\prime }_{w'\ge 0}$
. -
6. Let
 $\underline {D}$
be a full triangulated subcategory of
$\underline {D}$
be a full triangulated subcategory of
 $\underline {C}$
.
$\underline {C}$
.We will say that w restricts to
 $\underline {D}$
whenever the couple
$\underline {D}$
whenever the couple
 $(\underline {C}_{w\le 0}\cap \operatorname {Obj} \underline {D},\ \underline {C}_{w\ge 0}\cap \operatorname {Obj} \underline {D})$
is a weight structure on
$(\underline {C}_{w\le 0}\cap \operatorname {Obj} \underline {D},\ \underline {C}_{w\ge 0}\cap \operatorname {Obj} \underline {D})$
is a weight structure on
 $\underline {D}$
.
$\underline {D}$
. -
7. We say that M is left (resp., right) w-degenerate (or weight-degenerate if the choice of w is clear) if M belongs to
 $ \cap _{i\in {\mathbb {Z}}}\underline {C}_{w\ge i}$
(resp. to
$ \cap _{i\in {\mathbb {Z}}}\underline {C}_{w\ge i}$
(resp. to
 $\cap _{i\in {\mathbb {Z}}}\underline {C}_{w\le i}$
).
$\cap _{i\in {\mathbb {Z}}}\underline {C}_{w\le i}$
). -
8. We call
 $\cup _{i\in {\mathbb {Z}}} \underline {C}_{w\ge i}$
(resp.
$\cup _{i\in {\mathbb {Z}}} \underline {C}_{w\ge i}$
(resp.
 $\cup _{i\in {\mathbb {Z}}} \underline {C}_{w\le i}$
) the class of w-bounded below (resp., w-bounded above) objects of
$\cup _{i\in {\mathbb {Z}}} \underline {C}_{w\le i}$
) the class of w-bounded below (resp., w-bounded above) objects of
 $\underline {C}$
.
$\underline {C}$
. -
9. We will say that w is bounded if every object of
 $\underline {C}$
is w-bounded both above and below.
$\underline {C}$
is w-bounded both above and below.
Remark 1.2.3. 1. For an arbitrary additive
![]() $\underline {B}$
one can take
$\underline {B}$
one can take
![]() $\underline {C}=K(\underline {B})$
and set
$\underline {C}=K(\underline {B})$
and set
![]() $K(\underline {B})_{w^{st}\le 0}$
(resp.
$K(\underline {B})_{w^{st}\le 0}$
(resp.
![]() $K(\underline {B})_{w^{st}\ge 0}$
) to be the class of complexes
$K(\underline {B})_{w^{st}\ge 0}$
) to be the class of complexes
![]() $\underline {C}$
-isomorphic to complexes concentrated in degrees
$\underline {C}$
-isomorphic to complexes concentrated in degrees
![]() $\ge 0$
(resp.
$\ge 0$
(resp.
![]() $\le 0$
); see Remark 1.2.3(1) of [Reference Bondarko and Sosnilo9] for more detail. We will use this notation below.
$\le 0$
); see Remark 1.2.3(1) of [Reference Bondarko and Sosnilo9] for more detail. We will use this notation below.
The heart of this weight structure
![]() $w^{st}$
is the retraction-closure of
$w^{st}$
is the retraction-closure of
![]() $\underline {B}$
in
$\underline {B}$
in
![]() $K(\underline {B})$
; hence it is equivalent to
$K(\underline {B})$
; hence it is equivalent to
![]() $\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
.
$\operatorname {\mathrm {\operatorname {Kar}}}(\underline {B})$
.
2. The distinguished triangle in axiom (iv) is not determined by M.
Still for every
![]() $m\in {\mathbb {Z}}$
this axiom yields a distinguished triangle
$m\in {\mathbb {Z}}$
this axiom yields a distinguished triangle
with some
![]() $ w_{\le m}M\in \underline {C}_{w\le m}$
and
$ w_{\le m}M\in \underline {C}_{w\le m}$
and
![]() $ w_{\ge m+1}M\in \underline {C}_{w\ge m+1}$
. We notate this triangle with
$ w_{\ge m+1}M\in \underline {C}_{w\ge m+1}$
. We notate this triangle with
![]() $WD_m(M)$
and call
$WD_m(M)$
and call
![]() $WD_m(M)$
an m-weight decomposition of M.
$WD_m(M)$
an m-weight decomposition of M.
We will often use this notation below even though
![]() $w_{\ge m+1}M$
and
$w_{\ge m+1}M$
and
![]() $ w_{\le m}M$
are not canonically determined by M. We call any possible choice either of
$ w_{\le m}M$
are not canonically determined by M. We call any possible choice either of
![]() $w_{\ge m+1}M$
or of
$w_{\ge m+1}M$
or of
![]() $ w_{\le m}M$
a weight truncation of M. Moreover, when we write arrows of the type
$ w_{\le m}M$
a weight truncation of M. Moreover, when we write arrows of the type
![]() $w_{\le m}M\to M$
or
$w_{\le m}M\to M$
or
![]() $M\to w_{\ge m+1}M$
we always assume that they come from some m-weight decomposition of M.
$M\to w_{\ge m+1}M$
we always assume that they come from some m-weight decomposition of M.
3. In the current paper (along with several previous ones) we use the ‘homological convention’ for weight structures, whereas in [Reference Bondarko4] the cohomological convention was used. In the latter convention, the roles of
![]() $\underline {C}_{w\le 0}$
and
$\underline {C}_{w\le 0}$
and
![]() $\underline {C}_{w\ge 0}$
are interchanged, that is, one takes
$\underline {C}_{w\ge 0}$
are interchanged, that is, one takes
![]() $\underline {C}^{w\le 0}=\underline {C}_{w\ge 0}$
and
$\underline {C}^{w\le 0}=\underline {C}_{w\ge 0}$
and
![]() $\underline {C}^{w\ge 0}=\underline {C}_{w\le 0}$
.
$\underline {C}^{w\ge 0}=\underline {C}_{w\le 0}$
.
We also recall that weight structures were independently introduced in [Reference Pauksztello24]; D. Pauksztello has called them co-t-structures.
Proposition 1.2.4. Let
![]() $m\le n\in {\mathbb {Z}}$
,
$m\le n\in {\mathbb {Z}}$
,
![]() $M,M'\in \operatorname {Obj} \underline {C}$
.
$M,M'\in \operatorname {Obj} \underline {C}$
.
-
1. The axiomatics of weight structures is self-dual, that is, on
 $\underline {C}'=\underline {C}^{op}$
(so
$\underline {C}'=\underline {C}^{op}$
(so
 $\operatorname {Obj}\underline {C}'=\operatorname {Obj}\underline {C}$
) there exists the opposite weight structure
$\operatorname {Obj}\underline {C}'=\operatorname {Obj}\underline {C}$
) there exists the opposite weight structure
 $w^{op}$
for which
$w^{op}$
for which
 $\underline {C}^{\prime }_{w^{op}\le 0}=\underline {C}_{w\ge 0}$
and
$\underline {C}^{\prime }_{w^{op}\le 0}=\underline {C}_{w\ge 0}$
and
 $\underline {C}^{\prime }_{w^{op}\ge 0}=\underline {C}_{w\le 0}$
.
$\underline {C}^{\prime }_{w^{op}\ge 0}=\underline {C}_{w\le 0}$
. -
2.
 $\underline {C}_{w\ge 0}=(\underline {C}_{w\le -1})^{\perp }$
and
$\underline {C}_{w\ge 0}=(\underline {C}_{w\le -1})^{\perp }$
and
 $\underline {C}_{w\le 0}={}^{\perp } \underline {C}_{w\ge 1}$
.
$\underline {C}_{w\le 0}={}^{\perp } \underline {C}_{w\ge 1}$
. -
3.
 $\underline {C}_{w\le 0}$
is closed with respect to all coproducts that exist in
$\underline {C}_{w\le 0}$
is closed with respect to all coproducts that exist in
 $\underline {C}$
.
$\underline {C}$
. -
4.
 $\underline {C}_{w\le 0}$
,
$\underline {C}_{w\le 0}$
,
 $\underline {C}_{w\ge 0}$
, and
$\underline {C}_{w\ge 0}$
, and
 $\underline {C}_{w=0}$
are additive.
$\underline {C}_{w=0}$
are additive. -
5. If
 $M\in \underline {C}_{w\ge m}$
, then
$M\in \underline {C}_{w\ge m}$
, then
 $w_{\le n}M\in \underline {C}_{[m,n]}$
for every n-weight decomposition of M. Dually, if
$w_{\le n}M\in \underline {C}_{[m,n]}$
for every n-weight decomposition of M. Dually, if
 $M\in \underline {C}_{w\le n}$
, then
$M\in \underline {C}_{w\le n}$
, then
 $w_{\ge m}M\in \underline {C}_{[m,n]}$
.
$w_{\ge m}M\in \underline {C}_{[m,n]}$
. -
6. Assume
 $g\in \underline {C}(M,M')$
. If
$g\in \underline {C}(M,M')$
. If
 $M'\in \underline {C}_{w\ge m}$
, then g factors through
$M'\in \underline {C}_{w\ge m}$
, then g factors through
 $w_{\ge m}M$
for any choice of the latter object.
$w_{\ge m}M$
for any choice of the latter object.Dually, if
 $M\in \underline {C}_{w\le m}$
, then g factors through
$M\in \underline {C}_{w\le m}$
, then g factors through
 $w_{\le m}M'$
.
$w_{\le m}M'$
. -
7. If
 $\underline {C}$
is Karoubian, then it is also weight-Karoubian.
$\underline {C}$
is Karoubian, then it is also weight-Karoubian.
Proof. Assertions 1–5 were proved in [Reference Bondarko4] (cf. Remark 1.2.3(4) of [Reference Bondarko and Sosnilo9] and pay attention to Remark 1.2.3(3) above!), whereas the easy assertion 6 is given by Proposition 1.2.4(8) of [Reference Bondarko7].
Now we will study certain morphisms between weight decompositions.
Definition 1.2.5. Adopt the notation and assumptions of Remark 1.2.3(2); let
![]() $m'\in {\mathbb {Z}}$
. Then a morphism of triangles
$m'\in {\mathbb {Z}}$
. Then a morphism of triangles

will be said to be a morphism
![]() $WD_m(M)\to WD_{m'}(M')$
that extends
$WD_m(M)\to WD_{m'}(M')$
that extends
![]() $g:M\to M'$
. We will say that the morphisms h and j are w-truncations of g.
$g:M\to M'$
. We will say that the morphisms h and j are w-truncations of g.
Remark 1.2.6. Clearly, one can compose morphisms of weight decompositions. That is, for a morphism
![]() $WD_m(M)\to WD_{m'}(M')$
as above,
$WD_m(M)\to WD_{m'}(M')$
as above,
![]() $m"\in {\mathbb {Z}}$
, and any morphism
$m"\in {\mathbb {Z}}$
, and any morphism
![]() $WD_{m'}(M')\to WD_{m"}(M")$
that extends any
$WD_{m'}(M')\to WD_{m"}(M")$
that extends any
![]() $g'\in \underline {C}(M',M")$
one can compose the corresponding arrows (provided that the corresponding choices of
$g'\in \underline {C}(M',M")$
one can compose the corresponding arrows (provided that the corresponding choices of
![]() $WD_{m'}(M')$
coincide) to obtain a morphism
$WD_{m'}(M')$
coincide) to obtain a morphism
![]() $WD_m(M)\to WD_{m"}(M")$
that extends
$WD_m(M)\to WD_{m"}(M")$
that extends
![]() $g'\circ g$
.
$g'\circ g$
.
Lemma 1.2.7. Adopt the notation of Definition 1.2.5, and assume
![]() $m'\ge m$
.
$m'\ge m$
.
1. Then an extension of g to a morphism
![]() $WD_m(M)\to WD_{m'}(M')$
exists. Moreover, this extension is unique if
$WD_m(M)\to WD_{m'}(M')$
exists. Moreover, this extension is unique if
![]() $m'>m$
; consequently, in this case the morphism h (resp. j) is the only one that makes the left- (resp. right-) hand square in diagram 1.2.2 commutative.
$m'>m$
; consequently, in this case the morphism h (resp. j) is the only one that makes the left- (resp. right-) hand square in diagram 1.2.2 commutative.
2. Assume that the rows of diagram 1.2.2 are equal,
![]() $g=\operatorname {id}_M$
,
$g=\operatorname {id}_M$
,
![]() $m=m'$
,
$m=m'$
,
![]() $h^2=h$
, and
$h^2=h$
, and
![]() $(\underline {C},w)$
is weight-Karoubian. Then there exists a decomposition
$(\underline {C},w)$
is weight-Karoubian. Then there exists a decomposition
![]() $w_{\le m} M\cong M_1\bigoplus M_0$
such that h corresponds to
$w_{\le m} M\cong M_1\bigoplus M_0$
such that h corresponds to
![]() $\operatorname {id}_{M_1}\bigoplus 0_{M_0}$
, and the rows of (1.2.2) can be presented as the direct sum of the corresponding two arrows in some m-weight decomposition
$\operatorname {id}_{M_1}\bigoplus 0_{M_0}$
, and the rows of (1.2.2) can be presented as the direct sum of the corresponding two arrows in some m-weight decomposition
![]() $M_1\to M\to M_2$
with
$M_1\to M\to M_2$
with
![]() $(M_0\to 0 \to M_0[1])$
.
$(M_0\to 0 \to M_0[1])$
.
Proof. 1. This is Lemma 1.5.1(1,2) of [Reference Bondarko4].
2. Take a triangulated category
![]() $\underline {C}'$
that is equivalent to
$\underline {C}'$
that is equivalent to
![]() $\operatorname {\mathrm {\operatorname {Kar}}}(\underline {C})$
and contains
$\operatorname {\mathrm {\operatorname {Kar}}}(\underline {C})$
and contains
![]() $\underline {C}$
as a (full) strict subcategory. Consider the decomposition
$\underline {C}$
as a (full) strict subcategory. Consider the decomposition
![]() $w_{\le m}M\cong M_1\bigoplus M_0$
corresponding to h in
$w_{\le m}M\cong M_1\bigoplus M_0$
corresponding to h in
![]() $\underline {C}'$
. Since the diagram 1.2.2 is commutative,
$\underline {C}'$
. Since the diagram 1.2.2 is commutative,
![]() $c=c\circ h$
; thus, c factors through
$c=c\circ h$
; thus, c factors through
![]() $M_1$
. Hence, the rows of diagram 1.2.2 can be decomposed into the direct sum of the
$M_1$
. Hence, the rows of diagram 1.2.2 can be decomposed into the direct sum of the
![]() $\underline {C}'$
-distinguished triangle
$\underline {C}'$
-distinguished triangle
![]() $M_0\to 0 \to M_0[1]$
with a distinguished triangle
$M_0\to 0 \to M_0[1]$
with a distinguished triangle
![]() $M_1\to M\to M_2$
. Thus,
$M_1\to M\to M_2$
. Thus,
![]() $M_0$
is a retract of
$M_0$
is a retract of
![]() $w_{\ge m+1}M[-1]$
as well. Hence, the morphism
$w_{\ge m+1}M[-1]$
as well. Hence, the morphism
![]() $\operatorname {id}_{M_0}$
factors through some morphism
$\operatorname {id}_{M_0}$
factors through some morphism
![]() $a: w_{\le m} M\to w_{\ge m+1}M[-1]$
. Next, Proposition 1.2.4(6) implies that a factors through
$a: w_{\le m} M\to w_{\ge m+1}M[-1]$
. Next, Proposition 1.2.4(6) implies that a factors through
![]() $N=w_{\ge m}(w_{\le m} M)$
; thus,
$N=w_{\ge m}(w_{\le m} M)$
; thus,
![]() $M_0$
is a retract of N. Since N belongs to
$M_0$
is a retract of N. Since N belongs to
![]() $\underline {C}_{w=m}$
by Proposition 1.2.4(5) and
$\underline {C}_{w=m}$
by Proposition 1.2.4(5) and
![]() ${\underline {Hw}}$
is Karoubian,
${\underline {Hw}}$
is Karoubian,
![]() $M_0$
belongs to
$M_0$
belongs to
![]() $\underline {C}_{w=m}\subset \operatorname {Obj} \underline {C}$
. It follows that
$\underline {C}_{w=m}\subset \operatorname {Obj} \underline {C}$
. It follows that
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are objects of
$M_2$
are objects of
![]() $\underline {C}$
as well. Applying axiom (i) of Definition 1.2.1 we obtain
$\underline {C}$
as well. Applying axiom (i) of Definition 1.2.1 we obtain
![]() $M_1\in \underline {C}_{w \le m}$
and
$M_1\in \underline {C}_{w \le m}$
and
![]() $M_2\in \underline {C}_{w \ge m+1}$
; hence,
$M_2\in \underline {C}_{w \ge m+1}$
; hence,
![]() $M_1\to M\to M_2\to M_1[1]$
is an m-weight decomposition of M indeed.
$M_1\to M\to M_2\to M_1[1]$
is an m-weight decomposition of M indeed.
1.3 On weight complexes and weak homotopy equivalences
To define the weight complex functor, we need the following definition. Recall here that
![]() $\underline {B}$
is an additive category and
$\underline {B}$
is an additive category and
![]() $C(\underline {B})$
is the category of
$C(\underline {B})$
is the category of
![]() $\underline {B}$
-complexes.
$\underline {B}$
-complexes.
Definition 1.3.1. Let M and N be objects of
![]() $K(\underline {B})$
and
$K(\underline {B})$
and
![]() $m_1,m_2\in C(\underline {B})(M,N)$
.
$m_1,m_2\in C(\underline {B})(M,N)$
.
1. We write
![]() $m_1\backsim m_2$
if
$m_1\backsim m_2$
if
![]() $m_1-m_2=d_Nx+yd_M$
for some collections
$m_1-m_2=d_Nx+yd_M$
for some collections
![]() $x^*,y^*\in \underline {B}(M^*, N^{*-1})$
, where
$x^*,y^*\in \underline {B}(M^*, N^{*-1})$
, where
![]() $d_M$
and
$d_M$
and
![]() $d_N$
are the corresponding differentials. We call this relation the weak homotopy equivalence relation.
$d_N$
are the corresponding differentials. We call this relation the weak homotopy equivalence relation.
2. Assume
![]() $k\le l\in (\{-\infty \}\cup {\mathbb {Z}}\cup \{+\infty \})$
; also,
$k\le l\in (\{-\infty \}\cup {\mathbb {Z}}\cup \{+\infty \})$
; also,
![]() $k\in {\mathbb {Z}}$
if
$k\in {\mathbb {Z}}$
if
![]() $k=l$
.
$k=l$
.
Then we write
![]() $m_1\backsim _{[k,l]}m_2$
if
$m_1\backsim _{[k,l]}m_2$
if
![]() $m_1-m_2$
is weakly homotopic to
$m_1-m_2$
is weakly homotopic to
![]() $ m_0\in C(M,N)$
such that
$ m_0\in C(M,N)$
such that
![]() $m_0^i=0$
for
$m_0^i=0$
for
![]() $k\le i \le l$
(and
$k\le i \le l$
(and
![]() $i\in {\mathbb {Z}}$
).
$i\in {\mathbb {Z}}$
).
We need the following properties of these equivalence relations.
Lemma 1.3.2. Adopt the notation of Definition 1.3.1.
-
1. Factoring morphisms in
 $K(\underline {B})$
by the weak homotopy relation yields an additive category
$K(\underline {B})$
by the weak homotopy relation yields an additive category
 $K_{\mathfrak {w}}(\underline {B})$
. Moreover, the corresponding full functor
$K_{\mathfrak {w}}(\underline {B})$
. Moreover, the corresponding full functor
 $p_w:K(\underline {B})\to K_{\mathfrak {w}}(\underline {B})$
is additive and conservative.
$p_w:K(\underline {B})\to K_{\mathfrak {w}}(\underline {B})$
is additive and conservative. -
2. Let
 ${\mathcal {A}}:\underline {B}\to \underline {A}$
be an additive functor, where
${\mathcal {A}}:\underline {B}\to \underline {A}$
be an additive functor, where
 $\underline {A}$
is any abelian category, and
$\underline {A}$
is any abelian category, and
 $m_1$
is weakly homotopic to
$m_1$
is weakly homotopic to
 $m_2$
. Then
$m_2$
. Then
 $m_1$
and
$m_1$
and
 $m_2$
induce equal morphisms of the homology
$m_2$
induce equal morphisms of the homology
 $H_*({\mathcal {A}}(M^i))\to H_*({\mathcal {A}}(N^i))$
.
$H_*({\mathcal {A}}(M^i))\to H_*({\mathcal {A}}(N^i))$
.Hence, the correspondence
 $N\mapsto H_0({\mathcal {A}}(N^i))$
gives a well-defined functor
$N\mapsto H_0({\mathcal {A}}(N^i))$
gives a well-defined functor
 $K_{\mathfrak {w}}(\underline {B})\to \underline {A}$
.
$K_{\mathfrak {w}}(\underline {B})\to \underline {A}$
. -
3. Applying an additive functor
 $F:\underline {B}\to \underline {B}'$
to complexes termwisely, one obtains an additive functor
$F:\underline {B}\to \underline {B}'$
to complexes termwisely, one obtains an additive functor
 $K_{\mathfrak {w}}(F):K_{\mathfrak {w}}(\underline {B})\to K_{\mathfrak {w}}(\underline {B}')$
.
$K_{\mathfrak {w}}(F):K_{\mathfrak {w}}(\underline {B})\to K_{\mathfrak {w}}(\underline {B}')$
. -
4.
 $m_1\backsim _{[k,l]}m_2$
if and only if
$m_1\backsim _{[k,l]}m_2$
if and only if
 $m_1\backsim _{[i,i]}m_2$
for any
$m_1\backsim _{[i,i]}m_2$
for any
 $i\in {\mathbb {Z}}$
such that
$i\in {\mathbb {Z}}$
such that
 $k\le i \le l$
.
$k\le i \le l$
. -
5. If
 $k\in {\mathbb {Z}}$
, then
$k\in {\mathbb {Z}}$
, then
 $m_1\backsim _{[k,k]}0$
if and only if there exists
$m_1\backsim _{[k,k]}0$
if and only if there exists
 $m_0\in C(\underline {B})(M,N)$
such that
$m_0\in C(\underline {B})(M,N)$
such that
 $m_1=m_0$
in
$m_1=m_0$
in
 $K(\underline {B})(M,N)$
and
$K(\underline {B})(M,N)$
and
 $m_0^k=0$
.
$m_0^k=0$
. -
6. M belongs to
 $ K(\underline {B})_{w^{st}\ge 0}$
if and only if
$ K(\underline {B})_{w^{st}\ge 0}$
if and only if
 $\operatorname {id}_M \backsim _{[1,+\infty ]}0_M$
, and
$\operatorname {id}_M \backsim _{[1,+\infty ]}0_M$
, and
 $M\in K(\underline {B})_{w^{st}\le 0}$
if and only if
$M\in K(\underline {B})_{w^{st}\le 0}$
if and only if
 $\operatorname {id}_M \backsim _{[-\infty ,-1]}0_M$
.
$\operatorname {id}_M \backsim _{[-\infty ,-1]}0_M$
.
Proof. Assertion 3 is obvious, and the remaining ones are contained in Proposition B.2 of [Reference Bondarko7].
Let us describe the approach to weight complexes that we use below.
Remark 1.3.3.
-
1. In the current paper, we consider an additive weight complex functor
 $t:\underline {C}\to K_{\mathfrak {w}}({\underline {Hw}})$
for any triangulated category
$t:\underline {C}\to K_{\mathfrak {w}}({\underline {Hw}})$
for any triangulated category
 $\underline {C}$
endowed with a weight structure w. Still to define a canonical functor of this sort one has to replace
$\underline {C}$
endowed with a weight structure w. Still to define a canonical functor of this sort one has to replace
 $\underline {C}$
by a certain equivalent category
$\underline {C}$
by a certain equivalent category
 $\underline {C}_w$
; see §1.3 of [Reference Bondarko7] (and cf. Remark A.2.1(3) of ibid. where the inaccuracies made in [Reference Bondarko4, §3] are discussed). Thus, to define t one should compose the additive ‘canonical weight complex functor’
$\underline {C}_w$
; see §1.3 of [Reference Bondarko7] (and cf. Remark A.2.1(3) of ibid. where the inaccuracies made in [Reference Bondarko4, §3] are discussed). Thus, to define t one should compose the additive ‘canonical weight complex functor’
 $t_{can}:\underline {C}_w\to K_{\mathfrak {w}}({\underline {Hw}})$
with a splitting s of the canonical equivalence
$t_{can}:\underline {C}_w\to K_{\mathfrak {w}}({\underline {Hw}})$
with a splitting s of the canonical equivalence
 $\underline {C}_w\to \underline {C}$
(see Proposition 1.3.4(3,6) of [Reference Bondarko7]). Clearly, any two splittings s of this sort are isomorphic; thus, we can assume that s is chosen, and so
$\underline {C}_w\to \underline {C}$
(see Proposition 1.3.4(3,6) of [Reference Bondarko7]). Clearly, any two splittings s of this sort are isomorphic; thus, we can assume that s is chosen, and so
 $t=t_{can}\circ s$
is fixed.
$t=t_{can}\circ s$
is fixed. -
2. Moreover, we have no need to describe weight complexes of all morphisms in
 $\underline {C}$
explicitly. We prefer to list a collection of properties of t instead. So, we only sketch the description of
$\underline {C}$
explicitly. We prefer to list a collection of properties of t instead. So, we only sketch the description of
 $t(M)$
for
$t(M)$
for
 $M\in \operatorname {Obj} \underline {C}$
. The details can be found in loc. cit.
$M\in \operatorname {Obj} \underline {C}$
. The details can be found in loc. cit.We choose arbitrary weight truncations
 $w_{\le n}M$
of M for all
$w_{\le n}M$
of M for all
 $n\in {\mathbb {Z}}$
and take
$n\in {\mathbb {Z}}$
and take
 $g_{n}:w_{\le n}M\to w_{\le n+1}M$
to be the corresponding w-truncations of
$g_{n}:w_{\le n}M\to w_{\le n+1}M$
to be the corresponding w-truncations of
 $\operatorname {id}_M$
in the sense of Definition 1.2.5. Denote
$\operatorname {id}_M$
in the sense of Definition 1.2.5. Denote
 $\operatorname {\mathrm {\operatorname {Cone}}}(g_n)$
by
$\operatorname {\mathrm {\operatorname {Cone}}}(g_n)$
by
 $M^{-n-1}[n+1]$
. It is easily seen that
$M^{-n-1}[n+1]$
. It is easily seen that
 $M^i\in \underline {C}_{w=0}$
for all
$M^i\in \underline {C}_{w=0}$
for all
 $i\in {\mathbb {Z}}$
and that the distinguished triangles coming from
$i\in {\mathbb {Z}}$
and that the distinguished triangles coming from
 $g_n$
connect these objects to form a complex
$g_n$
connect these objects to form a complex
 $(M^i)$
.
$(M^i)$
.Clearly, this complex depends on the choice of the objects
 $w_{\le n}M$
. However, for any choice of this form, we have
$w_{\le n}M$
. However, for any choice of this form, we have
 $(M^i)\cong t(M)$
in
$(M^i)\cong t(M)$
in
 $K({\underline {Hw}})$
. This isomorphism becomes canonical in
$K({\underline {Hw}})$
. This isomorphism becomes canonical in
 $K_{\mathfrak {w}}({\underline {Hw}})$
.
$K_{\mathfrak {w}}({\underline {Hw}})$
. -
3. t can ‘usually’ be enhanced to an exact ‘strong’ weight complex functor
 $t^{st}:\underline {C}\to K({\underline {Hw}})$
. This is currently known to be the case if
$t^{st}:\underline {C}\to K({\underline {Hw}})$
. This is currently known to be the case if
 $\underline {C}$
possesses an
$\underline {C}$
possesses an
 $\infty $
-enhancement and w is either bounded (see Definition 1.2.2(9) and Corollary 3.5 of [Reference Sosnilo26]) or is purely compactly generated as in Theorem 4.1.2 below (see Remark 3.6 of ibid.).Footnote
3
$\infty $
-enhancement and w is either bounded (see Definition 1.2.2(9) and Corollary 3.5 of [Reference Sosnilo26]) or is purely compactly generated as in Theorem 4.1.2 below (see Remark 3.6 of ibid.).Footnote
3
Consequently, the reader will not lose much if she assumes that
 $t^{st}$
exists throughout the paper.
$t^{st}$
exists throughout the paper. -
4. On the other hand, if
 $K_{\mathfrak {w}}(\underline {B})$
differs from
$K_{\mathfrak {w}}(\underline {B})$
differs from
 $K(\underline {B})$
(cf. Proposition 4.1.7(1) below) then
$K(\underline {B})$
(cf. Proposition 4.1.7(1) below) then
 $K_{\mathfrak {w}}(\underline {B})$
cannot be endowed with a triangulated category structure compatible with that for
$K_{\mathfrak {w}}(\underline {B})$
cannot be endowed with a triangulated category structure compatible with that for
 $K(\underline {B})$
, that is, the functor
$K(\underline {B})$
, that is, the functor
 $p_w:K(\underline {B})\to K_{\mathfrak {w}}(\underline {B})$
cannot be exact.
$p_w:K(\underline {B})\to K_{\mathfrak {w}}(\underline {B})$
cannot be exact.Indeed, Lemma 1.3.2(1) allows to reduce this claim to the following statement: If
 $p:\underline {C}\to \underline {C}'$
is a full conservative exact functor, then p is also faithful. Now, assume that
$p:\underline {C}\to \underline {C}'$
is a full conservative exact functor, then p is also faithful. Now, assume that
 $p(m)=0$
for some
$p(m)=0$
for some
 $\underline {C}$
-morphism
$\underline {C}$
-morphism
 $m:X\to Y$
and take the corresponding distinguished triangle Then
$m:X\to Y$
and take the corresponding distinguished triangle Then $$ \begin{align*}X\stackrel{m}{\to}Y\stackrel{n}{\to}Z\to X[1].\end{align*} $$
$$ \begin{align*}X\stackrel{m}{\to}Y\stackrel{n}{\to}Z\to X[1].\end{align*} $$
 $p(n)$
is split injective. Since p is full and conservative, the easy Lemma 1.5.2(1) of [Reference Bondarko7] says that n is split injective as well. Hence,
$p(n)$
is split injective. Since p is full and conservative, the easy Lemma 1.5.2(1) of [Reference Bondarko7] says that n is split injective as well. Hence,
 $m=0$
, and we obtain faithfulness.
$m=0$
, and we obtain faithfulness.
Now we list the main properties of our functor
![]() $t: \underline {C}\to K_{\mathfrak {w}}({\underline {Hw}})$
.
$t: \underline {C}\to K_{\mathfrak {w}}({\underline {Hw}})$
.
Proposition 1.3.4. Assume that
![]() $(\underline {C},w)$
is a weight structure, and
$(\underline {C},w)$
is a weight structure, and
![]() $M\stackrel {g}{\to } M'\stackrel {h}{\to }\operatorname {\mathrm {\operatorname {Cone}}}(g)$
are two sides of a
$M\stackrel {g}{\to } M'\stackrel {h}{\to }\operatorname {\mathrm {\operatorname {Cone}}}(g)$
are two sides of a
![]() $\underline {C}$
-distinguished triangle.
$\underline {C}$
-distinguished triangle.
-
1. Then
 $t\circ [n]_{\underline {C}}\cong [n]_{K_{\mathfrak {w}}({\underline {Hw}})}\circ t$
, where
$t\circ [n]_{\underline {C}}\cong [n]_{K_{\mathfrak {w}}({\underline {Hw}})}\circ t$
, where
 $[n]_{K_{\mathfrak {w}}({\underline {Hw}})}$
is the obvious shift by
$[n]_{K_{\mathfrak {w}}({\underline {Hw}})}$
is the obvious shift by
 $[n]$
endofunctor of the category
$[n]$
endofunctor of the category
 $K_{\mathfrak {w}}({\underline {Hw}})$
.
$K_{\mathfrak {w}}({\underline {Hw}})$
. -
2. There exists a lift of the
 $K_{\mathfrak {w}}({\underline {Hw}})$
-morphism chain to two sides of a distinguished triangle in
$K_{\mathfrak {w}}({\underline {Hw}})$
-morphism chain to two sides of a distinguished triangle in $$ \begin{align*}t(M)\stackrel{t(g)}{\to} t(M') \stackrel{t(h)}{\to} t(\operatorname{\mathrm{\operatorname{Cone}}}(g))\end{align*} $$
$$ \begin{align*}t(M)\stackrel{t(g)}{\to} t(M') \stackrel{t(h)}{\to} t(\operatorname{\mathrm{\operatorname{Cone}}}(g))\end{align*} $$
 $K({\underline {Hw}})$
.
$K({\underline {Hw}})$
.
-
3. If
 $M\in \underline {C}_{w\le n}$
(resp.
$M\in \underline {C}_{w\le n}$
(resp.
 $M\in \underline {C}_{w\ge n}$
), then
$M\in \underline {C}_{w\ge n}$
), then
 $t(M)$
belongs to
$t(M)$
belongs to
 $K({\underline {Hw}})_{w^{st}\le n}$
(resp. to
$K({\underline {Hw}})_{w^{st}\le n}$
(resp. to
 $K({\underline {Hw}})_{w^{st}\ge n}$
).
$K({\underline {Hw}})_{w^{st}\ge n}$
).Moreover, if M is left or right w-degenerate (see Definition 1.2.2(7)), then
 $t(M)=0$
.
$t(M)=0$
. -
4. Let
 $\underline {C}'$
be a triangulated category endowed with a weight structure
$\underline {C}'$
be a triangulated category endowed with a weight structure
 $w'$
; let
$w'$
; let
 $F:\underline {C}\to \underline {C}'$
be a weight-exact functor. Then the composition
$F:\underline {C}\to \underline {C}'$
be a weight-exact functor. Then the composition
 $t'\circ F$
is isomorphic to
$t'\circ F$
is isomorphic to
 $K_{\mathfrak {w}}({\underline {HF}})\circ t$
, where
$K_{\mathfrak {w}}({\underline {HF}})\circ t$
, where
 $t'$
is a weight complex functor corresponding to
$t'$
is a weight complex functor corresponding to
 $w'$
, and the functor
$w'$
, and the functor
 $K_{\mathfrak {w}}({\underline {HF}}):K_{\mathfrak {w}}({\underline {Hw}})\to K_{\mathfrak {w}}({\underline {Hw}}')$
is defined as in Lemma 1.3.2(3).
$K_{\mathfrak {w}}({\underline {HF}}):K_{\mathfrak {w}}({\underline {Hw}})\to K_{\mathfrak {w}}({\underline {Hw}}')$
is defined as in Lemma 1.3.2(3). -
5. For any morphism of triangles
(1.3.1)where a, b, c and d are the corresponding w-truncations of
 $\operatorname {id}_M$
,
$\operatorname {id}_M$
,
 $\operatorname {id}_{M'}$
and g (see Definition 1.2.5), respectively, we have
$\operatorname {id}_{M'}$
and g (see Definition 1.2.5), respectively, we have
 $\operatorname {\mathrm {\operatorname {Cone}}}(a),\operatorname {\mathrm {\operatorname {Cone}}}(b)\in \underline {C}_{w=n}$
. Moreover,
$\operatorname {\mathrm {\operatorname {Cone}}}(a),\operatorname {\mathrm {\operatorname {Cone}}}(b)\in \underline {C}_{w=n}$
. Moreover,
 $t(g)$
is isomorphic as a
$t(g)$
is isomorphic as a
 $K_{\mathfrak {w}}({\underline {Hw}})$
-arrow to a morphism x whose
$K_{\mathfrak {w}}({\underline {Hw}})$
-arrow to a morphism x whose
 $-n$
th component
$-n$
th component
 $x^{-n}\in \operatorname {Mor}({\underline {Hw}})$
equals
$x^{-n}\in \operatorname {Mor}({\underline {Hw}})$
equals
 $h[-n]$
.
$h[-n]$
.
Furthermore, if
 $t(g)$
is isomorphic to a
$t(g)$
is isomorphic to a
 $K_{\mathfrak {w}}({\underline {Hw}})$
-morphism y such that
$K_{\mathfrak {w}}({\underline {Hw}})$
-morphism y such that
 $y^{-n}=0$
, then any choice of the rows in diagram 1.3.1 can be completed to the whole diagram with
$y^{-n}=0$
, then any choice of the rows in diagram 1.3.1 can be completed to the whole diagram with
 $h=0$
in it.
$h=0$
in it.
2 On morphisms killing weights
In this section, we introduce and study the main new notions of this paper.
In §2.1, we define morphisms killing weights
![]() $m,\dots , n$
and objects without these weights. We give several equivalent definitions of these notions.
$m,\dots , n$
and objects without these weights. We give several equivalent definitions of these notions.
In §2.2, we establish several interesting properties of our notions. In particular, we prove that any object without weights
![]() $m,\dots , n$
admits a weight decomposition avoiding these weights (in the sense defined by J. Wildeshaus) if
$m,\dots , n$
admits a weight decomposition avoiding these weights (in the sense defined by J. Wildeshaus) if
![]() $\underline {C}$
is weight-Karoubian.
$\underline {C}$
is weight-Karoubian.
In §2.3, we prove that M is without weights
![]() $m,\dots , n$
if and only if
$m,\dots , n$
if and only if
![]() $t(M)$
possesses this property.
$t(M)$
possesses this property.
In §2.4, we relate killing a weight m and objects without weights in a range to pure functors; those were introduced in §2.1 of [Reference Bondarko7].
2.1 Killing weights: equivalent definitions
Proposition 2.1.1. Let
![]() $M,N\in \operatorname {Obj} \underline {C}$
,
$M,N\in \operatorname {Obj} \underline {C}$
,
![]() $g\in \underline {C}(M,N)$
and
$g\in \underline {C}(M,N)$
and
![]() $m\le n\in {\mathbb {Z}}$
. Then the following conditions are equivalent.
$m\le n\in {\mathbb {Z}}$
. Then the following conditions are equivalent.
-
1. There exists a choice of
 $w_{\le n}M$
and
$w_{\le n}M$
and
 $w_{\ge m}N$
such that the composed morphism
$w_{\ge m}N$
such that the composed morphism
 $w_{\le n}M\stackrel {x}{\to } M\stackrel {g}{\to }N\stackrel {y}{\to } w_{\ge m}N$
is zero (here x and y come from the corresponding weight decompositions; see Remark 1.2.3(2)).
$w_{\le n}M\stackrel {x}{\to } M\stackrel {g}{\to }N\stackrel {y}{\to } w_{\ge m}N$
is zero (here x and y come from the corresponding weight decompositions; see Remark 1.2.3(2)). -
2. There exists a choice of
 $w_{\le n}M$
and
$w_{\le n}M$
and
 $w_{\le m-1}N$
and of a morphism h making the following square commutative: (2.1.1)
$w_{\le m-1}N$
and of a morphism h making the following square commutative: (2.1.1)
-
3. There exists a choice of
 $w_{\ge n+1}M$
and
$w_{\ge n+1}M$
and
 $w_{\ge m}N$
and of a morphism j making commutative the square (2.1.2)
$w_{\ge m}N$
and of a morphism j making commutative the square (2.1.2)
-
4. Any choices of
 $WD_n(M)$
and
$WD_n(M)$
and
 $WD_{m-1}(N)$
can be joined by a morphism that extends g in the sense of Definition 1.2.5.
$WD_{m-1}(N)$
can be joined by a morphism that extends g in the sense of Definition 1.2.5. -
5. For any choice of
 $WD_n(M)$
and
$WD_n(M)$
and
 $WD_{m-1}(N)$
and for the corresponding truncations
$WD_{m-1}(N)$
and for the corresponding truncations
 $a: w_{\le m-1} M\to w_{\le n} M$
and
$a: w_{\le m-1} M\to w_{\le n} M$
and
 $b:w_{\le m-1} N\to w_{\le n} N$
of
$b:w_{\le m-1} N\to w_{\le n} N$
of
 $\operatorname {id}_M$
and
$\operatorname {id}_M$
and
 $\operatorname {id}_N$
(see Lemma 1.2.7(1)), there exists a commutative diagram (2.1.3)along with
$\operatorname {id}_N$
(see Lemma 1.2.7(1)), there exists a commutative diagram (2.1.3)along with
 $h\in \underline {C}(w_{\le n} M, w_{\le m-1} N) $
that turns the corresponding ‘halves’ of the left-hand square of diagram 2.1.3 into commutative triangles.
$h\in \underline {C}(w_{\le n} M, w_{\le m-1} N) $
that turns the corresponding ‘halves’ of the left-hand square of diagram 2.1.3 into commutative triangles.
-
6. For any choice of the diagram 2.1.3 as above, its left-hand commutative square can be completed to a morphism of triangles as follows:
(2.1.4)
-
7. There exists a choice of diagram 2.1.3 whose left-hand square can be completed to a morphism of triangles as in diagram 2.1.4.
Proof. Conditions 1, 2 and 3 are equivalent by Proposition 1.1.9 of [Reference Beilinson, Bernstein and Deligne2].
Loc. cit. also implies that any of these conditions implies the existence of a morphism
![]() $WD_g:WD^{\prime }_n(M)\to WD^{\prime }_{m-1}(N)$
that extends g, where
$WD_g:WD^{\prime }_n(M)\to WD^{\prime }_{m-1}(N)$
that extends g, where
![]() $WD^{\prime }_n(M)$
(resp.
$WD^{\prime }_n(M)$
(resp.
![]() $ WD^{\prime }_{m-1}(N)$
) is the corresponding n-weight decomposition of M (resp.
$ WD^{\prime }_{m-1}(N)$
) is the corresponding n-weight decomposition of M (resp.
![]() $m-1$
-weight decomposition of N).
$m-1$
-weight decomposition of N).
Next, Lemma 1.2.7(1) gives the existence of some choices of ‘modification of weight decomposition’ morphisms
![]() $WD_n(M)\to WD^{\prime }_n(M)$
and
$WD_n(M)\to WD^{\prime }_n(M)$
and
![]() $WD^{\prime }_{m-1}(N)\to WD_{m-1}(N)$
that extend
$WD^{\prime }_{m-1}(N)\to WD_{m-1}(N)$
that extend
![]() $\operatorname {id}_M$
and
$\operatorname {id}_M$
and
![]() $\operatorname {id}_N$
, respectively. Composing
$\operatorname {id}_N$
, respectively. Composing
![]() $WD_g$
with these morphisms (see Remark 1.2.6) we obtain condition 4. Conversely, this condition obviously implies conditions 1, 2 and 3.
$WD_g$
with these morphisms (see Remark 1.2.6) we obtain condition 4. Conversely, this condition obviously implies conditions 1, 2 and 3.
Next, condition 5 clearly implies condition 2. Conversely, to obtain the commutative diagrams in condition 5 we apply Lemma 1.2.7(1) and take a and b to be the canonical truncations
![]() $w_{\le m-1} M\to w_{\le n} M$
and
$w_{\le m-1} M\to w_{\le n} M$
and
![]() $w_{\le m-1} N\to w_{\le n} N$
of
$w_{\le m-1} N\to w_{\le n} N$
of
![]() $\operatorname {id}_M$
and
$\operatorname {id}_M$
and
![]() $\operatorname {id}_N$
, respectively. We also take
$\operatorname {id}_N$
, respectively. We also take
![]() $c=h\circ a$
, and
$c=h\circ a$
, and
![]() $d=b\circ h$
.
$d=b\circ h$
.
Next, condition 6 clearly yields condition 7. Now, consider the exact sequence
![]() $\underline {C}(w_{\le n} M,w_{\le m-1} N)\to \underline {C}(w_{\le n} M,w_{\le n} N) \to \underline {C}(w_{\le n} M,\operatorname {\mathrm {\operatorname {Cone}}} (b))$
(for an arbitrary choice of diagram 2.1.3). If condition 7 is fulfilled, the composed morphism
$\underline {C}(w_{\le n} M,w_{\le m-1} N)\to \underline {C}(w_{\le n} M,w_{\le n} N) \to \underline {C}(w_{\le n} M,\operatorname {\mathrm {\operatorname {Cone}}} (b))$
(for an arbitrary choice of diagram 2.1.3). If condition 7 is fulfilled, the composed morphism
![]() $w_{\le n} M\stackrel {d}{\to } w_{\le n} N\to \operatorname {\mathrm {\operatorname {Cone}}} (b)$
is zero; hence, there exists a morphism
$w_{\le n} M\stackrel {d}{\to } w_{\le n} N\to \operatorname {\mathrm {\operatorname {Cone}}} (b)$
is zero; hence, there exists a morphism
![]() $h\in \underline {C}(w_{\le n} M,w_{\le m-1} N)$
making the corresponding triangle commutative. Combining this with the commutativity of the right-hand square in diagram 2.1.3 we obtain condition 2.
$h\in \underline {C}(w_{\le n} M,w_{\le m-1} N)$
making the corresponding triangle commutative. Combining this with the commutativity of the right-hand square in diagram 2.1.3 we obtain condition 2.
It remains to verify that condition 5 implies condition 6. The aforementioned long exact sequence gives the vanishing of the corresponding composed morphism
![]() $w_{\le n} M\to \operatorname {\mathrm {\operatorname {Cone}}} (b)$
, whereas the exact sequence
$w_{\le n} M\to \operatorname {\mathrm {\operatorname {Cone}}} (b)$
, whereas the exact sequence
 $$ \begin{align*} \underline{C}(w_{\le n} M,w_{\le m-1} N)\to \underline{C}(w_{\le m-1} M,w_{\le m-1} N) \\ \to \underline{C}(\operatorname{\mathrm{\operatorname{Cone}}}(a)[-1],w_{\le m-1} N)\to \dots \end{align*} $$
$$ \begin{align*} \underline{C}(w_{\le n} M,w_{\le m-1} N)\to \underline{C}(w_{\le m-1} M,w_{\le m-1} N) \\ \to \underline{C}(\operatorname{\mathrm{\operatorname{Cone}}}(a)[-1],w_{\le m-1} N)\to \dots \end{align*} $$
yields the vanishing of the composed morphism
![]() $\operatorname {\mathrm {\operatorname {Cone}}}(a)[-1]\to w_{\le m-1} N$
. We obtain that diagram 2.1.4 is a morphism of triangles indeed.
$\operatorname {\mathrm {\operatorname {Cone}}}(a)[-1]\to w_{\le m-1} N$
. We obtain that diagram 2.1.4 is a morphism of triangles indeed.
Now, we give the main original definitions of this paper.
Definition 2.1.2. Let
![]() $m\le n\in {\mathbb {Z}}$
,
$m\le n\in {\mathbb {Z}}$
,
![]() $g\in \underline {C}(M,N)$
.
$g\in \underline {C}(M,N)$
.
1. We will say that g kills weights
![]() $m,\dots , n$
(and also that g kills weight m if
$m,\dots , n$
(and also that g kills weight m if
![]() $n=m$
) if it satisfies the equivalent conditions of Proposition 2.1.1; denote the class of
$n=m$
) if it satisfies the equivalent conditions of Proposition 2.1.1; denote the class of
![]() $\underline {C}$
-morphisms killing weights
$\underline {C}$
-morphisms killing weights
![]() $m,\dots , n$
by
$m,\dots , n$
by
![]() .
.
2. We say that M is without weights
![]() $m,\dots ,n$
if
$m,\dots ,n$
if
![]() $\operatorname {id}_M$
kills weights
$\operatorname {id}_M$
kills weights
![]() $m,\dots , n$
; the class of
$m,\dots , n$
; the class of
![]() $\underline {C}$
-objects without weights
$\underline {C}$
-objects without weights
![]() $m,\dots ,n$
will be denoted by
$m,\dots ,n$
will be denoted by
![]() $\underline {C}_{w\notin [m,n]}$
.
$\underline {C}_{w\notin [m,n]}$
.
Remark 2.1.3. Proposition 1.2.4(1) easily implies that these definitions are self-dual in the following natural sense:
![]() (resp.
(resp.
![]() $M\in \underline {C}_{w\notin [m,n]}$
) if and only if g kills
$M\in \underline {C}_{w\notin [m,n]}$
) if and only if g kills
![]() $w^{op}$
-weights
$w^{op}$
-weights
![]() $-n,\dots ,-m$
(resp. M is without
$-n,\dots ,-m$
(resp. M is without
![]() $w^{op}$
-weights
$w^{op}$
-weights
![]() $-n,\dots ,-m$
) in
$-n,\dots ,-m$
) in
![]() $\underline {C}'=\underline {C}^{op}$
.
$\underline {C}'=\underline {C}^{op}$
.
2.2 Basic properties of our notions
Theorem 2.2.1. Let
![]() $M,N,O\in \operatorname {Obj} \underline {C}$
,
$M,N,O\in \operatorname {Obj} \underline {C}$
,
![]() $h\in \underline {C}(N,O)$
, and assume that a morphism
$h\in \underline {C}(N,O)$
, and assume that a morphism
![]() $g\in \underline {C}(M,N)$
kills weights
$g\in \underline {C}(M,N)$
kills weights
![]() $m,\dots , n$
for some
$m,\dots , n$
for some
![]() $m\le n\in {\mathbb {Z}}$
. Then the following statements are valid.
$m\le n\in {\mathbb {Z}}$
. Then the following statements are valid.
-
1. Assume
 $m\le m'\le n'\le n$
. Then g also kills weights
$m\le m'\le n'\le n$
. Then g also kills weights
 $m',\dots , n'$
.
$m',\dots , n'$
. -
2.
 is closed with respect to direct sums and retracts (i.e.,
is closed with respect to direct sums and retracts (i.e.,
 $\bigoplus g_i$
kills weights
$\bigoplus g_i$
kills weights
 $m,\dots , n$
if and only if all
$m,\dots , n$
if and only if all
 $g_i$
do that).
$g_i$
do that). -
3.
 is a two-sided ideal of morphisms, that is, for any
is a two-sided ideal of morphisms, that is, for any
 $h'\in \underline {C}(O,M)$
both
$h'\in \underline {C}(O,M)$
both
 $h\circ g$
and
$h\circ g$
and
 $g\circ h'$
kill weights
$g\circ h'$
kill weights
 $m,\dots , n$
.
$m,\dots , n$
. -
4. Assume that h kills weights
 $m',\dots , m-1$
for some
$m',\dots , m-1$
for some
 $m'<m$
. Then
$m'<m$
. Then
 $h\circ g$
kills weights
$h\circ g$
kills weights
 $m',\dots , n$
.
$m',\dots , n$
. -
5. Let
 $F:\underline {C}\to \underline {D}$
be a weight-exact functor (with respect to a certain weight structure on
$F:\underline {C}\to \underline {D}$
be a weight-exact functor (with respect to a certain weight structure on
 $\underline {D}$
) and assume that h kills weights
$\underline {D}$
) and assume that h kills weights
 $m,\dots , n$
. Then
$m,\dots , n$
. Then
 $F(h)$
kills these weights as well.
$F(h)$
kills these weights as well. -
6. For F and h as in the previous assertion, assume that F is a full embedding and
 . Then
. Then
 .
. -
7. Assume that O is without weights
 $m,\dots , n$
and also is without weights
$m,\dots , n$
and also is without weights
 $n+1,\dots , n'$
for some
$n+1,\dots , n'$
for some
 $n'>n$
. Then
$n'>n$
. Then
 $O\in \underline {C}_{w\notin [m,n']}$
.
$O\in \underline {C}_{w\notin [m,n']}$
. -
8. O is without weights
 $m,\dots , n$
if and only if O is without weight i whenever
$m,\dots , n$
if and only if O is without weight i whenever
 $m\le i\le n$
.
$m\le i\le n$
. -
9. Assume that there exists a distinguished triangle
(2.2.1)with $$ \begin{align} X\to O \to Y\to X[1] \end{align} $$
$$ \begin{align} X\to O \to Y\to X[1] \end{align} $$
 $X\in \underline {C}_{w\le m-1}$
,
$X\in \underline {C}_{w\le m-1}$
,
 $Y\in \underline {C}_{w\ge n+1}$
. We call it a decomposition avoiding weights
$Y\in \underline {C}_{w\ge n+1}$
. We call it a decomposition avoiding weights
 $m,\dots , n$
for M.
$m,\dots , n$
for M.
Then triangle 2.2.1 gives an l-weight decomposition of O for every
 $l\in {\mathbb {Z}}$
,
$l\in {\mathbb {Z}}$
,
 $m-1\le l\le n$
. Moreover, O is without weights
$m-1\le l\le n$
. Moreover, O is without weights
 $m,\dots ,n$
, and this triangle is unique up to a canonical isomorphism.
$m,\dots ,n$
, and this triangle is unique up to a canonical isomorphism. -
10. Assume that
 $\underline {C}$
is weight-Karoubian. Then the converse to the previous assertion is also valid, that is, every O without weights
$\underline {C}$
is weight-Karoubian. Then the converse to the previous assertion is also valid, that is, every O without weights
 $m,\dots ,n$
admits a decomposition avoiding weights
$m,\dots ,n$
admits a decomposition avoiding weights
 $m,\dots , n$
.
$m,\dots , n$
.
Proof.
-
1. This is easy from Lemma 1.2.7(1); see Remark 1.2.6 and condition 2 of Proposition 2.1.1.
-
2. Proposition 1.2.4(4) implies that direct sums of l-weight decompositions are l-weight decompositions. Here, we take
 $l=n,m-1$
. This implies the assertion easily; see condition 1 in Proposition 2.1.1.
$l=n,m-1$
. This implies the assertion easily; see condition 1 in Proposition 2.1.1.Assertions 3 and 4 easily follow from Lemma 1.2.7(1) as well; see Remark 1.2.6 and condition 2 in Proposition 2.1.1.
5. If we vanish in condition 1 of Proposition 2.1.1, then we obtain this condition for
 $F(h)$
.
$F(h)$
.6. For any choice of
 $w_{\le n}M$
and
$w_{\le n}M$
and
 $w_{\ge m}N$
, the composed morphism is zero (see condition 2 of Proposition 2.1.1); hence,
$w_{\ge m}N$
, the composed morphism is zero (see condition 2 of Proposition 2.1.1); hence, $$ \begin{align*}F(w_{\le n}M)\to F(M)\stackrel{F(h)}{\to}F(N)\to F( w_{\ge m}N)\end{align*} $$
$$ \begin{align*}F(w_{\le n}M)\to F(M)\stackrel{F(h)}{\to}F(N)\to F( w_{\ge m}N)\end{align*} $$
 .
.
7. Since
 $\operatorname {id}_O\circ \operatorname {id}_O=\operatorname {id}_O$
, the statement follows from assertion 4.
$\operatorname {id}_O\circ \operatorname {id}_O=\operatorname {id}_O$
, the statement follows from assertion 4.8. If O is without weight i whenever
 $m\le i\le n$
, then, iterating the previous assertion, we obtain that O is without weights
$m\le i\le n$
, then, iterating the previous assertion, we obtain that O is without weights
 $m,\dots , n$
. Conversely, if
$m,\dots , n$
. Conversely, if
 $O\in \underline {C}_{w\notin [m,n]}$
and
$O\in \underline {C}_{w\notin [m,n]}$
and
 $m\le i\le n$
, then
$m\le i\le n$
, then
 $\operatorname {id}_O$
kills weight i (i.e., O is without weight i) according to assertion 1.
$\operatorname {id}_O$
kills weight i (i.e., O is without weight i) according to assertion 1.9. Each statement in this assertion easily follows from previous ones.
Indeed, triangle 2.2.1 gives the corresponding l-weight decompositions of O just by definition. We obtain that O is without weights
 $m,\dots , n$
immediately. Here, we can use either condition 2 or 3 of Proposition 2.1.1. This triangle (2.2.1) is canonical by Lemma 1.2.7(1); we take
$m,\dots , n$
immediately. Here, we can use either condition 2 or 3 of Proposition 2.1.1. This triangle (2.2.1) is canonical by Lemma 1.2.7(1); we take
 $M=M'=O$
,
$M=M'=O$
,
 $g=\operatorname {id}_O$
,
$g=\operatorname {id}_O$
,
 $m=n-1$
, and
$m=n-1$
, and
 $m'=n$
in it.
$m'=n$
in it.10. The idea is to ‘modify’ any fixed n-decomposition of O using Lemma 1.2.7(2).
We also fix an m-weight decomposition of O. According to condition 2 in Proposition 2.1.1, there exists a commutative square
Next, Lemma 1.2.7(1) gives the existence and uniqueness of the square Now, if we ‘compose’ these squares in the sense of Remark 1.2.6, then the aforementioned uniqueness statement implies
Now, if we ‘compose’ these squares in the sense of Remark 1.2.6, then the aforementioned uniqueness statement implies
 $t=t\circ z\circ t$
. Thus, the endomorphism
$t=t\circ z\circ t$
. Thus, the endomorphism
 $u=t\circ z$
is idempotent, and the square is commutative. Now, we apply Lemma 1.2.7(2); for X being the image of u, we obtain an n-weight decomposition
$u=t\circ z$
is idempotent, and the square is commutative. Now, we apply Lemma 1.2.7(2); for X being the image of u, we obtain an n-weight decomposition
 $X\to O\to Y$
. It remains to note that
$X\to O\to Y$
. It remains to note that
 $X\in \underline {C}_{w\le m-1}$
since u factors through
$X\in \underline {C}_{w\le m-1}$
since u factors through
 $w_{\le m-1}O$
.
$w_{\le m-1}O$
.
Remark 2.2.2.
-
1. In the original Definition 1.10 of [Reference Wildeshaus28] O was said to be without weights
 $m,\dots ,n$
if there exists a decomposition (2.2.1) for it. Thus, our definition of this notion is equivalent to loc. cit. if
$m,\dots ,n$
if there exists a decomposition (2.2.1) for it. Thus, our definition of this notion is equivalent to loc. cit. if
 $\underline {C}$
is weight-Karoubian. Recall here that this is automatically the case if
$\underline {C}$
is weight-Karoubian. Recall here that this is automatically the case if
 $\underline {C}$
is Karoubian according to the easy Proposition 1.2.4(7). Yet in §3.3 below, we demonstrate that this equivalence fails in general; see also §3.3.2 of [Reference Bondarko6] for a w-bounded (cf. Definition 1.2.2(9)) example of this sort.
$\underline {C}$
is Karoubian according to the easy Proposition 1.2.4(7). Yet in §3.3 below, we demonstrate that this equivalence fails in general; see also §3.3.2 of [Reference Bondarko6] for a w-bounded (cf. Definition 1.2.2(9)) example of this sort.Hence, the uniqueness statement in Theorem 2.2.1(9) coincides with Corollary 1.9 of [Reference Wildeshaus28]. Moreover, Lemma 1.2.7 and Theorem 2.2.1(9) imply Proposition 1.7 of ibid. that is essentially as follows: If
 $X_i\to O_i \to Y_i$
are decompositions avoiding weights
$X_i\to O_i \to Y_i$
are decompositions avoiding weights
 $m,\dots ,n$
, then any
$m,\dots ,n$
, then any
 $g:O_1\to O_2$
uniquely extends to a morphism of these triangles.
$g:O_1\to O_2$
uniquely extends to a morphism of these triangles. -
2. Combining parts 2 and 3 of our theorem, one immediately obtains that the sum of any two parallel morphisms killing weights
 $m,\dots , n$
kills these weights as well.
$m,\dots , n$
kills these weights as well.Moreover, part 2 implies that
 $\underline {C}_{w\notin [m,n]}$
is additive and retraction-closed in
$\underline {C}_{w\notin [m,n]}$
is additive and retraction-closed in
 $\underline {C}$
, whereas part 3 yields that every
$\underline {C}$
, whereas part 3 yields that every
 $\underline {C}$
-morphism from M kills weights
$\underline {C}$
-morphism from M kills weights
 $m,\dots ,n$
if (and only if) M is without these weights.
$m,\dots ,n$
if (and only if) M is without these weights.
2.3 Relation to the weight complex functor
Theorem 2.3.1. Let
![]() $g\in \underline {C}(M,N)$
(for some
$g\in \underline {C}(M,N)$
(for some
![]() $M,N\in \operatorname {Obj} \underline {C}$
);
$M,N\in \operatorname {Obj} \underline {C}$
);
![]() $m\le n\in {\mathbb {Z}}$
.
$m\le n\in {\mathbb {Z}}$
.
-
1. Then g kills weight m if and only if
 $t(g)\backsim _{[-m,-m]} 0$
; see Definition 1.3.1 for this notation.
$t(g)\backsim _{[-m,-m]} 0$
; see Definition 1.3.1 for this notation. -
2. If
 $\{f_i\}$
for
$\{f_i\}$
for
 $n\ge i\ge m$
form a chain of composable
$n\ge i\ge m$
form a chain of composable
 $\underline {C}$
-morphism such that
$\underline {C}$
-morphism such that
 $t(f_i)\backsim _{[-i,-i]}0$
for all i in this range, then
$t(f_i)\backsim _{[-i,-i]}0$
for all i in this range, then
 $f_m\circ \dots \circ f_{n-1}\circ f_{n}$
kills weights
$f_m\circ \dots \circ f_{n-1}\circ f_{n}$
kills weights
 $m,\dots , n$
.
$m,\dots , n$
. -
3. M is without weights
 $m,\dots , n$
if and only if
$m,\dots , n$
if and only if
 $t(\operatorname {id}_M)\backsim _{[-n,-m]}0$
.
$t(\operatorname {id}_M)\backsim _{[-n,-m]}0$
. -
4. Assume in addition that
 $\underline {C}$
is weight-Karoubian. Then M is without weights
$\underline {C}$
is weight-Karoubian. Then M is without weights
 $m,\dots , n$
if and only if
$m,\dots , n$
if and only if
 $t(M)$
is homotopy equivalent to a complex
$t(M)$
is homotopy equivalent to a complex
 $C=(C^i)$
with
$C=(C^i)$
with
 $C^i=0$
for
$C^i=0$
for
 $-n\le i\le -m$
.
$-n\le i\le -m$
.
Proof.
-
1. Immediate from Proposition 1.3.4(5); see condition 7 in Proposition 2.1.1.
-
2. Straightforward from assertion 1 combined with Theorem 2.2.1(4).
-
3. If
 $M\in \underline {C}_{w\notin [m,n]}$
, then combining assertion 1 with Lemma 1.3.2(4) we obtain
$M\in \underline {C}_{w\notin [m,n]}$
, then combining assertion 1 with Lemma 1.3.2(4) we obtain
 $t(\operatorname {id}_M)\backsim _{[-n,-m]}0$
. Conversely, if
$t(\operatorname {id}_M)\backsim _{[-n,-m]}0$
. Conversely, if
 $t(\operatorname {id}_M)\backsim _{[-n,-m]}0$
, then
$t(\operatorname {id}_M)\backsim _{[-n,-m]}0$
, then
 $t(\operatorname {id}_M)\backsim _{[i,i]} 0$
for all i between
$t(\operatorname {id}_M)\backsim _{[i,i]} 0$
for all i between
 $-n$
and
$-n$
and
 $-m$
; thus, applying the previous assertion to the composition
$-m$
; thus, applying the previous assertion to the composition
 $\operatorname {id}_{M}^{\circ n-m+1}$
we obtain that M is without weights
$\operatorname {id}_{M}^{\circ n-m+1}$
we obtain that M is without weights
 $m,\dots , n$
.
$m,\dots , n$
. -
4. The ‘if’ implication follows from the previous assertion immediately; cf. Definition 1.3.1(2).
Conversely, assume that M is without weights
 $m,\dots , n$
. By Theorem 2.2.1(10), M possesses a decomposition avoiding weights
$m,\dots , n$
. By Theorem 2.2.1(10), M possesses a decomposition avoiding weights
 $m,\dots , n$
. Then for the corresponding objects X and Y (see diagram 2.2.1) Proposition 1.3.4(3) says that
$m,\dots , n$
. Then for the corresponding objects X and Y (see diagram 2.2.1) Proposition 1.3.4(3) says that
 $t(X)\in K({\underline {Hw}})_{w^{st}\le m-1}$
and
$t(X)\in K({\underline {Hw}})_{w^{st}\le m-1}$
and
 $t(Y)\in K({\underline {Hw}})_{w^{st}\ge n+1}$
. Recalling the definition of
$t(Y)\in K({\underline {Hw}})_{w^{st}\ge n+1}$
. Recalling the definition of
 $w^{st}$
in Remark 1.2.3(1) and applying Proposition 1.3.4(2), we obtain a
$w^{st}$
in Remark 1.2.3(1) and applying Proposition 1.3.4(2), we obtain a
 $K({\underline {Hw}})$
-distinguished triangle where
$K({\underline {Hw}})$
-distinguished triangle where $$ \begin{align*}T_X\to t(M)\to T_Y\to T_X[1],\end{align*} $$
$$ \begin{align*}T_X\to t(M)\to T_Y\to T_X[1],\end{align*} $$
 $T_X$
and
$T_X$
and
 $T_Y$
have zero terms in degrees at most
$T_Y$
have zero terms in degrees at most
 $-m$
and at least
$-m$
and at least
 $-n$
, respectively. Thus, we obtain the ‘only if’ implication.
$-n$
, respectively. Thus, we obtain the ‘only if’ implication.
Remark 2.3.2. 1. Let us demonstrate that Theorem 2.3.1(2) generalizes Theorem 3.3.1(II) of [Reference Bondarko4]. The latter says that for
![]() $f= f_m\circ \dots \circ f_{n-1}\circ f_{n}$
we have
$f= f_m\circ \dots \circ f_{n-1}\circ f_{n}$
we have
![]() $f=0$
whenever
$f=0$
whenever
![]() $f_i$
are
$f_i$
are
![]() $\underline {C}_{[m,n]}$
-morphisms (see Definition 1.2.2(3)) such that
$\underline {C}_{[m,n]}$
-morphisms (see Definition 1.2.2(3)) such that
![]() $t(f_i)=0$
.
$t(f_i)=0$
.
Now, if this is the case, then
![]() $t(f_i)\backsim _{[-i,-i]}0$
for
$t(f_i)\backsim _{[-i,-i]}0$
for
![]() $m\le i \le n$
; hence, f kills weights
$m\le i \le n$
; hence, f kills weights
![]() $m,\dots , n$
by Theorem 2.3.1(2). Next, if
$m,\dots , n$
by Theorem 2.3.1(2). Next, if
![]() $f\in \underline {C}(M,N)$
for
$f\in \underline {C}(M,N)$
for
![]() $M,N\in \underline {C}_{[m,n]}$
, then we can take
$M,N\in \underline {C}_{[m,n]}$
, then we can take
![]() $w_{\le n}M=M$
and
$w_{\le n}M=M$
and
![]() $w_{\ge m}N=N$
. Thus,
$w_{\ge m}N=N$
. Thus,
![]() $f=0$
indeed; see condition 4 in Proposition 2.1.1.
$f=0$
indeed; see condition 4 in Proposition 2.1.1.
Thus, we obtain an alternative proof of loc. cit. that does not depend either on it or on Proposition 3.2.4 of ibid. (cf. Remark A.2.1(3) of [Reference Bondarko7]).
2. More criteria for killing weights for morphisms and for the absence of weights in objects are given by Theorems 2.1.2 and 2.2.2 of [Reference Bondarko and Vostokov12]. These matters are also studied in Theorem 3.1.1 of ibid., where the additional assumption of the existence of a t-structure adjacent to w (see Definition 1.2.2(3) of ibid.) was imposed. Note here that this assumption is fulfilled whenever w is purely compactly generated (see Theorem 4.1.2 below). In particular, it is valid if
![]() $w= w_{\Lambda }^G$
(see Proposition 4.2.1(2) and Remark 4.2.3(6) below).
$w= w_{\Lambda }^G$
(see Proposition 4.2.1(2) and Remark 4.2.3(6) below).
Let us now improve the conservativity property of weight complexes given by Theorem 3.3.1(V) of [Reference Bondarko4].
Definition 2.3.3. 1. We say that w is left (resp., right) nondegenerate if all left (resp. right) w-degenerate objects (see Definition 1.2.2(7)) are zero.
We say that w is nondegenerate if it is both left and right nondegenerate.
2. We will say that
![]() $M\in \operatorname {Obj} \underline {C}$
is w-degenerate or weight-degenerate if
$M\in \operatorname {Obj} \underline {C}$
is w-degenerate or weight-degenerate if
![]() $t(M)$
is zero in
$t(M)$
is zero in
![]() $K_{\mathfrak {w}}({\underline {Hw}})$
; hence, it is zero in
$K_{\mathfrak {w}}({\underline {Hw}})$
; hence, it is zero in
![]() $K({\underline {Hw}})$
as well.
$K({\underline {Hw}})$
as well.
Theorem 2.3.4. Let
![]() $g:M\to M'$
be a
$g:M\to M'$
be a
![]() $\underline {C}$
-morphism,
$\underline {C}$
-morphism,
![]() $m\in {\mathbb {Z}}$
.
$m\in {\mathbb {Z}}$
.
I.1. Then
![]() $t(g)$
is an isomorphism if and only if
$t(g)$
is an isomorphism if and only if
![]() $\operatorname {\mathrm {\operatorname {Cone}}}(g)$
is w-degenerate.
$\operatorname {\mathrm {\operatorname {Cone}}}(g)$
is w-degenerate.
2. Any extension of a left w-degenerate object Y of
![]() $\underline {C}$
by a right w-degenerate object X is w-degenerate.
$\underline {C}$
by a right w-degenerate object X is w-degenerate.
3. If M is an extension of a left w-degenerate object Y by
![]() $X_m\in \underline {C}_{w\le m}$
(resp. an extension of
$X_m\in \underline {C}_{w\le m}$
(resp. an extension of
![]() $Y_m\in \underline {C}_{w\ge m}$
by a right w-degenerate object X), then
$Y_m\in \underline {C}_{w\ge m}$
by a right w-degenerate object X), then
![]() $t(M)\in K({\underline {Hw}})_{w^{st}\le m}$
(resp.
$t(M)\in K({\underline {Hw}})_{w^{st}\le m}$
(resp.
![]() $t(M)\in K({\underline {Hw}})_{w^{st}\ge m}$
; see Remark 1.2.3(1)).
$t(M)\in K({\underline {Hw}})_{w^{st}\ge m}$
; see Remark 1.2.3(1)).
II. Assume that
![]() $\underline {C}$
is weight-Karoubian.
$\underline {C}$
is weight-Karoubian.
1. Then M is w-degenerate if and only if M is an extension of a left w-degenerate Y by a right w-degenerate X; cf. assertion I.2.
2.
![]() $t(M)\in K({\underline {Hw}})_{w^{st}\le m}$
(resp.
$t(M)\in K({\underline {Hw}})_{w^{st}\le m}$
(resp.
![]() $t(M)\in K({\underline {Hw}})_{w^{st}\ge m}$
) if and only if M is an extension of a left w-degenerate Y by
$t(M)\in K({\underline {Hw}})_{w^{st}\ge m}$
) if and only if M is an extension of a left w-degenerate Y by
![]() $X_m\in \underline {C}_{w\le m}$
(resp. an extension of
$X_m\in \underline {C}_{w\le m}$
(resp. an extension of
![]() $Y_m\in \underline {C}_{w\ge m}$
by a right w-degenerate X; cf. assertion I.3).
$Y_m\in \underline {C}_{w\ge m}$
by a right w-degenerate X; cf. assertion I.3).
Proof. I.1. Immediate from Proposition 1.3.4(2) combined with the conservativity of the projection functor
![]() $p_w:K(\underline {B})\to K_{\mathfrak {w}}(\underline {B})$
given by Lemma 1.3.2(1).
$p_w:K(\underline {B})\to K_{\mathfrak {w}}(\underline {B})$
given by Lemma 1.3.2(1).
2. If N is left or right w-degenerate, then
![]() $t(N)=0$
according to Proposition 1.3.4(3). Hence, the assertion follows from the previous one.
$t(N)=0$
according to Proposition 1.3.4(3). Hence, the assertion follows from the previous one.
3. Similarly to the previous assertion, it suffices to combine Proposition 1.3.4(3) with assertion I.1.
II. If
![]() $t(M)\in K({\underline {Hw}})_{w^{st} \le m}$
, then for every
$t(M)\in K({\underline {Hw}})_{w^{st} \le m}$
, then for every
![]() $n> m$
we have
$n> m$
we have
![]() $\operatorname {id}_{t(M)}\backsim _{[-n,-m-1]}0$
; see Lemma 1.3.2(6).
$\operatorname {id}_{t(M)}\backsim _{[-n,-m-1]}0$
; see Lemma 1.3.2(6).
Since
![]() $\underline {C}$
is weight-Karoubian, for every
$\underline {C}$
is weight-Karoubian, for every
![]() $n>0$
Theorem 2.2.1(10) gives a distinguished triangle
$n>0$
Theorem 2.2.1(10) gives a distinguished triangle
with
![]() $X_m\in \underline {C}_{w\le m}$
and
$X_m\in \underline {C}_{w\le m}$
and
![]() $Y_{n+1}\in \underline {C}_{w\ge n+1}$
. All of these triangles are isomorphic to the one for
$Y_{n+1}\in \underline {C}_{w\ge n+1}$
. All of these triangles are isomorphic to the one for
![]() $n=m+1$
by the uniqueness statement in Theorem 2.2.1(9). Hence,
$n=m+1$
by the uniqueness statement in Theorem 2.2.1(9). Hence,
![]() $T=Y_{m+1}$
is left w-degenerate and we obtain the ‘only if’ implication for this case. Next, the ‘if’ implication is given by assertion I.3.
$T=Y_{m+1}$
is left w-degenerate and we obtain the ‘only if’ implication for this case. Next, the ‘if’ implication is given by assertion I.3.
The proofs of the two remaining statements are similar and left to the reader.
Remark 2.3.5. 1. Thus, we get a precise answer to the question when
![]() $t(g)$
is an isomorphism in the weight-Karoubian case. In particular, the weight complex functor is conservative if and only if w is nondegenerate.
$t(g)$
is an isomorphism in the weight-Karoubian case. In particular, the weight complex functor is conservative if and only if w is nondegenerate.
2. To obtain the latter statement in the general case, one should combine part I.1 of our theorem with Theorem 3.1.3 below. Moreover, that theorem contains several equivalent conditions for
![]() $t(M)$
to belong to
$t(M)$
to belong to
![]() $ K({\underline {Hw}})_{w^{st}\le 0}$
. However, those formulations require Definition 3.1.1(2); see §3.3 below.
$ K({\underline {Hw}})_{w^{st}\le 0}$
. However, those formulations require Definition 3.1.1(2); see §3.3 below.
2.4 On the relation to pure functors
Let us prove that the assumption that a
![]() $\underline {C}$
-morphism g kills a given weight m can be expressed in terms of pure functors.
$\underline {C}$
-morphism g kills a given weight m can be expressed in terms of pure functors.
Definition 2.4.1. Assume that
![]() $\underline {C}$
is endowed with a weight structure w.
$\underline {C}$
is endowed with a weight structure w.
We will say that a (co)homological functor H from
![]() $\underline {C}$
into an abelian category
$\underline {C}$
into an abelian category
![]() $\underline {A}$
is w-pure or just pure if H kills both
$\underline {A}$
is w-pure or just pure if H kills both
![]() $\underline {C}_{w\ge 1}$
and
$\underline {C}_{w\ge 1}$
and
![]() $\underline {C}_{w\le -1}$
.
$\underline {C}_{w\le -1}$
.
Theorem 2.4.2.
1. Let
![]() ${\mathcal {A}}:{\underline {Hw}}\to \underline {A}$
be an additive functor, where
${\mathcal {A}}:{\underline {Hw}}\to \underline {A}$
be an additive functor, where
![]() $\underline {A}$
is an abelian category. For
$\underline {A}$
is an abelian category. For
![]() $M\in \operatorname {Obj} \underline {C}$
and
$M\in \operatorname {Obj} \underline {C}$
and
![]() $t(M)=(M^j)$
, we set
$t(M)=(M^j)$
, we set
![]() $H(M)=H^{{\mathcal {A}}}(M)$
to be the zeroth homology of the complex
$H(M)=H^{{\mathcal {A}}}(M)$
to be the zeroth homology of the complex
![]() $({\mathcal {A}}(M^{j}))$
. Then
$({\mathcal {A}}(M^{j}))$
. Then
![]() $H(-)$
yields a pure homological functor, and the assignment
$H(-)$
yields a pure homological functor, and the assignment
![]() ${\mathcal {A}}\mapsto H^{\mathcal {A}}$
is natural in
${\mathcal {A}}\mapsto H^{\mathcal {A}}$
is natural in
![]() ${\mathcal {A}}$
.
${\mathcal {A}}$
.
2. The correspondence
![]() ${\mathcal {A}}\to H^{\mathcal {A}}$
is an equivalence of categories between the following categories of functors:
${\mathcal {A}}\to H^{\mathcal {A}}$
is an equivalence of categories between the following categories of functors:
![]() $\operatorname {\mathrm {\operatorname {AddFun}}}({\underline {Hw}},\underline {A})$
and the category of pure homological functors from
$\operatorname {\mathrm {\operatorname {AddFun}}}({\underline {Hw}},\underline {A})$
and the category of pure homological functors from
![]() $\underline {C}$
into
$\underline {C}$
into
![]() $\underline {A}$
.
$\underline {A}$
.
3. Dually, the correspondence sending a contravariant functor
![]() ${\mathcal {A}}'$
into the functor
${\mathcal {A}}'$
into the functor
![]() $H_{{\mathcal {A}}'}$
that maps M into the zeroth homology of the complex
$H_{{\mathcal {A}}'}$
that maps M into the zeroth homology of the complex
![]() $({\mathcal {A}}'(M^{-j}))$
gives an equivalence of categories between
$({\mathcal {A}}'(M^{-j}))$
gives an equivalence of categories between
![]() $\operatorname {\mathrm {\operatorname {AddFun}}}({\underline {Hw}}^{op},\underline {A})$
and the category of pure cohomological functors from
$\operatorname {\mathrm {\operatorname {AddFun}}}({\underline {Hw}}^{op},\underline {A})$
and the category of pure cohomological functors from
![]() $\underline {C}$
into
$\underline {C}$
into
![]() $\underline {A}$
.
$\underline {A}$
.
Proof. Assertions 1 and 2 are contained in Theorem 2.1.2 of [Reference Bondarko7], and assertion 3 is their dual; cf. Proposition 1.2.4(1) or Remark 2.1.3(1) of ibid.
We also need the following definitions.
Definition 2.4.3. Assume that
![]() $\underline {C}$
is smashing, that is, closed with respect to (small) coproducts.
$\underline {C}$
is smashing, that is, closed with respect to (small) coproducts.
1. We will say that
![]() $\underline {C}$
is a Brown category if any cohomological functor from
$\underline {C}$
is a Brown category if any cohomological functor from
![]() $\underline {C}$
into
$\underline {C}$
into
![]() $\operatorname {Ab}$
that converts
$\operatorname {Ab}$
that converts
![]() $\underline {C}$
-coproducts into products of groups is representable in
$\underline {C}$
-coproducts into products of groups is representable in
![]() $\underline {C}$
.
$\underline {C}$
.
2. We will say that a weight structure w on
![]() $\underline {C}$
is smashing if the class
$\underline {C}$
is smashing if the class
![]() $\underline {C}_{w\ge 0}$
is closed with respect to
$\underline {C}_{w\ge 0}$
is closed with respect to
![]() $\underline {C}$
-coproducts (cf. Proposition 1.2.4(3)).
$\underline {C}$
-coproducts (cf. Proposition 1.2.4(3)).
Proposition 2.4.4. Assume that
![]() $\underline {C}$
is endowed with a weight structure w,
$\underline {C}$
is endowed with a weight structure w,
![]() $g:M\to N$
is a
$g:M\to N$
is a
![]() $\underline {C}$
-morphism, and
$\underline {C}$
-morphism, and
![]() $j\in {\mathbb {Z}}$
.
$j\in {\mathbb {Z}}$
.
I. Then the following assumptions are equivalent to
![]() .
.
1.
![]() $H^j_{{\mathcal {A}}}(g)=0$
for every pure cohomological functor
$H^j_{{\mathcal {A}}}(g)=0$
for every pure cohomological functor
![]() $H_{{\mathcal {A}}}$
as above.
$H_{{\mathcal {A}}}$
as above.
2.
![]() $H^j_{{\mathcal {A}}}(g)=0$
for every pure cohomological functor
$H^j_{{\mathcal {A}}}(g)=0$
for every pure cohomological functor
![]() $H_{{\mathcal {A}}}$
coming from
$H_{{\mathcal {A}}}$
coming from
![]() ${\mathcal {A}}\in \operatorname {\mathrm {\operatorname {AddFun}}}({\underline {Hw}}^{op}, \operatorname {Ab})$
such that
${\mathcal {A}}\in \operatorname {\mathrm {\operatorname {AddFun}}}({\underline {Hw}}^{op}, \operatorname {Ab})$
such that
![]() ${\mathcal {A}}$
converts
${\mathcal {A}}$
converts
![]() ${\underline {Hw}}$
-coproducts into products of groups.
${\underline {Hw}}$
-coproducts into products of groups.
3.
![]() $H_j^{{\mathcal {A}}}(g)=0$
for every pure homological functor
$H_j^{{\mathcal {A}}}(g)=0$
for every pure homological functor
![]() $H^{{\mathcal {A}}}$
.
$H^{{\mathcal {A}}}$
.
II. Assume in addition that
![]() $\underline {C}$
is a Brown category and w is smashing. Then the functors
$\underline {C}$
is a Brown category and w is smashing. Then the functors
![]() $H_{{\mathcal {A}}}$
as in condition I.3 are the pure representable ones.
$H_{{\mathcal {A}}}$
as in condition I.3 are the pure representable ones.
Proof. I. Proposition 1.3.4(1) enables us to assume
![]() $j=0$
.
$j=0$
.
Next, if
![]() , then condition 1 is fulfilled by Proposition 1.3.4(2) combined with Theorem 2.3.1(1). Moreover, condition 1 clearly implies condition 2.
, then condition 1 is fulfilled by Proposition 1.3.4(2) combined with Theorem 2.3.1(1). Moreover, condition 1 clearly implies condition 2.
Furthermore, if
![]() , then
, then
![]() $t(g)\not \backsim _{[0,0]} 0$
by Theorem 2.3.1(1); here, we use the notation of Definition 1.3.1(2). Thus, Proposition B.2(8) of [Reference Bondarko7] gives the existence of a functor
$t(g)\not \backsim _{[0,0]} 0$
by Theorem 2.3.1(1); here, we use the notation of Definition 1.3.1(2). Thus, Proposition B.2(8) of [Reference Bondarko7] gives the existence of a functor
![]() ${\mathcal {A}}$
as in assertion 2 such that
${\mathcal {A}}$
as in assertion 2 such that
![]() $H_{{\mathcal {A}}}(g)\neq 0$
. Hence, condition 2 implies
$H_{{\mathcal {A}}}(g)\neq 0$
. Hence, condition 2 implies
![]() .
.
Lastly,
![]() if and only if condition I.3 is fulfilled since I.3 is the categorical dual of condition I.1; see also Remark 2.1.3.
if and only if condition I.3 is fulfilled since I.3 is the categorical dual of condition I.1; see also Remark 2.1.3.
II. This is Proposition 2.3.2(8) of ibid.
3 Non-Karoubian generalizations and a conservativity application
In §3.1, we extend Theorem 2.3.4(II) to the case where
![]() $\underline {C}$
is not necessarily weight-Karoubian.
$\underline {C}$
is not necessarily weight-Karoubian.
In §3.2, we apply our results to prove that certain weight-exact functors are ‘conservative up to weight-degenerate objects’; we also discuss the relation of this proposition to the corresponding results of [Reference Wildeshaus29] and [Reference Bondarko7].
In §3.3, we consider an example; it demonstrates that the modifications made in §3.1 to generalize Theorem 2.3.4(II) cannot be avoided.
3.1 Main statements in non-weight-Karoubian categories
Definition 3.1.1. 1. We call a triangulated category
![]() $\underline {C}'\subset \operatorname {\mathrm {\operatorname {Kar}}}(\underline {C})$
a weight-Karoubian extension of
$\underline {C}'\subset \operatorname {\mathrm {\operatorname {Kar}}}(\underline {C})$
a weight-Karoubian extension of
![]() $\underline {C}$
if
$\underline {C}$
if
![]() $\underline {C}'$
contains
$\underline {C}'$
contains
![]() $\underline {C}$
, the retraction-closures of
$\underline {C}$
, the retraction-closures of
![]() $\underline {C}_{w\le 0}$
and
$\underline {C}_{w\le 0}$
and
![]() $\underline {C}_{w\ge 0}$
in
$\underline {C}_{w\ge 0}$
in
![]() $\underline {C}'$
give a weight structure
$\underline {C}'$
give a weight structure
![]() $w'$
on it, and
$w'$
on it, and
![]() ${\underline {Hw}}'$
is Karoubian.
${\underline {Hw}}'$
is Karoubian.
2. We say that an object M of
![]() $\underline {C}$
is essentially w-positive (resp. essentially w-negative) if M is a retract of some
$\underline {C}$
is essentially w-positive (resp. essentially w-negative) if M is a retract of some
![]() $\tilde M\in \operatorname {Obj} \underline {C}$
that is an extension of an element of
$\tilde M\in \operatorname {Obj} \underline {C}$
that is an extension of an element of
![]() $\underline {C}_{w\ge 0}$
by a right w-degenerate object of
$\underline {C}_{w\ge 0}$
by a right w-degenerate object of
![]() $\underline {C}$
(resp. of a left w-degenerate object by an element of
$\underline {C}$
(resp. of a left w-degenerate object by an element of
![]() $\underline {C}_{w\le 0}$
; see Definition 1.2.2(7)).
$\underline {C}_{w\le 0}$
; see Definition 1.2.2(7)).
Proposition 3.1.2.
1. Let
![]() $\underline {C}'$
be a weight-Karoubian extension of
$\underline {C}'$
be a weight-Karoubian extension of
![]() $\underline {C}$
. Then the embedding
$\underline {C}$
. Then the embedding
![]() $\underline {C}\to \underline {C}'$
is weight-exact with respect to
$\underline {C}\to \underline {C}'$
is weight-exact with respect to
![]() $(w,w')$
, and
$(w,w')$
, and
![]() $\underline {C}^{\prime }_{w'= 0}$
equals the retraction-closure of
$\underline {C}^{\prime }_{w'= 0}$
equals the retraction-closure of
![]() $\underline {C}_{w= 0}$
in
$\underline {C}_{w= 0}$
in
![]() $\underline {C}'$
.
$\underline {C}'$
.
2. Any
![]() $(\underline {C},w)$
possesses a weight-Karoubian extension.
$(\underline {C},w)$
possesses a weight-Karoubian extension.
Proof. Assertion 1 immediately follows from Theorem 2.2.2(I.1) of [Reference Bondarko and Sosnilo9], and invoking part III.1 of loc. cit., one also obtains assertion 2.
Now, we generalize Theorem 2.3.4(II) to arbitrary weighted categories; see Definition 2.3.3, Remark 1.3.3, and Theorem 2.4.2 for the definitions.
Theorem 3.1.3. The following assumptions on
![]() $M\in \operatorname {Obj} \underline {C}$
are equivalent.
$M\in \operatorname {Obj} \underline {C}$
are equivalent.
-
1. M is w-degenerate (resp.
 $t(M)\in K({\underline {Hw}})_{w^{st}\le 0}$
).
$t(M)\in K({\underline {Hw}})_{w^{st}\le 0}$
). -
2. M can be presented as an extension of a left
 $w'$
-degenerate object
$w'$
-degenerate object
 $Y'$
of
$Y'$
of
 $\underline {C}$
by a right
$\underline {C}$
by a right
 $w'$
-degenerate object
$w'$
-degenerate object
 $X'$
(resp. by
$X'$
(resp. by
 $X^{\prime }_0\in \underline {C}^{\prime }_{w'\le 0}$
; cf. diagram 2.3.1) in a weight-Karoubian extension
$X^{\prime }_0\in \underline {C}^{\prime }_{w'\le 0}$
; cf. diagram 2.3.1) in a weight-Karoubian extension
 $(\underline {C}',w')$
of
$(\underline {C}',w')$
of
 $(\underline {C},w)$
.
$(\underline {C},w)$
. -
3. In any weight-Karoubian extension of
 $\underline {C}$
, there exists a presentation of M as in condition 2.
$\underline {C}$
, there exists a presentation of M as in condition 2. -
4. M is a
 $\underline {C}$
-retract of an extension
$\underline {C}$
-retract of an extension
 $\tilde M$
of a left w-degenerate object Y of
$\tilde M$
of a left w-degenerate object Y of
 $\underline {C}$
by a right w-degenerate X (resp. M is essentially w-negative in the sense of Definition 3.1.1(2)).
$\underline {C}$
by a right w-degenerate X (resp. M is essentially w-negative in the sense of Definition 3.1.1(2)). -
5. The object
 $M\bigoplus M[-1]$
is an extension of a left w-degenerate
$M\bigoplus M[-1]$
is an extension of a left w-degenerate
 $Y\in \operatorname {Obj} \underline {C}$
by a right w-degenerate X (resp. by
$Y\in \operatorname {Obj} \underline {C}$
by a right w-degenerate X (resp. by
 $X_0\in \underline {C}_{w\le 0}$
).
$X_0\in \underline {C}_{w\le 0}$
). -
6. M is without weight i for all
 $i\in {\mathbb {Z}}$
(resp. for all
$i\in {\mathbb {Z}}$
(resp. for all
 $i>0$
).
$i>0$
). -
7.
 $H_i(M)=0$
for all
$H_i(M)=0$
for all
 $i\in {\mathbb {Z}}$
(resp.
$i\in {\mathbb {Z}}$
(resp.
 $i>0$
) and every w-pure homological functor H from
$i>0$
) and every w-pure homological functor H from
 $\underline {C}$
.
$\underline {C}$
. -
8.
 $H_{{\mathcal {A}}}^i(M)=\{0\}$
for all
$H_{{\mathcal {A}}}^i(M)=\{0\}$
for all
 $i\in {\mathbb {Z}}$
(resp. for
$i\in {\mathbb {Z}}$
(resp. for
 $i>0$
) and every additive functor
$i>0$
) and every additive functor
 ${\mathcal {A}}:{\underline {Hw}}^{op}\to \operatorname {Ab}$
that respects products; here we use the notation of Theorem 2.4.2(3).
${\mathcal {A}}:{\underline {Hw}}^{op}\to \operatorname {Ab}$
that respects products; here we use the notation of Theorem 2.4.2(3).
Proof. Let us study the conditions in brackets (that correspond to the essential w-negativity of M).
Clearly, the corresponding version of condition 5 implies condition 4. 2 follows from 3 since a weight-Karoubian extension
![]() $(\underline {C}',w')$
of
$(\underline {C}',w')$
of
![]() $\underline {C}$
exists; see Proposition 3.1.2(2).
$\underline {C}$
exists; see Proposition 3.1.2(2).
Condition 1 is easily seen to be equivalent to condition 6 according to Theorem 2.3.1(3,1) combined with Lemma 1.3.2(4,6). Moreover, condition 1 is equivalent to
![]() $t(M)\backsim _{[i,i]}0$
for all
$t(M)\backsim _{[i,i]}0$
for all
![]() $i<0$
by the latter lemma; thus, applying Proposition 2.4.4(I), we obtain that this condition is also equivalent to conditions 7 and 8.
$i<0$
by the latter lemma; thus, applying Proposition 2.4.4(I), we obtain that this condition is also equivalent to conditions 7 and 8.
Next, for any weight-Karoubian extension
![]() $\underline {C}'$
of
$\underline {C}'$
of
![]() $\underline {C}$
the complex
$\underline {C}$
the complex
![]() $t_w(M)$
belongs
$t_w(M)$
belongs
![]() $ K({\underline {Hw}})_{w^{st}\le 0}$
if and only if it belongs to
$ K({\underline {Hw}})_{w^{st}\le 0}$
if and only if it belongs to
![]() $K({\underline {Hw}}')_{w^{st}\le 0}$
; see Proposition 1.2.5(1) of [Reference Bondarko and Sosnilo10] that easily follows from Proposition 1.2.4(2) above. Applying Proposition 1.3.4(4), we obtain that condition 4 implies 1.
$K({\underline {Hw}}')_{w^{st}\le 0}$
; see Proposition 1.2.5(1) of [Reference Bondarko and Sosnilo10] that easily follows from Proposition 1.2.4(2) above. Applying Proposition 1.3.4(4), we obtain that condition 4 implies 1.
Now, we fix some
![]() $(\underline {C}',w')$
and apply Theorem 2.3.4(II.2) to
$(\underline {C}',w')$
and apply Theorem 2.3.4(II.2) to
![]() $\underline {C}'$
. We obtain that condition 1 implies condition 3.
$\underline {C}'$
. We obtain that condition 1 implies condition 3.
It remains to deduce condition 5 from condition 2. Any
![]() $N'\in \operatorname {Obj} \underline {C}'$
is the image of an idempotent
$N'\in \operatorname {Obj} \underline {C}'$
is the image of an idempotent
![]() $p\in \underline {C}(N,N)$
for some
$p\in \underline {C}(N,N)$
for some
![]() $N\in \operatorname {Obj} \underline {C}$
(see §1.1), and
$N\in \operatorname {Obj} \underline {C}$
(see §1.1), and
![]() $\operatorname {\mathrm {\operatorname {Cone}}}(p)\cong N'\bigoplus N'[1]\in \operatorname {Obj} \underline {C}$
; cf. Lemma 2.2 of [Reference Thomason27]. Hence, the direct sum of the
$\operatorname {\mathrm {\operatorname {Cone}}}(p)\cong N'\bigoplus N'[1]\in \operatorname {Obj} \underline {C}$
; cf. Lemma 2.2 of [Reference Thomason27]. Hence, the direct sum of the
![]() $\underline {C}'$
-‘decomposition’ of M given by condition 2 with its shift by
$\underline {C}'$
-‘decomposition’ of M given by condition 2 with its shift by
![]() $[-1]$
yields condition 5.
$[-1]$
yields condition 5.
The equivalence of the conditions corresponding to
![]() $t(M)=0$
is similar; note that the functors
$t(M)=0$
is similar; note that the functors
![]() $ K({\underline {Hw}})\to K({\underline {Hw}}')\to K_{\mathfrak {w}}({\underline {Hw}}')$
are conservative.
$ K({\underline {Hw}})\to K({\underline {Hw}}')\to K_{\mathfrak {w}}({\underline {Hw}}')$
are conservative.
Corollary 3.1.4. If w is a weight structure on
![]() $\underline {C}$
and M is its object, then the following conditions are equivalent.
$\underline {C}$
and M is its object, then the following conditions are equivalent.
-
1.
 $t(M)\in K({\underline {Hw}})_{w^{st}\ge 0}$
.
$t(M)\in K({\underline {Hw}})_{w^{st}\ge 0}$
. -
2. M is without weight i for all
 $i<0$
.
$i<0$
. -
3. M is an extension of some
 $Y^{\prime }_0\in \underline {C}^{\prime }_{w'\ge 0}$
by a right
$Y^{\prime }_0\in \underline {C}^{\prime }_{w'\ge 0}$
by a right
 $w'$
-degenerate object
$w'$
-degenerate object
 $X'$
in some weight-Karoubian extension
$X'$
in some weight-Karoubian extension
 $(\underline {C}',w')$
of
$(\underline {C}',w')$
of
 $\underline {C}$
.
$\underline {C}$
. -
4. In any weight-Karoubian extension of
 $\underline {C}$
there exists a presentation of M as in condition 3.
$\underline {C}$
there exists a presentation of M as in condition 3. -
5. M is essentially w-positive in the sense of Definition 3.1.1(2).
-
6. The object
 $M\bigoplus M[1]$
is an extension of
$M\bigoplus M[1]$
is an extension of
 $Y_0\in \underline {C}_{w\ge 0}$
by a right w-degenerate X.
$Y_0\in \underline {C}_{w\ge 0}$
by a right w-degenerate X. -
7.
 $H_{{\mathcal {A}}}^i(M)=\{0\}$
for all
$H_{{\mathcal {A}}}^i(M)=\{0\}$
for all
 $i<0$
and all additive functors
$i<0$
and all additive functors
 ${\mathcal {A}}:{\underline {Hw}}^{op}\to \operatorname {Ab}$
that respect products.
${\mathcal {A}}:{\underline {Hw}}^{op}\to \operatorname {Ab}$
that respect products.
Proof. Conditions 1–6 are the categorical duals of the corresponding conditions in Theorem 3.1.3, whereas conditions 2 and 7 are equivalent according to Proposition 2.4.4(I).
Remark 3.1.5. 1. Clearly, the formulation of conditions 8 in Theorem 3.1.3 and condition 7 of Corollary 3.1.4 can be combined with Proposition 2.4.4(II) to obtain the following statement: If
![]() $\underline {C}$
is a Brown category and w is smashing, then an object M is w-degenerate (resp. essentially w-negative, resp. essentially w-positive) if and only if
$\underline {C}$
is a Brown category and w is smashing, then an object M is w-degenerate (resp. essentially w-negative, resp. essentially w-positive) if and only if
![]() $H^i(M)=\{0\}$
for any pure representable H and any
$H^i(M)=\{0\}$
for any pure representable H and any
![]() $i\in {\mathbb {Z}}$
(resp. any
$i\in {\mathbb {Z}}$
(resp. any
![]() $i>0$
, resp. any
$i>0$
, resp. any
![]() $i<0$
).
$i<0$
).
2. [Reference Bondarko and Sosnilo9] contains a lot of information on weight-Karoubian extensions and related matters. In particular, the smallest strict triangulated subcategory
![]() $\underline {C}'$
of
$\underline {C}'$
of
![]() $\operatorname {\mathrm {\operatorname {Kar}}}(\underline {C})$
that contains both
$\operatorname {\mathrm {\operatorname {Kar}}}(\underline {C})$
that contains both
![]() $\underline {C}$
and
$\underline {C}$
and
![]() $\operatorname {\mathrm {\operatorname {Kar}}}({\underline {Hw}})$
is essentially the minimal weight-Karoubian extension of
$\operatorname {\mathrm {\operatorname {Kar}}}({\underline {Hw}})$
is essentially the minimal weight-Karoubian extension of
![]() $\underline {C}$
; thus, it makes sense to apply conditions 3 of Theorem 3.1.3 and 4 of Corollary 3.1.4 for this choice of
$\underline {C}$
; thus, it makes sense to apply conditions 3 of Theorem 3.1.3 and 4 of Corollary 3.1.4 for this choice of
![]() $\underline {C}'$
.
$\underline {C}'$
.
3. Moreover, in §3.1 of ibid. it was demonstrated that there does not have to exist a weight structure on
![]() $\operatorname {\mathrm {\operatorname {Kar}}}(\underline {C})$
whose restriction to
$\operatorname {\mathrm {\operatorname {Kar}}}(\underline {C})$
whose restriction to
![]() $\underline {C}$
equals w; thus, weight-Karoubian extensions are necessary for our arguments.
$\underline {C}$
equals w; thus, weight-Karoubian extensions are necessary for our arguments.
Now, let us prove a few results closely related to our theorem. The reader may consult Definition 1.2.2(8, 6) for some notions mentioned below.
Proposition 3.1.6. Let w be a weight structure on
![]() $\underline {C}$
.
$\underline {C}$
.
1. Assume that w is left (resp. right) nondegenerate.
Then every weight-degenerate object of
![]() $\underline {C}$
is right (resp. left) w-degenerate, and every essentially w-negative (resp. essentially w-positive) object belongs to
$\underline {C}$
is right (resp. left) w-degenerate, and every essentially w-negative (resp. essentially w-positive) object belongs to
![]() $\underline {C}_{w\le 0}$
(resp. to
$\underline {C}_{w\le 0}$
(resp. to
![]() $\underline {C}_{w\ge 0}$
).
$\underline {C}_{w\ge 0}$
).
2. Assume that w is left nondegenerate, an object M of
![]() $\underline {C}$
is weight-degenerate and either M is w-bounded below or w is also right nondegenerate. Then M is zero.
$\underline {C}$
is weight-degenerate and either M is w-bounded below or w is also right nondegenerate. Then M is zero.
3. For an object M of
![]() $\underline {C}$
, assume that
$\underline {C}$
, assume that
![]() ${\underline {Hw}}$
-complexes
${\underline {Hw}}$
-complexes
![]() $t_j=(M_j^i)$
for
$t_j=(M_j^i)$
for
![]() $j=1,2$
are
$j=1,2$
are
![]() $K({\underline {Hw}})$
-isomorphic to
$K({\underline {Hw}})$
-isomorphic to
![]() $t(M)$
, and
$t(M)$
, and
![]() $F:\underline {C}\to (\underline {C}',w')$
is a weight-exact functor that annihilates the groups
$F:\underline {C}\to (\underline {C}',w')$
is a weight-exact functor that annihilates the groups
![]() $\underline {C}(M_1^i,M_2^i)$
for all
$\underline {C}(M_1^i,M_2^i)$
for all
![]() $i\in {\mathbb {Z}}$
.
$i\in {\mathbb {Z}}$
.
Then
![]() $F(M)$
is
$F(M)$
is
![]() $w'$
-degenerate.
$w'$
-degenerate.
4. Assume that
![]() $\underline {C}_1,\ \underline {C}_2$
, and
$\underline {C}_1,\ \underline {C}_2$
, and
![]() $\underline {C}_3$
are full triangulated subcategories of
$\underline {C}_3$
are full triangulated subcategories of
![]() $\underline {C}$
such that w restricts to them; suppose that the Verdier localization functor
$\underline {C}$
such that w restricts to them; suppose that the Verdier localization functor
![]() $F:\underline {C}\to \underline {C}'=\underline {C}/\underline {C}_3$
exists (i.e., all morphism classes in this localization are sets) and all
$F:\underline {C}\to \underline {C}'=\underline {C}/\underline {C}_3$
exists (i.e., all morphism classes in this localization are sets) and all
![]() ${\underline {Hw}}$
-morphisms between elements of the corresponding classes
${\underline {Hw}}$
-morphisms between elements of the corresponding classes
![]() $\underline {C}_{1,w_1=0}$
and
$\underline {C}_{1,w_1=0}$
and
![]() $\underline {C}_{2,w_2=0}$
are killed by F.
$\underline {C}_{2,w_2=0}$
are killed by F.
Then there is a unique weight structure
![]() $w'$
on
$w'$
on
![]() $\underline {C}'$
such that F is weight-exact, and for any
$\underline {C}'$
such that F is weight-exact, and for any
![]() $M\in \operatorname {Obj} \underline {C}_1\cap \operatorname {Obj}\underline {C}_2$
the object
$M\in \operatorname {Obj} \underline {C}_1\cap \operatorname {Obj}\underline {C}_2$
the object
![]() $F(M)$
is
$F(M)$
is
![]() $w'$
-degenerate. Moreover, if
$w'$
-degenerate. Moreover, if
![]() $w'$
is left nondegenerate, then
$w'$
is left nondegenerate, then
![]() $F(M)$
is
$F(M)$
is
![]() $w'$
-right degenerate, and M belongs to
$w'$
-right degenerate, and M belongs to
![]() $\operatorname {\mathrm {\operatorname {Kar}}}_{\underline {C}}(\operatorname {Obj} \underline {C}_3)$
whenever M is w-bounded below.
$\operatorname {\mathrm {\operatorname {Kar}}}_{\underline {C}}(\operatorname {Obj} \underline {C}_3)$
whenever M is w-bounded below.
Proof. 1. By axiom 1.2.1(i), retracts of left (resp. right) w-degenerate objects are left (resp. right) w-degenerate. The assertion follows easily.
2. According to the previous assertion, M is right weight-degenerate, that is, it belongs to
![]() $\cap _{i\in {\mathbb {Z}}}\underline {C}_{w\le i}$
. On the other hand, M belongs to
$\cap _{i\in {\mathbb {Z}}}\underline {C}_{w\le i}$
. On the other hand, M belongs to
![]() $\underline {C}_{w\ge i+1}$
for some
$\underline {C}_{w\ge i+1}$
for some
![]() $i\in {\mathbb {Z}}$
(and it actually belongs to all of these classes in the second case by the previous assertion). Since
$i\in {\mathbb {Z}}$
(and it actually belongs to all of these classes in the second case by the previous assertion). Since
![]() $\underline {C}_{w\le i}\perp \underline {C}_{w\ge i+1}$
,
$\underline {C}_{w\le i}\perp \underline {C}_{w\ge i+1}$
,
![]() $M\perp M$
; hence,
$M\perp M$
; hence,
![]() $M=0$
.
$M=0$
.
3. Let m be a
![]() $K_{\mathfrak {w}}({\underline {Hw}})$
-isomorphism
$K_{\mathfrak {w}}({\underline {Hw}})$
-isomorphism
![]() $t_1\to t_2$
. Then, for the functor
$t_1\to t_2$
. Then, for the functor
![]() $K_{\mathfrak {w}}({\underline {HF}}):K_{\mathfrak {w}}({\underline {Hw}})\to K_{\mathfrak {w}}({\underline {Hw}}')$
given by Lemma 1.3.2(3), we clearly have
$K_{\mathfrak {w}}({\underline {HF}}):K_{\mathfrak {w}}({\underline {Hw}})\to K_{\mathfrak {w}}({\underline {Hw}}')$
given by Lemma 1.3.2(3), we clearly have
![]() $K_{\mathfrak {w}}({\underline {HF}})(m)=0$
. Here,
$K_{\mathfrak {w}}({\underline {HF}})(m)=0$
. Here,
![]() ${\underline {HF}}$
is the restriction of F to hearts. Since
${\underline {HF}}$
is the restriction of F to hearts. Since
![]() $K_{\mathfrak {w}}({\underline {HF}})(m)$
is also an isomorphism, we obtain
$K_{\mathfrak {w}}({\underline {HF}})(m)$
is also an isomorphism, we obtain
![]() $K_{\mathfrak {w}}({\underline {HF}})(t_1)=0$
. On the other hand, by Proposition 1.3.4(4) we have
$K_{\mathfrak {w}}({\underline {HF}})(t_1)=0$
. On the other hand, by Proposition 1.3.4(4) we have
![]() $t_{w'}(F(M))\cong K_{\mathfrak {w}}({\underline {HF}})(t(M))\cong K_{\mathfrak {w}}({\underline {HF}})(t_1)$
; hence,
$t_{w'}(F(M))\cong K_{\mathfrak {w}}({\underline {HF}})(t(M))\cong K_{\mathfrak {w}}({\underline {HF}})(t_1)$
; hence,
![]() $t_{w'}(F(M))=0$
, as desired.
$t_{w'}(F(M))=0$
, as desired.
4.
![]() $w'$
exists according to Proposition 8.1.1(1) of [Reference Bondarko4], and
$w'$
exists according to Proposition 8.1.1(1) of [Reference Bondarko4], and
![]() $w'$
is uniquely determined by w according to Proposition 3.1.1(1) of [Reference Bondarko and Sosnilo10].
$w'$
is uniquely determined by w according to Proposition 3.1.1(1) of [Reference Bondarko and Sosnilo10].
Next, Proposition 1.3.4(4) gives the existence of
![]() ${\underline {Hw}}$
-complexes
${\underline {Hw}}$
-complexes
![]() $t_1$
and
$t_1$
and
![]() $t_2$
such that
$t_2$
such that
![]() $t(M)\cong t_1\cong t_2$
(both in
$t(M)\cong t_1\cong t_2$
(both in
![]() $K_{\mathfrak {w}}({\underline {Hw}})$
and in
$K_{\mathfrak {w}}({\underline {Hw}})$
and in
![]() $K({\underline {Hw}})$
; see Lemma 1.3.2(1)). The terms
$K({\underline {Hw}})$
; see Lemma 1.3.2(1)). The terms
![]() $M_1^i$
belong to
$M_1^i$
belong to
![]() $\underline {C}_{1,w_1=0}$
, and the terms of
$\underline {C}_{1,w_1=0}$
, and the terms of
![]() $t_2$
belong to
$t_2$
belong to
![]() $\underline {C}_{2,w_2=0}$
. Thus,
$\underline {C}_{2,w_2=0}$
. Thus,
![]() $F(M)$
is
$F(M)$
is
![]() $w'$
-degenerate by assertion 3.
$w'$
-degenerate by assertion 3.
By assertion 1, it follows that
![]() $F(M)$
is right
$F(M)$
is right
![]() $w'$
-degenerate whenever
$w'$
-degenerate whenever
![]() $w'$
is left nondegenerate. Lastly, if M is weight-bounded below, then
$w'$
is left nondegenerate. Lastly, if M is weight-bounded below, then
![]() $F(M)$
also is. Hence, our assumptions imply that
$F(M)$
also is. Hence, our assumptions imply that
![]() $F(M)=0$
according to assertion 2. Thus, M belongs to
$F(M)=0$
according to assertion 2. Thus, M belongs to
![]() $\operatorname {\mathrm {\operatorname {Kar}}}_{\underline {C}}(\operatorname {Obj} \underline {C}_3)$
. Here, we apply the well-known Lemma 2.1.33 of [Reference Neeman23].
$\operatorname {\mathrm {\operatorname {Kar}}}_{\underline {C}}(\operatorname {Obj} \underline {C}_3)$
. Here, we apply the well-known Lemma 2.1.33 of [Reference Neeman23].
We will describe some consequences of Proposition 3.1.6(4) in Corollary 4.1.4 and Remark 4.1.5 below.
3.2 A conservativity application
Our results imply that certain weight-exact functors are ‘almost conservative’.
Proposition 3.2.1. Let
![]() $F:(\underline {C},w)\to (\underline {C}',w')$
be a weight-exact functor.
$F:(\underline {C},w)\to (\underline {C}',w')$
be a weight-exact functor.
Assume that the induced functor
![]() ${\underline {HF}}:{\underline {Hw}}\to {\underline {Hw}}'$
is full. Every
${\underline {HF}}:{\underline {Hw}}\to {\underline {Hw}}'$
is full. Every
![]() ${\underline {Hw}}$
-endomorphism killed by
${\underline {Hw}}$
-endomorphism killed by
![]() ${\underline {HF}}$
is nilpotent, and for some
${\underline {HF}}$
is nilpotent, and for some
![]() $M\in \operatorname {Obj} \underline {C}$
the object
$M\in \operatorname {Obj} \underline {C}$
the object
![]() $F(M)$
belongs to
$F(M)$
belongs to
![]() $\underline {C}^{\prime }_{w'\notin [m,n]}$
for some
$\underline {C}^{\prime }_{w'\notin [m,n]}$
for some
![]() $m\le n\in {\mathbb {Z}}$
(resp.
$m\le n\in {\mathbb {Z}}$
(resp.
![]() $F(M)$
is
$F(M)$
is
![]() $w'$
-degenerate, resp. essentially
$w'$
-degenerate, resp. essentially
![]() $w'$
-positive, resp. essentially
$w'$
-positive, resp. essentially
![]() $w'$
-negative).
$w'$
-negative).
Then M is without weights
![]() $m,\dots , n$
(resp. M is weight-degenerate, resp. essentially w-positive, resp. essentially w-negative).
$m,\dots , n$
(resp. M is weight-degenerate, resp. essentially w-positive, resp. essentially w-negative).
Consequently,
![]() $M=0$
if
$M=0$
if
![]() $F(M)$
is
$F(M)$
is
![]() $w'$
-degenerate and w is nondegenerate.
$w'$
-degenerate and w is nondegenerate.
Proof. Let us prove the first statement in our proposition for
![]() $m=n$
; thus, assume that
$m=n$
; thus, assume that
![]() $F(M)$
is without weight m. We should prove that this assumption implies
$F(M)$
is without weight m. We should prove that this assumption implies
![]() $M\in \underline {C}_{w\notin [m,m]}$
; we call this implication Claim (*).
$M\in \underline {C}_{w\notin [m,m]}$
; we call this implication Claim (*).
According to Theorem 2.3.1(3), this claim is equivalent to the following one:
![]() $t(\operatorname {id}_M)\backsim _{[-m,-m]}0$
whenever
$t(\operatorname {id}_M)\backsim _{[-m,-m]}0$
whenever
![]() $t_{w'}(\operatorname {id}_{F(M)})\backsim _{[-m,-m]}0$
.
$t_{w'}(\operatorname {id}_{F(M)})\backsim _{[-m,-m]}0$
.
Now, we can assume that
![]() $t_{w'}(F(M))$
is obtained from the weight complex
$t_{w'}(F(M))$
is obtained from the weight complex
![]() $t(M)=(M^i,d^i)$
; see Proposition 1.3.4(4). Thus, there exist morphisms
$t(M)=(M^i,d^i)$
; see Proposition 1.3.4(4). Thus, there exist morphisms
![]() $h'\in {\underline {Hw}}'(F(M^{-m}), F(M^{-m-1}))$
and
$h'\in {\underline {Hw}}'(F(M^{-m}), F(M^{-m-1}))$
and
![]() $j'\in {\underline {Hw}}'(F(M^{1-m}),F(M^{-m}))$
such that
$j'\in {\underline {Hw}}'(F(M^{1-m}),F(M^{-m}))$
such that
![]() $\operatorname {id}_{F(M^{-m})}=j'\circ F(d^{-m}) +F(d^{-m-1})\circ h'$
. Since the restriction of F to
$\operatorname {id}_{F(M^{-m})}=j'\circ F(d^{-m}) +F(d^{-m-1})\circ h'$
. Since the restriction of F to
![]() ${\underline {Hw}}$
is full and conservative, we can lift
${\underline {Hw}}$
is full and conservative, we can lift
![]() $h'$
and
$h'$
and
![]() $j'$
to some
$j'$
to some
![]() ${\underline {Hw}}$
-morphisms h and j, and for lifts of this sort the endomorphism
${\underline {Hw}}$
-morphisms h and j, and for lifts of this sort the endomorphism
is nilpotent. Hence, there exists
![]() $n>0$
such that
$n>0$
such that
Therefore,
![]() $\operatorname {id}_{M^{-m}}$
can be presented in the form
$\operatorname {id}_{M^{-m}}$
can be presented in the form
![]() $a\circ d^{-m}+ d^{-m-1}\circ b$
for some
$a\circ d^{-m}+ d^{-m-1}\circ b$
for some
![]() $a\in {\underline {Hw}}(M^{-m},M^{-m-1})$
and
$a\in {\underline {Hw}}(M^{-m},M^{-m-1})$
and
![]() $b\in {\underline {Hw}}(M^{1-m},M^{-m})$
; one can just write down explicit formulas for a and b in this setting. Thus,
$b\in {\underline {Hw}}(M^{1-m},M^{-m})$
; one can just write down explicit formulas for a and b in this setting. Thus,
![]() $t(\operatorname {id}_M)\backsim _{[-m,-m]}0$
.
$t(\operatorname {id}_M)\backsim _{[-m,-m]}0$
.
Next, the general case of the ‘without weights
![]() $m,\dots , n$
part’ follows from Claim (*) immediately according to Theorem 2.2.1(8).
$m,\dots , n$
part’ follows from Claim (*) immediately according to Theorem 2.2.1(8).
Lastly, our remaining statements follow from Claim (*) as well; see condition 6 in Theorem 3.1.3, condition 2 in Corollary 3.1.4 and Proposition 3.1.6(2).
Remark 3.2.2.
-
1. Our proposition essentially says that F is ‘conservative (and detects weights; cf. Remark 1.5.3(1) of [Reference Bondarko7]) up to weight-degenerate objects’. The latter feature of the result is unavoidable. Indeed, arguing similarly to Proposition 4.2.1(1) of [Reference Bondarko and Sosnilo10] one can easily prove that for any set W of weight-degenerate objects of
 $\underline {C}$
the localization of
$\underline {C}$
the localization of
 $\underline {C}$
by the triangulated subcategory generated by W gives a weight-exact functor that restricts to a full embedding
$\underline {C}$
by the triangulated subcategory generated by W gives a weight-exact functor that restricts to a full embedding
 ${\underline {Hw}}\to \underline {C}'$
.
${\underline {Hw}}\to \underline {C}'$
. -
2. Let us relate our proposition to earlier results.
In Theorem 1.5.1(1,2) of [Reference Bondarko7], only the case where M is bounded either above or below was considered. On the other hand,
 ${\underline {HF}}$
was just assumed to be full and conservative. Thus, neither our proposition implies loc. cit. nor the converse is valid. Note also that, in the case where the endomorphisms killed by
${\underline {HF}}$
was just assumed to be full and conservative. Thus, neither our proposition implies loc. cit. nor the converse is valid. Note also that, in the case where the endomorphisms killed by
 ${\underline {HF}}$
are nilpotent, all the conclusions of loc. cit. can be easily deduced from our proposition.
${\underline {HF}}$
are nilpotent, all the conclusions of loc. cit. can be easily deduced from our proposition.Next, we recall that in Theorem 2.8 of [Reference Wildeshaus29] (as well as in the weaker Theorem 2.5 of ibid.) it was assumed that F is weight-exact,
 ${\underline {HF}}$
is full and conservative,
${\underline {HF}}$
is full and conservative,
 ${\underline {Hw}}$
is Karoubian and semiprimary and w is bounded (see Definition 1.2.2(9)). Now, these assumptions imply that endomorphisms killed by
${\underline {Hw}}$
is Karoubian and semiprimary and w is bounded (see Definition 1.2.2(9)). Now, these assumptions imply that endomorphisms killed by
 ${\underline {HF}}$
are nilpotent. Indeed, the conservativity of
${\underline {HF}}$
are nilpotent. Indeed, the conservativity of
 ${\underline {HF}}$
means that these endomorphisms belong to the radical of
${\underline {HF}}$
means that these endomorphisms belong to the radical of
 ${\underline {Hw}}$
, and semiprimality means that all elements of this radical are nilpotent. Thus, our proposition implies Theorem 2.8 of ibid.
${\underline {Hw}}$
, and semiprimality means that all elements of this radical are nilpotent. Thus, our proposition implies Theorem 2.8 of ibid. -
3. One can obtain plenty of examples to our proposition by taking
 $F=K(G):K(\underline {B})\to K(\underline {B}')$
; here,
$F=K(G):K(\underline {B})\to K(\underline {B}')$
; here,
 $G:\underline {B}\to \underline {B}'$
is a full additive functor such that every
$G:\underline {B}\to \underline {B}'$
is a full additive functor such that every
 $\underline {B}$
-endomorphism killed by G is nilpotent, and one takes w and
$\underline {B}$
-endomorphism killed by G is nilpotent, and one takes w and
 $w'$
to be the corresponding stupid weight structures. Note that in this case we have
$w'$
to be the corresponding stupid weight structures. Note that in this case we have
 ${\underline {HF}}\cong \operatorname {\mathrm {\operatorname {Kar}}}(G)$
(see Remark 1.2.3(1)); thus,
${\underline {HF}}\cong \operatorname {\mathrm {\operatorname {Kar}}}(G)$
(see Remark 1.2.3(1)); thus,
 ${\underline {HF}}$
fulfills our assumptions as well.
${\underline {HF}}$
fulfills our assumptions as well.Since w is nondegenerate, our proposition implies that F is conservative. The author wonders whether a proof of this statement ‘without killing weights’ exists. This may allow to modify the assumptions on
 ${\underline {HF}}$
in Proposition 3.2.1.
${\underline {HF}}$
in Proposition 3.2.1.Other examples to our proposition are given by Corollary 4.1.4(2).
3.3 An ‘indecomposable’ weight-degenerate object
Let
![]() $K^b(L-\operatorname {vect})$
be the category of bounded complexes of vectors spaces over a field L. We take
$K^b(L-\operatorname {vect})$
be the category of bounded complexes of vectors spaces over a field L. We take
![]() $\underline {C}'=(K^b(L-\operatorname {vect}))^3$
and
$\underline {C}'=(K^b(L-\operatorname {vect}))^3$
and
![]() $\underline {C}$
to be the subcategory of
$\underline {C}$
to be the subcategory of
![]() $\underline {C}'$
consisting of objects whose ‘total Euler characteristic’ is even in the following sense: The sum of dimensions of all homology of all the three components of
$\underline {C}'$
consisting of objects whose ‘total Euler characteristic’ is even in the following sense: The sum of dimensions of all homology of all the three components of
![]() $M=(M_1,M_2,M_3)$
should be even. We define
$M=(M_1,M_2,M_3)$
should be even. We define
![]() $\underline {C}^{\prime }_{w'\le 0}$
as the class of all
$\underline {C}^{\prime }_{w'\le 0}$
as the class of all
![]() $M=(M_1,M_2,M_3)$
such that
$M=(M_1,M_2,M_3)$
such that
![]() $M_1=0$
and
$M_1=0$
and
![]() $M_2$
is acyclic in negative degrees;
$M_2$
is acyclic in negative degrees;
![]() $M\in \underline {C}^{\prime }_{w'\ge 0}$
if
$M\in \underline {C}^{\prime }_{w'\ge 0}$
if
![]() $M_3= 0$
and
$M_3= 0$
and
![]() $M_2$
is acyclic in positive degrees. We set
$M_2$
is acyclic in positive degrees. We set
![]() $\underline {C}_{w\le 0}=\underline {C}^{\prime }_{w\le 0}\cap \operatorname {Obj} \underline {C}$
and
$\underline {C}_{w\le 0}=\underline {C}^{\prime }_{w\le 0}\cap \operatorname {Obj} \underline {C}$
and
![]() $\underline {C}_{w\ge 0}=\underline {C}^{\prime }_{w\ge 0}\cap \operatorname {Obj} \underline {C}$
. Obviously,
$\underline {C}_{w\ge 0}=\underline {C}^{\prime }_{w\ge 0}\cap \operatorname {Obj} \underline {C}$
. Obviously,
![]() $w'$
is a weight structure on
$w'$
is a weight structure on
![]() $\underline {C}'$
. w is a weight structure on
$\underline {C}'$
. w is a weight structure on
![]() $\underline {C}$
since for
$\underline {C}$
since for
![]() $(M_1,M_2,M_3)\in \operatorname {Obj} \underline {C}$
any triangle of the form
$(M_1,M_2,M_3)\in \operatorname {Obj} \underline {C}$
any triangle of the form
where
![]() $M'\to M_2\to M"$
is a
$M'\to M_2\to M"$
is a
![]() $w^{st}$
-decomposition of
$w^{st}$
-decomposition of
![]() $M_2$
with the corresponding parities of the Euler characteristics, gives a w-decomposition. Clearly,
$M_2$
with the corresponding parities of the Euler characteristics, gives a w-decomposition. Clearly,
![]() $(\underline {C}',w')$
is a weight-Karoubian extension of
$(\underline {C}',w')$
is a weight-Karoubian extension of
![]() $\underline {C}$
.
$\underline {C}$
.
Take
![]() $M=(L,0,L)$
and a distinguished triangle
$M=(L,0,L)$
and a distinguished triangle
![]() $X'\to M \to Y'$
with
$X'\to M \to Y'$
with
![]() $X'=(0,0,L)$
and
$X'=(0,0,L)$
and
![]() $Y'=(L,0,0)$
. Then
$Y'=(L,0,0)$
. Then
![]() $X'$
(resp.
$X'$
(resp.
![]() $Y'$
) is right (resp. left)
$Y'$
) is right (resp. left)
![]() $w'$
-degenerate. Thus, M is weight-degenerate and without weight
$w'$
-degenerate. Thus, M is weight-degenerate and without weight
![]() $0$
both in
$0$
both in
![]() $\underline {C}'$
and in
$\underline {C}'$
and in
![]() $\underline {C}$
; see conditions 1 and 2 in Theorem 3.1.3 and Theorem 2.2.1(9,6).
$\underline {C}$
; see conditions 1 and 2 in Theorem 3.1.3 and Theorem 2.2.1(9,6).
Next, for a distinguished triangle
![]() $X\to M \to Y$
with
$X\to M \to Y$
with
![]() $X\in \underline {C}^{\prime }_{w'\le -1}$
,
$X\in \underline {C}^{\prime }_{w'\le -1}$
,
![]() $Y\in \underline {C}^{\prime }_{w'\ge 1}$
, we have
$Y\in \underline {C}^{\prime }_{w'\ge 1}$
, we have
![]() $X\cong X'$
and
$X\cong X'$
and
![]() $Y\cong Y'$
by Theorem 2.2.1(9). Since
$Y\cong Y'$
by Theorem 2.2.1(9). Since
![]() $X'$
(as well as
$X'$
(as well as
![]() $Y'$
) is not an object of
$Y'$
) is not an object of
![]() $\underline {C}$
, X is not an object of
$\underline {C}$
, X is not an object of
![]() $\underline {C}$
either. Thus, neither of the parts of Theorem 2.3.4(II) nor Theorem 2.2.1(10) extends to
$\underline {C}$
either. Thus, neither of the parts of Theorem 2.3.4(II) nor Theorem 2.2.1(10) extends to
![]() $\underline {C}$
.
$\underline {C}$
.
Consequently, the notions of essential w-positivity and w-negativity are necessary for Theorem 3.1.3 and Corollary 3.1.4.
Note also that
![]() $t_w(M)=0$
; hence, Theorem 2.3.1(4) does not extend to
$t_w(M)=0$
; hence, Theorem 2.3.1(4) does not extend to
![]() $\underline {C}$
as well.
$\underline {C}$
as well.
4 On ‘topological’ examples and converse Hurewicz theorems
In this section, we discuss the applications of our results to equivariant stable homotopy categories as well as to general purely compactly generated weight structures. We significantly extend the main results of [Reference Bondarko7, §4].
In §4.1, we recall some properties of weight structures generated by sets of compact objects in their hearts and apply the main results of the previous sections to this setting. As an application, we establish important prerequisites for [Reference Bondarko5].
In §4.2, we apply our results to prove some new properties of the spherical weight structure
![]() $w^G$
on the equivariant stable homotopy category
$w^G$
on the equivariant stable homotopy category
![]() $SH(G)$
of G-spectra (
$SH(G)$
of G-spectra (
![]() $w^G$
was introduced in [Reference Bondarko7]; actually, we work in a somewhat more general context). We obtain a certain converse Hurewicz theorem in this setting. Moreover, the theory of objects without weights gives canonical ‘decompositions’ of spectra whose singular homology vanishes in two subsequent degrees; see Theorem 4.2.4(5) and Remark 4.2.3(2) below.
$w^G$
was introduced in [Reference Bondarko7]; actually, we work in a somewhat more general context). We obtain a certain converse Hurewicz theorem in this setting. Moreover, the theory of objects without weights gives canonical ‘decompositions’ of spectra whose singular homology vanishes in two subsequent degrees; see Theorem 4.2.4(5) and Remark 4.2.3(2) below.
4.1 On purely compactly generated weight structures
In this section, we always assume that
![]() $\underline {C}$
is a smashing triangulated category; see Definition 2.4.3.
$\underline {C}$
is a smashing triangulated category; see Definition 2.4.3.
Definition 4.1.1. Let
![]() $\mathcal {P}$
be a full subcategory of
$\mathcal {P}$
be a full subcategory of
![]() $\underline {C}$
.
$\underline {C}$
.
-
1. We will say that
 $\mathcal {P}$
is connective in
$\mathcal {P}$
is connective in
 $\underline {C}$
if
$\underline {C}$
if
 $ \mathcal {P}\perp (\cup _{i>0} \mathcal {P}[i])$
.Footnote
4
$ \mathcal {P}\perp (\cup _{i>0} \mathcal {P}[i])$
.Footnote
4
-
2. Let
 $\mathcal {P}'$
be the category of ‘formal coproducts’ of objects of
$\mathcal {P}'$
be the category of ‘formal coproducts’ of objects of
 $\mathcal {P}$
, that is, the objects of
$\mathcal {P}$
, that is, the objects of
 $\mathcal {P}'$
are of the form
$\mathcal {P}'$
are of the form
 $\coprod _i P_i$
for families of
$\coprod _i P_i$
for families of
 $P_i\in \operatorname {Obj} \mathcal {P}$
, and (4.1.1)Then we will call the idempotent completion of
$P_i\in \operatorname {Obj} \mathcal {P}$
, and (4.1.1)Then we will call the idempotent completion of $$ \begin{align}\mathcal{P}'(\coprod M_i,\coprod N_j)=\prod_i (\bigoplus_j \mathcal{P}(M_i,N_j)).\end{align} $$
$$ \begin{align}\mathcal{P}'(\coprod M_i,\coprod N_j)=\prod_i (\bigoplus_j \mathcal{P}(M_i,N_j)).\end{align} $$
 $\mathcal {P}'$
the smashing idempotent completion of
$\mathcal {P}'$
the smashing idempotent completion of
 $\mathcal {P}$
.
$\mathcal {P}$
.
-
3. We will say that a full triangulated subcategory
 $\underline {D}\subset \underline {C}$
is localizing whenever
$\underline {D}\subset \underline {C}$
is localizing whenever
 $\underline {D}$
is closed with respect to
$\underline {D}$
is closed with respect to
 $\underline {C}$
-coproducts. Respectively, we will call the smallest localizing subcategory of
$\underline {C}$
-coproducts. Respectively, we will call the smallest localizing subcategory of
 $\underline {C}$
that contains a given subcategory
$\underline {C}$
that contains a given subcategory
 $\mathcal {P}\subset \underline {C}$
the localizing subcategory of
$\mathcal {P}\subset \underline {C}$
the localizing subcategory of
 $\underline {C}$
generated by
$\underline {C}$
generated by
 $\mathcal {P}$
.
$\mathcal {P}$
. -
4. An object M of
 $\underline {C}$
is said to be compact if the functor
$\underline {C}$
is said to be compact if the functor
 $H^M=\underline {C}(M,-):\underline {C}\to \operatorname {Ab}$
respects coproducts.
$H^M=\underline {C}(M,-):\underline {C}\to \operatorname {Ab}$
respects coproducts. -
5. We will say that
 $\underline {C}$
is compactly generated by its subcategory
$\underline {C}$
is compactly generated by its subcategory
 $\mathcal {P}$
if
$\mathcal {P}$
if
 $\mathcal {P}$
is small, generates
$\mathcal {P}$
is small, generates
 $\underline {C}$
as its own localizing subcategory and objects of
$\underline {C}$
as its own localizing subcategory and objects of
 $\mathcal {P}$
are compact.
$\mathcal {P}$
are compact.
Now, let us recall the main properties of purely compactly generated weight structures. These are the ones provided by the following theorem.
Theorem 4.1.2. Let
![]() $\mathcal {P}$
be a connective subcategory of
$\mathcal {P}$
be a connective subcategory of
![]() $\underline {C}$
that compactly generates it. Then the following statements are valid; cf. Definition 2.4.3.
$\underline {C}$
that compactly generates it. Then the following statements are valid; cf. Definition 2.4.3.
-
1.
 $\underline {C}$
is a Karoubian Brown category.
$\underline {C}$
is a Karoubian Brown category. -
2. There exists a unique smashing weight structure w on
 $\underline {C}$
such that
$\underline {C}$
such that
 $\mathcal {P}\subset {\underline {Hw}}$
; w is left nondegenerate.
$\mathcal {P}\subset {\underline {Hw}}$
; w is left nondegenerate. -
3. The corresponding
 $\underline {C}_{w\le 0}$
(resp.
$\underline {C}_{w\le 0}$
(resp.
 $\underline {C}_{w\ge 0}$
) is the smallest subclass of
$\underline {C}_{w\ge 0}$
) is the smallest subclass of
 $\operatorname {Obj} \underline {C}$
that is closed with respect to coproducts and extensions and contains
$\operatorname {Obj} \underline {C}$
that is closed with respect to coproducts and extensions and contains
 $\operatorname {Obj}\mathcal {P}[i]$
for
$\operatorname {Obj}\mathcal {P}[i]$
for
 $i\le 0$
(resp. for
$i\le 0$
(resp. for
 $i\ge 0$
), and
$i\ge 0$
), and
 ${\underline {Hw}}$
is equivalent to the smashing idempotent completion of
${\underline {Hw}}$
is equivalent to the smashing idempotent completion of
 $\mathcal {P}$
.
$\mathcal {P}$
.Moreover,
 $\underline {C}_{w\ge 0}=(\cup _{i<0}\mathcal {P}[i])^{\perp }$
.
$\underline {C}_{w\ge 0}=(\cup _{i<0}\mathcal {P}[i])^{\perp }$
. -
4. Let H be a cohomological functor from
 $\underline {C}$
into an abelian category
$\underline {C}$
into an abelian category
 $\underline {A}$
that converts all small coproducts into products. Then it is pure if and only if it kills
$\underline {A}$
that converts all small coproducts into products. Then it is pure if and only if it kills
 $\cup _{i\neq 0}\mathcal {P}[i]$
.
$\cup _{i\neq 0}\mathcal {P}[i]$
. -
5. Let
 $F:\underline {C}\to \underline {D}$
be an exact functor that respects coproducts, where
$F:\underline {C}\to \underline {D}$
be an exact functor that respects coproducts, where
 $\underline {D}$
is a triangulated category endowed with a smashing weight structure v. Then F is weight-exact if and only if it sends
$\underline {D}$
is a triangulated category endowed with a smashing weight structure v. Then F is weight-exact if and only if it sends
 $\mathcal {P}$
into
$\mathcal {P}$
into
 $\underline {Hv}$
.
$\underline {Hv}$
. -
6. The category
 ${\underline {Ht}}\subset \underline {C}$
of w-pure representable functors from
${\underline {Ht}}\subset \underline {C}$
of w-pure representable functors from
 $\underline {C}$
is equivalent to the category
$\underline {C}$
is equivalent to the category
 $\underline {A}_{\mathcal {P}}$
of additive contravariant functors from
$\underline {A}_{\mathcal {P}}$
of additive contravariant functors from
 $\mathcal {P}$
into
$\mathcal {P}$
into
 $\operatorname {Ab}$
(i.e., we take those functors that respect the addition of morphisms).Footnote
5
Moreover,
$\operatorname {Ab}$
(i.e., we take those functors that respect the addition of morphisms).Footnote
5
Moreover,
 $\underline {A}_{\mathcal {P}}$
(and thus also
$\underline {A}_{\mathcal {P}}$
(and thus also
 ${\underline {Ht}}$
) is Grothendieck abelian and has enough projectives. Consequently,
${\underline {Ht}}$
) is Grothendieck abelian and has enough projectives. Consequently,
 $\underline {A}_{\mathcal {P}}$
is cogenerated by an object I that is injective in it; we fix the choice of I.
$\underline {A}_{\mathcal {P}}$
is cogenerated by an object I that is injective in it; we fix the choice of I.Furthermore, restricting functors representable by objects of
 $\mathcal {P}$
to
$\mathcal {P}$
to
 ${\underline {Hw}}$
one obtains a fully faithful functor
${\underline {Hw}}$
one obtains a fully faithful functor
 ${\mathcal {A}_{\mathcal {P}}}:{\underline {Hw}}\to \underline {A}_{\mathcal {P}}$
whose essential image is the subcategory of projective objects of
${\mathcal {A}_{\mathcal {P}}}:{\underline {Hw}}\to \underline {A}_{\mathcal {P}}$
whose essential image is the subcategory of projective objects of
 $\underline {A}_{\mathcal {P}}$
.
$\underline {A}_{\mathcal {P}}$
. -
7. The following assumptions on an object M of
 $\underline {C}$
are equivalent.
$\underline {C}$
are equivalent.(i).
 $t(M)\in K({\underline {Hw}})_{w^{st}\ge 0}$
.
$t(M)\in K({\underline {Hw}})_{w^{st}\ge 0}$
.(ii).
 $H_j^{{\mathcal {A}_{\mathcal {P}}}}(M)=0$
for
$H_j^{{\mathcal {A}_{\mathcal {P}}}}(M)=0$
for
 $j<0$
; see Theorem 2.4.2(3) for this notation.
$j<0$
; see Theorem 2.4.2(3) for this notation.(iii).
 $M\perp (\cup _{j<0}\{I[j]\})$
.
$M\perp (\cup _{j<0}\{I[j]\})$
. -
8. Assume that there exists an integer
 $j>0$
such that
$j>0$
such that
 $\mathcal {P}\perp \cup _{i\ge j}\mathcal {P}[-i]$
. Then w is nondegenerate.
$\mathcal {P}\perp \cup _{i\ge j}\mathcal {P}[-i]$
. Then w is nondegenerate.
Proof. Assertions 1–7 were mostly established in [Reference Neeman23] and [Reference Bondarko and Sosnilo10]; see §3.2 of [Reference Bondarko7] for the detail.
Next, if
![]() $\mathcal {P}\perp (\cup _{i\ge j}\mathcal {P}[-i])$
, then the compactness of elements of
$\mathcal {P}\perp (\cup _{i\ge j}\mathcal {P}[-i])$
, then the compactness of elements of
![]() $\mathcal {P}$
along with the description of
$\mathcal {P}$
along with the description of
![]() $\underline {C}_{w\le 0}$
in assertion 3 imply that
$\underline {C}_{w\le 0}$
in assertion 3 imply that
![]() $\cup _{i\ge j}\mathcal {P}[i]\perp \underline {C}_{w\le 0}$
. Thus, every right weight-degenerate element of
$\cup _{i\ge j}\mathcal {P}[i]\perp \underline {C}_{w\le 0}$
. Thus, every right weight-degenerate element of
![]() $\underline {C}$
belongs to
$\underline {C}$
belongs to
![]() $(\cup _{i\in {\mathbb {Z}}}\mathcal {P}[i]){}^{\perp }$
. Now, the well-known Proposition 8.4.1 of [Reference Neeman23] says that the latter class is zero since
$(\cup _{i\in {\mathbb {Z}}}\mathcal {P}[i]){}^{\perp }$
. Now, the well-known Proposition 8.4.1 of [Reference Neeman23] says that the latter class is zero since
![]() $\underline {C}$
is compactly generated by
$\underline {C}$
is compactly generated by
![]() $\mathcal {P}$
; hence, w is right nondegenerate. Since w is also left nondegenerate by assertion 2, we obtain assertion 8.
$\mathcal {P}$
; hence, w is right nondegenerate. Since w is also left nondegenerate by assertion 2, we obtain assertion 8.
Remark 4.1.3. We will now discuss certain examples to our theorem. Note, however, that the spherical weight structure on
![]() $SH$
is purely compactly generated and still right weight-degenerate; see Remark 4.2.3(4) below.
$SH$
is purely compactly generated and still right weight-degenerate; see Remark 4.2.3(4) below.
Corollary 4.1.4. Let
![]() $n>0$
.
$n>0$
.
1. The assumptions of Theorem 4.1.2 are fulfilled if
![]() $\underline {C}$
is one of the following categories:
$\underline {C}$
is one of the following categories:
(i) the derived category of a small differential graded category
![]() $\underline {B}$
(see §3.2 [Reference Keller16]) such that the complex
$\underline {B}$
(see §3.2 [Reference Keller16]) such that the complex
![]() $\underline {B}^*(M,N)$
is acyclic in positive degrees whenever
$\underline {B}^*(M,N)$
is acyclic in positive degrees whenever
![]() $M,N\in \underline {B}$
. Here, we take
$M,N\in \underline {B}$
. Here, we take
![]() $\mathcal {P}$
to be the subcategory of
$\mathcal {P}$
to be the subcategory of
![]() $\underline {C}$
corresponding to
$\underline {C}$
corresponding to
![]() $\underline {B}$
;
$\underline {B}$
;
(ii) the derived category of E-modules, where E is an S-algebra and
![]() $\pi _i(E)=\{0\}$
if
$\pi _i(E)=\{0\}$
if
![]() $i<0$
; see Example 1.2.3(f) of [Reference Hovey, Palmieri and Strickland15] for the detail. In this case, we take
$i<0$
; see Example 1.2.3(f) of [Reference Hovey, Palmieri and Strickland15] for the detail. In this case, we take
![]() $\mathcal {P}=\{E\}$
.
$\mathcal {P}=\{E\}$
.
Moreover, the additional assumption of Theorem 4.1.2(8) is fulfilled in these cases as well whenever all the complexes
![]() $\underline {B}^*(M,N)$
are acyclic in degrees less than
$\underline {B}^*(M,N)$
are acyclic in degrees less than
![]() $-n$
or if
$-n$
or if
![]() $\pi _i(E)=\{0\}$
for
$\pi _i(E)=\{0\}$
for
![]() $i>n$
, respectively.
$i>n$
, respectively.
2. Let A and B be differential graded algebras whose cohomology
![]() $H^*(A)$
and
$H^*(A)$
and
![]() $H^*(B)$
is concentrated in negative degrees, and assume that B is a right A-module.
$H^*(B)$
is concentrated in negative degrees, and assume that B is a right A-module.
Take
![]() $\underline {C}=D(A)$
,
$\underline {C}=D(A)$
,
![]() $w_A$
to be the weight structure corresponding to
$w_A$
to be the weight structure corresponding to
![]() $\mathcal {P}=\{A\}$
according to assertion 1 and Theorem 4.1.2(2),
$\mathcal {P}=\{A\}$
according to assertion 1 and Theorem 4.1.2(2),
![]() $\underline {C}'=D(B)$
,
$\underline {C}'=D(B)$
,
![]() $w_B$
to be the weight structure corresponding to
$w_B$
to be the weight structure corresponding to
![]() $\mathcal {P}'=\{B\}$
. Assume that n-th power of the kernel of the ring homomorphism
$\mathcal {P}'=\{B\}$
. Assume that n-th power of the kernel of the ring homomorphism
![]() $\underline {C}(A,A)\to \underline {C}'(B,B)$
induced by F is zero.
$\underline {C}(A,A)\to \underline {C}'(B,B)$
induced by F is zero.
Then for the exact functor
![]() $F:\underline {C}=D(A)\to \underline {C}'=D(B)$
described in §3.8 of [Reference Keller16], the assumptions of Proposition 3.2.1 are fulfilled. Here, we take
$F:\underline {C}=D(A)\to \underline {C}'=D(B)$
described in §3.8 of [Reference Keller16], the assumptions of Proposition 3.2.1 are fulfilled. Here, we take
![]() $X=B$
and consider X as an
$X=B$
and consider X as an
![]() $A-B$
-bimodule when we apply loc. cit.
$A-B$
-bimodule when we apply loc. cit.
3. Assume that
![]() $\underline {C}$
is compactly purely generated by its subcategory
$\underline {C}$
is compactly purely generated by its subcategory
![]() $\mathcal {P}$
, and that for
$\mathcal {P}$
, and that for
![]() $i=1,2,3$
we have full subcategories
$i=1,2,3$
we have full subcategories
![]() $\mathcal {P}_i$
of
$\mathcal {P}_i$
of
![]() $\mathcal {P}$
such that all morphisms between
$\mathcal {P}$
such that all morphisms between
![]() $\mathcal {P}_1$
and
$\mathcal {P}_1$
and
![]() $\mathcal {P}_2$
factor through
$\mathcal {P}_2$
factor through
![]() $\mathcal {P}_3$
. Denote by
$\mathcal {P}_3$
. Denote by
![]() $\underline {C}_i$
the localizing triangulated subcategory of
$\underline {C}_i$
the localizing triangulated subcategory of
![]() $\underline {C}$
generated by
$\underline {C}$
generated by
![]() $\mathcal {P}_i$
(
$\mathcal {P}_i$
(
![]() $i=1,2,3$
).
$i=1,2,3$
).
Then the localization functor
![]() $F:\underline {C}\to \underline {C}'=\underline {C}/\underline {C}_3$
exists (cf. Proposition 3.1.6(4)), there is a unique weight structure
$F:\underline {C}\to \underline {C}'=\underline {C}/\underline {C}_3$
exists (cf. Proposition 3.1.6(4)), there is a unique weight structure
![]() $w'$
on
$w'$
on
![]() $\underline {C}'$
such that F is weight-exact and for any
$\underline {C}'$
such that F is weight-exact and for any
![]() $M\in \operatorname {Obj} \underline {C}_1\cap \operatorname {Obj}\underline {C}_2$
, the object
$M\in \operatorname {Obj} \underline {C}_1\cap \operatorname {Obj}\underline {C}_2$
, the object
![]() $F(M)$
is right
$F(M)$
is right
![]() $w'$
-degenerate. Moreover, M is an object of
$w'$
-degenerate. Moreover, M is an object of
![]() $\underline {C}_3$
whenever
$\underline {C}_3$
whenever
![]() $M\in \operatorname {Obj} \underline {C}_1\cap \operatorname {Obj}\underline {C}_2$
and M is w-bounded below.
$M\in \operatorname {Obj} \underline {C}_1\cap \operatorname {Obj}\underline {C}_2$
and M is w-bounded below.
Proof. 1. In case (i), the objects of
![]() $\underline {C}$
coming from
$\underline {C}$
coming from
![]() $\underline {B}$
are compact by Corollary 3.7 of [Reference Keller16]. Moreover, in the discussion preceding loc. cit. the equality
$\underline {B}$
are compact by Corollary 3.7 of [Reference Keller16]. Moreover, in the discussion preceding loc. cit. the equality
![]() $(\cup _{i\in {\mathbb {Z}}}\mathcal {P}[i]){}^{\perp }=\{0\}$
is mentioned. Hence,
$(\cup _{i\in {\mathbb {Z}}}\mathcal {P}[i]){}^{\perp }=\{0\}$
is mentioned. Hence,
![]() $\mathcal {P}$
compactly generates
$\mathcal {P}$
compactly generates
![]() $\underline {C}$
by Proposition 8.4.1 of [Reference Neeman23]. Next, formula (3) in [Reference Keller16, §3.2] says that for every
$\underline {C}$
by Proposition 8.4.1 of [Reference Neeman23]. Next, formula (3) in [Reference Keller16, §3.2] says that for every
![]() $j\in {\mathbb {Z}}$
and
$j\in {\mathbb {Z}}$
and
![]() $M,N\in \underline {B}$
the jth cohomology of the complex
$M,N\in \underline {B}$
the jth cohomology of the complex
![]() $(\underline {B}^i(M,N))$
is isomorphic to
$(\underline {B}^i(M,N))$
is isomorphic to
![]() $\underline {C}(M,N[j])$
. This easily implies all the remaining statements for this case.
$\underline {C}(M,N[j])$
. This easily implies all the remaining statements for this case.
The statement that
![]() $\{E\}$
compactly generates
$\{E\}$
compactly generates
![]() $\underline {C}$
in case (ii) can be found in Example 1.2.3(f) of [Reference Hovey, Palmieri and Strickland15]. Furthermore, loc. cit. states that
$\underline {C}$
in case (ii) can be found in Example 1.2.3(f) of [Reference Hovey, Palmieri and Strickland15]. Furthermore, loc. cit. states that
![]() $\underline {C}(E,X)$
is the zeroth homotopy group of the underlying spectrum X for any object X of
$\underline {C}(E,X)$
is the zeroth homotopy group of the underlying spectrum X for any object X of
![]() $\underline {C}$
. This yields all the remaining statements for this case.
$\underline {C}$
. This yields all the remaining statements for this case.
2. The description of F given in §3.8 of [Reference Keller16] immediately implies that F is exact, respects coproducts and
![]() $F(A)\cong B$
. Applying Theorem 4.1.2(5), we obtain that F is weight-exact.
$F(A)\cong B$
. Applying Theorem 4.1.2(5), we obtain that F is weight-exact.
Next, the hearts of
![]() $w_A$
and
$w_A$
and
![]() $w_B$
are equivalent to the categories of projective modules over
$w_B$
are equivalent to the categories of projective modules over
![]() $\underline {C}(A,A)$
and
$\underline {C}(A,A)$
and
![]() $ \underline {C}'(B,B)$
, respectively, according to Theorem 4.1.2(3). Hence, the nilpotence condition in Proposition 3.2.1 follows from our nilpotence of the kernel assumption.
$ \underline {C}'(B,B)$
, respectively, according to Theorem 4.1.2(3). Hence, the nilpotence condition in Proposition 3.2.1 follows from our nilpotence of the kernel assumption.
3. It clearly suffices to prove that
![]() $\underline {C}_3$
is retraction-closed in
$\underline {C}_3$
is retraction-closed in
![]() $\underline {C}$
,
$\underline {C}$
,
![]() $(\underline {C},w,\underline {C}_i)$
satisfy the assumptions of Proposition 3.1.6(4), and the corresponding
$(\underline {C},w,\underline {C}_i)$
satisfy the assumptions of Proposition 3.1.6(4), and the corresponding
![]() $w'$
is left nondegenerate.
$w'$
is left nondegenerate.
![]() $\underline {C}_3$
is retraction-closed in
$\underline {C}_3$
is retraction-closed in
![]() $\underline {C}$
since
$\underline {C}$
since
![]() $\underline {C}_3$
is Karoubian (see Theorem 4.1.2(1)). Next, w restricts to
$\underline {C}_3$
is Karoubian (see Theorem 4.1.2(1)). Next, w restricts to
![]() $\underline {C}_1$
and
$\underline {C}_1$
and
![]() $\underline {C}_2$
by Theorem 4.1.2(5).
$\underline {C}_2$
by Theorem 4.1.2(5).
The localization functor F is well-known to exist and (also) to respect coproducts and the compactness of objects; see Proposition 9.1.19, Theorem 8.3.3, Corollary 3.2.11 and Theorem 4.4.9 of [Reference Neeman23]. Thus, Theorem 4.1.2(3) implies that all
![]() ${\underline {Hw}}$
-morphisms between elements of the corresponding classes
${\underline {Hw}}$
-morphisms between elements of the corresponding classes
![]() $\underline {C}_{1,w_1=0}$
and
$\underline {C}_{1,w_1=0}$
and
![]() $\underline {C}_{2,w_2=0}$
are killed by F; see equality 4.1.1.
$\underline {C}_{2,w_2=0}$
are killed by F; see equality 4.1.1.
Lastly, by Proposition 3.1.6(4) there exists a unique weight structure
![]() $w'$
such that F is weight-exact. Thus,
$w'$
such that F is weight-exact. Thus,
![]() $F(\mathcal {P})\subset \underline {C}^{\prime }_{w'=0}$
; hence,
$F(\mathcal {P})\subset \underline {C}^{\prime }_{w'=0}$
; hence,
![]() $F(\mathcal {P})$
is a connective subcategory of
$F(\mathcal {P})$
is a connective subcategory of
![]() $\underline {C}'$
. Since
$\underline {C}'$
. Since
![]() $\mathcal {P}$
compactly generates
$\mathcal {P}$
compactly generates
![]() $\underline {C}$
,
$\underline {C}$
,
![]() $F(\mathcal {P})$
compactly generates
$F(\mathcal {P})$
compactly generates
![]() $\underline {C}'$
and applying Theorem 4.1.2(5), we obtain that
$\underline {C}'$
and applying Theorem 4.1.2(5), we obtain that
![]() $w'$
is purely compactly generated by
$w'$
is purely compactly generated by
![]() $F(\mathcal {P})$
. Hence,
$F(\mathcal {P})$
. Hence,
![]() $w'$
is left nondegenerate by Theorem 4.1.2(2).
$w'$
is left nondegenerate by Theorem 4.1.2(2).
Remark 4.1.5. Corollary 4.1.4(3) slightly generalizes Proposition 1.9 of [Reference Bondarko5] which seriously depended on an earlier version of the current paper. Thus, we obtain an unconditional proof of loc. cit. This is crucial for ibid.
Now, let us relate purely compactly generated weight structures to the main definitions of the current paper.
Corollary 4.1.6. Adopt the notation and the assumptions of Theorem 4.1.2. Let
![]() $m\le n\in {\mathbb {Z}}$
.
$m\le n\in {\mathbb {Z}}$
.
-
1. The class of essentially w-positive objects coincides with
 ${}^{\perp } \cup _{j<0}\{I[j]\}$
, where I is an injective cogenerator of
${}^{\perp } \cup _{j<0}\{I[j]\}$
, where I is an injective cogenerator of
 $\underline {A}_{\mathcal {P}}$
. This class is also characterized by the vanishing of
$\underline {A}_{\mathcal {P}}$
. This class is also characterized by the vanishing of
 $H_j^{{\mathcal {A}_{\mathcal {P}}}}(-)$
for
$H_j^{{\mathcal {A}_{\mathcal {P}}}}(-)$
for
 $j<0$
.
$j<0$
. -
2. The class of w-degenerate objects coincides with
 ${}^{\perp } \cup _{j\in {\mathbb {Z}}}\{I[j]\}$
and also with
${}^{\perp } \cup _{j\in {\mathbb {Z}}}\{I[j]\}$
and also with
 ${}^{\perp } \cup _{j\in {\mathbb {Z}}}\{ {\underline {Ht}}[j]\}$
. Moreover, this class is characterized by the vanishing of
${}^{\perp } \cup _{j\in {\mathbb {Z}}}\{ {\underline {Ht}}[j]\}$
. Moreover, this class is characterized by the vanishing of
 $H_j^{{\mathcal {A}_{\mathcal {P}}}}(-)$
for all
$H_j^{{\mathcal {A}_{\mathcal {P}}}}(-)$
for all
 $j\in {\mathbb {Z}}$
.
$j\in {\mathbb {Z}}$
. -
3. A
 $\underline {C}$
-morphism g kills weight m if and only if
$\underline {C}$
-morphism g kills weight m if and only if
 $H^m(g)=0$
for every pure representable functor H.
$H^m(g)=0$
for every pure representable functor H. -
4. An object M of
 $\underline {C}$
is without weights
$\underline {C}$
is without weights
 $m,\dots , n$
if and only if
$m,\dots , n$
if and only if
 $H^j(M)=0$
whenever H is pure and representable and
$H^j(M)=0$
whenever H is pure and representable and
 $m\le j \le n$
.
$m\le j \le n$
. -
5.
 $\underline {C}_{w\le 0}={}^{\perp } (\cup _{j>0} {\underline {Ht}}[j])$
. Moreover, this class is also annihilated by
$\underline {C}_{w\le 0}={}^{\perp } (\cup _{j>0} {\underline {Ht}}[j])$
. Moreover, this class is also annihilated by
 $H_i$
for all
$H_i$
for all
 $i>0$
and for every w-pure homological functor H from
$i>0$
and for every w-pure homological functor H from
 $\underline {C}$
.
$\underline {C}$
.
Proof.
1. According to Corollary 3.1.4, an object M of
![]() $\underline {C}$
is essentially w-positive if and only if
$\underline {C}$
is essentially w-positive if and only if
![]() $t(M)\in K({\underline {Hw}})_{w^{st}\ge 0}$
. Combining this fact with Theorem 4.1.2(7), we obtain our assertion.
$t(M)\in K({\underline {Hw}})_{w^{st}\ge 0}$
. Combining this fact with Theorem 4.1.2(7), we obtain our assertion.
2. w is left nondegenerate by Theorem 4.1.2(2); hence, Proposition 3.1.6(1) implies that M is essentially w-positive if and only if it belongs to
![]() $\underline {C}_{w\ge 0}$
. On the other hand, M is weight-degenerate if and only if it is right weight-degenerate. Thus, M is weight-degenerate if and only if
$\underline {C}_{w\ge 0}$
. On the other hand, M is weight-degenerate if and only if it is right weight-degenerate. Thus, M is weight-degenerate if and only if
![]() $M[j]$
is essentially w-positive for all
$M[j]$
is essentially w-positive for all
![]() $j\in {\mathbb {Z}}$
. Hence, our assertion follows from the previous one.
$j\in {\mathbb {Z}}$
. Hence, our assertion follows from the previous one.
3. Since w is smashing and
![]() $\underline {C}$
is a Brown category, the assertion follows from Proposition 2.4.4 immediately.
$\underline {C}$
is a Brown category, the assertion follows from Proposition 2.4.4 immediately.
4. This is a straightforward consequence of the previous assertion combined with Theorem 2.3.1(1,3) along with Lemma 1.3.2(4).
5. Since w is left nondegenerate,
![]() $\underline {C}_{w\le 0}$
coincides with the class of all essentially w-negative objects according to Proposition 3.1.6(1). Thus, Theorem 3.1.3 gives the result in question; cf. Remark 3.1.5(1).
$\underline {C}_{w\le 0}$
coincides with the class of all essentially w-negative objects according to Proposition 3.1.6(1). Thus, Theorem 3.1.3 gives the result in question; cf. Remark 3.1.5(1).
Now, let us demonstrate that one can say more on this setting if an additional assumption is imposed.
Proposition 4.1.7. Adopt the notation and assumptions of Theorem 4.1.2, and suppose in addition that the category
![]() $\underline {A}_{\mathcal {P}}$
is of projective dimension at most
$\underline {A}_{\mathcal {P}}$
is of projective dimension at most
![]() $1$
, that is, any its object has a projective resolution of length
$1$
, that is, any its object has a projective resolution of length
![]() $1$
. Let
$1$
. Let
![]() $m\le n\in {\mathbb {Z}}$
and
$m\le n\in {\mathbb {Z}}$
and
![]() $g:E\to E'$
be a
$g:E\to E'$
be a
![]() $\underline {C}$
-morphism.
$\underline {C}$
-morphism.
-
1. Then the category
 $K_{\mathfrak {w}}({\underline {Hw}})$
equals
$K_{\mathfrak {w}}({\underline {Hw}})$
equals
 $K({\underline {Hw}})$
, and the natural functor
$K({\underline {Hw}})$
, and the natural functor
 $K({\underline {Hw}})\to D(\underline {A}_{\mathcal {P}})$
is an equivalence.
$K({\underline {Hw}})\to D(\underline {A}_{\mathcal {P}})$
is an equivalence. -
2. For any objects C and
 $C'$
in
$C'$
in
 $D(\underline {A}_{\mathcal {P}})$
, we have natural isomorphisms
$D(\underline {A}_{\mathcal {P}})$
, we have natural isomorphisms
 $C\cong \coprod H_j(C)[j]$
and
$C\cong \coprod H_j(C)[j]$
and  $$ \begin{align*}D(\underline{A}_{\mathcal{P}})(C,C')\cong \prod_{j\in {\mathbb{Z}}}\underline{A}_{\mathcal{P}}(H_j(C),H_j(C'))\bigoplus (\prod_{j\in {\mathbb{Z}}}\operatorname{\mathrm{\operatorname{Ext}^{1}_{\underline{A}_{\mathcal{P}}}}}(H_j(C),H_{j+1}(C'))).\end{align*} $$
$$ \begin{align*}D(\underline{A}_{\mathcal{P}})(C,C')\cong \prod_{j\in {\mathbb{Z}}}\underline{A}_{\mathcal{P}}(H_j(C),H_j(C'))\bigoplus (\prod_{j\in {\mathbb{Z}}}\operatorname{\mathrm{\operatorname{Ext}^{1}_{\underline{A}_{\mathcal{P}}}}}(H_j(C),H_{j+1}(C'))).\end{align*} $$
-
3. g kills weight m if and only if
 $H_m^{{\mathcal {A}_{\mathcal {P}}}}(g)=0$
, the class of
$H_m^{{\mathcal {A}_{\mathcal {P}}}}(g)=0$
, the class of
 $t(g)$
in the group
$t(g)$
in the group
 $\operatorname {\mathrm {\operatorname {Ext}^{1}_{\underline {A}_{\mathcal {P}}}}}(H_{m-1}(t(E)),H_{m}(t(E')))$
(here we use the identification provided by the previous two assertions) vanishes, and the morphism
$\operatorname {\mathrm {\operatorname {Ext}^{1}_{\underline {A}_{\mathcal {P}}}}}(H_{m-1}(t(E)),H_{m}(t(E')))$
(here we use the identification provided by the previous two assertions) vanishes, and the morphism
 $H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(g)$
factors through a projective object of
$H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(g)$
factors through a projective object of
 $\underline {A}_{\mathcal {P}}$
.
$\underline {A}_{\mathcal {P}}$
. -
4. E is without weights
 $m,\dots ,n$
(resp.
$m,\dots ,n$
(resp.
 $E\in \underline {C}_{w\le m-1}$
) if and only if
$E\in \underline {C}_{w\le m-1}$
) if and only if
 $H_j^{{\mathcal {A}_{\mathcal {P}}}}(E)=0$
for
$H_j^{{\mathcal {A}_{\mathcal {P}}}}(E)=0$
for
 $m\le j \le n$
(resp. for
$m\le j \le n$
(resp. for
 $j\ge m$
) and
$j\ge m$
) and
 $H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(E)$
is a projective object of
$H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(E)$
is a projective object of
 $\underline {A}_{\mathcal {P}}$
.
$\underline {A}_{\mathcal {P}}$
.
Proof. 1. These statements easily follow from Theorem 4.1.2(6) according to Remark 3.3.4 of [Reference Bondarko4].
2. The first splitting statement is well-known, and the second statement easily follows from the vanishing of higher extension groups in
![]() $\underline {A}_{\mathcal {P}}$
.
$\underline {A}_{\mathcal {P}}$
.
3. Once again, we should check whether
![]() $t(g)\backsim _{[-m,-m]} 0$
; see Theorem 2.3.1(1). Now, assertion 2 implies that
$t(g)\backsim _{[-m,-m]} 0$
; see Theorem 2.3.1(1). Now, assertion 2 implies that
where
![]() $C_i=\operatorname {\mathrm {\operatorname {Cone}}}(A_{i}\stackrel {f_i}\to B_i)[i]$
, and
$C_i=\operatorname {\mathrm {\operatorname {Cone}}}(A_{i}\stackrel {f_i}\to B_i)[i]$
, and
![]() $f_i$
are
$f_i$
are
![]() ${\underline {Hw}}$
-monomorphisms; thus,
${\underline {Hw}}$
-monomorphisms; thus,
![]() $f_i$
are also
$f_i$
are also
![]() $\underline {A}_{\mathcal {P}}$
-monomorphisms between projective objects. Similarly, we present
$\underline {A}_{\mathcal {P}}$
-monomorphisms between projective objects. Similarly, we present
![]() $t(E')$
as
$t(E')$
as
![]() $\coprod C^{\prime }_j$
, where
$\coprod C^{\prime }_j$
, where
![]() $C^{\prime }_j=\operatorname {\mathrm {\operatorname {Cone}}}(A^{\prime }_{j}\stackrel {f^{\prime }_j}\to B^{\prime }_j)[j]$
. Clearly, it suffices to treat all our assumptions on
$C^{\prime }_j=\operatorname {\mathrm {\operatorname {Cone}}}(A^{\prime }_{j}\stackrel {f^{\prime }_j}\to B^{\prime }_j)[j]$
. Clearly, it suffices to treat all our assumptions on
![]() $t(g)$
separately for the morphisms
$t(g)$
separately for the morphisms
![]() $g_{ij}: C_i\to C^{\prime }_j$
induced by
$g_{ij}: C_i\to C^{\prime }_j$
induced by
![]() $t(g)$
, for
$t(g)$
, for
![]() $\{i,j\}\subset \{m,m-1\}$
.
$\{i,j\}\subset \{m,m-1\}$
.
Next,
![]() $C_m\perp C^{\prime }_{m-1}$
since
$C_m\perp C^{\prime }_{m-1}$
since
![]() $f^{\prime }_{m-1}$
is monomorphic. It remains to verify that the three remaining cases of
$f^{\prime }_{m-1}$
is monomorphic. It remains to verify that the three remaining cases of
![]() $(i,j)$
give our three conditions on g.
$(i,j)$
give our three conditions on g.
Assertion 2 implies that
![]() $K({\underline {Hw}})(C_{m-1},C^{\prime }_{m})\cong \operatorname {\mathrm {\operatorname {Ext}^{1}_{\underline {A}_{\mathcal {P}}}}} (H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(E), H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(E')).$
Moreover,
$K({\underline {Hw}})(C_{m-1},C^{\prime }_{m})\cong \operatorname {\mathrm {\operatorname {Ext}^{1}_{\underline {A}_{\mathcal {P}}}}} (H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(E), H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(E')).$
Moreover,
![]() $g_{m-1,m}\backsim _{[l,l]} 0$
for all
$g_{m-1,m}\backsim _{[l,l]} 0$
for all
![]() $l\neq -m$
; thus,
$l\neq -m$
; thus,
![]() $g_{m-1,m}=0$
if and only if
$g_{m-1,m}=0$
if and only if
![]() $g_{m-1,m}$
kills weight m. Hence,
$g_{m-1,m}$
kills weight m. Hence,
![]() $g_{m,m-1}$
kills weight m if and only if the class of
$g_{m,m-1}$
kills weight m if and only if the class of
![]() $t(g)$
in
$t(g)$
in
![]() $\operatorname {\mathrm {\operatorname {Ext}^{1}_{\underline {A}_{\mathcal {P}}}}}(H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(E), H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(E'))$
vanishes.
$\operatorname {\mathrm {\operatorname {Ext}^{1}_{\underline {A}_{\mathcal {P}}}}}(H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(E), H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(E'))$
vanishes.
Next, if g kills weight m, then
![]() $H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(g)=0$
by Proposition 2.4.4(I). Conversely,
$H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(g)=0$
by Proposition 2.4.4(I). Conversely,
![]() $K({\underline {Hw}})(C_m,C^{\prime }_m)\cong \underline {A}_{\mathcal {P}} (H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(E), H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(E'))$
; thus, if
$K({\underline {Hw}})(C_m,C^{\prime }_m)\cong \underline {A}_{\mathcal {P}} (H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(E), H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(E'))$
; thus, if
![]() $H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(g)=0$
, then
$H_{m}^{{\mathcal {A}_{\mathcal {P}}}}(g)=0$
, then
![]() $g_{mm}=0$
.
$g_{mm}=0$
.
Lastly,
![]() $g_{m-1,m-1}\backsim _{[-m,-m]} 0$
if and only if
$g_{m-1,m-1}\backsim _{[-m,-m]} 0$
if and only if
![]() $g_{m-1,m-1}$
factors through the obvious morphism
$g_{m-1,m-1}$
factors through the obvious morphism
![]() $B^{\prime }_{m-1}[m-1]\to C^{\prime }_{m-1}$
. The latter condition clearly implies that
$B^{\prime }_{m-1}[m-1]\to C^{\prime }_{m-1}$
. The latter condition clearly implies that
![]() $H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(g)$
factors through
$H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(g)$
factors through
![]() $B^{\prime }_{m-1}$
. Conversely, if
$B^{\prime }_{m-1}$
. Conversely, if
![]() $H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(g)$
factors through a projective object of
$H_{m-1}^{{\mathcal {A}_{\mathcal {P}}}}(g)$
factors through a projective object of
![]() $\underline {A}_{\mathcal {P}}$
, then
$\underline {A}_{\mathcal {P}}$
, then
![]() $g_{m-1,m-1}$
factors through
$g_{m-1,m-1}$
factors through
![]() $\underline {C}_{w=m-1}$
. Note here that
$\underline {C}_{w=m-1}$
. Note here that
![]() $\underline {A}_{\mathcal {P}}$
embeds into
$\underline {A}_{\mathcal {P}}$
embeds into
![]() $K({\underline {Hw}})_{w^{st}\ge m-1}$
via projective resolutions. Thus,
$K({\underline {Hw}})_{w^{st}\ge m-1}$
via projective resolutions. Thus,
![]() $g_{m-1,m-1}$
factors through
$g_{m-1,m-1}$
factors through
![]() $B^{\prime }_{m-1}[m-1]$
. Here, we apply Proposition 1.2.4(6) to the category
$B^{\prime }_{m-1}[m-1]$
. Here, we apply Proposition 1.2.4(6) to the category
![]() $\underline {C}=K({\underline {Hw}})$
endowed with the stupid weight structure.
$\underline {C}=K({\underline {Hw}})$
endowed with the stupid weight structure.
Assertion 4 follows from the previous one more or less easily. Combining Corollary 3.1.4 (see condition 2 in it) with Proposition 3.1.6(1) we obtain that E belongs to
![]() $ \underline {C}_{w\le m-1}$
if and only if
$ \underline {C}_{w\le m-1}$
if and only if
![]() $\operatorname {id}_E$
kills weight i for all
$\operatorname {id}_E$
kills weight i for all
![]() $i\ge m$
. Recall also that E is without weights
$i\ge m$
. Recall also that E is without weights
![]() $m,\dots ,n$
if and only if
$m,\dots ,n$
if and only if
![]() $\operatorname {id}_E$
kills weight i for
$\operatorname {id}_E$
kills weight i for
![]() $m\le i \le n$
; see Theorem 2.2.1(8). Hence, it remains to note that for every
$m\le i \le n$
; see Theorem 2.2.1(8). Hence, it remains to note that for every
![]() $i\in {\mathbb {Z}}$
the morphism
$i\in {\mathbb {Z}}$
the morphism
![]() $H_i^{{\mathcal {A}_{\mathcal {P}}}}(\operatorname {id}_E)$
clearly equals the corresponding identity, whereas the classes of
$H_i^{{\mathcal {A}_{\mathcal {P}}}}(\operatorname {id}_E)$
clearly equals the corresponding identity, whereas the classes of
![]() $t(\operatorname {id}_E)$
in all the groups
$t(\operatorname {id}_E)$
in all the groups
![]() $\operatorname {\mathrm {\operatorname {Ext}^{1}_{\underline {A}_{\mathcal {P}}}}}(H_i(E),H_{i+1}(E))$
(see assertion 2) are zero.
$\operatorname {\mathrm {\operatorname {Ext}^{1}_{\underline {A}_{\mathcal {P}}}}}(H_i(E),H_{i+1}(E))$
(see assertion 2) are zero.
Remark 4.1.8. 1. Let us describe a motivic example to our proposition.
One can take
![]() $\underline {C}$
to be the localizing subcategory
$\underline {C}$
to be the localizing subcategory
![]() $DTM$
generated by the Tate motives
$DTM$
generated by the Tate motives
![]() ${\mathbb {Z}}(i),\ i\in {\mathbb {Z}}$
, in the category
${\mathbb {Z}}(i),\ i\in {\mathbb {Z}}$
, in the category
![]() $DM$
of motives with integral coefficients over any perfect field k; see §4.2 of [Reference Déglise13]. Then the category
$DM$
of motives with integral coefficients over any perfect field k; see §4.2 of [Reference Déglise13]. Then the category
![]() $\mathcal {P}=\{{\mathbb {Z}}(i)[2i],\ i\in {\mathbb {Z}}\}$
is connective in
$\mathcal {P}=\{{\mathbb {Z}}(i)[2i],\ i\in {\mathbb {Z}}\}$
is connective in
![]() $DTM$
since
$DTM$
since
![]() ${\mathbb {Z}}(i)[2i]\perp {\mathbb {Z}}(j)[2j]$
for every
${\mathbb {Z}}(i)[2i]\perp {\mathbb {Z}}(j)[2j]$
for every
![]() $i\neq j\in {\mathbb {Z}}$
, whereas
$i\neq j\in {\mathbb {Z}}$
, whereas
![]() $DM({\mathbb {Z}}(i)[2i],{\mathbb {Z}}(i)[2i])\cong {\mathbb {Z}}$
for all i; see Corollary 6.7.3 of [Reference Beilinson and Vologodsky3]. Hence, the corresponding category
$DM({\mathbb {Z}}(i)[2i],{\mathbb {Z}}(i)[2i])\cong {\mathbb {Z}}$
for all i; see Corollary 6.7.3 of [Reference Beilinson and Vologodsky3]. Hence, the corresponding category
![]() $\underline {A}_{\mathcal {P}}$
is equivalent to
$\underline {A}_{\mathcal {P}}$
is equivalent to
![]() $ \operatorname {Ab}^{{\mathbb {Z}}}$
; thus,
$ \operatorname {Ab}^{{\mathbb {Z}}}$
; thus,
![]() $\underline {A}_{\mathcal {P}}$
is of projective dimension
$\underline {A}_{\mathcal {P}}$
is of projective dimension
![]() $1$
.
$1$
.
Moreover,
![]() $\underline {A}_{\mathcal {P}}$
is of projective dimension
$\underline {A}_{\mathcal {P}}$
is of projective dimension
![]() $1$
for the R-linear motivic category
$1$
for the R-linear motivic category
![]() $DTM_R$
whenever R is a Dedekind domain or a field. Note also that for any R the corresponding functor
$DTM_R$
whenever R is a Dedekind domain or a field. Note also that for any R the corresponding functor
![]() $H^{{\mathcal {A}_{\mathcal {P}}}}$
essentially computes the so-called Chow-weight homology of Tate motives (inside
$H^{{\mathcal {A}_{\mathcal {P}}}}$
essentially computes the so-called Chow-weight homology of Tate motives (inside
![]() $DM_R\supset DM^{eff}_R$
); see [Reference Bondarko and Kumallagov8] and [Reference Bondarko and Sosnilo11].
$DM_R\supset DM^{eff}_R$
); see [Reference Bondarko and Kumallagov8] and [Reference Bondarko and Sosnilo11].
2. The case
![]() $E\in \underline {C}_{w\le m-1}$
in part 4 of our proposition is an abstract generalization of [Reference Margolis20, Proposition 6.16] (where
$E\in \underline {C}_{w\le m-1}$
in part 4 of our proposition is an abstract generalization of [Reference Margolis20, Proposition 6.16] (where
![]() $\underline {C}=SH$
was considered; see Theorem 4.2.4 below). Respectively, Proposition 6.17 of loc. cit. is the corresponding case of the orthogonality axiom for the weight structure
$\underline {C}=SH$
was considered; see Theorem 4.2.4 below). Respectively, Proposition 6.17 of loc. cit. is the corresponding case of the orthogonality axiom for the weight structure
![]() $w^{sph}$
. Note, however, that the methods of loc. cit. do not seem to extend to the case of a general G as well as to the setting of Theorem 4.1.2.
$w^{sph}$
. Note, however, that the methods of loc. cit. do not seem to extend to the case of a general G as well as to the setting of Theorem 4.1.2.
4.2 Equivariant spectra and converse Hurewicz theorems
Let us generalize Theorem 4.1.1 of [Reference Bondarko7] to the setting of S-local equivariant stable homotopy categories and extend it. We need some notation.
-
• Choose a set of prime numbers
 $S\subset {\mathbb {Z}}$
, and denote
$S\subset {\mathbb {Z}}$
, and denote
 ${\mathbb {Z}}[S^{-1}]$
by
${\mathbb {Z}}[S^{-1}]$
by
 $\Lambda $
. S may be empty. Then
$\Lambda $
. S may be empty. Then
 $\Lambda ={\mathbb {Z}}$
, and this case is quite important.
$\Lambda ={\mathbb {Z}}$
, and this case is quite important. -
• G is a fixed compact Lie group. We will write
 $SH(G)$
for the stable homotopy category of G-spectra indexed by a complete G-universe; see [Reference Lewis, May, Steinberger and McClure19] and [Reference May21] for lots of detail on these categories.
$SH(G)$
for the stable homotopy category of G-spectra indexed by a complete G-universe; see [Reference Lewis, May, Steinberger and McClure19] and [Reference May21] for lots of detail on these categories. -
• We write
 $SH_{\Lambda }(G)$
for the full subcategory of S-local objects of
$SH_{\Lambda }(G)$
for the full subcategory of S-local objects of
 $SH(G)$
, that is,
$SH(G)$
, that is,
 $M\in \operatorname {Obj}SH_{\Lambda }(G)$
whenever the morphism
$M\in \operatorname {Obj}SH_{\Lambda }(G)$
whenever the morphism
 $p\operatorname {id}_M$
is invertible for every
$p\operatorname {id}_M$
is invertible for every
 $p\in S$
. According to Proposition A.2.8 of [Reference Kelly17],
$p\in S$
. According to Proposition A.2.8 of [Reference Kelly17],
 $SH_{\Lambda }(G)$
is a triangulated subcategory of
$SH_{\Lambda }(G)$
is a triangulated subcategory of
 $SH(G)$
and there exists an exact left adjoint
$SH(G)$
and there exists an exact left adjoint
 $l_{S}=(-)[S^{-1}]$
to the embedding
$l_{S}=(-)[S^{-1}]$
to the embedding
 $SH_{\Lambda }(G)\to SH(G)$
.
$SH_{\Lambda }(G)\to SH(G)$
. -
• We take
 $\mathcal {P}$
to be the set of spectra of the form
$\mathcal {P}$
to be the set of spectra of the form
 $l_{S}(S_B^0)$
, where B is a closed subgroup of G (cf. Definition I.4.3 of [Reference Lewis, May, Steinberger and McClure19]. Recall that
$l_{S}(S_B^0)$
, where B is a closed subgroup of G (cf. Definition I.4.3 of [Reference Lewis, May, Steinberger and McClure19]. Recall that
 $S_B^0=\sum ^{\infty }G/B^+$
is constructed starting from the G-space
$S_B^0=\sum ^{\infty }G/B^+$
is constructed starting from the G-space
 $G/B$
). We will write
$G/B$
). We will write
 $\mathcal {P}$
for the corresponding preadditive subcategory of
$\mathcal {P}$
for the corresponding preadditive subcategory of
 $SH_{\Lambda }(G)$
. If
$SH_{\Lambda }(G)$
. If
 $\Lambda ={\mathbb {Z}}$
, then
$\Lambda ={\mathbb {Z}}$
, then
 $\mathcal {P}$
is the (stable) orbit category of ibid.
$\mathcal {P}$
is the (stable) orbit category of ibid.Recall also that
 $S_B^0[n]\in \operatorname {Obj} SH(G)$
is the corresponding sphere spectrum
$S_B^0[n]\in \operatorname {Obj} SH(G)$
is the corresponding sphere spectrum
 $S_B^n$
essentially by definition; see loc. cit.
$S_B^n$
essentially by definition; see loc. cit. -
• The equivariant homotopy groups of an object E of
 $SH(G)\supset SH_{\Lambda }(G)$
are defined as
$SH(G)\supset SH_{\Lambda }(G)$
are defined as
 $\pi _n^B(E)=SH(G)(S_B^n,E)$
(for all
$\pi _n^B(E)=SH(G)(S_B^n,E)$
(for all
 $n\in {\mathbb {Z}}$
; see §I.6 and Definition I.4.4(i) of ibid.).
$n\in {\mathbb {Z}}$
; see §I.6 and Definition I.4.4(i) of ibid.). -
• We will write
 $\operatorname {EM}_G$
for the full subcategory of
$\operatorname {EM}_G$
for the full subcategory of
 $SH_{\Lambda }(G)$
whose object class is
$SH_{\Lambda }(G)$
whose object class is
 $(\cup _{i\in {\mathbb {Z}}\setminus \{0\}} \mathcal {P}[i])^{\perp }$
. In the case
$(\cup _{i\in {\mathbb {Z}}\setminus \{0\}} \mathcal {P}[i])^{\perp }$
. In the case
 $\Lambda ={\mathbb {Z}}$
, the objects of
$\Lambda ={\mathbb {Z}}$
, the objects of
 $\operatorname {EM}_G$
are the Eilenberg–MacLane G-spectra; see §XIII.4 of [Reference May21].
$\operatorname {EM}_G$
are the Eilenberg–MacLane G-spectra; see §XIII.4 of [Reference May21]. -
• We write
 $\mathcal {M}_G$
for the category of additive contravariant functors from
$\mathcal {M}_G$
for the category of additive contravariant functors from
 $\mathcal {P}$
into
$\mathcal {P}$
into
 $\operatorname {Ab}$
(cf. Theorem 4.1.2(6)). We call its objects Mackey functors. Respectively,
$\operatorname {Ab}$
(cf. Theorem 4.1.2(6)). We call its objects Mackey functors. Respectively,
 ${\mathcal {A}_{\mathcal {P}}}: \mathcal {P}\to \mathcal {M}_G$
is the Yoneda embedding.
${\mathcal {A}_{\mathcal {P}}}: \mathcal {P}\to \mathcal {M}_G$
is the Yoneda embedding. -
• We call
 ${}^{\perp } (\cup _{i\in {\mathbb {Z}}} \operatorname {EM}_G[i])\subset \operatorname {Obj} SH_{\Lambda }(G) $
the class of acyclic spectra; that is, a spectrum is acyclic if it is annihilated by
${}^{\perp } (\cup _{i\in {\mathbb {Z}}} \operatorname {EM}_G[i])\subset \operatorname {Obj} SH_{\Lambda }(G) $
the class of acyclic spectra; that is, a spectrum is acyclic if it is annihilated by
 $H^i$
for all H represented by S-local Eilenberg–MacLane spectra and
$H^i$
for all H represented by S-local Eilenberg–MacLane spectra and
 $i\in {\mathbb {Z}}$
.
$i\in {\mathbb {Z}}$
.
Now, let us describe a weight structure on
![]() $SH_{\Lambda }(G)$
.
$SH_{\Lambda }(G)$
.
Proposition 4.2.1. Let
![]() $n\in {\mathbb {Z}}$
. Then the following statements are valid.
$n\in {\mathbb {Z}}$
. Then the following statements are valid.
-
1. The restriction of
 $l_{S}$
to the category
$l_{S}$
to the category
 $SH_{\Lambda }(G)\subset SH(G)$
is fully faithful. Moreover,
$SH_{\Lambda }(G)\subset SH(G)$
is fully faithful. Moreover,
 $SH_{\Lambda }(G)(l_{S}(S_B^n),l_{S}(C))\cong SH(G)(S_B^n,l_{S}(C))\cong \pi _n^B(C)\otimes _{{\mathbb {Z}}}\Lambda $
for any closed subgroup B of G and an object C of
$SH_{\Lambda }(G)(l_{S}(S_B^n),l_{S}(C))\cong SH(G)(S_B^n,l_{S}(C))\cong \pi _n^B(C)\otimes _{{\mathbb {Z}}}\Lambda $
for any closed subgroup B of G and an object C of
 $SH(G)$
.
$SH(G)$
. -
2. The category
 $\underline {C}=SH_{\Lambda }(G)$
and the class
$\underline {C}=SH_{\Lambda }(G)$
and the class
 $\mathcal {P}$
specified above satisfy the assumptions of Theorem 4.1.2. The heart
$\mathcal {P}$
specified above satisfy the assumptions of Theorem 4.1.2. The heart
 ${\underline {Hw}}_{\Lambda }^G$
of the corresponding weight structure
${\underline {Hw}}_{\Lambda }^G$
of the corresponding weight structure
 $w_{\Lambda }^G$
on
$w_{\Lambda }^G$
on
 $SH_{\Lambda }(G)$
consists of retracts of coproducts of elements of
$SH_{\Lambda }(G)$
consists of retracts of coproducts of elements of
 $\mathcal {P}$
, and
$\mathcal {P}$
, and
 ${\underline {Hw}}_{\Lambda }^G$
is equivalent to the smashing idempotent completion of
${\underline {Hw}}_{\Lambda }^G$
is equivalent to the smashing idempotent completion of
 $\mathcal {P}$
; see Definition 4.1.1(2).
$\mathcal {P}$
; see Definition 4.1.1(2). -
3. The class of
 $n-1$
-connected S-local spectra (see Definition I.4.4(iii) of [Reference Lewis, May, Steinberger and McClure19]; that is, this is the class
$n-1$
-connected S-local spectra (see Definition I.4.4(iii) of [Reference Lewis, May, Steinberger and McClure19]; that is, this is the class
 $(\cup _{i<n}\mathcal {P}[i]){}^{\perp }$
) coincides with
$(\cup _{i<n}\mathcal {P}[i]){}^{\perp }$
) coincides with
 $SH_{\Lambda }(G)_{w_{\Lambda }^G\ge n}$
. In particular,
$SH_{\Lambda }(G)_{w_{\Lambda }^G\ge n}$
. In particular,
 $SH_{\Lambda }(G)_{w_{\Lambda }^G\ge 0}$
is the class of S-local connective spectra. It is the smallest class of objects of
$SH_{\Lambda }(G)_{w_{\Lambda }^G\ge 0}$
is the class of S-local connective spectra. It is the smallest class of objects of
 $SH_{\Lambda }(G)$
that contains
$SH_{\Lambda }(G)$
that contains
 $\cup _{i\ge 0}\mathcal {P}[i]$
and is closed with respect to coproducts and extensions.
$\cup _{i\ge 0}\mathcal {P}[i]$
and is closed with respect to coproducts and extensions. -
4.
 $ SH_{\Lambda }(G)_{w_{\Lambda }^G\le 0}$
is the smallest subclass of
$ SH_{\Lambda }(G)_{w_{\Lambda }^G\le 0}$
is the smallest subclass of
 $\operatorname {Obj} SH_{\Lambda }(G)$
that is closed with respect to coproducts and extensions and contains
$\operatorname {Obj} SH_{\Lambda }(G)$
that is closed with respect to coproducts and extensions and contains
 $\mathcal {P}[i]$
for
$\mathcal {P}[i]$
for
 $i\le 0$
. This class also equals
$i\le 0$
. This class also equals
 ${}^{\perp } (\cup _{i\ge 0} \operatorname {EM}_G[i])= {}^{\perp } SH_{\Lambda }(G)_{w_{\Lambda }^G\ge 1}$
. Moreover, it is annihilated by
${}^{\perp } (\cup _{i\ge 0} \operatorname {EM}_G[i])= {}^{\perp } SH_{\Lambda }(G)_{w_{\Lambda }^G\ge 1}$
. Moreover, it is annihilated by
 $H_i$
for all
$H_i$
for all
 $i>0$
and for every pure homological functor H from
$i>0$
and for every pure homological functor H from
 $SH_{\Lambda }(G)$
.
$SH_{\Lambda }(G)$
. -
5. A (co)homological functor from
 $SH_{\Lambda }(G)$
into an abelian category
$SH_{\Lambda }(G)$
into an abelian category
 $\underline {A}$
that respects coproducts (resp. converts them into products) is
$\underline {A}$
that respects coproducts (resp. converts them into products) is
 $w_{\Lambda }^G$
-pure if and only if it kills
$w_{\Lambda }^G$
-pure if and only if it kills
 $\cup _{i\neq 0}\mathcal {P}[i]$
.
$\cup _{i\neq 0}\mathcal {P}[i]$
.In particular, all objects of
 $\operatorname {EM}_G$
represent
$\operatorname {EM}_G$
represent
 $w_{\Lambda }^G$
-pure functors.
$w_{\Lambda }^G$
-pure functors. -
6. The category
 $\operatorname {EM}_G$
is naturally equivalent to
$\operatorname {EM}_G$
is naturally equivalent to
 $\mathcal {M}_G$
via Yoneda; thus,
$\mathcal {M}_G$
via Yoneda; thus,
 $\operatorname {EM}_G$
is Grothendieck abelian and has an injective cogenerator I.
$\operatorname {EM}_G$
is Grothendieck abelian and has an injective cogenerator I.
Proof.
1. The restriction of
![]() $l_{S}$
to
$l_{S}$
to
![]() $SH_{\Lambda }(G)$
is fully faithful since
$SH_{\Lambda }(G)$
is fully faithful since
![]() $l_{S}$
is left adjoint to the embedding
$l_{S}$
is left adjoint to the embedding
![]() $SH_{\Lambda }(G)\to SH(G)$
. Next, the only nontrivial isomorphism for morphism groups in the assertion is given by Corollary A.2.13 of [Reference Kelly17].
$SH_{\Lambda }(G)\to SH(G)$
. Next, the only nontrivial isomorphism for morphism groups in the assertion is given by Corollary A.2.13 of [Reference Kelly17].
2. The fact that objects of the form
![]() $S_B^0$
form a connective subcategory of
$S_B^0$
form a connective subcategory of
![]() $SH(G)$
that compactly generates this category can be deduced from the results of [Reference Lewis, May, Steinberger and McClure19]; see [Reference Bondarko7, Theorem 4.1.1] for more detail. Applying the previous assertion, we obtain that
$SH(G)$
that compactly generates this category can be deduced from the results of [Reference Lewis, May, Steinberger and McClure19]; see [Reference Bondarko7, Theorem 4.1.1] for more detail. Applying the previous assertion, we obtain that
![]() $\mathcal {P}$
is connective in
$\mathcal {P}$
is connective in
![]() $SH_{\Lambda }(G)$
. Next, the functor
$SH_{\Lambda }(G)$
. Next, the functor
![]() $l_{S}$
sends any family of compact generators of
$l_{S}$
sends any family of compact generators of
![]() $SH(G)$
into a one for
$SH(G)$
into a one for
![]() $SH_{\Lambda }(G)$
according to Proposition A.2.8 of [Reference Kelly17]. Lastly, we apply Theorem 4.1.2(3) to compute the heart of
$SH_{\Lambda }(G)$
according to Proposition A.2.8 of [Reference Kelly17]. Lastly, we apply Theorem 4.1.2(3) to compute the heart of
![]() $w_{\Lambda }^G$
.
$w_{\Lambda }^G$
.
3. By definition, a G-spectrum N is
![]() $n-1$
-connected whenever
$n-1$
-connected whenever
![]() $\pi _i^B(N)\cong SH(G)(S_B^i,N)= \{0\}$
for all
$\pi _i^B(N)\cong SH(G)(S_B^i,N)= \{0\}$
for all
![]() $i<n$
and every closed subgroup B of G. Since
$i<n$
and every closed subgroup B of G. Since
![]() $SH(G)(S_B^n,N) \cong SH_{\Lambda }(G)(l_{S}(S_B^n),l_{S}(N))$
(see assertion 1), it remains to apply Theorem 4.1.2(3) to obtain all the statements in question.
$SH(G)(S_B^n,N) \cong SH_{\Lambda }(G)(l_{S}(S_B^n),l_{S}(N))$
(see assertion 1), it remains to apply Theorem 4.1.2(3) to obtain all the statements in question.
4. The first of these descriptions of
![]() $ SH_{\Lambda }(G)_{w_{\Lambda }^G\le 0}$
is given by Theorem 4.1.2(1). Next,
$ SH_{\Lambda }(G)_{w_{\Lambda }^G\le 0}$
is given by Theorem 4.1.2(1). Next,
![]() $ SH_{\Lambda }(G)_{w_{\Lambda }^G\le 0}= {}^{\perp } SH_{\Lambda }(G)_{w_{\Lambda }^G\ge 1}$
according to Proposition 1.2.4(2). It remains to apply Theorem 4.1.2(5) to conclude the proof.
$ SH_{\Lambda }(G)_{w_{\Lambda }^G\le 0}= {}^{\perp } SH_{\Lambda }(G)_{w_{\Lambda }^G\ge 1}$
according to Proposition 1.2.4(2). It remains to apply Theorem 4.1.2(5) to conclude the proof.
Assertion 5 follows from Theorem 4.1.2(4) immediately. Lastly, assertion 6 is just the corresponding case of Theorem 4.1.2(6).
Now, we apply the results of this paper to
![]() $w_{\Lambda }^G$
; consult Definitions 2.3.3, 2.1.2, 3.1.1(2) and 2.4.1 for the notions mentioned in it.
$w_{\Lambda }^G$
; consult Definitions 2.3.3, 2.1.2, 3.1.1(2) and 2.4.1 for the notions mentioned in it.
Theorem 4.2.2. Let
![]() $E\in \operatorname {Obj} SH(G)$
; I is an injective cogenerator of
$E\in \operatorname {Obj} SH(G)$
; I is an injective cogenerator of
![]() $\operatorname {EM}_G$
.
$\operatorname {EM}_G$
.
-
1. The following conditions are equivalent.
(i). E is acyclic.
(ii). E is
 $w_{\Lambda }^G$
-degenerate.
$w_{\Lambda }^G$
-degenerate.(iii). E is right
 $w_{\Lambda }^G$
-degenerate.
$w_{\Lambda }^G$
-degenerate.(iv).
 $E\perp SH_{\Lambda }(G)_{w_{\Lambda }^G\ge i}$
for every
$E\perp SH_{\Lambda }(G)_{w_{\Lambda }^G\ge i}$
for every
 $i\in {\mathbb {Z}}$
.
$i\in {\mathbb {Z}}$
.(v).
 $H^{{\mathcal {A}_{\mathcal {P}}}}_i(E)=0$
for every
$H^{{\mathcal {A}_{\mathcal {P}}}}_i(E)=0$
for every
 $i\in {\mathbb {Z}}$
.
$i\in {\mathbb {Z}}$
.(vi).
 $E\perp (\cup _{i\in {\mathbb {Z}}}I[i])$
.
$E\perp (\cup _{i\in {\mathbb {Z}}}I[i])$
. -
2. The following assumptions on a
 $SH_{\Lambda }(G)$
-morphism h are equivalent.
$SH_{\Lambda }(G)$
-morphism h are equivalent.(i). h kills weight
 $0$
.
$0$
.(ii).
 $H(h)=0$
for every
$H(h)=0$
for every
 $w_{\Lambda }^G$
-pure functor H from
$w_{\Lambda }^G$
-pure functor H from
 $SH_{\Lambda }(G)$
.
$SH_{\Lambda }(G)$
.(iii). For every
 $J\in \operatorname {EM}_G$
and
$J\in \operatorname {EM}_G$
and
 $P=SH_{\Lambda }(G)(-,J)$
, we have
$P=SH_{\Lambda }(G)(-,J)$
, we have
 $P(h)=0$
.
$P(h)=0$
. -
3. The following conditions are equivalent as well.
(i). E is essentially
 $w_{\Lambda }^G$
-positive.
$w_{\Lambda }^G$
-positive.(ii). E is an extension of a connective spectrum by an acyclic one.
(iii).
 $H(E[j])=0$
for every
$H(E[j])=0$
for every
 $w_{\Lambda }^G$
-pure functor H from
$w_{\Lambda }^G$
-pure functor H from
 $SH_{\Lambda }(G)$
and
$SH_{\Lambda }(G)$
and
 $j>0$
.
$j>0$
.(iv).
 $E\perp I[j]$
for all
$E\perp I[j]$
for all
 $j<0$
.
$j<0$
.(v).
 $H_j^{{\mathcal {A}_{\mathcal {P}}}}(E)=0$
for all
$H_j^{{\mathcal {A}_{\mathcal {P}}}}(E)=0$
for all
 $j<0$
.
$j<0$
. -
4. Let
 $m\le n\in {\mathbb {Z}}$
. Then the following conditions are equivalent.
$m\le n\in {\mathbb {Z}}$
. Then the following conditions are equivalent.(i). E is without weights
 $m\dots n$
.
$m\dots n$
.(ii). There exists a distinguished triangle
 $E_1\to E\to E_2\to E_1[1]$
such that
$E_1\to E\to E_2\to E_1[1]$
such that
 $E_1\in SH_{\Lambda }(G)_{w_{\Lambda }^G\le m-1}$
and
$E_1\in SH_{\Lambda }(G)_{w_{\Lambda }^G\le m-1}$
and
 $E_2\in SH_{\Lambda }(G)_{w_{\Lambda }^G\ge n+1}$
. Moreover, if this is the case, then this triangle is canonically determined by E.
$E_2\in SH_{\Lambda }(G)_{w_{\Lambda }^G\ge n+1}$
. Moreover, if this is the case, then this triangle is canonically determined by E.(iii).
 $E\perp (\cup _{m\le i \le n} \operatorname {EM}_G[-i])$
.
$E\perp (\cup _{m\le i \le n} \operatorname {EM}_G[-i])$
.(iv). E is annihilated by
 $H_{i}$
whenever
$H_{i}$
whenever
 $m\le i\le n$
and H is a pure homological functor from
$m\le i\le n$
and H is a pure homological functor from
 $SH_{\Lambda }(G)$
.
$SH_{\Lambda }(G)$
.
Proof.
1. According to Proposition 4.2.1(2), we can apply Corollary 4.1.6(2) to obtain that conditions (i), (ii), (v) and (vi) are equivalent. Next, conditions (ii) and (iii) are equivalent since
![]() $w_{\Lambda }^G$
is left nondegenerate (see Theorem 4.1.2(2) and Proposition 3.1.6(1)), and applying Proposition 1.2.4(2) we obtain the equivalence of (iii) and (iv).
$w_{\Lambda }^G$
is left nondegenerate (see Theorem 4.1.2(2) and Proposition 3.1.6(1)), and applying Proposition 1.2.4(2) we obtain the equivalence of (iii) and (iv).
Assertion 2 immediately follows from Proposition 2.4.4.
3. Since
![]() $SH_{\Lambda }(G)$
is Karoubian, conditions (i) and (ii) are equivalent according to Corollary 3.1.4(II) combined with Proposition 4.2.1(3) and assertion 1. Moreover, (i) is equivalent to (iv) and (v) by Theorem 4.1.2(1), and condition (iii) clearly implies condition (iv).
$SH_{\Lambda }(G)$
is Karoubian, conditions (i) and (ii) are equivalent according to Corollary 3.1.4(II) combined with Proposition 4.2.1(3) and assertion 1. Moreover, (i) is equivalent to (iv) and (v) by Theorem 4.1.2(1), and condition (iii) clearly implies condition (iv).
4. By definition, E is without weights
![]() $m \dots n$
if and only if
$m \dots n$
if and only if
![]() $\operatorname {id}_E$
kills these weights. Hence, applying assertion 2 we obtain the equivalence of conditions (i), (iii) and (iv). Lastly, conditions (i) and (ii) are equivalent according to Theorem 2.2.1(9,10).
$\operatorname {id}_E$
kills these weights. Hence, applying assertion 2 we obtain the equivalence of conditions (i), (iii) and (iv). Lastly, conditions (i) and (ii) are equivalent according to Theorem 2.2.1(9,10).
Remark 4.2.3.
-
1. Let us explain that part 3 of our theorem is a certain converse to the natural Hurewicz theorem for this context.
We recall that the ‘usual’ stable Hurewicz theorem essentially says that in the case
 $G=\{e\}$
(and
$G=\{e\}$
(and
 $\Lambda ={\mathbb {Z}}$
, so
$\Lambda ={\mathbb {Z}}$
, so
 $SH(G)=SH$
) a
$SH(G)=SH$
) a
 $w_{\Lambda }^G=w^{sph}$
-bounded below spectrum E is connective if and only if its singular homology is concentrated in nonnegative degrees. An equivariant version of this statement is given by Theorem 2.1(i) of [Reference Lewis18] (cf. also Theorem 1.11 of ibid. and Proposition 7.1.2(f) of [Reference Hovey, Palmieri and Strickland15]). Note that one replaces singular homology by
$w_{\Lambda }^G=w^{sph}$
-bounded below spectrum E is connective if and only if its singular homology is concentrated in nonnegative degrees. An equivariant version of this statement is given by Theorem 2.1(i) of [Reference Lewis18] (cf. also Theorem 1.11 of ibid. and Proposition 7.1.2(f) of [Reference Hovey, Palmieri and Strickland15]). Note that one replaces singular homology by
 $H^{{\mathcal {A}_{\mathcal {P}}}}$
in it (cf. part 4 of this remark).
$H^{{\mathcal {A}_{\mathcal {P}}}}$
in it (cf. part 4 of this remark).Now, it is easily seen that those essentially
 $w_{\Lambda }^G$
-positive objects that are
$w_{\Lambda }^G$
-positive objects that are
 $w_{\Lambda }^G$
-bounded below are connective. Hence, part 3 of our theorem naturally generalizes the aforementioned converse equivariant Hurewicz theorem to arbitrary objects of
$w_{\Lambda }^G$
-bounded below are connective. Hence, part 3 of our theorem naturally generalizes the aforementioned converse equivariant Hurewicz theorem to arbitrary objects of
 $SH_{\Lambda }(G)$
. Our generalization depends on the notion of acyclic spectra, and the corresponding part 1 of our theorem also appears to be quite new; cf. also part 4 of this remark.
$SH_{\Lambda }(G)$
. Our generalization depends on the notion of acyclic spectra, and the corresponding part 1 of our theorem also appears to be quite new; cf. also part 4 of this remark. -
2. The notions of killing weights and being without weights
 $m,\dots ,n$
(along with parts 2–4 of our theorem see also Proposition 4.2.1(4)) appear to be new in this context even when restricted to the case
$m,\dots ,n$
(along with parts 2–4 of our theorem see also Proposition 4.2.1(4)) appear to be new in this context even when restricted to the case
 $\underline {C}=SH$
. Note that one can obtain canonical ‘decompositions’ of some spectra (see condition 4. (ii) in our theorem) by looking at their cohomology with coefficients in Eilenberg–Maclane spectra.
$\underline {C}=SH$
. Note that one can obtain canonical ‘decompositions’ of some spectra (see condition 4. (ii) in our theorem) by looking at their cohomology with coefficients in Eilenberg–Maclane spectra. -
3. Recall that if
 $\Lambda ={\mathbb {Z}}$
, then the pure homological functor
$\Lambda ={\mathbb {Z}}$
, then the pure homological functor
 $H^{{\mathcal {A}_{\mathcal {P}}}}$
is the equivariant ordinary homology with Burnside ring coefficients functor
$H^{{\mathcal {A}_{\mathcal {P}}}}$
is the equivariant ordinary homology with Burnside ring coefficients functor
 $H^G_0$
considered in [Reference Lewis18] (cf. also Definition X.4.1 of [Reference May21]), and for every Mackey functor M the corresponding pure functor
$H^G_0$
considered in [Reference Lewis18] (cf. also Definition X.4.1 of [Reference May21]), and for every Mackey functor M the corresponding pure functor
 $H_M$
coincides with
$H_M$
coincides with
 $H_G^0(-,M)$
in Definitions X.4.2 and §XIII.4 of ibid. Clearly, it follows that the functors
$H_G^0(-,M)$
in Definitions X.4.2 and §XIII.4 of ibid. Clearly, it follows that the functors
 $H^{{\mathcal {A}_{\mathcal {P}}}}$
and
$H^{{\mathcal {A}_{\mathcal {P}}}}$
and
 $H_M$
are closely related to these notions as well.
$H_M$
are closely related to these notions as well. -
4. None of the descriptions of acyclic spectra in part 1 of our theorem characterizes them ‘explicitly’. In the case
 $G=\{e\}$
, our definition of this notion coincides with the definition in [Reference Margolis20]; see Theorem 4.2.4(2) below. Thus, Theorem 16.17 of ibid. gives an explicit example of a nonzero acyclic spectrum.
$G=\{e\}$
, our definition of this notion coincides with the definition in [Reference Margolis20]; see Theorem 4.2.4(2) below. Thus, Theorem 16.17 of ibid. gives an explicit example of a nonzero acyclic spectrum. -
5. Proposition 4.1.7 certainly gives some more information on (‘weights of’) objects of
 $SH_{\Lambda }(G)$
whenever the corresponding category
$SH_{\Lambda }(G)$
whenever the corresponding category
 $\mathcal {M}_G$
is of projective dimension at most
$\mathcal {M}_G$
is of projective dimension at most
 $1$
. So we note that this assumption is fulfilled whenever G is a finite group of order n and
$1$
. So we note that this assumption is fulfilled whenever G is a finite group of order n and
 $1/n\in \Lambda $
. One should join Theorem 2.1 of [Reference Greenlees14] with the finite projective dimension statement established in §6 of ibid. to obtain this fact.
$1/n\in \Lambda $
. One should join Theorem 2.1 of [Reference Greenlees14] with the finite projective dimension statement established in §6 of ibid. to obtain this fact. -
6. Let us mention some nice properties of
 $w^G$
.
$w^G$
.Firstly, it restricts to the subcategory of compact objects of
 $SH_{\Lambda }(G)$
; cf. Theorem 4.1.1(2) of [Reference Bondarko7]. Next, the class
$SH_{\Lambda }(G)$
; cf. Theorem 4.1.1(2) of [Reference Bondarko7]. Next, the class
 $SH_{\Lambda }(G)_{w^G\ge 0}$
can also be described as
$SH_{\Lambda }(G)_{w^G\ge 0}$
can also be described as
 $SH_{\Lambda }(G)_{t\ge 0}$
for a certain Postnikov t-structure t (see Definition 4.3.1(I) and Proposition 4.3.3 of ibid.), yet this t-structure does not restrict to compact objects of
$SH_{\Lambda }(G)_{t\ge 0}$
for a certain Postnikov t-structure t (see Definition 4.3.1(I) and Proposition 4.3.3 of ibid.), yet this t-structure does not restrict to compact objects of
 $SH_{\Lambda }(G)$
.
$SH_{\Lambda }(G)$
.Note also that our theory gives a certain converse Hurewicz-type theorem (and also other ‘decompositions’ as well as several new definitions; see part 2 of this remark) for the so-called connective stable homotopy theory as discussed in §7 of [Reference Hovey, Palmieri and Strickland15]; cf. version (ii) of Corollary 4.1.4(1) and see Remark 4.3.4(2) of [Reference Bondarko7] for more detail.
Now, we apply our results to the stable homotopy category
![]() $SH$
. Some of these statements were already stated in Theorem 4.2.1 of [Reference Bondarko7]. This corresponds to the case of trivial G and S in Proposition 4.2.1, so we will write
$SH$
. Some of these statements were already stated in Theorem 4.2.1 of [Reference Bondarko7]. This corresponds to the case of trivial G and S in Proposition 4.2.1, so we will write
![]() $\operatorname {EM}$
for
$\operatorname {EM}$
for
![]() $\operatorname {EM}_G$
and
$\operatorname {EM}_G$
and
![]() $w^{sph}$
for
$w^{sph}$
for
![]() $w_{\Lambda }^G$
in this case and use the remaining notation from the proposition.
$w_{\Lambda }^G$
in this case and use the remaining notation from the proposition.
Theorem 4.2.4. Set
![]() $\mathcal {P}=\{S^0\}$
, and assume
$\mathcal {P}=\{S^0\}$
, and assume
![]() $m\le n\in {\mathbb {Z}}$
and
$m\le n\in {\mathbb {Z}}$
and
![]() $g:E\to E'$
is an
$g:E\to E'$
is an
![]() $SH$
-morphism.
$SH$
-morphism.
-
1. Then the functor
 $SH(S^0,-)$
gives equivalences
$SH(S^0,-)$
gives equivalences
 ${\underline {Hw}}^{sph}\to \operatorname {FreeAb}$
(free abelian groups) and
${\underline {Hw}}^{sph}\to \operatorname {FreeAb}$
(free abelian groups) and
 $\operatorname {EM}\to \operatorname {Ab}$
; thus,
$\operatorname {EM}\to \operatorname {Ab}$
; thus,
 $\underline {A}_{\mathcal {P}}$
is equivalent to
$\underline {A}_{\mathcal {P}}$
is equivalent to
 $\operatorname {Ab}$
as well.
$\operatorname {Ab}$
as well. -
2. The last of the aforementioned equivalences makes the functor
 ${\mathcal {A}_{\mathcal {P}}}$
isomorphic to the singular homology functor
${\mathcal {A}_{\mathcal {P}}}$
isomorphic to the singular homology functor
 $H^{sing}=H^{sing}(-,{\mathbb {Z}})$
. Consequently, acyclic spectra in
$H^{sing}=H^{sing}(-,{\mathbb {Z}})$
. Consequently, acyclic spectra in
 $SH$
are characterized by the vanishing of their singular homology (cf. §6.2 of [Reference Margolis20]).
$SH$
are characterized by the vanishing of their singular homology (cf. §6.2 of [Reference Margolis20]). -
3. For every abelian group
 $\Gamma $
and the corresponding spectrum
$\Gamma $
and the corresponding spectrum
 $\operatorname {EM}^{\Gamma }\in \operatorname {Obj} \operatorname {EM}$
, the functor
$\operatorname {EM}^{\Gamma }\in \operatorname {Obj} \operatorname {EM}$
, the functor
 $SH(-,\operatorname {EM}^{\Gamma })$
is isomorphic to the singular cohomology with coefficients in
$SH(-,\operatorname {EM}^{\Gamma })$
is isomorphic to the singular cohomology with coefficients in
 $\Gamma $
.
$\Gamma $
. -
4. g kills weight m if and only if
 $H^{sing}_m(g)=0$
, the class of
$H^{sing}_m(g)=0$
, the class of
 $t(g)$
in the group
$t(g)$
in the group
 $\operatorname {\mathrm {\operatorname {Ext}^{1}_{\operatorname {Ab}}}}(H^{sing}_{m-1}(E),H^{sing}_m(E'))$
(see Proposition 4.1.7(3)) vanishes and the morphism
$\operatorname {\mathrm {\operatorname {Ext}^{1}_{\operatorname {Ab}}}}(H^{sing}_{m-1}(E),H^{sing}_m(E'))$
(see Proposition 4.1.7(3)) vanishes and the morphism
 $H^{sing}_{m-1}(g)$
factors through a free abelian group.
$H^{sing}_{m-1}(g)$
factors through a free abelian group.This condition is also equivalent to the vanishing of
 $H_{sing}^m(-,\Gamma )(g)$
for every abelian group
$H_{sing}^m(-,\Gamma )(g)$
for every abelian group
 $\Gamma $
.
$\Gamma $
. -
5. E is an extension of an n-connected spectrum Y by
 $X_{m-1}\in SH_{w^{sph}\le m-1}$
Footnote
6
if and only if
$X_{m-1}\in SH_{w^{sph}\le m-1}$
Footnote
6
if and only if
 $H^{sing}_j(E)=\{0\}$
for
$H^{sing}_j(E)=\{0\}$
for
 $m\le j \le n$
, and
$m\le j \le n$
, and
 $H^{sing}_{m-1}(E)$
is a free abelian group.
$H^{sing}_{m-1}(E)$
is a free abelian group. -
6. E is an extension of a connective spectrum by an acyclic one if and only if
 $H^{sing}_j(E)=\{0\}$
for all
$H^{sing}_j(E)=\{0\}$
for all
 $j<0$
. This is also equivalent to the vanishing of
$j<0$
. This is also equivalent to the vanishing of
 $H_{sing}^j(E,{\mathbb {Q}}/{\mathbb {Z}})$
for all
$H_{sing}^j(E,{\mathbb {Q}}/{\mathbb {Z}})$
for all
 $j<0$
.
$j<0$
.
Proof. Assertions 1–3 easily follow from Theorem 4.1.2. They are also contained in Theorem 4.2.1 of [Reference Bondarko7]. These facts also yield that Theorem 4.1.2(3) implies our assertion 6.
Next, the category
![]() $\operatorname {Ab}\cong \underline {A}_{\mathcal {P}}$
is of cohomological dimension
$\operatorname {Ab}\cong \underline {A}_{\mathcal {P}}$
is of cohomological dimension
![]() $1$
; hence, we can combine Proposition 4.1.7(3,4) with the preceding assertions along with Theorem 4.1.2(2,4) to obtain assertions 4 and 5.
$1$
; hence, we can combine Proposition 4.1.7(3,4) with the preceding assertions along with Theorem 4.1.2(2,4) to obtain assertions 4 and 5.
Now, we can relate
![]() $w^{sph}$
to central notions of [Reference Margolis20].
$w^{sph}$
to central notions of [Reference Margolis20].
Theorem 4.2.5.
1. The following assumptions on a spectrum E (that is, an object of
![]() $SH$
) are equivalent.
$SH$
) are equivalent.
(i)
![]() $E\in SH_{w^{sph}\le n}$
;
$E\in SH_{w^{sph}\le n}$
;
(ii)
![]() $H^{sing}_i(E)=\{0\}$
for
$H^{sing}_i(E)=\{0\}$
for
![]() $i>n$
and
$i>n$
and
![]() $H^{sing}_n(E)$
is a free abelian group;
$H^{sing}_n(E)$
is a free abelian group;
(iii)
![]() $H_{sing}^i(E,\Gamma )=\{0\}$
for every
$H_{sing}^i(E,\Gamma )=\{0\}$
for every
![]() $i>n$
and every abelian group
$i>n$
and every abelian group
![]() $\Gamma $
;
$\Gamma $
;
(iv) E is an n-skeleton (of some spectrum) in the sense of [Reference Margolis20, §6.3].
2. A
![]() $w^{sph}$
-Postnikov tower (see Definition 1.3.3 of [Reference Bondarko7]) for E is the same thing as a cellular tower for E in the sense of [Reference Margolis20, §6.3].
$w^{sph}$
-Postnikov tower (see Definition 1.3.3 of [Reference Bondarko7]) for E is the same thing as a cellular tower for E in the sense of [Reference Margolis20, §6.3].
Proof. Applying Theorem 4.2.4(1–3) we obtain that Proposition 4.2.1(4) gives the equivalence of conditions 1(i) and 1(iii), and also that Proposition 4.1.7(4) implies the equivalence of conditions 1(i) and 1(ii). Moreover, the latter equivalence statement implies that these conditions are fulfilled if and only if E is an n-skeleton, and also that assertion 2 is valid according to Theorem 4.2.1(4,5) of [Reference Bondarko7].