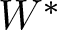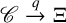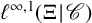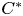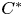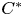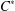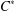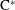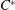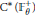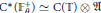Refine search
Actions for selected content:
12 results
Isometric dilations for representations of product systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CRITERION FOR HYPERSYMMETRY ON DISCRETE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 320-330
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of irreversible and reversible Pimsner operator algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 13 January 2021, pp. 2510-2535
- Print publication:
- December 2020
-
- Article
- Export citation
APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 328-337
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
INVERSION OF OPERATOR PENCILS ON HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 145-176
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
New Deformations of Convolution Algebras and Fourier Algebras on Locally Compact Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 2 / 01 April 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 434-452
- Print publication:
- 01 April 2017
-
- Article
-
- You have access
- Export citation
On the Isomorphism Problem for Multiplier Algebras of Nevanlinna-Pick Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 1 / 01 February 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 54-106
- Print publication:
- 01 February 2017
-
- Article
-
- You have access
- Export citation
Some Weighted Group Algebras are Operator Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 05 January 2015, pp. 499-519
-
- Article
-
- You have access
- Export citation
A NONSEPARABLE AMENABLE OPERATOR ALGEBRA WHICH IS NOT ISOMORPHIC TO A
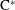 $C^*$ -ALGEBRA
$C^*$ -ALGEBRA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 March 2014, e2
-
- Article
-
- You have access
- Open access
- Export citation
SUBMODULES OF COMMUTATIVE C*-ALGEBRAS
-
- Journal:
- Glasgow Mathematical Journal / Volume 56 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 13 August 2013, pp. 471-479
- Print publication:
- May 2014
-
- Article
-
- You have access
- Export citation
Periodicity in Rank 2 Graph Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 6 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1239-1261
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
One-sided ideals and approximate identities in operator algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-448
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation