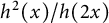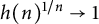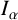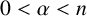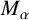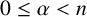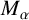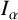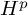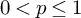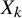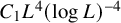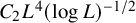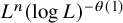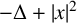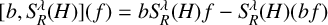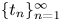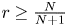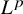Refine search
Actions for selected content:
131 results
Uniform bounds for polynomial Carleson operators and oscillatory integrals of Radon type
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
Weak porosity on metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variation of the one-dimensional centered maximal operator on simple functions with gaps between pieces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weighted decoupling estimates and the Bochner-Riesz means
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 06 October 2025, e167
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the best constant for uncentered maximal functions with measure on ℝ
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-9
-
- Article
- Export citation
Hardy-type inequalities for the drifting p-Laplace operator and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 August 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parabolic Muckenhoupt weights characterized by parabolic fractional maximal and integral operators with time lag
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1-54
-
- Article
- Export citation
BOUNDEDNESS OF DIFFERENTIAL TRANSFORMS FOR FRACTIONAL HEAT SEMIGROUPS GENERATED BY SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 210-244
- Print publication:
- April 2025
-
- Article
- Export citation
Compact bilinear operators and paraproducts revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 44-59
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Model structures, n-Gorenstein flat modules and PGF dimensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1241-1264
-
- Article
- Export citation
CORRECTION TO ‘CHOQUET INTEGRALS, HAUSDORFF CONTENT AND FRACTIONAL OPERATORS’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 568-570
- Print publication:
- June 2025
-
- Article
- Export citation
The multilinear spherical maximal function in one dimension
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 25 September 2024, pp. 1045-1059
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some convexity questions of Handelman
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 936-939
- Print publication:
- December 2024
-
- Article
- Export citation
CHOQUET INTEGRALS, HAUSDORFF CONTENT AND FRACTIONAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. 355-366
- Print publication:
- October 2024
-
- Article
- Export citation
TRILINEAR FOURIER MULTIPLIERS ON HARDY SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2217-2278
- Print publication:
- September 2024
-
- Article
- Export citation
Degrees of maps and multiscale geometry
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 January 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A WEIGHTED
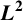 $\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
$\boldsymbol {L}^{\boldsymbol {2}}$ ESTIMATE OF COMMUTATORS OF BOCHNER–RIESZ OPERATORS FOR HERMITE OPERATOR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 January 2024, pp. 308-330
- Print publication:
- June 2024
-
- Article
- Export citation
Sharp convergence for sequences of Schrödinger means and related generalizations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 25 September 2023, pp. 453-469
- Print publication:
- April 2025
-
- Article
- Export citation
On a multi-parameter variant of the Bellow–Furstenberg problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 September 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete restriction estimates for forms in many variables
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 923-939
-
- Article
-
- You have access
- Open access
- HTML
- Export citation



































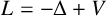
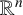
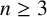
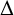
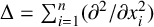

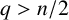
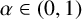
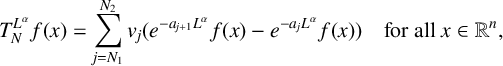
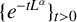
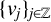
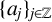
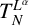
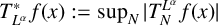
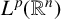
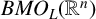
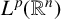
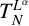
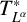
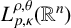
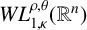





 . The homotopy category of this model structure is triangulated equivalent to the stable category
. The homotopy category of this model structure is triangulated equivalent to the stable category