Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-25T23:14:02.767Z Has data issue: false hasContentIssue false
  • English
  • Français

Perron’s capacity of random sets

Part of: Functions of several variables Harmonic analysis in several variables

Published online by Cambridge University Press:  01 September 2023

Anthony Gauvan
Anthony Gauvan*
Affiliation:
Department of Mathematics, Institut de Mathématiques d’Orsay, Orsay 91400, France (a.gauvan@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We answer in a probabilistic setting two questions raised by Stokolos in a private communication. Precisely, given a sequence of random variables 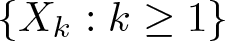$\left\{X_k : k \geq 1\right\}$ uniformly distributed in 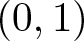$(0,1)$ and independent, we consider the following random sets of directions

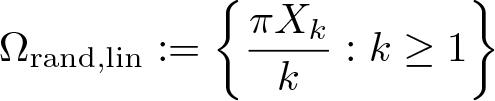\begin{equation*}\Omega_{\text{rand},\text{lin}} := \left\{ \frac{\pi X_k}{k}: k \geq 1\right\}\end{equation*}
and
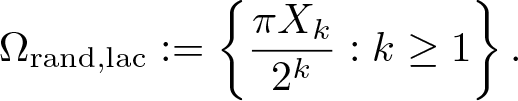\begin{equation*}\Omega_{\text{rand},\text{lac}} := \left\{\frac{\pi X_k}{2^k} : k\geq 1 \right\}.\end{equation*}

We prove that almost surely the directional maximal operators associated to those sets of directions are not bounded on 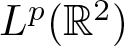$L^p({\mathbb{R}}^2)$ for any 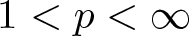$1 \lt p \lt \infty$.

Keywords

maximal operatordifferentiation of integralsharmonic analysislacunary sets of finite orderreal analysis

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory 26B05: Continuity and differentiation questions
Secondary: 42B35: Function spaces arising in harmonic analysis
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 4 , November 2023 , pp. 960 - 970
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bateman, M. D., Kakeya sets and directional maximal operators in the plane, Duke Math. J. 147(1) (2009), 55–77.CrossRefGoogle Scholar
D’Aniello, E. and Moonens, L., Differentiating Orlicz spaces with rectangles having fixed shapes in a set of directions, Z. Anal. Anwend. 39(4) (2020), 461–473.CrossRefGoogle Scholar
D’Aniello, E., Gauvan, A. and Moonens, L., (Un)boundedness of directional maximal operators through a notion of “Perron capacity” and an application, Proc. Amer. Math. Soc., 151 (2023). 2517–2526.Google Scholar
Fefferman, C., The multiplier problem for the ball, Ann. Math. 94(2) (1971), 330–336.CrossRefGoogle Scholar
Gauvan, A., Application of Perron trees to geometric maximal operators, Colloq. Math. 172(1) (2023), 1–13.CrossRefGoogle Scholar
Hare, K. and Rönning, J.-O., Applications of generalized Perron trees to maximal functions and density bases, J. Fourier Anal. App. 4 (1998), 215–227.CrossRefGoogle Scholar
Katz, N. H., A counterexample for maximal operators over a Cantor set of directions, Math. Res. Lett. 3(4) (1996), 527–536.CrossRefGoogle Scholar
Kroc, E. and Pramanik, M., Lacunarity, Kakeya-type sets and directional maximal operators. arXiv:1404.6241.Google Scholar
Nagel, A., Stein, E. M. and Wainger, S., Differentiation in lacunary directions, Proc. Natl. Acad. Sci. USA 75(3) (1978), 1060–1062.CrossRefGoogle ScholarPubMed