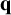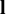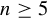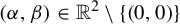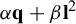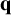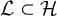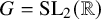Refine search
Actions for selected content:
61 results
Counting closed geodesics on rank-one manifolds without focal points
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-28
-
- Article
- Export citation
Approximate control of the marked length spectrum by short geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 29 October 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sub-actions for geodesic flows on locally CAT(
 $-1$) spaces
$-1$) spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 06 August 2025, pp. 3619-3662
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LYUAPONOV EXPONENTS FOR OPEN BILLIARD SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 568-569
- Print publication:
- December 2025
-
- Article
-
- You have access
- HTML
- Export citation
Smooth orbit equivalence rigidity for dissipative geodesic flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 3698-3727
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DYNAMICAL SYSTEMS ON SOME ELLIPTIC MODULAR SURFACES VIA OPERATORS ON LINE ARRANGEMENTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 357-375
- Print publication:
- June 2025
-
- Article
- Export citation
Quasidiagonals in strata of translation surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 2233-2248
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Surfaces of section for geodesic flows of closed surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 15 November 2024, pp. 1698-1733
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Marked length pattern rigidity for arithmetic manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1199-1223
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multifractal analysis of homological growth rates for hyperbolic surfaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 849-883
- Print publication:
- March 2025
-
- Article
- Export citation
Bishop–Jones’ theorem and the ergodic limit set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 704-718
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution in homology classes and discrete fractal dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic distribution for pairs of linear and quadratic forms at integral vectors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 111-139
- Print publication:
- January 2025
-
- Article
- Export citation
On the ergodic theory of the real Rel foliation
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Patterson–Sullivan theory for groups with a strongly contracting element
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3216-3271
- Print publication:
- November 2024
-
- Article
- Export citation
DIOPHANTINE TRANSFERENCE PRINCIPLE OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 216-233
- Print publication:
- October 2024
-
- Article
- Export citation
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 January 2024, pp. 2700-2736
- Print publication:
- September 2024
-
- Article
- Export citation
BRATTELI–VERSHIKISABILITY OF POLYGONAL BILLIARDS ON THE HYPERBOLIC PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 85-104
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting geodesics of given commutator length
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 December 2023, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform spectral gap and orthogeodesic counting for strong convergence of Kleinian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 August 2023, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation