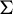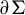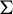1 Introduction
Let N be a closed connected 3-manifold and let X be a nowhere vanishing vector field on N with flow
![]() $\phi _t:N\to N$
. A surface of section for X is a (not necessarily connected) immersed compact surface
$\phi _t:N\to N$
. A surface of section for X is a (not necessarily connected) immersed compact surface
![]() $\Sigma \looparrowright N$
whose boundary
$\Sigma \looparrowright N$
whose boundary
![]() $\partial \Sigma $
is tangent to X, and whose interior
$\partial \Sigma $
is tangent to X, and whose interior
![]() $\operatorname {\mathrm {int}}(\Sigma )$
is embedded in
$\operatorname {\mathrm {int}}(\Sigma )$
is embedded in
![]() $N\setminus \partial \Sigma $
and transverse to X. A surface of section allows us to read part of the dynamics of X as discrete dynamics of the first return map to
$N\setminus \partial \Sigma $
and transverse to X. A surface of section allows us to read part of the dynamics of X as discrete dynamics of the first return map to
![]() $\Sigma $
. For this purpose, we consider the first return time function
$\Sigma $
. For this purpose, we consider the first return time function
Here, as usual, we set
![]() $\inf \varnothing =+\infty $
. The function
$\inf \varnothing =+\infty $
. The function
![]() $\tau $
is continuous on the whole
$\tau $
is continuous on the whole
![]() $\operatorname {\mathrm {int}}(\Sigma )$
and smooth on the open subsets where it is finite. The surface of section
$\operatorname {\mathrm {int}}(\Sigma )$
and smooth on the open subsets where it is finite. The surface of section
![]() $\Sigma $
is called a Birkhoff section when there exists a finite constant
$\Sigma $
is called a Birkhoff section when there exists a finite constant
![]() $\ell>0$
such that, for each
$\ell>0$
such that, for each
![]() $z\in N$
, the orbit segment
$z\in N$
, the orbit segment
![]() $\phi _{[0,\ell ]}(z)$
intersects
$\phi _{[0,\ell ]}(z)$
intersects
![]() $\Sigma $
. Under this condition, outside
$\Sigma $
. Under this condition, outside
![]() $\partial \Sigma $
the dynamical system defined by X is the suspension of the discrete dynamical system defined by the first return map
$\partial \Sigma $
the dynamical system defined by X is the suspension of the discrete dynamical system defined by the first return map
Notice that a Birkhoff section
![]() $\Sigma $
is not necessarily connected, but any connected component of
$\Sigma $
is not necessarily connected, but any connected component of
![]() $\Sigma $
is also a Birkhoff section. By means of a Birkhoff section, statements concerning two-dimensional discrete dynamics can be translated into corresponding statements for the dynamics of vector fields in dimension three.
$\Sigma $
is also a Birkhoff section. By means of a Birkhoff section, statements concerning two-dimensional discrete dynamics can be translated into corresponding statements for the dynamics of vector fields in dimension three.
The quest for Birkhoff sections has been a problem of major interest in dynamical systems since the seminal work of Poincaré [Reference PoincaréPoi12] and Birkhoff [Reference BirkhoffBir17]. In the context of Reeb vector fields on closed 3-manifolds, by a spectacular application of holomorphic curves techniques, Hofer, Wysocki and Zehnder [Reference Hofer, Wysocki and ZehnderHWZ98] established the existence of Birkhoff sections for all positively curved
![]() $3$
-spheres in the four-dimensional symplectic vector space, equipped with the canonical contact form. A result of the first and third author [Reference Contreras and MazzucchelliCM22] proved the existence of Birkhoff sections for all closed contact 3-manifolds satisfying the Kupka–Smale condition: non-degeneracy of the closed Reeb orbits, and transversality of the stable and unstable manifolds of the hyperbolic closed Reeb orbits. In particular, the existence of Birkhoff sections holds for the Reeb vector field of a
$3$
-spheres in the four-dimensional symplectic vector space, equipped with the canonical contact form. A result of the first and third author [Reference Contreras and MazzucchelliCM22] proved the existence of Birkhoff sections for all closed contact 3-manifolds satisfying the Kupka–Smale condition: non-degeneracy of the closed Reeb orbits, and transversality of the stable and unstable manifolds of the hyperbolic closed Reeb orbits. In particular, the existence of Birkhoff sections holds for the Reeb vector field of a
![]() $C^\infty $
generic contact form on any closed 3-manifold and for the geodesic vector field of a
$C^\infty $
generic contact form on any closed 3-manifold and for the geodesic vector field of a
![]() $C^\infty $
generic Riemannian metric on any closed surface.
$C^\infty $
generic Riemannian metric on any closed surface.
An independent work of Colin et al [Reference Colin, Dehornoy, Hryniewicz and RechtmanCDHR24] established the existence of Birkhoff sections for those Reeb vector fields on any closed 3-manifold whose closed orbits are non-degenerate and equidistributed (that is, the contact volume form can be approximated, as a measure, by closed orbits). It is not known whether the equidistribution of the closed orbits holds for the geodesic vector field of a
![]() $C^\infty $
generic Riemannian metric on a closed surface; indeed, even the fact that, for such a
$C^\infty $
generic Riemannian metric on a closed surface; indeed, even the fact that, for such a
![]() $C^\infty $
generic Riemannian metric, the lifts of the closed geodesics form a dense subset of the unit tangent bundle is an open problem. Nevertheless, Irie’s equidistribution theorem [Reference IrieIri21] implies that the equidistribution of the closed orbits holds for the Reeb vector field of a
$C^\infty $
generic Riemannian metric, the lifts of the closed geodesics form a dense subset of the unit tangent bundle is an open problem. Nevertheless, Irie’s equidistribution theorem [Reference IrieIri21] implies that the equidistribution of the closed orbits holds for the Reeb vector field of a
![]() $C^\infty $
generic contact form on any closed 3-manifold, and together with [Reference Colin, Dehornoy, Hryniewicz and RechtmanCDHR24] this provides an alternative proof of the
$C^\infty $
generic contact form on any closed 3-manifold, and together with [Reference Colin, Dehornoy, Hryniewicz and RechtmanCDHR24] this provides an alternative proof of the
![]() $C^\infty $
generic existence of Birkhoff sections for closed contact 3-manifolds. We stress that, on a closed 3-manifold diffeomorphic to the unit tangent bundle of a closed surface, the Reeb flow of a
$C^\infty $
generic existence of Birkhoff sections for closed contact 3-manifolds. We stress that, on a closed 3-manifold diffeomorphic to the unit tangent bundle of a closed surface, the Reeb flow of a
![]() $C^\infty $
generic contact form is not necessarily conjugate (or even orbitally equivalent) to the geodesic flow of a Riemannian metric.
$C^\infty $
generic contact form is not necessarily conjugate (or even orbitally equivalent) to the geodesic flow of a Riemannian metric.
In this paper, we focus on geodesic flows of closed orientable Riemannian surfaces
![]() $(M,g)$
; hereafter, the Riemannian metrics are assumed to be
$(M,g)$
; hereafter, the Riemannian metrics are assumed to be
![]() $C^\infty $
. The unit tangent bundle
$C^\infty $
. The unit tangent bundle
![]() $SM=\{v\in TM\ |\ \|v\|_g=1\}$
is equipped with the Liouville contact form
$SM=\{v\in TM\ |\ \|v\|_g=1\}$
is equipped with the Liouville contact form
![]() $\unicode{x3bb} _{v}=g(v,d\pi (v)\,\cdot \,)$
, where
$\unicode{x3bb} _{v}=g(v,d\pi (v)\,\cdot \,)$
, where
![]() $\pi :SM\to M$
is the base projection. The geodesic vector field X on
$\pi :SM\to M$
is the base projection. The geodesic vector field X on
![]() $SM$
is the associated Reeb vector field, which means that
$SM$
is the associated Reeb vector field, which means that
![]() $\unicode{x3bb} (X)\equiv 1$
and
$\unicode{x3bb} (X)\equiv 1$
and
![]() $d\unicode{x3bb} (X,\cdot )\equiv 0$
. The geodesic flow
$d\unicode{x3bb} (X,\cdot )\equiv 0$
. The geodesic flow
![]() $\phi _t:SM\to SM$
is the associated Reeb flow. Its orbits have the form
$\phi _t:SM\to SM$
is the associated Reeb flow. Its orbits have the form
![]() $\phi _t(\dot \gamma (0))\hspace{-1pt}=\hspace{-1pt}\dot \gamma (t)$
, where
$\phi _t(\dot \gamma (0))\hspace{-1pt}=\hspace{-1pt}\dot \gamma (t)$
, where
![]() $\gamma :\mathbb {R}\hspace{-1pt}\looparrowright\hspace{-1pt} M$
is a geodesic parameterized with unit speed
$\gamma :\mathbb {R}\hspace{-1pt}\looparrowright\hspace{-1pt} M$
is a geodesic parameterized with unit speed
![]() $\|\dot \gamma \|_g\hspace{-1pt}\equiv\hspace{-1pt} 1$
. The closed geodesics of
$\|\dot \gamma \|_g\hspace{-1pt}\equiv\hspace{-1pt} 1$
. The closed geodesics of
![]() $(M,g)$
are precisely the base projections of the closed orbits of the geodesic flow. A closed geodesic is called simple when it is an embedded circle in M.
$(M,g)$
are precisely the base projections of the closed orbits of the geodesic flow. A closed geodesic is called simple when it is an embedded circle in M.
In this setting, surfaces of section have had important dynamical applications, among which we mention the following: they played a crucial role in Bangert, Franks and Hingston’s proof [Reference BangertBan93, Reference FranksFra92, Reference HingstonHin93] of the existence of infinitely many closed geodesics on every Riemannian 2-sphere; and they were employed by Contreras and Oliveira [Reference Contreras and OliveiraCO04] to establish the existence of an elliptic closed geodesic on a
![]() $C^2$
-generic Riemannian 2-sphere, by Contreras and Mazzucchelli [Reference Contreras and MazzucchelliCM24] to prove the
$C^2$
-generic Riemannian 2-sphere, by Contreras and Mazzucchelli [Reference Contreras and MazzucchelliCM24] to prove the
![]() $C^2$
-structural stability conjecture for Riemannian geodesic flows of closed surfaces and by Knieper and Schulz [Reference Knieper and SchulzKS24] to characterize Anosov Riemannian geodesic flows of closed surfaces as the
$C^2$
-structural stability conjecture for Riemannian geodesic flows of closed surfaces and by Knieper and Schulz [Reference Knieper and SchulzKS24] to characterize Anosov Riemannian geodesic flows of closed surfaces as the
![]() $C^2$
-stably transitive ones.
$C^2$
-stably transitive ones.
Although the above-mentioned result in [Reference Contreras and MazzucchelliCM22] implies the existence of a Birkhoff section for ‘most’ geodesic flows of closed Riemannian surfaces, it does not provide any information concerning the topology of such a Birkhoff section. In contrast, the celebrated work of Birkhoff [Reference BirkhoffBir17] provides explicit Birkhoff sections for two classes of geodesic flows: every positively curved Riemannian 2-sphere admits an embedded Birkhoff section diffeomorphic to an annulus, and any negatively curved Riemannian surface admits a Birkhoff section of genus one (see also [Reference FriedFri83, §3]). This paper is largely inspired by the work of Birkhoff.
Our first main result provides specific Birkhoff sections for geodesic flows of closed surfaces that do not admit contractible simple closed geodesics without conjugate points. We refer the reader to §2.3 for the background on the classical notion of conjugate points. A simple closed geodesic
![]() $\gamma $
is called a waist when it is a local minimizer of the length functional over the free loop space. (In the literature, sometimes ‘waist’ refers to a closed geodesic that is a local length minimizer in the free loop space, but is not necessary a simple closed geodesic.) We recall that a non-degenerate simple closed geodesic is a waist if and only if it does not have conjugate points.
$\gamma $
is called a waist when it is a local minimizer of the length functional over the free loop space. (In the literature, sometimes ‘waist’ refers to a closed geodesic that is a local length minimizer in the free loop space, but is not necessary a simple closed geodesic.) We recall that a non-degenerate simple closed geodesic is a waist if and only if it does not have conjugate points.
Theorem A. Let
![]() $(M,g)$
be a closed connected orientable Riemannian surface of genus
$(M,g)$
be a closed connected orientable Riemannian surface of genus
![]() $G\geq 1$
that does not have any contractible simple closed geodesics without conjugate points. Its geodesic vector field admits a Birkhoff section
$G\geq 1$
that does not have any contractible simple closed geodesics without conjugate points. Its geodesic vector field admits a Birkhoff section
![]() $\Sigma \looparrowright SM$
, where
$\Sigma \looparrowright SM$
, where
![]() $\Sigma $
is a compact connected surface of genus one and
$\Sigma $
is a compact connected surface of genus one and
![]() $8G-4$
boundary components that cover waists.
$8G-4$
boundary components that cover waists.
Theorem A applies, in particular, to Riemannian surfaces without contractible simple closed geodesics, and we obtain the following corollary.
Corollary B. The geodesic vector field of any closed connected orientable Riemannian surface
![]() $(M,g)$
of genus
$(M,g)$
of genus
![]() $G\geq 1$
admits a Birkhoff section of genus one and
$G\geq 1$
admits a Birkhoff section of genus one and
![]() $8G-4$
boundary components that cover waists, provided at least one of the following two conditions is satisfied.
$8G-4$
boundary components that cover waists, provided at least one of the following two conditions is satisfied.
-
• The Riemannian surface
 $(M,g)$
has no conjugate points.
$(M,g)$
has no conjugate points. -
• The Gaussian curvature is bounded from above as
 $$ \begin{align*} \max (K_g) \leq \frac{2\pi}{\mathrm{area}(M,g)}. \end{align*} $$
$$ \begin{align*} \max (K_g) \leq \frac{2\pi}{\mathrm{area}(M,g)}. \end{align*} $$
Proof. If
![]() $(M,g)$
has no conjugate points, it does not have contractible closed geodesics (see, e.g., [Reference Guillarmou and MazzucchelliGM24, Theorem 3.28]), and Theorem A applies. If, instead,
$(M,g)$
has no conjugate points, it does not have contractible closed geodesics (see, e.g., [Reference Guillarmou and MazzucchelliGM24, Theorem 3.28]), and Theorem A applies. If, instead,
![]() $(M,g)$
contains a contractible simple closed geodesic
$(M,g)$
contains a contractible simple closed geodesic
![]() $\gamma $
, then we denote by
$\gamma $
, then we denote by
![]() $B\subsetneq M$
the open disk such that
$B\subsetneq M$
the open disk such that
![]() $\partial B=\gamma $
, and the Gauss–Bonnet theorem implies that
$\partial B=\gamma $
, and the Gauss–Bonnet theorem implies that
where
![]() $m_g$
denotes the Riemannian measure. In particular,
$m_g$
denotes the Riemannian measure. In particular,
![]() $K_g$
attains positive values on B. This proves that, under the curvature bound
$K_g$
attains positive values on B. This proves that, under the curvature bound
![]() $\max (K_g) \leq 2\pi /\mathrm {area}(M,g)$
, there are no contractible simple closed geodesics, and Theorem A provides a Birkhoff section, as claimed.
$\max (K_g) \leq 2\pi /\mathrm {area}(M,g)$
, there are no contractible simple closed geodesics, and Theorem A provides a Birkhoff section, as claimed.
Any oriented simple closed geodesic
![]() $\gamma $
on an oriented Riemannian surface
$\gamma $
on an oriented Riemannian surface
![]() $(M,g)$
defines two surfaces of section
$(M,g)$
defines two surfaces of section
![]() $A(\dot \gamma ),A(-\dot \gamma )\subset SM$
diffeomorphic to annuli, which are referred to as the Birkhoff annuli of
$A(\dot \gamma ),A(-\dot \gamma )\subset SM$
diffeomorphic to annuli, which are referred to as the Birkhoff annuli of
![]() $\gamma $
(see §4.1). Theorem A was inspired by the following statement for Riemannian 2-spheres due to Bangert [Reference BangertBan93, Theorem 2], which, in turn, generalizes the above-mentioned result of Birkhoff for positively curved Riemannian 2-spheres. Our methods will provide a slightly simpler proof.
$\gamma $
(see §4.1). Theorem A was inspired by the following statement for Riemannian 2-spheres due to Bangert [Reference BangertBan93, Theorem 2], which, in turn, generalizes the above-mentioned result of Birkhoff for positively curved Riemannian 2-spheres. Our methods will provide a slightly simpler proof.
Theorem C. (Bangert)
Let
![]() $(S^2,g)$
be a Riemannian 2-sphere and let
$(S^2,g)$
be a Riemannian 2-sphere and let
![]() $\gamma $
be a simple closed geodesic with conjugate points whose complement
$\gamma $
be a simple closed geodesic with conjugate points whose complement
![]() $S^2\setminus \gamma $
does not contain simple closed geodesics without conjugate points. Then both Birkhoff annuli of
$S^2\setminus \gamma $
does not contain simple closed geodesics without conjugate points. Then both Birkhoff annuli of
![]() $\gamma $
are Birkhoff sections.
$\gamma $
are Birkhoff sections.
Remark 1.1. Every Riemannian 2-sphere has at least two simple closed geodesics with conjugate points. This follows from an addendum to the celebrated theorem of Lusternik and Schnirelmann [Reference Lusternik and SchnirelmannLS29], see [Reference De Philippis, Marini, Mazzucchelli and SuhrDPMMS22, Theorem 1.3(iii) and Proposition 4.2]).
Our third theorem is an improvement of the above-mentioned result [Reference Contreras and MazzucchelliCM22] for the case of geodesic flows. If K is a hyperbolic invariant subset for the geodesic flow, then we denote, as usual, by
![]() $W^{s}(K)$
and
$W^{s}(K)$
and
![]() $W^{u}(K)$
its stable and unstable manifolds, respectively.
$W^{u}(K)$
its stable and unstable manifolds, respectively.
Theorem D. Let
![]() $(M,g)$
be a closed connected orientable Riemannian surface satisfying the following two conditions.
$(M,g)$
be a closed connected orientable Riemannian surface satisfying the following two conditions.
-
(i) All contractible simple closed geodesics without conjugate points are non-degenerate.
-
(ii) Any pair of not necessarily distinct contractible waists
 $\gamma _1,\gamma _2$
(if they exist) satisfies the transversality condition
$\gamma _1,\gamma _2$
(if they exist) satisfies the transversality condition
 $W^{u}(\dot \gamma _1)\pitchfork W^{s}(\dot \gamma _2)$
.
$W^{u}(\dot \gamma _1)\pitchfork W^{s}(\dot \gamma _2)$
.
Then the geodesic vector field of
![]() $(M,g)$
admits a Birkhoff section.
$(M,g)$
admits a Birkhoff section.
The Birkhoff section provided by Theorem D is constructed by applying a surgery procedure due to Fried (see §4.1) to the Birkhoff annuli of a suitable finite collection of closed geodesics. The topology of such a Birkhoff section depends on the configuration of the closed geodesics in the collection, which, in turn, depends on the geometry of the Riemannian surface.
When an orientable Riemannian surface does not satisfy the assumptions of Theorems A, C and D, but still satisfies a mild non-degeneracy condition, we are at least able to construct a surface of section
![]() $\Sigma $
whose escaping orbits are asymptotic to certain hyperbolic components of
$\Sigma $
whose escaping orbits are asymptotic to certain hyperbolic components of
![]() $\partial \Sigma $
.
$\partial \Sigma $
.
Theorem E. Let
![]() $(M,g)$
be a closed connected orientable Riemannian surface all of whose contractible simple closed geodesics without conjugate points are non-degenerate. Its geodesic vector field admits a surface of section
$(M,g)$
be a closed connected orientable Riemannian surface all of whose contractible simple closed geodesics without conjugate points are non-degenerate. Its geodesic vector field admits a surface of section
![]() $\Sigma \looparrowright SM$
satisfying the following properties.
$\Sigma \looparrowright SM$
satisfying the following properties.
-
(i) Topology: If
 $M=S^2$
, then
$M=S^2$
, then
 $\Sigma $
is the disjoint union of the Birkhoff annuli of some simple closed geodesics. If M has genus
$\Sigma $
is the disjoint union of the Birkhoff annuli of some simple closed geodesics. If M has genus
 $G\geq 1$
, then
$G\geq 1$
, then
 $\Sigma $
is the disjoint union of the Birkhoff annuli of some simple closed geodesics and of a compact connected surface of genus one and
$\Sigma $
is the disjoint union of the Birkhoff annuli of some simple closed geodesics and of a compact connected surface of genus one and
 $8G-4$
boundary components, all covering non-contractible waists.
$8G-4$
boundary components, all covering non-contractible waists. -
(ii) Completeness:
 $\Sigma $
intersects any orbit
$\Sigma $
intersects any orbit
 $\phi _{(-\infty ,\infty )}(z)$
of the geodesic flow.
$\phi _{(-\infty ,\infty )}(z)$
of the geodesic flow. -
(iii) Escape set: There exists a possibly empty union of connected components
 $K\subset \partial \Sigma $
, whose base projection
$K\subset \partial \Sigma $
, whose base projection
 $\pi (K)$
is the union of hyperbolic contractible waists, such that the complements
$\pi (K)$
is the union of hyperbolic contractible waists, such that the complements
 $W^{s}(K)\setminus K$
and
$W^{s}(K)\setminus K$
and
 $W^{u}(K)\setminus K$
are given by
$W^{u}(K)\setminus K$
are given by  $$ \begin{align*} W^{s}(K)\setminus K &= \{ z\in SM\ |\ \phi_{[t,\infty)}(z)\cap\Sigma=\varnothing\mbox{ for some }t\in\mathbb{R}\},\\ W^{u}(K)\setminus K &= \{ z\in SM\ |\ \phi_{(-\infty,t]}(z)\cap\Sigma=\varnothing\mbox{ for some }t\in\mathbb{R}\}. \end{align*} $$
$$ \begin{align*} W^{s}(K)\setminus K &= \{ z\in SM\ |\ \phi_{[t,\infty)}(z)\cap\Sigma=\varnothing\mbox{ for some }t\in\mathbb{R}\},\\ W^{u}(K)\setminus K &= \{ z\in SM\ |\ \phi_{(-\infty,t]}(z)\cap\Sigma=\varnothing\mbox{ for some }t\in\mathbb{R}\}. \end{align*} $$
-
(iv) Return time: There exists
 $\ell>0$
such that, for each
$\ell>0$
such that, for each
 $z\in SM$
sufficiently close to
$z\in SM$
sufficiently close to
 $\partial \Sigma \setminus K$
, we have
$\partial \Sigma \setminus K$
, we have
 $\phi _{(0,\ell ]}(z)\cap \Sigma \neq \varnothing $
.
$\phi _{(0,\ell ]}(z)\cap \Sigma \neq \varnothing $
.
For general non-degenerate Reeb flows on closed 3-manifolds, surfaces of section satisfying properties analogous to (ii), (iii) and (iv) of Theorem E were constructed by Colin, Dehornoy and Rechtman [Reference Colin, Dehornoy and RechtmanCDR23] by applying surgery to certain holomorphic curves provided by Hutchings’ embedded contact homology [Reference HutchingsHut14]. Colin, Dehornoy and Rechtman further employed such surfaces of section to produce a so-called broken book decomposition of the 3-manifold, which is a generalization of the classical notions of open book decomposition and of Hofer, Wysocki and Zehnder’s finite energy foliations [Reference Hofer, Wysocki and ZehnderHWZ03].
The mentioned works [Reference Colin, Dehornoy, Hryniewicz and RechtmanCDHR24, Reference Colin, Dehornoy and RechtmanCDR23, Reference Contreras and MazzucchelliCM22, Reference Hofer, Wysocki and ZehnderHWZ03, Reference Hofer, Wysocki and ZehnderHWZ98] are ultimately based on holomorphic curve techniques [Reference Hofer, Wysocki and ZehnderHWZ02], and the last three even on embedded contact homology [Reference HutchingsHut14]. In this paper, we do not need any of these techniques and instead employ the curve shortening flow [Reference GageGag90, Reference GraysonGra89]. Our approach allows us to obtain sharper results for geodesic flows. On the one hand, our theorems require only the non-existence or the non-degeneracy of contractible simple closed geodesics without conjugate points, but no conditions on the other closed geodesics. On the other hand, in all the statements except Theorem D, we obtain surfaces of section all of whose components have genus at most one, which may be important for future applications. Incidentally, our arguments require a study of maximal families of pairwise disjoint simple closed geodesics of closed orientable Riemannian surfaces (Theorems 3.4 and 3.5), which may have independent interest.
Finally, we remark that, even though we only considered Riemannian geodesic flows, our results are also valid for geodesic flows of reversible Finsler metrics, by using the generalization of the curve shortening flow developed by Oaks [Reference OaksOak94] and further investigated by Angenent [Reference AngenentAng08] and De Philippis et al [Reference De Philippis, Marini, Mazzucchelli and SuhrDPMMS22].
1.1 Organization of the paper
In §2, we recall the main properties of the curve shortening flow, we provide the details of some applications to the existence of simple closed geodesics that cannot be found in the literature and we recall some features of conjugate points. In §3, we study configurations of simple closed geodesics on closed Riemannian surfaces, whose properties will be an essential ingredient for our main theorems. Finally, in §4, we state and prove Theorems A, C, D and E.
2 Preliminaries
2.1 The curve shortening flow
It is well known that closed geodesics are critical points of the length and energy functionals, and therefore their existence can be investigated by means of critical point theory [Reference KlingenbergKli78]. In this paper, we will be interested in contractible closed geodesics on surfaces; their critical point theory requires the curve shortening flow [Reference GraysonGra89], whose main properties we now recall.
Let
![]() $(M,g)$
be a closed oriented Riemannian surface. For any smooth embedded circle
$(M,g)$
be a closed oriented Riemannian surface. For any smooth embedded circle
![]() $\gamma :S^1\hookrightarrow M$
, we denote by
$\gamma :S^1\hookrightarrow M$
, we denote by
![]() $\nu _\gamma $
its positively oriented normal vector field and by
$\nu _\gamma $
its positively oriented normal vector field and by
![]() $k_\gamma $
the signed geodesic curvature of
$k_\gamma $
the signed geodesic curvature of
![]() $\gamma $
. Here,
$\gamma $
. Here,
![]() $S^1=\mathbb {R}/\mathbb {Z}$
. We denote by
$S^1=\mathbb {R}/\mathbb {Z}$
. We denote by
![]() $\mathrm {Emb}(S^1,M)$
the space of smooth embedded circles in M endowed with the
$\mathrm {Emb}(S^1,M)$
the space of smooth embedded circles in M endowed with the
![]() $C^\infty $
topology. The length functional
$C^\infty $
topology. The length functional
is continuous over this space. Indeed, it is even differentiable, and its critical points are the simple closed geodesics (that is, the closed geodesics in
![]() $\mathrm {Emb}(S^1,M)$
) with arbitrary time reparameterization. The curve shortening flow is a continuous map
$\mathrm {Emb}(S^1,M)$
) with arbitrary time reparameterization. The curve shortening flow is a continuous map
defined on a maximal open neighborhood
![]() $\mathcal {U}\subset [0,\infty )\times \mathrm {Emb}(S^1,M)$
of
$\mathcal {U}\subset [0,\infty )\times \mathrm {Emb}(S^1,M)$
of
![]() $\{0\}\times \mathrm {Emb}(S^1,M)$
by means of the partial differential equation
$\{0\}\times \mathrm {Emb}(S^1,M)$
by means of the partial differential equation
Its main properties are the following.
-
(i)
 $\Psi _0=\mathrm {id}$
, and
$\Psi _0=\mathrm {id}$
, and
 $\Psi _{s_2}\circ \Psi _{s_1}=\Psi _{s_2+s_1}$
for all
$\Psi _{s_2}\circ \Psi _{s_1}=\Psi _{s_2+s_1}$
for all
 $s_1,s_2\geq 0$
.
$s_1,s_2\geq 0$
. -
(ii)
 $\Psi _s(\gamma \circ \theta )=\Psi _s(\gamma )\circ \theta $
for all
$\Psi _s(\gamma \circ \theta )=\Psi _s(\gamma )\circ \theta $
for all
 $(s,\gamma )\in \mathcal {U}$
and
$(s,\gamma )\in \mathcal {U}$
and
 $\theta \in \mathrm {Diff}(S^1)$
.
$\theta \in \mathrm {Diff}(S^1)$
. -
(iii)
 $({d}/{ds}) L(\Psi _s(\gamma ))\leq 0$
for all
$({d}/{ds}) L(\Psi _s(\gamma ))\leq 0$
for all
 $(s,\gamma )\in \mathcal {U}$
, and the equality holds if and only if
$(s,\gamma )\in \mathcal {U}$
, and the equality holds if and only if
 $\gamma $
is a simple closed geodesic (not necessarily parameterized with constant speed).
$\gamma $
is a simple closed geodesic (not necessarily parameterized with constant speed). -
(iv) For each
 $\gamma \in \mathrm {Emb}(S^1,M)$
, if
$\gamma \in \mathrm {Emb}(S^1,M)$
, if
 $s_\gamma \in (0,\infty ]$
denotes the supremum of the times
$s_\gamma \in (0,\infty ]$
denotes the supremum of the times
 $s>0$
for which
$s>0$
for which
 $(s,\gamma )\in \mathcal {U}$
, then
$(s,\gamma )\in \mathcal {U}$
, then
 $s_\gamma $
is finite if and only if
$s_\gamma $
is finite if and only if
 $\Psi _s(\gamma )$
converges to a constant as
$\Psi _s(\gamma )$
converges to a constant as
 $s\to s_\gamma $
.
$s\to s_\gamma $
.
We refer the reader to [Reference De Philippis, Marini, Mazzucchelli and SuhrDPMMS22, Reference GraysonGra89] and to the references therein for the proofs of these facts. For each
![]() $\ell>0$
and
$\ell>0$
and
![]() $\epsilon>0$
, we consider the open subsets
$\epsilon>0$
, we consider the open subsets
 $$ \begin{align*} \mathrm{Emb}(S^1,M)^{<\ell} & := \{ \gamma\in\mathrm{Emb}(S^1,M)\ |\ L(\gamma)<\ell \}, \\ \mathcal{W}(\ell,\epsilon) & := \{ \gamma\in\mathrm{Emb}(S^1,M)\ |\ |L(\gamma)-\ell|<\epsilon^2,\ \|k_\gamma\|_{L^\infty}<\epsilon \}. \end{align*} $$
$$ \begin{align*} \mathrm{Emb}(S^1,M)^{<\ell} & := \{ \gamma\in\mathrm{Emb}(S^1,M)\ |\ L(\gamma)<\ell \}, \\ \mathcal{W}(\ell,\epsilon) & := \{ \gamma\in\mathrm{Emb}(S^1,M)\ |\ |L(\gamma)-\ell|<\epsilon^2,\ \|k_\gamma\|_{L^\infty}<\epsilon \}. \end{align*} $$
The intersection
is precisely the subspace of those embedded circles that are reparameterizations of simple closed geodesics of length
![]() $\ell>0$
. Moreover, we have
$\ell>0$
. Moreover, we have
![]() $\mathcal {K}_\ell =\varnothing $
if and only if
$\mathcal {K}_\ell =\varnothing $
if and only if
![]() $\mathcal {W}(\ell ,\epsilon )=\varnothing $
for
$\mathcal {W}(\ell ,\epsilon )=\varnothing $
for
![]() $\epsilon>0$
sufficiently small.
$\epsilon>0$
sufficiently small.
In order to employ the curve shortening flow in the critical point theory of the length functional, the following property is crucial. Its proof can be extracted from Grayson’s [Reference GraysonGra89], and the details can also be found in [Reference De Philippis, Marini, Mazzucchelli and SuhrDPMMS22, Theorem 1.2(iv)].
-
(v) For each
 $\ell>0$
and
$\ell>0$
and
 $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
 $\delta \in (0,\ell )$
and a continuous function
$\delta \in (0,\ell )$
and a continuous function
 $\tau :\mathrm {Emb}(S^1,M)^{<\ell +\delta }\to [0,\infty )$
such that, for each
$\tau :\mathrm {Emb}(S^1,M)^{<\ell +\delta }\to [0,\infty )$
such that, for each
 $\gamma \in \mathrm {Emb}(S^1,M)^{<\ell +\delta }$
, we have
$\gamma \in \mathrm {Emb}(S^1,M)^{<\ell +\delta }$
, we have
 $\tau (\gamma )<s_\gamma $
and
$\tau (\gamma )<s_\gamma $
and  $$ \begin{align*} \quad\ \ \Psi_s(\gamma)\in\mathrm{Emb}(S^1,M)^{<\ell-\delta}\cup\mathcal{W}(\ell,\epsilon)\quad\text{for all } s\in[\tau(\gamma),s_\gamma). \end{align*} $$
$$ \begin{align*} \quad\ \ \Psi_s(\gamma)\in\mathrm{Emb}(S^1,M)^{<\ell-\delta}\cup\mathcal{W}(\ell,\epsilon)\quad\text{for all } s\in[\tau(\gamma),s_\gamma). \end{align*} $$
A path-connected subset
![]() $U\subseteq M$
is weakly convex when, for any pair of distinct points
$U\subseteq M$
is weakly convex when, for any pair of distinct points
![]() $x,y\in U$
that can be joined by an absolutely continuous curve contained in U of length strictly less than the injectivity radius
$x,y\in U$
that can be joined by an absolutely continuous curve contained in U of length strictly less than the injectivity radius
![]() $\mathrm {inj}(M,g)$
, the shortest geodesic segment joining x and y is entirely contained in U. One of the crucial properties of the curve shortening flow is that it preserves the embeddedness of loops. This was first proved by Gage [Reference GageGag90, §3] as a consequence of a suitable maximum principle. The same arguments actually imply the following analogous property.
$\mathrm {inj}(M,g)$
, the shortest geodesic segment joining x and y is entirely contained in U. One of the crucial properties of the curve shortening flow is that it preserves the embeddedness of loops. This was first proved by Gage [Reference GageGag90, §3] as a consequence of a suitable maximum principle. The same arguments actually imply the following analogous property.
-
(vi) The curve shortening flow preserves any weakly convex open subset
 $U\subseteq M$
: that is, for any smooth embedded circle
$U\subseteq M$
: that is, for any smooth embedded circle
 $\gamma $
in U and for any
$\gamma $
in U and for any
 $s\in (0,s_\gamma )$
, the embedded circle
$s\in (0,s_\gamma )$
, the embedded circle
 $\Psi _s(\gamma )$
is still contained in U.
$\Psi _s(\gamma )$
is still contained in U.
The following is a rather straightforward consequence of the properties of the curve shortening flow.
Lemma 2.1. Let
![]() $U\subseteq M$
be a weakly convex open subset that is not simply connected and let
$U\subseteq M$
be a weakly convex open subset that is not simply connected and let
![]() $\mathcal {C}\subset \mathrm {Emb}(S^1,U)$
be a connected component containing loops that are non-contractible in U. Then, there exists a sequence
$\mathcal {C}\subset \mathrm {Emb}(S^1,U)$
be a connected component containing loops that are non-contractible in U. Then, there exists a sequence
![]() $\gamma _n\in \mathcal {C}$
converging in the
$\gamma _n\in \mathcal {C}$
converging in the
![]() $C^2$
-topology to a simple closed geodesic
$C^2$
-topology to a simple closed geodesic
![]() $\gamma $
contained in
$\gamma $
contained in
![]() $\overline U$
of length
$\overline U$
of length
Remark 2.2. The simple closed geodesic
![]() $\gamma $
may not be a waist (see the definition in §2.2) if it intersects the boundary
$\gamma $
may not be a waist (see the definition in §2.2) if it intersects the boundary
![]() $\partial U$
.
$\partial U$
.
Proof of Lemma 2.1
We claim that
Indeed, assume by contradiction that
![]() $L(\zeta )<2\,\mathrm {inj}(M,g)$
for some
$L(\zeta )<2\,\mathrm {inj}(M,g)$
for some
![]() $\zeta \in \mathcal {C}$
. This implies that
$\zeta \in \mathcal {C}$
. This implies that
![]() $\zeta $
can be written as
$\zeta $
can be written as
for some smooth function
![]() $V:S^1\to T_{\zeta (0)}M$
. We define the smooth homotopy
$V:S^1\to T_{\zeta (0)}M$
. We define the smooth homotopy
which satisfies
![]() $\zeta _0\equiv \zeta (0)$
and
$\zeta _0\equiv \zeta (0)$
and
![]() $\zeta _1=\zeta $
. Since the open subset U is weakly convex, each
$\zeta _1=\zeta $
. Since the open subset U is weakly convex, each
![]() $\zeta _r$
is contained in U. Therefore,
$\zeta _r$
is contained in U. Therefore,
![]() $\zeta $
is contractible in U, which is a contradiction.
$\zeta $
is contractible in U, which is a contradiction.
We claim that
Indeed, assume that
![]() $\mathcal {W}(\ell ,\epsilon )\cap \mathcal {C}=\varnothing $
for some
$\mathcal {W}(\ell ,\epsilon )\cap \mathcal {C}=\varnothing $
for some
![]() $\epsilon>0$
. Consider the constant
$\epsilon>0$
. Consider the constant
![]() $\delta>0$
and the continuous function
$\delta>0$
and the continuous function
![]() $\tau :\mathrm {Emb}(S^1,M)^{<\ell +\delta }\to (0,\infty )$
provided by property (v). For each
$\tau :\mathrm {Emb}(S^1,M)^{<\ell +\delta }\to (0,\infty )$
provided by property (v). For each
![]() $\zeta _0\in \mathcal {C}$
of length
$\zeta _0\in \mathcal {C}$
of length
![]() $L(\zeta _0)<\ell +\delta $
, property (vi) guarantees that
$L(\zeta _0)<\ell +\delta $
, property (vi) guarantees that
![]() $\zeta _s:=\Psi _s(\zeta _0)\in \mathcal {C}$
for all
$\zeta _s:=\Psi _s(\zeta _0)\in \mathcal {C}$
for all
![]() $s>0$
for which it is well defined. Property (v) then implies that
$s>0$
for which it is well defined. Property (v) then implies that
![]() $L(\zeta _{\tau (\zeta )})<\ell -\delta $
, which contradicts the definition of
$L(\zeta _{\tau (\zeta )})<\ell -\delta $
, which contradicts the definition of
![]() $\ell $
.
$\ell $
.
We choose an arbitrary
![]() $\gamma _n\in \mathcal {W}(\ell ,1/n)$
parameterized with constant speed. Up to extracting a subsequence, we have that
$\gamma _n\in \mathcal {W}(\ell ,1/n)$
parameterized with constant speed. Up to extracting a subsequence, we have that
![]() $\gamma _n(0)\to x$
and
$\gamma _n(0)\to x$
and
![]() $\dot \gamma _n(0)\to v$
for some
$\dot \gamma _n(0)\to v$
for some
![]() $(x,v)\in TM$
with
$(x,v)\in TM$
with
![]() $\|v\|=\ell $
. The curve
$\|v\|=\ell $
. The curve
![]() $\gamma :S^1\to M$
,
$\gamma :S^1\to M$
,
![]() $\gamma (t):=\exp _x(tv)$
is a closed geodesic of length
$\gamma (t):=\exp _x(tv)$
is a closed geodesic of length
![]() $\ell $
, and
$\ell $
, and
![]() $\gamma _n\to \gamma $
in the
$\gamma _n\to \gamma $
in the
![]() $C^1$
topology. Since
$C^1$
topology. Since
![]() $\|k_{\gamma _n}-k_\gamma \|_{L^\infty }\leq 1/n$
, actually,
$\|k_{\gamma _n}-k_\gamma \|_{L^\infty }\leq 1/n$
, actually,
![]() $\gamma _n\to \gamma $
in the
$\gamma _n\to \gamma $
in the
![]() $C^2$
topology. Finally, since the closed geodesic
$C^2$
topology. Finally, since the closed geodesic
![]() $\gamma $
is the
$\gamma $
is the
![]() $C^2$
limit of embedded circles on an orientable surface,
$C^2$
limit of embedded circles on an orientable surface,
![]() $\gamma $
is a simple closed geodesic.
$\gamma $
is a simple closed geodesic.
We denote by
![]() $SM=\{v\in TM\ |\ \|v\|_g=1\}$
the unit tangent bundle, by
$SM=\{v\in TM\ |\ \|v\|_g=1\}$
the unit tangent bundle, by
![]() $\pi :SM\to M$
the base projection and by
$\pi :SM\to M$
the base projection and by
![]() $\phi _t:SM\to SM$
the geodesic flow, which is defined by
$\phi _t:SM\to SM$
the geodesic flow, which is defined by
![]() $\phi _t(\dot \gamma (0))\hspace{-1pt}=\hspace{-1pt}\dot \gamma (t)$
, where
$\phi _t(\dot \gamma (0))\hspace{-1pt}=\hspace{-1pt}\dot \gamma (t)$
, where
![]() $\gamma :\mathbb {R}\looparrowright M$
is a geodesic parameterized with unit speed
$\gamma :\mathbb {R}\looparrowright M$
is a geodesic parameterized with unit speed
![]() $\|\dot \gamma \|_g\hspace{-1pt}\equiv\hspace{-1pt} 1$
. In §3, we will need the following property of weakly convex sets.
$\|\dot \gamma \|_g\hspace{-1pt}\equiv\hspace{-1pt} 1$
. In §3, we will need the following property of weakly convex sets.
Lemma 2.3. If
![]() $U\subseteq M$
is a weakly convex subset and
$U\subseteq M$
is a weakly convex subset and
![]() $K\subset SM$
is a subset invariant under the geodesic flow (that is,
$K\subset SM$
is a subset invariant under the geodesic flow (that is,
![]() $\phi _t(K)=K$
for all
$\phi _t(K)=K$
for all
![]() $t\in \mathbb {R})$
, then any path-connected component of
$t\in \mathbb {R})$
, then any path-connected component of
![]() $U\setminus \pi (K)$
is weakly convex.
$U\setminus \pi (K)$
is weakly convex.
Proof. Let
![]() $V\subset U\setminus \pi (K)$
be a path-connected component and consider two arbitrary distinct points
$V\subset U\setminus \pi (K)$
be a path-connected component and consider two arbitrary distinct points
![]() $x_1,x_2\in V$
that can be joined by an absolutely continuous curve
$x_1,x_2\in V$
that can be joined by an absolutely continuous curve
![]() $\zeta $
contained in V of length strictly less than the injectivity radius
$\zeta $
contained in V of length strictly less than the injectivity radius
![]() $\mathrm {inj}(M,g)$
. Since U is weakly convex, the shortest geodesic segment
$\mathrm {inj}(M,g)$
. Since U is weakly convex, the shortest geodesic segment
![]() $\gamma $
joining
$\gamma $
joining
![]() $x_1$
and
$x_1$
and
![]() $x_2$
is contained in U. We assume, by contradiction, that
$x_2$
is contained in U. We assume, by contradiction, that
![]() $\gamma \cap \pi (K)\neq \varnothing $
, and choose a point
$\gamma \cap \pi (K)\neq \varnothing $
, and choose a point
![]() $v\in K$
such that
$v\in K$
such that
![]() $x:=\pi (v)\in \gamma $
. Let
$x:=\pi (v)\in \gamma $
. Let
![]() $B\subset M$
be the Riemannian open ball of radius
$B\subset M$
be the Riemannian open ball of radius
![]() $\mathrm {inj}(M,g)$
centered at x and let
$\mathrm {inj}(M,g)$
centered at x and let
![]() $\eta \subset \pi (K)\cap B$
be the maximal geodesic segment passing through x tangent to v. Notice that
$\eta \subset \pi (K)\cap B$
be the maximal geodesic segment passing through x tangent to v. Notice that
![]() $\eta $
separates B and intersects
$\eta $
separates B and intersects
![]() $\gamma $
only in x. In particular,
$\gamma $
only in x. In particular,
![]() $x_1$
and
$x_1$
and
![]() $x_2$
lie in distinct connected components of
$x_2$
lie in distinct connected components of
![]() $B\setminus \eta $
. This is not possible, since the curve
$B\setminus \eta $
. This is not possible, since the curve
![]() $\zeta $
joining
$\zeta $
joining
![]() $x_1$
and
$x_1$
and
![]() $x_2$
is contained in
$x_2$
is contained in
![]() $B\setminus \pi (K)\subset B\setminus \eta $
; indeed, any absolutely continuous curve joining
$B\setminus \pi (K)\subset B\setminus \eta $
; indeed, any absolutely continuous curve joining
![]() $x_1$
and
$x_1$
and
![]() $x_2$
and not entirely contained in B must have length larger than or equal to
$x_2$
and not entirely contained in B must have length larger than or equal to
![]() $\mathrm {inj}(M,g)$
.
$\mathrm {inj}(M,g)$
.
2.2 Types of closed geodesics
Let
![]() $\gamma $
be a closed geodesic of length
$\gamma $
be a closed geodesic of length
![]() $\ell>0$
in the closed oriented Riemannian surface
$\ell>0$
in the closed oriented Riemannian surface
![]() $(M,g)$
. We parameterize
$(M,g)$
. We parameterize
![]() $\gamma $
with unit speed, so that it is a curve of the form
$\gamma $
with unit speed, so that it is a curve of the form
where
![]() $v\in SM$
and the length
$v\in SM$
and the length
![]() $\ell $
is the minimal period of
$\ell $
is the minimal period of
![]() $\gamma $
. The Floquet multipliers of
$\gamma $
. The Floquet multipliers of
![]() $\gamma $
are the eigenvalues of the linearized Poincaré map
$\gamma $
are the eigenvalues of the linearized Poincaré map
![]() $d\phi _\ell (v)|_V$
, where V is the vector subspace
$d\phi _\ell (v)|_V$
, where V is the vector subspace
Since the linearized Poincaré map preserves a symplectic structure on the plane V, the Floquet multipliers are of the form
![]() $\sigma ,\sigma ^{-1}\in \mathbb {U}\cup \mathbb {R}\setminus \{0\}$
, where
$\sigma ,\sigma ^{-1}\in \mathbb {U}\cup \mathbb {R}\setminus \{0\}$
, where
![]() $\mathbb {U}$
denotes the unit circle in the complex plane. The closed geodesic
$\mathbb {U}$
denotes the unit circle in the complex plane. The closed geodesic
![]() $\gamma $
is called non-degenerate when
$\gamma $
is called non-degenerate when
![]() $\sigma \neq 1$
and hyperbolic when
$\sigma \neq 1$
and hyperbolic when
![]() $\sigma \in \mathbb {R}\setminus \{1,-1\}$
. (A closed geodesic
$\sigma \in \mathbb {R}\setminus \{1,-1\}$
. (A closed geodesic
![]() $\gamma $
of length
$\gamma $
of length
![]() $\ell $
and Floquet multiplier
$\ell $
and Floquet multiplier
![]() $\sigma =e^{i2\pi /k}$
for some integer
$\sigma =e^{i2\pi /k}$
for some integer
![]() $k\geq 2$
is non-degenerate. However, the kth iterate of
$k\geq 2$
is non-degenerate. However, the kth iterate of
![]() $\gamma $
is degenerate. In this paper, we will not need to consider iterates of closed geodesics.)
$\gamma $
is degenerate. In this paper, we will not need to consider iterates of closed geodesics.)
We recall that a simple closed geodesic
![]() $\gamma :S^1\hookrightarrow M$
is called a waist when any absolutely continuous curve
$\gamma :S^1\hookrightarrow M$
is called a waist when any absolutely continuous curve
![]() $\zeta :S^1\to M$
that is sufficiently
$\zeta :S^1\to M$
that is sufficiently
![]() $C^0$
-close to
$C^0$
-close to
![]() $\gamma $
satisfies
$\gamma $
satisfies
![]() $L(\zeta )\geq L(\gamma )$
; here L is the length functional (2.1).
$L(\zeta )\geq L(\gamma )$
; here L is the length functional (2.1).
Remark 2.4. Let
![]() $\gamma :S^1\hookrightarrow M$
be a waist, let
$\gamma :S^1\hookrightarrow M$
be a waist, let
![]() $W\subset M$
be a sufficiently small open neighborhood of
$W\subset M$
be a sufficiently small open neighborhood of
![]() $\gamma $
and let
$\gamma $
and let
![]() $\mathcal {W}$
be the space of absolutely continuous curves
$\mathcal {W}$
be the space of absolutely continuous curves
![]() $\zeta :S^1\to W$
homotopic to
$\zeta :S^1\to W$
homotopic to
![]() $\gamma $
within W. One can easily prove that any
$\gamma $
within W. One can easily prove that any
![]() $\zeta \in \mathcal {W}$
has length
$\zeta \in \mathcal {W}$
has length
![]() $L(\zeta )\geq L(\gamma )$
. Moreover, the equality
$L(\zeta )\geq L(\gamma )$
. Moreover, the equality
![]() $L(\zeta )= L(\gamma )$
holds if and only if
$L(\zeta )= L(\gamma )$
holds if and only if
![]() $\zeta $
becomes itself a waist after being reparameterized with constant speed
$\zeta $
becomes itself a waist after being reparameterized with constant speed
![]() $\|\dot \zeta \|_g\equiv L(\zeta )$
. If
$\|\dot \zeta \|_g\equiv L(\zeta )$
. If
![]() $\gamma $
is a non-degenerate waist, then any
$\gamma $
is a non-degenerate waist, then any
![]() $\zeta \in \mathcal {W}$
satisfying the equality
$\zeta \in \mathcal {W}$
satisfying the equality
![]() $L(\zeta )=L(\gamma )$
must be geometrically equivalent to
$L(\zeta )=L(\gamma )$
must be geometrically equivalent to
![]() $\gamma $
: that is,
$\gamma $
: that is,
![]() $\zeta \circ \theta =\gamma $
for some homeomorphism
$\zeta \circ \theta =\gamma $
for some homeomorphism
![]() $\theta :S^1\to S^1$
.
$\theta :S^1\to S^1$
.
Later, we employ waists to infer the existence of other simple closed geodesics, according to the following lemma. For closed geodesics that are possibly self-intersecting, the analogous lemma is well known (see, e.g., [Reference BangertBan93]).
Lemma 2.5. Let
![]() $(M,g)$
be an oriented Riemannian surface.
$(M,g)$
be an oriented Riemannian surface.
-
(i) If
 $A\subset M$
is a compact annulus bounded by two waists, then
$A\subset M$
is a compact annulus bounded by two waists, then
 $\operatorname {\mathrm {int}}(A)$
contains a non-contractible simple closed geodesic.
$\operatorname {\mathrm {int}}(A)$
contains a non-contractible simple closed geodesic. -
(ii) If D is a compact disk bounded by a waist, then
 $\operatorname {\mathrm {int}}(D)$
contains a simple closed geodesic.
$\operatorname {\mathrm {int}}(D)$
contains a simple closed geodesic.
Proof. Let
![]() $A\subset M$
be a compact annulus bounded by the waists
$A\subset M$
be a compact annulus bounded by the waists
![]() $\gamma _0,\gamma _1$
, with
$\gamma _0,\gamma _1$
, with
![]() $L(\gamma _1)\leq L(\gamma _0)$
. Let
$L(\gamma _1)\leq L(\gamma _0)$
. Let
![]() $W\subset A\setminus \gamma _1$
be a sufficiently small open neighborhood of
$W\subset A\setminus \gamma _1$
be a sufficiently small open neighborhood of
![]() $\gamma _0$
. If
$\gamma _0$
. If
![]() $W\setminus \gamma _0$
contains a simple closed geodesic, such a closed geodesic must be
$W\setminus \gamma _0$
contains a simple closed geodesic, such a closed geodesic must be
![]() $C^0$
-close to
$C^0$
-close to
![]() $\gamma _0$
and in, particular, be non-contractible in A, and the proof is complete. Now, assume that
$\gamma _0$
and in, particular, be non-contractible in A, and the proof is complete. Now, assume that
![]() $W\setminus \gamma _0$
does not contain any simple closed geodesic. In particular, every absolutely continuous curve
$W\setminus \gamma _0$
does not contain any simple closed geodesic. In particular, every absolutely continuous curve
![]() $\gamma :S^1\to W$
homotopic to
$\gamma :S^1\to W$
homotopic to
![]() $\gamma _0$
within W and not geometrically equivalent to
$\gamma _0$
within W and not geometrically equivalent to
![]() $\gamma _0$
satisfies the strict inequality
$\gamma _0$
satisfies the strict inequality
![]() $L(\gamma )> L(\gamma _0)$
(see Remark 2.4). Up to shrinking W, there exists
$L(\gamma )> L(\gamma _0)$
(see Remark 2.4). Up to shrinking W, there exists
![]() $\rho>0$
such that any smooth curve
$\rho>0$
such that any smooth curve
![]() $\gamma :S^1\hookrightarrow \overline W$
homotopic to
$\gamma :S^1\hookrightarrow \overline W$
homotopic to
![]() $\gamma _0$
within
$\gamma _0$
within
![]() $\overline W$
and that intersects
$\overline W$
and that intersects
![]() $\partial W\setminus \gamma _0$
has length
$\partial W\setminus \gamma _0$
has length
![]() $L(\gamma )\geq L(\gamma _0)+\rho $
. We now detect a simple closed geodesic in
$L(\gamma )\geq L(\gamma _0)+\rho $
. We now detect a simple closed geodesic in
![]() $\operatorname {\mathrm {int}}(A)$
by means of a minmax procedure, as follows. Let
$\operatorname {\mathrm {int}}(A)$
by means of a minmax procedure, as follows. Let
where the infimum ranges over the family
![]() $\mathcal {F}$
of continuous homotopies of smooth embedded loops
$\mathcal {F}$
of continuous homotopies of smooth embedded loops
![]() $\zeta _r:S^1\hookrightarrow A$
,
$\zeta _r:S^1\hookrightarrow A$
,
![]() $r\in [0,1]$
such that
$r\in [0,1]$
such that
![]() $\zeta _0=\gamma _0$
,
$\zeta _0=\gamma _0$
,
![]() $\zeta _1=\gamma _1$
, and
$\zeta _1=\gamma _1$
, and
![]() $\zeta _r\subset \operatorname {\mathrm {int}}(A)$
for all
$\zeta _r\subset \operatorname {\mathrm {int}}(A)$
for all
![]() $r\in (0,1)$
. Notice that, for any such homotopy
$r\in (0,1)$
. Notice that, for any such homotopy
![]() $(\zeta _r)_{r\in [0,1]}$
, there exists a minimal
$(\zeta _r)_{r\in [0,1]}$
, there exists a minimal
![]() $r_0\in (0,1]$
such that the curve
$r_0\in (0,1]$
such that the curve
![]() $\zeta _r$
intersects
$\zeta _r$
intersects
![]() $\partial W\setminus \gamma _0$
; therefore,
$\partial W\setminus \gamma _0$
; therefore,
This readily implies that
We claim that
![]() $\ell $
is the length of a non-contractible simple closed geodesic in A, which must actually be contained in
$\ell $
is the length of a non-contractible simple closed geodesic in A, which must actually be contained in
![]() $\operatorname {\mathrm {int}}(A)$
since
$\operatorname {\mathrm {int}}(A)$
since
![]() $L(\gamma _1)\leq L(\gamma _0)<\ell -\rho $
. Let us assume that this is not the case. In particular, for
$L(\gamma _1)\leq L(\gamma _0)<\ell -\rho $
. Let us assume that this is not the case. In particular, for
![]() $\epsilon>0$
small enough, no embedded loop
$\epsilon>0$
small enough, no embedded loop
![]() $\gamma \in \mathcal {W}(\ell ,\epsilon )$
is entirely contained in A and non-contractible therein. We apply property (v) of the curve shortening flow, which provides
$\gamma \in \mathcal {W}(\ell ,\epsilon )$
is entirely contained in A and non-contractible therein. We apply property (v) of the curve shortening flow, which provides
![]() $\delta>0$
and a suitable continuous function
$\delta>0$
and a suitable continuous function
![]() $\tau :\mathrm {Emb}(S^1,M)^{<\ell +\delta }\to (0,\infty )$
. Let
$\tau :\mathrm {Emb}(S^1,M)^{<\ell +\delta }\to (0,\infty )$
. Let
![]() $(\zeta _r)_{r\in [0,1]}$
be a homotopy in
$(\zeta _r)_{r\in [0,1]}$
be a homotopy in
![]() $\mathcal {F}$
that is optimal up to
$\mathcal {F}$
that is optimal up to
![]() $\delta $
, which means that
$\delta $
, which means that
We push the homotopy by means of the curve shortening flow, defining
Property (v) implies that
![]() $\eta _r\in \mathrm {Emb}(S^1,M)^{<\ell -\delta }\cup \mathcal {W}(\ell ,\epsilon )$
for each
$\eta _r\in \mathrm {Emb}(S^1,M)^{<\ell -\delta }\cup \mathcal {W}(\ell ,\epsilon )$
for each
![]() $r\in [0,1]$
. Since the compact annulus A is bounded by simple closed geodesics,
$r\in [0,1]$
. Since the compact annulus A is bounded by simple closed geodesics,
![]() $\operatorname {\mathrm {int}}(A)$
is weakly convex. Property (vi) implies that
$\operatorname {\mathrm {int}}(A)$
is weakly convex. Property (vi) implies that
![]() $\eta _r\subset \operatorname {\mathrm {int}}(A)$
for each
$\eta _r\subset \operatorname {\mathrm {int}}(A)$
for each
![]() $r\in (0,1)$
. Since
$r\in (0,1)$
. Since
![]() $\zeta _0=\gamma _0$
and
$\zeta _0=\gamma _0$
and
![]() $\zeta _1=\gamma _1$
are simple closed geodesics, we have
$\zeta _1=\gamma _1$
are simple closed geodesics, we have
![]() $\eta _0=\gamma _0$
and
$\eta _0=\gamma _0$
and
![]() $\eta _1=\gamma _1$
. Therefore, the homotopy
$\eta _1=\gamma _1$
. Therefore, the homotopy
![]() $(\eta _r)_{r\in [0,1]}$
belongs to
$(\eta _r)_{r\in [0,1]}$
belongs to
![]() $\mathcal {F}$
. Since no curve
$\mathcal {F}$
. Since no curve
![]() $\gamma \in \mathcal {W}(\ell ,\epsilon )$
is entirely contained in A and non-contractible therein, we conclude that
$\gamma \in \mathcal {W}(\ell ,\epsilon )$
is entirely contained in A and non-contractible therein, we conclude that
![]() $\eta _r\in \mathrm {Emb}(S^1,M)^{<\ell -\delta }$
for each
$\eta _r\in \mathrm {Emb}(S^1,M)^{<\ell -\delta }$
for each
![]() $r\in [0,1]$
, which contradicts the definition of the minmax value
$r\in [0,1]$
, which contradicts the definition of the minmax value
![]() $\ell $
.
$\ell $
.
The case of a compact disk
![]() $D\subset M$
bounded by a waist
$D\subset M$
bounded by a waist
![]() $\gamma $
is analogous, except that, in the definition of the minmax (2.2), the infimum ranges over the family of continuous homotopies of smooth embedded loops
$\gamma $
is analogous, except that, in the definition of the minmax (2.2), the infimum ranges over the family of continuous homotopies of smooth embedded loops
![]() $\zeta _r:S^1\hookrightarrow D$
,
$\zeta _r:S^1\hookrightarrow D$
,
![]() $r\in [0,1]$
, such that
$r\in [0,1]$
, such that
![]() $\zeta _0=\gamma $
,
$\zeta _0=\gamma $
,
![]() $\zeta _r\subset \operatorname {\mathrm {int}}(D)$
for all
$\zeta _r\subset \operatorname {\mathrm {int}}(D)$
for all
![]() $r\in (0,1]$
and
$r\in (0,1]$
and
![]() $L(\zeta _1)<L(\gamma )$
.
$L(\zeta _1)<L(\gamma )$
.
2.3 Conjugate points
Let us recall the classical notion of conjugate points. If
![]() $\gamma :\mathbb {R}\to M$
is an (open or closed) geodesic parameterized with unit speed, the points
$\gamma :\mathbb {R}\to M$
is an (open or closed) geodesic parameterized with unit speed, the points
![]() $\gamma (t_1),\gamma (t_2)$
are conjugate along
$\gamma (t_1),\gamma (t_2)$
are conjugate along
![]() $\gamma |_{[t_1,t_2]}$
when
$\gamma |_{[t_1,t_2]}$
when
On orientable Riemannian surfaces, simple closed geodesics with conjugate points are not waists, and they actually satisfy the following lemma due to Bangert [Reference BangertBan93, Lemma 2].
Lemma 2.6. Let
![]() $(M,g)$
be an orientable Riemannian surface and let
$(M,g)$
be an orientable Riemannian surface and let
![]() $\gamma :S^1\hookrightarrow M$
be a simple closed geodesic with conjugate points. Then, for any open neighborhood
$\gamma :S^1\hookrightarrow M$
be a simple closed geodesic with conjugate points. Then, for any open neighborhood
![]() $U\subset M$
of
$U\subset M$
of
![]() $\gamma $
, any connected component
$\gamma $
, any connected component
![]() $V\subset U\setminus \gamma $
contains a smooth embedded circle
$V\subset U\setminus \gamma $
contains a smooth embedded circle
![]() $\zeta :S^1\hookrightarrow V$
homotopic to
$\zeta :S^1\hookrightarrow V$
homotopic to
![]() $\gamma $
within U such that
$\gamma $
within U such that
![]() $L(\zeta )<L(\gamma )$
.
$L(\zeta )<L(\gamma )$
.
On an orientable Riemannian surface, a non-degenerate simple closed geodesic is a waist if and only if it does not have conjugate points (see, e.g., [Reference De Philippis, Marini, Mazzucchelli and SuhrDPMMS22, Lemma 4.1(iii) and Proposition 4.2(iii, vii)]). Moreover, a non-degenerate waist
![]() $\gamma $
is hyperbolic (see, e.g., [Reference KlingenbergKli95, Theorem 3.4.2]), and the corresponding orbit
$\gamma $
is hyperbolic (see, e.g., [Reference KlingenbergKli95, Theorem 3.4.2]), and the corresponding orbit
![]() $\dot \gamma $
of the geodesic flow
$\dot \gamma $
of the geodesic flow
![]() $\phi _t$
has a stable manifold
$\phi _t$
has a stable manifold
which is an injectively immersed surface in
![]() $SM$
. Here,
$SM$
. Here,
![]() $\omega (z)$
denotes the
$\omega (z)$
denotes the
![]() $\omega $
-limit of z: that is,
$\omega $
-limit of z: that is,
Lemma 2.7. Let
![]() $(M,g)$
be an orientable closed Riemannian surface and let
$(M,g)$
be an orientable closed Riemannian surface and let
![]() $\gamma $
be a non-degenerate waist. For any sufficiently small neighborhood
$\gamma $
be a non-degenerate waist. For any sufficiently small neighborhood
![]() $V\subset SM$
of
$V\subset SM$
of
![]() $\dot \gamma $
, if
$\dot \gamma $
, if
![]() $W\subset V\cap W^{s}(\dot \gamma )$
is the path-connected component containing
$W\subset V\cap W^{s}(\dot \gamma )$
is the path-connected component containing
![]() $\dot \gamma $
, then the base projection
$\dot \gamma $
, then the base projection
![]() $\pi |_W:W\to M$
is a diffeomorphism onto a neighborhood of
$\pi |_W:W\to M$
is a diffeomorphism onto a neighborhood of
![]() $\gamma $
. In particular, for each
$\gamma $
. In particular, for each
![]() $z\in W^{s}(\dot \gamma )\setminus \dot \gamma $
with associated geodesic
$z\in W^{s}(\dot \gamma )\setminus \dot \gamma $
with associated geodesic
![]() $\zeta (t):=\pi \circ \phi _t(z)$
, there exists
$\zeta (t):=\pi \circ \phi _t(z)$
, there exists
![]() $t\in \mathbb {R}$
such that
$t\in \mathbb {R}$
such that
![]() $\zeta |_{[t,\infty )}$
does not intersect
$\zeta |_{[t,\infty )}$
does not intersect
![]() $\gamma $
.
$\gamma $
.
Remark 2.8. Since
![]() $W^{u}(\dot \gamma )=-W^{s}(-\dot \gamma )$
, the analogous statement holds for the unstable manifold.
$W^{u}(\dot \gamma )=-W^{s}(-\dot \gamma )$
, the analogous statement holds for the unstable manifold.
Proof of Lemma 2.7
Since
![]() $\gamma $
is hyperbolic, the closed orbit
$\gamma $
is hyperbolic, the closed orbit
![]() $\dot \gamma $
has a Floquet multiplier
$\dot \gamma $
has a Floquet multiplier
![]() $\sigma \in (-1,1)$
. We parameterize
$\sigma \in (-1,1)$
. We parameterize
![]() $\gamma $
with unit speed, and denote by
$\gamma $
with unit speed, and denote by
![]() $\ell>0$
its length, so that
$\ell>0$
its length, so that
![]() $\dot \gamma (t)=\dot \gamma (t+\ell )$
. We consider the stable line bundle
$\dot \gamma (t)=\dot \gamma (t+\ell )$
. We consider the stable line bundle
![]() $E^{s}$
over
$E^{s}$
over
![]() $\dot \gamma $
, which is given by
$\dot \gamma $
, which is given by
The stable bundle is invariant under the linearized geodesic flow: that is,
If we had
![]() $E^{s}(\dot \gamma (t))=\ker (d\pi (\dot \gamma (t)))$
for some
$E^{s}(\dot \gamma (t))=\ker (d\pi (\dot \gamma (t)))$
for some
![]() $t\in \mathbb {R}/\ell \mathbb {Z}$
, the endpoints of the geodesic segment
$t\in \mathbb {R}/\ell \mathbb {Z}$
, the endpoints of the geodesic segment
![]() $\gamma |_{[t,t+\ell ]}$
would be conjugate. Therefore, since
$\gamma |_{[t,t+\ell ]}$
would be conjugate. Therefore, since
![]() $\gamma $
has no conjugate points, we infer that
$\gamma $
has no conjugate points, we infer that
This, together with the fact that
readily implies that the local stable manifold of
![]() $\dot \gamma $
is a graph over the base manifold M. Namely, for any sufficiently small neighborhood
$\dot \gamma $
is a graph over the base manifold M. Namely, for any sufficiently small neighborhood
![]() $V\subset SM$
of the closed orbit
$V\subset SM$
of the closed orbit
![]() $\dot \gamma $
, if
$\dot \gamma $
, if
![]() $W\subset V\cap W^{s}(\dot \gamma )$
is the path-connected component containing
$W\subset V\cap W^{s}(\dot \gamma )$
is the path-connected component containing
![]() $\dot \gamma $
, then the base projection
$\dot \gamma $
, then the base projection
![]() $\pi |_W:W\to M$
is a diffeomorphism onto a neighborhood of
$\pi |_W:W\to M$
is a diffeomorphism onto a neighborhood of
![]() $\gamma $
. For each
$\gamma $
. For each
![]() $z\in W^{s}(\dot \gamma )\setminus \dot \gamma $
, for all
$z\in W^{s}(\dot \gamma )\setminus \dot \gamma $
, for all
![]() $t>0$
large enough, we have
$t>0$
large enough, we have
![]() $\phi _t(z)\in W\setminus \dot \gamma $
, and therefore
$\phi _t(z)\in W\setminus \dot \gamma $
, and therefore
![]() $\pi \circ \phi _t(z)\in \pi (W)\setminus \gamma $
.
$\pi \circ \phi _t(z)\in \pi (W)\setminus \gamma $
.
We recall the following elementary property of geodesics with conjugate points on surfaces (see, e.g., [Reference De Philippis, Marini, Mazzucchelli and SuhrDPMMS22, Lemma 5.9] for a proof).
Lemma 2.9. Let
![]() $(M,g)$
be a Riemannian surface and let
$(M,g)$
be a Riemannian surface and let
![]() $\gamma :[-T,T]\to M$
be a geodesic arc such that, for some
$\gamma :[-T,T]\to M$
be a geodesic arc such that, for some
![]() $[t_1,t_2]\subset (-T,T)$
, the points
$[t_1,t_2]\subset (-T,T)$
, the points
![]() $\gamma (t_1)$
and
$\gamma (t_1)$
and
![]() $\gamma (t_2)$
are conjugate along
$\gamma (t_2)$
are conjugate along
![]() $\gamma |_{[t_1,t_2]}$
. There exists an open neighborhood
$\gamma |_{[t_1,t_2]}$
. There exists an open neighborhood
![]() $V\subset SM$
of
$V\subset SM$
of
![]() $\dot \gamma (0)$
such that, for each
$\dot \gamma (0)$
such that, for each
![]() $z\in V$
, the geodesic
$z\in V$
, the geodesic
![]() $\zeta (t):=\pi \circ \phi _t(z)$
intersects
$\zeta (t):=\pi \circ \phi _t(z)$
intersects
![]() $\gamma $
for some
$\gamma $
for some
![]() $t\in [-T,T]$
.
$t\in [-T,T]$
.
This lemma has the following immediate consequence for simple closed geodesics with conjugate points.
Corollary 2.10. Let
![]() $(M,g)$
be an orientable Riemannian surface and let
$(M,g)$
be an orientable Riemannian surface and let
![]() $\gamma $
be a simple closed geodesic with conjugate points.
$\gamma $
be a simple closed geodesic with conjugate points.
-
(i) There exists
 $T>0$
and an open neighborhood
$T>0$
and an open neighborhood
 $V\subset SM$
of the lift
$V\subset SM$
of the lift
 $\dot \gamma $
such that, for each
$\dot \gamma $
such that, for each
 $z\in V$
, the geodesic
$z\in V$
, the geodesic
 $\zeta (t):=\pi \circ \phi _t(z)$
intersects
$\zeta (t):=\pi \circ \phi _t(z)$
intersects
 $\gamma $
for some positive time
$\gamma $
for some positive time
 $t\in (0,T]$
and for some negative time
$t\in (0,T]$
and for some negative time
 $t\in [-T,0)$
.
$t\in [-T,0)$
. -
(ii) There exists
 $T>0$
and an open neighborhood
$T>0$
and an open neighborhood
 $U\subset M$
of
$U\subset M$
of
 $\gamma $
such that, for each
$\gamma $
such that, for each
 $z\in SU$
, the geodesic
$z\in SU$
, the geodesic
 $\zeta (t):=\pi \circ \phi _t(z)$
intersects
$\zeta (t):=\pi \circ \phi _t(z)$
intersects
 $\gamma $
for some
$\gamma $
for some
 $t\in [-T,T]$
.
$t\in [-T,T]$
.
3 Contractible simple closed geodesics on surfaces
Let
![]() $(M,g)$
be a closed Riemannian surface with geodesic flow
$(M,g)$
be a closed Riemannian surface with geodesic flow
![]() $\phi _t:SM\to SM$
. If
$\phi _t:SM\to SM$
. If
![]() $K\subset SM$
is a hyperbolic compact invariant subset for the geodesic flow, then its stable manifold is defined by
$K\subset SM$
is a hyperbolic compact invariant subset for the geodesic flow, then its stable manifold is defined by
where
![]() $\omega (z)$
denotes the
$\omega (z)$
denotes the
![]() $\omega $
-limit of z. The unstable manifold
$\omega $
-limit of z. The unstable manifold
![]() $W^{u}(K)$
is defined analogously by employing the
$W^{u}(K)$
is defined analogously by employing the
![]() $\alpha $
-limit instead of the
$\alpha $
-limit instead of the
![]() $\omega $
-limit, or, equivalently,
$\omega $
-limit, or, equivalently,
In this paper, we consider invariant compact sets K of the form
 $$ \begin{align*} K=\bigcup_{i=1}^n (\dot\gamma_i\cup-\dot\gamma_i), \end{align*} $$
$$ \begin{align*} K=\bigcup_{i=1}^n (\dot\gamma_i\cup-\dot\gamma_i), \end{align*} $$
where
![]() $\gamma _1,\ldots ,\gamma _n$
are hyperbolic closed geodesics of
$\gamma _1,\ldots ,\gamma _n$
are hyperbolic closed geodesics of
![]() $(M,g)$
. In this case, the stable and unstable manifolds of K decompose as the disjoint unions of the stable and unstable manifolds of the closed orbits
$(M,g)$
. In this case, the stable and unstable manifolds of K decompose as the disjoint unions of the stable and unstable manifolds of the closed orbits
![]() $\pm \dot \gamma _i$
: that is,
$\pm \dot \gamma _i$
: that is,
 $$ \begin{align*} W^{s}(K)=\bigcup_{i=1}^n (W^{s}(\dot\gamma_i)\cup W^{s}(-\dot\gamma_i)), \quad W^{u}(K)=\bigcup_{i=1}^n (W^{u}(\dot\gamma_i)\cup W^{u}(-\dot\gamma_i)). \end{align*} $$
$$ \begin{align*} W^{s}(K)=\bigcup_{i=1}^n (W^{s}(\dot\gamma_i)\cup W^{s}(-\dot\gamma_i)), \quad W^{u}(K)=\bigcup_{i=1}^n (W^{u}(\dot\gamma_i)\cup W^{u}(-\dot\gamma_i)). \end{align*} $$
Let
![]() $V\subset SM$
be an open subset. We define the forward trapped set
$V\subset SM$
be an open subset. We define the forward trapped set
![]() $\mathrm {trap}_+(V)$
and the backward trapped set
$\mathrm {trap}_+(V)$
and the backward trapped set
![]() $\mathrm {trap}_-(V)$
by
$\mathrm {trap}_-(V)$
by
Notice that
In §2.1, we introduced the notion of weak convexity for an open subset of a closed orientable Riemannian surface
![]() $(M,g)$
. In this section, we consider open disks
$(M,g)$
. In this section, we consider open disks
![]() $B\subset M$
satisfying the following, stronger, convexity assumption.
$B\subset M$
satisfying the following, stronger, convexity assumption.
Assumption 3.1. The open disk
![]() $B\subset M$
is weakly convex, and there exist
$B\subset M$
is weakly convex, and there exist
![]() $\delta>0$
,
$\delta>0$
,
![]() $T>0$
and an open neighborhood
$T>0$
and an open neighborhood
![]() $N\subset \overline B$
of
$N\subset \overline B$
of
![]() $\partial B$
such that every smooth curve
$\partial B$
such that every smooth curve
![]() $\gamma :[-T,T]\to M$
parameterized with unit speed
$\gamma :[-T,T]\to M$
parameterized with unit speed
![]() $\|\dot \gamma \|_g\equiv 1$
, with curvature bound
$\|\dot \gamma \|_g\equiv 1$
, with curvature bound
![]() $\|k_\gamma \|_{L^\infty }\leq \delta $
and such that
$\|k_\gamma \|_{L^\infty }\leq \delta $
and such that
![]() $\gamma (0)\in N$
, is not entirely contained in B.
$\gamma (0)\in N$
, is not entirely contained in B.
Example 3.2. Assumption 3.1 is satisfied when
![]() $B\subset M$
is a convex geodesic polygon, which means an open disk whose boundary
$B\subset M$
is a convex geodesic polygon, which means an open disk whose boundary
![]() $\partial B$
, seen as a piecewise smooth immersed submanifold of M, is a piecewise geodesic circle with at least one corner and all the inner angles at the corners of
$\partial B$
, seen as a piecewise smooth immersed submanifold of M, is a piecewise geodesic circle with at least one corner and all the inner angles at the corners of
![]() $\partial B$
are less than
$\partial B$
are less than
![]() $\pi $
. This definition allows B to be a fundamental domain of M defined as the complement of a suitable collection of finitely many simple closed geodesics (Figure 1).
$\pi $
. This definition allows B to be a fundamental domain of M defined as the complement of a suitable collection of finitely many simple closed geodesics (Figure 1).

Figure 1 An open convex geodesic polygon B that is the complement of two simple closed geodesics of a 2-torus of revolution.
Example 3.3. Corollary 2.10(ii) readily implies that Assumption 3.1 is satisfied when
![]() ${B\subset M}$
is an open disk whose boundary is a simple closed geodesic with conjugate points.
${B\subset M}$
is an open disk whose boundary is a simple closed geodesic with conjugate points.
The following two theorems are the main results of this section.
Theorem 3.4. Let
![]() $(M,g)$
be a closed orientable Riemannian surface and let
$(M,g)$
be a closed orientable Riemannian surface and let
![]() $B\subset M$
be an open disk satisfying Assumption 3.1. If B does not contain any simple closed geodesic without conjugate points, then
$B\subset M$
be an open disk satisfying Assumption 3.1. If B does not contain any simple closed geodesic without conjugate points, then
![]() $\mathrm {trap}_+(SB)=\mathrm {trap}_-(SB)=\varnothing $
.
$\mathrm {trap}_+(SB)=\mathrm {trap}_-(SB)=\varnothing $
.
Proof. Equation (3.1) implies that
![]() $\mathrm {trap}_+(SB)=-\mathrm {trap}_-(SB)$
. Let us assume that
$\mathrm {trap}_+(SB)=-\mathrm {trap}_-(SB)$
. Let us assume that
![]() $\mathrm {trap}_+(SB)\neq \varnothing $
and consider an arbitrary point
$\mathrm {trap}_+(SB)\neq \varnothing $
and consider an arbitrary point
![]() $z\in \mathrm {trap}_+(SB)$
. Assumption 3.1 implies that
$z\in \mathrm {trap}_+(SB)$
. Assumption 3.1 implies that
By Lemma 2.3, the connected component
![]() $U\subset B\setminus \pi (\omega (z))$
containing
$U\subset B\setminus \pi (\omega (z))$
containing
![]() $N\setminus \partial B$
is weakly convex. Let
$N\setminus \partial B$
is weakly convex. Let
![]() $\mathcal {C}\subset \mathrm {Emb}(S^1,U)$
be a connected component containing loops that are non-contractible in U. By Lemma 2.1, there exists a sequence
$\mathcal {C}\subset \mathrm {Emb}(S^1,U)$
be a connected component containing loops that are non-contractible in U. By Lemma 2.1, there exists a sequence
![]() $\gamma _n\in \mathcal {C}$
that converges in the
$\gamma _n\in \mathcal {C}$
that converges in the
![]() $C^2$
topology to a simple closed geodesic
$C^2$
topology to a simple closed geodesic
![]() $\gamma \subset \overline U$
of length
$\gamma \subset \overline U$
of length
Notice that
![]() $\gamma _n\subset U\setminus N$
for all n large enough, as, otherwise,
$\gamma _n\subset U\setminus N$
for all n large enough, as, otherwise,
![]() $\gamma _n$
would intersect
$\gamma _n$
would intersect
![]() $\partial B$
according to Assumption 3.1. Therefore,
$\partial B$
according to Assumption 3.1. Therefore,
![]() $\gamma $
is contained in B. This, together with Lemma 2.6 and equation (3.2), implies that
$\gamma $
is contained in B. This, together with Lemma 2.6 and equation (3.2), implies that
![]() $\gamma $
has no conjugate points.
$\gamma $
has no conjugate points.
Theorem 3.5. Let
![]() $(M,g)$
be a closed orientable Riemannian surface and let
$(M,g)$
be a closed orientable Riemannian surface and let
![]() $B\subset M$
be an open disk satisfying Assumption 3.1 that contains at least one closed geodesic but no degenerate simple closed geodesics without conjugate points. Then there exists a finite even number of pairwise disjoint simple closed geodesics
$B\subset M$
be an open disk satisfying Assumption 3.1 that contains at least one closed geodesic but no degenerate simple closed geodesics without conjugate points. Then there exists a finite even number of pairwise disjoint simple closed geodesics
![]() $\gamma _1,\ldots ,\gamma _{2k}\subset B$
satisfying the following properties.
$\gamma _1,\ldots ,\gamma _{2k}\subset B$
satisfying the following properties.
-
(i)
 $\gamma _{i+1}\subset B_{\gamma _i}$
, where
$\gamma _{i+1}\subset B_{\gamma _i}$
, where
 $B_{\gamma _i}\subset B$
are the open disks with boundary
$B_{\gamma _i}\subset B$
are the open disks with boundary
 $\partial B_{\gamma _i}=\gamma _i$
.
$\partial B_{\gamma _i}=\gamma _i$
. -
(ii) For each i odd,
 $\gamma _i$
is a waist.
$\gamma _i$
is a waist. -
(iii) For each i even,
 $\gamma _i$
has conjugate points.
$\gamma _i$
has conjugate points. -
(iv) Let
 $U:=B\setminus (\gamma _1\cup \cdots \cup \gamma _{2k})$
. The trapped sets of
$U:=B\setminus (\gamma _1\cup \cdots \cup \gamma _{2k})$
. The trapped sets of
 $SU$
are given by
$SU$
are given by  $$ \begin{align*} \quad\quad \mathrm{trap}_+(SU) = W^{s}(K)\setminus K, \quad \mathrm{trap}_-(SU) = W^{u}(K)\setminus K, \end{align*} $$
$$ \begin{align*} \quad\quad \mathrm{trap}_+(SU) = W^{s}(K)\setminus K, \quad \mathrm{trap}_-(SU) = W^{u}(K)\setminus K, \end{align*} $$
where
 $$ \begin{align*} K:=\bigcup_{i\ \mathrm{odd}} (\dot\gamma_i\cup-\dot\gamma_i). \end{align*} $$
$$ \begin{align*} K:=\bigcup_{i\ \mathrm{odd}} (\dot\gamma_i\cup-\dot\gamma_i). \end{align*} $$
-
(v) No complete geodesic (that is, a geodesic parameterized with constant speed and defined for all times) is entirely contained in U.
We prove Theorem 3.5 after some preliminaries.
Lemma 3.6. Let
![]() $(M,g)$
be a closed oriented Riemannian surface. There exists a constant
$(M,g)$
be a closed oriented Riemannian surface. There exists a constant
![]() $a_0>0$
such that, for each embedded compact annulus
$a_0>0$
such that, for each embedded compact annulus
![]() $A\subset M$
with
$A\subset M$
with
![]() $\mathrm {area}(A,g)\leq a_0$
and whose boundary
$\mathrm {area}(A,g)\leq a_0$
and whose boundary
![]() $\partial A$
is the union of two simple closed geodesics
$\partial A$
is the union of two simple closed geodesics
![]() $\gamma _1,\gamma _2$
,
$\gamma _1,\gamma _2$
,
Proof. We denote by J the complex structure of the oriented Riemannian surface
![]() $(M,g)$
: that is, for all tangent vectors
$(M,g)$
: that is, for all tangent vectors
![]() $v\in S_xM$
, we have that
$v\in S_xM$
, we have that
![]() $v,Jv$
is an oriented orthonormal basis of
$v,Jv$
is an oriented orthonormal basis of
![]() $T_xM$
. For each
$T_xM$
. For each
![]() $r\in (0,\mathrm {inj}(M,g)/2)$
,
$r\in (0,\mathrm {inj}(M,g)/2)$
,
![]() $x\in M$
and
$x\in M$
and
![]() $v\in S_xM$
, we denote by
$v\in S_xM$
, we denote by
![]() $T(v,r)$
the unique geodesic triangle with vertices
$T(v,r)$
the unique geodesic triangle with vertices
![]() $x,\exp _x(rJv),\exp _x(-( r/2) v)$
(see Figure 2). We consider the continuous function
$x,\exp _x(rJv),\exp _x(-( r/2) v)$
(see Figure 2). We consider the continuous function
We fix
![]() $r\in (0,\mathrm {inj}(M,g)/4)$
to be small enough so that, for each
$r\in (0,\mathrm {inj}(M,g)/4)$
to be small enough so that, for each
![]() $x\in M$
and
$x\in M$
and
![]() $v\in S_xM$
with corresponding geodesic
$v\in S_xM$
with corresponding geodesic
![]() $\gamma _v(t):=\exp _{x}(tv)$
, the smooth map
$\gamma _v(t):=\exp _{x}(tv)$
, the smooth map
is an embedding. The positive constant of the lemma will be
![]() $a_0:=a(r)$
.
$a_0:=a(r)$
.

Figure 2 The geodesic triangle
![]() $T(v,r)$
.
$T(v,r)$
.
Consider two simple closed geodesics
![]() $\gamma _1,\gamma _2$
bounding a compact annulus
$\gamma _1,\gamma _2$
bounding a compact annulus
![]() $A\subset M$
such that
$A\subset M$
such that
![]() $\mathrm {area}(A,g)\leq a(r)$
. We choose two points
$\mathrm {area}(A,g)\leq a(r)$
. We choose two points
![]() $x_0\in \gamma _1$
and
$x_0\in \gamma _1$
and
![]() $y_0\in \gamma _2$
such that
$y_0\in \gamma _2$
such that
We set
![]() $\ell _1:=L(\gamma _1)$
,
$\ell _1:=L(\gamma _1)$
,
![]() $\ell _2:=L(\gamma _2)$
, and we consider the unit-speed parameterizations
$\ell _2:=L(\gamma _2)$
, and we consider the unit-speed parameterizations
such that
![]() $\gamma _1(0)=x_0$
,
$\gamma _1(0)=x_0$
,
![]() $\gamma _2(0)=y_0$
and
$\gamma _2(0)=y_0$
and
![]() $J\dot \gamma _1(0)$
points inside the annulus A while
$J\dot \gamma _1(0)$
points inside the annulus A while
![]() $J\dot \gamma _2(0)$
points outside the annulus A. Notice that
$J\dot \gamma _2(0)$
points outside the annulus A. Notice that
Otherwise, we would have
![]() $T(\dot \gamma _1(0),r)\subset A$
, which would give the contradiction
$T(\dot \gamma _1(0),r)\subset A$
, which would give the contradiction
For each
![]() $t\in \mathbb {R}/\ell _1\mathbb {Z}$
, we consider the geodesic arc
$t\in \mathbb {R}/\ell _1\mathbb {Z}$
, we consider the geodesic arc
The geodesic
![]() $\gamma _2$
intersects
$\gamma _2$
intersects
![]() $\zeta _0((0,r))$
at
$\zeta _0((0,r))$
at
![]() $y_0=\gamma _2(0)$
. Notice that all intersections between
$y_0=\gamma _2(0)$
. Notice that all intersections between
![]() $\gamma _2$
and the geodesic arcs
$\gamma _2$
and the geodesic arcs
![]() $\zeta _t$
must be transverse (otherwise, some
$\zeta _t$
must be transverse (otherwise, some
![]() $\zeta _t$
would be contained in
$\zeta _t$
would be contained in
![]() $\gamma _2$
, which would contradict the fact that
$\gamma _2$
, which would contradict the fact that
![]() $\gamma _2$
and
$\gamma _2$
and
![]() $\gamma _1$
are disjoint). Therefore, by the implicit function theorem, there exists a maximal time
$\gamma _1$
are disjoint). Therefore, by the implicit function theorem, there exists a maximal time
![]() $t_0\in (0,\ell _1]$
and a smooth monotone increasing function
$t_0\in (0,\ell _1]$
and a smooth monotone increasing function
![]() $\sigma :[0,t_0]\to \mathbb {R}$
such that
$\sigma :[0,t_0]\to \mathbb {R}$
such that
![]() $\sigma (0)=0$
and, for all
$\sigma (0)=0$
and, for all
![]() $t\in [0,t_0]$
,
$t\in [0,t_0]$
,
![]() $\gamma _2$
intersects
$\gamma _2$
intersects
![]() $\zeta _t((0,r])$
transversely at
$\zeta _t((0,r])$
transversely at
![]() $\gamma _2(\sigma (t))$
. We denote by
$\gamma _2(\sigma (t))$
. We denote by
![]() $\rho :[0,t_0]\to (0,r]$
the smooth function such that
$\rho :[0,t_0]\to (0,r]$
the smooth function such that
![]() $\zeta _t(\rho (t))=\gamma _2(\sigma (t))$
for all
$\zeta _t(\rho (t))=\gamma _2(\sigma (t))$
for all
![]() $t\in [0,t_0]$
. Notice that
$t\in [0,t_0]$
. Notice that
We claim that
![]() $t_0=\ell _1$
. Indeed, if
$t_0=\ell _1$
. Indeed, if
![]() $t_0<\ell _1$
, we would have
$t_0<\ell _1$
, we would have
![]() $\gamma _2(\sigma (t_0))=\zeta _{t_0}(r)$
. Therefore
$\gamma _2(\sigma (t_0))=\zeta _{t_0}(r)$
. Therefore
![]() $T(\dot \gamma _1(t_0),r)\subset A$
(Figure 3), which would give the contradiction
$T(\dot \gamma _1(t_0),r)\subset A$
(Figure 3), which would give the contradiction

Figure 3 The geodesic triangle
![]() $T=T(\dot \gamma _1(t_0),r)$
contained in A.
$T=T(\dot \gamma _1(t_0),r)$
contained in A.
Next, we claim that
![]() $\sigma (\ell _1)\leq \ell _2$
. Indeed, assume by contradiction that
$\sigma (\ell _1)\leq \ell _2$
. Indeed, assume by contradiction that
![]() $\sigma (\ell _1)>\ell _2$
, so that there exists
$\sigma (\ell _1)>\ell _2$
, so that there exists
![]() $t_1\in (0,\ell _1)$
such that
$t_1\in (0,\ell _1)$
such that
![]() $\sigma (t_1)=\ell _2$
. Suitable segments of the geodesics
$\sigma (t_1)=\ell _2$
. Suitable segments of the geodesics
![]() $\gamma _1$
,
$\gamma _1$
,
![]() $\zeta _{t_1}$
and
$\zeta _{t_1}$
and
![]() $\zeta _0$
bound a triangle
$\zeta _0$
bound a triangle
![]() $T'\subset A$
, as in Figure 4. By (3.5),
$T'\subset A$
, as in Figure 4. By (3.5),
![]() $\gamma _2$
does not intersect the interior of
$\gamma _2$
does not intersect the interior of
![]() $T'$
. Since the maps (3.3) are embeddings, the geodesic segments
$T'$
. Since the maps (3.3) are embeddings, the geodesic segments
![]() $\zeta _t$
and
$\zeta _t$
and
![]() $\zeta _{t'}$
are disjoint whenever
$\zeta _{t'}$
are disjoint whenever
![]() $|t-t'|<r$
. Therefore, for each
$|t-t'|<r$
. Therefore, for each
![]() $t\in (t_1,\ell _1)$
, the geodesic segment
$t\in (t_1,\ell _1)$
, the geodesic segment
![]() $\zeta _t$
must intersect
$\zeta _t$
must intersect
![]() $\zeta _{\ell _1}=\zeta _0$
, but, when
$\zeta _{\ell _1}=\zeta _0$
, but, when
![]() $t>\ell _1-r$
, this contradicts the embeddedness of the maps (3.3).
$t>\ell _1-r$
, this contradicts the embeddedness of the maps (3.3).

Figure 4 The geodesic triangle
![]() $T'$
.
$T'$
.
Finally, we claim that
![]() $\sigma (\ell _1)=\ell _2$
. Indeed, assume by contradiction that the strict inequality
$\sigma (\ell _1)=\ell _2$
. Indeed, assume by contradiction that the strict inequality
![]() $\sigma (\ell _1)<\ell _2$
holds, so that we have distinct values
$\sigma (\ell _1)<\ell _2$
holds, so that we have distinct values
![]() $\rho (0)\neq \rho (\ell _1)$
. Since
$\rho (0)\neq \rho (\ell _1)$
. Since
![]() $\gamma _2(0)=\zeta _0(\rho (0))$
and
$\gamma _2(0)=\zeta _0(\rho (0))$
and
![]() $\gamma _2(\sigma (\ell _1))=\zeta _0(\rho (\ell _1))$
, equation (3.4) implies that
$\gamma _2(\sigma (\ell _1))=\zeta _0(\rho (\ell _1))$
, equation (3.4) implies that
![]() $\rho (0)<\rho (\ell _1)$
. Namely,
$\rho (0)<\rho (\ell _1)$
. Namely,
![]() $\gamma _2(0)$
lies in
$\gamma _2(0)$
lies in
![]() $\zeta _{0}|_{[0,\rho (\ell _1))}=\zeta _{\ell _1}|_{[0,\rho (\ell _1))}$
(Figure 5), which contradicts (3.5).
$\zeta _{0}|_{[0,\rho (\ell _1))}=\zeta _{\ell _1}|_{[0,\rho (\ell _1))}$
(Figure 5), which contradicts (3.5).

Figure 5 The point
![]() $\gamma _2(0)$
intersecting the geodesic arc
$\gamma _2(0)$
intersecting the geodesic arc
![]() $\zeta _{\ell _1}|_{[0,\rho (\ell _1))}$
.
$\zeta _{\ell _1}|_{[0,\rho (\ell _1))}$
.
We can now estimate the length of
![]() $\gamma _2$
as follows. Notice that
$\gamma _2$
as follows. Notice that
Let
![]() $k\geq 9$
be the integer such that
$k\geq 9$
be the integer such that
Notice that each restriction
![]() $\gamma _2|_{[\sigma (t),\sigma (t+\ell _1/k)]}$
is contained in the open Riemannian ball
$\gamma _2|_{[\sigma (t),\sigma (t+\ell _1/k)]}$
is contained in the open Riemannian ball
![]() $B_g(\gamma _1(t),2r)$
, which has diameter less than
$B_g(\gamma _1(t),2r)$
, which has diameter less than
![]() $\mathrm {inj}(M,g)$
. Therefore,
$\mathrm {inj}(M,g)$
. Therefore,
We infer that
 $$ \begin{align*} \ell_2 &= \sum_{h=0}^{k-1} d_g\bigg(\gamma_2\bigg(\sigma(\ell_1 \frac hk\bigg)\bigg),\gamma_2\bigg(\sigma\bigg(\ell_1\frac{h+1}k\bigg)\bigg)\bigg) <4rk <4\ell_1\frac{k}{k-1} \leq \frac92 \ell_1. \end{align*} $$
$$ \begin{align*} \ell_2 &= \sum_{h=0}^{k-1} d_g\bigg(\gamma_2\bigg(\sigma(\ell_1 \frac hk\bigg)\bigg),\gamma_2\bigg(\sigma\bigg(\ell_1\frac{h+1}k\bigg)\bigg)\bigg) <4rk <4\ell_1\frac{k}{k-1} \leq \frac92 \ell_1. \end{align*} $$
Switching the roles of
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
, we obtain the other inequality
$\gamma _2$
, we obtain the other inequality
![]() $\ell _1\leq \tfrac 92\ell _2$
.
$\ell _1\leq \tfrac 92\ell _2$
.
We now consider an open disk
![]() $B\subset M$
satisfying Assumption 3.1. For any smooth embedded circle
$B\subset M$
satisfying Assumption 3.1. For any smooth embedded circle
![]() $\gamma \subset B$
, we denote by
$\gamma \subset B$
, we denote by
![]() $B_\gamma \subset B$
its filling, namely, the open disk with boundary
$B_\gamma \subset B$
its filling, namely, the open disk with boundary
![]() $\partial B_\gamma =\gamma $
.
$\partial B_\gamma =\gamma $
.
Lemma 3.7. If B contains closed geodesics, then it contains a simple closed geodesic
![]() $\gamma $
without conjugate points and whose filling
$\gamma $
without conjugate points and whose filling
![]() $B_{\gamma }$
contains any other closed geodesic in B.
$B_{\gamma }$
contains any other closed geodesic in B.
Proof. We consider the compact subset
 $$ \begin{align*} K:=\overline{\bigcup_{\gamma} \dot\gamma}, \end{align*} $$
$$ \begin{align*} K:=\overline{\bigcup_{\gamma} \dot\gamma}, \end{align*} $$
where the union ranges over all closed geodesics
![]() $\gamma $
contained in B. The subset K is invariant under the geodesic flow (that is,
$\gamma $
contained in B. The subset K is invariant under the geodesic flow (that is,
![]() $\phi _t(K)=K$
for all
$\phi _t(K)=K$
for all
![]() $t\in \mathbb {R}$
), and therefore its projection
$t\in \mathbb {R}$
), and therefore its projection
![]() $\pi (K)$
is contained in the compact subset
$\pi (K)$
is contained in the compact subset
![]() $B\setminus N$
, where
$B\setminus N$
, where
![]() $N\subset \overline B$
is the open subset of
$N\subset \overline B$
is the open subset of
![]() $\partial B$
given by Assumption 3.1. By Lemma 2.3, the connected component
$\partial B$
given by Assumption 3.1. By Lemma 2.3, the connected component
![]() $U\subset B\setminus \pi (K)$
intersecting N is weakly convex. Since U is not simply connected, there exists a connected component
$U\subset B\setminus \pi (K)$
intersecting N is weakly convex. Since U is not simply connected, there exists a connected component
![]() $\mathcal {C}\subset \mathrm {Emb}(S^1,U)$
consisting of loops that are non-contractible in U and whose fillings contain
$\mathcal {C}\subset \mathrm {Emb}(S^1,U)$
consisting of loops that are non-contractible in U and whose fillings contain
![]() $\pi (K)$
. By Lemma 2.1, there exists a sequence
$\pi (K)$
. By Lemma 2.1, there exists a sequence
![]() $\gamma _n\in \mathcal {C}$
that converges in the
$\gamma _n\in \mathcal {C}$
that converges in the
![]() $C^2$
topology to a simple closed geodesic
$C^2$
topology to a simple closed geodesic
![]() $\gamma \subseteq \overline U$
of length
$\gamma \subseteq \overline U$
of length
and whose filling
![]() $B_\gamma $
contains
$B_\gamma $
contains
![]() $\pi (K)\setminus \gamma $
. We now conclude as in the proof of Theorem 3.4. We must have
$\pi (K)\setminus \gamma $
. We now conclude as in the proof of Theorem 3.4. We must have
![]() $\gamma _n\subset U\setminus N$
for all n large enough, as, otherwise,
$\gamma _n\subset U\setminus N$
for all n large enough, as, otherwise,
![]() $\gamma _n$
would intersect
$\gamma _n$
would intersect
![]() $\partial B$
according to Assumption 3.1. Therefore,
$\partial B$
according to Assumption 3.1. Therefore,
![]() $\gamma $
is contained in B. This, together with Lemma 2.6 and equation (3.6), implies that
$\gamma $
is contained in B. This, together with Lemma 2.6 and equation (3.6), implies that
![]() $\gamma $
has no conjugate points.
$\gamma $
has no conjugate points.
From now on, we assume that B contains closed geodesics and that all simple closed geodesics without conjugate points that are entirely contained in B are non-degenerate (and therefore they are hyperbolic waists). The open ball B may contain infinitely many simple closed geodesics. Nevertheless, we have the following statement.
Lemma 3.8. Any collection of pairwise disjoint simple closed geodesics contained in B is finite.
Proof. Let
![]() $\mathcal {G}$
be a collection of pairwise disjoint simple closed geodesics contained in the open ball B. Let
$\mathcal {G}$
be a collection of pairwise disjoint simple closed geodesics contained in the open ball B. Let
![]() $\mathcal {G}'\subseteq \mathcal {G}$
be a maximal subcollection of simple closed geodesics such that
$\mathcal {G}'\subseteq \mathcal {G}$
be a maximal subcollection of simple closed geodesics such that
![]() $B_{\gamma _1}\cap B_{\gamma _2}=\varnothing $
for all distinct
$B_{\gamma _1}\cap B_{\gamma _2}=\varnothing $
for all distinct
![]() $\gamma _1,\gamma _2\in \mathcal {G}'$
: namely, for each
$\gamma _1,\gamma _2\in \mathcal {G}'$
: namely, for each
![]() $\zeta \in \mathcal {G}\setminus \mathcal {G}'$
, we have
$\zeta \in \mathcal {G}\setminus \mathcal {G}'$
, we have
![]() $B_{\zeta }\cap B_{\gamma }\neq \varnothing $
for some
$B_{\zeta }\cap B_{\gamma }\neq \varnothing $
for some
![]() $\gamma \in \mathcal {G}'$
. The Gauss–Bonnet formula implies that
$\gamma \in \mathcal {G}'$
. The Gauss–Bonnet formula implies that
 $$ \begin{align*} 2\pi=\int_{B_{\gamma}} K_g\,dm_g\leq \max(K_g)\,\mathrm{area}(B_{\gamma},g) \quad\text{for all } \gamma\in\mathcal{G}, \end{align*} $$
$$ \begin{align*} 2\pi=\int_{B_{\gamma}} K_g\,dm_g\leq \max(K_g)\,\mathrm{area}(B_{\gamma},g) \quad\text{for all } \gamma\in\mathcal{G}, \end{align*} $$
where
![]() $m_g$
is the Riemannian measure and
$m_g$
is the Riemannian measure and
![]() $K_g$
the Gaussian curvature of
$K_g$
the Gaussian curvature of
![]() $(M,g)$
. Therefore,
$(M,g)$
. Therefore,
![]() $\mathcal {G}'$
is a finite collection of cardinality
$\mathcal {G}'$
is a finite collection of cardinality
We define
![]() $U\subset B$
to be the complement of the simple closed geodesics in
$U\subset B$
to be the complement of the simple closed geodesics in
![]() $\mathcal {G}'$
, that is,
$\mathcal {G}'$
, that is,
 $$ \begin{align*} U:=B\setminus\bigcup_{\gamma\in\mathcal{G}'}\gamma. \end{align*} $$
$$ \begin{align*} U:=B\setminus\bigcup_{\gamma\in\mathcal{G}'}\gamma. \end{align*} $$
We consider the family
![]() $\pi _0(\mathrm {Emb}(S^1,U))$
of path-connected components of the space of embedded loops in U. Notice that
$\pi _0(\mathrm {Emb}(S^1,U))$
of path-connected components of the space of embedded loops in U. Notice that
![]() $\pi _0(\mathrm {Emb}(S^1,U))$
is infinite when
$\pi _0(\mathrm {Emb}(S^1,U))$
is infinite when
![]() $k\geq 3$
. Nevertheless, since
$k\geq 3$
. Nevertheless, since
![]() $\mathcal {G}$
is a collection of pairwise disjoint simple closed geodesics, there are only finitely many homotopy classes
$\mathcal {G}$
is a collection of pairwise disjoint simple closed geodesics, there are only finitely many homotopy classes
![]() $h\in \pi _0(\mathrm {Emb}(S^1,U))$
containing elements of
$h\in \pi _0(\mathrm {Emb}(S^1,U))$
containing elements of
![]() $\mathcal {G}\setminus \mathcal {G}'$
. For every such homotopy class h, let
$\mathcal {G}\setminus \mathcal {G}'$
. For every such homotopy class h, let
![]() $\mathcal {G}_h$
be the subcollection of those
$\mathcal {G}_h$
be the subcollection of those
![]() $\gamma \in \mathcal {G}\setminus \mathcal {G}'$
contained in h. For each pair of distinct
$\gamma \in \mathcal {G}\setminus \mathcal {G}'$
contained in h. For each pair of distinct
![]() $\gamma _1,\gamma _2\in \mathcal {G}_h$
, we denote by
$\gamma _1,\gamma _2\in \mathcal {G}_h$
, we denote by
![]() $A_{\gamma _1,\gamma _2}\subset B$
the compact annulus with boundary
$A_{\gamma _1,\gamma _2}\subset B$
the compact annulus with boundary
![]() $\partial A_{\gamma _1,\gamma _2}=\gamma _1\cup \gamma _2$
. Consider the constant
$\partial A_{\gamma _1,\gamma _2}=\gamma _1\cup \gamma _2$
. Consider the constant
![]() $a_0>0$
provided by Lemma 3.6. Since
$a_0>0$
provided by Lemma 3.6. Since
![]() $\mathrm {area}(U,g)<\infty $
, there exist finitely many
$\mathrm {area}(U,g)<\infty $
, there exist finitely many
![]() $\gamma _{h,1},\ldots ,\gamma _{h,n_h}\in \mathcal {G}_h$
such that, for each
$\gamma _{h,1},\ldots ,\gamma _{h,n_h}\in \mathcal {G}_h$
such that, for each
![]() $\gamma \in \mathcal {G}_h\setminus \{\gamma _{h,1},\ldots ,\gamma _{h,n_h}\}$
, we have
$\gamma \in \mathcal {G}_h\setminus \{\gamma _{h,1},\ldots ,\gamma _{h,n_h}\}$
, we have
![]() $\mathrm {area}(A_{\gamma ,\gamma _{h,i}},g)\leq a_0$
for some i. We consider the finite subcollection
$\mathrm {area}(A_{\gamma ,\gamma _{h,i}},g)\leq a_0$
for some i. We consider the finite subcollection
![]() $\mathcal {G}"\subset \mathcal {G}$
that comprises
$\mathcal {G}"\subset \mathcal {G}$
that comprises
![]() $\mathcal {G}'$
and all the elements
$\mathcal {G}'$
and all the elements
![]() $\gamma _{h,j}$
. Summing up, we have shown that, for each
$\gamma _{h,j}$
. Summing up, we have shown that, for each
![]() $\gamma \in \mathcal {G}\setminus \mathcal {G}"$
, there exists
$\gamma \in \mathcal {G}\setminus \mathcal {G}"$
, there exists
![]() $\zeta \in \mathcal {G}"$
such that
$\zeta \in \mathcal {G}"$
such that
![]() $\mathrm {area}(A_{\gamma ,\zeta })\leq a_0$
. This, together with Lemma 3.6, implies that
$\mathrm {area}(A_{\gamma ,\zeta })\leq a_0$
. This, together with Lemma 3.6, implies that
Let
![]() $\mathcal {K}\subset W^{1,2}(S^1,M)$
be the subspace of closed geodesics
$\mathcal {K}\subset W^{1,2}(S^1,M)$
be the subspace of closed geodesics
![]() $\gamma :S^1\to M$
of length
$\gamma :S^1\to M$
of length
![]() $L(\gamma )\leq \ell $
parameterized with constant speed. As a consequence of the Palais–Smale condition for the geodesic energy functional [Reference KlingenbergKli78, Theorem 1.4.7],
$L(\gamma )\leq \ell $
parameterized with constant speed. As a consequence of the Palais–Smale condition for the geodesic energy functional [Reference KlingenbergKli78, Theorem 1.4.7],
![]() $\mathcal {K}$
is compact in the
$\mathcal {K}$
is compact in the
![]() $W^{1,2}$
topology.
$W^{1,2}$
topology.
Assume, by contradiction, that there exist an infinite sequence
![]() $\gamma _n\in \mathcal {G}\subset \mathcal {K}$
. Up to extracting a subsequence,
$\gamma _n\in \mathcal {G}\subset \mathcal {K}$
. Up to extracting a subsequence,
![]() $\gamma _n$
converges to a simple closed geodesic
$\gamma _n$
converges to a simple closed geodesic
![]() $\gamma $
in the
$\gamma $
in the
![]() $W^{1,2}$
topology. A priori,
$W^{1,2}$
topology. A priori,
![]() $\gamma $
is contained in the closure
$\gamma $
is contained in the closure
![]() $\overline B$
, but Lemma 3.7 guarantees that
$\overline B$
, but Lemma 3.7 guarantees that
![]() $\gamma $
is actually contained in the open ball B. Since the
$\gamma $
is actually contained in the open ball B. Since the
![]() $\gamma _n$
are pairwise disjoint, they are also disjoint from their limit
$\gamma _n$
are pairwise disjoint, they are also disjoint from their limit
![]() $\gamma $
. This, together with Corollary 2.10(ii), implies that
$\gamma $
. This, together with Corollary 2.10(ii), implies that
![]() $\gamma $
is without conjugate points, and therefore it must be non-degenerate by our assumption. This gives a contradiction, since a non-degenerate closed geodesic
$\gamma $
is without conjugate points, and therefore it must be non-degenerate by our assumption. This gives a contradiction, since a non-degenerate closed geodesic
![]() $\gamma $
cannot be the
$\gamma $
cannot be the
![]() $W^{1,2}$
-limit of closed geodesics that are disjoint from
$W^{1,2}$
-limit of closed geodesics that are disjoint from
![]() $\gamma $
.
$\gamma $
.
Proof of Theorem 3.5
Let
![]() $\gamma _1,\ldots ,\gamma _n$
be a maximal sequence of pairwise disjoint simple closed geodesics contained in the open ball B such that
$\gamma _1,\ldots ,\gamma _n$
be a maximal sequence of pairwise disjoint simple closed geodesics contained in the open ball B such that
![]() $\gamma _{i+1}\subset B_{\gamma _i}$
for each
$\gamma _{i+1}\subset B_{\gamma _i}$
for each
![]() $i=1,\ldots ,n-1$
. Lemma 3.8 implies that such a sequence must be finite. The maximality of this sequence implies that every other simple closed geodesic
$i=1,\ldots ,n-1$
. Lemma 3.8 implies that such a sequence must be finite. The maximality of this sequence implies that every other simple closed geodesic
![]() $\gamma $
contained in B and not intersecting any
$\gamma $
contained in B and not intersecting any
![]() $\gamma _i$
must have filling
$\gamma _i$
must have filling
![]() $B_\gamma $
contained in the complement
$B_\gamma $
contained in the complement
![]() $U:=B\setminus (\gamma _1\cup \cdots \cup \gamma _n)$
. Notice that the first simple closed geodesic
$U:=B\setminus (\gamma _1\cup \cdots \cup \gamma _n)$
. Notice that the first simple closed geodesic
![]() $\gamma _1$
must be the waist provided by Lemma 3.7, whose filling
$\gamma _1$
must be the waist provided by Lemma 3.7, whose filling
![]() $B_{\gamma _1}$
contains any other closed geodesic contained in B. We recall that, by our assumption on B, any simple closed geodesic contained in B that is not a waist must have conjugate points.
$B_{\gamma _1}$
contains any other closed geodesic contained in B. We recall that, by our assumption on B, any simple closed geodesic contained in B that is not a waist must have conjugate points.
For each
![]() $i\in \{1,\ldots ,n-1\}$
,
$i\in \{1,\ldots ,n-1\}$
,
![]() $\gamma _i$
or
$\gamma _i$
or
![]() $\gamma _{i+1}$
must be a waist. Indeed, if none of them were waists, Lemma 2.6 would imply that the open annulus
$\gamma _{i+1}$
must be a waist. Indeed, if none of them were waists, Lemma 2.6 would imply that the open annulus
![]() $A_i:=B_{\gamma _{i}}\setminus \overline {B_{\gamma _{i+1}}}$
contains a non-contractible embedded circle
$A_i:=B_{\gamma _{i}}\setminus \overline {B_{\gamma _{i+1}}}$
contains a non-contractible embedded circle
![]() $\zeta _0$
with length
$\zeta _0$
with length
![]() $L(\zeta _0)<\min \{L(\gamma _{i}),L(\gamma _{i+1})\}$
, and Lemma 2.1 would imply that there exists a non-contractible closed geodesic
$L(\zeta _0)<\min \{L(\gamma _{i}),L(\gamma _{i+1})\}$
, and Lemma 2.1 would imply that there exists a non-contractible closed geodesic
![]() $\zeta \subset \overline {A_i}$
such that
$\zeta \subset \overline {A_i}$
such that
![]() $L(\zeta )\leq L(\zeta _0)$
; these inequalities would imply that
$L(\zeta )\leq L(\zeta _0)$
; these inequalities would imply that
![]() $\zeta $
is contained in
$\zeta $
is contained in
![]() $A_i$
, which would contradict the maximality of the sequence
$A_i$
, which would contradict the maximality of the sequence
![]() $\gamma _1,\ldots ,\gamma _n$
. Moreover,
$\gamma _1,\ldots ,\gamma _n$
. Moreover,
![]() $\gamma _i$
and
$\gamma _i$
and
![]() $\gamma _{i+1}$
cannot both be waists. Otherwise Lemma 2.5(i) would imply that the open annulus
$\gamma _{i+1}$
cannot both be waists. Otherwise Lemma 2.5(i) would imply that the open annulus
![]() $A_i$
contains a non-contractible simple closed geodesic
$A_i$
contains a non-contractible simple closed geodesic
![]() $\zeta $
, which would contradict the maximality of the sequence
$\zeta $
, which would contradict the maximality of the sequence
![]() $\gamma _1,\ldots ,\gamma _n$
. Finally, the last simple closed geodesic
$\gamma _1,\ldots ,\gamma _n$
. Finally, the last simple closed geodesic
![]() $\gamma _n$
of the sequence cannot be a waist, as, otherwise, Lemma 2.5(ii) would imply that its filling
$\gamma _n$
of the sequence cannot be a waist, as, otherwise, Lemma 2.5(ii) would imply that its filling
![]() $B_\gamma $
contains another simple closed geodesic, which would again contradict the maximality of the sequence
$B_\gamma $
contains another simple closed geodesic, which would again contradict the maximality of the sequence
![]() $\gamma _1,\ldots ,\gamma _n$
. Summing up, we have proved that n is even, and that
$\gamma _1,\ldots ,\gamma _n$
. Summing up, we have proved that n is even, and that
![]() $\gamma _i$
is a waist if i is odd, whereas
$\gamma _i$
is a waist if i is odd, whereas
![]() $\gamma _i$
has conjugate points if i is even.
$\gamma _i$
has conjugate points if i is even.
We denote by
![]() $\mathcal {K}=\{\gamma _1,\gamma _3,\ldots ,\gamma _{n-1}\}$
the collection of waists in the sequence
$\mathcal {K}=\{\gamma _1,\gamma _3,\ldots ,\gamma _{n-1}\}$
the collection of waists in the sequence
![]() $\gamma _1,\ldots ,\gamma _{n}$
, and we set
$\gamma _1,\ldots ,\gamma _{n}$
, and we set
 $$ \begin{align*} K:=\bigcup_{\gamma\in\mathcal{K}} (\dot\gamma\cup-\dot\gamma). \end{align*} $$
$$ \begin{align*} K:=\bigcup_{\gamma\in\mathcal{K}} (\dot\gamma\cup-\dot\gamma). \end{align*} $$
Lemma 2.7 implies that
Conversely, consider an arbitrary point
![]() $z\in \mathrm {trap}_+(SU)$
, so that
$z\in \mathrm {trap}_+(SU)$
, so that
![]() $\phi _t(z)\in SU$
for all
$\phi _t(z)\in SU$
for all
![]() $t>0$
large enough. We shall prove that the
$t>0$
large enough. We shall prove that the
![]() $\omega $
-limit
$\omega $
-limit
![]() $\omega (z)$
is either
$\omega (z)$
is either
![]() $\dot \gamma $
or
$\dot \gamma $
or
![]() $-\dot \gamma $
for some
$-\dot \gamma $
for some
![]() $\gamma \in \mathcal {K}$
, which will imply the opposite inclusion
$\gamma \in \mathcal {K}$
, which will imply the opposite inclusion
Let
![]() $\pi :SM\to M$
be the base projection. Since
$\pi :SM\to M$
be the base projection. Since
![]() $z\in \mathrm {trap}_+(SU)$
, there exists a connected component
$z\in \mathrm {trap}_+(SU)$
, there exists a connected component
![]() $W\subset U$
such that
$W\subset U$
such that
![]() $\phi _t(z)\in SW$
for all
$\phi _t(z)\in SW$
for all
![]() $t>0$
large enough, and therefore
$t>0$
large enough, and therefore
![]() $\pi (\omega (z))\subset \overline W$
. We have three possible cases.
$\pi (\omega (z))\subset \overline W$
. We have three possible cases.
Case 1:
![]() $W=B_{\gamma _n}$
. Since
$W=B_{\gamma _n}$
. Since
![]() $\gamma _n$
has conjugate points, Corollary 2.10(ii) implies that the geodesic
$\gamma _n$
has conjugate points, Corollary 2.10(ii) implies that the geodesic
![]() $\pi \circ \phi _t(z)$
does not enter a sufficiently small neighborhood of
$\pi \circ \phi _t(z)$
does not enter a sufficiently small neighborhood of
![]() $\partial B_{\gamma _n}$
for all
$\partial B_{\gamma _n}$
for all
![]() $t>0$
large enough. Therefore,
$t>0$
large enough. Therefore,
![]() $\pi (\omega (z))$
is contained in the open disk
$\pi (\omega (z))$
is contained in the open disk
![]() $B_{\gamma _n}$
. Since
$B_{\gamma _n}$
. Since
![]() $\omega (z)$
is compact, so is its projection
$\omega (z)$
is compact, so is its projection
![]() $\pi (\omega (z))$
. Lemma 2.3 implies that any path-connected component of the open set
$\pi (\omega (z))$
. Lemma 2.3 implies that any path-connected component of the open set
![]() $B_{\gamma _n}\setminus \pi (\omega (z))$
is weakly convex, and Lemma 2.6 implies that
$B_{\gamma _n}\setminus \pi (\omega (z))$
is weakly convex, and Lemma 2.6 implies that
![]() $B_{\gamma _n}\setminus \pi (\omega (z))$
contains a non-contractible embedded loop
$B_{\gamma _n}\setminus \pi (\omega (z))$
contains a non-contractible embedded loop
![]() $\zeta _0$
with length
$\zeta _0$
with length
![]() $L(\zeta _0)<L(\gamma _n)$
. We can now apply Lemma 2.1, which provides a sequence of non-contractible smooth embedded circles in
$L(\zeta _0)<L(\gamma _n)$
. We can now apply Lemma 2.1, which provides a sequence of non-contractible smooth embedded circles in
![]() $B_{\gamma _n}\setminus \pi (\omega (z))$
converging in the
$B_{\gamma _n}\setminus \pi (\omega (z))$
converging in the
![]() $C^2$
topology to a simple closed geodesic
$C^2$
topology to a simple closed geodesic
![]() $\zeta \subset \overline {B_{\gamma _n}\setminus \pi (\omega (z))}$
with length
$\zeta \subset \overline {B_{\gamma _n}\setminus \pi (\omega (z))}$
with length
![]() $L(\zeta )\leq L(\zeta _0)<L(\gamma _n)$
. These inequalities readily imply that
$L(\zeta )\leq L(\zeta _0)<L(\gamma _n)$
. These inequalities readily imply that
![]() $\zeta $
is contained in the open disk
$\zeta $
is contained in the open disk
![]() $B_{\gamma _n}$
, which contradicts the maximality of the sequence
$B_{\gamma _n}$
, which contradicts the maximality of the sequence
![]() $\gamma _1,\ldots ,\gamma _n$
. This proves that case 1 cannot occur.
$\gamma _1,\ldots ,\gamma _n$
. This proves that case 1 cannot occur.
Case 2:
![]() $W=B\setminus \overline {B_{\gamma _1}}$
. Since B satisfies Assumption 3.1, the geodesic
$W=B\setminus \overline {B_{\gamma _1}}$
. Since B satisfies Assumption 3.1, the geodesic
![]() $\pi \circ \phi _t(z)$
does not enter a sufficiently small neighborhood of
$\pi \circ \phi _t(z)$
does not enter a sufficiently small neighborhood of
![]() $\partial B$
for all
$\partial B$
for all
![]() $t>0$
large enough, as, otherwise, it would intersect
$t>0$
large enough, as, otherwise, it would intersect
![]() $\partial B$
for
$\partial B$
for
![]() $t>0$
arbitrarily large. Therefore, the compact set
$t>0$
arbitrarily large. Therefore, the compact set
![]() $\pi (\omega (z))$
is contained in
$\pi (\omega (z))$
is contained in
![]() $\overline W\setminus \partial B$
. Let
$\overline W\setminus \partial B$
. Let
![]() $V\subset W\setminus \pi (\omega (z))$
be the connected component whose boundary
$V\subset W\setminus \pi (\omega (z))$
be the connected component whose boundary
![]() $\partial V$
contains
$\partial V$
contains
![]() $\partial B$
. By Lemma 2.3, V is weakly convex. Lemma 2.1 provides a sequence of non-contractible smooth embedded loops
$\partial B$
. By Lemma 2.3, V is weakly convex. Lemma 2.1 provides a sequence of non-contractible smooth embedded loops
![]() $\zeta _k\subset V$
converging in the
$\zeta _k\subset V$
converging in the
![]() $C^2$
topology to a simple closed geodesic
$C^2$
topology to a simple closed geodesic
![]() $\zeta \subset \overline V$
. Notice that
$\zeta \subset \overline V$
. Notice that
![]() $\zeta $
cannot intersect
$\zeta $
cannot intersect
![]() $\partial B$
, as, otherwise,
$\partial B$
, as, otherwise,
![]() $\zeta _{k}$
would intersect
$\zeta _{k}$
would intersect
![]() $\partial B$
as well for k large enough, according to Assumption 3.1. Therefore, Lemma 3.7 implies that
$\partial B$
as well for k large enough, according to Assumption 3.1. Therefore, Lemma 3.7 implies that
![]() $\zeta =\gamma _1$
, and we have
$\zeta =\gamma _1$
, and we have
![]() $V=B\setminus \overline {B_{\gamma _1}}$
and
$V=B\setminus \overline {B_{\gamma _1}}$
and
![]() $\pi (\omega (z))=\gamma _1$
. Since
$\pi (\omega (z))=\gamma _1$
. Since
![]() $\omega (z)$
is connected and invariant under the geodesic flow, we infer that either
$\omega (z)$
is connected and invariant under the geodesic flow, we infer that either
![]() $\omega (z)=\dot \gamma _1$
or
$\omega (z)=\dot \gamma _1$
or
![]() $\omega (z)=-\dot \gamma _1$
.
$\omega (z)=-\dot \gamma _1$
.
Case 3:
![]() $W=B_{\gamma _i}\setminus \overline {B_{\gamma _{i+1}}}$
for some
$W=B_{\gamma _i}\setminus \overline {B_{\gamma _{i+1}}}$
for some
![]() $i\in \{1,\ldots ,n-1\}$
. Let us assume that i is odd, so that
$i\in \{1,\ldots ,n-1\}$
. Let us assume that i is odd, so that
![]() $\gamma _i$
is a waist and
$\gamma _i$
is a waist and
![]() $\gamma _{i+1}$
has conjugate points (the case of i even is analogous). Since
$\gamma _{i+1}$
has conjugate points (the case of i even is analogous). Since
![]() $\gamma _{i+1}$
has conjugate points, Corollary 2.10(ii) implies that there exists a neighborhood of
$\gamma _{i+1}$
has conjugate points, Corollary 2.10(ii) implies that there exists a neighborhood of
![]() $\gamma _{i+1}$
that does not intersect
$\gamma _{i+1}$
that does not intersect
![]() $\pi (\omega (z))$
. If
$\pi (\omega (z))$
. If
![]() $\pi (\omega (z))$
intersects the interior W, then we can apply Lemma 2.1, as in case 1, and infer the existence of a simple closed geodesic
$\pi (\omega (z))$
intersects the interior W, then we can apply Lemma 2.1, as in case 1, and infer the existence of a simple closed geodesic
![]() $\zeta \subset W$
, which contradicts the maximality of the sequence
$\zeta \subset W$
, which contradicts the maximality of the sequence
![]() $\gamma _1,\ldots ,\gamma _n$
. This proves that
$\gamma _1,\ldots ,\gamma _n$
. This proves that
![]() $\pi (\omega (z))\subseteq \gamma _i$
. Since
$\pi (\omega (z))\subseteq \gamma _i$
. Since
![]() $\omega (z)$
is connected and invariant under the geodesic flow, we infer that either
$\omega (z)$
is connected and invariant under the geodesic flow, we infer that either
![]() $\omega (z)=\dot \gamma _i$
or
$\omega (z)=\dot \gamma _i$
or
![]() $\omega (z)=-\dot \gamma _i$
.
$\omega (z)=-\dot \gamma _i$
.
Summing up, we have proved that
Since
![]() $\mathrm {trap}_-(SU)=-\mathrm {trap}_+(SU)$
and
$\mathrm {trap}_-(SU)=-\mathrm {trap}_+(SU)$
and
![]() $W^{u}(K)=-W^{s}(K)$
, we also have
$W^{u}(K)=-W^{s}(K)$
, we also have
It remains to show that no complete geodesic is entirely contained in U. Assume, by contradiction, that this does not hold, so that there exists a point
![]() $z\in SU$
such that
$z\in SU$
such that
![]() $\phi _t(z)\in SU$
for all
$\phi _t(z)\in SU$
for all
![]() $t\in \mathbb {R}$
. In particular,
$t\in \mathbb {R}$
. In particular,
![]() $z\in \mathrm {trap}_+(SU)\cap \mathrm {trap}_-(SU)$
, and therefore
$z\in \mathrm {trap}_+(SU)\cap \mathrm {trap}_-(SU)$
, and therefore
![]() $z\in W^{u}(\dot \gamma \cup -\dot \gamma )\cap W^{s}(\dot \gamma \cup -\dot \gamma )\setminus (\dot \gamma \cup -\dot \gamma )$
for some waist
$z\in W^{u}(\dot \gamma \cup -\dot \gamma )\cap W^{s}(\dot \gamma \cup -\dot \gamma )\setminus (\dot \gamma \cup -\dot \gamma )$
for some waist
![]() $\gamma \in \mathcal {K}$
. Let
$\gamma \in \mathcal {K}$
. Let
![]() $W\subset U$
be the connected component such that
$W\subset U$
be the connected component such that
![]() $\phi _t(z)\in SW$
for all
$\phi _t(z)\in SW$
for all
![]() $t\in \mathbb {R}$
. The waist
$t\in \mathbb {R}$
. The waist
![]() $\gamma $
is a connected component of
$\gamma $
is a connected component of
![]() $\partial W$
, and therefore we must have either
$\partial W$
, and therefore we must have either
![]() $W=B\setminus \overline {B_{\gamma _1}}$
or
$W=B\setminus \overline {B_{\gamma _1}}$
or
![]() $W=B_{\gamma _i}\setminus \overline {B_{\gamma _{i+1}}}$
for some
$W=B_{\gamma _i}\setminus \overline {B_{\gamma _{i+1}}}$
for some
![]() $i\in \{1,\ldots ,n-1\}$
. The compact subset
$i\in \{1,\ldots ,n-1\}$
. The compact subset
 $$ \begin{align*}C:=\overline{\bigcup_{t\in\mathbb{R}}\phi_t(z)}\subseteq\dot\gamma\cup-\dot\gamma\cup\bigcup_{t\in\mathbb{R}}\phi_t(z)\end{align*} $$
$$ \begin{align*}C:=\overline{\bigcup_{t\in\mathbb{R}}\phi_t(z)}\subseteq\dot\gamma\cup-\dot\gamma\cup\bigcup_{t\in\mathbb{R}}\phi_t(z)\end{align*} $$
is invariant under the geodesic flow, and therefore any path-connected component of
![]() $W\setminus \pi (C)$
is weakly convex according to Lemma 2.3. The end of the argument is entirely analogous to the one in cases 2 and 3 above. There exists a neighborhood of
$W\setminus \pi (C)$
is weakly convex according to Lemma 2.3. The end of the argument is entirely analogous to the one in cases 2 and 3 above. There exists a neighborhood of
![]() $\partial W\setminus \gamma $
that does not intersect
$\partial W\setminus \gamma $
that does not intersect
![]() $\pi (C)$
. Since
$\pi (C)$
. Since
![]() $\pi (C)$
intersects the open set W, with a suitable application of Lemma 2.1, we infer the existence of a simple closed geodesic in W, which contradicts the maximality of the sequence
$\pi (C)$
intersects the open set W, with a suitable application of Lemma 2.1, we infer the existence of a simple closed geodesic in W, which contradicts the maximality of the sequence
![]() $\gamma _1,\ldots ,\gamma _n$
.
$\gamma _1,\ldots ,\gamma _n$
.
4 Construction of surfaces of section
4.1 Fried surgery of Birkhoff annuli
The surfaces of section provided by our main theorems will be obtained by performing surgeries à la Fried [Reference FriedFri83] on a suitable collection of Birkhoff annuli of closed geodesics. In this subsection, we briefly recall this procedure.
Let
![]() $(M,g)$
be an oriented Riemannian surface and let J be its associated complex structure: that is,
$(M,g)$
be an oriented Riemannian surface and let J be its associated complex structure: that is,
![]() $v,Jv$
is an oriented orthonormal basis of
$v,Jv$
is an oriented orthonormal basis of
![]() $T_xM$
for all tangent vectors
$T_xM$
for all tangent vectors
![]() $v\in S_xM$
. Let
$v\in S_xM$
. Let
![]() $\gamma :\mathbb {R}/\ell \mathbb {Z}\to M$
be a closed geodesic parameterized with unit speed
$\gamma :\mathbb {R}/\ell \mathbb {Z}\to M$
be a closed geodesic parameterized with unit speed
![]() $\|\dot \gamma \|_g\equiv 1$
. The Birkhoff annulus of
$\|\dot \gamma \|_g\equiv 1$
. The Birkhoff annulus of
![]() $\gamma $
is the immersed compact annulus in
$\gamma $
is the immersed compact annulus in
![]() $SM$
given by
$SM$
given by
Its boundary
![]() $\partial A(\dot \gamma )=\dot \gamma \cup -\dot \gamma $
is embedded, whereas its interior
$\partial A(\dot \gamma )=\dot \gamma \cup -\dot \gamma $
is embedded, whereas its interior
![]() $\operatorname {\mathrm {int}}(A(\dot \gamma ))$
is immersed and transverse to the geodesic vector field X on
$\operatorname {\mathrm {int}}(A(\dot \gamma ))$
is immersed and transverse to the geodesic vector field X on
![]() $SM$
.
$SM$
.
Now assume that
![]() $\gamma $
is simple. In this case,
$\gamma $
is simple. In this case,
![]() $A(\dot \gamma )$
is embedded; therefore, it is a surface of section for X. By considering the opposite orientation on
$A(\dot \gamma )$
is embedded; therefore, it is a surface of section for X. By considering the opposite orientation on
![]() $\gamma $
, we obtain a second Birkhoff annulus
$\gamma $
, we obtain a second Birkhoff annulus
![]() $A(-\dot \gamma )$
such that
$A(-\dot \gamma )$
such that
For any pair of distinct simple closed geodesics
![]() $\gamma _1,\gamma _2$
of
$\gamma _1,\gamma _2$
of
![]() $(M,g)$
that intersect each other, the Birkhoff annuli
$(M,g)$
that intersect each other, the Birkhoff annuli
![]() $A_i^\pm :=A(\pm \dot \gamma _i)$
intersect as in Figure 6. We see their union
$A_i^\pm :=A(\pm \dot \gamma _i)$
intersect as in Figure 6. We see their union
as a non-injectively immersed surface with boundary
Notice that, for any
![]() $\ell>\max \{L(\gamma _1),L(\gamma _2)\}$
, there exists an open neighborhood
$\ell>\max \{L(\gamma _1),L(\gamma _2)\}$
, there exists an open neighborhood
![]() $N\subset \Upsilon $
of
$N\subset \Upsilon $
of
![]() $\partial \Upsilon $
such that, for each
$\partial \Upsilon $
such that, for each
![]() $z\in N$
, the orbit segment
$z\in N$
, the orbit segment
![]() $\phi _{(0,\ell ]}(z)$
intersects
$\phi _{(0,\ell ]}(z)$
intersects
![]() $\Upsilon $
.
$\Upsilon $
.

Figure 6 The four Birkhoff annuli
![]() $A_1^+,A_1^-,A_{2}^+,A_{2}^-$
of the simple closed geodesics
$A_1^+,A_1^-,A_{2}^+,A_{2}^-$
of the simple closed geodesics
![]() $\gamma _1,\gamma _2$
. The central vertical line of double points is the fiber
$\gamma _1,\gamma _2$
. The central vertical line of double points is the fiber
![]() $S_xM$
of a point
$S_xM$
of a point
![]() $x\in \gamma _1\cap \gamma _2$
. The geodesic vector field should be thought as horizontal and makes a full turn as we move through the line of double points.
$x\in \gamma _1\cap \gamma _2$
. The geodesic vector field should be thought as horizontal and makes a full turn as we move through the line of double points.
We apply the following surgery procedures, due to Fried, in order to resolve the self-intersections with interior points of
![]() $\Upsilon $
, and we produce a surface of section
$\Upsilon $
, and we produce a surface of section
![]() $\Sigma \subset SM$
with the same boundary
$\Sigma \subset SM$
with the same boundary
![]() $\partial \Sigma =\partial \Upsilon $
. Away from an arbitrarily small neighborhood U of the subspace of self-intersections of
$\partial \Sigma =\partial \Upsilon $
. Away from an arbitrarily small neighborhood U of the subspace of self-intersections of
![]() $\operatorname {\mathrm {int}}(\Upsilon )$
with
$\operatorname {\mathrm {int}}(\Upsilon )$
with
![]() $\Upsilon $
, we set
$\Upsilon $
, we set
![]() $\Sigma \cap (SM\setminus U):=\Upsilon \cap (SM\setminus U)$
. Along the lines of double points in
$\Sigma \cap (SM\setminus U):=\Upsilon \cap (SM\setminus U)$
. Along the lines of double points in
![]() $\operatorname {\mathrm {int}}(\Upsilon )$
, we resolve the self-intersections and obtain
$\operatorname {\mathrm {int}}(\Upsilon )$
, we resolve the self-intersections and obtain
![]() $\Sigma $
as in Figure 7. Finally, near the intersections
$\Sigma $
as in Figure 7. Finally, near the intersections
![]() $\operatorname {\mathrm {int}}(\Upsilon )\cap \partial \Upsilon $
, the surface
$\operatorname {\mathrm {int}}(\Upsilon )\cap \partial \Upsilon $
, the surface
![]() $\Sigma $
is obtained as in Figure 8. Up to choosing the neighborhood U where the surgery takes place to be small enough, for each
$\Sigma $
is obtained as in Figure 8. Up to choosing the neighborhood U where the surgery takes place to be small enough, for each
![]() $z\in \Upsilon $
, the orbit segment
$z\in \Upsilon $
, the orbit segment
![]() $\phi _{(-1,1)}(z)$
intersects
$\phi _{(-1,1)}(z)$
intersects
![]() $\Sigma $
; analogously, for each
$\Sigma $
; analogously, for each
![]() $z\in \Sigma $
, the orbit segment
$z\in \Sigma $
, the orbit segment
![]() $\phi _{(-1,1)}(z)$
intersects
$\phi _{(-1,1)}(z)$
intersects
![]() $\Upsilon $
.
$\Upsilon $
.

Figure 7 Fried surgery to resolve the double points in
![]() $\operatorname {\mathrm {int}}(\Upsilon )$
.
$\operatorname {\mathrm {int}}(\Upsilon )$
.

Figure 8 Fried surgery to resolve the lines of double points near the boundary point
![]() $z\in \partial \Upsilon $
.
$z\in \partial \Upsilon $
.
If a closed geodesic
![]() $\gamma $
is not simple, one can apply Fried surgeries to resolve the self-intersections of its Birkhoff annulus
$\gamma $
is not simple, one can apply Fried surgeries to resolve the self-intersections of its Birkhoff annulus
![]() $A(\dot \gamma )$
and produce a surface of section. More generally, one can apply Fried surgeries to produce a surface of section out of the Birkhoff annuli of any finite collection of closed geodesics.
$A(\dot \gamma )$
and produce a surface of section. More generally, one can apply Fried surgeries to produce a surface of section out of the Birkhoff annuli of any finite collection of closed geodesics.
4.2 Complete system of closed geodesics
Let
![]() $(M,g)$
be a closed connected oriented Riemannian surface with unit tangent bundle
$(M,g)$
be a closed connected oriented Riemannian surface with unit tangent bundle
![]() $\pi :SM\to M$
and geodesic flow
$\pi :SM\to M$
and geodesic flow
![]() $\phi _t:SM\to SM$
. We introduce the following notion, which we will employ in the next subsection.
$\phi _t:SM\to SM$
. We introduce the following notion, which we will employ in the next subsection.
Definition 4.1. A complete system of closed geodesics
![]() $\mathcal {G}$
is a non-empty finite collection of closed geodesics of
$\mathcal {G}$
is a non-empty finite collection of closed geodesics of
![]() $(M,g)$
, together with a (possibly empty) subcollection
$(M,g)$
, together with a (possibly empty) subcollection
![]() $\mathcal {K}\subset \mathcal {G}$
, satisfying the following properties. We set
$\mathcal {K}\subset \mathcal {G}$
, satisfying the following properties. We set
 $$ \begin{align*} K:=\bigcup_{\gamma\in\mathcal{K}} (\dot\gamma\cup-\dot\gamma), \quad R:=\bigcup_{\gamma\in\mathcal{G}\setminus\mathcal{K}} (\dot\gamma\cup-\dot\gamma), \quad U:=M\setminus\bigcup_{\gamma\in\mathcal{G}}\gamma. \end{align*} $$
$$ \begin{align*} K:=\bigcup_{\gamma\in\mathcal{K}} (\dot\gamma\cup-\dot\gamma), \quad R:=\bigcup_{\gamma\in\mathcal{G}\setminus\mathcal{K}} (\dot\gamma\cup-\dot\gamma), \quad U:=M\setminus\bigcup_{\gamma\in\mathcal{G}}\gamma. \end{align*} $$
-
(i) Every
 $\gamma \in \mathcal {K}$
is a non-degenerate contractible waist disjoint from all the other closed geodesics in
$\gamma \in \mathcal {K}$
is a non-degenerate contractible waist disjoint from all the other closed geodesics in
 $\mathcal {G}\setminus \{\gamma \}$
. In particular, K is a hyperbolic invariant subset for the geodesic flow.
$\mathcal {G}\setminus \{\gamma \}$
. In particular, K is a hyperbolic invariant subset for the geodesic flow. -
(ii) No complete orbit
 $\phi _{(-\infty ,\infty )}(z)$
is entirely contained in
$\phi _{(-\infty ,\infty )}(z)$
is entirely contained in
 $SU$
, and the trapped sets of
$SU$
, and the trapped sets of
 $SU$
are given by For this reason, we briefly call
$SU$
are given by For this reason, we briefly call $$ \begin{align*} \mathrm{trap}_+(SU)=W^{s}(K)\setminus K, \quad \mathrm{trap}_-(SU)=W^{u}(K)\setminus K. \end{align*} $$
$$ \begin{align*} \mathrm{trap}_+(SU)=W^{s}(K)\setminus K, \quad \mathrm{trap}_-(SU)=W^{u}(K)\setminus K. \end{align*} $$
 $\mathcal {K}$
the limit subcollection of
$\mathcal {K}$
the limit subcollection of
 $\mathcal {G}$
and K the limit set.
$\mathcal {G}$
and K the limit set.
-
(iii) The invariant subset R admits an open neighborhood
 $N\subset SM$
and a positive number
$N\subset SM$
and a positive number
 $\ell>0$
such that, for each
$\ell>0$
such that, for each
 $z\in N$
, the orbit segment
$z\in N$
, the orbit segment
 $\phi _{(0,\ell ]}(z)$
is not contained in
$\phi _{(0,\ell ]}(z)$
is not contained in
 $SU$
.
$SU$
.
We stress that the closed geodesics in
![]() $\mathcal {G}\setminus \mathcal {K}$
are not necessarily simple and can have mutual intersections as well. A complete system of closed geodesics with empty limit subcollection will produce a Birkhoff section. For this purpose, we need the following lemma.
$\mathcal {G}\setminus \mathcal {K}$
are not necessarily simple and can have mutual intersections as well. A complete system of closed geodesics with empty limit subcollection will produce a Birkhoff section. For this purpose, we need the following lemma.
Lemma 4.2. If the limit subcollection
![]() $\mathcal {K}$
is empty, then there is a constant
$\mathcal {K}$
is empty, then there is a constant
![]() $\ell '>0$
such that every geodesic segment of length
$\ell '>0$
such that every geodesic segment of length
![]() $\ell '$
intersects some geodesic in
$\ell '$
intersects some geodesic in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Proof. We denote by
![]() $\Upsilon $
the union of the Birkhoff annuli of the closed geodesics in
$\Upsilon $
the union of the Birkhoff annuli of the closed geodesics in
![]() $\mathcal {G}$
, that is,
$\mathcal {G}$
, that is,
 $$ \begin{align*} \Upsilon := \bigcup_{\gamma\in\mathcal{G}} ( A(\dot\gamma)\cup A(-\dot\gamma) ). \end{align*} $$
$$ \begin{align*} \Upsilon := \bigcup_{\gamma\in\mathcal{G}} ( A(\dot\gamma)\cup A(-\dot\gamma) ). \end{align*} $$
Since
![]() $\mathcal {K}\hspace{-1pt}=\hspace{-1pt}\varnothing $
, we have empty trapped sets
$\mathcal {K}\hspace{-1pt}=\hspace{-1pt}\varnothing $
, we have empty trapped sets
![]() $\mathrm {trap}_\pm (SU)\hspace{-1pt}=\hspace{-1pt}\varnothing $
. Therefore, for each
$\mathrm {trap}_\pm (SU)\hspace{-1pt}=\hspace{-1pt}\varnothing $
. Therefore, for each
![]() $z\hspace{-1pt}\in\hspace{-1pt} SM\setminus \Upsilon $
, there exists
$z\hspace{-1pt}\in\hspace{-1pt} SM\setminus \Upsilon $
, there exists
![]() $\ell _z>1$
such that the orbit segment
$\ell _z>1$
such that the orbit segment
![]() $\phi _{[1,\ell _z-1]}(z)$
intersects
$\phi _{[1,\ell _z-1]}(z)$
intersects
![]() $\operatorname {\mathrm {int}}(\Upsilon )$
transversely. The transversality guarantees that there exists an open neighborhood
$\operatorname {\mathrm {int}}(\Upsilon )$
transversely. The transversality guarantees that there exists an open neighborhood
![]() $N_z\subset SM$
of z such that, for each
$N_z\subset SM$
of z such that, for each
![]() $z'\in N_z$
, the orbit segment
$z'\in N_z$
, the orbit segment
![]() $\phi _{[0,\ell _z]}(z')$
intersects
$\phi _{[0,\ell _z]}(z')$
intersects
![]() $\operatorname {\mathrm {int}}(\Upsilon )$
. Now consider the constant
$\operatorname {\mathrm {int}}(\Upsilon )$
. Now consider the constant
![]() $\ell>0$
and the open neighborhood N of R given by property (iii) above. Since
$\ell>0$
and the open neighborhood N of R given by property (iii) above. Since
![]() $SM$
is compact, there exist finitely many points
$SM$
is compact, there exist finitely many points
![]() $z_1,\ldots ,z_n\in SM$
such that
$z_1,\ldots ,z_n\in SM$
such that
![]() $N\cup N_{z_1}\cup \cdots \cup N_{z_n}=SM$
. For
$N\cup N_{z_1}\cup \cdots \cup N_{z_n}=SM$
. For
![]() $\ell ':=\max \{\ell ,\ell _{z_1},\ldots ,\ell _{z_n}\}$
, we conclude that, for each
$\ell ':=\max \{\ell ,\ell _{z_1},\ldots ,\ell _{z_n}\}$
, we conclude that, for each
![]() $z\in SM$
, the orbit segment
$z\in SM$
, the orbit segment
![]() $\phi _{[0,\ell ']}(z)$
intersects
$\phi _{[0,\ell ']}(z)$
intersects
![]() $\Upsilon $
. Namely, every geodesic segment of length
$\Upsilon $
. Namely, every geodesic segment of length
![]() $\ell '$
intersects some geodesic in
$\ell '$
intersects some geodesic in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
The arguments of Contreras and Mazzucchelli’s [Reference Contreras and MazzucchelliCM22, §4] allow us to produce, out of a suitable complete system of closed geodesics with non-empty limit subcollection, a new such complete system with strictly smaller limit subcollection. The setting of [Reference Contreras and MazzucchelliCM22, §4] employs Colin, Dehornoy and Rechtman’s broken book decompositions [Reference Colin, Dehornoy and RechtmanCDR23], but it turns out that the arguments go through in our simpler setting as well. We include the details in the rest of this section, for the reader’s convenience. We begin with the following preliminary lemma due to Colin, Dehornoy and Rechtman [Reference Colin, Dehornoy and RechtmanCDR23, Lemma 4.9], which is based on an argument originally due to Hofer, Wysocki and Zehnder [Reference Hofer, Wysocki and ZehnderHWZ03, Proposition 7.5].
Lemma 4.3. If the limit set K is non-empty and satisfies the transversality condition
then there exists
![]() $\gamma \in \mathcal {K}$
such that
$\gamma \in \mathcal {K}$
such that
![]() $W\cap W^{s}(\dot \gamma )\neq \varnothing $
for each path-connected component
$W\cap W^{s}(\dot \gamma )\neq \varnothing $
for each path-connected component
![]() $W\subseteq W^{u}(\dot \gamma )\setminus \dot \gamma $
. Namely, the closed orbit
$W\subseteq W^{u}(\dot \gamma )\setminus \dot \gamma $
. Namely, the closed orbit
![]() $\dot \gamma $
has homoclinics in all path-connected components of
$\dot \gamma $
has homoclinics in all path-connected components of
![]() $W^{u}(\dot \gamma )\setminus \dot \gamma $
.
$W^{u}(\dot \gamma )\setminus \dot \gamma $
.
Proof. We first show that, for each
![]() $\gamma \in \mathcal {K}$
and for each connected component
$\gamma \in \mathcal {K}$
and for each connected component
![]() $W\subseteq W^{u}(\dot \gamma )\setminus \dot \gamma $
, there exists a heteroclinic
$W\subseteq W^{u}(\dot \gamma )\setminus \dot \gamma $
, there exists a heteroclinic
We prove this by contradiction, assuming that
![]() $W\cap W^{s}(K)=\varnothing $
.
$W\cap W^{s}(K)=\varnothing $
.
The path-connected component W is an immersed cylinder in
![]() $SM$
with one end equal to
$SM$
with one end equal to
![]() $\dot \gamma $
. Let
$\dot \gamma $
. Let
![]() $S\subset W$
be an embedded essential circle that is
$S\subset W$
be an embedded essential circle that is
![]() $C^1$
-close to
$C^1$
-close to
![]() $\dot \gamma $
and transverse to the geodesic vector field, so that its base projection
$\dot \gamma $
and transverse to the geodesic vector field, so that its base projection
![]() $\pi (S)$
does not intersect
$\pi (S)$
does not intersect
![]() $\gamma $
(Lemma 2.7) nor any other closed geodesic in the collection
$\gamma $
(Lemma 2.7) nor any other closed geodesic in the collection
![]() $\mathcal {G}$
. We consider the union of the Birkhoff annuli
$\mathcal {G}$
. We consider the union of the Birkhoff annuli
 $$ \begin{align*} \Upsilon':=\bigcup_{\zeta\in\mathcal{G}\setminus\{\gamma\}} ( A(\dot\zeta)\cup A(-\dot\zeta) ) \end{align*} $$
$$ \begin{align*} \Upsilon':=\bigcup_{\zeta\in\mathcal{G}\setminus\{\gamma\}} ( A(\dot\zeta)\cup A(-\dot\zeta) ) \end{align*} $$
and an open neighborhood
![]() $V\subset SM$
of
$V\subset SM$
of
![]() $\Upsilon '$
such that
$\Upsilon '$
such that
![]() $V\cap \phi _{(-\infty ,0]}(S)=\varnothing $
. We apply Fried surgery, as explained in §4.1, to resolve the self-intersection points of
$V\cap \phi _{(-\infty ,0]}(S)=\varnothing $
. We apply Fried surgery, as explained in §4.1, to resolve the self-intersection points of
![]() $\Upsilon '$
with its interior (if there are any) and produce surfaces of section
$\Upsilon '$
with its interior (if there are any) and produce surfaces of section
![]() $\Sigma '\subset V$
such that
$\Sigma '\subset V$
such that
We set
For each
![]() $z\in S$
, we have
$z\in S$
, we have
![]() $\phi _{(-\infty ,0]}(z)\subset SU$
, whereas
$\phi _{(-\infty ,0]}(z)\subset SU$
, whereas
![]() $\phi _{(-\infty ,\infty )}(z)$
is not entirely contained in
$\phi _{(-\infty ,\infty )}(z)$
is not entirely contained in
![]() $SU$
and thus intersects
$SU$
and thus intersects
![]() $\Upsilon $
. This, together with (4.2), implies that there exists a minimal
$\Upsilon $
. This, together with (4.2), implies that there exists a minimal
![]() $t_z>0$
such that the orbit
$t_z>0$
such that the orbit
![]() $t\mapsto \phi _{t}(z)$
intersects
$t\mapsto \phi _{t}(z)$
intersects
![]() $\Sigma $
transversely for
$\Sigma $
transversely for
![]() $t=t_z$
. This transversality, together with the compactness of the circle S, implies that the function
$t=t_z$
. This transversality, together with the compactness of the circle S, implies that the function
![]() $z\mapsto t_z$
is smooth on S, and we obtain an embedded circle
$z\mapsto t_z$
is smooth on S, and we obtain an embedded circle
We consider the first return time
which is smooth on the open subset
![]() $\Sigma _0:=\tau ^{-1}(0,\infty )$
. The first return map
$\Sigma _0:=\tau ^{-1}(0,\infty )$
. The first return map
is a diffeomorphism onto its image that preserves the area form
![]() $d\unicode{x3bb} |_{\operatorname {\mathrm {int}}(\Sigma )}$
, where
$d\unicode{x3bb} |_{\operatorname {\mathrm {int}}(\Sigma )}$
, where
![]() $\unicode{x3bb} $
is the Liouville contact form of
$\unicode{x3bb} $
is the Liouville contact form of
![]() $SM$
.
$SM$
.
Since
![]() $S_0\cap W^{s}(K)=\varnothing $
, we have
$S_0\cap W^{s}(K)=\varnothing $
, we have
![]() $S_0\cap \mathrm {trap}_+(SU)=\varnothing $
, and therefore
$S_0\cap \mathrm {trap}_+(SU)=\varnothing $
, and therefore
![]() $\psi ^n(S_0)\subset \Sigma _0$
for all
$\psi ^n(S_0)\subset \Sigma _0$
for all
![]() $n\geq 0$
. We obtained an infinite sequence
$n\geq 0$
. We obtained an infinite sequence
![]() $S_n:=\psi ^n(S_0)$
of pairwise disjoint embedded circles in the interior of the surface of section
$S_n:=\psi ^n(S_0)$
of pairwise disjoint embedded circles in the interior of the surface of section
![]() $\Sigma $
. Since the unstable manifold
$\Sigma $
. Since the unstable manifold
![]() $W^{u}(\dot \gamma )$
is an immersed surface tangent to the geodesic vector field, the 2-form
$W^{u}(\dot \gamma )$
is an immersed surface tangent to the geodesic vector field, the 2-form
![]() $d\unicode{x3bb} |_W$
vanishes identically. If
$d\unicode{x3bb} |_W$
vanishes identically. If
![]() $S_n$
bounds a disk
$S_n$
bounds a disk
![]() $B_n\subset \operatorname {\mathrm {int}}(\Sigma )$
, then we denote by
$B_n\subset \operatorname {\mathrm {int}}(\Sigma )$
, then we denote by
![]() $A_n\subset W$
the compact annulus with boundary
$A_n\subset W$
the compact annulus with boundary
![]() $\partial A_n=\dot \gamma \cup S_n$
, and Stokes’ theorem implies that
$\partial A_n=\dot \gamma \cup S_n$
, and Stokes’ theorem implies that
 $$ \begin{align*} \mathrm{area}(B_n,d\unicode{x3bb})=\int_{B_n} d\unicode{x3bb}=\int_{A_n\cup B_n} d\unicode{x3bb} = \int_{\dot\gamma} \unicode{x3bb} = L(\gamma), \end{align*} $$
$$ \begin{align*} \mathrm{area}(B_n,d\unicode{x3bb})=\int_{B_n} d\unicode{x3bb}=\int_{A_n\cup B_n} d\unicode{x3bb} = \int_{\dot\gamma} \unicode{x3bb} = L(\gamma), \end{align*} $$
where
![]() $L(\gamma )>0$
is the length of the simple closed geodesic
$L(\gamma )>0$
is the length of the simple closed geodesic
![]() $\gamma $
. In particular, if
$\gamma $
. In particular, if
![]() $S_{n_1},S_{n_2}$
bound disks
$S_{n_1},S_{n_2}$
bound disks
![]() $B_{n_1},B_{n_2}\subset \operatorname {\mathrm {int}}(\Sigma )$
for some distinct
$B_{n_1},B_{n_2}\subset \operatorname {\mathrm {int}}(\Sigma )$
for some distinct
![]() $n_1,n_2\geq 0$
, we have
$n_1,n_2\geq 0$
, we have
![]() $B_{n_1}\cap B_{n_2}=\varnothing $
. This, together with the finiteness of the area
$B_{n_1}\cap B_{n_2}=\varnothing $
. This, together with the finiteness of the area
readily implies that there exist at most finitely many
![]() $n\geq 0$
such that
$n\geq 0$
such that
![]() $S_n$
is contractible in
$S_n$
is contractible in
![]() $\operatorname {\mathrm {int}}(\Sigma )$
. Therefore, since the embedded circles
$\operatorname {\mathrm {int}}(\Sigma )$
. Therefore, since the embedded circles
![]() $S_n$
are pairwise disjoint, there exist distinct
$S_n$
are pairwise disjoint, there exist distinct
![]() $n_1,n_2\geq 0$
and an embedded compact annulus
$n_1,n_2\geq 0$
and an embedded compact annulus
![]() $A\subset \operatorname {\mathrm {int}}(\Sigma )$
with boundary
$A\subset \operatorname {\mathrm {int}}(\Sigma )$
with boundary
![]() $\partial A=S_{n_1}\cup S_{n_2}$
. Let
$\partial A=S_{n_1}\cup S_{n_2}$
. Let
![]() $A'\subset W$
be the embedded compact annulus with boundary
$A'\subset W$
be the embedded compact annulus with boundary
![]() $\partial A'=S_{n_1}\cup S_{n_2}$
, so that the union
$\partial A'=S_{n_1}\cup S_{n_2}$
, so that the union
![]() $A\cup A'$
is a piecewise smooth embedded torus in
$A\cup A'$
is a piecewise smooth embedded torus in
![]() $SM$
. By Stokes theorem,
$SM$
. By Stokes theorem,
which contradicts the fact that
![]() $d\unicode{x3bb} |_{A}$
is an area form. This proves the existence of heteroclinics (4.1).
$d\unicode{x3bb} |_{A}$
is an area form. This proves the existence of heteroclinics (4.1).
Our transversality assumption on the heteroclinics, together with the shadowing lemma from hyperbolic dynamics [Reference Fisher and HasselblattFH19, Theorem 5.3.3], implies that, for all
![]() $\gamma _1,\gamma _2,\gamma _3\in \mathcal {K}$
and for each path-connected component
$\gamma _1,\gamma _2,\gamma _3\in \mathcal {K}$
and for each path-connected component
![]() $W\subset W^{u}(\dot \gamma _1)\setminus \dot \gamma _1$
, if there are heteroclinics
$W\subset W^{u}(\dot \gamma _1)\setminus \dot \gamma _1$
, if there are heteroclinics
![]() $W\cap W^{s}(\dot \gamma _2)\neq \varnothing $
and
$W\cap W^{s}(\dot \gamma _2)\neq \varnothing $
and
![]() $W^{u}(\dot \gamma _2)\cap W^{s}(\dot \gamma _3)\neq \varnothing $
, then there are also heteroclinics
$W^{u}(\dot \gamma _2)\cap W^{s}(\dot \gamma _3)\neq \varnothing $
, then there are also heteroclinics
![]() ${W\cap W^{s}(\dot \gamma _3)\neq \varnothing }$
.
${W\cap W^{s}(\dot \gamma _3)\neq \varnothing }$
.
For each
![]() $\gamma \in \mathcal {K}$
, we fix arbitrary path-connected components
$\gamma \in \mathcal {K}$
, we fix arbitrary path-connected components
![]() $W_{\pm \dot \gamma }\subset W^{u}(\pm \dot \gamma )\setminus \pm \dot \gamma $
. We have already proved that every such path-connected component must contain a heteroclinic to K. Therefore, there exists a sequence of oriented waists
$W_{\pm \dot \gamma }\subset W^{u}(\pm \dot \gamma )\setminus \pm \dot \gamma $
. We have already proved that every such path-connected component must contain a heteroclinic to K. Therefore, there exists a sequence of oriented waists
![]() $\gamma _i\in \mathcal {K}$
with heteroclinics
$\gamma _i\in \mathcal {K}$
with heteroclinics
![]() $W_{\dot \gamma _i}\cap W^{s}(\dot \gamma _{i+1})\neq \varnothing $
. The same waist may appear at different times with opposite orientations in the sequence. Nevertheless, since the collection
$W_{\dot \gamma _i}\cap W^{s}(\dot \gamma _{i+1})\neq \varnothing $
. The same waist may appear at different times with opposite orientations in the sequence. Nevertheless, since the collection
![]() $\mathcal {G}$
is finite, there exists
$\mathcal {G}$
is finite, there exists
![]() $n\leq 2\,\#\mathcal {G}+1$
such that
$n\leq 2\,\#\mathcal {G}+1$
such that
![]() $\gamma _1=\gamma _n$
as oriented waists. This implies that
$\gamma _1=\gamma _n$
as oriented waists. This implies that
![]() $W_{\dot \gamma _1}\cap W^{s}(\dot \gamma _1)\neq \varnothing $
.
$W_{\dot \gamma _1}\cap W^{s}(\dot \gamma _1)\neq \varnothing $
.
Lemma 4.4. If the limit set K is non-empty and satisfies the transversality condition
then there exists
![]() $\gamma \in \mathcal {K}$
and another complete system of closed geodesics with limit subcollection contained in
$\gamma \in \mathcal {K}$
and another complete system of closed geodesics with limit subcollection contained in
![]() $\mathcal {K}\setminus \{\gamma \}$
.
$\mathcal {K}\setminus \{\gamma \}$
.
Proof. By Lemma 4.3, there exists
![]() $\gamma \in \mathcal {K}$
whose associated periodic orbit
$\gamma \in \mathcal {K}$
whose associated periodic orbit
![]() $\dot \gamma $
has homoclinics in all path-connected components of
$\dot \gamma $
has homoclinics in all path-connected components of
![]() $W^{u}(\dot \gamma )\setminus \dot \gamma $
. Since
$W^{u}(\dot \gamma )\setminus \dot \gamma $
. Since
![]() $\gamma $
is a non-degenerate waist, Lemma 2.7 implies that there exists a tubular neighborhood
$\gamma $
is a non-degenerate waist, Lemma 2.7 implies that there exists a tubular neighborhood
![]() $A\subset M$
of
$A\subset M$
of
![]() $\gamma $
and an open neighborhood
$\gamma $
and an open neighborhood
![]() $V\subset SM$
of
$V\subset SM$
of
![]() $\dot \gamma $
such that, if we denote by
$\dot \gamma $
such that, if we denote by
![]() $W\subset V\cap W^{u}(\dot \gamma )$
the path-connected component containing
$W\subset V\cap W^{u}(\dot \gamma )$
the path-connected component containing
![]() $\dot \gamma $
, the restriction of the base projection
$\dot \gamma $
, the restriction of the base projection
![]() $\pi |_W:W\to ~A$
is a diffeomorphism. An analogous statement holds for the stable manifold
$\pi |_W:W\to ~A$
is a diffeomorphism. An analogous statement holds for the stable manifold
![]() $W^{s}(\dot \gamma )$
. Therefore, for any homoclinic point
$W^{s}(\dot \gamma )$
. Therefore, for any homoclinic point
![]() $z\in W^{u}(\dot \gamma )\cap W^{s}(\dot \gamma )\setminus \dot \gamma $
, the corresponding geodesic
$z\in W^{u}(\dot \gamma )\cap W^{s}(\dot \gamma )\setminus \dot \gamma $
, the corresponding geodesic
![]() $\zeta (t):=\pi \circ \phi _t(z)$
is contained in
$\zeta (t):=\pi \circ \phi _t(z)$
is contained in
![]() $A\setminus \gamma $
provided
$A\setminus \gamma $
provided
![]() $|t|$
is large enough.
$|t|$
is large enough.
The complement
![]() $A\setminus \gamma $
is the disjoint union of two open annuli
$A\setminus \gamma $
is the disjoint union of two open annuli
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, and therefore
$A_2$
, and therefore
![]() $W\setminus \dot \gamma $
is the disjoint union of the open annuli
$W\setminus \dot \gamma $
is the disjoint union of the open annuli
![]() $W_1:=\pi |_W^{-1}(A_1)$
and
$W_1:=\pi |_W^{-1}(A_1)$
and
![]() $W_2:=\pi |_W^{-1}(A_2)$
. Our assumption on
$W_2:=\pi |_W^{-1}(A_2)$
. Our assumption on
![]() $\gamma $
implies that both
$\gamma $
implies that both
![]() $W_1$
and
$W_1$
and
![]() $W_2$
intersect the stable manifold
$W_2$
intersect the stable manifold
![]() $W^{s}(\dot \gamma )$
, and we fix homoclinic points
$W^{s}(\dot \gamma )$
, and we fix homoclinic points
![]() $z_i\in W_i\cap W^{s}(\dot \gamma )$
such that, if we denote by
$z_i\in W_i\cap W^{s}(\dot \gamma )$
such that, if we denote by
![]() $\zeta _i(t):=\pi \circ \phi _t(z)$
the associated geodesics, we have
$\zeta _i(t):=\pi \circ \phi _t(z)$
the associated geodesics, we have
![]() $\zeta _i(t)\in A_i$
for all
$\zeta _i(t)\in A_i$
for all
![]() $t\leq 0$
. We have two possible cases.
$t\leq 0$
. We have two possible cases.
Case 1: There exists
![]() $i\in \{1,2\}$
such that
$i\in \{1,2\}$
such that
![]() $\zeta _i(t)\in A_{3-i}$
for all
$\zeta _i(t)\in A_{3-i}$
for all
![]() $t>0$
large enough. For each
$t>0$
large enough. For each
![]() $\delta>0$
, there exist arbitrarily large
$\delta>0$
, there exist arbitrarily large
![]() $a,b>0$
such that the points
$a,b>0$
such that the points
![]() $\phi _{-a}(z_i)$
and
$\phi _{-a}(z_i)$
and
![]() $\phi _{b}(z_i)$
are
$\phi _{b}(z_i)$
are
![]() $\delta $
-close (where the distance on
$\delta $
-close (where the distance on
![]() $SM$
is the one induced by the Riemannian metric g). We consider the orbit segment
$SM$
is the one induced by the Riemannian metric g). We consider the orbit segment
and we extend it as a discontinuous periodic curve of period
![]() $\tau :=a+b$
.
$\tau :=a+b$
.
Case 2: For all
![]() $i\in \{1,2\}$
, we have
$i\in \{1,2\}$
, we have
![]() $\zeta _i(t)\in A_{i}$
for all
$\zeta _i(t)\in A_{i}$
for all
![]() $t>0$
large enough. For each
$t>0$
large enough. For each
![]() $\delta>0$
, there exist arbitrarily large
$\delta>0$
, there exist arbitrarily large
![]() $a_1,b_1,a_2,b_2>0$
such that the points
$a_1,b_1,a_2,b_2>0$
such that the points
![]() $\phi _{-a_i}(z_i)$
and
$\phi _{-a_i}(z_i)$
and
![]() $\phi _{b_i}(z_i)$
are
$\phi _{b_i}(z_i)$
are
![]() $\delta $
-close. We consider the orbit segments
$\delta $
-close. We consider the orbit segments
and we define
![]() $\Gamma _\delta $
to be the discontinuous periodic curve of period
$\Gamma _\delta $
to be the discontinuous periodic curve of period
![]() $\tau :=a_1+b_1+a_2+b_2$
obtained by extending periodically the concatenation of
$\tau :=a_1+b_1+a_2+b_2$
obtained by extending periodically the concatenation of
![]() $\Gamma _{\delta ,1}$
and
$\Gamma _{\delta ,1}$
and
![]() $\Gamma _{\delta ,2}$
.
$\Gamma _{\delta ,2}$
.
In both cases, for each
![]() $\delta>0$
, we obtained a periodic
$\delta>0$
, we obtained a periodic
![]() $\delta $
-pseudo orbit
$\delta $
-pseudo orbit
![]() $\Gamma _\delta $
of the geodesic flow with arbitrarily large minimal period. Moreover, the projection
$\Gamma _\delta $
of the geodesic flow with arbitrarily large minimal period. Moreover, the projection
![]() $\pi \circ \Gamma _\delta $
makes a
$\pi \circ \Gamma _\delta $
makes a
![]() $\delta $
-jump from
$\delta $
-jump from
![]() $A_1$
to
$A_1$
to
![]() $A_2$
. The shadowing lemma from hyperbolic dynamics [Reference Fisher and HasselblattFH19, Theorem 5.3.3] implies that, for each
$A_2$
. The shadowing lemma from hyperbolic dynamics [Reference Fisher and HasselblattFH19, Theorem 5.3.3] implies that, for each
![]() $\epsilon>0$
, there exist
$\epsilon>0$
, there exist
![]() $\delta>0$
and
$\delta>0$
and
![]() $z\in SM$
such that the orbit
$z\in SM$
such that the orbit
![]() $t\mapsto \phi _t(z)$
is periodic and pointwise
$t\mapsto \phi _t(z)$
is periodic and pointwise
![]() $\epsilon $
-close to
$\epsilon $
-close to
![]() $\Gamma _\delta $
up to a time reparameterization with Lipschitz constant
$\Gamma _\delta $
up to a time reparameterization with Lipschitz constant
![]() $\epsilon $
. Up to choosing
$\epsilon $
. Up to choosing
![]() $\epsilon>0$
small enough, the corresponding closed geodesic
$\epsilon>0$
small enough, the corresponding closed geodesic
![]() $\zeta (t):=\pi \circ \phi _t(z)$
must intersect
$\zeta (t):=\pi \circ \phi _t(z)$
must intersect
![]() $\gamma $
transversely.
$\gamma $
transversely.
Let
![]() $\mathcal {K}'$
be the subcollection of those simple closed geodesics
$\mathcal {K}'$
be the subcollection of those simple closed geodesics
![]() $\eta \in \mathcal {K}$
that intersect
$\eta \in \mathcal {K}$
that intersect
![]() $\zeta $
, which is non-empty since it contains
$\zeta $
, which is non-empty since it contains
![]() $\gamma $
. The collection
$\gamma $
. The collection
![]() $\mathcal {G}\cup \{\zeta \}$
is a complete system of closed geodesics with limit subcollection
$\mathcal {G}\cup \{\zeta \}$
is a complete system of closed geodesics with limit subcollection
![]() $\mathcal {K}\setminus \mathcal {K}'$
.
$\mathcal {K}\setminus \mathcal {K}'$
.
4.3 Proof of Theorems A, C, D and E
We first single out a suitable family of non-contractible waists, which is always available in every closed orientable Riemannian surface of positive genus.
Lemma 4.5. On any closed orientable Riemannian surface
![]() $(M,g)$
of genus
$(M,g)$
of genus
![]() $G\geq 1$
, there exist waists
$G\geq 1$
, there exist waists
![]() $\gamma _1,\ldots ,\gamma _{2G}$
such that:
$\gamma _1,\ldots ,\gamma _{2G}$
such that:
-
(i)
 $\gamma _i\cap \gamma _{i+1}$
is a singleton for all
$\gamma _i\cap \gamma _{i+1}$
is a singleton for all
 $i\in \{1,\ldots ,2G-1\}$
;
$i\in \{1,\ldots ,2G-1\}$
; -
(ii)
 $\gamma _i\cap \gamma _j=\varnothing $
if
$\gamma _i\cap \gamma _j=\varnothing $
if
 $|i-j|\geq 2$
;
$|i-j|\geq 2$
; -
(iii)
 $M\setminus (\gamma _1\cup \cdots \cup \gamma _{2G})$
is simply connected;
$M\setminus (\gamma _1\cup \cdots \cup \gamma _{2G})$
is simply connected; -
(iv) every
 $\gamma _i$
is a waist.
$\gamma _i$
is a waist.
Proof. We first consider non-contractible embedded loops
![]() $\zeta _1,\ldots ,\zeta _{2G}\subset M$
such that
$\zeta _1,\ldots ,\zeta _{2G}\subset M$
such that
![]() $\zeta _i\cap \zeta _{i+1}$
is a singleton for all
$\zeta _i\cap \zeta _{i+1}$
is a singleton for all
![]() $i\in \{1,\ldots ,2G-1\}$
,
$i\in \{1,\ldots ,2G-1\}$
,
![]() $\zeta _i\cap \zeta _j=\varnothing $
if
$\zeta _i\cap \zeta _j=\varnothing $
if
![]() $|i-j|\geq 2$
, and
$|i-j|\geq 2$
, and
![]() $M\setminus (\zeta _1\cup \cdots \cup \zeta _{2G})$
is simply connected (Figure 9). We denote by
$M\setminus (\zeta _1\cup \cdots \cup \zeta _{2G})$
is simply connected (Figure 9). We denote by
![]() $\mathcal {C}_i\subset \mathrm {Emb}(S^1,M)$
the connected component containing
$\mathcal {C}_i\subset \mathrm {Emb}(S^1,M)$
the connected component containing
![]() $\zeta _i$
. Notice that the
$\zeta _i$
. Notice that the
![]() $\mathcal {C}_i$
are pairwise distinct and the embedded loops
$\mathcal {C}_i$
are pairwise distinct and the embedded loops
![]() $\zeta _1,\ldots ,\zeta _{2G}$
are in minimal position: that is,
$\zeta _1,\ldots ,\zeta _{2G}$
are in minimal position: that is,
By Lemma 2.1, for each
![]() $i=1,\ldots ,2G$
, there exists a waist
$i=1,\ldots ,2G$
, there exists a waist
![]() $\gamma _i\in \mathcal {C}_i$
such that
$\gamma _i\in \mathcal {C}_i$
such that

Figure 9 The embedded loops
![]() $\zeta _1,\ldots ,\zeta _{2G}$
.
$\zeta _1,\ldots ,\zeta _{2G}$
.
We recall that a geodesic bigon is a compact disk
![]() $D\subset M$
whose boundary is the union of two geodesic arcs. For each
$D\subset M$
whose boundary is the union of two geodesic arcs. For each
![]() $i<j$
, there is no geodesic bigon bounded by an arc in
$i<j$
, there is no geodesic bigon bounded by an arc in
![]() $\alpha _i\subset \gamma _i$
and an arc
$\alpha _i\subset \gamma _i$
and an arc
![]() $\alpha _j\subset \gamma _j$
. Indeed, if there were such a geodesic bigon with
$\alpha _j\subset \gamma _j$
. Indeed, if there were such a geodesic bigon with
![]() $L(\alpha _i)\leq L(\alpha _j)$
, we could further shrink the simple closed geodesics
$L(\alpha _i)\leq L(\alpha _j)$
, we could further shrink the simple closed geodesics
![]() $\gamma _j$
and obtain a shorter embedded loop in the same homotopy class
$\gamma _j$
and obtain a shorter embedded loop in the same homotopy class
![]() $\mathcal {C}_j$
, which would contradict (4.3). By the bigon criterium [Reference Farb and MargalitFM12, Proposition 1.7], the waists
$\mathcal {C}_j$
, which would contradict (4.3). By the bigon criterium [Reference Farb and MargalitFM12, Proposition 1.7], the waists
![]() $\gamma _1,\ldots ,\gamma _{2G}$
are in minimal position. Therefore,
$\gamma _1,\ldots ,\gamma _{2G}$
are in minimal position. Therefore,
To prove that
![]() $B:=M\setminus (\gamma _1\cup \cdots \cup \gamma _{2G})$
is simply connected, we cut open the surface M at the simple closed geodesics
$B:=M\setminus (\gamma _1\cup \cdots \cup \gamma _{2G})$
is simply connected, we cut open the surface M at the simple closed geodesics
![]() $\gamma _2,\gamma _4,\ldots ,\gamma _{2G}$
, and we thus obtain a compact surface
$\gamma _2,\gamma _4,\ldots ,\gamma _{2G}$
, and we thus obtain a compact surface
![]() $M'$
of genus zero with
$M'$
of genus zero with
![]() $2G$
boundary components. Each waist
$2G$
boundary components. Each waist
![]() $\gamma _{2i}$
, with
$\gamma _{2i}$
, with
![]() $i=1,\ldots ,G$
, corresponds to two boundary components
$i=1,\ldots ,G$
, corresponds to two boundary components
![]() $\gamma _{2i}^+,\gamma _{2i}^-\subset \partial M'$
. Each waist
$\gamma _{2i}^+,\gamma _{2i}^-\subset \partial M'$
. Each waist
![]() $\gamma _{2i+1}$
, with
$\gamma _{2i+1}$
, with
![]() $i=1,\ldots ,G-1$
, splits into two embedded arcs
$i=1,\ldots ,G-1$
, splits into two embedded arcs
![]() $\gamma _{2i+1}^+,\gamma _{2i+1}^-$
; the arc
$\gamma _{2i+1}^+,\gamma _{2i+1}^-$
; the arc
![]() $\gamma _{2i+1}^\pm $
joins the boundary components
$\gamma _{2i+1}^\pm $
joins the boundary components
![]() $\gamma _{2i}^\pm $
and
$\gamma _{2i}^\pm $
and
![]() $\gamma _{2i+2}^\pm $
. Finally, the waist
$\gamma _{2i+2}^\pm $
. Finally, the waist
![]() $\gamma _1$
corresponds to an embedded arc
$\gamma _1$
corresponds to an embedded arc
![]() $\gamma _1^+$
joining the boundary components
$\gamma _1^+$
joining the boundary components
![]() $\gamma _2^+$
and
$\gamma _2^+$
and
![]() $\gamma _2^-$
. We now cut open
$\gamma _2^-$
. We now cut open
![]() $M'$
along the embedded arcs
$M'$
along the embedded arcs
![]() $\gamma _{2i+1}^\pm $
and obtain a compact disk
$\gamma _{2i+1}^\pm $
and obtain a compact disk
![]() $M"$
. The interior
$M"$
. The interior
![]() $\operatorname {\mathrm {int}}(M")$
is diffeomorphic to B.
$\operatorname {\mathrm {int}}(M")$
is diffeomorphic to B.
By means of Fried surgery, we produce a connected surface of section out of the union of the Birkhoff annuli of the waists given by Lemma 4.5.
Lemma 4.6. Let
![]() $\gamma _1,\ldots ,\gamma _{2G}$
be the waists provided by Lemma 4.5 and consider the union of the associated Birkhoff annuli
$\gamma _1,\ldots ,\gamma _{2G}$
be the waists provided by Lemma 4.5 and consider the union of the associated Birkhoff annuli
 $$ \begin{align} \Upsilon:=\bigcup_{i=1}^{2G} (A(\dot\gamma_i)\cup A(-\dot\gamma_i)). \end{align} $$
$$ \begin{align} \Upsilon:=\bigcup_{i=1}^{2G} (A(\dot\gamma_i)\cup A(-\dot\gamma_i)). \end{align} $$
For each open neighborhood
![]() $V\subset SM$
of
$V\subset SM$
of
![]() $\Upsilon $
, there exists a surface of section
$\Upsilon $
, there exists a surface of section
with the following properties.
-
(i)
 $\Sigma $
is a compact connected surface of genus one and
$\Sigma $
is a compact connected surface of genus one and
 $8G-4$
boundary components.
$8G-4$
boundary components. -
(ii) The restriction
is a double cover. The preimages $$ \begin{align*}\iota|_{\partial\Sigma}:\partial\Sigma\to\bigcup_{i=1}^{2G}(\dot\gamma_i\cup-\dot\gamma_i)\end{align*} $$
$$ \begin{align*}\iota|_{\partial\Sigma}:\partial\Sigma\to\bigcup_{i=1}^{2G}(\dot\gamma_i\cup-\dot\gamma_i)\end{align*} $$
 $\iota ^{-1}(\dot \gamma _i)$
and
$\iota ^{-1}(\dot \gamma _i)$
and
 $\iota ^{-1}(-\dot \gamma _i)$
are connected if
$\iota ^{-1}(-\dot \gamma _i)$
are connected if
 $i\in \{1,2G\}$
, and they have two connected components each if
$i\in \{1,2G\}$
, and they have two connected components each if
 $G>1$
and
$G>1$
and
 $2\leq i\leq 2G-1$
.
$2\leq i\leq 2G-1$
.
-
(iii) There exist
 $\ell>0$
such that, for each
$\ell>0$
such that, for each
 $z\in SM$
sufficiently close to
$z\in SM$
sufficiently close to
 $\partial \Sigma $
, we have
$\partial \Sigma $
, we have
 $\phi _{[-\ell ,0)}(z)\cap \Sigma \neq \varnothing $
and
$\phi _{[-\ell ,0)}(z)\cap \Sigma \neq \varnothing $
and
 $\phi _{(0,\ell ]}(z)\cap \Sigma \neq \varnothing $
.
$\phi _{(0,\ell ]}(z)\cap \Sigma \neq \varnothing $
. -
(iv) For each
 $z\in \Upsilon $
, we have
$z\in \Upsilon $
, we have
 $\phi _{(-1,1)}(z)\cap \Sigma \neq \varnothing $
, and, for each
$\phi _{(-1,1)}(z)\cap \Sigma \neq \varnothing $
, and, for each
 $z'\in \Sigma $
, we have
$z'\in \Sigma $
, we have
 $\phi _{(-1,1)}(z')\cap \Upsilon \neq \varnothing $
.
$\phi _{(-1,1)}(z')\cap \Upsilon \neq \varnothing $
.
Proof. We see
![]() $\Upsilon $
as a non-injectively immersed surface in
$\Upsilon $
as a non-injectively immersed surface in
![]() $SM$
with boundary and interior
$SM$
with boundary and interior
 $$ \begin{align*}\partial\Upsilon=\bigcup_{i=1}^{2G} (\dot\gamma_i\cup-\dot\gamma_i), \quad \operatorname{\mathrm{int}}(\Upsilon)=\bigcup_{i=1}^{2G}(\operatorname{\mathrm{int}}(A_i^+)\cup\operatorname{\mathrm{int}}(A_i^-)), \end{align*} $$
$$ \begin{align*}\partial\Upsilon=\bigcup_{i=1}^{2G} (\dot\gamma_i\cup-\dot\gamma_i), \quad \operatorname{\mathrm{int}}(\Upsilon)=\bigcup_{i=1}^{2G}(\operatorname{\mathrm{int}}(A_i^+)\cup\operatorname{\mathrm{int}}(A_i^-)), \end{align*} $$
where
![]() $A_i^\pm :=A(\pm \dot \gamma _i)$
. We set
$A_i^\pm :=A(\pm \dot \gamma _i)$
. We set
![]() $\ell _0:=\max \{L(\gamma _1),\ldots ,L(\gamma _{2G})\}$
. Since
$\ell _0:=\max \{L(\gamma _1),\ldots ,L(\gamma _{2G})\}$
. Since
![]() $\gamma _i$
intersects
$\gamma _i$
intersects
![]() $\gamma _{i-1}$
and
$\gamma _{i-1}$
and
![]() $\gamma _{i+1}$
for all
$\gamma _{i+1}$
for all
![]() $2\leq i\leq 2G-1$
, we have
$2\leq i\leq 2G-1$
, we have
![]() $\phi _{[2,\ell _0+2]}(z)\cap \operatorname {\mathrm {int}}(\Upsilon )\neq \varnothing $
for all
$\phi _{[2,\ell _0+2]}(z)\cap \operatorname {\mathrm {int}}(\Upsilon )\neq \varnothing $
for all
![]() $z\in \partial \Upsilon $
. Therefore, there exists an open neighborhood
$z\in \partial \Upsilon $
. Therefore, there exists an open neighborhood
![]() $N\subset SM$
of
$N\subset SM$
of
![]() $\partial \Upsilon $
such that
$\partial \Upsilon $
such that
Let
![]() $V\subset SM$
be an open neighborhood of
$V\subset SM$
be an open neighborhood of
![]() $\Upsilon $
. We apply Fried surgeries in an arbitrarily small neighborhood of the self-intersection points of
$\Upsilon $
. We apply Fried surgeries in an arbitrarily small neighborhood of the self-intersection points of
![]() $\Upsilon $
, as explained in §4.1, and obtain a surface of section
$\Upsilon $
, as explained in §4.1, and obtain a surface of section
![]() $\iota :\Sigma \looparrowright V$
with the same boundary
$\iota :\Sigma \looparrowright V$
with the same boundary
![]() $\partial \Sigma =\partial \Upsilon $
and satisfying point (iv) in the statement of the lemma. This, together with (4.5), implies point (iii) for
$\partial \Sigma =\partial \Upsilon $
and satisfying point (iv) in the statement of the lemma. This, together with (4.5), implies point (iii) for
![]() $\ell :=\ell _0+4$
.
$\ell :=\ell _0+4$
.
We claim that the interior
![]() $\operatorname {\mathrm {int}}(\Sigma )$
is path connected. Indeed, near the point in
$\operatorname {\mathrm {int}}(\Sigma )$
is path connected. Indeed, near the point in
![]() $\operatorname {\mathrm {int}}(A_1^+)\cap \partial A_2^+\cap \partial A_2^-$
, Fried surgery glues together the intersecting annuli
$\operatorname {\mathrm {int}}(A_1^+)\cap \partial A_2^+\cap \partial A_2^-$
, Fried surgery glues together the intersecting annuli
![]() $A_1^+$
,
$A_1^+$
,
![]() $A_2^-$
and
$A_2^-$
and
![]() $A_2^+$
in the same connected component of
$A_2^+$
in the same connected component of
![]() $\operatorname {\mathrm {int}}(\Sigma )$
, as is clear from Figures 6 and 8; analogously, near the point in
$\operatorname {\mathrm {int}}(\Sigma )$
, as is clear from Figures 6 and 8; analogously, near the point in
![]() $\operatorname {\mathrm {int}}(A_1^-)\cap \partial A_2^+\cap \partial A_2^-$
, Fried surgery glues together the intersecting annuli
$\operatorname {\mathrm {int}}(A_1^-)\cap \partial A_2^+\cap \partial A_2^-$
, Fried surgery glues together the intersecting annuli
![]() $A_1^-$
,
$A_1^-$
,
![]() $A_2^-$
and
$A_2^-$
and
![]() $A_2^+$
. Therefore, the surgery sends the four annuli
$A_2^+$
. Therefore, the surgery sends the four annuli
![]() $A_1^+$
,
$A_1^+$
,
![]() $A_1^-$
,
$A_1^-$
,
![]() $A_2^+$
and
$A_2^+$
and
![]() $A_2^-$
to the same path-connected component of
$A_2^-$
to the same path-connected component of
![]() $\operatorname {\mathrm {int}}(\Sigma )$
. Assume, by induction, that Fried surgery sends the annuli
$\operatorname {\mathrm {int}}(\Sigma )$
. Assume, by induction, that Fried surgery sends the annuli
![]() $A_1^+,A_1^-,\ldots ,A_{i}^+,A_{i}^-$
to the same path-connected component
$A_1^+,A_1^-,\ldots ,A_{i}^+,A_{i}^-$
to the same path-connected component
![]() $W\subset \operatorname {\mathrm {int}}(\Sigma )$
. Near the point in
$W\subset \operatorname {\mathrm {int}}(\Sigma )$
. Near the point in
![]() $A_i^+\cap \partial A_{i+1}^+\cap \partial A_{i+1}^-$
, Fried surgery glues together the intersecting annuli
$A_i^+\cap \partial A_{i+1}^+\cap \partial A_{i+1}^-$
, Fried surgery glues together the intersecting annuli
![]() $A_{i}^+$
,
$A_{i}^+$
,
![]() $A_{i+1}^-$
and
$A_{i+1}^-$
and
![]() $A_{i+1}^+$
. Therefore, the surgery sends
$A_{i+1}^+$
. Therefore, the surgery sends
![]() $A_{i+1}^-$
and
$A_{i+1}^-$
and
![]() $A_{i+1}^+$
to the connected component W as well, and we conclude that
$A_{i+1}^+$
to the connected component W as well, and we conclude that
![]() $W=\operatorname {\mathrm {int}}(\Sigma )$
.
$W=\operatorname {\mathrm {int}}(\Sigma )$
.
We now determine the number of connected components of the boundary
![]() $\partial \Sigma $
and how they cover the closed orbits
$\partial \Sigma $
and how they cover the closed orbits
![]() $\pm \dot \gamma _i$
. The simple closed geodesic
$\pm \dot \gamma _i$
. The simple closed geodesic
![]() $\gamma _1$
intersects
$\gamma _1$
intersects
![]() $\gamma _2$
in one point, but does not intersect any of the other simple closed geodesics
$\gamma _2$
in one point, but does not intersect any of the other simple closed geodesics
![]() $\gamma _3,\ldots ,\gamma _{2G}$
; therefore,
$\gamma _3,\ldots ,\gamma _{2G}$
; therefore,
![]() $\dot \gamma _1$
intersects the interior of the Birkhoff annulus
$\dot \gamma _1$
intersects the interior of the Birkhoff annulus
![]() $\operatorname {\mathrm {int}}(A_2^+)$
in one point, but does not intersect any of the other Birkhoff annuli
$\operatorname {\mathrm {int}}(A_2^+)$
in one point, but does not intersect any of the other Birkhoff annuli
![]() $A_i^\pm $
. Analogously,
$A_i^\pm $
. Analogously,
![]() $-\dot \gamma _1$
intersects
$-\dot \gamma _1$
intersects
![]() $\operatorname {\mathrm {int}}(A_2^-)$
in one point but none of the other
$\operatorname {\mathrm {int}}(A_2^-)$
in one point but none of the other
![]() $A_i^\pm $
. Therefore, there is a unique connected component of
$A_i^\pm $
. Therefore, there is a unique connected component of
![]() $\partial \Sigma $
that covers
$\partial \Sigma $
that covers
![]() $\dot \gamma _1$
, and such a connected component winds around
$\dot \gamma _1$
, and such a connected component winds around
![]() $\dot \gamma _1$
twice; analogously, there is a unique connected component of
$\dot \gamma _1$
twice; analogously, there is a unique connected component of
![]() $\partial \Sigma $
that covers
$\partial \Sigma $
that covers
![]() $-\dot \gamma _1$
, and such a connected component winds around
$-\dot \gamma _1$
, and such a connected component winds around
![]() $-\dot \gamma _1$
twice (Figure 10). The same conclusions hold for
$-\dot \gamma _1$
twice (Figure 10). The same conclusions hold for
![]() $\gamma _{2G}$
. For each
$\gamma _{2G}$
. For each
![]() $i\in \{2,\ldots ,2G-1\}$
,
$i\in \{2,\ldots ,2G-1\}$
,
![]() $\gamma _i$
intersects
$\gamma _i$
intersects
![]() $\gamma _{i-1}$
and
$\gamma _{i-1}$
and
![]() $\gamma _{i+1}$
in one point each, but does not intersect any other
$\gamma _{i+1}$
in one point each, but does not intersect any other
![]() $\gamma _j$
; therefore,
$\gamma _j$
; therefore,
![]() $\dot \gamma _i$
intersects the interiors of the Birkhoff annuli
$\dot \gamma _i$
intersects the interiors of the Birkhoff annuli
![]() $\operatorname {\mathrm {int}}(A_{i-1}^-)$
and
$\operatorname {\mathrm {int}}(A_{i-1}^-)$
and
![]() $\operatorname {\mathrm {int}}(A_{i+1}^+)$
in one point each, but does not intersect any of the other Birkhoff annuli
$\operatorname {\mathrm {int}}(A_{i+1}^+)$
in one point each, but does not intersect any of the other Birkhoff annuli
![]() $A_j^\pm $
; analogously,
$A_j^\pm $
; analogously,
![]() $-\dot \gamma _i$
intersects
$-\dot \gamma _i$
intersects
![]() $A_{i-1}^+$
and
$A_{i-1}^+$
and
![]() $A_{i+1}^-$
in one point each, but does not intersect any other
$A_{i+1}^-$
in one point each, but does not intersect any other
![]() $A_j^\pm $
. Therefore, there are two connected components of
$A_j^\pm $
. Therefore, there are two connected components of
![]() $\partial \Sigma $
that are mapped diffeomorphically to
$\partial \Sigma $
that are mapped diffeomorphically to
![]() $\dot \gamma _i$
and two other connected components of
$\dot \gamma _i$
and two other connected components of
![]() $\partial \Sigma $
that are mapped diffeomorphically to
$\partial \Sigma $
that are mapped diffeomorphically to
![]() $-\dot \gamma _i$
(Figure 11). All together,
$-\dot \gamma _i$
(Figure 11). All together,
![]() $\partial \Sigma $
has
$\partial \Sigma $
has
![]() $8G-4$
boundary components.
$8G-4$
boundary components.

Figure 10 The surface
![]() $\Sigma $
near the boundary component
$\Sigma $
near the boundary component
![]() $-\dot \gamma _1$
.
$-\dot \gamma _1$
.

Figure 11 The surface
![]() $\Sigma $
near the boundary component
$\Sigma $
near the boundary component
![]() $-\dot \gamma _i$
, for
$-\dot \gamma _i$
, for
![]() $2\leq i\leq 2G-1$
. Notice that there are two open annuli in
$2\leq i\leq 2G-1$
. Notice that there are two open annuli in
![]() $\operatorname {\mathrm {int}}(\Sigma )$
having boundary on
$\operatorname {\mathrm {int}}(\Sigma )$
having boundary on
![]() $-\dot \gamma _i$
.
$-\dot \gamma _i$
.
Since
![]() $\operatorname {\mathrm {int}}(\Sigma )$
is transverse to the geodesic vector field X,
$\operatorname {\mathrm {int}}(\Sigma )$
is transverse to the geodesic vector field X,
![]() $\Sigma $
is orientable. Indeed, the Liouville contact form
$\Sigma $
is orientable. Indeed, the Liouville contact form
![]() $\unicode{x3bb} $
of
$\unicode{x3bb} $
of
![]() $SM$
induces an area form
$SM$
induces an area form
![]() $d\unicode{x3bb} |_{\operatorname {\mathrm {int}}(\Sigma )}$
. To compute the genus of
$d\unicode{x3bb} |_{\operatorname {\mathrm {int}}(\Sigma )}$
. To compute the genus of
![]() $\Sigma $
, we first triangulate every Birkhoff annulus
$\Sigma $
, we first triangulate every Birkhoff annulus
![]() $A_i^\pm $
with 6 vertices, 14 edges and 8 faces. We choose such triangulations so that, along the intersections
$A_i^\pm $
with 6 vertices, 14 edges and 8 faces. We choose such triangulations so that, along the intersections
![]() $A_i^+\cap A_i^-$
,
$A_i^+\cap A_i^-$
,
![]() $A_i^\pm \cap A_{i+1}^\pm $
and
$A_i^\pm \cap A_{i+1}^\pm $
and
![]() $A_i^\pm \cap A_{i+1}^\mp $
, the vertices and edges of
$A_i^\pm \cap A_{i+1}^\mp $
, the vertices and edges of
![]() $A_{i}^\pm $
and
$A_{i}^\pm $
and
![]() $A_{i+1}^\pm $
match as in Figure 12. All together,
$A_{i+1}^\pm $
match as in Figure 12. All together,
![]() $\Upsilon $
is triangulated with
$\Upsilon $
is triangulated with
![]() $24\,G$
vertices,
$24\,G$
vertices,
![]() $56\,G$
edges and
$56\,G$
edges and
![]() $32\,G$
faces (once again, we stress that
$32\,G$
faces (once again, we stress that
![]() $\Upsilon $
must be seen as an immersed compact surface with boundary, and therefore distinct Birkhoff annuli do not share vertices, edges or faces). The same number of edges and faces can be used to triangulate
$\Upsilon $
must be seen as an immersed compact surface with boundary, and therefore distinct Birkhoff annuli do not share vertices, edges or faces). The same number of edges and faces can be used to triangulate
![]() $\Sigma $
as well; however, the triangulation of
$\Sigma $
as well; however, the triangulation of
![]() $\Upsilon $
provides one extra vertex for each of the points
$\Upsilon $
provides one extra vertex for each of the points
![]() $x_i,y_i,w_i,z_i$
depicted in Figure 12, where
$x_i,y_i,w_i,z_i$
depicted in Figure 12, where
![]() $i=1,\ldots ,2G-1$
, and therefore we need to throw away
$i=1,\ldots ,2G-1$
, and therefore we need to throw away
![]() $8\,G-4$
vertices. All together,
$8\,G-4$
vertices. All together,
![]() $\Sigma $
is triangulated with
$\Sigma $
is triangulated with
![]() $16\,G+4$
vertices,
$16\,G+4$
vertices,
![]() $56\,G$
edges and
$56\,G$
edges and
![]() $32\,G$
faces, and therefore has Euler characteristic
$32\,G$
faces, and therefore has Euler characteristic
Since
we conclude that
![]() $\Sigma $
has genus one.
$\Sigma $
has genus one.
In the following, we shall employ the notion of a complete system of closed geodesics, which we introduced in Definition 4.1. Theorem A is a consequence of the following statement.

Figure 12 Triangulation of
![]() $A_i^+\cup A_i^-\cup A_{i+1}^+\cup A_{i+1}^-$
.
$A_i^+\cup A_i^-\cup A_{i+1}^+\cup A_{i+1}^-$
.
Theorem 4.7. Let
![]() $(M,g)$
be a closed oriented Riemannian surface of positive genus, let
$(M,g)$
be a closed oriented Riemannian surface of positive genus, let
![]() $\gamma _1,\ldots ,\gamma _{2G}$
be the waists provided by Lemma 4.5 and let
$\gamma _1,\ldots ,\gamma _{2G}$
be the waists provided by Lemma 4.5 and let
![]() $\Sigma $
be the surface of section provided by Lemma 4.6. If the open disk
$\Sigma $
be the surface of section provided by Lemma 4.6. If the open disk
![]() $M\setminus (\gamma _1\cup \cdots \cup \gamma _{2G})$
does not contain any simple closed geodesic without conjugate points, then
$M\setminus (\gamma _1\cup \cdots \cup \gamma _{2G})$
does not contain any simple closed geodesic without conjugate points, then
![]() $\Sigma $
is a Birkhoff section.
$\Sigma $
is a Birkhoff section.
Proof. With the terminology of Example 3.2, the open disk
![]() $B:=M\setminus (\gamma _1\cup \cdots \cup \gamma _{2G})$
is a convex geodesic polygon and, in particular, satisfies Assumption 3.1. Since B does not contain any simple closed geodesic without conjugate points, Theorem 3.4 implies that we have empty trapped sets
$B:=M\setminus (\gamma _1\cup \cdots \cup \gamma _{2G})$
is a convex geodesic polygon and, in particular, satisfies Assumption 3.1. Since B does not contain any simple closed geodesic without conjugate points, Theorem 3.4 implies that we have empty trapped sets
![]() $\mathrm {trap}_+(SB)=\mathrm {trap}_-(SB)=\varnothing $
. Therefore, the collection of waists
$\mathrm {trap}_+(SB)=\mathrm {trap}_-(SB)=\varnothing $
. Therefore, the collection of waists
![]() $\{\gamma _1,\ldots ,\gamma _{2G}\}$
is a complete system of closed geodesics with empty limit subcollection. Let
$\{\gamma _1,\ldots ,\gamma _{2G}\}$
is a complete system of closed geodesics with empty limit subcollection. Let
![]() $\Upsilon $
be the union of the Birkhoff annuli of the waists
$\Upsilon $
be the union of the Birkhoff annuli of the waists
![]() $\gamma _1,\ldots ,\gamma _{2G}$
, as in (4.4). By Lemma 4.2, there exists
$\gamma _1,\ldots ,\gamma _{2G}$
, as in (4.4). By Lemma 4.2, there exists
![]() $\ell>0$
such that, for each
$\ell>0$
such that, for each
![]() $z\in SM$
, the orbit segment
$z\in SM$
, the orbit segment
![]() $\phi _{[0,\ell ]}(z)$
intersects
$\phi _{[0,\ell ]}(z)$
intersects
![]() $\Upsilon $
. This, together with Lemma 4.6(iv), implies that, for each
$\Upsilon $
. This, together with Lemma 4.6(iv), implies that, for each
![]() $z\in SM$
, the orbit segment
$z\in SM$
, the orbit segment
![]() $\phi _{(0,\ell +2)}(z)$
intersects
$\phi _{(0,\ell +2)}(z)$
intersects
![]() $\Sigma $
. Therefore,
$\Sigma $
. Therefore,
![]() $\Sigma $
is a Birkhoff section.
$\Sigma $
is a Birkhoff section.
The proof of Theorem C is analogous. We rewrite the statement for the reader’s convenience.
Theorem C. Let
![]() $(S^2,g)$
be a Riemannian 2-sphere and let
$(S^2,g)$
be a Riemannian 2-sphere and let
![]() $\gamma $
be a simple closed geodesic with conjugate points whose complement
$\gamma $
be a simple closed geodesic with conjugate points whose complement
![]() $S^2\setminus \gamma $
does not contain simple closed geodesics without conjugate points. Then both Birkhoff annuli
$S^2\setminus \gamma $
does not contain simple closed geodesics without conjugate points. Then both Birkhoff annuli
![]() $A(\dot \gamma )$
and
$A(\dot \gamma )$
and
![]() $A(-\dot \gamma )$
are Birkhoff sections.
$A(-\dot \gamma )$
are Birkhoff sections.
Proof. Both connected components
![]() $B_1$
and
$B_1$
and
![]() $B_2$
of the complement
$B_2$
of the complement
![]() $S^2\setminus \gamma $
satisfy the convexity Assumption 3.1. Since
$S^2\setminus \gamma $
satisfy the convexity Assumption 3.1. Since
![]() $B_1$
and
$B_1$
and
![]() $B_2$
do not contain any simple closed geodesic without conjugate points, Theorem 3.4 implies that we have empty trapped sets
$B_2$
do not contain any simple closed geodesic without conjugate points, Theorem 3.4 implies that we have empty trapped sets
![]() $\mathrm {trap}_\pm (S(B_1\cup B_2))=\varnothing $
. Therefore,
$\mathrm {trap}_\pm (S(B_1\cup B_2))=\varnothing $
. Therefore,
![]() $\{\gamma \}$
is a complete system of closed geodesics with empty limit subcollection. By Lemma 4.2, there exists
$\{\gamma \}$
is a complete system of closed geodesics with empty limit subcollection. By Lemma 4.2, there exists
![]() $\ell>0$
such that any geodesic segment of length
$\ell>0$
such that any geodesic segment of length
![]() $\ell $
intersects
$\ell $
intersects
![]() $\gamma $
. This implies that both Birkhoff annuli
$\gamma $
. This implies that both Birkhoff annuli
![]() $A(\dot \gamma )$
and
$A(\dot \gamma )$
and
![]() $A(-\dot \gamma )$
are Birkhoff sections.
$A(-\dot \gamma )$
are Birkhoff sections.
We recall that a consequence of the Lusternik–Schnirelmann theorem is that every Riemannian 2-sphere admits a simple closed geodesic with conjugate points (see Remark 1.1).
Lemma 4.8. Let
![]() $(M,g)$
be a closed connected oriented Riemannian surface all of whose contractible simple closed geodesics without conjugate points are non-degenerate. If
$(M,g)$
be a closed connected oriented Riemannian surface all of whose contractible simple closed geodesics without conjugate points are non-degenerate. If
![]() $M\neq S^2$
, we consider the collection of waists
$M\neq S^2$
, we consider the collection of waists
![]() $\mathcal {G}'=\{\gamma _1,\ldots ,\gamma _{2G}\}$
given by Lemma 4.5; if, instead,
$\mathcal {G}'=\{\gamma _1,\ldots ,\gamma _{2G}\}$
given by Lemma 4.5; if, instead,
![]() $M=S^2$
, we set
$M=S^2$
, we set
![]() $\mathcal {G}'=\{\gamma \}$
, where
$\mathcal {G}'=\{\gamma \}$
, where
![]() $\gamma $
is any simple closed geodesic with conjugate points. There exists a possibly empty finite collection
$\gamma $
is any simple closed geodesic with conjugate points. There exists a possibly empty finite collection
![]() $\mathcal {G}"$
of contractible simple closed geodesics that are pairwise disjoint and disjoint from all the closed geodesics in
$\mathcal {G}"$
of contractible simple closed geodesics that are pairwise disjoint and disjoint from all the closed geodesics in
![]() $\mathcal {G}'$
such that
$\mathcal {G}'$
such that
![]() $\mathcal {G}:=\mathcal {G}'\cup \mathcal {G}"$
is a complete system of closed geodesics whose limit subcollection
$\mathcal {G}:=\mathcal {G}'\cup \mathcal {G}"$
is a complete system of closed geodesics whose limit subcollection
![]() $\mathcal {K}$
is given by the waists in
$\mathcal {K}$
is given by the waists in
![]() $\mathcal {G}"$
.
$\mathcal {G}"$
.
Proof. First, assume that M has genus
![]() $G\geq 1$
, so that
$G\geq 1$
, so that
![]() $\mathcal {G}'=\{\gamma _1,\ldots ,\gamma _{2G}\}$
. The complement
$\mathcal {G}'=\{\gamma _1,\ldots ,\gamma _{2G}\}$
. The complement
![]() $B\setminus (\gamma _1\cup \cdots \cup \gamma _{2G})$
satisfies the convexity Assumption 3.1. Since every closed geodesic
$B\setminus (\gamma _1\cup \cdots \cup \gamma _{2G})$
satisfies the convexity Assumption 3.1. Since every closed geodesic
![]() $\gamma \in \mathcal {G}'$
intersects some other closed geodesic in
$\gamma \in \mathcal {G}'$
intersects some other closed geodesic in
![]() $\mathcal {G}'$
, if we fix
$\mathcal {G}'$
, if we fix
![]() $\ell> L(\gamma )$
, for every
$\ell> L(\gamma )$
, for every
![]() $z\in SM$
sufficiently close to
$z\in SM$
sufficiently close to
![]() $\dot \gamma \cup -\dot \gamma $
, then the orbit segment
$\dot \gamma \cup -\dot \gamma $
, then the orbit segment
![]() $\phi _{(0,\ell ]}(z)$
is not contained in
$\phi _{(0,\ell ]}(z)$
is not contained in
![]() $SB$
. If B does not contain simple closed geodesics, then Theorem 3.4 implies that
$SB$
. If B does not contain simple closed geodesics, then Theorem 3.4 implies that
![]() $\mathrm {trap}_\pm (SB)=\varnothing $
, and therefore
$\mathrm {trap}_\pm (SB)=\varnothing $
, and therefore
![]() $\mathcal {G}'$
is a complete system of closed geodesics with empty limit subcollection
$\mathcal {G}'$
is a complete system of closed geodesics with empty limit subcollection
![]() $\mathcal {K}=\varnothing $
. Now assume that B contains at least a closed geodesic. By Theorem 3.5, B contains a finite collection of pairwise disjoint simple closed geodesics
$\mathcal {K}=\varnothing $
. Now assume that B contains at least a closed geodesic. By Theorem 3.5, B contains a finite collection of pairwise disjoint simple closed geodesics
![]() $\mathcal {G}"$
such that:
$\mathcal {G}"$
such that:
-
• no complete geodesic is entirely contained in
 $$ \begin{align*}U:=B\setminus\bigcup_{\zeta\in\mathcal{G}"}\zeta;\end{align*} $$
$$ \begin{align*}U:=B\setminus\bigcup_{\zeta\in\mathcal{G}"}\zeta;\end{align*} $$
-
• if we denote by
 $\mathcal {K}$
the subcollection of the waists in
$\mathcal {K}$
the subcollection of the waists in
 $\mathcal {G}"$
, and we set the trapped sets of
$\mathcal {G}"$
, and we set the trapped sets of $$ \begin{align*} K:=\bigcup_{\gamma\in\mathcal{K}} (\dot\gamma\cup-\dot\gamma), \end{align*} $$
$$ \begin{align*} K:=\bigcup_{\gamma\in\mathcal{K}} (\dot\gamma\cup-\dot\gamma), \end{align*} $$
 $SU$
are given by
$SU$
are given by  $$ \begin{align*} \mathrm{trap}_+(SU)= W^{s}(K)\setminus K,\quad \mathrm{trap}_-(SU)= W^{u}(K)\setminus K. \end{align*} $$
$$ \begin{align*} \mathrm{trap}_+(SU)= W^{s}(K)\setminus K,\quad \mathrm{trap}_-(SU)= W^{u}(K)\setminus K. \end{align*} $$
Since every
![]() $\gamma \in \mathcal {G}"\setminus \mathcal {K}$
has conjugate points, Corollary 2.10 implies that there exists
$\gamma \in \mathcal {G}"\setminus \mathcal {K}$
has conjugate points, Corollary 2.10 implies that there exists
![]() $\ell>0$
such that, for every
$\ell>0$
such that, for every
![]() $z\in SM$
sufficiently close to
$z\in SM$
sufficiently close to
![]() $\dot \gamma \cup -\dot \gamma $
, the orbit segment
$\dot \gamma \cup -\dot \gamma $
, the orbit segment
![]() $\phi _{(0,\ell ]}(z)$
is not contained in
$\phi _{(0,\ell ]}(z)$
is not contained in
![]() $SU$
. This proves that the union
$SU$
. This proves that the union
![]() $\mathcal {G}:=\mathcal {G}'\cup \mathcal {G}"$
is a complete system of closed geodesics with limit subcollection
$\mathcal {G}:=\mathcal {G}'\cup \mathcal {G}"$
is a complete system of closed geodesics with limit subcollection
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Now assume that
![]() $M=S^2$
so that the collection
$M=S^2$
so that the collection
![]() $\mathcal {G}'$
consists in just one simple closed geodesic
$\mathcal {G}'$
consists in just one simple closed geodesic
![]() $\gamma $
with conjugate points. Let
$\gamma $
with conjugate points. Let
![]() $B_1$
and
$B_1$
and
![]() $B_2$
be the connected components of the complement
$B_2$
be the connected components of the complement
![]() $S^2\setminus \gamma $
. Since
$S^2\setminus \gamma $
. Since
![]() $\gamma $
has conjugate points, each
$\gamma $
has conjugate points, each
![]() $B_i$
satisfies the convexity Assumption 3.1. Corollary 2.10 implies that there exists
$B_i$
satisfies the convexity Assumption 3.1. Corollary 2.10 implies that there exists
![]() $\ell>0$
such that, for every
$\ell>0$
such that, for every
![]() $z\in SM$
sufficiently close to
$z\in SM$
sufficiently close to
![]() $\dot \gamma \cup -\dot \gamma $
, the orbit segment
$\dot \gamma \cup -\dot \gamma $
, the orbit segment
![]() $\phi _{(0,\ell ]}(z)$
is not contained in
$\phi _{(0,\ell ]}(z)$
is not contained in
![]() $S(B_1\cup B_2)$
. If
$S(B_1\cup B_2)$
. If
![]() $S^2\setminus \gamma $
does not contain any simple closed geodesic, then Theorem 3.4 implies that
$S^2\setminus \gamma $
does not contain any simple closed geodesic, then Theorem 3.4 implies that
![]() $\mathrm {trap}_\pm (sb:1)\cup \mathrm {trap}_\pm (sb:2)=\varnothing $
, and therefore
$\mathrm {trap}_\pm (sb:1)\cup \mathrm {trap}_\pm (sb:2)=\varnothing $
, and therefore
![]() $\mathcal {G}'$
is a complete system of closed geodesics with empty limit subcollection
$\mathcal {G}'$
is a complete system of closed geodesics with empty limit subcollection
![]() $\mathcal {K}=\varnothing $
. If
$\mathcal {K}=\varnothing $
. If
![]() $S^2\setminus \gamma $
contains closed geodesics, then we argue as in the previous paragraph in both
$S^2\setminus \gamma $
contains closed geodesics, then we argue as in the previous paragraph in both
![]() $B_1$
and
$B_1$
and
![]() $B_2$
, and we find another collection
$B_2$
, and we find another collection
![]() $\mathcal {G}"$
of pairwise disjoint simple closed geodesics in
$\mathcal {G}"$
of pairwise disjoint simple closed geodesics in
![]() $B_1\cup B_2$
that, together with
$B_1\cup B_2$
that, together with
![]() $\mathcal {G}'$
, form a complete system of closed geodesics
$\mathcal {G}'$
, form a complete system of closed geodesics
![]() $\mathcal {G}:=\mathcal {G}'\cup \mathcal {G}"$
whose limit subcollection
$\mathcal {G}:=\mathcal {G}'\cup \mathcal {G}"$
whose limit subcollection
![]() $\mathcal {K}$
is given by the waists in
$\mathcal {K}$
is given by the waists in
![]() $\mathcal {G}"$
.
$\mathcal {G}"$
.
We now have all the ingredients to prove Theorem D, which we restate for the reader’s convenience.
Theorem D. Let
![]() $(M,g)$
be a closed connected orientable Riemannian surface satisfying the following two conditions.
$(M,g)$
be a closed connected orientable Riemannian surface satisfying the following two conditions.
-
(i) All contractible simple closed geodesics without conjugate points are non-degenerate.
-
(ii) Any pair of not necessarily distinct contractible waists
 $\gamma _1,\gamma _2 ($
if it exists) satisfies the transversality condition
$\gamma _1,\gamma _2 ($
if it exists) satisfies the transversality condition
 $W^{u}(\dot \gamma _1)\pitchfork W^{s}(\dot \gamma _2)$
.
$W^{u}(\dot \gamma _1)\pitchfork W^{s}(\dot \gamma _2)$
.
Then the geodesic vector field of
![]() $(M,g)$
admits a Birkhoff section.
$(M,g)$
admits a Birkhoff section.
Proof. Lemma 4.8 provides a complete system of closed geodesics. If its limit subcollection is non-empty, by applying Lemma 4.4 a finite number of times, we end up with another complete system of closed geodesics
![]() $\mathcal {G}$
with empty limit subcollection. We denote by
$\mathcal {G}$
with empty limit subcollection. We denote by
![]() $\Upsilon $
the union of the Birkhoff annuli of the closed geodesics in
$\Upsilon $
the union of the Birkhoff annuli of the closed geodesics in
![]() $\mathcal {G}$
, that is,
$\mathcal {G}$
, that is,
 $$ \begin{align*} \Upsilon:=\bigcup_{\gamma\in\mathcal{G}} ( A(\dot\gamma)\cup A(-\dot\gamma) ). \end{align*} $$
$$ \begin{align*} \Upsilon:=\bigcup_{\gamma\in\mathcal{G}} ( A(\dot\gamma)\cup A(-\dot\gamma) ). \end{align*} $$
By Lemma 4.2, there exists
![]() $\ell>0$
such that, for each
$\ell>0$
such that, for each
![]() $z\in SM$
, the orbit segment
$z\in SM$
, the orbit segment
![]() $\phi _{(0,\ell ]}(z)$
intersects
$\phi _{(0,\ell ]}(z)$
intersects
![]() $\Upsilon $
. We apply Fried surgery to resolve the self-intersection of
$\Upsilon $
. We apply Fried surgery to resolve the self-intersection of
![]() $\Upsilon $
(if there is any), and we end up with a surface of section
$\Upsilon $
(if there is any), and we end up with a surface of section
![]() $\Sigma \looparrowright SM$
such that, for each
$\Sigma \looparrowright SM$
such that, for each
![]() $z\in \Upsilon $
, the orbit segment
$z\in \Upsilon $
, the orbit segment
![]() $\phi _{(-1,1)}(z)$
intersects
$\phi _{(-1,1)}(z)$
intersects
![]() $\Sigma $
. Therefore, for each
$\Sigma $
. Therefore, for each
![]() $z\in SM$
, the orbit segment
$z\in SM$
, the orbit segment
![]() $\phi _{(0,\ell +2)}(z)$
intersects
$\phi _{(0,\ell +2)}(z)$
intersects
![]() $\Sigma $
, and we conclude that
$\Sigma $
, and we conclude that
![]() $\Sigma $
is a Birkhoff section.
$\Sigma $
is a Birkhoff section.
Finally, Theorem E is a consequence of the following statement.
Theorem 4.9. Let
![]() $(M,g)$
be a closed connected orientable surface. If M has genus
$(M,g)$
be a closed connected orientable surface. If M has genus
![]() $G\geq 1$
, then we consider the collection of waists
$G\geq 1$
, then we consider the collection of waists
![]() $\mathcal {G}'=\{\gamma _1,\ldots ,\gamma _{2G}\}$
given by Lemma 4.5 and the surface of section
$\mathcal {G}'=\{\gamma _1,\ldots ,\gamma _{2G}\}$
given by Lemma 4.5 and the surface of section
![]() $\Sigma '\looparrowright SM$
provided by Lemma 4.6, which has genus one and
$\Sigma '\looparrowright SM$
provided by Lemma 4.6, which has genus one and
![]() $8G-4$
boundary components, all covering the closed geodesics in
$8G-4$
boundary components, all covering the closed geodesics in
![]() $\mathcal {G}'$
; if, instead,
$\mathcal {G}'$
; if, instead,
![]() $M=S^2$
, then we set
$M=S^2$
, then we set
![]() $\mathcal {G}'=\{\gamma _0\}$
, where
$\mathcal {G}'=\{\gamma _0\}$
, where
![]() $\gamma _0$
is any simple closed geodesic with conjugate points, and we set
$\gamma _0$
is any simple closed geodesic with conjugate points, and we set
![]() $\Sigma ':=A(\dot \gamma _0)\cup A(-\dot \gamma _0)$
. Assume that the complement
$\Sigma ':=A(\dot \gamma _0)\cup A(-\dot \gamma _0)$
. Assume that the complement
 $$ \begin{align*}B:=M\setminus\bigcup_{\gamma\in\mathcal{G}'}\gamma\end{align*} $$
$$ \begin{align*}B:=M\setminus\bigcup_{\gamma\in\mathcal{G}'}\gamma\end{align*} $$
contains at least a closed geodesic and no degenerate simple closed geodesics without conjugate points. Then there exists a finite collection
![]() $\mathcal {G}"$
of simple closed geodesics that are pairwise disjoint and disjoint from the closed geodesics in
$\mathcal {G}"$
of simple closed geodesics that are pairwise disjoint and disjoint from the closed geodesics in
![]() $\mathcal {G}'$
with the following properties.
$\mathcal {G}'$
with the following properties.
-
(i) Every orbit of the geodesic flow intersects
 $\Sigma '\cup \Sigma "$
, where
$\Sigma '\cup \Sigma "$
, where  $$ \begin{align*}\Sigma":=\bigcup_{\gamma\in\mathcal{G}"} (A(\dot\gamma)\cup A(-\dot\gamma)) \subset SM\setminus\Sigma'.\end{align*} $$
$$ \begin{align*}\Sigma":=\bigcup_{\gamma\in\mathcal{G}"} (A(\dot\gamma)\cup A(-\dot\gamma)) \subset SM\setminus\Sigma'.\end{align*} $$
-
(ii) We denote by
 $\mathcal {K}$
the subcollection of waists in
$\mathcal {K}$
the subcollection of waists in
 $\mathcal {G}'$
, and The trapped sets of
$\mathcal {G}'$
, and The trapped sets of $$ \begin{align*} K:=\bigcup_{\gamma\in\mathcal{K}} ( \dot\gamma\cup-\dot\gamma ). \end{align*} $$
$$ \begin{align*} K:=\bigcup_{\gamma\in\mathcal{K}} ( \dot\gamma\cup-\dot\gamma ). \end{align*} $$
 $SM\setminus (\Sigma '\cup \Sigma ")$
are given by
$SM\setminus (\Sigma '\cup \Sigma ")$
are given by  $$ \begin{align*} \mathrm{trap}_+(SM\setminus(\Sigma'\cup\Sigma")) &=W^{s}(K)\setminus K, \\ \mathrm{trap}_-(SM\setminus(\Sigma'\cup\Sigma")) &=W^{u}(K)\setminus K. \end{align*} $$
$$ \begin{align*} \mathrm{trap}_+(SM\setminus(\Sigma'\cup\Sigma")) &=W^{s}(K)\setminus K, \\ \mathrm{trap}_-(SM\setminus(\Sigma'\cup\Sigma")) &=W^{u}(K)\setminus K. \end{align*} $$
-
(iii) There exists
 $\ell>0$
such that, for each
$\ell>0$
such that, for each
 $z\in SM$
sufficiently close to the boundary components
$z\in SM$
sufficiently close to the boundary components
 $\partial \Sigma '\cup \partial \Sigma "\setminus K$
, we have
$\partial \Sigma '\cup \partial \Sigma "\setminus K$
, we have
 $\phi _{(0,\ell ]}(z)\cap (\Sigma '\cup \Sigma ")\neq \varnothing $
.
$\phi _{(0,\ell ]}(z)\cap (\Sigma '\cup \Sigma ")\neq \varnothing $
.
Proof. Lemma 4.8 provides a (possibly empty) finite collection
![]() $\mathcal {G}"$
of contractible simple closed geodesics that are pairwise disjoint and disjoint from all the closed geodesics in
$\mathcal {G}"$
of contractible simple closed geodesics that are pairwise disjoint and disjoint from all the closed geodesics in
![]() $\mathcal {G}'$
such that
$\mathcal {G}'$
such that
![]() $\mathcal {G}:=\mathcal {G}'\cup \mathcal {G}"$
is a complete system of closed geodesics whose limit subcollection
$\mathcal {G}:=\mathcal {G}'\cup \mathcal {G}"$
is a complete system of closed geodesics whose limit subcollection
![]() $\mathcal {K}$
is given by the waists in
$\mathcal {K}$
is given by the waists in
![]() $\mathcal {G}"$
. We set
$\mathcal {G}"$
. We set
 $$ \begin{align*} \Upsilon':=\bigcup_{\gamma\in\mathcal{G}'} ( A(\dot\gamma)\cup A(-\dot\gamma) ), \quad \Sigma":=\bigcup_{\gamma\in\mathcal{G}"} ( A(\dot\gamma)\cup A(-\dot\gamma) ). \end{align*} $$
$$ \begin{align*} \Upsilon':=\bigcup_{\gamma\in\mathcal{G}'} ( A(\dot\gamma)\cup A(-\dot\gamma) ), \quad \Sigma":=\bigcup_{\gamma\in\mathcal{G}"} ( A(\dot\gamma)\cup A(-\dot\gamma) ). \end{align*} $$
If
![]() $M=S^2$
, then we have set
$M=S^2$
, then we have set
![]() $\Sigma ':=\Upsilon '$
. If, instead,
$\Sigma ':=\Upsilon '$
. If, instead,
![]() $M\neq S^2$
, then we require the surface of section
$M\neq S^2$
, then we require the surface of section
![]() $\Sigma '$
provided by Lemma 4.5 to be contained in a sufficiently small neighborhood of
$\Sigma '$
provided by Lemma 4.5 to be contained in a sufficiently small neighborhood of
![]() $\Upsilon '$
so that
$\Upsilon '$
so that
![]() $\Sigma '\cap \Sigma "=\varnothing $
, and by Lemma 4.6(iv),
$\Sigma '\cap \Sigma "=\varnothing $
, and by Lemma 4.6(iv),
We set
 $$ \begin{align*} K:=\bigcup_{\gamma\in\mathcal{K}} (\dot\gamma\cup-\dot\gamma), \quad R:=\bigcup_{\gamma\in\mathcal{G}'\cup\mathcal{G}"\setminus\mathcal{K}}(\dot\gamma\cup-\dot\gamma)=\partial\Sigma'\cup\partial\Sigma"\setminus K. \end{align*} $$
$$ \begin{align*} K:=\bigcup_{\gamma\in\mathcal{K}} (\dot\gamma\cup-\dot\gamma), \quad R:=\bigcup_{\gamma\in\mathcal{G}'\cup\mathcal{G}"\setminus\mathcal{K}}(\dot\gamma\cup-\dot\gamma)=\partial\Sigma'\cup\partial\Sigma"\setminus K. \end{align*} $$
By properties (ii) in Definition 4.1, every complete orbit
![]() $\phi _{(-\infty ,\infty )}(z)$
intersects
$\phi _{(-\infty ,\infty )}(z)$
intersects
![]() $\Sigma '\cup \Sigma "$
, and
$\Sigma '\cup \Sigma "$
, and
 $$ \begin{align*} \mathrm{trap}_+(SM\setminus(\Sigma'\cup\Sigma"))&=\mathrm{trap}_+(SM\setminus(\Upsilon'\cup\Sigma"))=W^{s}(K)\setminus K, \\ \mathrm{trap}_-(SM\setminus(\Sigma'\cup\Sigma"))&= \mathrm{trap}_-(SM\setminus(\Upsilon'\cup\Sigma"))=W^{u}(K)\setminus K. \end{align*} $$
$$ \begin{align*} \mathrm{trap}_+(SM\setminus(\Sigma'\cup\Sigma"))&=\mathrm{trap}_+(SM\setminus(\Upsilon'\cup\Sigma"))=W^{s}(K)\setminus K, \\ \mathrm{trap}_-(SM\setminus(\Sigma'\cup\Sigma"))&= \mathrm{trap}_-(SM\setminus(\Upsilon'\cup\Sigma"))=W^{u}(K)\setminus K. \end{align*} $$
Moreover, by properties (iii) in Definition 4.1, there exist
![]() $\ell>0$
and an open neighborhood
$\ell>0$
and an open neighborhood
![]() $N\subset SM$
of R such that
$N\subset SM$
of R such that
If we take a sufficiently small open neighborhood
![]() $N'\subset N$
of R, then we also have
$N'\subset N$
of R, then we also have
Acknowledgements
We are grateful to Marie-Claude Arnaud for a discussion concerning the stable manifold of hyperbolic closed geodesics without conjugate points. We are also particularly grateful to the many anonymous referees for their careful reading of the manuscript and for their helpful reports. Gonzalo Contreras is partially supported by CONACYT, Mexico, grant A1-S-10145. Gerhard Knieper, Marco Mazzucchelli and Benjamin H. Schulz are partially supported by the SFB/TRR 191 ‘Symplectic Structures in Geometry, Algebra and Dynamics’, funded by the Deutsche Forschungsgemeinschaft. Marco Mazzucchelli is also partially supported by the ANR grants CoSyDy (ANRCE40-0014) and COSY (ANR-21-CE40-0002), and by the IEA project IEA00549 from CNRS.