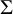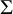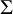1 Introduction
In this paper, we will be interested in studying the growth of the number of certain classes of geodesics in a closed, connected and oriented hyperbolic surface
![]() $\Sigma =\Gamma \backslash {\mathbb {H}}^2$
, which we assume to be fixed throughout the paper.
$\Sigma =\Gamma \backslash {\mathbb {H}}^2$
, which we assume to be fixed throughout the paper.
In [Reference Huber10], Huber proved that the cardinality of the set
![]() ${\mathbf {C}}(L)$
of nontrivial oriented periodic geodesics
${\mathbf {C}}(L)$
of nontrivial oriented periodic geodesics
![]() $\gamma \subset \Sigma $
of length
$\gamma \subset \Sigma $
of length
![]() $\ell _{\Sigma }(\gamma )\leqslant L$
behaves like
$\ell _{\Sigma }(\gamma )\leqslant L$
behaves like
Here,
![]() $\sim $
means that the ratio between both quantities tends to
$\sim $
means that the ratio between both quantities tends to
![]() $1$
as
$1$
as
![]() $L\to \infty $
. Huber’s result has been generalized in all possible directions, allowing, for example, for surfaces of finite area [Reference Hejhal9] and for higher-dimensional negatively curved manifolds or replacing periodic geodesic by orbits of Anosov flows [Reference Margulis12]. Variations of Huber’s result have also been obtained when one imposes additional restrictions on the geodesics one is counting. Here, one should mention Mirzakhani’s work on counting simple geodesics [Reference Mirzakhani13] or more generally geodesics of given type [Reference Mirzakhani14
Reference Mirzakhani, Reference Erlandsson and Souto8], but what is closer to what we will care about in this paper are earlier results of Katsuda–Sunanda [Reference Katsuda and Sunada11] and Phillips–Sarnak [Reference Phillips and Sarnak16] giving the asymptotic behavior of the number of geodesics with length at most L and satisfying some homological condition. For example, Katsuda–Sunada [Reference Katsuda and Sunada11] proved that
$L\to \infty $
. Huber’s result has been generalized in all possible directions, allowing, for example, for surfaces of finite area [Reference Hejhal9] and for higher-dimensional negatively curved manifolds or replacing periodic geodesic by orbits of Anosov flows [Reference Margulis12]. Variations of Huber’s result have also been obtained when one imposes additional restrictions on the geodesics one is counting. Here, one should mention Mirzakhani’s work on counting simple geodesics [Reference Mirzakhani13] or more generally geodesics of given type [Reference Mirzakhani14
Reference Mirzakhani, Reference Erlandsson and Souto8], but what is closer to what we will care about in this paper are earlier results of Katsuda–Sunanda [Reference Katsuda and Sunada11] and Phillips–Sarnak [Reference Phillips and Sarnak16] giving the asymptotic behavior of the number of geodesics with length at most L and satisfying some homological condition. For example, Katsuda–Sunada [Reference Katsuda and Sunada11] proved that
where
![]() $g_{\Sigma }$
is the genus of
$g_{\Sigma }$
is the genus of
![]() $\Sigma $
. Phillips–Sarnak [Reference Phillips and Sarnak16] get this same result with an estimate on the error term.
$\Sigma $
. Phillips–Sarnak [Reference Phillips and Sarnak16] get this same result with an estimate on the error term.
Here, we will be counting certain kinds of homologically trivial curves. Every homologically trivial curve
![]() $\gamma $
can be represented, up to free homotopy, as the product of commutators in
$\gamma $
can be represented, up to free homotopy, as the product of commutators in
![]() $\pi _1(\Sigma )$
. The smallest number of commutators needed is the commutator length of
$\pi _1(\Sigma )$
. The smallest number of commutators needed is the commutator length of
![]() $\gamma $
. This quantity agrees with the genus of the smallest connected oriented surface S with connected boundary
$\gamma $
. This quantity agrees with the genus of the smallest connected oriented surface S with connected boundary
![]() $\partial S$
for which there is a (continuous) map
$\partial S$
for which there is a (continuous) map
![]() $S\to \Sigma $
sending
$S\to \Sigma $
sending
![]() $\partial S$
to
$\partial S$
to
![]() $\gamma $
. This explains why we think of the commutator length
$\gamma $
. This explains why we think of the commutator length
![]() $cl(\gamma )$
of
$cl(\gamma )$
of
![]() $\gamma $
as the genus of
$\gamma $
as the genus of
![]() $\gamma $
.
$\gamma $
.
In this paper, we study, for fixed but otherwise arbitrary
![]() $g\geqslant 1$
, the asymptotic behavior of the cardinality of the set
$g\geqslant 1$
, the asymptotic behavior of the cardinality of the set
 $$ \begin{align} {\mathbf{B}}_{g}(L)=\left\{\gamma\subset\Sigma\ \middle\vert \begin{array}{l} \text{closed geodesic with } \ell_{\Sigma}(\gamma)\leqslant L\text{ and}\\ \text{commutator length }cl(\gamma)=g \end{array} \right\} \end{align} $$
$$ \begin{align} {\mathbf{B}}_{g}(L)=\left\{\gamma\subset\Sigma\ \middle\vert \begin{array}{l} \text{closed geodesic with } \ell_{\Sigma}(\gamma)\leqslant L\text{ and}\\ \text{commutator length }cl(\gamma)=g \end{array} \right\} \end{align} $$
This is our main result:
Theorem 1.1. Let
![]() $\Sigma $
be a closed, connected and oriented hyperbolic surface and for
$\Sigma $
be a closed, connected and oriented hyperbolic surface and for
![]() $g\geqslant 1$
, and
$g\geqslant 1$
, and
![]() $L>0$
let
$L>0$
let
![]() ${\mathbf {B}}_g(L)$
be as in Equation (1.3). We have
${\mathbf {B}}_g(L)$
be as in Equation (1.3). We have
as
![]() $L\to \infty $
.
$L\to \infty $
.
Here, as we will throughout the paper, we have endowed the unit tangent bundle
![]() $T^1\Sigma $
with the Liouville measure, normalized in such a way that
$T^1\Sigma $
with the Liouville measure, normalized in such a way that
![]() $\operatorname {\mathrm {vol}}(T^1\Sigma )=2\pi \cdot \operatorname {\mathrm {vol}}(\Sigma )=-4\pi ^2\chi (\Sigma )$
. In particular, we have that, as in Equation (1.2), the quantities in Theorem 1.1 depend on the topology of the underlying surface
$\operatorname {\mathrm {vol}}(T^1\Sigma )=2\pi \cdot \operatorname {\mathrm {vol}}(\Sigma )=-4\pi ^2\chi (\Sigma )$
. In particular, we have that, as in Equation (1.2), the quantities in Theorem 1.1 depend on the topology of the underlying surface
![]() $\Sigma $
but there is no dependence on its geometry.
$\Sigma $
but there is no dependence on its geometry.
Note that by definition the curves in
![]() ${\mathbf {B}}_g(L)$
bound a surface of genus g but that this surface is just the image of a continuous, or if you want smooth, map. We prove that only a small but definite proportion of the elements in
${\mathbf {B}}_g(L)$
bound a surface of genus g but that this surface is just the image of a continuous, or if you want smooth, map. We prove that only a small but definite proportion of the elements in
![]() ${\mathbf {B}}_g(L)$
arise as the boundary of an immersed surface of genus g (and connected boundary):
${\mathbf {B}}_g(L)$
arise as the boundary of an immersed surface of genus g (and connected boundary):
Theorem 1.2. Let
![]() $\Sigma $
be a closed, connected and oriented hyperbolic surface and for
$\Sigma $
be a closed, connected and oriented hyperbolic surface and for
![]() $g\geqslant 1$
, and
$g\geqslant 1$
, and
![]() $L>0$
let
$L>0$
let
![]() ${\mathbf {B}}_g(L)$
be as in Equation (1.3). We have
${\mathbf {B}}_g(L)$
be as in Equation (1.3). We have
as
![]() $L\to \infty $
.
$L\to \infty $
.
Theorem 1.2 should perhaps be compared with the immersion theorem in [Reference Calegari4, Theorem 4.79]. The immersion theorem asserts that every homologically trivial geodesic
![]() $\gamma $
in
$\gamma $
in
![]() $\Sigma $
virtually bounds an immersed surface, meaning that there is an immersion into
$\Sigma $
virtually bounds an immersed surface, meaning that there is an immersion into
![]() $\Sigma $
of a compact surface S in such a way that the boundary of S is mapped onto
$\Sigma $
of a compact surface S in such a way that the boundary of S is mapped onto
![]() $\gamma $
with positive degree. In some sense, Theorem 1.2 seems to suggest that, most of the time, the genus of S does not agree with the genus of
$\gamma $
with positive degree. In some sense, Theorem 1.2 seems to suggest that, most of the time, the genus of S does not agree with the genus of
![]() $\gamma $
.
$\gamma $
.
In the course of the proof of Theorem 1.1, we will need a different counting result that we believe has its own interest. Suppose namely that X is a compact trivalent graph. Under a critical realization of X in
![]() $\Sigma $
, we understand a (continuous) map
$\Sigma $
, we understand a (continuous) map
sending each edge to a nondegenerate geodesic segment in such a way that any two (germs of) edges incident to the same vertex are sent to geodesic segments meeting at angle
![]() $\frac {2\pi }3$
(see Lemma 2.2 for an explanation of the etymology of this terminology). Although it may not be completely evident to the reader at this point, the set
$\frac {2\pi }3$
(see Lemma 2.2 for an explanation of the etymology of this terminology). Although it may not be completely evident to the reader at this point, the set
 $$ \begin{align} {\mathbf{G}}^X(L)=\left\{\begin{array}{c}\phi:X\to\Sigma\text{ critical realization}\\ \text{with length }\ell_{\Sigma}(\phi)\leqslant L\end{array}\right\} \end{align} $$
$$ \begin{align} {\mathbf{G}}^X(L)=\left\{\begin{array}{c}\phi:X\to\Sigma\text{ critical realization}\\ \text{with length }\ell_{\Sigma}(\phi)\leqslant L\end{array}\right\} \end{align} $$
is finite, where the length of a critical realization is defined to be the sum
 $$ \begin{align*}\ell_{\Sigma}(\phi)=\sum_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}\ell_{\Sigma}(\phi(e))\end{align*} $$
$$ \begin{align*}\ell_{\Sigma}(\phi)=\sum_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}\ell_{\Sigma}(\phi(e))\end{align*} $$
of the lengths of the geodesic segments
![]() $\phi (e)$
when e ranges over the set of edges of X. The following is the key to Theorem 1.1:
$\phi (e)$
when e ranges over the set of edges of X. The following is the key to Theorem 1.1:
Theorem 1.3. Let
![]() $\Sigma $
be a closed, connected and oriented hyperbolic surface. For every connected trivalent graph X, we have
$\Sigma $
be a closed, connected and oriented hyperbolic surface. For every connected trivalent graph X, we have
 $$ \begin{align*}\vert{\mathbf{G}}^X(L)\vert\sim \left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}^X(L)\vert\sim \left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}\end{align*} $$
as
![]() $L\to \infty $
. Here,
$L\to \infty $
. Here,
![]() $\chi (X)$
is the Euler-characteristic of the graph X.
$\chi (X)$
is the Euler-characteristic of the graph X.
Let us sketch the proof of Theorem 1.3. Recall first that there are basically two approaches (that we know of) to establish Huber’s theorem (1.1): Either one approaches it à la Huber [Reference Huber10], that is, from the point of spectral analysis or, as Margulis did later [Reference Margulis12], exploiting the ergodic properties of the geodesic flow. Indeed, already the predecessor to Huber’s theorem, namely Delsarte’s lattice point counting theorem [Reference Delsarte7] can be approached from these two different points of view. In Section 3 below, we will sketch the argument to derive Delsarte’s theorem from the fact that the geodesic flow is mixing, discussing also the count of those geodesic arcs in
![]() $\Sigma $
going from x to y and whose initial and terminal speed are in predetermined sectors of the respective unit tangent spaces – see Theorem 3.1 for the precise statement. This is indeed all the dynamics we will need in the proof of the theorems above. To be clear, we do not make use of any of the slightly rarified refinements of the mixing property of the geodesic flow. Specifically, we do not need exponential mixing or such.
$\Sigma $
going from x to y and whose initial and terminal speed are in predetermined sectors of the respective unit tangent spaces – see Theorem 3.1 for the precise statement. This is indeed all the dynamics we will need in the proof of the theorems above. To be clear, we do not make use of any of the slightly rarified refinements of the mixing property of the geodesic flow. Specifically, we do not need exponential mixing or such.
The basic idea of the proof of Theorem 1.3 is to note that, for a fixed graph X, the set of all its realizations in
![]() $\Sigma $
, that is, maps
$\Sigma $
, that is, maps
![]() $X\to \Sigma $
mapping each edge geodesically, is naturally a manifold. Generically, each connected component contains a unique critical realization. To count how many such critical realizations, there are with total length less than L we consider for small
$X\to \Sigma $
mapping each edge geodesically, is naturally a manifold. Generically, each connected component contains a unique critical realization. To count how many such critical realizations, there are with total length less than L we consider for small
![]() $\varepsilon $
the set
$\varepsilon $
the set
![]() $\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(L)$
of geodesic realizations of length at most L and where the angles, instead of being
$\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(L)$
of geodesic realizations of length at most L and where the angles, instead of being
![]() $\frac {2\pi }3$
on the nose, are in the interval of size
$\frac {2\pi }3$
on the nose, are in the interval of size
![]() $\varepsilon $
around that number. Delsarte’s theorem allows us to compute the volume
$\varepsilon $
around that number. Delsarte’s theorem allows us to compute the volume
![]() $\operatorname {\mathrm {vol}}(\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(L))$
of that set of geodesic realizations. A little bit of hyperbolic geometry then shows that most of the connected components of
$\operatorname {\mathrm {vol}}(\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(L))$
of that set of geodesic realizations. A little bit of hyperbolic geometry then shows that most of the connected components of
![]() $\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(L)$
have basically the same volume. We thus know, with a small error, how many connected components we have, and thus how many critical realizations. This concludes the sketch of the proof of Theorem 1.3.
$\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(L)$
have basically the same volume. We thus know, with a small error, how many connected components we have, and thus how many critical realizations. This concludes the sketch of the proof of Theorem 1.3.
Remark. The strategy used to prove Theorem 1.3 can be used to give a pretty easy proof of Huber’s theorem (1.1). We work this out in the appendix, and although there is no logical need of doing so, we encourage the reader to have a look at it before working out the details of the proof of Theorem 1.3.
Let us also sketch the proof of Theorem 1.1. A fat graph is basically a graph which comes equipped with a regular neighborhood
![]() $\operatorname {\mathrm {\mathbf {neigh}}}(X)$
homeomorphic to an oriented surface. Such a fat graph has genus g if this regular neighborhood is homeomorphic to a compact surface of genus g with connected boundary. The point of considering fat graphs is that whenever we have a realization
$\operatorname {\mathrm {\mathbf {neigh}}}(X)$
homeomorphic to an oriented surface. Such a fat graph has genus g if this regular neighborhood is homeomorphic to a compact surface of genus g with connected boundary. The point of considering fat graphs is that whenever we have a realization
![]() $\phi :X\to \Sigma $
of the graph underlying a genus g fat graph then we get a curve, namely
$\phi :X\to \Sigma $
of the graph underlying a genus g fat graph then we get a curve, namely
![]() $\phi (\partial \operatorname {\mathrm {\mathbf {neigh}}}(X))$
which has at most genus g. The basic idea of the proof of Theorem 1.1 is to consider the set
$\phi (\partial \operatorname {\mathrm {\mathbf {neigh}}}(X))$
which has at most genus g. The basic idea of the proof of Theorem 1.1 is to consider the set
 $$ \begin{align*}{\mathbf{X}}_{g}=\left\{(X,\phi)\middle\vert\begin{array}{c}X\text{ is a fat graph of genus }g\text{ and}\\ \phi:X\to\Sigma\text{ is a critical realization}\\ \text{of the underlying graph}\end{array}\middle\}\right/_{\text{equiv}}\end{align*} $$
$$ \begin{align*}{\mathbf{X}}_{g}=\left\{(X,\phi)\middle\vert\begin{array}{c}X\text{ is a fat graph of genus }g\text{ and}\\ \phi:X\to\Sigma\text{ is a critical realization}\\ \text{of the underlying graph}\end{array}\middle\}\right/_{\text{equiv}}\end{align*} $$
of (equivalence classes) of realizations (see Section 7 for details) and prove that the map
is basically bijective onto
![]() ${\mathbf {B}}_g$
and that generically, the geodesic
${\mathbf {B}}_g$
and that generically, the geodesic
![]() $\Lambda (X,\phi )$
has length almost exactly equal to
$\Lambda (X,\phi )$
has length almost exactly equal to
![]() $2\cdot \ell (\phi )-C$
for some explicit constant C. Once we are here, we get the statement of Theorem 1.1 from Theorem 1.3 together with a result by Bacher and Vdovina [Reference Bacher and Vdovina1]. Other than proving Theorem 1.3, the bulk of the work is to establish the properties of the map
$2\cdot \ell (\phi )-C$
for some explicit constant C. Once we are here, we get the statement of Theorem 1.1 from Theorem 1.3 together with a result by Bacher and Vdovina [Reference Bacher and Vdovina1]. Other than proving Theorem 1.3, the bulk of the work is to establish the properties of the map
![]() $\Lambda $
. The key step is to bound the number of curves with at most length L and which arise in two essentially different ways as the boundary of genus g surfaces:
$\Lambda $
. The key step is to bound the number of curves with at most length L and which arise in two essentially different ways as the boundary of genus g surfaces:
Theorem 1.4. For any g, there are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
genus g closed geodesics
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
genus g closed geodesics
![]() $\gamma $
in
$\gamma $
in
![]() $\Sigma $
with length
$\Sigma $
with length
![]() $\ell (\gamma )\leqslant L$
and with the property that there are two nonhomotopic fillings
$\ell (\gamma )\leqslant L$
and with the property that there are two nonhomotopic fillings
![]() $\beta _1:S_1\to \Sigma $
and
$\beta _1:S_1\to \Sigma $
and
![]() $\beta _2:S_2\to \Sigma $
of genus
$\beta _2:S_2\to \Sigma $
of genus
![]() $\leqslant g$
.
$\leqslant g$
.
Here, a genus g filling of
![]() $\gamma $
is a continuous map
$\gamma $
is a continuous map
![]() $\beta : S\to \Sigma $
from a genus g surface S with connected boundary such that
$\beta : S\to \Sigma $
from a genus g surface S with connected boundary such that
![]() $\beta (\partial S) = \gamma $
.
$\beta (\partial S) = \gamma $
.
Theorem 1.4 may look kind of weak because we are only bounding by
![]() $\frac {\operatorname {\mathrm {\mathbf {const}}}}{L}$
the proportion of those elements in
$\frac {\operatorname {\mathrm {\mathbf {const}}}}{L}$
the proportion of those elements in
![]() ${\mathbf {B}}_g(L)$
that we are double counting when we count surfaces of genus g instead of counting curves. It should however be noted that this is the order of the error term in Equation (1.2) (see [Reference Phillips and Sarnak16]), and this is indeed the order of error term that we expect in the results we prove here. For what it is worth, it is not hard to show that the set of those
${\mathbf {B}}_g(L)$
that we are double counting when we count surfaces of genus g instead of counting curves. It should however be noted that this is the order of the error term in Equation (1.2) (see [Reference Phillips and Sarnak16]), and this is indeed the order of error term that we expect in the results we prove here. For what it is worth, it is not hard to show that the set of those
![]() $\gamma $
in Theorem 1.4 is at least of the order of
$\gamma $
in Theorem 1.4 is at least of the order of
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-10}\cdot e^{\frac L2}$
. Indeed, if
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-10}\cdot e^{\frac L2}$
. Indeed, if
![]() $\omega \in \pi _1(\Sigma )$
arises in two ways as a commutator, for example if we choose
$\omega \in \pi _1(\Sigma )$
arises in two ways as a commutator, for example if we choose
![]() $\omega =[aabab,ba^{-1}a^{-1}]=[aaba,bba^{-1}]$
and if
$\omega =[aabab,ba^{-1}a^{-1}]=[aaba,bba^{-1}]$
and if
![]() $\eta $
is a randomly chosen product of
$\eta $
is a randomly chosen product of
![]() $g-1$
generators, then
$g-1$
generators, then
![]() $\omega \eta $
arises in two different ways as a product of g commutators and hence admits two nonhomotopic fillings, and there are
$\omega \eta $
arises in two different ways as a product of g commutators and hence admits two nonhomotopic fillings, and there are
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-10}\cdot e^{\frac L2}$
many choices for
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-10}\cdot e^{\frac L2}$
many choices for
![]() $\eta $
.
$\eta $
.
Section-by-section summary
In Section 2, we discuss realizations of graphs and the topology and geometry of spaces of realizations, and in Section 3 we discuss Delsarte’s classical lattice point counting result and a couple of minimal generalizations thereof. At this point, we will have all tools needed to prove Theorem 1.3; this is done in Section 4. In Section 5 and Section 6, we work out the geometric aspects of the proof of Theorem 1.1, the main result being Theorem 1.4. Although we do not use any results about pleated surfaces, some of the arguments in these two sections will come pretty naturally to those readers used to working with such objects. In Section 7, we prove Theorem 1.1, combining the results of the previous two sections with Theorem 1.3. Theorem 1.2 is proved in Section 8. Finally, Section 9 is dedicated to discussing what parts of what we do hold if we soften the assumption that
![]() $\Sigma $
is a closed hyperbolic surface. To conclude, we present in Appendix A a proof of Huber’s theorem using the same idea as in the proof of Theorem 1.3.
$\Sigma $
is a closed hyperbolic surface. To conclude, we present in Appendix A a proof of Huber’s theorem using the same idea as in the proof of Theorem 1.3.
Remark. After conclusion of this paper, we learned that the problem of calculating how many elements arise as commutators in some group has also been treated in other cases. More concretely, Park [Reference Park15] uses Wicks forms to get asymptotics, as
![]() $L\to \infty $
, for the number of elements in the free group
$L\to \infty $
, for the number of elements in the free group
![]() ${\mathbb {F}}_r$
of rank r which arise as a commutator and have word length L. In the same paper, he also treats the case that the group is a free product of two nontrivial finite groups. It would be interesting to figure out if it is possible to apply the methods here to recover Park’s beautiful theorems.
${\mathbb {F}}_r$
of rank r which arise as a commutator and have word length L. In the same paper, he also treats the case that the group is a free product of two nontrivial finite groups. It would be interesting to figure out if it is possible to apply the methods here to recover Park’s beautiful theorems.
Notation
Under a graph X, we understand a one-dimensional CW-complex with finitely many cells. We denote by
![]() $\operatorname {\mathrm {\mathbf {vert}}}=\operatorname {\mathrm {\mathbf {vert}}}(X)$
the set of vertices, by
$\operatorname {\mathrm {\mathbf {vert}}}=\operatorname {\mathrm {\mathbf {vert}}}(X)$
the set of vertices, by
![]() $\operatorname {\mathrm {\mathbf {edge}}}=\operatorname {\mathrm {\mathbf {edge}}}(X)$
the set of edges of X, and by
$\operatorname {\mathrm {\mathbf {edge}}}=\operatorname {\mathrm {\mathbf {edge}}}(X)$
the set of edges of X, and by
![]() $\operatorname {\mathrm {\mathbf {half}}}=\operatorname {\mathrm {\mathbf {half}}}(X)$
the set of half-edges of a graph X – a half-edge is nothing other than the germ of an edge. Given a vertex
$\operatorname {\mathrm {\mathbf {half}}}=\operatorname {\mathrm {\mathbf {half}}}(X)$
the set of half-edges of a graph X – a half-edge is nothing other than the germ of an edge. Given a vertex
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
, we let
$v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
, we let
![]() $\operatorname {\mathrm {\mathbf {half}}}_v=\operatorname {\mathrm {\mathbf {half}}}_v(X)$
be the set of half-edges emanating out of v. Note that two elements of
$\operatorname {\mathrm {\mathbf {half}}}_v=\operatorname {\mathrm {\mathbf {half}}}_v(X)$
be the set of half-edges emanating out of v. Note that two elements of
![]() $\operatorname {\mathrm {\mathbf {half}}}_v$
might well correspond to the same edge – that is, X might have edges which are incident to the same vertex on both ends. The cardinality of
$\operatorname {\mathrm {\mathbf {half}}}_v$
might well correspond to the same edge – that is, X might have edges which are incident to the same vertex on both ends. The cardinality of
![]() $\operatorname {\mathrm {\mathbf {half}}}_v$
is the degree of X at v and we say that X is trivalent if its degree is 3 at every vertex. The reader can safely assume that the graphs they encounter are trivalent.
$\operatorname {\mathrm {\mathbf {half}}}_v$
is the degree of X at v and we say that X is trivalent if its degree is 3 at every vertex. The reader can safely assume that the graphs they encounter are trivalent.
When it comes to surfaces, we will be working all the time with the same underlying surface, our fixed closed connected and oriented hyperbolic surface
![]() $\Sigma =\Gamma \backslash {\mathbb {H}}^2$
. We identify
$\Sigma =\Gamma \backslash {\mathbb {H}}^2$
. We identify
![]() $T^1\Sigma $
with
$T^1\Sigma $
with
![]() $\Gamma \backslash T^1{\mathbb {H}}^2=\Gamma \backslash \operatorname {\mathrm {PSL}}_2\mathbb R$
and endow
$\Gamma \backslash T^1{\mathbb {H}}^2=\Gamma \backslash \operatorname {\mathrm {PSL}}_2\mathbb R$
and endow
![]() $T^1\Sigma $
with the distance induced by a
$T^1\Sigma $
with the distance induced by a
![]() $\operatorname {\mathrm {PSL}}_2\mathbb R$
left-invariant Riemannian metric on
$\operatorname {\mathrm {PSL}}_2\mathbb R$
left-invariant Riemannian metric on
![]() $\operatorname {\mathrm {PSL}}_2\mathbb R$
, say one that gives length
$\operatorname {\mathrm {PSL}}_2\mathbb R$
, say one that gives length
![]() $2\pi $
to each unit tangent space
$2\pi $
to each unit tangent space
![]() $T_{x_0}^1\Sigma $
and such that the projection
$T_{x_0}^1\Sigma $
and such that the projection
![]() $T^1{\mathbb {H}}^2\to {\mathbb {H}}^2$
is a Riemannian submersion. This means that the unit tangent bundle has volume
$T^1{\mathbb {H}}^2\to {\mathbb {H}}^2$
is a Riemannian submersion. This means that the unit tangent bundle has volume
![]() $\operatorname {\mathrm {vol}}(T^1\Sigma )=2\pi \cdot \operatorname {\mathrm {vol}}(\Sigma )=4\pi ^2\cdot \vert \chi (S)\vert $
. Angles between tangent vectors based at the same point of
$\operatorname {\mathrm {vol}}(T^1\Sigma )=2\pi \cdot \operatorname {\mathrm {vol}}(\Sigma )=4\pi ^2\cdot \vert \chi (S)\vert $
. Angles between tangent vectors based at the same point of
![]() $\Sigma $
will always be unoriented, meaning that they take values in
$\Sigma $
will always be unoriented, meaning that they take values in
![]() $[0,\pi ]$
– note that this is consistent with the unit tangent spaces having length
$[0,\pi ]$
– note that this is consistent with the unit tangent spaces having length
![]() $2\pi $
.
$2\pi $
.
Often we will denote the discrete sets we are counting by boldface capitals, such as
![]() ${\mathbf {C}}$
or
${\mathbf {C}}$
or
![]() ${\mathbf {B}}$
. They will often come with a wealth of decorations such as for example
${\mathbf {B}}$
. They will often come with a wealth of decorations such as for example
![]() ${\mathbf {G}}^X(L)$
or
${\mathbf {G}}^X(L)$
or
![]() ${\mathbf {B}}_g(L)$
. Often these sets arise as discrete subsets of larger spaces which will be denoted by calligraphic letters. Often the boldfaced and the calligraphic letters go together:
${\mathbf {B}}_g(L)$
. Often these sets arise as discrete subsets of larger spaces which will be denoted by calligraphic letters. Often the boldfaced and the calligraphic letters go together:
![]() ${\mathbf {G}}$
will be a subset of the space
${\mathbf {G}}$
will be a subset of the space
![]() $\mathcal G$
.
$\mathcal G$
.
A comment about constants. In this paper, there are two kinds of constants: the ones whose value we are trying to actually compute and those about which we just need to know that they exist. Evidently, the first kind we have to track carefully. It would, however, be too painful, and for no clear gain, to do the same with all possible constants. And in general constants tend to breed more and more constants. This is why we we just write
![]() $\operatorname {\mathrm {\mathbf {const}}}$
for a constant whose actual value is irrelevant, allowing the precise value of
$\operatorname {\mathrm {\mathbf {const}}}$
for a constant whose actual value is irrelevant, allowing the precise value of
![]() $\operatorname {\mathrm {\mathbf {const}}}$
to change from line to line. We hope that this does not cause any confusion.
$\operatorname {\mathrm {\mathbf {const}}}$
to change from line to line. We hope that this does not cause any confusion.
And now a comment about Euclidean vectors. All vector arising here, indicated with an arrow as in
![]() $\vec v=(v_1,\dots ,v_k)$
, are positive in the sense that the entries
$\vec v=(v_1,\dots ,v_k)$
, are positive in the sense that the entries
![]() $v_i$
are positive. In other words, they live in
$v_i$
are positive. In other words, they live in
![]() $\mathbb R_+^k$
or maybe in
$\mathbb R_+^k$
or maybe in
![]() $\mathbb N^k$
. We will write
$\mathbb N^k$
. We will write
for the
![]() $L^1$
-norm on vectors. This is the only norm we will encounter here.
$L^1$
-norm on vectors. This is the only norm we will encounter here.
2 Realizations of graphs in surfaces
In this section, we discuss certain spaces of maps of graphs into a surface. These spaces play a key rôle in this paper. Although long, the material here should be nice and pleasant to read – only the proof of Proposition 2.3 takes some amount of work.
Realizations
We will be interested in connected graphs living inside our hyperbolic surface
![]() $\Sigma $
, or more precisely in continuous maps
$\Sigma $
, or more precisely in continuous maps
of graphs X into
![]() $\Sigma $
which when restricted to each edge are geodesic. We will say that such a map (2.1) is a realization of X in
$\Sigma $
which when restricted to each edge are geodesic. We will say that such a map (2.1) is a realization of X in
![]() $\Sigma $
. We stress that realizations do not need to be injective and that in fact the map
$\Sigma $
. We stress that realizations do not need to be injective and that in fact the map
![]() $\phi $
could be constant on certain edges or even on larger pieces of the graph. A regular realization is one whose restriction to every edge is nonconstant. If
$\phi $
could be constant on certain edges or even on larger pieces of the graph. A regular realization is one whose restriction to every edge is nonconstant. If
![]() $\phi :X\to \Sigma $
is a regular realization and if
$\phi :X\to \Sigma $
is a regular realization and if
![]() $\vec e\in \operatorname {\mathrm {\mathbf {half}}}(X)$
is a half-edge incident to a vertex
$\vec e\in \operatorname {\mathrm {\mathbf {half}}}(X)$
is a half-edge incident to a vertex
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
, then we denote by
$v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
, then we denote by
![]() $\phi (\vec e)\in T^1_{\phi (v)}\Sigma $
the unit tangent vector at
$\phi (\vec e)\in T^1_{\phi (v)}\Sigma $
the unit tangent vector at
![]() $\phi (v)$
pointing in the direction of the image of
$\phi (v)$
pointing in the direction of the image of
![]() $\vec e$
.
$\vec e$
.
We endow the set
![]() $\mathcal G^X$
of all realizations of the (always connected) graph X with the compact-open topology and note that unless X itself is contractible, the space
$\mathcal G^X$
of all realizations of the (always connected) graph X with the compact-open topology and note that unless X itself is contractible, the space
![]() $\mathcal G^X$
is not connected: The connected components of
$\mathcal G^X$
is not connected: The connected components of
![]() $\mathcal G^X$
correspond to the different possible free homotopy classes of maps of X into
$\mathcal G^X$
correspond to the different possible free homotopy classes of maps of X into
![]() $\Sigma $
. Indeed, pulling segments tight relative to their endpoints we get that any homotopy
$\Sigma $
. Indeed, pulling segments tight relative to their endpoints we get that any homotopy
between two realizations is homotopic, relative to
![]() $\{0,1\}\times X$
, to a homotopy, which we are still denoting by the same symbol, such that
$\{0,1\}\times X$
, to a homotopy, which we are still denoting by the same symbol, such that
-
1.
 $t\mapsto \varphi _t(v)$
is geodesic for every vertex
$t\mapsto \varphi _t(v)$
is geodesic for every vertex
 $v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
, and
$v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
, and -
2.
 $\varphi _t:X\to \Sigma $
is a realization for all t.
$\varphi _t:X\to \Sigma $
is a realization for all t.
A homotopy
![]() $[0,1]\times X\to \Sigma $
satisfying (1) and (2) is said to be a geodesic homotopy.
$[0,1]\times X\to \Sigma $
satisfying (1) and (2) is said to be a geodesic homotopy.
Geodesic homotopies admit a different intrinsic description. Indeed, uniqueness of geodesic representatives in each homotopy class of arcs implies that each realization
![]() $\phi \in \mathcal G^X$
has a neighborhood which is parametrized by the image of the vertices. This implies that the map
$\phi \in \mathcal G^X$
has a neighborhood which is parametrized by the image of the vertices. This implies that the map
is a cover. Pulling back the product of hyperbolic metrics, we think of it as a manifold locally modeled on the product
![]() $({\mathbb {H}}^2)^{\operatorname {\mathrm {\mathbf {vert}}}(X)}={\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2$
of
$({\mathbb {H}}^2)^{\operatorname {\mathrm {\mathbf {vert}}}(X)}={\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2$
of
![]() $\operatorname {\mathrm {\mathbf {vert}}}(X)$
worth of copies of the hyperbolic plane. Geodesic homotopies are, from this point of view, nothing other than geodesics in
$\operatorname {\mathrm {\mathbf {vert}}}(X)$
worth of copies of the hyperbolic plane. Geodesic homotopies are, from this point of view, nothing other than geodesics in
![]() $\mathcal G^X$
.
$\mathcal G^X$
.
Since all of this will be quite important, we record it here as a proposition:
Proposition 2.1. Let X be a graph. The map (2.2) is a cover and geodesic homotopies are geodesics with respect to the pull-back metric.
Length function
On the space
![]() $\mathcal G^X$
of realizations of the graph X in
$\mathcal G^X$
of realizations of the graph X in
![]() $\Sigma $
, we have the length function
$\Sigma $
, we have the length function
 $$ \begin{align*}\ell_{\Sigma}:\mathcal G^X\to\mathbb R_{\geqslant 0},\ \ \ell_{\Sigma}(\phi)=\sum_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}\ell_{\Sigma}(\phi(e)).\end{align*} $$
$$ \begin{align*}\ell_{\Sigma}:\mathcal G^X\to\mathbb R_{\geqslant 0},\ \ \ell_{\Sigma}(\phi)=\sum_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}\ell_{\Sigma}(\phi(e)).\end{align*} $$
First, note that Arzela–Ascoli implies that
![]() $\ell _{\Sigma }$
is a proper function. It follows thus that the restriction of
$\ell _{\Sigma }$
is a proper function. It follows thus that the restriction of
![]() $\ell _{\Sigma }$
to any and every connected component of
$\ell _{\Sigma }$
to any and every connected component of
![]() $\mathcal G^X$
has a minimum. Now, convexity of the distance function
$\mathcal G^X$
has a minimum. Now, convexity of the distance function
![]() $d_{{\mathbb {H}}^2}(\cdot ,\cdot )$
implies that
$d_{{\mathbb {H}}^2}(\cdot ,\cdot )$
implies that
![]() $\ell _{\Sigma }$
is convex. More precisely, if
$\ell _{\Sigma }$
is convex. More precisely, if
![]() $(\varphi _t)$
is a geodesic homotopy between two realizations in
$(\varphi _t)$
is a geodesic homotopy between two realizations in
![]() $\Sigma $
, then the function
$\Sigma $
, then the function
![]() $t\mapsto \ell _{\Sigma }(\varphi _t)$
is convex. Indeed, it is strictly convex unless the image of
$t\mapsto \ell _{\Sigma }(\varphi _t)$
is convex. Indeed, it is strictly convex unless the image of
![]() $[0,1]\times X$
is contained in a geodesic in
$[0,1]\times X$
is contained in a geodesic in
![]() $\Sigma $
, or rather if the image of some (and hence any) lift to the universal cover is contained in a geodesic in
$\Sigma $
, or rather if the image of some (and hence any) lift to the universal cover is contained in a geodesic in
![]() ${\mathbb {H}}^2$
.
${\mathbb {H}}^2$
.
Note now also that the length function is smooth when restricted to the set of regular realizations – its derivative is given by the first variation formula
 $$ \begin{align*}\frac d{dt}\ell_{\Sigma}(\phi_t)=\sum_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\sum_{\vec e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} \left\langle-\phi(\vec e),\frac d{dt}\phi_t(v)\right\rangle,\end{align*} $$
$$ \begin{align*}\frac d{dt}\ell_{\Sigma}(\phi_t)=\sum_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\sum_{\vec e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} \left\langle-\phi(\vec e),\frac d{dt}\phi_t(v)\right\rangle,\end{align*} $$
where
![]() $\phi (\vec e)\in T_v^1\Sigma $
is the unit tangent vector based at v and pointing as the image of the half-edge
$\phi (\vec e)\in T_v^1\Sigma $
is the unit tangent vector based at v and pointing as the image of the half-edge
![]() $\vec e$
. It follows that a regular realization
$\vec e$
. It follows that a regular realization
![]() $\phi $
is a critical point for the length function
$\phi $
is a critical point for the length function
![]() $\ell _{\Sigma }:\mathcal G^X\to \mathbb R_{\geqslant 0}$
if and only if for every
$\ell _{\Sigma }:\mathcal G^X\to \mathbb R_{\geqslant 0}$
if and only if for every
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
we have
$v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
we have
![]() $\sum _{\vec e\in \operatorname {\mathrm {\mathbf {half}}}_v}\phi (\vec e)=0$
. Note that this implies, in the for us relevant case that X is trivalent, that the (unsigned) angle
$\sum _{\vec e\in \operatorname {\mathrm {\mathbf {half}}}_v}\phi (\vec e)=0$
. Note that this implies, in the for us relevant case that X is trivalent, that the (unsigned) angle
![]() $\angle (\phi '(\vec e_1),\phi '(\vec e_2))$
between the images of any two half-edges incident to the same vertex is equal to
$\angle (\phi '(\vec e_1),\phi '(\vec e_2))$
between the images of any two half-edges incident to the same vertex is equal to
![]() $\frac {2\pi }3$
.
$\frac {2\pi }3$
.
Definition. A regular realization
![]() $\phi :X\to \Sigma $
of a trivalent graph X into
$\phi :X\to \Sigma $
of a trivalent graph X into
![]() $\Sigma $
is critical if we have
$\Sigma $
is critical if we have
for every vertex
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
and for any two distinct
$v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
and for any two distinct
![]() $\vec e_1,\vec e_2\in \operatorname {\mathrm {\mathbf {half}}}_v(X)$
.
$\vec e_1,\vec e_2\in \operatorname {\mathrm {\mathbf {half}}}_v(X)$
.
We collect in the next lemma a few of the properties of critical realizations:
Lemma 2.2. Let X be a trivalent graph. A regular realization
![]() $\phi \in \mathcal G^X$
is a critical point for the length function if and only if
$\phi \in \mathcal G^X$
is a critical point for the length function if and only if
![]() $\phi $
is a critical realization. Moreover, if
$\phi $
is a critical realization. Moreover, if
![]() $\phi \in \mathcal G^X$
is a critical realization and
$\phi \in \mathcal G^X$
is a critical realization and
![]() $\mathcal G^{\phi }$
is the connected component of
$\mathcal G^{\phi }$
is the connected component of
![]() $\mathcal G^X$
containing
$\mathcal G^X$
containing
![]() $\phi $
, then the following holds:
$\phi $
, then the following holds:
-
1.
 $\phi $
is the unique critical realization in
$\phi $
is the unique critical realization in
 $\mathcal G^{\phi }$
.
$\mathcal G^{\phi }$
. -
2.
 $\phi $
is the global minimum of the length function on
$\phi $
is the global minimum of the length function on
 $\mathcal G^{\phi }$
.
$\mathcal G^{\phi }$
. -
3. Besides
 $\phi $
, there are no other local minima in
$\phi $
, there are no other local minima in
 $\mathcal G^{\phi }$
of the length function.
$\mathcal G^{\phi }$
of the length function. -
4. The connected component
 $\mathcal G^{\phi }$
is isometric to the product
$\mathcal G^{\phi }$
is isometric to the product
 ${\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2$
of
${\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2$
of
 $\operatorname {\mathrm {\mathbf {vert}}}(X)$
many copies of the hyperbolic plane.
$\operatorname {\mathrm {\mathbf {vert}}}(X)$
many copies of the hyperbolic plane.
Note that lack of global smoothness of the length function means that we cannot directly derive (2) and (3) from (1). This is why they appear as independent statements.
Proof. Statement (1) was actually discussed in the paragraph preceding the definition of critical realization. Let us focus in the subsequent ones. Recall that if
is a (nonconstant) geodesic homotopy with
![]() $\phi _0=\phi $
, then the length function
$\phi _0=\phi $
, then the length function
is convex. In our situation it is strictly convex: Since
![]() $\phi $
is critical, we get that its image, or rather the image of its lifts to the universal cover, are not contained in a geodesic because if they were, then the angles between any two half-edges starting at the same vertex could only take the values
$\phi $
is critical, we get that its image, or rather the image of its lifts to the universal cover, are not contained in a geodesic because if they were, then the angles between any two half-edges starting at the same vertex could only take the values
![]() $0$
or
$0$
or
![]() $\pi $
. Now, strict convexity and the fact that
$\pi $
. Now, strict convexity and the fact that
![]() $\phi =\phi _0$
is a critical point of the length function implies that
$\phi =\phi _0$
is a critical point of the length function implies that
![]() $t=0$
is the minimum and only critical point of the function (2.3). From here, we get directly (2) and (3). To prove (4), note that if
$t=0$
is the minimum and only critical point of the function (2.3). From here, we get directly (2) and (3). To prove (4), note that if
![]() $\mathcal G^{\phi }$
were not simply connected, then there would be a nontrivial geodesic homotopy starting and ending at
$\mathcal G^{\phi }$
were not simply connected, then there would be a nontrivial geodesic homotopy starting and ending at
![]() $\phi $
, contradicting the strict convexity of the length function. Note now that the restricting the cover (2.2) to
$\phi $
, contradicting the strict convexity of the length function. Note now that the restricting the cover (2.2) to
![]() $\mathcal G^{\phi }$
we get a locally isometric cover
$\mathcal G^{\phi }$
we get a locally isometric cover
![]() $\mathcal G^{\phi }\to \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
. Since the domain of this cover is connected and simply connected, we get that it is nothing other than the universal cover of
$\mathcal G^{\phi }\to \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
. Since the domain of this cover is connected and simply connected, we get that it is nothing other than the universal cover of
![]() $\Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
. This proves (4) and concludes the proof of the lemma.
$\Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
. This proves (4) and concludes the proof of the lemma.
Remark. Although we will not need it here, let us comment briefly on the topology of the connected components of
![]() $\mathcal G^X$
. The fundamental group of the connected component
$\mathcal G^X$
. The fundamental group of the connected component
![]() $\mathcal G^{\phi }$
containing a realization
$\mathcal G^{\phi }$
containing a realization
![]() $\phi \in \mathcal G^X$
is isomorphic to the centralizer
$\phi \in \mathcal G^X$
is isomorphic to the centralizer
![]() $\mathcal Z_{\pi _1(\Sigma )}(\phi _*(\pi _1(X)))$
in
$\mathcal Z_{\pi _1(\Sigma )}(\phi _*(\pi _1(X)))$
in
![]() $\pi _1(\Sigma )$
of the image of
$\pi _1(\Sigma )$
of the image of
![]() $\pi _1(X)$
under
$\pi _1(X)$
under
![]() $\phi _*:\pi _1(X)\to \pi _1(\Sigma )$
. It follows that
$\phi _*:\pi _1(X)\to \pi _1(\Sigma )$
. It follows that
![]() $\mathcal G^{\phi }$
is isometric to the quotient under the diagonal action of
$\mathcal G^{\phi }$
is isometric to the quotient under the diagonal action of
![]() $\mathcal Z_{\pi _1(\Sigma )}(\phi _*(\pi _1(X)))$
of
$\mathcal Z_{\pi _1(\Sigma )}(\phi _*(\pi _1(X)))$
of
![]() ${\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2$
of
${\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2$
of
![]() $\operatorname {\mathrm {\mathbf {vert}}}(X)$
-copies of the hyperbolic plane. In particular, we have:
$\operatorname {\mathrm {\mathbf {vert}}}(X)$
-copies of the hyperbolic plane. In particular, we have:
-
○ If
 $\phi $
is homotopically trivial, then
$\phi $
is homotopically trivial, then
 $\mathcal G^{\phi }\simeq \pi _1(\Sigma )\backslash ({\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2)$
.
$\mathcal G^{\phi }\simeq \pi _1(\Sigma )\backslash ({\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2)$
. -
○ If
 $\phi _*(\pi _1(X))\neq \operatorname {\mathrm {Id}}_{\pi _1(\Sigma )}$
is abelian, then
$\phi _*(\pi _1(X))\neq \operatorname {\mathrm {Id}}_{\pi _1(\Sigma )}$
is abelian, then
 $\mathcal G^{\phi }\simeq \mathbb Z\backslash ({\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2)$
.
$\mathcal G^{\phi }\simeq \mathbb Z\backslash ({\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2)$
. -
○
 $\phi _*(\pi _1(X))$
is non-abelian, then
$\phi _*(\pi _1(X))$
is non-abelian, then
 $\mathcal G^{\phi }\simeq {\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2.$
$\mathcal G^{\phi }\simeq {\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2.$
In the appendix, we will give a concrete description of the components of
![]() $\mathcal G^X$
for the case that X is a loop, that is, the graph with a single vertex and a single edge.
$\mathcal G^X$
for the case that X is a loop, that is, the graph with a single vertex and a single edge.
Lemma 2.2, with all its beauty, does not say anything about the existence of critical realizations. Our next goal is to prove that any realization that from far away kind of looks like a critical realization is actually homotopic to a critical realization.
Quasicritical realizations
Recall that a regular realization
![]() $\phi :X\to \Sigma $
of a trivalent graph X is critical if the angles between the images of any two half-edges incident to the same vertex are equal to
$\phi :X\to \Sigma $
of a trivalent graph X is critical if the angles between the images of any two half-edges incident to the same vertex are equal to
![]() $\frac {2\pi }3$
. We will say that a regular realization is quasicritical if those angles are bounded from below by
$\frac {2\pi }3$
. We will say that a regular realization is quasicritical if those angles are bounded from below by
![]() $\frac {1}{2}\pi $
and that the realization is
$\frac {1}{2}\pi $
and that the realization is
![]() $\ell _0$
-long if
$\ell _0$
-long if
![]() $\ell (\phi (e))>\ell _0$
for all edges e of X. Recall that we measure all angles in
$\ell (\phi (e))>\ell _0$
for all edges e of X. Recall that we measure all angles in
![]() $[0,\pi ]$
.
$[0,\pi ]$
.
Our next goal here is to prove that every sufficiently long quasicritical realization is homotopic to a critical realization. This will follow easily from the following technical result:
Proposition 2.3. For any trivalent graph X and constant
![]() $C\geq 0$
, there exist constants
$C\geq 0$
, there exist constants
![]() $\ell _0, D>0$
such that given an
$\ell _0, D>0$
such that given an
![]() $\ell _0$
-long quasicritical realization
$\ell _0$
-long quasicritical realization
![]() $\phi : X\to \Sigma $
, a trivalent graph Y and realization
$\phi : X\to \Sigma $
, a trivalent graph Y and realization
![]() $\psi : Y\to \Sigma $
satisfying
$\psi : Y\to \Sigma $
satisfying
-
1.
 $\ell (\psi )\leq \ell (\phi )+C$
, and
$\ell (\psi )\leq \ell (\phi )+C$
, and -
2. there is a homotopy equivalence
 $\sigma : X\to Y$
with
$\sigma : X\to Y$
with
 $\phi $
and
$\phi $
and
 $\sigma \circ \psi $
homotopic,
$\sigma \circ \psi $
homotopic,
then there exists a homeomorphism
![]() $F: Y\to X$
mapping each edge with constant speed such that
$F: Y\to X$
mapping each edge with constant speed such that
![]() $\sigma \circ F$
is homotopic to the identity and such that the geodesic homotopy
$\sigma \circ F$
is homotopic to the identity and such that the geodesic homotopy
![]() $X\times [0,1]\to \sigma $
,
$X\times [0,1]\to \sigma $
,
![]() $(x, t)\mapsto \phi _t(x)$
joining
$(x, t)\mapsto \phi _t(x)$
joining
![]() $\phi _0(\cdot ) = \phi \circ F(\cdot )$
to
$\phi _0(\cdot ) = \phi \circ F(\cdot )$
to
![]() $\phi _1(\cdot ) = \psi (\cdot )$
has tracks bounded by D.
$\phi _1(\cdot ) = \psi (\cdot )$
has tracks bounded by D.
Since the proof of Proposition 2.3 is technical and pretty long, it may be a good idea to skip it in a first reading. Nevertheless, before proving it, we demonstrate that it might be useful:
Corollary 2.4. Let X be a trivalent graph. There are positive constants
![]() $\ell _0$
and D such that every component of
$\ell _0$
and D such that every component of
![]() $\mathcal G^X$
which contains an
$\mathcal G^X$
which contains an
![]() $\ell _0$
-long quasicritical realization
$\ell _0$
-long quasicritical realization
![]() $\phi : X\to \Sigma $
also contains a critical realization
$\phi : X\to \Sigma $
also contains a critical realization
![]() $\psi $
, which moreover is unique and homotopic to
$\psi $
, which moreover is unique and homotopic to
![]() $\phi $
by a homotopy whose tracks have length bounded by D.
$\phi $
by a homotopy whose tracks have length bounded by D.
Proof. Let
![]() $\ell _0$
and D be given by Proposition 2.3 for
$\ell _0$
and D be given by Proposition 2.3 for
![]() $C=0$
and if needed increase
$C=0$
and if needed increase
![]() $\ell _0$
so that it is larger than
$\ell _0$
so that it is larger than
![]() $2D$
. Let
$2D$
. Let
![]() $\phi : X\to \Sigma $
be an
$\phi : X\to \Sigma $
be an
![]() $\ell _0$
-long quasicritical realization. Let
$\ell _0$
-long quasicritical realization. Let
![]() $\psi : X\to \Sigma $
be the minimizer for the length function in the component
$\psi : X\to \Sigma $
be the minimizer for the length function in the component
![]() $\mathcal G^{\phi }$
– it exists because the length function is proper. We claim that
$\mathcal G^{\phi }$
– it exists because the length function is proper. We claim that
![]() $\psi $
is critical. In the light of Lemma 2.2, it suffices to prove that
$\psi $
is critical. In the light of Lemma 2.2, it suffices to prove that
![]() $\psi $
is regular.
$\psi $
is regular.
Being a minimizer we have that
![]() $\ell _{\Sigma }(\psi )\leqslant \ell _{\Sigma }(\phi )$
. We thus get from Proposition 2.3 that there exists a homeomorphism
$\ell _{\Sigma }(\psi )\leqslant \ell _{\Sigma }(\phi )$
. We thus get from Proposition 2.3 that there exists a homeomorphism
![]() $F: X\to X$
homotopic to the identity, mapping edges with constant speed and such that the geodesic homotopy from
$F: X\to X$
homotopic to the identity, mapping edges with constant speed and such that the geodesic homotopy from
![]() $\phi \circ F$
to
$\phi \circ F$
to
![]() $\psi $
has tracks bounded by D. Now, since X is trivalent we get that the homeomorphism F, being homotopic to the identity and mapping edges with constant speed, is actually equal to the identity. What we thus have is a homotopy from
$\psi $
has tracks bounded by D. Now, since X is trivalent we get that the homeomorphism F, being homotopic to the identity and mapping edges with constant speed, is actually equal to the identity. What we thus have is a homotopy from
![]() $\phi $
and
$\phi $
and
![]() $\psi $
with tracks bounded by D. Now, since each edge of
$\psi $
with tracks bounded by D. Now, since each edge of
![]() $\phi (X)$
has at least length
$\phi (X)$
has at least length
![]() $\ell _0>2D$
and since the tracks of the homotopy are bounded by D, we get that
$\ell _0>2D$
and since the tracks of the homotopy are bounded by D, we get that
![]() $\psi $
is regular and hence critical by Lemma 2.2, as we needed to prove. Lemma 2.2 also yields that
$\psi $
is regular and hence critical by Lemma 2.2, as we needed to prove. Lemma 2.2 also yields that
![]() $\psi $
is unique.
$\psi $
is unique.
Let us next prove the proposition:
Proof of Proposition 2.3
Let
![]() $\phi : X\to \Sigma $
be a quasicritical realization, and assume it is
$\phi : X\to \Sigma $
be a quasicritical realization, and assume it is
![]() $\ell _0$
-long for an
$\ell _0$
-long for an
![]() $\ell _0$
large enough to satisfy some conditions we will give in the course of the proof. Let
$\ell _0$
large enough to satisfy some conditions we will give in the course of the proof. Let
![]() $H: X\times [0,1]\to \Sigma $
be the homotopy between
$H: X\times [0,1]\to \Sigma $
be the homotopy between
![]() $\phi $
and
$\phi $
and
![]() $\psi \circ \sigma $
.
$\psi \circ \sigma $
.
To be able to consistently choose lifts of
![]() $\phi $
,
$\phi $
,
![]() $\psi $
and
$\psi $
and
![]() $\sigma $
to the universal covers
$\sigma $
to the universal covers
![]() $\widetilde X, \widetilde Y$
and
$\widetilde X, \widetilde Y$
and
![]() ${\mathbb {H}}^2$
of
${\mathbb {H}}^2$
of
![]() $X,Y$
and
$X,Y$
and
![]() $\Sigma $
, let us start by picking base points. Fixing
$\Sigma $
, let us start by picking base points. Fixing
![]() $x_0\in X$
, consider the base points
$x_0\in X$
, consider the base points
![]() $\sigma (x_0)\in Y$
and
$\sigma (x_0)\in Y$
and
![]() $\phi (x_0)\in \Sigma $
, and pick lifts
$\phi (x_0)\in \Sigma $
, and pick lifts
![]() $\widetilde {x}_0\in \widetilde X$
,
$\widetilde {x}_0\in \widetilde X$
,
![]() $\widetilde {\sigma (x_0)}\in \widetilde Y$
and
$\widetilde {\sigma (x_0)}\in \widetilde Y$
and
![]() $\widetilde {\phi (x_0)}\in \mathbb {H}^2$
of each one of those endpoints. Having chosen those base points we have uniquely determined lifts
$\widetilde {\phi (x_0)}\in \mathbb {H}^2$
of each one of those endpoints. Having chosen those base points we have uniquely determined lifts
![]() $\widetilde {\phi }: \widetilde {X}\to \mathbb {H}^2$
and
$\widetilde {\phi }: \widetilde {X}\to \mathbb {H}^2$
and
![]() $\widetilde {\sigma }: \widetilde {X}\to \widetilde {Y}$
of
$\widetilde {\sigma }: \widetilde {X}\to \widetilde {Y}$
of
![]() $\phi $
and
$\phi $
and
![]() $\sigma $
satisfying
$\sigma $
satisfying
![]() $\widetilde {\phi }(\widetilde x_0) = \widetilde {\phi (x_0)}$
and
$\widetilde {\phi }(\widetilde x_0) = \widetilde {\phi (x_0)}$
and
![]() $\widetilde {\sigma }(\widetilde {x}_0) = \widetilde {\sigma (x_0)}$
. We can also lift to
$\widetilde {\sigma }(\widetilde {x}_0) = \widetilde {\sigma (x_0)}$
. We can also lift to
![]() ${\mathbb {H}}^2$
, starting at
${\mathbb {H}}^2$
, starting at
![]() $\widetilde \phi (\widetilde {x_0})$
, the path in
$\widetilde \phi (\widetilde {x_0})$
, the path in
![]() $\Sigma $
given by
$\Sigma $
given by
![]() $t\mapsto H(x_0, t)$
. The endpoint of this path is a lift of
$t\mapsto H(x_0, t)$
. The endpoint of this path is a lift of
![]() $\psi \circ \sigma (x_0)$
, and we take the lift
$\psi \circ \sigma (x_0)$
, and we take the lift
![]() $\widetilde {\psi }: \widetilde {Y}\to \mathbb {H}^2$
which maps
$\widetilde {\psi }: \widetilde {Y}\to \mathbb {H}^2$
which maps
![]() $\widetilde {\sigma }(\widetilde x_0)$
to this point. All those lifts are related by the following equivariance property:
$\widetilde {\sigma }(\widetilde x_0)$
to this point. All those lifts are related by the following equivariance property:
for all
![]() $x\in \widetilde {X}$
and for all
$x\in \widetilde {X}$
and for all
![]() $g\in \pi _1(X, x_0)$
, where
$g\in \pi _1(X, x_0)$
, where
![]() $\phi _*: \pi _1(X, x_0)\to \pi _1(\Sigma , \phi (x_0))$
is the homomorphism induced by
$\phi _*: \pi _1(X, x_0)\to \pi _1(\Sigma , \phi (x_0))$
is the homomorphism induced by
![]() $\phi $
and the chosen base points.
$\phi $
and the chosen base points.
Note that, since
![]() $\phi $
is almost critical and
$\phi $
is almost critical and
![]() $\ell _0$
-long we get, as long as
$\ell _0$
-long we get, as long as
![]() $\ell _0$
is large enough, that the lift
$\ell _0$
is large enough, that the lift
![]() $\widetilde \phi :\widetilde X\to {\mathbb {H}}^2$
is an injective quasi-isometric embedding. For ease of notation, denote by
$\widetilde \phi :\widetilde X\to {\mathbb {H}}^2$
is an injective quasi-isometric embedding. For ease of notation, denote by
![]() $T_X=\widetilde {\phi }(\widetilde {X})\subset \mathbb {H}^2$
the image of
$T_X=\widetilde {\phi }(\widetilde {X})\subset \mathbb {H}^2$
the image of
![]() $\widetilde \phi $
and let us rephrase what we just said: If
$\widetilde \phi $
and let us rephrase what we just said: If
![]() $\ell _0$
is sufficiently large, then
$\ell _0$
is sufficiently large, then
![]() $T_X$
is a quasiconvex tree, with quasiconvexity constants only depending on a lower bound for
$T_X$
is a quasiconvex tree, with quasiconvexity constants only depending on a lower bound for
![]() $\ell _0$
. We denote by
$\ell _0$
. We denote by
![]() $\hat \pi :{\mathbb {H}}^2\to T_X$
a nearest point retraction which is equivariant under
$\hat \pi :{\mathbb {H}}^2\to T_X$
a nearest point retraction which is equivariant under
![]() $\phi _*(\pi _1(X, x_0))$
. We would like to define
$\phi _*(\pi _1(X, x_0))$
. We would like to define
as
![]() $\hat \pi \circ \widetilde \psi $
, but since
$\hat \pi \circ \widetilde \psi $
, but since
![]() $\hat \pi $
is definitively not continuous, we have to be slightly careful. We define
$\hat \pi $
is definitively not continuous, we have to be slightly careful. We define
![]() $\pi $
as follows: First, set
$\pi $
as follows: First, set
![]() $\pi (v) = \hat \pi (\tilde {\psi }(v))$
for all vertices
$\pi (v) = \hat \pi (\tilde {\psi }(v))$
for all vertices
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}(\widetilde Y)$
of
$v\in \operatorname {\mathrm {\mathbf {vert}}}(\widetilde Y)$
of
![]() $\widetilde Y$
, and then extend (at constant speed) over the edges of Y. Note that Equation (2.4), together with the equivariance of
$\widetilde Y$
, and then extend (at constant speed) over the edges of Y. Note that Equation (2.4), together with the equivariance of
![]() $\pi $
, implies that
$\pi $
, implies that
![]() $\pi \circ \widetilde {\sigma }: \tilde {X}\to T_X$
satisfies
$\pi \circ \widetilde {\sigma }: \tilde {X}\to T_X$
satisfies
for all
![]() $x\in \widetilde {X}$
and
$x\in \widetilde {X}$
and
![]() $g\in \pi _1(X, x_0)$
.
$g\in \pi _1(X, x_0)$
.
Claim 1. As long as
![]() $\ell _0$
is large enough, we have that
$\ell _0$
is large enough, we have that
![]() $\pi $
maps each vertex of
$\pi $
maps each vertex of
![]() $\widetilde Y$
within
$\widetilde Y$
within
![]() $\operatorname {\mathrm {\mathbf {const}}}$
of one and only one vertex of
$\operatorname {\mathrm {\mathbf {const}}}$
of one and only one vertex of
![]() $T_X$
.
$T_X$
.
Starting with the proof of the claim, note that there is a constant
![]() $A\geqslant 0$
depending only on the quasiconvexity constants for
$A\geqslant 0$
depending only on the quasiconvexity constants for
![]() $T_X$
with
$T_X$
with
for all
![]() $x,y\in {\mathbb {H}}^2$
. In fact, there exists constants
$x,y\in {\mathbb {H}}^2$
. In fact, there exists constants
![]() $K, A'>0$
which once again depend only on the quasiconvexity constant of
$K, A'>0$
which once again depend only on the quasiconvexity constant of
![]() $T_X$
such that whenever
$T_X$
such that whenever
![]() $d_{\mathbb {H}^2}(\hat \pi (x),\hat \pi (y))>K$
we have the better bound
$d_{\mathbb {H}^2}(\hat \pi (x),\hat \pi (y))>K$
we have the better bound
For
![]() $a, b\in T_X$
, let
$a, b\in T_X$
, let
![]() $d_{T_X}(a,b)$
denote the interior distance in
$d_{T_X}(a,b)$
denote the interior distance in
![]() $T_X$
between them. We will care about a modified version of this distance: Let B be the collection of balls in
$T_X$
between them. We will care about a modified version of this distance: Let B be the collection of balls in
![]() ${\mathbb {H}}^2$
of radius 1 centered at each vertex of
${\mathbb {H}}^2$
of radius 1 centered at each vertex of
![]() $T_X$
, and define
$T_X$
, and define
![]() $d_{T_X\text {rel}B}(a, b)$
to be the length of the part of the path in
$d_{T_X\text {rel}B}(a, b)$
to be the length of the part of the path in
![]() $T_X$
between them that lies outside of B. For all
$T_X$
between them that lies outside of B. For all
![]() $\ell _0$
large enough (depending only on hyperbolicity of
$\ell _0$
large enough (depending only on hyperbolicity of
![]() ${\mathbb {H}}^2$
), we have from the choice of the radiusFootnote 1 that
${\mathbb {H}}^2$
), we have from the choice of the radiusFootnote 1 that
for all
![]() $a, b \in T_X$
.
$a, b \in T_X$
.
Given two edges
![]() $e, e'$
of
$e, e'$
of
![]() $\widetilde Y$
adjacent to the same vertex, we define
$\widetilde Y$
adjacent to the same vertex, we define
and let then
where the maximum is taken over all such pairs of edges. The reason to introduce this quantity is that we have
 $$ \begin{align} \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}(Y)} d_{T_X\text{rel}B}(\pi(v), \pi(v')) \geq \ell(\phi) + \operatorname{\mathrm{Fold}}(\pi) - A" \end{align} $$
$$ \begin{align} \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}(Y)} d_{T_X\text{rel}B}(\pi(v), \pi(v')) \geq \ell(\phi) + \operatorname{\mathrm{Fold}}(\pi) - A" \end{align} $$
for some positive constant
![]() $A"$
depending only on that number of vertices (and the fact that we chose the balls B to have radius
$A"$
depending only on that number of vertices (and the fact that we chose the balls B to have radius
![]() $1$
) – here, we have identified each edge of Y with one of its representatives in
$1$
) – here, we have identified each edge of Y with one of its representatives in
![]() $\widetilde Y$
.
$\widetilde Y$
.
Now, using Equations (2.5), (2.7) and (2.8), we get that
 $$ \begin{align*} \ell(\psi) &= \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}(Y)}d_{{\mathbb{H}}^2}(\tilde\psi(v), \tilde\psi(v')) \\ & \geq -\operatorname{\mathrm{\mathbf{const}}} + \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}(Y)} d_{{\mathbb{H}}^2}(\pi(v), \pi(v'))\\ & \geq -\operatorname{\mathrm{\mathbf{const}}} + \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}(Y)} d_{T_X\text{rel}B}(\pi(v), \pi(v'))\\ & \geq -\operatorname{\mathrm{\mathbf{const}}} + \ell(\phi) + \operatorname{\mathrm{Fold}}(\pi), \end{align*} $$
$$ \begin{align*} \ell(\psi) &= \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}(Y)}d_{{\mathbb{H}}^2}(\tilde\psi(v), \tilde\psi(v')) \\ & \geq -\operatorname{\mathrm{\mathbf{const}}} + \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}(Y)} d_{{\mathbb{H}}^2}(\pi(v), \pi(v'))\\ & \geq -\operatorname{\mathrm{\mathbf{const}}} + \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}(Y)} d_{T_X\text{rel}B}(\pi(v), \pi(v'))\\ & \geq -\operatorname{\mathrm{\mathbf{const}}} + \ell(\phi) + \operatorname{\mathrm{Fold}}(\pi), \end{align*} $$
where each
![]() $\operatorname {\mathrm {\mathbf {const}}}$
is a positive constant (but not necessarily the same) depending on the quasiconvexity constant and combinatorics of Y.
$\operatorname {\mathrm {\mathbf {const}}}$
is a positive constant (but not necessarily the same) depending on the quasiconvexity constant and combinatorics of Y.
Since
![]() $\ell (\psi )\leq \ell (\phi )+C$
, it follows that
$\ell (\psi )\leq \ell (\phi )+C$
, it follows that
![]() $\operatorname {\mathrm {Fold}}(\pi ) \leq \operatorname {\mathrm {\mathbf {const}}}$
, where the constant depends on C and on the lower bound for
$\operatorname {\mathrm {Fold}}(\pi ) \leq \operatorname {\mathrm {\mathbf {const}}}$
, where the constant depends on C and on the lower bound for
![]() $\ell _0$
and on combinatorics of Y. In particular, for each
$\ell _0$
and on combinatorics of Y. In particular, for each
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}$
there is a vertex
$v\in \operatorname {\mathrm {\mathbf {vert}}}$
there is a vertex
![]() $v'\in T_X$
such that
$v'\in T_X$
such that
![]() $d_{T_X\text {rel}B}(\pi (v), v') \leq \operatorname {\mathrm {\mathbf {const}}}$
and we can choose
$d_{T_X\text {rel}B}(\pi (v), v') \leq \operatorname {\mathrm {\mathbf {const}}}$
and we can choose
![]() $\ell _0$
large such that
$\ell _0$
large such that
![]() $v'$
is unique. We have proved Claim 1.
$v'$
is unique. We have proved Claim 1.
Armed with Claim 1, we can define a map
![]() $\widetilde {F}: \widetilde Y\to T_X$
by first mapping
$\widetilde {F}: \widetilde Y\to T_X$
by first mapping
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}(\widetilde Y)$
, to the unique vertex in
$v\in \operatorname {\mathrm {\mathbf {vert}}}(\widetilde Y)$
, to the unique vertex in
![]() $T_X$
closest to
$T_X$
closest to
![]() $\pi (v)$
, extending it so that it maps each
$\pi (v)$
, extending it so that it maps each
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}(\widetilde Y)$
with constant speed. Note that equivariance of
$e\in \operatorname {\mathrm {\mathbf {edge}}}(\widetilde Y)$
with constant speed. Note that equivariance of
![]() $\pi $
implies that
$\pi $
implies that
![]() $\widetilde {F}$
satisfies
$\widetilde {F}$
satisfies
![]() $\widetilde F(\sigma _*(g)(y)) = g(\widetilde F(y))$
for all
$\widetilde F(\sigma _*(g)(y)) = g(\widetilde F(y))$
for all
![]() $y\in \widetilde Y$
and
$y\in \widetilde Y$
and
![]() $g\in \pi _1(X, x_0)$
, where
$g\in \pi _1(X, x_0)$
, where
![]() $\sigma _*: \pi _1(X, x_0)\to \pi _1(Y, \sigma (x_0))$
is the isomorphism induced by
$\sigma _*: \pi _1(X, x_0)\to \pi _1(Y, \sigma (x_0))$
is the isomorphism induced by
![]() $\sigma $
and the chosen base points. It follows that
$\sigma $
and the chosen base points. It follows that
![]() $\widetilde F$
descends to a map
$\widetilde F$
descends to a map
![]() $F: Y\to X$
.
$F: Y\to X$
.
Claim 2.
![]() $F:Y\to X$
is a homeomorphism with
$F:Y\to X$
is a homeomorphism with
![]() $F\circ \sigma $
homotopic to the identity.
$F\circ \sigma $
homotopic to the identity.
The fact that
![]() $F\circ \sigma $
is homotopic to the identity follows directly from the fact
$F\circ \sigma $
is homotopic to the identity follows directly from the fact
![]() $\widetilde F\circ \widetilde \sigma : \widetilde X\to \widetilde X$
satisfies that
$\widetilde F\circ \widetilde \sigma : \widetilde X\to \widetilde X$
satisfies that
![]() $(\widetilde F\circ \sigma )(gx)=g((\widetilde F\circ \widetilde \sigma )(x))$
for
$(\widetilde F\circ \sigma )(gx)=g((\widetilde F\circ \widetilde \sigma )(x))$
for
![]() $g\in \pi _1(X,x_0)$
. What we really have to prove is that F is a homeomorphism. To see that this is the case, note that since the maps
$g\in \pi _1(X,x_0)$
. What we really have to prove is that F is a homeomorphism. To see that this is the case, note that since the maps
![]() $\widetilde F,\pi :\widetilde Y\to \widetilde X$
send points within
$\widetilde F,\pi :\widetilde Y\to \widetilde X$
send points within
![]() $\operatorname {\mathrm {\mathbf {const}}}$
of each other, and since in our way to proving Claim 1 we proved that
$\operatorname {\mathrm {\mathbf {const}}}$
of each other, and since in our way to proving Claim 1 we proved that
![]() $\operatorname {\mathrm {Fold}}(\pi )<\operatorname {\mathrm {\mathbf {const}}}$
, we get that
$\operatorname {\mathrm {Fold}}(\pi )<\operatorname {\mathrm {\mathbf {const}}}$
, we get that
![]() $\operatorname {\mathrm {Fold}}(\widetilde F)<\operatorname {\mathrm {\mathbf {const}}}$
. On the other hand, since
$\operatorname {\mathrm {Fold}}(\widetilde F)<\operatorname {\mathrm {\mathbf {const}}}$
. On the other hand, since
![]() $\widetilde F$
maps vertices to vertices and has constant speed on the edges we get that if
$\widetilde F$
maps vertices to vertices and has constant speed on the edges we get that if
![]() $\operatorname {\mathrm {Fold}}(\widetilde F)\neq 0$
, then
$\operatorname {\mathrm {Fold}}(\widetilde F)\neq 0$
, then
![]() $\operatorname {\mathrm {Fold}}(F)$
has to be at least as large as the shortest edge of X. This implies, using the fact that
$\operatorname {\mathrm {Fold}}(F)$
has to be at least as large as the shortest edge of X. This implies, using the fact that
![]() $\operatorname {\mathrm {Fold}}(\widetilde F)$
is uniformly bounded, that as long as
$\operatorname {\mathrm {Fold}}(\widetilde F)$
is uniformly bounded, that as long as
![]() $\ell _0$
is large enough, then
$\ell _0$
is large enough, then
![]() $\operatorname {\mathrm {Fold}}(\widetilde F)=0$
. This implies in turn that
$\operatorname {\mathrm {Fold}}(\widetilde F)=0$
. This implies in turn that
![]() $\widetilde F$
is locally injective. Local injectivity of
$\widetilde F$
is locally injective. Local injectivity of
![]() $\widetilde F$
, together with the fact that F, being a homotopy inverse to
$\widetilde F$
, together with the fact that F, being a homotopy inverse to
![]() $\sigma $
, is a homotopy equivalence, implies that F is a homeomorphism. We have proved Claim 2.
$\sigma $
, is a homotopy equivalence, implies that F is a homeomorphism. We have proved Claim 2.
What is left is to bound the tracks of the geodesic homotopy from
![]() $\phi \circ F$
to
$\phi \circ F$
to
![]() $\psi $
– the argument is similar to the proof of the existence of F. First, note that we know that for every vertex
$\psi $
– the argument is similar to the proof of the existence of F. First, note that we know that for every vertex
![]() $v\in \widetilde Y$
, the nearest point projection
$v\in \widetilde Y$
, the nearest point projection
![]() $\hat \pi $
maps
$\hat \pi $
maps
![]() $\widetilde \psi (v)$
close to the vertex
$\widetilde \psi (v)$
close to the vertex
![]() $\tilde \phi (\widetilde F(v))$
of
$\tilde \phi (\widetilde F(v))$
of
![]() $T_X$
. It follows that if we choose
$T_X$
. It follows that if we choose
![]() $\ell _0$
large enough we can also assume that
$\ell _0$
large enough we can also assume that
![]() $d_{\mathbb {H}^2}(\hat \pi (\tilde \psi (v)),\hat \pi (\tilde \psi ((v'))))> K$
for any two distinct vertices
$d_{\mathbb {H}^2}(\hat \pi (\tilde \psi (v)),\hat \pi (\tilde \psi ((v'))))> K$
for any two distinct vertices
![]() $v,v'\in \operatorname {\mathrm {\mathbf {vert}}}(\widetilde Y)$
. This means that Equation (2.6) applies, and hence that we have
$v,v'\in \operatorname {\mathrm {\mathbf {vert}}}(\widetilde Y)$
. This means that Equation (2.6) applies, and hence that we have
 $$ \begin{align*} \ell(\psi(Y)) &= \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}}d_{{\mathbb{H}}^2}(\tilde\psi(v), \tilde\psi(v')) \\ & \geq -\operatorname{\mathrm{\mathbf{const}}} + \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}} d_{\mathbb{H}^2}(\hat\pi(\tilde\psi(v)),\hat\pi(\tilde\psi(v')))+ \\ & \hspace{1cm}+ 3\sum_{v\in\operatorname{\mathrm{\mathbf{vert}}}} d_{{\mathbb{H}}^2}(\tilde\psi(v),\hat\pi(\tilde\psi(v)))\\ & \geq -\operatorname{\mathrm{\mathbf{const}}} + \ell(\phi(X)) + 3\sum_{v\in\operatorname{\mathrm{\mathbf{vert}}}} d_{\mathbb{H}^2}(\tilde\psi(v), \hat\pi(\tilde\psi(v))), \end{align*} $$
$$ \begin{align*} \ell(\psi(Y)) &= \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}}d_{{\mathbb{H}}^2}(\tilde\psi(v), \tilde\psi(v')) \\ & \geq -\operatorname{\mathrm{\mathbf{const}}} + \sum_{[v, v']\in\operatorname{\mathrm{\mathbf{edge}}}} d_{\mathbb{H}^2}(\hat\pi(\tilde\psi(v)),\hat\pi(\tilde\psi(v')))+ \\ & \hspace{1cm}+ 3\sum_{v\in\operatorname{\mathrm{\mathbf{vert}}}} d_{{\mathbb{H}}^2}(\tilde\psi(v),\hat\pi(\tilde\psi(v)))\\ & \geq -\operatorname{\mathrm{\mathbf{const}}} + \ell(\phi(X)) + 3\sum_{v\in\operatorname{\mathrm{\mathbf{vert}}}} d_{\mathbb{H}^2}(\tilde\psi(v), \hat\pi(\tilde\psi(v))), \end{align*} $$
where as before each
![]() $\operatorname {\mathrm {\mathbf {const}}}$
is a positive constant, the first inequality follows by Equation (2.6), the second by Equations (2.7) and (2.8). Hence, again by assumption (1) in the lemma, we must have that
$\operatorname {\mathrm {\mathbf {const}}}$
is a positive constant, the first inequality follows by Equation (2.6), the second by Equations (2.7) and (2.8). Hence, again by assumption (1) in the lemma, we must have that
![]() $d_{\mathbb {H}^2}(\tilde \psi (v), \hat \pi (\tilde \psi (v)))<\operatorname {\mathrm {\mathbf {const}}}$
for all
$d_{\mathbb {H}^2}(\tilde \psi (v), \hat \pi (\tilde \psi (v)))<\operatorname {\mathrm {\mathbf {const}}}$
for all
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}(\widetilde Y)$
. Since
$v\in \operatorname {\mathrm {\mathbf {vert}}}(\widetilde Y)$
. Since
![]() $\widetilde {F}(v)$
and
$\widetilde {F}(v)$
and
![]() $\hat \pi (\tilde \psi (v))$
are near each other, we have that
$\hat \pi (\tilde \psi (v))$
are near each other, we have that
![]() $d_{\mathbb {H}^2}(\tilde \psi (v), \widetilde F(v))<\operatorname {\mathrm {\mathbf {const}}}$
for all
$d_{\mathbb {H}^2}(\tilde \psi (v), \widetilde F(v))<\operatorname {\mathrm {\mathbf {const}}}$
for all
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}(\widetilde Y)$
. Convexity of the length function implies that the geodesic homotopy between
$v\in \operatorname {\mathrm {\mathbf {vert}}}(\widetilde Y)$
. Convexity of the length function implies that the geodesic homotopy between
![]() $\tilde \psi $
and
$\tilde \psi $
and
![]() $\tilde \phi \circ \widetilde F$
has then tracks bounded by the same constant
$\tilde \phi \circ \widetilde F$
has then tracks bounded by the same constant
![]() $\operatorname {\mathrm {\mathbf {const}}}$
, as we had claimed.
$\operatorname {\mathrm {\mathbf {const}}}$
, as we had claimed.
 $\varepsilon $
-critical realizations
$\varepsilon $
-critical realizations
Corollary 2.4 asserts that whenever we have a realization with very long edges and which looks vaguely critical, then it is not far from a critical realization. Our next goal is to give a more precise description of the situation in the case that our realization looks even more as if it were critical. To be precise, suppose that X is a trivalent graph and
![]() $\varepsilon $
positive and small. A regular realization
$\varepsilon $
positive and small. A regular realization
![]() $\phi :X\to \Sigma $
is
$\phi :X\to \Sigma $
is
![]() $\varepsilon $
-critical if
$\varepsilon $
-critical if
 $$ \begin{align*}\angle(\phi(\vec e_1),\phi(\vec e_2))\in\left[\frac{2\pi}3-\varepsilon,\frac{2\pi}3+\varepsilon\right]\end{align*} $$
$$ \begin{align*}\angle(\phi(\vec e_1),\phi(\vec e_2))\in\left[\frac{2\pi}3-\varepsilon,\frac{2\pi}3+\varepsilon\right]\end{align*} $$
for every two half-edges
![]() $\vec e_1,\vec e_2\in \operatorname {\mathrm {\mathbf {half}}}_v$
incident to any vertex
$\vec e_1,\vec e_2\in \operatorname {\mathrm {\mathbf {half}}}_v$
incident to any vertex
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
.
$v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
.
The goal of this section is to determine how the set
![]() $\mathcal G^X_{\varepsilon -\operatorname {\mathrm {crit}}}$
of
$\mathcal G^X_{\varepsilon -\operatorname {\mathrm {crit}}}$
of
![]() $\varepsilon $
-critical realizations of X looks. To do that, we need a bit of of notation and preparatory work. First, we understand a tripod to be a tuple
$\varepsilon $
-critical realizations of X looks. To do that, we need a bit of of notation and preparatory work. First, we understand a tripod to be a tuple
![]() $\tau =(p,\{v,v',v"\})$
, where
$\tau =(p,\{v,v',v"\})$
, where
![]() $p\in {\mathbb {H}}^2$
is a point and where
$p\in {\mathbb {H}}^2$
is a point and where
![]() $\{v,v',v"\}\subset T^1_p{\mathbb {H}}^2$
is an unordered collection consisting of three distinct unit vectors based at p. A tripod
$\{v,v',v"\}\subset T^1_p{\mathbb {H}}^2$
is an unordered collection consisting of three distinct unit vectors based at p. A tripod
![]() $\tau =(p,\{v,v',v"\})$
is critical if the three vectors
$\tau =(p,\{v,v',v"\})$
is critical if the three vectors
![]() $v,v',v,"$
have pairwise angle equal to
$v,v',v,"$
have pairwise angle equal to
![]() $\frac {2\pi }3$
. Any tripod
$\frac {2\pi }3$
. Any tripod
![]() $\tau $
determines three geodesic rays, that is, three points in
$\tau $
determines three geodesic rays, that is, three points in
![]() $\partial _{\infty }{\mathbb {H}}^2$
, that is an ideal triangle
$\partial _{\infty }{\mathbb {H}}^2$
, that is an ideal triangle
![]() $T_{\tau }\subset {\mathbb {H}}^2$
(see the left-hand side of Figure 1). Conversely, every ideal triangle
$T_{\tau }\subset {\mathbb {H}}^2$
(see the left-hand side of Figure 1). Conversely, every ideal triangle
![]() $T\subset {\mathbb {H}}^2$
determines a tripod
$T\subset {\mathbb {H}}^2$
determines a tripod
![]() $\tau _p^T=(p,\{v,v',v"\})$
for every
$\tau _p^T=(p,\{v,v',v"\})$
for every
![]() $p\in {\mathbb {H}}^2$
: The vectors
$p\in {\mathbb {H}}^2$
: The vectors
![]() $v,v',v,"$
are the unit vectors based at p and pointing to the (ideal) vertices of the ideal triangle T. Note that T consists of exactly those points p such that the vectors in the tripod
$v,v',v,"$
are the unit vectors based at p and pointing to the (ideal) vertices of the ideal triangle T. Note that T consists of exactly those points p such that the vectors in the tripod
![]() $\tau _p^T$
have pairwise (always unoriented) angles adding up to
$\tau _p^T$
have pairwise (always unoriented) angles adding up to
![]() $2\pi $
. For a given
$2\pi $
. For a given
![]() $\varepsilon $
, we let
$\varepsilon $
, we let
 $$ \begin{align*}T(\varepsilon)=\left\{p\in T\ \middle\vert\begin{array}{l}\text{the angles between the vectors}\\ \text{in }\tau_p^T\text{ lie in }[\frac{2\pi}3-\varepsilon,\frac{2\pi}3+\varepsilon]\end{array}\right\}\end{align*} $$
$$ \begin{align*}T(\varepsilon)=\left\{p\in T\ \middle\vert\begin{array}{l}\text{the angles between the vectors}\\ \text{in }\tau_p^T\text{ lie in }[\frac{2\pi}3-\varepsilon,\frac{2\pi}3+\varepsilon]\end{array}\right\}\end{align*} $$
be the set of points such that the angles of the tripod
![]() $\tau _p^T$
are within
$\tau _p^T$
are within
![]() $\varepsilon $
of
$\varepsilon $
of
![]() $\frac {2\pi }3$
. The set
$\frac {2\pi }3$
. The set
![]() $T(\varepsilon )$
is, at least for
$T(\varepsilon )$
is, at least for
![]() $\varepsilon \in (0,\frac \pi 6)$
, a hexagon centered at the center of the triangle – the sides of the hexagon are not geodesic but rather subsegments of curves of constant curvature; see Figure 1. However, if we scale everything by
$\varepsilon \in (0,\frac \pi 6)$
, a hexagon centered at the center of the triangle – the sides of the hexagon are not geodesic but rather subsegments of curves of constant curvature; see Figure 1. However, if we scale everything by
![]() $\varepsilon ^{-1}$
, then
$\varepsilon ^{-1}$
, then
![]() $\varepsilon ^{-1}\cdot T(\varepsilon )$
converges to the regular euclidean hexagon of side length
$\varepsilon ^{-1}\cdot T(\varepsilon )$
converges to the regular euclidean hexagon of side length
![]() $\frac 23$
. This means in particular that
$\frac 23$
. This means in particular that

Figure 1 Left: A critical tripod and (part of) the ideal triangle it determines. Right: The hexagon
![]() $T(\varepsilon )$
. Each of the lines making up the boundary of the hexagon corresponds to points p having an angle between vectors in
$T(\varepsilon )$
. Each of the lines making up the boundary of the hexagon corresponds to points p having an angle between vectors in
![]() $\tau ^T_P$
of measure
$\tau ^T_P$
of measure
![]() $\frac {2\pi }{3}-\varepsilon $
(dotted lines) and
$\frac {2\pi }{3}-\varepsilon $
(dotted lines) and
![]() $\frac {2\pi }{3}+\varepsilon $
(solid lines).
$\frac {2\pi }{3}+\varepsilon $
(solid lines).
Remark. To get the shape of
![]() $T(\varepsilon )$
, one can use elementary synthetic hyperbolic geometry. But one can also resort to hyperbolic trigonometry. For example, evoking formula 2.2.2 (iv) in the back of Buser’s book [Reference Buser3] one gets
$T(\varepsilon )$
, one can use elementary synthetic hyperbolic geometry. But one can also resort to hyperbolic trigonometry. For example, evoking formula 2.2.2 (iv) in the back of Buser’s book [Reference Buser3] one gets
Suppose now that
![]() $\phi :X\to \Sigma $
is a critical realization of a trivalent graph X in our closed hyperbolic surface, and recall that by Lemma 2.2 we have that the connected component
$\phi :X\to \Sigma $
is a critical realization of a trivalent graph X in our closed hyperbolic surface, and recall that by Lemma 2.2 we have that the connected component
![]() $\mathcal G^{\phi }$
of geodesic realizations homotopic to
$\mathcal G^{\phi }$
of geodesic realizations homotopic to
![]() $\phi $
is isometric to a product of hyperbolic planes
$\phi $
is isometric to a product of hyperbolic planes
![]() ${\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2$
, one factor for each vertex of X. To each vertex x of X, we can associate first the tripod
${\mathbb {H}}^2\times \dots \times {\mathbb {H}}^2$
, one factor for each vertex of X. To each vertex x of X, we can associate first the tripod
![]() $\tau _x^{\phi }=(\phi (x),\{\phi (\vec e)\}_{\vec e\in \operatorname {\mathrm {\mathbf {half}}}_x(X)})$
consisting of the image under
$\tau _x^{\phi }=(\phi (x),\{\phi (\vec e)\}_{\vec e\in \operatorname {\mathrm {\mathbf {half}}}_x(X)})$
consisting of the image under
![]() $\phi $
of the vertex x and of the unit vectors
$\phi $
of the vertex x and of the unit vectors
![]() $\phi (\vec e)$
tangent to the images of the half-edges incident to x, and then
$\phi (\vec e)$
tangent to the images of the half-edges incident to x, and then
![]() $T_{\tau ^{\phi }_x}$
the ideal triangle associated to the critical tripod
$T_{\tau ^{\phi }_x}$
the ideal triangle associated to the critical tripod
![]() $\tau ^{\phi }_x$
. The assumption that
$\tau ^{\phi }_x$
. The assumption that
![]() $\phi $
is critical implies that the point
$\phi $
is critical implies that the point
![]() $\phi (x)$
is the center of
$\phi (x)$
is the center of
![]() $T_{\tau ^{\phi }_x}$
for every vertex
$T_{\tau ^{\phi }_x}$
for every vertex
![]() $x\in \operatorname {\mathrm {\mathbf {vert}}}$
. We let
$x\in \operatorname {\mathrm {\mathbf {vert}}}$
. We let
be the subset of
![]() $\mathcal G^{\phi }$
consisting of geodesic realizations homotopic to
$\mathcal G^{\phi }$
consisting of geodesic realizations homotopic to
![]() $\phi $
via a homotopy that maps each vertex x within
$\phi $
via a homotopy that maps each vertex x within
![]() $T_{\tau _x^{\phi }}$
. Accordingly, we set
$T_{\tau _x^{\phi }}$
. Accordingly, we set
and we note that
 $$ \begin{align*}\operatorname{\mathrm{vol}}(\mathcal T^{\phi}(\varepsilon))\sim \left(\frac 2{\sqrt 3}\varepsilon^2\right)^{\vert\operatorname{\mathrm{\mathbf{vert}}}(X)\vert}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{vol}}(\mathcal T^{\phi}(\varepsilon))\sim \left(\frac 2{\sqrt 3}\varepsilon^2\right)^{\vert\operatorname{\mathrm{\mathbf{vert}}}(X)\vert}.\end{align*} $$
The reason we care about all these sets is that, asymptotically,
![]() $\mathcal T^{\phi }(\varepsilon )$
agrees with the set
$\mathcal T^{\phi }(\varepsilon )$
agrees with the set
![]() $\mathcal G^{\phi }_{\varepsilon -\operatorname {\mathrm {crit}}}$
of
$\mathcal G^{\phi }_{\varepsilon -\operatorname {\mathrm {crit}}}$
of
![]() $\varepsilon $
-critical realizations
$\varepsilon $
-critical realizations
![]() $\psi $
homotopic to
$\psi $
homotopic to
![]() $\phi $
. Indeed, we get from Corollary 2.4 that the geodesic homotopy from
$\phi $
. Indeed, we get from Corollary 2.4 that the geodesic homotopy from
![]() $\psi $
to
$\psi $
to
![]() $\phi $
has lengths bounded by a uniform constant. This means that for all
$\phi $
has lengths bounded by a uniform constant. This means that for all
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
the geodesic segments
$e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
the geodesic segments
![]() $\phi (e)$
and
$\phi (e)$
and
![]() $\psi (e)$
are very long but have endpoints relatively close to each other. This means that, when looked from (each) one of its vertices x, the segment
$\psi (e)$
are very long but have endpoints relatively close to each other. This means that, when looked from (each) one of its vertices x, the segment
![]() $\psi (e)$
is very close to being asymptotic to
$\psi (e)$
is very close to being asymptotic to
![]() $\phi (e)$
. In particular, the angle between
$\phi (e)$
. In particular, the angle between
![]() $\psi (e)$
and the geodesic ray starting at
$\psi (e)$
and the geodesic ray starting at
![]() $\psi (x)$
and asymptotic to the ray starting in
$\psi (x)$
and asymptotic to the ray starting in
![]() $\phi (x)$
in direction
$\phi (x)$
in direction
![]() $\phi (e)$
is smaller than
$\phi (e)$
is smaller than
![]() $\delta =\delta (\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}\ell (\psi (e)))$
for some positive function with
$\delta =\delta (\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}\ell (\psi (e)))$
for some positive function with
![]() $\delta (t)\to 0$
as
$\delta (t)\to 0$
as
![]() $t\to \infty $
. With the rather clumsy notation, we find ourselves working with we have that
$t\to \infty $
. With the rather clumsy notation, we find ourselves working with we have that
![]() $\delta $
bounds from above the angles between corresponding edges of the tripods
$\delta $
bounds from above the angles between corresponding edges of the tripods
![]() $\tau ^{\psi }_x$
and
$\tau ^{\psi }_x$
and
![]() $\tau ^{T^{\phi }_x}_{\psi (x)}$
. Since by assumption the angles of
$\tau ^{T^{\phi }_x}_{\psi (x)}$
. Since by assumption the angles of
![]() $\tau ^{\psi }_x$
belong to
$\tau ^{\psi }_x$
belong to
![]() $[\frac {2\pi }3-\varepsilon ,\frac {2\pi }3+\varepsilon ]$
, we get that the angles of
$[\frac {2\pi }3-\varepsilon ,\frac {2\pi }3+\varepsilon ]$
, we get that the angles of
![]() $\tau ^{T^{\phi }_x}_{\psi (x)}$
belong to
$\tau ^{T^{\phi }_x}_{\psi (x)}$
belong to
![]() $[\frac {2\pi }3-\varepsilon -2\delta ,\frac {2\pi }3+\varepsilon +2\delta ]$
, meaning that
$[\frac {2\pi }3-\varepsilon -2\delta ,\frac {2\pi }3+\varepsilon +2\delta ]$
, meaning that
![]() $\psi (x)\in T_{\tau _x^{\phi }}(\varepsilon +2\delta )$
.
$\psi (x)\in T_{\tau _x^{\phi }}(\varepsilon +2\delta )$
.
To summarize, what we have proved is that for all
![]() $\varepsilon _1>\varepsilon $
there is
$\varepsilon _1>\varepsilon $
there is
![]() $\ell _1$
such that if
$\ell _1$
such that if
![]() $\phi :X\to \Sigma $
is critical with
$\phi :X\to \Sigma $
is critical with
![]() $\ell (\phi (e))\geqslant \ell _1$
for all
$\ell (\phi (e))\geqslant \ell _1$
for all
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}$
, then
$e\in \operatorname {\mathrm {\mathbf {edge}}}$
, then
The same argument proves that for all
![]() $\varepsilon _2<\varepsilon $
there is
$\varepsilon _2<\varepsilon $
there is
![]() $\ell _2$
such that if
$\ell _2$
such that if
![]() $\phi :X\to \Sigma $
is critical with
$\phi :X\to \Sigma $
is critical with
![]() $\ell (\phi (e))\geqslant \ell _2$
for all
$\ell (\phi (e))\geqslant \ell _2$
for all
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}$
, then
$e\in \operatorname {\mathrm {\mathbf {edge}}}$
, then
We record these facts:
Lemma 2.5. There are functions
![]() $h:(0,\frac \pi 6)\to \mathbb R_{>0}$
and
$h:(0,\frac \pi 6)\to \mathbb R_{>0}$
and
![]() $\delta :(0,\varepsilon _0)\to \mathbb R_{>0}$
with
$\delta :(0,\varepsilon _0)\to \mathbb R_{>0}$
with
![]() $\lim _{t\to 0}h(t)=0$
and
$\lim _{t\to 0}h(t)=0$
and
![]() $\lim _{t\to \infty }\delta (t)=0$
such that for every critical realizations
$\lim _{t\to \infty }\delta (t)=0$
such that for every critical realizations
![]() $\phi :X\to \Sigma $
we have
$\phi :X\to \Sigma $
we have
where
![]() $r(\varepsilon ,\phi )=h(\varepsilon )+\delta (\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}\ell (\phi (e)))$
.
$r(\varepsilon ,\phi )=h(\varepsilon )+\delta (\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}\ell (\phi (e)))$
.
To conclude this section, we collect what we will actually need about the set of
![]() $\varepsilon $
-critical realizations in a single statement.
$\varepsilon $
-critical realizations in a single statement.
Proposition 2.6. Let X be a trivalent graph. There are
![]() $\ell>0$
and functions
$\ell>0$
and functions
![]() $\rho _0,\rho _1:\mathbb R_{>0}\to \mathbb R_{>0}$
with
$\rho _0,\rho _1:\mathbb R_{>0}\to \mathbb R_{>0}$
with
![]() $\lim _{t\to 0}\rho _0(t)=0$
and
$\lim _{t\to 0}\rho _0(t)=0$
and
![]() $\lim _{t\to \infty }\rho _1(t)=0$
and such that the following holds for all
$\lim _{t\to \infty }\rho _1(t)=0$
and such that the following holds for all
![]() $\varepsilon \in [0,\frac \pi 6]$
:
$\varepsilon \in [0,\frac \pi 6]$
:
If
![]() $\phi \in \mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(X)$
is an
$\phi \in \mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(X)$
is an
![]() $\ell $
-long
$\ell $
-long
![]() $\varepsilon $
-critical realization, then
$\varepsilon $
-critical realization, then
 $$ \begin{align} \left\vert\operatorname{\mathrm{vol}}(\mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}^{\phi})-\left(\frac 2{\sqrt 3}\varepsilon^2\right)^V\right\vert\leqslant \rho_0(\varepsilon)\cdot\rho_1\left(\min_{e\in\operatorname{\mathrm{\mathbf{edge}}}}\ell(\phi(e))\right)\cdot\varepsilon^{2V}. \end{align} $$
$$ \begin{align} \left\vert\operatorname{\mathrm{vol}}(\mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}^{\phi})-\left(\frac 2{\sqrt 3}\varepsilon^2\right)^V\right\vert\leqslant \rho_0(\varepsilon)\cdot\rho_1\left(\min_{e\in\operatorname{\mathrm{\mathbf{edge}}}}\ell(\phi(e))\right)\cdot\varepsilon^{2V}. \end{align} $$
Moreover,
![]() $\mathcal G^{\phi }_{\varepsilon -\operatorname {\mathrm {crit}}}$
contains a unique critical realization
$\mathcal G^{\phi }_{\varepsilon -\operatorname {\mathrm {crit}}}$
contains a unique critical realization
![]() $\psi $
and we have
$\psi $
and we have
 $$ \begin{align} \max_{e\in\operatorname{\mathrm{\mathbf{edge}}}}\vert\ell_{\Sigma}(\phi(e))-\ell_{\Sigma}(\psi(e))\vert\leqslant\rho_0(\varepsilon)+\rho_1\left(\min_{e\in\operatorname{\mathrm{\mathbf{edge}}}}\ell(\phi(e))\right)\cdot\varepsilon. \end{align} $$
$$ \begin{align} \max_{e\in\operatorname{\mathrm{\mathbf{edge}}}}\vert\ell_{\Sigma}(\phi(e))-\ell_{\Sigma}(\psi(e))\vert\leqslant\rho_0(\varepsilon)+\rho_1\left(\min_{e\in\operatorname{\mathrm{\mathbf{edge}}}}\ell(\phi(e))\right)\cdot\varepsilon. \end{align} $$
Here, as before, V is the number of vertices of X and
![]() $\operatorname {\mathrm {\mathbf {edge}}}=\operatorname {\mathrm {\mathbf {edge}}}(X)$
is its set of edges.
$\operatorname {\mathrm {\mathbf {edge}}}=\operatorname {\mathrm {\mathbf {edge}}}(X)$
is its set of edges.
Proof. Suppose to begin with that
![]() $\ell $
is at least as large as the
$\ell $
is at least as large as the
![]() $\ell _0$
in Corollary 2.4. We thus get that
$\ell _0$
in Corollary 2.4. We thus get that
![]() $\mathcal G^{\phi }$
contains a unique critical realization
$\mathcal G^{\phi }$
contains a unique critical realization
![]() $\psi $
. Now, we get from Lemma 2.5 that
$\psi $
. Now, we get from Lemma 2.5 that
where
![]() $r(\varepsilon ,\phi )=h(\varepsilon )+\delta (\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}}\ell (\phi (e)))$
for some functions
$r(\varepsilon ,\phi )=h(\varepsilon )+\delta (\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}}\ell (\phi (e)))$
for some functions
![]() $h:(0,\frac \pi 6)\to \mathbb R_{>0}\text { with }$
and
$h:(0,\frac \pi 6)\to \mathbb R_{>0}\text { with }$
and
![]() $\delta :(0,\varepsilon _0)\to \mathbb R_{>0}$
with
$\delta :(0,\varepsilon _0)\to \mathbb R_{>0}$
with
![]() $\lim _{t\to \infty }h(t)=0$
and
$\lim _{t\to \infty }h(t)=0$
and
![]() $\lim _{t\to \infty }\delta (t)=0$
. The bounds (2.10) and (2.11) follow now from Equations (2.12) and (2.9).
$\lim _{t\to \infty }\delta (t)=0$
. The bounds (2.10) and (2.11) follow now from Equations (2.12) and (2.9).
3 Variations of Delsarte’s theorem
In this section, we establish the asymptotics of the number of realizations
![]() $\phi :X\to \Sigma $
satisfying some length condition, mapping each vertex to some predetermined point in
$\phi :X\to \Sigma $
satisfying some length condition, mapping each vertex to some predetermined point in
![]() $\Sigma $
, and so that the tuple of directions of images of half-edges belongs to some given open set of such tuples – see Theorem 3.2 for details. Other than some bookkeeping, what is needed is a slight extension of Delsarte’s lattice counting theorem [Reference Delsarte7], namely Theorem 3.1 below. This result is known to experts, and much more sophisticated versions than what we need here can be found in the literature – see, for example, [Reference Roblin17, Théorème 4.1.1]. However, for the sake of completeness, we will explain how to derive Theorem 3.1 from the fact that the geodesic flow is mixing. We refer to the very nice books [Reference Bekka and Mayer2, Reference Roblin17] for the needed background.
$\Sigma $
, and so that the tuple of directions of images of half-edges belongs to some given open set of such tuples – see Theorem 3.2 for details. Other than some bookkeeping, what is needed is a slight extension of Delsarte’s lattice counting theorem [Reference Delsarte7], namely Theorem 3.1 below. This result is known to experts, and much more sophisticated versions than what we need here can be found in the literature – see, for example, [Reference Roblin17, Théorème 4.1.1]. However, for the sake of completeness, we will explain how to derive Theorem 3.1 from the fact that the geodesic flow is mixing. We refer to the very nice books [Reference Bekka and Mayer2, Reference Roblin17] for the needed background.
We start by recalling a few well-known facts about dynamics of geodesic flows on hyperbolic surfaces. First, recall that we can identify
![]() $T^1{\mathbb {H}}^2$
with
$T^1{\mathbb {H}}^2$
with
![]() $\operatorname {\mathrm {PSL}}_2\mathbb R$
, and
$\operatorname {\mathrm {PSL}}_2\mathbb R$
, and
![]() $T^1\Sigma =T^1(\Gamma \backslash {\mathbb {H}}^2)$
with
$T^1\Sigma =T^1(\Gamma \backslash {\mathbb {H}}^2)$
with
![]() $\Gamma \backslash \operatorname {\mathrm {PSL}}_2\mathbb R$
. More specifically, when using the identification
$\Gamma \backslash \operatorname {\mathrm {PSL}}_2\mathbb R$
. More specifically, when using the identification
where the computation happens in the upper half-plane model and
![]() $i\in {\mathbb {H}}^2$
is the imaginary unit, then the geodesic and horocyclic flows amount to right multiplication by the matrices
$i\in {\mathbb {H}}^2$
is the imaginary unit, then the geodesic and horocyclic flows amount to right multiplication by the matrices
 $$ \begin{align*}\rho_t=\left(\begin{array}{cc}e^{\frac t2} & 0 \\ 0 & e^{-\frac t2}\end{array}\right)\text{ and }h_s=\left(\begin{array}{cc}1 & s \\ 0 & 1\end{array}\right),\end{align*} $$
$$ \begin{align*}\rho_t=\left(\begin{array}{cc}e^{\frac t2} & 0 \\ 0 & e^{-\frac t2}\end{array}\right)\text{ and }h_s=\left(\begin{array}{cc}1 & s \\ 0 & 1\end{array}\right),\end{align*} $$
respectively.
Note that
![]() $K=\operatorname {\mathrm {SO}}_2\subset \operatorname {\mathrm {PSL}}_2\mathbb R$
, the stabilizer of i under the action
$K=\operatorname {\mathrm {SO}}_2\subset \operatorname {\mathrm {PSL}}_2\mathbb R$
, the stabilizer of i under the action
![]() $\operatorname {\mathrm {PSL}}_2\mathbb R\curvearrowright {\mathbb {H}}^2$
, is a maximal compact subgroup – K corresponds under the identification
$\operatorname {\mathrm {PSL}}_2\mathbb R\curvearrowright {\mathbb {H}}^2$
, is a maximal compact subgroup – K corresponds under the identification
![]() $\operatorname {\mathrm {PSL}}_2\mathbb R\simeq T^1{\mathbb {H}}^2$
to the unit tangent space
$\operatorname {\mathrm {PSL}}_2\mathbb R\simeq T^1{\mathbb {H}}^2$
to the unit tangent space
![]() $T^1_i{\mathbb {H}}^2$
of the base point
$T^1_i{\mathbb {H}}^2$
of the base point
![]() $i\in {\mathbb {H}}^2$
. The KAN decomposition (basically the output of the Gramm–Schmidt process from linear algebra) asserts that every element in
$i\in {\mathbb {H}}^2$
. The KAN decomposition (basically the output of the Gramm–Schmidt process from linear algebra) asserts that every element in
![]() $g\in \operatorname {\mathrm {PSL}}_2\mathbb R$
can be written in a unique way as
$g\in \operatorname {\mathrm {PSL}}_2\mathbb R$
can be written in a unique way as
for
![]() $k\in K$
and
$k\in K$
and
![]() $t,s\in \mathbb R$
. In those coordinates, the Haar measure of
$t,s\in \mathbb R$
. In those coordinates, the Haar measure of
![]() $\operatorname {\mathrm {PSL}}_2\mathbb R$
is given by
$\operatorname {\mathrm {PSL}}_2\mathbb R$
is given by
where
![]() $dk$
stands for integrating over the arc length in
$dk$
stands for integrating over the arc length in
![]() $K\simeq T^1_i{\mathbb {H}}^2$
, normalized to have total measure
$K\simeq T^1_i{\mathbb {H}}^2$
, normalized to have total measure
![]() $2\pi $
.
$2\pi $
.
The basic fact we will need is that the geodesic flow
![]() $\rho _t$
on
$\rho _t$
on
![]() $T^1\Sigma $
is mixing [Reference Bekka and Mayer2, III.2.3], or rather one of its direct consequences, namely the fact that for each
$T^1\Sigma $
is mixing [Reference Bekka and Mayer2, III.2.3], or rather one of its direct consequences, namely the fact that for each
![]() $x_0\in {\mathbb {H}}^2$
the projection to
$x_0\in {\mathbb {H}}^2$
the projection to
![]() $\Sigma $
of the sphere
$\Sigma $
of the sphere
![]() $S(x_0,L)$
centered at
$S(x_0,L)$
centered at
![]() $x_0$
and with radius L gets equidistributed in
$x_0$
and with radius L gets equidistributed in
![]() $\Sigma $
when
$\Sigma $
when
![]() $L\to \infty $
[Reference Bekka and Mayer2, III.3.3]. To be more precise, note that we might assume without loss of generality that
$L\to \infty $
[Reference Bekka and Mayer2, III.3.3]. To be more precise, note that we might assume without loss of generality that
![]() $x_0=i$
, meaning that we are identifying
$x_0=i$
, meaning that we are identifying
![]() $T_{x_0}^1{\mathbb {H}}^2=K$
. The fact that the geodesic flow is mixing implies then that for every nondegenerate interval
$T_{x_0}^1{\mathbb {H}}^2=K$
. The fact that the geodesic flow is mixing implies then that for every nondegenerate interval
![]() $I\subset K$
the spherical arcs
$I\subset K$
the spherical arcs
![]() $I\rho _t$
equidistribute in
$I\rho _t$
equidistribute in
![]() $\Gamma \backslash \operatorname {\mathrm {PSL}}_2\mathbb R$
in the sense that for any continuous function
$\Gamma \backslash \operatorname {\mathrm {PSL}}_2\mathbb R$
in the sense that for any continuous function
![]() $f\in C^0(T^1\Sigma )=C^0(\Gamma \backslash \operatorname {\mathrm {PSL}}_2\mathbb R)$
we have
$f\in C^0(T^1\Sigma )=C^0(\Gamma \backslash \operatorname {\mathrm {PSL}}_2\mathbb R)$
we have
where
![]() $\ell (I)$
is the arc length of I and where the second integral is with respect to
$\ell (I)$
is the arc length of I and where the second integral is with respect to
![]() $\operatorname {\mathrm {vol}}_{T^1\Sigma }$
. Anyways, we care about equidistribution of the spheres for the following reason. If
$\operatorname {\mathrm {vol}}_{T^1\Sigma }$
. Anyways, we care about equidistribution of the spheres for the following reason. If
![]() $f\in C^0(\Sigma )$
is a continuous function and if we let
$f\in C^0(\Sigma )$
is a continuous function and if we let
![]() $\tilde f$
be the composition of f with the cover
$\tilde f$
be the composition of f with the cover
![]() ${\mathbb {H}}^2\to \Sigma $
, then Equation (3.2) implies, with
${\mathbb {H}}^2\to \Sigma $
, then Equation (3.2) implies, with
![]() $I=K$
, that
$I=K$
, that
 $$ \begin{align*}\lim_{L\to\infty}\frac 1{\operatorname{\mathrm{vol}}_{{\mathbb{H}}^2}(B(x_0,L))}\cdot\int_{B(x_0,L)}\tilde f(x)\, dx=\frac 1{\operatorname{\mathrm{vol}}(\Sigma)}\int_{\Sigma} f(x)dx.\end{align*} $$
$$ \begin{align*}\lim_{L\to\infty}\frac 1{\operatorname{\mathrm{vol}}_{{\mathbb{H}}^2}(B(x_0,L))}\cdot\int_{B(x_0,L)}\tilde f(x)\, dx=\frac 1{\operatorname{\mathrm{vol}}(\Sigma)}\int_{\Sigma} f(x)dx.\end{align*} $$
Applying this to a nonnegative function
![]() $f_{y_0,\varepsilon }\in C^0(\Sigma )$
with total integral
$f_{y_0,\varepsilon }\in C^0(\Sigma )$
with total integral
![]() $1$
and supported by
$1$
and supported by
![]() $B(y_0,\varepsilon )$
, we get that
$B(y_0,\varepsilon )$
, we get that
 $$ \begin{align*}\int_{B(x_0,L)}\tilde f_{y_0,\varepsilon}(x)\, dx\sim\frac{\operatorname{\mathrm{vol}}_{{\mathbb{H}}^2}(B(x_0,L))}{\operatorname{\mathrm{vol}}(\Sigma)}.\end{align*} $$
$$ \begin{align*}\int_{B(x_0,L)}\tilde f_{y_0,\varepsilon}(x)\, dx\sim\frac{\operatorname{\mathrm{vol}}_{{\mathbb{H}}^2}(B(x_0,L))}{\operatorname{\mathrm{vol}}(\Sigma)}.\end{align*} $$
Now, from the properties of
![]() $f_{y_0,\varepsilon }$
we get that
$f_{y_0,\varepsilon }$
we get that
When taken together, the last two displayed equations imply that for all
![]() $\varepsilon $
one has
$\varepsilon $
one has
 $$ \begin{align*}\frac{\pi\cdot e^{L-\varepsilon}}{\operatorname{\mathrm{vol}}(\Sigma)}\leqslant\vert\Gamma\cdot y_0\cap B(x_0,L)\vert\leqslant\frac{\pi\cdot e^{L+\varepsilon}}{\operatorname{\mathrm{vol}}(\Sigma)}\end{align*} $$
$$ \begin{align*}\frac{\pi\cdot e^{L-\varepsilon}}{\operatorname{\mathrm{vol}}(\Sigma)}\leqslant\vert\Gamma\cdot y_0\cap B(x_0,L)\vert\leqslant\frac{\pi\cdot e^{L+\varepsilon}}{\operatorname{\mathrm{vol}}(\Sigma)}\end{align*} $$
and hence that
 $$ \begin{align} \vert\Gamma\cdot y_0\cap B(x_0,L)\vert\sim\frac{\pi\cdot e^L}{\operatorname{\mathrm{vol}}(\Sigma)}\text{ as }L\to\infty. \end{align} $$
$$ \begin{align} \vert\Gamma\cdot y_0\cap B(x_0,L)\vert\sim\frac{\pi\cdot e^L}{\operatorname{\mathrm{vol}}(\Sigma)}\text{ as }L\to\infty. \end{align} $$
This is Delsarte’s lattice point counting theorem [Reference Delsarte7] – we refer to [Reference Bekka and Mayer2, III.3.5] for more details.
An observation: Note that counting elements of
![]() $\Gamma \cdot y_0$
contained in the ball
$\Gamma \cdot y_0$
contained in the ball
![]() $B(x_0,L)$
is exactly the same thing as counting geodesic arcs in
$B(x_0,L)$
is exactly the same thing as counting geodesic arcs in
![]() $\Sigma $
of length at most L going from
$\Sigma $
of length at most L going from
![]() $x_0$
to
$x_0$
to
![]() $y_0$
, or to be precise, from the projection of
$y_0$
, or to be precise, from the projection of
![]() $x_0$
to the projection of
$x_0$
to the projection of
![]() $y_0$
. In this way, if we are given a segment
$y_0$
. In this way, if we are given a segment
![]() $I\subset K=T_{x_0}^1\Sigma $
and we use the equidistribution of the spherical segments
$I\subset K=T_{x_0}^1\Sigma $
and we use the equidistribution of the spherical segments
![]() $I\rho _t$
, then when we run the argument above we get the cardinality of the set
$I\rho _t$
, then when we run the argument above we get the cardinality of the set
![]() ${\mathbf {A}}_{I,y_0}(L)$
of geodesic arcs of length at most L, starting in
${\mathbf {A}}_{I,y_0}(L)$
of geodesic arcs of length at most L, starting in
![]() $x_0$
with initial speed in I, and ending in
$x_0$
with initial speed in I, and ending in
![]() $y_0$
. As expected, the result is that
$y_0$
. As expected, the result is that
 $$ \begin{align*}\vert{\mathbf{A}}_{I,y_0}(L)\vert\sim \frac{\ell(I)}{2\pi}\cdot\frac{\pi\cdot e^L}{\operatorname{\mathrm{vol}}(\Sigma)}\ \ \ \text{ when }L\to\infty.\end{align*} $$
$$ \begin{align*}\vert{\mathbf{A}}_{I,y_0}(L)\vert\sim \frac{\ell(I)}{2\pi}\cdot\frac{\pi\cdot e^L}{\operatorname{\mathrm{vol}}(\Sigma)}\ \ \ \text{ when }L\to\infty.\end{align*} $$
Suppose now that we dial it up a bit giving ourselves a second sector
![]() $J\subset T^1_{y_0}\Sigma $
and care, for some fixed h, about the cardinality of the set
$J\subset T^1_{y_0}\Sigma $
and care, for some fixed h, about the cardinality of the set
![]() ${\mathbf {A}}_{I,J}(L,h)$
of geodesic arcs with length in
${\mathbf {A}}_{I,J}(L,h)$
of geodesic arcs with length in
![]() $[L,L+h]$
, joining
$[L,L+h]$
, joining
![]() $x_0$
to
$x_0$
to
![]() $y_0$
, and with initial and terminal velocities in I and J, respectively. We can obtain the asymptotics of
$y_0$
, and with initial and terminal velocities in I and J, respectively. We can obtain the asymptotics of
![]() $\vert {\mathbf {A}}_{I,J}(L,h)\vert $
following the same basic idea as in the proof of Delsarte’s theorem above. We need, however, to replace the bump function
$\vert {\mathbf {A}}_{I,J}(L,h)\vert $
following the same basic idea as in the proof of Delsarte’s theorem above. We need, however, to replace the bump function
![]() $f_{y_0,\varepsilon }$
by something else.
$f_{y_0,\varepsilon }$
by something else.
Using the coordinates (3.1), consider for h and
![]() $\delta $
positive and small the set
$\delta $
positive and small the set
and note that it has volume
![]() $\ell (J)\cdot 2\delta \cdot (1-e^{-h})$
. Note also that the intersection of
$\ell (J)\cdot 2\delta \cdot (1-e^{-h})$
. Note also that the intersection of
![]() ${\mathcal {J}}(J,h,\delta )$
with the outer normal vector field of any horosphere consists of segments of the form
${\mathcal {J}}(J,h,\delta )$
with the outer normal vector field of any horosphere consists of segments of the form
![]() $H_{v\rho _t}=\{v\rho _t h_s\text { with }s\in [-\delta ,\delta ]\}$
, where
$H_{v\rho _t}=\{v\rho _t h_s\text { with }s\in [-\delta ,\delta ]\}$
, where
![]() $v\in J$
and
$v\in J$
and
![]() $t\in [0,h]$
and that each such segment has length
$t\in [0,h]$
and that each such segment has length
![]() $2\delta $
. Finally, observe that each one of the sets
$2\delta $
. Finally, observe that each one of the sets
![]() $H_{v\rho _t}$
contains exactly one vector, namely
$H_{v\rho _t}$
contains exactly one vector, namely
![]() $v\rho _t$
, which lands in J when we geodesic flow it for some time in
$v\rho _t$
, which lands in J when we geodesic flow it for some time in
![]() $[-h,0]$
. It follows that for all intervals
$[-h,0]$
. It follows that for all intervals
![]() $\mathbb I\subset \mathbb R$
and
$\mathbb I\subset \mathbb R$
and
![]() $w\in T^1\Sigma $
we have
$w\in T^1\Sigma $
we have
 $$ \begin{align*}\left\vert\left\vert\left\{r\in\mathbb I\,\middle\vert\begin{array}{c}\exists s\in[-\delta,\delta],t\in[-h,0]\\ \text{ with }wh_s\rho_t\in J\end{array}\right\}\right\vert-\frac{\ell(\{s\in\mathbb I\text{ with }wh_s\in{\mathcal{J}}\})}{2\delta}\right\vert\leqslant 2,\end{align*} $$
$$ \begin{align*}\left\vert\left\vert\left\{r\in\mathbb I\,\middle\vert\begin{array}{c}\exists s\in[-\delta,\delta],t\in[-h,0]\\ \text{ with }wh_s\rho_t\in J\end{array}\right\}\right\vert-\frac{\ell(\{s\in\mathbb I\text{ with }wh_s\in{\mathcal{J}}\})}{2\delta}\right\vert\leqslant 2,\end{align*} $$
where
![]() ${\mathcal {J}}={\mathcal {J}}(J,h,\delta )$
and where the number
${\mathcal {J}}={\mathcal {J}}(J,h,\delta )$
and where the number
![]() $2$
is there to take into account possible over counting near the ends of the horospherical segment.
$2$
is there to take into account possible over counting near the ends of the horospherical segment.
Using then the fact that when
![]() $L\to \infty $
the sphere
$L\to \infty $
the sphere
![]() $S(x_0,L+h)\subset {\mathbb {H}}^2$
looks more and more like a horosphere, one gets the following analogue of Equation (3.3): For any
$S(x_0,L+h)\subset {\mathbb {H}}^2$
looks more and more like a horosphere, one gets the following analogue of Equation (3.3): For any
![]() $\delta '<\delta <\delta "$
and
$\delta '<\delta <\delta "$
and
![]() $h'<h<h"$
and
$h'<h<h"$
and
![]() $J'\Subset J\Subset J"$
, we have for all sufficiently large L
$J'\Subset J\Subset J"$
, we have for all sufficiently large L
 $$ \begin{align*}\int_{I\rho_{L+h}}\chi_{{\mathcal{J}}(J',h',\delta')}\leqslant 2\delta\cdot\vert{\mathbf{A}}_{I,J}(L,h)\vert\leqslant\int_{I\rho_{L+h}}\chi_{{\mathcal{J}}(J",h",\delta")},\end{align*} $$
$$ \begin{align*}\int_{I\rho_{L+h}}\chi_{{\mathcal{J}}(J',h',\delta')}\leqslant 2\delta\cdot\vert{\mathbf{A}}_{I,J}(L,h)\vert\leqslant\int_{I\rho_{L+h}}\chi_{{\mathcal{J}}(J",h",\delta")},\end{align*} $$
where
![]() $\chi _{\mathcal {J}}$
is the characteristic function of
$\chi _{\mathcal {J}}$
is the characteristic function of
![]() ${\mathcal {J}}$
. From here, we get that
${\mathcal {J}}$
. From here, we get that
 $$ \begin{align*} \vert{\mathbf{A}}_{I,J}(L,h)\vert &\sim \frac 1{2\delta}\int_{I\rho_{L+h}}\chi_{{\mathcal{J}}(J,h,\delta)}\sim\frac 1{2\delta}\cdot\frac{e^{L+h}}2\cdot\int_I\chi_{{\mathcal{J}}(J,h,\delta)}(k\rho_{L+h})\ dk\\ &\stackrel{\text{(3.2)}}\sim\frac 1{2\delta}\cdot\frac{e^{L+h}}2\cdot\ell(I)\cdot\frac{\operatorname{\mathrm{vol}}_{T^1\Sigma}({\mathcal{J}}(J,h,\delta))}{\operatorname{\mathrm{vol}}_{T^1\Sigma}(T^1\Sigma)}\\ &\sim \frac{\ell(I)\cdot\ell(J)}{4\pi}\cdot\frac{e^{L+h}-e^L}{\operatorname{\mathrm{vol}}(\Sigma)}. \end{align*} $$
$$ \begin{align*} \vert{\mathbf{A}}_{I,J}(L,h)\vert &\sim \frac 1{2\delta}\int_{I\rho_{L+h}}\chi_{{\mathcal{J}}(J,h,\delta)}\sim\frac 1{2\delta}\cdot\frac{e^{L+h}}2\cdot\int_I\chi_{{\mathcal{J}}(J,h,\delta)}(k\rho_{L+h})\ dk\\ &\stackrel{\text{(3.2)}}\sim\frac 1{2\delta}\cdot\frac{e^{L+h}}2\cdot\ell(I)\cdot\frac{\operatorname{\mathrm{vol}}_{T^1\Sigma}({\mathcal{J}}(J,h,\delta))}{\operatorname{\mathrm{vol}}_{T^1\Sigma}(T^1\Sigma)}\\ &\sim \frac{\ell(I)\cdot\ell(J)}{4\pi}\cdot\frac{e^{L+h}-e^L}{\operatorname{\mathrm{vol}}(\Sigma)}. \end{align*} $$
We record this slightly generalized version of Delsarte’s theorem for later reference:
Theorem 3.1 (Delarte’s theorem for in-out sectors)
Let
![]() $\Sigma $
be a closed hyperbolic surface, let h be positive and let
$\Sigma $
be a closed hyperbolic surface, let h be positive and let
![]() $I\subset T_{x_0}\Sigma $
and
$I\subset T_{x_0}\Sigma $
and
![]() $J\subset T_{y_0}\Sigma $
be nondegenerate segments. Let then
$J\subset T_{y_0}\Sigma $
be nondegenerate segments. Let then
![]() ${\mathbf {A}}_{I,J}(L,h)$
be the set of geodesic arcs
${\mathbf {A}}_{I,J}(L,h)$
be the set of geodesic arcs
![]() $\alpha :[0,r]\to \Sigma $
with length
$\alpha :[0,r]\to \Sigma $
with length
![]() $r\in [L,L+h]$
, with endpoints
$r\in [L,L+h]$
, with endpoints
![]() $\alpha (0)=x_0$
and
$\alpha (0)=x_0$
and
![]() $\alpha (r)=y_0$
, and with initial and terminal speeds satisfying
$\alpha (r)=y_0$
, and with initial and terminal speeds satisfying
![]() $\alpha '(0)\in I$
and
$\alpha '(0)\in I$
and
![]() $\alpha '(r)\in J$
. Then we have
$\alpha '(r)\in J$
. Then we have
 $$ \begin{align*}\vert{\mathbf{A}}_{I,J}(L,h)\vert\sim \frac{\ell(I)\cdot\ell(J)}{4\pi}\cdot\frac{e^{L+h}-e^L}{\operatorname{\mathrm{vol}}(\Sigma)}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{A}}_{I,J}(L,h)\vert\sim \frac{\ell(I)\cdot\ell(J)}{4\pi}\cdot\frac{e^{L+h}-e^L}{\operatorname{\mathrm{vol}}(\Sigma)}\end{align*} $$
when
![]() $L\to \infty $
.
$L\to \infty $
.
As we mentioned earlier, Theorem 3.1 is a very special case of the much more general [Reference Roblin17, Théorème 4.1.1]. We would not be surprised if there were also other references we are not aware of.
Remark. Note also that the asymptotic behavior in Theorem 3.1 is uniform as long as I and J belong to a compact set of choices. For example, since the surface
![]() $\Sigma $
is compact, we get that for all
$\Sigma $
is compact, we get that for all
![]() $\delta>0$
the asymptotic behavior in Theorem 3.1 is uniform as long as I and J are intervals of length at least
$\delta>0$
the asymptotic behavior in Theorem 3.1 is uniform as long as I and J are intervals of length at least
![]() $\delta $
contained, respectively, in
$\delta $
contained, respectively, in
![]() $T_{x_I}^1\Sigma $
and
$T_{x_I}^1\Sigma $
and
![]() $T_{x_J}^1\Sigma $
for some
$T_{x_J}^1\Sigma $
for some
![]() $x_I$
and
$x_I$
and
![]() $x_J$
in
$x_J$
in
![]() $\Sigma $
.
$\Sigma $
.
Now, let X be a trivalent graph with vertex set
![]() $\operatorname {\mathrm {\mathbf {vert}}}(X)$
and let
$\operatorname {\mathrm {\mathbf {vert}}}(X)$
and let
![]() $\vec x=(x_v)_{v\in \operatorname {\mathrm {\mathbf {vert}}}(X)}\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
be a
$\vec x=(x_v)_{v\in \operatorname {\mathrm {\mathbf {vert}}}(X)}\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
be a
![]() $\operatorname {\mathrm {\mathbf {vert}}}(X)$
-tuple of points in the surface. Let also
$\operatorname {\mathrm {\mathbf {vert}}}(X)$
-tuple of points in the surface. Let also
 $$ \begin{align*}U\subset\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\bigoplus_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} T^1_{x_v}\Sigma\right)\stackrel{\text{def}}=\mathbb T_{\vec x}\end{align*} $$
$$ \begin{align*}U\subset\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\bigoplus_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} T^1_{x_v}\Sigma\right)\stackrel{\text{def}}=\mathbb T_{\vec x}\end{align*} $$
be an open set where, as always,
![]() $\operatorname {\mathrm {\mathbf {half}}}_v(X)$
is the set of all half-edges of X starting at the vertex v.
$\operatorname {\mathrm {\mathbf {half}}}_v(X)$
is the set of all half-edges of X starting at the vertex v.
Given for each edge
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
a positive number
$e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
a positive number
![]() $L_e$
and writing
$L_e$
and writing
![]() $\vec L=(L_e)_{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}$
, we are going to be interested in the set
$\vec L=(L_e)_{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}$
, we are going to be interested in the set
![]() ${\mathbf {G}}^X_{U}(\vec L_e,h)$
of realizations
${\mathbf {G}}^X_{U}(\vec L_e,h)$
of realizations
![]() $\phi :X\to \Sigma $
$\phi :X\to \Sigma $
-
(a) mapping each vertex
 $v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
to the point
$v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
to the point
 $x_v$
,
$x_v$
, -
(b) with
 $(\phi (\vec e))_{\bar e\in \operatorname {\mathrm {\mathbf {half}}}(X)}\in U$
and
$(\phi (\vec e))_{\bar e\in \operatorname {\mathrm {\mathbf {half}}}(X)}\in U$
and -
(c) with
 $\ell (e)\in [L_e,L_e+h]$
for all
$\ell (e)\in [L_e,L_e+h]$
for all
 $e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
.
$e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
.
In this setting, we have the following version of Delsarte’s theorem relating the cardinality of
![]() ${\mathbf {G}}^X_{U}(\vec L_e,h)$
with the volume
${\mathbf {G}}^X_{U}(\vec L_e,h)$
with the volume
![]() $\operatorname {\mathrm {vol}}_{\vec x}(U)$
of U, where the volume is measured in the flat torus
$\operatorname {\mathrm {vol}}_{\vec x}(U)$
of U, where the volume is measured in the flat torus
![]() $\mathbb T_{\vec x}$
.
$\mathbb T_{\vec x}$
.
Theorem 3.2 (Delarte’s theorem for graph realizations)
Let
![]() $\Sigma $
be a closed hyperbolic surface, let X be a finite graph, fix
$\Sigma $
be a closed hyperbolic surface, let X be a finite graph, fix
![]() $\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
and an open set
$\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
and an open set
![]() $U_{\vec x}\subset \mathbb T_{\vec x}$
. If
$U_{\vec x}\subset \mathbb T_{\vec x}$
. If
![]() $\operatorname {\mathrm {vol}}_{\vec x}(\bar U_{\vec x}\setminus U_{\vec x})=0$
, then for every
$\operatorname {\mathrm {vol}}_{\vec x}(\bar U_{\vec x}\setminus U_{\vec x})=0$
, then for every
![]() $h>0$
we have
$h>0$
we have
 $$ \begin{align*}\vert{\mathbf{G}}^X_{U_{\vec x}}(\vec L,h)\vert\sim \frac{\operatorname{\mathrm{vol}}_{\vec x}(U_{\vec x})}{(4\pi)^{E}}\cdot\frac{(e^h-1)^{E}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{E}}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}^X_{U_{\vec x}}(\vec L,h)\vert\sim \frac{\operatorname{\mathrm{vol}}_{\vec x}(U_{\vec x})}{(4\pi)^{E}}\cdot\frac{(e^h-1)^{E}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{E}}\end{align*} $$
when
![]() $\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}L_e\to \infty $
. Here,
$\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}L_e\to \infty $
. Here,
![]() $\bar U_{\vec x}$
is the closure of
$\bar U_{\vec x}$
is the closure of
![]() $U_{\vec x}$
in
$U_{\vec x}$
in
![]() $\mathbb T_{\vec x}$
and
$\mathbb T_{\vec x}$
and
![]() $\operatorname {\mathrm {vol}}_{\vec x}(\cdot )$
stands for the volume therein. Also,
$\operatorname {\mathrm {vol}}_{\vec x}(\cdot )$
stands for the volume therein. Also,
![]() $E=\vert \operatorname {\mathrm {\mathbf {edge}}}(X)\vert $
is the number of edges in X, and
$E=\vert \operatorname {\mathrm {\mathbf {edge}}}(X)\vert $
is the number of edges in X, and
![]() $\Vert \vec L\Vert =\sum _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}L_e$
.
$\Vert \vec L\Vert =\sum _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}L_e$
.
We stress that
![]() $\operatorname {\mathrm {vol}}_{\vec x}$
is normalized in such a way that
$\operatorname {\mathrm {vol}}_{\vec x}$
is normalized in such a way that
![]() $\operatorname {\mathrm {vol}}_{\vec x}(\mathbb T_{\vec x})=(2\pi )^{2 E}$
. We also stress that this is consistent with the fact that we use the interval
$\operatorname {\mathrm {vol}}_{\vec x}(\mathbb T_{\vec x})=(2\pi )^{2 E}$
. We also stress that this is consistent with the fact that we use the interval
![]() $[0,\pi ]$
to measure unoriented angles.
$[0,\pi ]$
to measure unoriented angles.
Proof. Let us say that a closed set of the form
 $$ \begin{align*}\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\prod_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} I_{\bar e}\right)\subset\mathbb T_{\vec x}=\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\bigoplus_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} T^1_{x_v}\Sigma\right),\end{align*} $$
$$ \begin{align*}\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\prod_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} I_{\bar e}\right)\subset\mathbb T_{\vec x}=\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\bigoplus_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} T^1_{x_v}\Sigma\right),\end{align*} $$
where each
![]() $I_{\bar e}$
is a segment in
$I_{\bar e}$
is a segment in
![]() $T^1_{x_v}\Sigma $
is a cube. We say that a closed subset of
$T^1_{x_v}\Sigma $
is a cube. We say that a closed subset of
![]() $\prod _{v\in \operatorname {\mathrm {\mathbf {vert}}}(X)}\left (\oplus _{\bar e\in \operatorname {\mathrm {\mathbf {half}}}_v(X)} T^1_{x_v}\Sigma \right )$
it cubical if it can be given as the union of finitely many cubes with disjoint interiors. The assumption that the open set
$\prod _{v\in \operatorname {\mathrm {\mathbf {vert}}}(X)}\left (\oplus _{\bar e\in \operatorname {\mathrm {\mathbf {half}}}_v(X)} T^1_{x_v}\Sigma \right )$
it cubical if it can be given as the union of finitely many cubes with disjoint interiors. The assumption that the open set
![]() $U=U_{\vec x}$
in the statement is such that
$U=U_{\vec x}$
in the statement is such that
![]() $\bar U\setminus U$
is a null-set implies that U can be approximated from inside and outside by cubical sets
$\bar U\setminus U$
is a null-set implies that U can be approximated from inside and outside by cubical sets
![]() $U'\subset U\subset U"$
with
$U'\subset U\subset U"$
with
![]() $\operatorname {\mathrm {vol}}(U")-\operatorname {\mathrm {vol}}(U')$
as small as we want. It follows that it suffices to prove the theorem if U is (the interior of) a cubical set.
$\operatorname {\mathrm {vol}}(U")-\operatorname {\mathrm {vol}}(U')$
as small as we want. It follows that it suffices to prove the theorem if U is (the interior of) a cubical set.
Note now that if
![]() $U=U_1\cup U_2$
is the disjoint union of two sets
$U=U_1\cup U_2$
is the disjoint union of two sets
![]() $U_1$
and
$U_1$
and
![]() $U_2$
and if the statement of the theorem holds true for
$U_2$
and if the statement of the theorem holds true for
![]() $U_1$
and
$U_1$
and
![]() $U_2$
, then it also holds true for U. Since every cubical set is made out of finitely many cubes with disjoint interior, we deduce that it really suffices to prove the theorem for individual cubes
$U_2$
, then it also holds true for U. Since every cubical set is made out of finitely many cubes with disjoint interior, we deduce that it really suffices to prove the theorem for individual cubes
 $$ \begin{align*}U=\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\prod_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} I_{\bar e}\right).\end{align*} $$
$$ \begin{align*}U=\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\prod_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} I_{\bar e}\right).\end{align*} $$
Note that, up to shuffling the factors we can see U as
 $$ \begin{align*}U=\prod_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}\left(I_{e^+}\times I_{e^-}\right).\end{align*} $$
$$ \begin{align*}U=\prod_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}\left(I_{e^+}\times I_{e^-}\right).\end{align*} $$
Here, we are denoting by
![]() $e^+$
and
$e^+$
and
![]() $e^-$
the two half-edges of the edge
$e^-$
the two half-edges of the edge
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
. Now, unpacking the notation one sees that a realization
$e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
. Now, unpacking the notation one sees that a realization
![]() $\phi $
belongs to
$\phi $
belongs to
![]() ${\mathbf {G}}_{U}(\vec L_e,h)$
if and only if for all
${\mathbf {G}}_{U}(\vec L_e,h)$
if and only if for all
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
the arc
$e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
the arc
![]() $\phi (e)$
belongs to
$\phi (e)$
belongs to
![]() ${\mathbf {A}}_{I_{e^+},I_{e^-}}(L_e,h)$
. It follows thus from Delsarte’s theorem for in-out sectors that
${\mathbf {A}}_{I_{e^+},I_{e^-}}(L_e,h)$
. It follows thus from Delsarte’s theorem for in-out sectors that
 $$ \begin{align*} \vert{\mathbf{G}}_{U}^X(\vec L,h)\vert &=\prod_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}\left\vert{\mathbf{A}}_{I_{e^+},I_{e^-}}(L_e,h)\right\vert\\ &\sim\prod_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}\left(\frac{\ell(I_{e^+})\cdot\ell(I_{e^-})}{4\pi}\cdot \frac{(e^h-1)\cdot e^{L_e}}{\operatorname{\mathrm{vol}}(\Sigma)}\right)\\ &=\frac{\prod_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}(\ell(I_{e^+})\cdot\ell(I_{e^-}))}{(4\pi)^{E}}\cdot \frac{(e^h-1)^{E}\cdot e^{\sum_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}L_e}}{\operatorname{\mathrm{vol}}(\Sigma)^{E}}\\ &=\frac{\operatorname{\mathrm{vol}}(U)}{(4\pi)^{E}}\cdot \frac{(e^h-1)^{E}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{E}}, \end{align*} $$
$$ \begin{align*} \vert{\mathbf{G}}_{U}^X(\vec L,h)\vert &=\prod_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}\left\vert{\mathbf{A}}_{I_{e^+},I_{e^-}}(L_e,h)\right\vert\\ &\sim\prod_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}\left(\frac{\ell(I_{e^+})\cdot\ell(I_{e^-})}{4\pi}\cdot \frac{(e^h-1)\cdot e^{L_e}}{\operatorname{\mathrm{vol}}(\Sigma)}\right)\\ &=\frac{\prod_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}(\ell(I_{e^+})\cdot\ell(I_{e^-}))}{(4\pi)^{E}}\cdot \frac{(e^h-1)^{E}\cdot e^{\sum_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}L_e}}{\operatorname{\mathrm{vol}}(\Sigma)^{E}}\\ &=\frac{\operatorname{\mathrm{vol}}(U)}{(4\pi)^{E}}\cdot \frac{(e^h-1)^{E}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{E}}, \end{align*} $$
where, as in the statement we have set
![]() $E=\vert \operatorname {\mathrm {\mathbf {edge}}}(X)\vert $
. We are done.
$E=\vert \operatorname {\mathrm {\mathbf {edge}}}(X)\vert $
. We are done.
Let us consider now the concrete case we will care mostly about. Suppose namely that X is a trivalent graph and that we want all the angles to be between
![]() $\frac 23\pi -\varepsilon $
and
$\frac 23\pi -\varepsilon $
and
![]() $\frac 23\pi +\varepsilon $
. In other words, we are interested in the set of
$\frac 23\pi +\varepsilon $
. In other words, we are interested in the set of
![]() $\varepsilon $
-critical realizations
$\varepsilon $
-critical realizations
![]() $\phi :X\to \Sigma $
which map the vertices to our prescribed tuple
$\phi :X\to \Sigma $
which map the vertices to our prescribed tuple
![]() $\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
. Then we have to consider the set
$\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
. Then we have to consider the set
 $$ \begin{align*}U_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}^X\subset\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\bigoplus_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} T^1_{x_v}\Sigma\right)\end{align*} $$
$$ \begin{align*}U_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}^X\subset\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\bigoplus_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} T^1_{x_v}\Sigma\right)\end{align*} $$
of those tuples
![]() $(v_{\vec e})_{\vec e\in \operatorname {\mathrm {\mathbf {half}}}(X)}$
with
$(v_{\vec e})_{\vec e\in \operatorname {\mathrm {\mathbf {half}}}(X)}$
with
![]() $\angle (v_{\vec e_1},v_{\vec e_2})\in [\frac {2\pi }3-\varepsilon ,\frac {2\pi }3+\varepsilon ]$
for all distinct
$\angle (v_{\vec e_1},v_{\vec e_2})\in [\frac {2\pi }3-\varepsilon ,\frac {2\pi }3+\varepsilon ]$
for all distinct
![]() $\vec e_1,\vec e_2\in \operatorname {\mathrm {\mathbf {half}}}(X)$
incident to the same vertex.
$\vec e_1,\vec e_2\in \operatorname {\mathrm {\mathbf {half}}}(X)$
incident to the same vertex.
Let us compute the volume of
![]() $U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X$
. Noting that the conditions on
$U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X$
. Noting that the conditions on
![]() $U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X$
associated to different vertices are independent, we get that it suffices to think vertex-by-vertex and then multiply all the numbers obtained for all vertices. For each vertex v, label arbitrarily the half-edges incident to v by
$U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X$
associated to different vertices are independent, we get that it suffices to think vertex-by-vertex and then multiply all the numbers obtained for all vertices. For each vertex v, label arbitrarily the half-edges incident to v by
![]() $\vec e_1,\vec e_2$
and
$\vec e_1,\vec e_2$
and
![]() $\vec e_3$
. We have no restriction for the position of
$\vec e_3$
. We have no restriction for the position of
![]() $v_{\vec e_1}\in T_{x_v}\Sigma $
. Once we have fixed
$v_{\vec e_1}\in T_{x_v}\Sigma $
. Once we have fixed
![]() $v_{\vec e_1}\in T_{x_v}^1(\Sigma )$
, we get that
$v_{\vec e_1}\in T_{x_v}^1(\Sigma )$
, we get that
![]() $v_{\vec e_2}$
can belong to two segments, each one of length
$v_{\vec e_2}$
can belong to two segments, each one of length
![]() $2\varepsilon $
, in
$2\varepsilon $
, in
![]() $T^1_{x_v}(\Sigma )$
– recall that all our angles are unoriented. Then, once we have fixed
$T^1_{x_v}(\Sigma )$
– recall that all our angles are unoriented. Then, once we have fixed
![]() $v_{\vec e_1}$
and
$v_{\vec e_1}$
and
![]() $v_{\vec e_2}$
, we have to choose
$v_{\vec e_2}$
, we have to choose
![]() $v_{\vec e_3}$
in an interval of length
$v_{\vec e_3}$
in an interval of length
![]() $2\varepsilon -\vert \angle (v_{\vec e_1},v_{\vec e_2})-\frac {2\pi }3\vert $
. This means that when we have chosen
$2\varepsilon -\vert \angle (v_{\vec e_1},v_{\vec e_2})-\frac {2\pi }3\vert $
. This means that when we have chosen
![]() $v_{\vec e_1}$
and which segment
$v_{\vec e_1}$
and which segment
![]() $v_{\vec e_2}$
is in, then we have
$v_{\vec e_2}$
is in, then we have
![]() $3\varepsilon ^2$
worth of choices of
$3\varepsilon ^2$
worth of choices of
![]() $(v_{\vec e_2},v_{\vec e_3})$
. This means that the set of possible choices in
$(v_{\vec e_2},v_{\vec e_3})$
. This means that the set of possible choices in
![]() $T_{x_v}^1\Sigma \times T_{x_v}^1\Sigma \times T_{x_v}^1\Sigma $
has volume equal to
$T_{x_v}^1\Sigma \times T_{x_v}^1\Sigma \times T_{x_v}^1\Sigma $
has volume equal to
![]() $12\pi \varepsilon ^2$
. Since, as we already mentioned earlier, the conditions at all vertices of X are independent, we get that
$12\pi \varepsilon ^2$
. Since, as we already mentioned earlier, the conditions at all vertices of X are independent, we get that
From Theorem 3.2, we get thus that for all
![]() $h>0$
and all
$h>0$
and all
![]() $\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
we have
$\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
we have
 $$ \begin{align*}\vert{\mathbf{G}}^X_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}(\vec L,h)\vert\sim \frac{(12\pi\varepsilon^2)^{V}}{(4\pi)^{E}}\cdot\frac{(e^h-1)^{E}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{E}}\text{ as }\min_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}L_e\to\infty,\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}^X_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}(\vec L,h)\vert\sim \frac{(12\pi\varepsilon^2)^{V}}{(4\pi)^{E}}\cdot\frac{(e^h-1)^{E}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{E}}\text{ as }\min_{e\in\operatorname{\mathrm{\mathbf{edge}}}(X)}L_e\to\infty,\end{align*} $$
where we are writing V and E for the number of vertices and edges of X, and
![]() ${\mathbf {G}}^X_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}$
instead of
${\mathbf {G}}^X_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}$
instead of
![]() ${\mathbf {G}}^X_{U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}}$
. Taking into account that X is trivalent and hence satisfies
${\mathbf {G}}^X_{U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}}$
. Taking into account that X is trivalent and hence satisfies
![]() $V=-2\chi (X)$
and
$V=-2\chi (X)$
and
![]() $E=-3\chi (X)$
, we can clean this up to
$E=-3\chi (X)$
, we can clean this up to
 $$ \begin{align*}\vert{\mathbf{G}}^X_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}(\vec L,h)\vert\sim \varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-3\chi(X)}}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}^X_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}(\vec L,h)\vert\sim \varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-3\chi(X)}}\end{align*} $$
as
![]() $\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}L_e\to \infty $
. Moreover, since the geometry of the set
$\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}L_e\to \infty $
. Moreover, since the geometry of the set
![]() $U_{\vec x}^X(\varepsilon -\operatorname {\mathrm {crit}})$
is independent of the point
$U_{\vec x}^X(\varepsilon -\operatorname {\mathrm {crit}})$
is independent of the point
![]() $\vec x$
, we get that the speed of convergence to this asymptotic is independent of
$\vec x$
, we get that the speed of convergence to this asymptotic is independent of
![]() $\vec x$
. Altogether, we have the following result:
$\vec x$
. Altogether, we have the following result:
Corollary 3.3. Let
![]() $\Sigma $
be a closed hyperbolic surface and X be a trivalent graph, fix
$\Sigma $
be a closed hyperbolic surface and X be a trivalent graph, fix
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $h>0$
and for
$h>0$
and for
![]() $\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
, let
$\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
, let
![]() ${\mathbf {G}}^X_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}(\vec L,h)$
be the set of
${\mathbf {G}}^X_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}(\vec L,h)$
be the set of
![]() $\varepsilon $
-critical realizations
$\varepsilon $
-critical realizations
![]() $\phi :X\to \Sigma $
mapping the vertex v to the point
$\phi :X\to \Sigma $
mapping the vertex v to the point
![]() $x_v=\phi (v)$
. Then we have
$x_v=\phi (v)$
. Then we have
 $$ \begin{align} \vert{\mathbf{G}}_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}^X(\vec L,h)\vert \sim \varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-3\chi(X)}} \end{align} $$
$$ \begin{align} \vert{\mathbf{G}}_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}^X(\vec L,h)\vert \sim \varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-3\chi(X)}} \end{align} $$
as
![]() $\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}L_e\to \infty $
.
$\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}L_e\to \infty $
.
Note that the set
![]() $U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X$
needed to establish Corollary 3.3 is basically the same for all choices of
$U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X$
needed to establish Corollary 3.3 is basically the same for all choices of
![]() $\vec x$
. For example, if we take another
$\vec x$
. For example, if we take another
![]() $\vec y\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
and we identity
$\vec y\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
and we identity
![]() $\mathbb T_{\vec x}$
with
$\mathbb T_{\vec x}$
with
![]() $\mathbb T_{\vec y}$
isometrically by parallel transport (along any collection of curves whatsoever), then
$\mathbb T_{\vec y}$
isometrically by parallel transport (along any collection of curves whatsoever), then
![]() $U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X$
is sent to
$U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X$
is sent to
![]() $U_{\vec y,\varepsilon -\operatorname {\mathrm {crit}}}^X$
. It follows that we can approximate
$U_{\vec y,\varepsilon -\operatorname {\mathrm {crit}}}^X$
. It follows that we can approximate
![]() $U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X$
and
$U_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X$
and
![]() $U_{\vec y,\varepsilon -\operatorname {\mathrm {crit}}}^X$
at the same time by cubical sets consisting of the same number of cubes with the same side lengths. It thus follows from the comment following Theorem 3.1 that the asymptotics in Corollary 3.3 is uniform in
$U_{\vec y,\varepsilon -\operatorname {\mathrm {crit}}}^X$
at the same time by cubical sets consisting of the same number of cubes with the same side lengths. It thus follows from the comment following Theorem 3.1 that the asymptotics in Corollary 3.3 is uniform in
![]() $\vec x$
. We record this fact:
$\vec x$
. We record this fact:
Addendum to Corollary 3.3. The asymptotics in Equation (3.5) is uniform in
![]() $\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
.
$\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}(X)}$
.
4 Counting critical realizations
In this section, we prove Theorem 1.3 from the introduction. Before restating the theorem, recall that if X is a trivalent graph then we denote by
 $$ \begin{align} {\mathbf{G}}^X(L)=\left\{\begin{array}{c}\phi:X\to\Sigma\text{ critical realization}\\ \text{with length }\ell_{\Sigma}(\phi)\leqslant L\end{array}\right\} \end{align} $$
$$ \begin{align} {\mathbf{G}}^X(L)=\left\{\begin{array}{c}\phi:X\to\Sigma\text{ critical realization}\\ \text{with length }\ell_{\Sigma}(\phi)\leqslant L\end{array}\right\} \end{align} $$
the set of all critical realizations of length
![]() $\ell _{\Sigma }(\phi )$
at most L.
$\ell _{\Sigma }(\phi )$
at most L.
Theorem 1.3. Let
![]() $\Sigma $
be a closed, connected and oriented hyperbolic surface. For every connected trivalent graph X, we have
$\Sigma $
be a closed, connected and oriented hyperbolic surface. For every connected trivalent graph X, we have
 $$ \begin{align*}\vert{\mathbf{G}}^X(L)\vert\sim \left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}^X(L)\vert\sim \left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}\end{align*} $$
as
![]() $L\to \infty $
.
$L\to \infty $
.
Fixing for the remaining of this section the trivalent graph X, we will write
![]() $\operatorname {\mathrm {\mathbf {vert}}}=\operatorname {\mathrm {\mathbf {vert}}}(X)$
and
$\operatorname {\mathrm {\mathbf {vert}}}=\operatorname {\mathrm {\mathbf {vert}}}(X)$
and
![]() $\operatorname {\mathrm {\mathbf {edge}}}=\operatorname {\mathrm {\mathbf {edge}}}(X)$
for the sets of vertices and edges and
$\operatorname {\mathrm {\mathbf {edge}}}=\operatorname {\mathrm {\mathbf {edge}}}(X)$
for the sets of vertices and edges and
![]() $V=\vert \operatorname {\mathrm {\mathbf {vert}}}\vert $
and
$V=\vert \operatorname {\mathrm {\mathbf {vert}}}\vert $
and
![]() $E=\vert \operatorname {\mathrm {\mathbf {edge}}}\vert $
for their cardinalities. Similarly, we will denote by
$E=\vert \operatorname {\mathrm {\mathbf {edge}}}\vert $
for their cardinalities. Similarly, we will denote by
![]() $\mathcal G=\mathcal G^X$
the manifold of realizations of X in
$\mathcal G=\mathcal G^X$
the manifold of realizations of X in
![]() $\Sigma $
, and by
$\Sigma $
, and by
![]() ${\mathbf {G}}(L)={\mathbf {G}}^X(L)$
the set of critical realizations with length at most L.
${\mathbf {G}}(L)={\mathbf {G}}^X(L)$
the set of critical realizations with length at most L.
The main step in the proof of Theorem 1.3 is to count critical realizations of X such that the corresponding vectors of lengths
![]() $(\ell (\phi (e)))_{e\in \operatorname {\mathrm {\mathbf {edge}}}}$
belong to a box of size
$(\ell (\phi (e)))_{e\in \operatorname {\mathrm {\mathbf {edge}}}}$
belong to a box of size
![]() $h>0$
. More concretely, we want to count how many elements there are in the set
$h>0$
. More concretely, we want to count how many elements there are in the set
 $$ \begin{align} {\mathbf{G}}(\vec L,h)=\left\{\begin{array}{c}\phi:X\to\Sigma\text{ critical realization with}\\ \ell(\phi(e))\in(L_e,L_e+h]\text{ for all }e\in\operatorname{\mathrm{\mathbf{edge}}}\end{array}\right\}, \end{align} $$
$$ \begin{align} {\mathbf{G}}(\vec L,h)=\left\{\begin{array}{c}\phi:X\to\Sigma\text{ critical realization with}\\ \ell(\phi(e))\in(L_e,L_e+h]\text{ for all }e\in\operatorname{\mathrm{\mathbf{edge}}}\end{array}\right\}, \end{align} $$
where
![]() $\vec L=(L_e)_{e\in \operatorname {\mathrm {\mathbf {edge}}}}$
is a positive vector. We start by establishing some form of an upper bound for the number of homotopy classes of realizations when we bound the length of each individual edge – recall that by Lemma 2.2 any two homotopic critical realizations are identical.
$\vec L=(L_e)_{e\in \operatorname {\mathrm {\mathbf {edge}}}}$
is a positive vector. We start by establishing some form of an upper bound for the number of homotopy classes of realizations when we bound the length of each individual edge – recall that by Lemma 2.2 any two homotopic critical realizations are identical.
Lemma 4.1. For all
![]() $\vec L\in \mathbb R_+^{\operatorname {\mathrm {\mathbf {edge}}}(X)}$
, there are at most
$\vec L\in \mathbb R_+^{\operatorname {\mathrm {\mathbf {edge}}}(X)}$
, there are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\Vert \vec L\Vert }$
homotopy classes of realizations
$\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\Vert \vec L\Vert }$
homotopy classes of realizations
![]() $\phi :X\to \Sigma $
with
$\phi :X\to \Sigma $
with
![]() $\ell (\phi (e))\leqslant L_e$
for all
$\ell (\phi (e))\leqslant L_e$
for all
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
.
$e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
.
It is worth pointing out that Lemma 4.1 fails if
![]() $\Sigma $
is allowed to have cusps – see Section 9.
$\Sigma $
is allowed to have cusps – see Section 9.
Proof. Let us fix a point
![]() $x_0\in \Sigma $
, and note that every point in
$x_0\in \Sigma $
, and note that every point in
![]() $\Sigma $
– think of the images under a realization of the vertices of X – can be moved to
$\Sigma $
– think of the images under a realization of the vertices of X – can be moved to
![]() $x_0$
along a path of length at most
$x_0$
along a path of length at most
![]() $\operatorname {\mathrm {diam}}(\Sigma )$
. It follows that every realization
$\operatorname {\mathrm {diam}}(\Sigma )$
. It follows that every realization
![]() $\phi :X\to \Sigma $
is homotopic to a new realization
$\phi :X\to \Sigma $
is homotopic to a new realization
![]() $\psi :X\to \Sigma $
mapping all vertices of X to
$\psi :X\to \Sigma $
mapping all vertices of X to
![]() $x_0$
and with
$x_0$
and with
for every edge
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
. Note that the homotopy class of
$e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
. Note that the homotopy class of
![]() $\psi $
is determined by the homotopy classes of the loops
$\psi $
is determined by the homotopy classes of the loops
![]() $\psi (e)$
when e ranges over the edges of X. Now, Equation (4.3) implies that, up to homotopy, we have at most
$\psi (e)$
when e ranges over the edges of X. Now, Equation (4.3) implies that, up to homotopy, we have at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot e^{L_e}$
choices for the geodesic segment
$\operatorname {\mathrm {\mathbf {const}}}\cdot e^{L_e}$
choices for the geodesic segment
![]() $\psi (e)$
. This implies that there are at most
$\psi (e)$
. This implies that there are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\Vert \vec L\Vert }$
choices for the homotopy class of
$\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\Vert \vec L\Vert }$
choices for the homotopy class of
![]() $\psi $
, and hence for the homotopy class of
$\psi $
, and hence for the homotopy class of
![]() $\phi $
. We are done.
$\phi $
. We are done.
Although it is evidently pretty coarse, Lemma 4.1 will play a key role in the proof of Theorem 1.3. However, the main tool in the proof of the theorem is the following:
Proposition 4.2. For all
![]() $h>0$
, we have
$h>0$
, we have
 $$ \begin{align*}\vert{\mathbf{G}}(\vec L,h)\vert\sim\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h}-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}(\vec L,h)\vert\sim\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h}-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}\end{align*} $$
as
![]() $\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}}L_e\to \infty $
. Here,
$\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}}L_e\to \infty $
. Here,
![]() ${\mathbf {G}}(\vec L,h)$
is as in Equation (4.2).
${\mathbf {G}}(\vec L,h)$
is as in Equation (4.2).
Proof. Denote by
![]() $\mathcal G(\vec L,h)\subset \mathcal G$
the set of all realizations
$\mathcal G(\vec L,h)\subset \mathcal G$
the set of all realizations
![]() $\phi :X\to \Sigma $
with
$\phi :X\to \Sigma $
with
![]() $\ell _{\Sigma }(\phi )\in [L_e,L_e+h]$
for all
$\ell _{\Sigma }(\phi )\in [L_e,L_e+h]$
for all
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}$
and then let
$e\in \operatorname {\mathrm {\mathbf {edge}}}$
and then let
 $$ \begin{align*} G_{\varepsilon}(\vec L,h)&=\left\{ \mathcal G^{\phi}\in\pi_0(\mathcal G)\text{ with }\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\subset \mathcal G(\vec L,h)\right\}\\ \hat G_{\varepsilon}(\vec L,h)&=\left\{ \mathcal G^{\phi}\in\pi_0(\mathcal G)\text{ with }\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\cap\mathcal G(\vec L,h)\neq\varnothing\right\} \end{align*} $$
$$ \begin{align*} G_{\varepsilon}(\vec L,h)&=\left\{ \mathcal G^{\phi}\in\pi_0(\mathcal G)\text{ with }\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\subset \mathcal G(\vec L,h)\right\}\\ \hat G_{\varepsilon}(\vec L,h)&=\left\{ \mathcal G^{\phi}\in\pi_0(\mathcal G)\text{ with }\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\cap\mathcal G(\vec L,h)\neq\varnothing\right\} \end{align*} $$
be the sets of connected components of
![]() $\mathcal G$
whose set of
$\mathcal G$
whose set of
![]() $\varepsilon $
-critical realizations is fully contained in (resp. which meet)
$\varepsilon $
-critical realizations is fully contained in (resp. which meet)
![]() $\mathcal G(\vec L,h)$
. It follows from Corollary 2.4 that there is some
$\mathcal G(\vec L,h)$
. It follows from Corollary 2.4 that there is some
![]() $\ell _0$
such that as long as
$\ell _0$
such that as long as
![]() $\vec L$
satisfies that
$\vec L$
satisfies that
![]() $\min L_e\geqslant \ell _0$
, then each component listed in
$\min L_e\geqslant \ell _0$
, then each component listed in
![]() $\hat G_{\varepsilon }(\vec L,h)$
contains exactly one critical realization of the graph X. Assuming from now on that we are in this situation, we get that
$\hat G_{\varepsilon }(\vec L,h)$
contains exactly one critical realization of the graph X. Assuming from now on that we are in this situation, we get that
Now, from Equation (2.10) in Proposition 2.6 we get that for all
![]() $\delta>0$
there is
$\delta>0$
there is
![]() $\ell _1>\ell _0$
with
$\ell _1>\ell _0$
with
 $$ \begin{align*}(1-\delta)\cdot\operatorname{\mathrm{vol}}\left(\bigcup_{\mathcal G^{\phi}\in G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\right)<\left(\frac 2{\sqrt 3}\varepsilon^2\right)^V\cdot\vert G_{\varepsilon}(\vec L,h)\vert\end{align*} $$
$$ \begin{align*}(1-\delta)\cdot\operatorname{\mathrm{vol}}\left(\bigcup_{\mathcal G^{\phi}\in G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\right)<\left(\frac 2{\sqrt 3}\varepsilon^2\right)^V\cdot\vert G_{\varepsilon}(\vec L,h)\vert\end{align*} $$
 $$ \begin{align*}(1+\delta)\cdot\operatorname{\mathrm{vol}}\left(\bigcup_{\mathcal G^{\phi}\in\hat G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\right)>\left(\frac 2{\sqrt 3}\varepsilon^2\right)^V\cdot \vert \hat G_{\varepsilon}(\vec L,h)\vert\end{align*} $$
$$ \begin{align*}(1+\delta)\cdot\operatorname{\mathrm{vol}}\left(\bigcup_{\mathcal G^{\phi}\in\hat G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\right)>\left(\frac 2{\sqrt 3}\varepsilon^2\right)^V\cdot \vert \hat G_{\varepsilon}(\vec L,h)\vert\end{align*} $$
whenever
![]() $\varepsilon $
is small enough and
$\varepsilon $
is small enough and
![]() $\min L_e\geqslant \ell _1$
. Altogether, we get that for all
$\min L_e\geqslant \ell _1$
. Altogether, we get that for all
![]() $\varepsilon $
positive and small we have
$\varepsilon $
positive and small we have
 $$ \begin{align*} (1-\delta)\cdot\left(\frac 2{\sqrt 3}\varepsilon^2\right)^{-V}\cdot\operatorname{\mathrm{vol}}\left(\bigcup_{\mathcal G^{\phi}\in G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\right)&<\vert{\mathbf{G}}(\vec L, h)\vert\\[5pt] (1+\delta)\cdot\left(\frac 2{\sqrt 3}\varepsilon^2\right)^{-V}\cdot\operatorname{\mathrm{vol}}\left(\bigcup_{\mathcal G^{\phi}\in\hat G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\right)&>\vert{\mathbf{G}}(\vec L, h)\vert \end{align*} $$
$$ \begin{align*} (1-\delta)\cdot\left(\frac 2{\sqrt 3}\varepsilon^2\right)^{-V}\cdot\operatorname{\mathrm{vol}}\left(\bigcup_{\mathcal G^{\phi}\in G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\right)&<\vert{\mathbf{G}}(\vec L, h)\vert\\[5pt] (1+\delta)\cdot\left(\frac 2{\sqrt 3}\varepsilon^2\right)^{-V}\cdot\operatorname{\mathrm{vol}}\left(\bigcup_{\mathcal G^{\phi}\in\hat G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\right)&>\vert{\mathbf{G}}(\vec L, h)\vert \end{align*} $$
for all
![]() $\vec L$
with
$\vec L$
with
![]() $\min L_e\geqslant \ell _1$
.
$\min L_e\geqslant \ell _1$
.
We get now from Equation (2.11) in Proposition 2.6 that there is
![]() $\ell _2>\ell _1$
such that, as long as
$\ell _2>\ell _1$
such that, as long as
![]() $\varepsilon $
is under some threshold, we have that whenever
$\varepsilon $
is under some threshold, we have that whenever
![]() $\phi ,\psi \in \mathcal G$
are homotopic
$\phi ,\psi \in \mathcal G$
are homotopic
![]() $\varepsilon $
-critical realizations with
$\varepsilon $
-critical realizations with
![]() $\ell (\phi (e)),\ell (\psi (e))\geqslant \ell _2$
for all
$\ell (\phi (e)),\ell (\psi (e))\geqslant \ell _2$
for all
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}$
, then we have that the lengths
$e\in \operatorname {\mathrm {\mathbf {edge}}}$
, then we have that the lengths
![]() $\ell (\phi (e))$
and
$\ell (\phi (e))$
and
![]() $\ell (\psi (e))$
differ by at most
$\ell (\psi (e))$
differ by at most
![]() $2\varepsilon $
for each edge
$2\varepsilon $
for each edge
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}$
. This implies that for any such
$e\in \operatorname {\mathrm {\mathbf {edge}}}$
. This implies that for any such
![]() $\vec L$
and
$\vec L$
and
![]() $\varepsilon $
we have
$\varepsilon $
we have
 $$ \begin{align*} \mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}(\vec L+[2\varepsilon],h-4\varepsilon)&\subset \bigcup_{\mathcal G^{\phi}\in G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\\ \mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}(\vec L-[2\varepsilon],h+4\varepsilon)&\supset \bigcup_{\mathcal G^{\phi}\in\hat G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}, \end{align*} $$
$$ \begin{align*} \mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}(\vec L+[2\varepsilon],h-4\varepsilon)&\subset \bigcup_{\mathcal G^{\phi}\in G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}\\ \mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}(\vec L-[2\varepsilon],h+4\varepsilon)&\supset \bigcup_{\mathcal G^{\phi}\in\hat G_{\varepsilon}(\vec L,h)}\mathcal G^{\phi}_{\varepsilon-\operatorname{\mathrm{crit}}}, \end{align*} $$
where
![]() $\vec L+[t]\in \mathbb R^{\operatorname {\mathrm {\mathbf {edge}}}}$
is the vector with entries
$\vec L+[t]\in \mathbb R^{\operatorname {\mathrm {\mathbf {edge}}}}$
is the vector with entries
![]() $(\vec L+[t])_e=\vec L_e+t$
.
$(\vec L+[t])_e=\vec L_e+t$
.
Let us summarize what we have obtained so far:
 $$ \begin{align*} (1-\delta)\cdot\left(\frac 2{\sqrt 3}\varepsilon^2\right)^{-V}\cdot\operatorname{\mathrm{vol}}\left(\mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}(\vec L+[2\varepsilon],h-4\varepsilon)\right)&<\vert{\mathbf{G}}(\vec L, h)\vert\\ (1+\delta)\cdot\left(\frac 2{\sqrt 3}\varepsilon^2\right)^{-V}\cdot\operatorname{\mathrm{vol}}\left(\mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}(\vec L-[2\varepsilon],h+4\varepsilon)\right)&>\vert{\mathbf{G}}(\vec L, h)\vert. \end{align*} $$
$$ \begin{align*} (1-\delta)\cdot\left(\frac 2{\sqrt 3}\varepsilon^2\right)^{-V}\cdot\operatorname{\mathrm{vol}}\left(\mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}(\vec L+[2\varepsilon],h-4\varepsilon)\right)&<\vert{\mathbf{G}}(\vec L, h)\vert\\ (1+\delta)\cdot\left(\frac 2{\sqrt 3}\varepsilon^2\right)^{-V}\cdot\operatorname{\mathrm{vol}}\left(\mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}(\vec L-[2\varepsilon],h+4\varepsilon)\right)&>\vert{\mathbf{G}}(\vec L, h)\vert. \end{align*} $$
Our next goal is to compute the volumes on the left. Using the cover (2.2), we can compute volumes
![]() $\operatorname {\mathrm {vol}}(\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(\vec L,h))$
by integrating over
$\operatorname {\mathrm {vol}}(\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(\vec L,h))$
by integrating over
![]() $\Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}}$
the cardinality of the intersection
$\Sigma ^{\operatorname {\mathrm {\mathbf {vert}}}}$
the cardinality of the intersection
of the fiber
![]() $\Pi ^{-1}(\vec x)$
with the set we care about. In light of Corollary 3.3, we get in this way that
$\Pi ^{-1}(\vec x)$
with the set we care about. In light of Corollary 3.3, we get in this way that
 $$ \begin{align*} \operatorname{\mathrm{vol}}(\mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}(\vec L,h)) &=\int_{\Sigma^{\operatorname{\mathrm{\mathbf{vert}}}}} \left\vert{\mathbf{G}}_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}^X(\vec L,h)\right\vert\, d\vec x\\[4pt] &\stackrel{\text{Cor. 3.3}}\sim\int_{\Sigma^{\operatorname{\mathrm{\mathbf{vert}}}}} \varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-3\chi(X)}}\, d\vec x\\[4pt] &=\varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-3\chi(X)}}\operatorname{\mathrm{vol}}(\Sigma)^{V}\\[4pt] &=\varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{vol}}(\mathcal G_{\varepsilon-\operatorname{\mathrm{crit}}}(\vec L,h)) &=\int_{\Sigma^{\operatorname{\mathrm{\mathbf{vert}}}}} \left\vert{\mathbf{G}}_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}^X(\vec L,h)\right\vert\, d\vec x\\[4pt] &\stackrel{\text{Cor. 3.3}}\sim\int_{\Sigma^{\operatorname{\mathrm{\mathbf{vert}}}}} \varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-3\chi(X)}}\, d\vec x\\[4pt] &=\varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-3\chi(X)}}\operatorname{\mathrm{vol}}(\Sigma)^{V}\\[4pt] &=\varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}, \end{align*} $$
where we have used that
![]() $V=-2\chi (X)$
and where the asymptotics hold true when
$V=-2\chi (X)$
and where the asymptotics hold true when
![]() $\min _eL_e\to \infty $
. This means that whenever
$\min _eL_e\to \infty $
. This means that whenever
![]() $\min _eL_e$
is large enough we have
$\min _eL_e$
is large enough we have
 $$ \begin{align*} (1-\delta)\cdot\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h-4\varepsilon}-1)^{-3\chi(X)}\cdot e^{\sum_{e\in\operatorname{\mathrm{\mathbf{edge}}}}(L_e+2\varepsilon)}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}&<\vert{\mathbf{G}}(\vec L, h)\vert,\\[7pt] (1+\delta)\cdot\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h+4\varepsilon}-1)^{-3\chi(X)}\cdot e^{\sum_{e\in\operatorname{\mathrm{\mathbf{edge}}}}(L_e-2\varepsilon)}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}&>\vert{\mathbf{G}}(\vec L, h)\vert. \end{align*} $$
$$ \begin{align*} (1-\delta)\cdot\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h-4\varepsilon}-1)^{-3\chi(X)}\cdot e^{\sum_{e\in\operatorname{\mathrm{\mathbf{edge}}}}(L_e+2\varepsilon)}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}&<\vert{\mathbf{G}}(\vec L, h)\vert,\\[7pt] (1+\delta)\cdot\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h+4\varepsilon}-1)^{-3\chi(X)}\cdot e^{\sum_{e\in\operatorname{\mathrm{\mathbf{edge}}}}(L_e-2\varepsilon)}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}&>\vert{\mathbf{G}}(\vec L, h)\vert. \end{align*} $$
Since this is true for all
![]() $\varepsilon>0$
, we get that
$\varepsilon>0$
, we get that
 $$ \begin{align*}(1-\delta)\cdot\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h}-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}\leqslant\vert{\mathbf{G}}(\vec L, h)\vert\end{align*} $$
$$ \begin{align*}(1-\delta)\cdot\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h}-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}\leqslant\vert{\mathbf{G}}(\vec L, h)\vert\end{align*} $$
 $$ \begin{align*}(1+\delta)\cdot\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h}-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}\geqslant\vert{\mathbf{G}}(\vec L, h)\vert\end{align*} $$
$$ \begin{align*}(1+\delta)\cdot\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h}-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}\geqslant\vert{\mathbf{G}}(\vec L, h)\vert\end{align*} $$
and hence, since for all
![]() $\delta>0$
we can choose L large enough so that the above bounds hold, we have
$\delta>0$
we can choose L large enough so that the above bounds hold, we have
 $$ \begin{align*}\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h}-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}\sim\vert{\mathbf{G}}(\vec L, h)\vert\end{align*} $$
$$ \begin{align*}\frac {2^{4\chi(X)}}{3^{3\chi(X)}}\cdot\pi^{\chi(X)}\cdot \frac{(e^{h}-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-\chi(X)}}\sim\vert{\mathbf{G}}(\vec L, h)\vert\end{align*} $$
as we wanted to prove.
Armed with Lemma 4.1 and Proposition 4.2, we can now prove the theorem:
Proof of Theorem 1.3
Let
![]() $h>0$
be small, and for
$h>0$
be small, and for
![]() $\vec n\in \mathbb {N}^{\operatorname {\mathrm {\mathbf {edge}}}}$
consider, with the same notation as in Equation (4.2), the set
$\vec n\in \mathbb {N}^{\operatorname {\mathrm {\mathbf {edge}}}}$
consider, with the same notation as in Equation (4.2), the set
![]() ${\mathbf {G}}(h\cdot \vec n,h)$
. Setting
${\mathbf {G}}(h\cdot \vec n,h)$
. Setting
where
![]() $\Vert \vec n\Vert =\sum _e n_e$
, note that
$\Vert \vec n\Vert =\sum _e n_e$
, note that
 $$ \begin{align} \sum_{\vec n\in\Delta(N-E)}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\leqslant\vert{\mathbf{G}}(h\cdot N)\vert\leqslant\sum_{\vec n\in\Delta(N)}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert, \end{align} $$
$$ \begin{align} \sum_{\vec n\in\Delta(N-E)}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\leqslant\vert{\mathbf{G}}(h\cdot N)\vert\leqslant\sum_{\vec n\in\Delta(N)}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert, \end{align} $$
where
![]() ${\mathbf {G}}(h\cdot N)={\mathbf {G}}^X(h\cdot N)$
is as in Equation (4.1) and where, once again,
${\mathbf {G}}(h\cdot N)={\mathbf {G}}^X(h\cdot N)$
is as in Equation (4.1) and where, once again,
![]() $E=\vert \operatorname {\mathrm {\mathbf {edge}}}\vert $
is the number of edges of the graph X. Finally, write
$E=\vert \operatorname {\mathrm {\mathbf {edge}}}\vert $
is the number of edges of the graph X. Finally, write
Proposition 4.2 now reads as
where the asymptotic holds for fixed h when
![]() $\min \vec n_e\to \infty $
. This means that for all h and
$\min \vec n_e\to \infty $
. This means that for all h and
![]() $\delta $
there is
$\delta $
there is
![]() $n(h,\delta )$
with
$n(h,\delta )$
with
and
for all
![]() $\vec n$
with
$\vec n$
with
![]() $\min \vec n_e\geqslant n(h,\delta )$
. It follows thus from the left side of Equation (4.4) that
$\min \vec n_e\geqslant n(h,\delta )$
. It follows thus from the left side of Equation (4.4) that
 $$ \begin{align*} \vert{\mathbf{G}}(h\cdot N)\vert &\geqslant\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N-E),\\ \min\vec n_e\geqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\\ &> (\kappa-\delta)(e^h-1)^{-3\chi(X)}\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N-E),\\ \min\vec n_e\geqslant n(h,\delta)\end{array}}e^{h\cdot\Vert\vec n\Vert}\\ &= (\kappa-\delta)(e^h-1)^{-3\chi(X)}\sum_{K=0}^{N-E}P(K)\cdot e^{h\cdot K}, \end{align*} $$
$$ \begin{align*} \vert{\mathbf{G}}(h\cdot N)\vert &\geqslant\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N-E),\\ \min\vec n_e\geqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\\ &> (\kappa-\delta)(e^h-1)^{-3\chi(X)}\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N-E),\\ \min\vec n_e\geqslant n(h,\delta)\end{array}}e^{h\cdot\Vert\vec n\Vert}\\ &= (\kappa-\delta)(e^h-1)^{-3\chi(X)}\sum_{K=0}^{N-E}P(K)\cdot e^{h\cdot K}, \end{align*} $$
where
![]() $P(K)$
is the number of those
$P(K)$
is the number of those
![]() $\vec n\in \mathbb N^{\operatorname {\mathrm {\mathbf {edge}}}}$
with
$\vec n\in \mathbb N^{\operatorname {\mathrm {\mathbf {edge}}}}$
with
![]() $\Vert n\Vert =K$
and
$\Vert n\Vert =K$
and
![]() $\min \vec n_e\geqslant n(h,\delta )$
. As K tends to
$\min \vec n_e\geqslant n(h,\delta )$
. As K tends to
![]() $\infty $
, we have
$\infty $
, we have
![]() $P(K)\sim \frac 1{(E-1)!}K^{E-1}$
. Taking into account that
$P(K)\sim \frac 1{(E-1)!}K^{E-1}$
. Taking into account that
![]() $E=-3\chi (X)$
, we get that for all N large enough we have
$E=-3\chi (X)$
, we get that for all N large enough we have
 $$ \begin{align*} \vert{\mathbf{G}}(h\cdot N)\vert &\succeq\frac{\kappa-\delta}{(-3\chi(X)-1)!}(e^h-1)^{-3\chi(X)}\sum_{K=0}^{N-E}K^{-3\chi(X)-1}\cdot e^{h\cdot K}\\ &=\frac{\kappa-\delta}{(-3\chi(X)-1)!}\left(\frac{e^h-1}h\right)^{-3\chi(X)}\sum_{K=0}^{N-E}(hK)^{-3\chi(X)-1}\cdot e^{h\cdot K}\cdot h\\ &\succeq \frac{\kappa-\delta}{(-3\chi(X)-1)!}\left(\frac{e^h-1}h\right)^{-3\chi(X)}\int_0^{(N-E)h} x^{-3\chi(X)-1}e^xdx, \end{align*} $$
$$ \begin{align*} \vert{\mathbf{G}}(h\cdot N)\vert &\succeq\frac{\kappa-\delta}{(-3\chi(X)-1)!}(e^h-1)^{-3\chi(X)}\sum_{K=0}^{N-E}K^{-3\chi(X)-1}\cdot e^{h\cdot K}\\ &=\frac{\kappa-\delta}{(-3\chi(X)-1)!}\left(\frac{e^h-1}h\right)^{-3\chi(X)}\sum_{K=0}^{N-E}(hK)^{-3\chi(X)-1}\cdot e^{h\cdot K}\cdot h\\ &\succeq \frac{\kappa-\delta}{(-3\chi(X)-1)!}\left(\frac{e^h-1}h\right)^{-3\chi(X)}\int_0^{(N-E)h} x^{-3\chi(X)-1}e^xdx, \end{align*} $$
where the symbol
![]() $\succeq $
means that asymptotically the ratio between the left side and the right side is at least
$\succeq $
means that asymptotically the ratio between the left side and the right side is at least
![]() $1$
. When
$1$
. When
![]() $N\to \infty $
then the value of the integral is asymptotic to
$N\to \infty $
then the value of the integral is asymptotic to
![]() $((N-E)\cdot h)^{-3\chi (X)-1}\cdot e^{(N-E)h}$
, and this means that for all N large enough we have
$((N-E)\cdot h)^{-3\chi (X)-1}\cdot e^{(N-E)h}$
, and this means that for all N large enough we have
 $$ \begin{align*}\vert{\mathbf{G}}(h\cdot N)\vert\succeq \frac{\kappa-\delta}{(-3\chi(X)-1)!}\left(\frac{e^h-1}h\right)^{-3\chi(X)}(Nh-Eh)^{-3\chi(X)-1}\cdot e^{Nh-Eh}.\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}(h\cdot N)\vert\succeq \frac{\kappa-\delta}{(-3\chi(X)-1)!}\left(\frac{e^h-1}h\right)^{-3\chi(X)}(Nh-Eh)^{-3\chi(X)-1}\cdot e^{Nh-Eh}.\end{align*} $$
This being true for all
![]() $\delta $
and all h and replacing
$\delta $
and all h and replacing
![]() $Nh$
by L, we have
$Nh$
by L, we have
as
![]() $L\to \infty $
. In other words, we have established the desired asymptotic lower bound.
$L\to \infty $
. In other words, we have established the desired asymptotic lower bound.
Starting with the upper bound we get, again for h positive and small, from the right side in Equation (4.4) that
 $$ \begin{align*}\vert{\mathbf{G}}(h\cdot N)\vert\leqslant\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\geqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert+\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\leqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert.\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}(h\cdot N)\vert\leqslant\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\geqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert+\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\leqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert.\end{align*} $$
The same calculation as above yields that
 $$ \begin{align} \begin{aligned} \sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\geqslant n(h,\delta)\end{array}}&\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\preceq \\ &\preceq\frac{\kappa+\delta}{(-3\chi(X)-1)!}\left(\frac{e^h-1}h\right)^{-3\chi(X)}(h(N+E))^{-3\chi(X)-1}\cdot e^{h(N + E)} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\geqslant n(h,\delta)\end{array}}&\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\preceq \\ &\preceq\frac{\kappa+\delta}{(-3\chi(X)-1)!}\left(\frac{e^h-1}h\right)^{-3\chi(X)}(h(N+E))^{-3\chi(X)-1}\cdot e^{h(N + E)} \end{aligned} \end{align} $$
as
![]() $N\to \infty $
. On the other hand, we get from Lemma 4.1 that there is
$N\to \infty $
. On the other hand, we get from Lemma 4.1 that there is
![]() $C>0$
with
$C>0$
with
![]() $\vert {\mathbf {G}}(h\cdot \vec n,h)\vert \leqslant C\cdot e^{h\cdot \vert \vec n\vert }$
for all
$\vert {\mathbf {G}}(h\cdot \vec n,h)\vert \leqslant C\cdot e^{h\cdot \vert \vec n\vert }$
for all
![]() $\vec n$
. This means thus that
$\vec n$
. This means thus that
 $$ \begin{align*}\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\leqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\leqslant C\cdot\sum_{K=1}^NQ(K)\cdot e^{h\cdot K},\end{align*} $$
$$ \begin{align*}\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\leqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\leqslant C\cdot\sum_{K=1}^NQ(K)\cdot e^{h\cdot K},\end{align*} $$
where
![]() $Q(K)$
is the number of those
$Q(K)$
is the number of those
![]() $\vec n\in \mathbb N^{\operatorname {\mathrm {\mathbf {edge}}}}$
with
$\vec n\in \mathbb N^{\operatorname {\mathrm {\mathbf {edge}}}}$
with
![]() $\min \vec n_e< n(h,\delta )$
and
$\min \vec n_e< n(h,\delta )$
and
![]() $\vert \vec n\vert =K$
. When
$\vert \vec n\vert =K$
. When
![]() $K\to \infty $
the function
$K\to \infty $
the function
![]() $Q(K)$
is asymptotic to
$Q(K)$
is asymptotic to
![]() $C'\cdot K^{E-2}$
for some positive constant
$C'\cdot K^{E-2}$
for some positive constant
![]() $C'$
, meaning that we have
$C'$
, meaning that we have
 $$ \begin{align*}\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\leqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\leqslant \frac{(1+\delta)\cdot C\cdot C'}{h^{E-1}}\cdot\sum_{K=1}^N h\cdot(hK)^{E-2}\cdot e^{h\cdot K}\end{align*} $$
$$ \begin{align*}\sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\leqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\leqslant \frac{(1+\delta)\cdot C\cdot C'}{h^{E-1}}\cdot\sum_{K=1}^N h\cdot(hK)^{E-2}\cdot e^{h\cdot K}\end{align*} $$
for all L large enough. A similar estimation as the one above yields thus that there is another positive constant
![]() $C"$
with
$C"$
with
 $$ \begin{align} \sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\leqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\leqslant C"\cdot (N\cdot h)^{-3\chi(X)-2}\cdot e^{N\cdot H}. \end{align} $$
$$ \begin{align} \sum_{\tiny\begin{array}{c}\vec n\in\Delta(N),\\ \min\vec n_e\leqslant n(h,\delta)\end{array}}\vert{\mathbf{G}}(h\cdot\vec n,h)\vert\leqslant C"\cdot (N\cdot h)^{-3\chi(X)-2}\cdot e^{N\cdot H}. \end{align} $$
The quantity in the right-hand side of Equation (4.6) is negligible when compared to the right-hand side of Equation (4.5), and this means that we have
 $$ \begin{align*}\vert{\mathbf{G}}(h\cdot N)\vert\preceq \frac{\kappa+2\delta}{(-3\chi(X)-1)!}\left(\frac{e^h-1}h\right)^{-3\chi(X)}(h(N+E))^{-3\chi(X)-1}\cdot e^{h(N+E)}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}(h\cdot N)\vert\preceq \frac{\kappa+2\delta}{(-3\chi(X)-1)!}\left(\frac{e^h-1}h\right)^{-3\chi(X)}(h(N+E))^{-3\chi(X)-1}\cdot e^{h(N+E)}\end{align*} $$
for all large N. Since this holds true for all
![]() $\delta $
and all h, replacing
$\delta $
and all h, replacing
![]() $hN$
by L we deduce that
$hN$
by L we deduce that
Having now also established the upper asymptotic bound, we are done with the proof of the theorem.
Before moving on to other matters, we include an observation that we will use later on. The basic strategy of the proof of Theorem 1.3 was to decompose the problem of counting all critical realizations of at most some given length into the problem of counting those whose edge lengths are in a given box and then adding over all boxes. For most boxes, Proposition 4.2 gives a pretty precise estimation for the number of critical realizations in the box, and from Lemma 4.1 we get an upper bound for all boxes. We used these two to get the desired upper bound in the theorem, deducing that we could ignore the boxes where Proposition 4.2 does not apply. A very similar argument implies that the set of critical realizations where some edge is shorter than
![]() $\ell _0$
is also negligible. We state this observation as a lemma:
$\ell _0$
is also negligible. We state this observation as a lemma:
Lemma 4.3. For all
![]() $\ell $
, all but a negligible set of critical realizations are
$\ell $
, all but a negligible set of critical realizations are
![]() $\ell $
-long.
$\ell $
-long.
It is probably clear from the context what negligible means here, but to be precise, we mean that the set is negligible inside the set of all critical realizations in the sense of Equation (7.2) below.
5 Fillings
Let
![]() $S_g$
be a compact, connected and oriented surface of genus g and with one boundary component. Below, we will be interested in continuous maps
$S_g$
be a compact, connected and oriented surface of genus g and with one boundary component. Below, we will be interested in continuous maps
which send
![]() $\partial S_g$
to a closed geodesic
$\partial S_g$
to a closed geodesic
![]() $\gamma =\beta (S_g)$
. We will refer to such a map as a filling of genus g of
$\gamma =\beta (S_g)$
. We will refer to such a map as a filling of genus g of
![]() $\gamma $
, a genus g filling of
$\gamma $
, a genus g filling of
![]() $\gamma $
, or just simply as a filling of
$\gamma $
, or just simply as a filling of
![]() $\gamma $
when the genus g is either undetermined or understood from the context. The genus of a curve
$\gamma $
when the genus g is either undetermined or understood from the context. The genus of a curve
![]() $\gamma \subset \Sigma $
is the infimum of all g’s for which there is a genus g filling Equation (5.1) with
$\gamma \subset \Sigma $
is the infimum of all g’s for which there is a genus g filling Equation (5.1) with
![]() $\gamma =\beta (\partial S_g)$
. Note that the genus of a curve is infinite unless
$\gamma =\beta (\partial S_g)$
. Note that the genus of a curve is infinite unless
![]() $\gamma $
is homologically trivial, that is, unless
$\gamma $
is homologically trivial, that is, unless
![]() $\gamma $
is represented by elements in the commutator subgroup of
$\gamma $
is represented by elements in the commutator subgroup of
![]() $\pi _1(\Sigma )$
. Indeed, as an element of
$\pi _1(\Sigma )$
. Indeed, as an element of
![]() $\pi _1(S_g)$
the boundary
$\pi _1(S_g)$
the boundary
![]() $\partial S_g$
is a product of g commutators. It follows that if a curve
$\partial S_g$
is a product of g commutators. It follows that if a curve
![]() $\gamma $
in
$\gamma $
in
![]() $\Sigma $
has genus g, then it is, when considered as an element in
$\Sigma $
has genus g, then it is, when considered as an element in
![]() $\pi _1(\Sigma )$
, a product of g commutators. Conversely, if
$\pi _1(\Sigma )$
, a product of g commutators. Conversely, if
![]() $\gamma $
is a product of g commutators, then there is a map as in Equation (5.1) with
$\gamma $
is a product of g commutators, then there is a map as in Equation (5.1) with
![]() $S_g$
of genus g. In a nutshell, what we have is that the genus and the commutator length of
$S_g$
of genus g. In a nutshell, what we have is that the genus and the commutator length of
![]() $\gamma $
agree. We record this fact for ease of reference:
$\gamma $
agree. We record this fact for ease of reference:
Lemma 5.1. The genus of a curve agrees with its commutator length.
Continuing with the same notation and terminology, suppose that a curve
![]() $\gamma $
in
$\gamma $
in
![]() $\Sigma $
has genus g. We then refer to any
$\Sigma $
has genus g. We then refer to any
![]() $\beta :S\to \Sigma $
as in Equation (5.1) with S of genus g as a minimal genus filling. Minimal genus fillings have very nice topological properties. Indeed, suppose that
$\beta :S\to \Sigma $
as in Equation (5.1) with S of genus g as a minimal genus filling. Minimal genus fillings have very nice topological properties. Indeed, suppose that
![]() $\beta :S_g\to \Sigma $
is a filling as in Equation (5.1) and suppose that there is an essential simple curve
$\beta :S_g\to \Sigma $
is a filling as in Equation (5.1) and suppose that there is an essential simple curve
![]() $m\subset S_g$
with
$m\subset S_g$
with
![]() $\beta (m)$
homotopically trivial. Then, performing surgery on the surface
$\beta (m)$
homotopically trivial. Then, performing surgery on the surface
![]() $S_g$
and the map
$S_g$
and the map
![]() $\beta $
we get a smaller genus filling
$\beta $
we get a smaller genus filling
![]() $\beta ':S_{g'}\to \Sigma $
with
$\beta ':S_{g'}\to \Sigma $
with
![]() $\beta '(\partial S_{g'})=\beta (\partial S_g)$
and
$\beta '(\partial S_{g'})=\beta (\partial S_g)$
and
![]() $g'<g$
. It follows that if
$g'<g$
. It follows that if
![]() $\beta :S_g\to \Sigma $
is a minimal genus filling for
$\beta :S_g\to \Sigma $
is a minimal genus filling for
![]() $\gamma =\beta (\partial S_g)$
, then
$\gamma =\beta (\partial S_g)$
, then
![]() $\beta $
is geometrically incompressible in the sense that there are no elements in
$\beta $
is geometrically incompressible in the sense that there are no elements in
![]() $\ker (\beta _*:\pi _1(S_g)\to \pi _1(\Sigma ))$
which are represented by simple curves. We record this fact:
$\ker (\beta _*:\pi _1(S_g)\to \pi _1(\Sigma ))$
which are represented by simple curves. We record this fact:
Lemma 5.2. Minimal genus fillings are geometrically incompressible.
From now on, we will be working exclusively with minimal genus fillings and the reader can safely add the words ‘minimal genus’ every time they see the word ‘filling’.
We will not be that much interested in individual fillings, but rather in homotopy classes of fillings. In particular, we will allow ourselves to select particularly nice fillings. More precisely, we will be working with hyperbolic fillings, by which we will understand a particular kind of pleated surface. We remind the reader that according to Thurston [Reference Thurston18] (see also [Reference Canary, Epstein and Green5]) a pleated surface is a map from a hyperbolic surface to a hyperbolic manifold with the property that every point in the domain is contained in a geodesic segment which gets mapped isometrically.
Definition. A filling
![]() $\beta :S\to \Sigma $
is hyperbolic if S is endowed with a hyperbolic metric with geodesic boundary and if the map
$\beta :S\to \Sigma $
is hyperbolic if S is endowed with a hyperbolic metric with geodesic boundary and if the map
![]() $\beta $
is such that every
$\beta $
is such that every
![]() $x\in S$
is contained in the interior of a geodesic arc I such that
$x\in S$
is contained in the interior of a geodesic arc I such that
![]() $\beta $
maps I isometrically to a geodesic arc in
$\beta $
maps I isometrically to a geodesic arc in
![]() $\Sigma $
.
$\Sigma $
.
An important observation is that if
![]() $\beta :S\to \Sigma $
is a hyperbolic filling, if
$\beta :S\to \Sigma $
is a hyperbolic filling, if
![]() $x\in \partial S$
and if
$x\in \partial S$
and if
![]() $I\subset S$
is a geodesic segment with x in its interior, then
$I\subset S$
is a geodesic segment with x in its interior, then
![]() $I\subset \partial S$
. It follows that hyperbolic fillings map the boundary isometrically.
$I\subset \partial S$
. It follows that hyperbolic fillings map the boundary isometrically.
Lemma 5.3. The restriction of any hyperbolic filling
![]() $\beta :S\to \Sigma $
to
$\beta :S\to \Sigma $
to
![]() $\partial S$
is geodesic.
$\partial S$
is geodesic.
We should not delay making sure that hyperbolic fillings exist:
Proposition 5.4. Every minimal genus filling is homotopic to a hyperbolic filling.
To prove this proposition, we will first show that if
![]() $\beta :S\to \Sigma $
is any filling and if the surface S admits a triangulation with certain properties, then
$\beta :S\to \Sigma $
is any filling and if the surface S admits a triangulation with certain properties, then
![]() $\beta $
is homotopic to a hyperbolic filling. For lack of a better name, we will say that a triangulation
$\beta $
is homotopic to a hyperbolic filling. For lack of a better name, we will say that a triangulation
![]() $\mathcal T$
of S is useful if it satisfies the following three conditions:
$\mathcal T$
of S is useful if it satisfies the following three conditions:
-
(i)
 $\mathcal T$
has exactly
$\mathcal T$
has exactly
 $g+1$
vertices
$g+1$
vertices
 $v_0,\dots ,v_g$
, with
$v_0,\dots ,v_g$
, with
 $v_0\in \partial S$
and the others in the interior of S.
$v_0\in \partial S$
and the others in the interior of S. -
(ii) There is a collection of edges
 $I_0,\dots ,I_g$
of
$I_0,\dots ,I_g$
of
 $\mathcal T$
such that both endpoints of
$\mathcal T$
such that both endpoints of
 $I_i$
are attached to
$I_i$
are attached to
 $v_i$
for all
$v_i$
for all
 $i=0,\dots ,g$
. Moreover,
$i=0,\dots ,g$
. Moreover,
 $I_0=\partial S$
.
$I_0=\partial S$
.
These two conditions are evidently pretty soft. It is the condition we will state next what makes useful triangulations actually useful. We first need a bit of notation: If I is any edge of
![]() $\mathcal T$
other than
$\mathcal T$
other than
![]() $I_0,\dots ,I_g$
, then let
$I_0,\dots ,I_g$
, then let
![]() $G_I$
be the connected component of
$G_I$
be the connected component of
![]() $I\cup I_0\cup \dots \cup I_g$
containing I.
$I\cup I_0\cup \dots \cup I_g$
containing I.
-
(iii) For any edge I other than
 $I_0,\dots ,I_g$
, we have that the image under
$I_0,\dots ,I_g$
, we have that the image under
 $\beta _*:\pi _1(G_I)\to \pi _1(\Sigma )$
is not abelian.
$\beta _*:\pi _1(G_I)\to \pi _1(\Sigma )$
is not abelian.
Note that
![]() $\pi _1(G_I)$
is a a free group of rank
$\pi _1(G_I)$
is a a free group of rank
![]() $2$
. This means that its image
$2$
. This means that its image
![]() $\beta _*(\pi _1(G_I)))$
has at most rank
$\beta _*(\pi _1(G_I)))$
has at most rank
![]() $2$
. Since we are assuming that it is not abelian, we actually get that it is a rank
$2$
. Since we are assuming that it is not abelian, we actually get that it is a rank
![]() $2$
free group. Free groups being Hopfian we deduce that
$2$
free group. Free groups being Hopfian we deduce that
![]() $\beta _*:\pi _1(G_I)\to \pi _1(\Sigma )$
is an isomorphism onto its image. In other words,
$\beta _*:\pi _1(G_I)\to \pi _1(\Sigma )$
is an isomorphism onto its image. In other words,
![]() $\beta _*$
is injective on
$\beta _*$
is injective on
![]() $\pi _1(G_I)$
.
$\pi _1(G_I)$
.
The following result makes clear why we care about such triangulations:
Lemma 5.5. If the domain S of a filling
![]() $\beta :S\to \Sigma $
admits a useful triangulation
$\beta :S\to \Sigma $
admits a useful triangulation
![]() $\mathcal T$
, then
$\mathcal T$
, then
![]() $\beta $
is homotopic to a hyperbolic filling.
$\beta $
is homotopic to a hyperbolic filling.
Proof. As we just discussed, our conditions imply that
![]() $\beta _*$
is injective on
$\beta _*$
is injective on
![]() $\pi _1(G_I)$
for all I. This implies in particular that each one of the exceptional edges
$\pi _1(G_I)$
for all I. This implies in particular that each one of the exceptional edges
![]() $I_0,\dots ,I_g$
of
$I_0,\dots ,I_g$
of
![]() $\mathcal T$
closes up to a simple closed curve
$\mathcal T$
closes up to a simple closed curve
![]() $\gamma _0,\dots ,\gamma _g$
in S which is mapped to a homotopically essential curve. This in turn means that the images of
$\gamma _0,\dots ,\gamma _g$
in S which is mapped to a homotopically essential curve. This in turn means that the images of
![]() $\gamma _0,\dots ,\gamma _g$
are homotopic to nontrivial closed geodesics. Since all these
$\gamma _0,\dots ,\gamma _g$
are homotopic to nontrivial closed geodesics. Since all these
![]() $g+1$
curves are mutually disjoint, we can then homotope
$g+1$
curves are mutually disjoint, we can then homotope
![]() $\beta $
so that
$\beta $
so that
![]() $\beta (\gamma _i)$
is a closed geodesic
$\beta (\gamma _i)$
is a closed geodesic
![]() $\hat \gamma _i$
for all i.
$\hat \gamma _i$
for all i.
Let now I be one of the remaining edges of
![]() $\mathcal T$
, let
$\mathcal T$
, let
![]() $v_i$
and
$v_i$
and
![]() $v_j$
be its (possibly equal) endpoints and note that
$v_j$
be its (possibly equal) endpoints and note that
![]() $G_I=\gamma _i\cup I\cup \gamma _j$
. Since
$G_I=\gamma _i\cup I\cup \gamma _j$
. Since
![]() $\beta _*$
is injective on
$\beta _*$
is injective on
![]() $\pi _1(G_I,v_i)$
, we know that the elements
$\pi _1(G_I,v_i)$
, we know that the elements
![]() $\beta _*(\gamma _i)$
and
$\beta _*(\gamma _i)$
and
![]() $\beta _*(I*\gamma _j*I^{-1})$
do not commute and hence have distinct fixed points in
$\beta _*(I*\gamma _j*I^{-1})$
do not commute and hence have distinct fixed points in
![]() $\partial _{\infty }{\mathbb {H}}^2$
. This seemingly weak property is all we need to run the standard construction of pleated surfaces by spinning the edges of the triangulation over the geodesics
$\partial _{\infty }{\mathbb {H}}^2$
. This seemingly weak property is all we need to run the standard construction of pleated surfaces by spinning the edges of the triangulation over the geodesics
![]() $\hat \gamma _i$
– compare with the proof of Theorem I.5.3.6 in [Reference Canary, Epstein and Green5].
$\hat \gamma _i$
– compare with the proof of Theorem I.5.3.6 in [Reference Canary, Epstein and Green5].
We can now prove Proposition 5.4.
Proof. Let
![]() $\beta :S\to \Sigma $
be a minimal genus filling of a geodesic
$\beta :S\to \Sigma $
be a minimal genus filling of a geodesic
![]() $\gamma =\beta (\partial S)$
, say of genus g. In light of Lemma 5.5, to prove that
$\gamma =\beta (\partial S)$
, say of genus g. In light of Lemma 5.5, to prove that
![]() $\beta $
is homotopic to a hyperbolic filling it suffices to show that S admits a useful triangulation. Let us start by taking g disjoint compact one-holed tori
$\beta $
is homotopic to a hyperbolic filling it suffices to show that S admits a useful triangulation. Let us start by taking g disjoint compact one-holed tori
![]() $T_1,\ldots ,T_g\subset S$
. We claim that the restriction of
$T_1,\ldots ,T_g\subset S$
. We claim that the restriction of
![]() $\beta $
to each
$\beta $
to each
![]() $T_i$
is
$T_i$
is
![]() $\pi _1$
-injective. Indeed, since we know that
$\pi _1$
-injective. Indeed, since we know that
![]() $\beta $
is geometrically incompressible we deduce that
$\beta $
is geometrically incompressible we deduce that
![]() $\partial T_i$
is not in the kernel of the induced homomorphism at the fundamental group level. It follows that the image of
$\partial T_i$
is not in the kernel of the induced homomorphism at the fundamental group level. It follows that the image of
![]() $\beta _*(\pi _1(T_i))$
cannot be abelian. Now, this implies that
$\beta _*(\pi _1(T_i))$
cannot be abelian. Now, this implies that
![]() $\beta _*(\pi _1(T_i))$
is free and evidently of rank 2. Hence, again since free groups are Hopfian, we get that the restriction of
$\beta _*(\pi _1(T_i))$
is free and evidently of rank 2. Hence, again since free groups are Hopfian, we get that the restriction of
![]() $\beta _*$
to
$\beta _*$
to
![]() $\pi _1(T_i)$
is injective for all i.
$\pi _1(T_i)$
is injective for all i.

Figure 2 Construction of the useful triangulation in Proposition 5.4: The
![]() $2g+1$
holed sphere obtained from S by cutting along
$2g+1$
holed sphere obtained from S by cutting along
![]() $\gamma _1, \ldots , \gamma _g$
. The vertices
$\gamma _1, \ldots , \gamma _g$
. The vertices
![]() $v_1,\dots ,v_g$
and their copies
$v_1,\dots ,v_g$
and their copies
![]() $v_1',\dots ,v_g'$
are joined by the sequence of edges
$v_1',\dots ,v_g'$
are joined by the sequence of edges
![]() $[v_1,v_2],[v_2,v_3],\dots ,[v_g,v_1'],[v_1',v_2'],\dots ,[v_{g-1}',v_g']$
. To complete the triangulation, add as many edges as needed joining
$[v_1,v_2],[v_2,v_3],\dots ,[v_g,v_1'],[v_1',v_2'],\dots ,[v_{g-1}',v_g']$
. To complete the triangulation, add as many edges as needed joining
![]() $v_0$
to the other vertices.
$v_0$
to the other vertices.
Now, why do we care about that? Knowing that the restriction of
![]() $\beta _*$
to
$\beta _*$
to
![]() $\pi _1(T_i)$
is injective for any i implies that when the images under
$\pi _1(T_i)$
is injective for any i implies that when the images under
![]() $\beta $
of the nonboundary parallel simple closed curves in
$\beta $
of the nonboundary parallel simple closed curves in
![]() $T_i$
determine infinitely many conjugacy classes of maximal abelian subgroups of
$T_i$
determine infinitely many conjugacy classes of maximal abelian subgroups of
![]() $\pi _1(\Sigma )$
. We can thus choose for each
$\pi _1(\Sigma )$
. We can thus choose for each
![]() $i=1,\dots ,g$
a nonboundary parallel simple closed curve
$i=1,\dots ,g$
a nonboundary parallel simple closed curve
![]() $\gamma _i\subset T_i$
such that if we also set
$\gamma _i\subset T_i$
such that if we also set
![]() $\gamma _0=\partial S$
, then we have that
$\gamma _0=\partial S$
, then we have that
-
(*) no two of the the maximal abelian subgroups of
 $\pi _1(\Sigma )$
containing
$\pi _1(\Sigma )$
containing
 $\beta _*(\gamma _0),\dots ,\beta _*(\gamma _g)$
are conjugate to each other.
$\beta _*(\gamma _0),\dots ,\beta _*(\gamma _g)$
are conjugate to each other.
Choosing now a vertex
![]() $v_i$
in each one of the curves
$v_i$
in each one of the curves
![]() $\gamma _i$
, we get from
$\gamma _i$
, we get from
![]() $(*)$
that if I is any simple path joining
$(*)$
that if I is any simple path joining
![]() $v_i$
to
$v_i$
to
![]() $v_j$
for
$v_j$
for
![]() $i\neq j$
, then the image of
$i\neq j$
, then the image of
![]() $\beta _*(\pi _1(\gamma _i\cup I\cup \gamma _j))$
is not abelian.
$\beta _*(\pi _1(\gamma _i\cup I\cup \gamma _j))$
is not abelian.
The upshot of all of this is that any triangulation
![]() $\mathcal T$
with
$\mathcal T$
with
-
1. vertex set
 $v_0,\dots ,v_g$
,
$v_0,\dots ,v_g$
, -
2. such that there are edges
 $I_0,\dots ,I_g$
incident on both ends to
$I_0,\dots ,I_g$
incident on both ends to
 $v_i$
and with image
$v_i$
and with image
 $\gamma _i$
, and
$\gamma _i$
, and -
3. such that all other edges connect distinct endpoints,
is useful. To see that such a triangulation exists, cut S along
![]() $\gamma _1,\dots ,\gamma _g$
. When doing this, we get a
$\gamma _1,\dots ,\gamma _g$
. When doing this, we get a
![]() $2g+1$
holed sphere
$2g+1$
holed sphere
![]() $\Delta $
and each vertex
$\Delta $
and each vertex
![]() $v_1,\dots ,v_g$
arises twice – denote the two copies of
$v_1,\dots ,v_g$
arises twice – denote the two copies of
![]() $v_i$
by
$v_i$
by
![]() $v_i$
and
$v_i$
and
![]() $v_i'$
as in Figure 2. Now, any triangulation of
$v_i'$
as in Figure 2. Now, any triangulation of
![]() $\Delta $
with vertex set
$\Delta $
with vertex set
![]() $v_0,v_1,v_1',v_2,v_2',\dots ,v_g,v_g'$
and which
$v_0,v_1,v_1',v_2,v_2',\dots ,v_g,v_g'$
and which
-
○ contains a sequence of
 $2g-1$
edges yielding a path and
$2g-1$
edges yielding a path and $$ \begin{align*}[v_1,v_2],[v_2,v_3],\dots,[v_g,v_1'],[v_1',v_2'],\dots,[v_{g-1}',v_g']\end{align*} $$
$$ \begin{align*}[v_1,v_2],[v_2,v_3],\dots,[v_g,v_1'],[v_1',v_2'],\dots,[v_{g-1}',v_g']\end{align*} $$
-
○ such that all other edges are incident to
 $v_0$
$v_0$
yields a triangulation of S satisfying (1)–(3) above. Having proved that there is a useful triangulation, we get from Lemma 5.5 that
![]() $\beta $
is homotopic to a hyperbolic filling, as we needed to prove.
$\beta $
is homotopic to a hyperbolic filling, as we needed to prove.
Being able to work with hyperbolic fillings is going to be key in the next section, where we bound the number of closed geodesics
![]() $\gamma $
in
$\gamma $
in
![]() $\Sigma $
with length
$\Sigma $
with length
![]() $\ell _{\Sigma }(\gamma )\leqslant L$
and which admit at least two homotopically distinct fillings.
$\ell _{\Sigma }(\gamma )\leqslant L$
and which admit at least two homotopically distinct fillings.
Definition. Two fillings
![]() $\beta _1:S_1\to \Sigma $
and
$\beta _1:S_1\to \Sigma $
and
![]() $\beta _2:S_2\to \Sigma $
are homotopic if there is a homeomorphism
$\beta _2:S_2\to \Sigma $
are homotopic if there is a homeomorphism
![]() $F:S_1\to S_2$
such that
$F:S_1\to S_2$
such that
![]() $\beta _1$
is homotopic to
$\beta _1$
is homotopic to
![]() $\beta _2\circ F$
.
$\beta _2\circ F$
.
Evidently, to bound the number of pairs of nonhomotopic fillings with the same boundary we will need some criterion to decide when two fillings are homotopic. To be able to state it note that if
![]() $\beta _1:S_1\to \Sigma $
and
$\beta _1:S_1\to \Sigma $
and
![]() $\beta _2:S_2\to \Sigma $
are homotopic hyperbolic fillings, then there is
$\beta _2:S_2\to \Sigma $
are homotopic hyperbolic fillings, then there is
a closed hyperbolic surface
![]() $S=S_1\cup _{\partial S_1=\partial S_2} S_2$
obtained by isometrically gluing
$S=S_1\cup _{\partial S_1=\partial S_2} S_2$
obtained by isometrically gluing
![]() $S_1$
and
$S_1$
and
![]() $S_2$
along the boundary, in such a way that there is a pleated surface
$S_2$
along the boundary, in such a way that there is a pleated surface
![]() $\Theta :S\to \Sigma $
with
$\Theta :S\to \Sigma $
with
![]() $\Theta \vert _{S_i}=\beta _i$
.
$\Theta \vert _{S_i}=\beta _i$
.
For lack of a better name, we refer to
![]() $\Theta :S\to \Sigma $
as the pseudo-double associated to
$\Theta :S\to \Sigma $
as the pseudo-double associated to
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
, and to the curve
$\beta _2$
, and to the curve
![]() $\partial S_1=\partial S_2\subset S$
as the crease of the pseudo-double.
$\partial S_1=\partial S_2\subset S$
as the crease of the pseudo-double.
Our criterion to decide if the two hyperbolic fillings
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
of a geodesic
$\beta _2$
of a geodesic
![]() $\gamma $
are homotopic will be in terms of the structure of the
$\gamma $
are homotopic will be in terms of the structure of the
![]() $\varepsilon _0$
thin part of the domain of the associated pseudo-double, where we choose once and forever the constant
$\varepsilon _0$
thin part of the domain of the associated pseudo-double, where we choose once and forever the constant
The following is our criterion.
Lemma 5.6. Suppose that
![]() $\beta _1:S_1\to \Sigma $
and
$\beta _1:S_1\to \Sigma $
and
![]() $\beta _2:S_2\to \Sigma $
are hyperbolic minimal genus fillings of genus g of a geodesic
$\beta _2:S_2\to \Sigma $
are hyperbolic minimal genus fillings of genus g of a geodesic
![]() $\gamma $
, let
$\gamma $
, let
![]() $\Theta :S\to \Sigma $
be the associated pseudo-double and denote its crease
$\Theta :S\to \Sigma $
be the associated pseudo-double and denote its crease
![]() $\partial S_1 = \partial S_2\subset S$
also by
$\partial S_1 = \partial S_2\subset S$
also by
![]() $\gamma $
. If
$\gamma $
. If
-
1. the
 $\varepsilon _0$
-thin part of S has
$\varepsilon _0$
-thin part of S has
 $6g-3$
connected components
$6g-3$
connected components
 $U_1,\dots ,U_{6g-3}$
, and
$U_1,\dots ,U_{6g-3}$
, and -
2.
 $\gamma $
traverses each
$\gamma $
traverses each
 $U_i$
exactly twice,
$U_i$
exactly twice,
then
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
are homotopic.
$\beta _2$
are homotopic.
Proof. Note that the surface S has genus
![]() $2g$
. In particular, the assumption on the
$2g$
. In particular, the assumption on the
![]() $\varepsilon _0$
-thin part implies that there is a pants decomposition P in S consisting of closed geodesics of length at most
$\varepsilon _0$
-thin part implies that there is a pants decomposition P in S consisting of closed geodesics of length at most
![]() $2\varepsilon _0$
. Now, since
$2\varepsilon _0$
. Now, since
![]() $\Theta $
is evidently 1-Lipschitz and since
$\Theta $
is evidently 1-Lipschitz and since
![]() $2\varepsilon _0$
is less than the systole of
$2\varepsilon _0$
is less than the systole of
![]() $\Sigma $
we get that each one of the components of P is mapped to a homotopically trivial curve. The assumption that the crease
$\Sigma $
we get that each one of the components of P is mapped to a homotopically trivial curve. The assumption that the crease
![]() $\gamma $
, a simple curve, intersects each component of the pants decomposition exactly twice implies that
$\gamma $
, a simple curve, intersects each component of the pants decomposition exactly twice implies that
![]() $\gamma $
cuts each pair of pants into two hexagons. Paint blue those in
$\gamma $
cuts each pair of pants into two hexagons. Paint blue those in
![]() $S_1$
and yellow those in
$S_1$
and yellow those in
![]() $S_2$
.
$S_2$
.
We can now construct a homotopy relative to the crease as follows. Each component of P consists of a blue arc and a yellow arc whose juxtaposition is homotopically trivial. This implies that we can homotope all yellow arcs, relative to their endpoints to the corresponding blue arcs. Extend this homotopy to a homotopy fixing
![]() $\partial S_2$
and defined on the whole of
$\partial S_2$
and defined on the whole of
![]() $S_2$
. Now, the boundary of each yellow hexagon is mapped to the boundary of each blue hexagon. Since
$S_2$
. Now, the boundary of each yellow hexagon is mapped to the boundary of each blue hexagon. Since
![]() $\Sigma $
has trivial
$\Sigma $
has trivial
![]() $\pi _2$
, we deduce that those two hexagons are homotopic. Proceeding like this with each hexagon, we get a homotopy relative to the crease of the yellow parts of S to the blue part. This is what we wanted to get.
$\pi _2$
, we deduce that those two hexagons are homotopic. Proceeding like this with each hexagon, we get a homotopy relative to the crease of the yellow parts of S to the blue part. This is what we wanted to get.
6 Bounding the number of multifillings
The goal of this section is to prove Theorem 1.4:
Theorem 1.4. For any g, there are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
genus g closed geodesics
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
genus g closed geodesics
![]() $\gamma $
in
$\gamma $
in
![]() $\Sigma $
with length
$\Sigma $
with length
![]() $\ell (\gamma )\leqslant L$
and with two nonhomotopic fillings
$\ell (\gamma )\leqslant L$
and with two nonhomotopic fillings
![]() $\beta _1:S_1\to \Sigma $
and
$\beta _1:S_1\to \Sigma $
and
![]() $\beta _2:S_2\to \Sigma $
of genus
$\beta _2:S_2\to \Sigma $
of genus
![]() $\leqslant g$
.
$\leqslant g$
.
The proof of Theorem 1.4 turns out to be kind of involved. We hope that the reader will not despair with all the weird objects and rather opaque statements they will find below.
Wired surfaces
Under a wired surface, we will understand a compact connected simplicial complex
![]() $\Delta $
obtained as follows: Start with a compact, possibly disconnected, triangulated surface
$\Delta $
obtained as follows: Start with a compact, possibly disconnected, triangulated surface
![]() $\operatorname {\mathrm {Surf}}(\Delta )$
and an, evidently finite, subset
$\operatorname {\mathrm {Surf}}(\Delta )$
and an, evidently finite, subset
![]() $P_{\Delta }$
of the set of vertices of the triangulation of
$P_{\Delta }$
of the set of vertices of the triangulation of
![]() $\operatorname {\mathrm {Surf}}(\Delta )$
such that every connected component of
$\operatorname {\mathrm {Surf}}(\Delta )$
such that every connected component of
![]() $\operatorname {\mathrm {Surf}}(\Delta )\setminus P_{\Delta }$
has negative Euler characteristic. We think of the elements in
$\operatorname {\mathrm {Surf}}(\Delta )\setminus P_{\Delta }$
has negative Euler characteristic. We think of the elements in
![]() $P_{\Delta }$
as plugs. Now, attach 1-simplices, to which we will refer as wires, by attaching both endpoints to plugs and do so in such a way that each plug arises exactly once as the end-point of a wire – we denote the set of wires by
$P_{\Delta }$
as plugs. Now, attach 1-simplices, to which we will refer as wires, by attaching both endpoints to plugs and do so in such a way that each plug arises exactly once as the end-point of a wire – we denote the set of wires by
![]() $\operatorname {\mathrm {\mathbf {wire}}}(\Delta )$
. A wired surface
$\operatorname {\mathrm {\mathbf {wire}}}(\Delta )$
. A wired surface
![]() $\Delta $
without wires, that is, one with
$\Delta $
without wires, that is, one with
![]() $\Delta =\operatorname {\mathrm {Surf}}(\Delta )$
, is said to be degenerate. Otherwise, it is nondegenerate.
$\Delta =\operatorname {\mathrm {Surf}}(\Delta )$
, is said to be degenerate. Otherwise, it is nondegenerate.
How will wired surfaces arise? We will say that a pair
![]() $({\mathbb {F}},\mathbb T)$
is a decoration of a surface S if
$({\mathbb {F}},\mathbb T)$
is a decoration of a surface S if
-
○
 ${\mathbb {F}}$
is a partial foliation of S supported by the union of a finite collection of disjoint, essential and nonparallel, cylinders, and
${\mathbb {F}}$
is a partial foliation of S supported by the union of a finite collection of disjoint, essential and nonparallel, cylinders, and -
○
 $\mathbb T$
is a triangulation of the complement of the interior of those cylinders.
$\mathbb T$
is a triangulation of the complement of the interior of those cylinders.
Now, if
![]() $({\mathbb {F}},\mathbb T)$
is a decoration of S, then we get an associated wired surface
$({\mathbb {F}},\mathbb T)$
is a decoration of S, then we get an associated wired surface
![]() $\Delta =S/\sim _{\mathbb {F}}$
by collapsing each leaf of
$\Delta =S/\sim _{\mathbb {F}}$
by collapsing each leaf of
![]() ${\mathbb {F}}$
to a point and dividing each one of the arising bigons into two triangles by adding a vertex in the interior of the bigon. We will say that the quotient map
${\mathbb {F}}$
to a point and dividing each one of the arising bigons into two triangles by adding a vertex in the interior of the bigon. We will say that the quotient map
![]() $\pi :S\to \Delta $
is a resolution of
$\pi :S\to \Delta $
is a resolution of
![]() $\Delta $
with associated foliation
$\Delta $
with associated foliation
![]() ${\mathbb {F}}$
. Every wired surface admits an essentially unique resolution, unique in the sense that any two differ by a PL-homeomorphism mapping one of the foliations to the other one.
${\mathbb {F}}$
. Every wired surface admits an essentially unique resolution, unique in the sense that any two differ by a PL-homeomorphism mapping one of the foliations to the other one.
Suppose now that
![]() $\Delta $
is a wired surface. A simple curve on
$\Delta $
is a wired surface. A simple curve on
![]() $\Delta $
is a map
$\Delta $
is a map
![]() $\eta :\mathbb S^1\to \Delta $
such that there are a resolution
$\eta :\mathbb S^1\to \Delta $
such that there are a resolution
![]() $\pi :S\to \Delta $
with associated foliation
$\pi :S\to \Delta $
with associated foliation
![]() ${\mathbb {F}}$
and an essential simple curve
${\mathbb {F}}$
and an essential simple curve
![]() $\eta ':\mathbb S^1\to S$
which is transversal to
$\eta ':\mathbb S^1\to S$
which is transversal to
![]() ${\mathbb {F}}$
and with
${\mathbb {F}}$
and with
![]() $\eta =\pi \circ \eta '$
.
$\eta =\pi \circ \eta '$
.
Note that transversality to the associated foliation implies that if
![]() $\eta $
is a simple curve of a wired surface
$\eta $
is a simple curve of a wired surface
![]() $\Delta $
then
$\Delta $
then
![]() $\eta \cap \pi ^{-1}(\Delta \setminus \operatorname {\mathrm {Surf}}(\Delta ))$
consists of a collection of segments, each one of them mapped homeomorphically to a wire. If I is such a wire, then we denote by
$\eta \cap \pi ^{-1}(\Delta \setminus \operatorname {\mathrm {Surf}}(\Delta ))$
consists of a collection of segments, each one of them mapped homeomorphically to a wire. If I is such a wire, then we denote by
![]() $n_I(\eta )$
the weight of
$n_I(\eta )$
the weight of
![]() $\eta $
in I, that is, the number of connected components of
$\eta $
in I, that is, the number of connected components of
![]() $\eta \cap \pi ^{-1}(\Delta \setminus \operatorname {\mathrm {Surf}}(\Delta ))$
which are mapped homeomorphically to I, or in other words, the number of times that
$\eta \cap \pi ^{-1}(\Delta \setminus \operatorname {\mathrm {Surf}}(\Delta ))$
which are mapped homeomorphically to I, or in other words, the number of times that
![]() $\eta $
crosses I. We refer to the vector
$\eta $
crosses I. We refer to the vector
as the weight vector for
![]() $\eta $
in
$\eta $
in
![]() $\Delta $
. The intersection of the image of
$\Delta $
. The intersection of the image of
![]() $\eta $
with the surface part
$\eta $
with the surface part
![]() $\operatorname {\mathrm {Surf}}(\Delta )$
is a simple arc system with endpoints in the set
$\operatorname {\mathrm {Surf}}(\Delta )$
is a simple arc system with endpoints in the set
![]() $P_{\Delta }$
. Note that up to homotopying
$P_{\Delta }$
. Note that up to homotopying
![]() $\eta $
to another simple curve in
$\eta $
to another simple curve in
![]() $\Delta $
we might assume that all the components of the arc system
$\Delta $
we might assume that all the components of the arc system
![]() $\eta \cap \operatorname {\mathrm {Surf}}(\Delta )$
are essential. This is equivalent to asking that for each wire I we have
$\eta \cap \operatorname {\mathrm {Surf}}(\Delta )$
are essential. This is equivalent to asking that for each wire I we have
![]() $n_I(\eta )\leqslant n_I(\eta ')$
for any other simple curve
$n_I(\eta )\leqslant n_I(\eta ')$
for any other simple curve
![]() $\eta '$
in
$\eta '$
in
![]() $\Delta $
homotopic to
$\Delta $
homotopic to
![]() $\eta $
. We will suppose from now on, without further mention, that all simple curves in
$\eta $
. We will suppose from now on, without further mention, that all simple curves in
![]() $\Delta $
satisfy these minimality requirements.
$\Delta $
satisfy these minimality requirements.
So far, wired surfaces are just topological objects. Let us change this. Under a hyperbolic wired surface we understand a wired surface
![]() $\Delta $
whose surface part
$\Delta $
whose surface part
![]() $\operatorname {\mathrm {Surf}}(\Delta )$
is endowed with a piece-wise hyperbolic metric, that is, one with respect to which the simplexes in the triangulation of
$\operatorname {\mathrm {Surf}}(\Delta )$
is endowed with a piece-wise hyperbolic metric, that is, one with respect to which the simplexes in the triangulation of
![]() $\operatorname {\mathrm {Surf}}(\Delta )$
are isometric to hyperbolic triangles.
$\operatorname {\mathrm {Surf}}(\Delta )$
are isometric to hyperbolic triangles.
Let
![]() $\Delta $
be a hyperbolic wired surface, and as always let
$\Delta $
be a hyperbolic wired surface, and as always let
![]() $\Sigma $
be our fixed hyperbolic surface. We will say that a map
$\Sigma $
be our fixed hyperbolic surface. We will say that a map
![]() $\Xi :\Delta \to \Sigma $
is tight if the following holds:
$\Xi :\Delta \to \Sigma $
is tight if the following holds:
-
○
 $\Xi $
maps every wire to a geodesic segment, and
$\Xi $
maps every wire to a geodesic segment, and -
○
 $\Xi $
is an isometry when restricted to each one of the simplexes in the triangulation of
$\Xi $
is an isometry when restricted to each one of the simplexes in the triangulation of
 $\operatorname {\mathrm {Surf}}(\Delta )$
.
$\operatorname {\mathrm {Surf}}(\Delta )$
.
We will be interested in counting pairs
![]() $(\Xi :\Delta \to \Sigma ,\gamma )$
consisting of tight maps and simple curves. Evidently, without further restrictions, there could be infinitely many such pairs. What we are going to count is pairs were the curve has bounded length. We are, however, going to use a pretty strange notion of length. Consider namely for some given small but positive
$(\Xi :\Delta \to \Sigma ,\gamma )$
consisting of tight maps and simple curves. Evidently, without further restrictions, there could be infinitely many such pairs. What we are going to count is pairs were the curve has bounded length. We are, however, going to use a pretty strange notion of length. Consider namely for some given small but positive
![]() $\varepsilon $
, the following quantity
$\varepsilon $
, the following quantity
 $$ \begin{align} \ell_{\Xi}^{\varepsilon}(\gamma)=\varepsilon\cdot\ell_{\operatorname{\mathrm{Surf}}(\Delta)}(\gamma\cap\operatorname{\mathrm{Surf}}(\Delta))+\sum_{I\in\operatorname{\mathrm{\mathbf{wire}}}}n_I(\gamma)\cdot\max\left\{\ell_{\Sigma}(\Xi(I))-\frac 1\varepsilon,0\right\}. \end{align} $$
$$ \begin{align} \ell_{\Xi}^{\varepsilon}(\gamma)=\varepsilon\cdot\ell_{\operatorname{\mathrm{Surf}}(\Delta)}(\gamma\cap\operatorname{\mathrm{Surf}}(\Delta))+\sum_{I\in\operatorname{\mathrm{\mathbf{wire}}}}n_I(\gamma)\cdot\max\left\{\ell_{\Sigma}(\Xi(I))-\frac 1\varepsilon,0\right\}. \end{align} $$
It is evident that this notion of length is exactly tailored to what we will need later on, but let us try to parse what Equation (6.2) actually means. What is the role of
![]() $\varepsilon $
? If we think of the length as a measure of the cost of a journey, then the first
$\varepsilon $
? If we think of the length as a measure of the cost of a journey, then the first
![]() $\varepsilon $
just makes traveling along the surface part pretty cheap, meaning that for the same price we can cruise longer over there. Along the same lines, when traveling through the wires, we only pay when the wires are very long.
$\varepsilon $
just makes traveling along the surface part pretty cheap, meaning that for the same price we can cruise longer over there. Along the same lines, when traveling through the wires, we only pay when the wires are very long.
Lemma 6.1. Let
![]() $\Delta $
be a nondegenerate hyperbolic wired surface with set of wires
$\Delta $
be a nondegenerate hyperbolic wired surface with set of wires
![]() $\operatorname {\mathrm {\mathbf {wire}}}=\operatorname {\mathrm {\mathbf {wire}}}(\Delta )$
. Fix a tight map
$\operatorname {\mathrm {\mathbf {wire}}}=\operatorname {\mathrm {\mathbf {wire}}}(\Delta )$
. Fix a tight map
![]() $f:\Delta \to \Sigma $
and a positive integer vector
$f:\Delta \to \Sigma $
and a positive integer vector
![]() $\vec n=(n_I)_{I\in \operatorname {\mathrm {\mathbf {wire}}}}\in \mathbb N_+^{\operatorname {\mathrm {\mathbf {wire}}}}$
, and denote by
$\vec n=(n_I)_{I\in \operatorname {\mathrm {\mathbf {wire}}}}\in \mathbb N_+^{\operatorname {\mathrm {\mathbf {wire}}}}$
, and denote by
the smallest entry of
![]() $\vec n$
and the number of times that this value is taken.
$\vec n$
and the number of times that this value is taken.
For any
![]() $\varepsilon>0$
, there are at most
$\varepsilon>0$
, there are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{d-1}\cdot e^{\frac {L}{\min }}$
homotopy classes of pairs
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{d-1}\cdot e^{\frac {L}{\min }}$
homotopy classes of pairs
![]() $(\Xi :\Delta \to \Sigma ,\gamma )$
, where
$(\Xi :\Delta \to \Sigma ,\gamma )$
, where
![]() $\Xi $
is a tight map with
$\Xi $
is a tight map with
![]() $\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta )}=f\vert _{\operatorname {\mathrm {Surf}}(\Delta )}$
and where
$\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta )}=f\vert _{\operatorname {\mathrm {Surf}}(\Delta )}$
and where
![]() $\gamma $
is a simple multicurve in
$\gamma $
is a simple multicurve in
![]() $\Delta $
with
$\Delta $
with
![]() $n_I(\gamma )\geqslant n_I$
for every wire I and with
$n_I(\gamma )\geqslant n_I$
for every wire I and with
![]() $\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
.
$\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
.
Note that the fact that the obtained bound, or rather its rate of growth, does not depend on
![]() $\varepsilon $
implies that actually the only way to get many homotopy classes is to play with the wires. In fact, since the given bound only depends on d and
$\varepsilon $
implies that actually the only way to get many homotopy classes is to play with the wires. In fact, since the given bound only depends on d and
![]() $\min $
, the only wires that matter are those which the curve crosses as little as possible.
$\min $
, the only wires that matter are those which the curve crosses as little as possible.
Another comment before launching the proof. Namely, what happens if the wired surface
![]() $\Delta $
in Lemma 6.1 is degenerate? If there are no wires, then
$\Delta $
in Lemma 6.1 is degenerate? If there are no wires, then
![]() $\Delta $
is nothing other than a surface with a (piece-wise hyperbolic) metric. In such a surface, there are at most
$\Delta $
is nothing other than a surface with a (piece-wise hyperbolic) metric. In such a surface, there are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{3\cdot \vert \chi (\Delta )\vert }$
simple multicurves of length at most L – see, for example, [Reference Erlandsson and Souto8]. This means that for a degenerate wired surface one actually gets a polynomial bound instead of an exponential one.
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{3\cdot \vert \chi (\Delta )\vert }$
simple multicurves of length at most L – see, for example, [Reference Erlandsson and Souto8]. This means that for a degenerate wired surface one actually gets a polynomial bound instead of an exponential one.
We are now ready to launch the proof of Lemma 6.1:
Proof. Note that, since the map
![]() $\Xi $
is fixed on
$\Xi $
is fixed on
![]() $\operatorname {\mathrm {Surf}}(\Delta )$
, we get that the homotopy type of the map, or even the map itself, is determined by what happens to the wires. In particular, as in the proof of Lemma 4.1 we get that if we give ourselves a positive vector
$\operatorname {\mathrm {Surf}}(\Delta )$
, we get that the homotopy type of the map, or even the map itself, is determined by what happens to the wires. In particular, as in the proof of Lemma 4.1 we get that if we give ourselves a positive vector
![]() $\vec \lambda =(\lambda _I)_{I\in \operatorname {\mathrm {\mathbf {wire}}}}\in \mathbb R_+^{\operatorname {\mathrm {\mathbf {wire}}}}$
, then there are at most
$\vec \lambda =(\lambda _I)_{I\in \operatorname {\mathrm {\mathbf {wire}}}}\in \mathbb R_+^{\operatorname {\mathrm {\mathbf {wire}}}}$
, then there are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\Vert \vec \lambda \Vert }$
homotopy classes of tight maps
$\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\Vert \vec \lambda \Vert }$
homotopy classes of tight maps
![]() $\Xi :\Delta \to \Sigma $
with
$\Xi :\Delta \to \Sigma $
with
![]() $\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta )}=f$
and such that
$\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta )}=f$
and such that
As always, we have set
![]() $\Vert \vec \lambda \Vert =\lambda _1+\dots +\lambda _r$
.
$\Vert \vec \lambda \Vert =\lambda _1+\dots +\lambda _r$
.
Now, we are not counting homotopy classes of maps but, rather, of pairs
![]() $(\Xi :\Delta \to \Sigma ,\gamma )$
, where the multicurve
$(\Xi :\Delta \to \Sigma ,\gamma )$
, where the multicurve
![]() $\gamma $
satisfies
$\gamma $
satisfies
![]() $\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
. Note that, if
$\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
. Note that, if
![]() $\Xi $
satisfies Equation (6.3), then our given length bound
$\Xi $
satisfies Equation (6.3), then our given length bound
![]() $\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
implies that
$\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
implies that
 $$ \begin{align*} \ell_{\operatorname{\mathrm{Surf}}(\Delta)}(\gamma\cap\operatorname{\mathrm{Surf}}(\Delta)) &= \frac 1\varepsilon\left(\ell_{\Xi}^{\varepsilon}(\gamma)-\sum_{I\in\operatorname{\mathrm{\mathbf{wire}}}}n_I(\gamma)\cdot\max\left\{\ell_{\Sigma}(\Xi(I))-\frac 1\varepsilon,0\right\}\right)\\ &\leqslant \frac 1\varepsilon\left(L-\sum_{I\in\operatorname{\mathrm{\mathbf{wire}}}}n_I\cdot\max\left\{\lambda_I-\frac 1\varepsilon,0\right\}\right)\\ &\leqslant \frac 1\varepsilon\left(L-\langle\vec n,\vec\lambda\rangle+\frac 1\varepsilon\cdot\Vert\vec n\Vert\right). \end{align*} $$
$$ \begin{align*} \ell_{\operatorname{\mathrm{Surf}}(\Delta)}(\gamma\cap\operatorname{\mathrm{Surf}}(\Delta)) &= \frac 1\varepsilon\left(\ell_{\Xi}^{\varepsilon}(\gamma)-\sum_{I\in\operatorname{\mathrm{\mathbf{wire}}}}n_I(\gamma)\cdot\max\left\{\ell_{\Sigma}(\Xi(I))-\frac 1\varepsilon,0\right\}\right)\\ &\leqslant \frac 1\varepsilon\left(L-\sum_{I\in\operatorname{\mathrm{\mathbf{wire}}}}n_I\cdot\max\left\{\lambda_I-\frac 1\varepsilon,0\right\}\right)\\ &\leqslant \frac 1\varepsilon\left(L-\langle\vec n,\vec\lambda\rangle+\frac 1\varepsilon\cdot\Vert\vec n\Vert\right). \end{align*} $$
Now, since for any given length there are only polynomially many simple arc systems of bounded length we deduce that for each
![]() $\Xi $
satisfying Equation (6.3) there are at most
$\Xi $
satisfying Equation (6.3) there are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot (L-\langle \vec n,\vec \lambda \rangle )^{\operatorname {\mathrm {\mathbf {const}}}}$
homotopy classes of simple multicurves
$\operatorname {\mathrm {\mathbf {const}}}\cdot (L-\langle \vec n,\vec \lambda \rangle )^{\operatorname {\mathrm {\mathbf {const}}}}$
homotopy classes of simple multicurves
![]() $\gamma $
in
$\gamma $
in
![]() $\Delta $
with
$\Delta $
with
![]() $\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
and satisfying
$\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
and satisfying
![]() $n_{I}(\gamma )\geqslant n_{I}$
for each wire I. Putting all of this together, we get the following:
$n_{I}(\gamma )\geqslant n_{I}$
for each wire I. Putting all of this together, we get the following:
Fact. There are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot (L-\langle \vec n,\vec \lambda \rangle )^{\operatorname {\mathrm {\mathbf {const}}}}\cdot e^{\Vert \lambda \Vert }$
homotopy classes of pairs
$\operatorname {\mathrm {\mathbf {const}}}\cdot (L-\langle \vec n,\vec \lambda \rangle )^{\operatorname {\mathrm {\mathbf {const}}}}\cdot e^{\Vert \lambda \Vert }$
homotopy classes of pairs
![]() $(\Xi :\Delta \to \Sigma ,\gamma )$
, where
$(\Xi :\Delta \to \Sigma ,\gamma )$
, where
![]() $\Xi $
is a tight map with
$\Xi $
is a tight map with
![]() $\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta )}=f$
, satisfying Equation (6.3) and where
$\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta )}=f$
, satisfying Equation (6.3) and where
![]() $\gamma $
is a simple curve in
$\gamma $
is a simple curve in
![]() $\Delta $
with
$\Delta $
with
![]() $n_I(\gamma )\geqslant n_I$
for every wire I and with
$n_I(\gamma )\geqslant n_I$
for every wire I and with
![]() $\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
.
$\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
.
Now, we get that the quantity we want to bound, that is, the number of homotopy classes of pairs
![]() $(\Xi :\Delta \to \Sigma ,\gamma )$
, where
$(\Xi :\Delta \to \Sigma ,\gamma )$
, where
![]() $\Xi $
is a tight map with
$\Xi $
is a tight map with
![]() $\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta )}=f$
and where
$\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta )}=f$
and where
![]() $\gamma $
is a simple curve in
$\gamma $
is a simple curve in
![]() $\Delta $
with
$\Delta $
with
![]() $n_I(\gamma )\geqslant n_I$
for every wire I and with
$n_I(\gamma )\geqslant n_I$
for every wire I and with
![]() $\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
is bounded from above by
$\ell _{\Xi }^{\varepsilon }(\gamma )\leqslant L$
is bounded from above by
 $$ \begin{align*}\sum_{\lambda\in\mathbb N^{\operatorname{\mathrm{\mathbf{wire}}}},\ \Vert\lambda\Vert\leqslant L}\operatorname{\mathrm{\mathbf{const}}}\cdot (L-\langle\vec n,\vec\lambda\rangle)^{\operatorname{\mathrm{\mathbf{const}}}}\cdot e^{\Vert\lambda\Vert}.\end{align*} $$
$$ \begin{align*}\sum_{\lambda\in\mathbb N^{\operatorname{\mathrm{\mathbf{wire}}}},\ \Vert\lambda\Vert\leqslant L}\operatorname{\mathrm{\mathbf{const}}}\cdot (L-\langle\vec n,\vec\lambda\rangle)^{\operatorname{\mathrm{\mathbf{const}}}}\cdot e^{\Vert\lambda\Vert}.\end{align*} $$
This quantity is then bounded from above by the value of the integral
 $$ \begin{align*}\operatorname{\mathrm{\mathbf{const}}}\int_{\{\vec x\in\mathbb R_+^{\operatorname{\mathrm{\mathbf{wire}}}},\ \langle\vec n,\vec x\rangle\}\leqslant L}(L-\langle \vec n,\vec x\rangle)^{\operatorname{\mathrm{\mathbf{const}}}}\cdot e^{\Vert\vec x\Vert}dx,\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{\mathbf{const}}}\int_{\{\vec x\in\mathbb R_+^{\operatorname{\mathrm{\mathbf{wire}}}},\ \langle\vec n,\vec x\rangle\}\leqslant L}(L-\langle \vec n,\vec x\rangle)^{\operatorname{\mathrm{\mathbf{const}}}}\cdot e^{\Vert\vec x\Vert}dx,\end{align*} $$
and now it is a calculus problem that we leave to the reader to check that this integral is bounded by
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{d-1}\cdot e^{\frac {L}{n_{\min }}}$
, where
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{d-1}\cdot e^{\frac {L}{n_{\min }}}$
, where
![]() $n_{\min }=\min _In_I\geqslant 1$
and where
$n_{\min }=\min _In_I\geqslant 1$
and where
![]() $d=\vert \{I\text { wire with }n_I=n_{\min }\}\vert $
. We are done.
$d=\vert \{I\text { wire with }n_I=n_{\min }\}\vert $
. We are done.
At this point, we know how to bound the number of homotopy classes of tight maps of wired surfaces. It is time to explain why we care about being able to do so.
Pseudo-doubles
Earlier, just before the statement of Lemma 5.6, we introduced the pseudo-double associated to two fillings. Let us extend that terminology a bit: Under a pseudo-double, we understand a pair
![]() $(\Theta :S\to \Sigma ,\gamma )$
where
$(\Theta :S\to \Sigma ,\gamma )$
where
-
○
 $\Theta :S\to \Sigma $
is a pleated surface with S closed,
$\Theta :S\to \Sigma $
is a pleated surface with S closed, -
○
 $\gamma \subset S$
, the crease, is a simple curve cutting S into two connected components and
$\gamma \subset S$
, the crease, is a simple curve cutting S into two connected components and -
○
 $\Theta $
maps
$\Theta $
maps
 $\gamma $
to a geodesic in
$\gamma $
to a geodesic in
 $\Sigma $
and its restriction
$\Sigma $
and its restriction
 $\Theta \vert _{S\setminus \gamma }$
to the complement of
$\Theta \vert _{S\setminus \gamma }$
to the complement of
 $\gamma $
is geometrically incompressible.
$\gamma $
is geometrically incompressible.
Two pseudo-doubles
![]() $(\Theta :S\to \Sigma ,\gamma )$
and
$(\Theta :S\to \Sigma ,\gamma )$
and
![]() $(\Theta ':S'\to \Sigma ,\gamma ')$
are homotopic if there is a homeomorphism
$(\Theta ':S'\to \Sigma ,\gamma ')$
are homotopic if there is a homeomorphism
![]() $f:S\to S'$
with
$f:S\to S'$
with
![]() $\gamma '$
homotopic to
$\gamma '$
homotopic to
![]() $f(\gamma )$
and with
$f(\gamma )$
and with
![]() $\Theta $
homotopic to
$\Theta $
homotopic to
![]() $\Theta '\circ f$
.
$\Theta '\circ f$
.
Note that this terminology is consistent with the use of the word pseudo-double in the previous section.
Recall now that we fixed earlier some
![]() $\varepsilon _0$
satisfying Equation (5.2) and note that if
$\varepsilon _0$
satisfying Equation (5.2) and note that if
![]() $(\Theta :S\to \Sigma ,\gamma )$
is a pseudo-double then the crease
$(\Theta :S\to \Sigma ,\gamma )$
is a pseudo-double then the crease
![]() $\gamma $
, being separating, crosses every component U of the thin part
$\gamma $
, being separating, crosses every component U of the thin part
![]() $S^{\leqslant \varepsilon _0}$
an even number of times
$S^{\leqslant \varepsilon _0}$
an even number of times
![]() $\iota (\gamma ,U)\in 2\mathbb N$
. In fact, since by the choice of
$\iota (\gamma ,U)\in 2\mathbb N$
. In fact, since by the choice of
![]() $\varepsilon _0$
we get that
$\varepsilon _0$
we get that
![]() $\Theta $
maps the core of every component of the thin part to a homotopically trivial curve and since the restriction of
$\Theta $
maps the core of every component of the thin part to a homotopically trivial curve and since the restriction of
![]() $\Theta $
to
$\Theta $
to
![]() $S\setminus \gamma $
is geometrically incompressible we get that actually
$S\setminus \gamma $
is geometrically incompressible we get that actually
by which we mean that
![]() $\gamma $
traverses each such U at least twice.
$\gamma $
traverses each such U at least twice.
Our next goal is to bound, for growing L, the number of homotopy classes of pseudo-doubles
![]() $(\Theta :S\to \Sigma ,\gamma )$
where S has given topological type, where there are precisely d components U of the thin part with
$(\Theta :S\to \Sigma ,\gamma )$
where S has given topological type, where there are precisely d components U of the thin part with
![]() $\iota (\gamma ,U)=2$
and where
$\iota (\gamma ,U)=2$
and where
![]() $\ell _S(\gamma )\leqslant L$
:
$\ell _S(\gamma )\leqslant L$
:
Proposition 6.2. Let
![]() $\varepsilon _0$
be as in Equation (5.2), and suppose that
$\varepsilon _0$
be as in Equation (5.2), and suppose that
![]() $S_0$
is a closed orientable surface.
$S_0$
is a closed orientable surface.
-
1. For every
 $d\geqslant 1$
, there are at most
$d\geqslant 1$
, there are at most
 $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{d-1}\cdot e^{\frac L2}$
homotopy classes of pseudo-doubles
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{d-1}\cdot e^{\frac L2}$
homotopy classes of pseudo-doubles
 $(\Theta :S\to \Sigma ,\gamma )$
, where S is homeomorphic to
$(\Theta :S\to \Sigma ,\gamma )$
, where S is homeomorphic to
 $S_0$
where the thin part
$S_0$
where the thin part
 $S^{\leqslant \varepsilon _0}$
of S has exactly d components U with
$S^{\leqslant \varepsilon _0}$
of S has exactly d components U with
 $\iota (\gamma ,U)=2$
and where
$\iota (\gamma ,U)=2$
and where
 $\gamma $
has length
$\gamma $
has length
 $\ell _S(\gamma )\leqslant L$
.
$\ell _S(\gamma )\leqslant L$
. -
2. There are at most
 $\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\frac L3}$
homotopy classes of pseudo-doubles
$\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\frac L3}$
homotopy classes of pseudo-doubles
 $(\Theta :S\to \Sigma ,\gamma )$
where S is homeomorphic to
$(\Theta :S\to \Sigma ,\gamma )$
where S is homeomorphic to
 $S_0$
, where there is no component U of the thin part
$S_0$
, where there is no component U of the thin part
 $S^{\leqslant \varepsilon _0}$
with
$S^{\leqslant \varepsilon _0}$
with
 $\iota (\gamma ,U)=2$
, and where
$\iota (\gamma ,U)=2$
, and where
 $\gamma $
has length
$\gamma $
has length
 $\ell _S(\gamma )\leqslant L$
.
$\ell _S(\gamma )\leqslant L$
.
Recall that we declared a decoration
![]() $({\mathbb {F}},\mathbb T)$
of a surface S to be a pair consisting of partial foliation
$({\mathbb {F}},\mathbb T)$
of a surface S to be a pair consisting of partial foliation
![]() ${\mathbb {F}}$
supported by the union of disjoint essential and nonparallel cylinders and of a triangulation
${\mathbb {F}}$
supported by the union of disjoint essential and nonparallel cylinders and of a triangulation
![]() $\mathbb T$
of the complement of the interior of those cylinders. To see where these decorations come from, assume that S is a hyperbolic surface.
$\mathbb T$
of the complement of the interior of those cylinders. To see where these decorations come from, assume that S is a hyperbolic surface.
-
○ The
 $\varepsilon _0$
-thick part of S is metrically bounded in the sense that it has a triangulation
$\varepsilon _0$
-thick part of S is metrically bounded in the sense that it has a triangulation
 $\mathbb T$
whose vertices are
$\mathbb T$
whose vertices are
 $\frac 1{10}\varepsilon _0$
-separated and whose edges have length at most
$\frac 1{10}\varepsilon _0$
-separated and whose edges have length at most
 $\frac 13\varepsilon _0$
and are geodesic unless contained in the boundary
$\frac 13\varepsilon _0$
and are geodesic unless contained in the boundary
 $\partial (S^{\geqslant \varepsilon _0})$
of the
$\partial (S^{\geqslant \varepsilon _0})$
of the
 $\varepsilon _0$
-thick part – in that case, they have just constant curvature.
$\varepsilon _0$
-thick part – in that case, they have just constant curvature. -
○ The components of the
 $\varepsilon _0$
-thin part
$\varepsilon _0$
-thin part
 $S^{\leqslant \varepsilon _0}$
are not metrically bounded but still have a very simple structure: They are cylinders foliated by constant curvature circles, namely the curves at constant distance from the geodesic at the core of the cylinder.
$S^{\leqslant \varepsilon _0}$
are not metrically bounded but still have a very simple structure: They are cylinders foliated by constant curvature circles, namely the curves at constant distance from the geodesic at the core of the cylinder.
Putting these things together, that is, the triangulation
![]() $\mathbb T$
of the thick part and the foliation
$\mathbb T$
of the thick part and the foliation
![]() ${\mathbb {F}}$
of the thin part, we get what we will refer as a thin-thick decoration
${\mathbb {F}}$
of the thin part, we get what we will refer as a thin-thick decoration
![]() $({\mathbb {F}},\mathbb T)$
of S – note that the triangulation
$({\mathbb {F}},\mathbb T)$
of S – note that the triangulation
![]() $\mathbb T$
is not unique, and this is why we use an undetermined article. More importantly, note also that the number of components of the thin part is bounded just in terms of the topology of S and that the number of vertices in the triangulation
$\mathbb T$
is not unique, and this is why we use an undetermined article. More importantly, note also that the number of components of the thin part is bounded just in terms of the topology of S and that the number of vertices in the triangulation
![]() $\mathbb T$
is bounded by some number depending on the chosen
$\mathbb T$
is bounded by some number depending on the chosen
![]() $\varepsilon _0$
and again the topological type of S. Since we have fixed
$\varepsilon _0$
and again the topological type of S. Since we have fixed
![]() $\varepsilon _0$
, it follows that every compact surface
$\varepsilon _0$
, it follows that every compact surface
![]() $S_0$
admits finitely many decorations
$S_0$
admits finitely many decorations
![]() $({\mathbb {F}}_1,\mathbb T_1),\dots ,({\mathbb {F}}_r,\mathbb T_r)$
such that if S is any hyperbolic surface homeomorphic to
$({\mathbb {F}}_1,\mathbb T_1),\dots ,({\mathbb {F}}_r,\mathbb T_r)$
such that if S is any hyperbolic surface homeomorphic to
![]() $S_0$
, then there is a homeomorphism
$S_0$
, then there is a homeomorphism
![]() $\sigma :S_0\to S$
and some i such that
$\sigma :S_0\to S$
and some i such that
![]() $(\sigma ({\mathbb {F}}_i),\sigma (\mathbb T_i))$
is a
$(\sigma ({\mathbb {F}}_i),\sigma (\mathbb T_i))$
is a
![]() $\varepsilon _0$
-thin-thick decoration of S. We state this fact for later reference:
$\varepsilon _0$
-thin-thick decoration of S. We state this fact for later reference:
Lemma 6.3. For every closed surface
![]() $S_0$
, there are finitely many decorations
$S_0$
, there are finitely many decorations
![]() $({\mathbb {F}}_1,\mathbb T_1),\dots ,({\mathbb {F}}_r,\mathbb T_r)$
such that for any hyperbolic surface S homeomorphic to
$({\mathbb {F}}_1,\mathbb T_1),\dots ,({\mathbb {F}}_r,\mathbb T_r)$
such that for any hyperbolic surface S homeomorphic to
![]() $S_0$
there are
$S_0$
there are
![]() $i\in \{1,\dots ,r\}$
and a homeomorphism
$i\in \{1,\dots ,r\}$
and a homeomorphism
![]() $\sigma :S_0\to S$
such that
$\sigma :S_0\to S$
such that
![]() $\sigma ({\mathbb {F}}_i,\mathbb T_i)$
is a
$\sigma ({\mathbb {F}}_i,\mathbb T_i)$
is a
![]() $\varepsilon _0$
-thin-thick decoration of S.
$\varepsilon _0$
-thin-thick decoration of S.
After these comments, we can finally launch the proof of Proposition 6.2:
Proof of Proposition 6.2
Starting with the proof of (1), note that from Lemma 6.3 we get that it suffices to prove for each fixed decoration
![]() $({\mathbb {F}},\mathbb T)$
of
$({\mathbb {F}},\mathbb T)$
of
![]() $S_0$
that
$S_0$
that
-
(*) there are at most
 $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{d-1}\cdot e^{\frac L2}$
homotopy classes of pseudo-doubles
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{d-1}\cdot e^{\frac L2}$
homotopy classes of pseudo-doubles
 $(\Theta :S\to \Sigma ,\gamma )$
where there is a homeomorphism
$(\Theta :S\to \Sigma ,\gamma )$
where there is a homeomorphism
 $\sigma :S_0\to S$
such that
$\sigma :S_0\to S$
such that
 $(\sigma ({\mathbb {F}}),\sigma (\mathbb T))$
is a decoration of the
$(\sigma ({\mathbb {F}}),\sigma (\mathbb T))$
is a decoration of the
 $\varepsilon _0$
-thin-thick decomposition of S, where the thin part
$\varepsilon _0$
-thin-thick decomposition of S, where the thin part
 $S^{\leqslant \varepsilon _0}$
of S has exactly d components U with
$S^{\leqslant \varepsilon _0}$
of S has exactly d components U with
 $\iota (\gamma ,U)=2$
and where
$\iota (\gamma ,U)=2$
and where
 $\gamma $
has length
$\gamma $
has length
 $\ell _S(\gamma )\leqslant L$
.
$\ell _S(\gamma )\leqslant L$
.
Assuming from now on that we have an
![]() $\varepsilon _0$
-thin-thick decoration
$\varepsilon _0$
-thin-thick decoration
![]() $({\mathbb {F}}, \mathbb T)$
, let
$({\mathbb {F}}, \mathbb T)$
, let
![]() $\Delta =S_0/\sim _{\mathbb {F}}$
be the wired surface obtained from S by collapsing each leaf of
$\Delta =S_0/\sim _{\mathbb {F}}$
be the wired surface obtained from S by collapsing each leaf of
![]() ${\mathbb {F}}$
to a point and let
${\mathbb {F}}$
to a point and let
![]() $\pi :S_0\to \Delta $
be the corresponding quotient map.
$\pi :S_0\to \Delta $
be the corresponding quotient map.
The reason we consider
![]() $\Delta $
is that, as we already mentioned earlier, we have that by the choice of
$\Delta $
is that, as we already mentioned earlier, we have that by the choice of
![]() $\varepsilon _0$
all the leaves of the foliation
$\varepsilon _0$
all the leaves of the foliation
![]() $\sigma ({\mathbb {F}})$
are mapped by
$\sigma ({\mathbb {F}})$
are mapped by
![]() $\Theta $
to homotopically trivial curves. This implies that there is a map
$\Theta $
to homotopically trivial curves. This implies that there is a map
mapping the wires of
![]() $\Delta $
to geodesic segments and with
$\Delta $
to geodesic segments and with
![]() $\Theta \circ \sigma $
homotopic to
$\Theta \circ \sigma $
homotopic to
![]() $\Xi \circ \pi $
by a homotopy whose tracks are bounded by
$\Xi \circ \pi $
by a homotopy whose tracks are bounded by
![]() $\operatorname {\mathrm {\mathbf {const}}}$
. In particular, the edges in
$\operatorname {\mathrm {\mathbf {const}}}$
. In particular, the edges in
![]() $\mathbb T$
are mapped to paths homotopic to geodesic paths of at most length
$\mathbb T$
are mapped to paths homotopic to geodesic paths of at most length
![]() $\operatorname {\mathrm {\mathbf {const}}}$
. Pulling tight relative to the vertices, we can assume that
$\operatorname {\mathrm {\mathbf {const}}}$
. Pulling tight relative to the vertices, we can assume that
![]() $\Xi $
maps two-dimensional simplices in the triangulation of
$\Xi $
maps two-dimensional simplices in the triangulation of
![]() $\Delta $
to hyperbolic triangles. Note that the bound on the lengths of the images of the edges of
$\Delta $
to hyperbolic triangles. Note that the bound on the lengths of the images of the edges of
![]() $\mathbb T$
imply that the restriction of
$\mathbb T$
imply that the restriction of
![]() $\Xi $
to
$\Xi $
to
![]() $\operatorname {\mathrm {Surf}}(\Delta )$
is
$\operatorname {\mathrm {Surf}}(\Delta )$
is
![]() $\operatorname {\mathrm {\mathbf {const}}}$
-Lipschitz.
$\operatorname {\mathrm {\mathbf {const}}}$
-Lipschitz.
This uniform Lipschitz bound implies that
![]() $\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta _0)}$
belongs to finitely many homotopy classes and that the tracks of the homotopy to any chosen representative of the correct homotopy class are bounded by
$\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta _0)}$
belongs to finitely many homotopy classes and that the tracks of the homotopy to any chosen representative of the correct homotopy class are bounded by
![]() $\operatorname {\mathrm {\mathbf {const}}}$
. Choosing the representatives to be tight maps with respect to some hyperbolic structure on
$\operatorname {\mathrm {\mathbf {const}}}$
. Choosing the representatives to be tight maps with respect to some hyperbolic structure on
![]() $\Delta _0$
, we get:
$\Delta _0$
, we get:
Fact. There are finitely many hyperbolic structures
![]() $\Delta _1,\dots ,\Delta _r$
on
$\Delta _1,\dots ,\Delta _r$
on
![]() $\Delta $
and finitely many tight maps
$\Delta $
and finitely many tight maps
![]() $f_1,\dots ,f_r:\Delta _i\to \Sigma $
such that for any
$f_1,\dots ,f_r:\Delta _i\to \Sigma $
such that for any
![]() $\Theta :S\to \Sigma $
and
$\Theta :S\to \Sigma $
and
![]() $\sigma :S_0\to S$
as in (
$\sigma :S_0\to S$
as in (
![]() $*$
) there are
$*$
) there are
![]() $i\in \{1,\dots ,r\}$
and a tight map
$i\in \{1,\dots ,r\}$
and a tight map
![]() $\Xi :\Delta _i\to \Sigma $
with
$\Xi :\Delta _i\to \Sigma $
with
![]() $\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta _i)}=f_i\vert _{\operatorname {\mathrm {Surf}}(\Delta _i)}$
and such that
$\Xi \vert _{\operatorname {\mathrm {Surf}}(\Delta _i)}=f_i\vert _{\operatorname {\mathrm {Surf}}(\Delta _i)}$
and such that
![]() $\Theta \circ \sigma :S_0\to \Sigma $
is homotopic to
$\Theta \circ \sigma :S_0\to \Sigma $
is homotopic to
![]() $\Xi \circ \pi :S_0\to \Sigma $
by a homotopy whose tracks have at most length
$\Xi \circ \pi :S_0\to \Sigma $
by a homotopy whose tracks have at most length
![]() $\operatorname {\mathrm {\mathbf {const}}}$
.
$\operatorname {\mathrm {\mathbf {const}}}$
.
Continuing with the same notation, note that the bound on the tracks of the homotopy between
![]() $\Theta \circ \sigma $
and
$\Theta \circ \sigma $
and
![]() $\Xi \circ \pi $
means that when we compare the length of the geodesic
$\Xi \circ \pi $
means that when we compare the length of the geodesic
![]() $\gamma $
in S with that of the curve
$\gamma $
in S with that of the curve
![]() $\eta =(\pi \circ \sigma ^{-1})(\gamma )$
in the hyperbolic wired surface
$\eta =(\pi \circ \sigma ^{-1})(\gamma )$
in the hyperbolic wired surface
![]() $\Delta _i$
then there is at most an increase by an additive amount every time
$\Delta _i$
then there is at most an increase by an additive amount every time
![]() $\gamma $
crosses a simplex of the wired surface. It means that lengths
$\gamma $
crosses a simplex of the wired surface. It means that lengths
-
○ increase at most by an additive amount every time we cross a component of the thin part, and
-
○ increase by a multiplicative amount while we are in the thick part.
Said in other words: There is some R with
 $$ \begin{align*} \ell_{\Sigma}(\Xi(\eta\cap\operatorname{\mathrm{Surf}}(\Delta)))&\leqslant R\cdot \ell_S(\gamma\cap S^{\geqslant\varepsilon_0})\\ \ell_{\Sigma}(\Xi(\eta\setminus\operatorname{\mathrm{Surf}}(\Delta)))&\leqslant \sum_{\kappa\in\pi_0(\gamma\cap S^{\leqslant\varepsilon_0})}(\ell_S(\kappa)+R). \end{align*} $$
$$ \begin{align*} \ell_{\Sigma}(\Xi(\eta\cap\operatorname{\mathrm{Surf}}(\Delta)))&\leqslant R\cdot \ell_S(\gamma\cap S^{\geqslant\varepsilon_0})\\ \ell_{\Sigma}(\Xi(\eta\setminus\operatorname{\mathrm{Surf}}(\Delta)))&\leqslant \sum_{\kappa\in\pi_0(\gamma\cap S^{\leqslant\varepsilon_0})}(\ell_S(\kappa)+R). \end{align*} $$
Recalling that the wires I of
![]() $\Delta _0$
correspond to the thin parts of
$\Delta _0$
correspond to the thin parts of
![]() $S^{\leqslant \varepsilon _0}$
and that the weight
$S^{\leqslant \varepsilon _0}$
and that the weight
![]() $n_I(\eta )$
is nothing other than the number of times that
$n_I(\eta )$
is nothing other than the number of times that
![]() $\eta $
crosses the wire I, we get from the last two inequalities that
$\eta $
crosses the wire I, we get from the last two inequalities that
 $$ \begin{align} \frac 1R\cdot\ell_{\Xi}(\eta\cap\operatorname{\mathrm{Surf}}(\Delta))+\sum_{I\in\operatorname{\mathrm{\mathbf{wire}}}(\Delta_0)}n_I(\eta)\cdot\max\left\{\ell_{\Xi}(I)-R,0\right\}\leqslant\ell_S(\gamma), \end{align} $$
$$ \begin{align} \frac 1R\cdot\ell_{\Xi}(\eta\cap\operatorname{\mathrm{Surf}}(\Delta))+\sum_{I\in\operatorname{\mathrm{\mathbf{wire}}}(\Delta_0)}n_I(\eta)\cdot\max\left\{\ell_{\Xi}(I)-R,0\right\}\leqslant\ell_S(\gamma), \end{align} $$
where the ‘max’ arises because a length is always nonnegative. Anyways, note that with the notation introduced in Equation (6.2) we can rewrite Equation (6.5) as
Note also that from Equation (6.4) we get that
![]() $n_I(\eta )\geqslant 2$
for all
$n_I(\eta )\geqslant 2$
for all
![]() $I\in \operatorname {\mathrm {\mathbf {wire}}}(\Delta _0)$
. This means that using the notation of Lemma 6.1 we can restate the assumptions in Proposition 6.2 (1) as follows:
$I\in \operatorname {\mathrm {\mathbf {wire}}}(\Delta _0)$
. This means that using the notation of Lemma 6.1 we can restate the assumptions in Proposition 6.2 (1) as follows:
![]() $\min =2$
and this value is achieved
$\min =2$
and this value is achieved
![]() $d\geqslant 1$
times. Lemma 6.1 implies thus that there are at most
$d\geqslant 1$
times. Lemma 6.1 implies thus that there are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{d-1}\cdot e^{\frac L2}$
homotopy classes of pairs
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{d-1}\cdot e^{\frac L2}$
homotopy classes of pairs
![]() $(\Xi ,\eta )$
arising from pseudo-doubles
$(\Xi ,\eta )$
arising from pseudo-doubles
![]() $(\Theta :S\to \Sigma ,\gamma )$
, where
$(\Theta :S\to \Sigma ,\gamma )$
, where
![]() $\Theta $
is as in the fact and where
$\Theta $
is as in the fact and where
![]() $\ell _S(\gamma )\leqslant L$
. This implies a fortiori that we have at most that many choices for the homotopy class of
$\ell _S(\gamma )\leqslant L$
. This implies a fortiori that we have at most that many choices for the homotopy class of
![]() $\Xi $
. Since the homotopy class of
$\Xi $
. Since the homotopy class of
![]() $\Xi $
determines that of
$\Xi $
determines that of
![]() $\Theta $
, we are done with the proof of (1). The proof of (2) is pretty much identical; the only difference is that now
$\Theta $
, we are done with the proof of (1). The proof of (2) is pretty much identical; the only difference is that now
![]() $\min \geqslant 4$
. Plugging this in the argument above, we get the bound
$\min \geqslant 4$
. Plugging this in the argument above, we get the bound
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{k-1}\cdot e^{\frac L4}$
for some k. This is evidently a stronger bound that
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{k-1}\cdot e^{\frac L4}$
for some k. This is evidently a stronger bound that
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\frac L3}$
, and we are done.
$\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\frac L3}$
, and we are done.
The fruits of our labor
After all this work, we are now ready to prove Theorem 1.4.
Proof of Theorem 1.4
Suppose that
![]() $\gamma $
is a closed geodesic with length
$\gamma $
is a closed geodesic with length
![]() $\ell _{\Sigma }(\gamma )\leqslant L$
and such that there are two nonhomotopic minimal genus fillings
$\ell _{\Sigma }(\gamma )\leqslant L$
and such that there are two nonhomotopic minimal genus fillings
![]() $\beta _1:S_1\to \Sigma $
and
$\beta _1:S_1\to \Sigma $
and
![]() $\beta _2:S_2\to \Sigma $
with
$\beta _2:S_2\to \Sigma $
with
![]() $\beta _i(\partial S_i)=\gamma $
. From Proposition 5.4, we get that, without loss of generality, we might assume that both
$\beta _i(\partial S_i)=\gamma $
. From Proposition 5.4, we get that, without loss of generality, we might assume that both
![]() $\beta _1:S_1\to \Sigma $
and
$\beta _1:S_1\to \Sigma $
and
![]() $\beta _2:S_2\to \Sigma $
are hyperbolic fillings.
$\beta _2:S_2\to \Sigma $
are hyperbolic fillings.
Let then
![]() $S=S_i\cup _{\partial S_1=\partial S_2}S_2$
be the hyperbolic surface obtained by gluing both surfaces
$S=S_i\cup _{\partial S_1=\partial S_2}S_2$
be the hyperbolic surface obtained by gluing both surfaces
![]() $S_1$
and
$S_1$
and
![]() $S_2$
along the boundary in such a way that there is a pleated surface
$S_2$
along the boundary in such a way that there is a pleated surface
![]() $\Theta :S\to \Sigma $
with
$\Theta :S\to \Sigma $
with
![]() $\Theta \vert _{S_i}=\beta _i$
. Note once again that the map
$\Theta \vert _{S_i}=\beta _i$
. Note once again that the map
![]() $\Theta $
maps the crease
$\Theta $
maps the crease
![]() $\hat \gamma =\partial S_1=\partial S_2$
geodesically to
$\hat \gamma =\partial S_1=\partial S_2$
geodesically to
![]() $\gamma $
. Moreover, Lemma 5.2 implies that the restriction of
$\gamma $
. Moreover, Lemma 5.2 implies that the restriction of
![]() $\Theta $
to
$\Theta $
to
![]() $S\setminus \hat \gamma $
is geometrically incompressible. Taken together, all of this means that the pair
$S\setminus \hat \gamma $
is geometrically incompressible. Taken together, all of this means that the pair
![]() $(\Theta :S\to \Sigma ,\hat \gamma )$
is a pseudo-double.
$(\Theta :S\to \Sigma ,\hat \gamma )$
is a pseudo-double.
Now, Lemma 5.6 implies, together with the assumption that
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
are not homotopic, that the
$\beta _2$
are not homotopic, that the
![]() $\varepsilon _0$
-thin part of S has at most
$\varepsilon _0$
-thin part of S has at most
![]() $6g-4$
connected components which are traversed twice by the crease
$6g-4$
connected components which are traversed twice by the crease
![]() $\hat \gamma $
. We thus get from Proposition 6.2 that there are at most
$\hat \gamma $
. We thus get from Proposition 6.2 that there are at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
choices for the homotopy class of
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
choices for the homotopy class of
![]() $(\Theta :S\to \Sigma ,\hat \gamma )$
. Since the geodesic
$(\Theta :S\to \Sigma ,\hat \gamma )$
. Since the geodesic
![]() $\gamma $
is determined by the homotopy class of
$\gamma $
is determined by the homotopy class of
![]() $\Theta (\hat \gamma )$
, we have proved that there are
$\Theta (\hat \gamma )$
, we have proved that there are
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
choices for
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
choices for
![]() $\gamma $
, as we had claimed.
$\gamma $
, as we had claimed.
7 Proof of the main theorem
In this section, we prove Theorem 1.1 from the introduction.
Theorem 1.1. Let
![]() $\Sigma $
be a closed, connected and oriented hyperbolic surface and for
$\Sigma $
be a closed, connected and oriented hyperbolic surface and for
![]() $g\geqslant 1$
and
$g\geqslant 1$
and
![]() $L>0$
let
$L>0$
let
![]() ${\mathbf {B}}_g(L)$
be as in Equation (1.3). We have
${\mathbf {B}}_g(L)$
be as in Equation (1.3). We have
as
![]() $L\to \infty $
.
$L\to \infty $
.
Before we can even explain the idea of the proof of Theorem 1.1, we need to recall what fat graphs are and a few of their properties:
Fat graphs
A fat graph X is a graph endowed with a cyclic ordering of the set
![]() $\operatorname {\mathrm {\mathbf {half}}}_v$
for each v – fat graphs are also sometimes called ribbon graphs. Every fat graph is endowed with a canonically built thickening
$\operatorname {\mathrm {\mathbf {half}}}_v$
for each v – fat graphs are also sometimes called ribbon graphs. Every fat graph is endowed with a canonically built thickening
![]() $\operatorname {\mathrm {\mathbf {neigh}}}(X)$
, the thickening of X. For the sake of concreteness, let us discuss this in the particular case that X is trivalent. We start by taking an oriented filled-in hexagon
$\operatorname {\mathrm {\mathbf {neigh}}}(X)$
, the thickening of X. For the sake of concreteness, let us discuss this in the particular case that X is trivalent. We start by taking an oriented filled-in hexagon
![]() $G_v$
for every vertex v; see Figure 3. If we label by
$G_v$
for every vertex v; see Figure 3. If we label by
![]() $a,b,c$
the three elements in
$a,b,c$
the three elements in
![]() $\operatorname {\mathrm {\mathbf {half}}}_v$
, given in the correct cyclic order, then we label the boundary components of
$\operatorname {\mathrm {\mathbf {half}}}_v$
, given in the correct cyclic order, then we label the boundary components of
![]() $G_v$
by
$G_v$
by
![]() $a,ab,b,bc,c,ca$
, also given in the correct cyclic order. Now, for every edge
$a,ab,b,bc,c,ca$
, also given in the correct cyclic order. Now, for every edge
![]() $e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
let
$e\in \operatorname {\mathrm {\mathbf {edge}}}(X)$
let
![]() $v_1,v_2\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
be the two (possibly identical) vertices at which the two half-edges
$v_1,v_2\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
be the two (possibly identical) vertices at which the two half-edges
![]() $\vec e_1\in \operatorname {\mathrm {\mathbf {half}}}_{v_1}$
and
$\vec e_1\in \operatorname {\mathrm {\mathbf {half}}}_{v_1}$
and
![]() $\vec e_2\in \operatorname {\mathrm {\mathbf {half}}}_{v_2}$
corresponding to e are based, and identify in an orientation reversing way the
$\vec e_2\in \operatorname {\mathrm {\mathbf {half}}}_{v_2}$
corresponding to e are based, and identify in an orientation reversing way the
![]() $\vec e_1$
-edge of
$\vec e_1$
-edge of
![]() $\partial G_{v_1}$
with the
$\partial G_{v_1}$
with the
![]() $\vec e_2$
-edge of
$\vec e_2$
-edge of
![]() $\partial G_{v_2}$
. Proceeding like this for all edges, we end up with the thickening
$\partial G_{v_2}$
. Proceeding like this for all edges, we end up with the thickening
![]() $\operatorname {\mathrm {\mathbf {neigh}}}(X)$
of X.
$\operatorname {\mathrm {\mathbf {neigh}}}(X)$
of X.

Figure 3 Constructing the thickening of X. Pictured are two oriented hexagons corresponding to two vertices connected by an edge. The lighter lines indicate the gluing of those two hexagons.
Definition. A trivalent fat graph X has genus g if
![]() $\operatorname {\mathrm {\mathbf {neigh}}}(X)$
is homeomorphic to a surface of genus g with one boundary component.
$\operatorname {\mathrm {\mathbf {neigh}}}(X)$
is homeomorphic to a surface of genus g with one boundary component.
One of the quantities that appear in the right side of Theorem 1.1 is the number of genus g fat graphs or, rather, that number weighted by the number of automorphims of each such fat graph, where a map
![]() $F:X\to X'$
between two fat graphs is a fat graph homeomorphism if first it is a homeomorphism between two the underlying graphs and then if it sends one fat structure to the other one. In any case, what is really lucky for us is that Bacher and Vdovina [Reference Bacher and Vdovina1] have computed that
$F:X\to X'$
between two fat graphs is a fat graph homeomorphism if first it is a homeomorphism between two the underlying graphs and then if it sends one fat structure to the other one. In any case, what is really lucky for us is that Bacher and Vdovina [Reference Bacher and Vdovina1] have computed that
where the sum takes place over all homeomorphism classes of genus g fat graphs.
Remark. Bacher and Vdovina’s result is phrased in terms of one-vertex triangulations of the closed surface of genus g up to orientation preserving homeomorphism. Let us explain briefly how one goes from such triangulations to genus g fat graphs and back. The dual graph of a triangulation of a surface is a trivalent fat graph – its thickening is the surface minus the vertices of the triangulation. It follows that if the triangulation has a single vertex and the surface is closed of genus g, then the fat graph has genus g. Conversely, the thickening of a fat graph is equipped with a natural arc system (one arc dual to each edge). When collapsing each boundary component of the thickening to a point one gets a closed surface together with a triangulation with as many vertices as connected components of the boundary. It follows that if X is a genus g fat graph, then one gets a one-vertex triangulation of a genus g surface.
Let X now be a fat graph, and, for the sake of concreteness, assume that it has genus g. By construction, we have a canonical embedding of X into
![]() $\operatorname {\mathrm {\mathbf {neigh}}}(X)$
whose image is a spine. In particular, there is a retraction
$\operatorname {\mathrm {\mathbf {neigh}}}(X)$
whose image is a spine. In particular, there is a retraction
such that the preimage of every vertex is a tripod and the preimage of every point in the interior of and edge in X is a segment. The image of
![]() $\partial \operatorname {\mathrm {\mathbf {neigh}}}(X)$
under
$\partial \operatorname {\mathrm {\mathbf {neigh}}}(X)$
under
![]() $\operatorname {\mathrm {spine}}$
runs twice over every edge of X. We will refer to this parametrized curve in X as
$\operatorname {\mathrm {spine}}$
runs twice over every edge of X. We will refer to this parametrized curve in X as
![]() $\partial X$
.
$\partial X$
.
Remark. Note that reversing the orientation of X, that is, reversing the cyclic order at each vertex, has the effect of reversing the orientation of
![]() $\partial X$
.
$\partial X$
.
The map
We will reduce the proof of Theorem 1.1 to the fact that we know how to count critical realizations of graphs, that is, to Theorem 1.3. Let us explain the basic idea. For given g, consider the set
 $$ \begin{align*}{\mathbf{X}}_{g}=\left\{(X,\phi)\middle\vert\begin{array}{c}X\text{ is a fat graph of genus }g\text{ and}\\ \phi:X\to\Sigma\text{ is a critical realization}\\ \text{of the underlying graph}\end{array}\middle\}\right/_{\text{equiv}}\end{align*} $$
$$ \begin{align*}{\mathbf{X}}_{g}=\left\{(X,\phi)\middle\vert\begin{array}{c}X\text{ is a fat graph of genus }g\text{ and}\\ \phi:X\to\Sigma\text{ is a critical realization}\\ \text{of the underlying graph}\end{array}\middle\}\right/_{\text{equiv}}\end{align*} $$
of equivalence classes of realizations, where two realizations
![]() $\phi :X\to \Sigma $
and
$\phi :X\to \Sigma $
and
![]() $\phi ':X'\to \Sigma $
are equivalent if there is a fat graph homeomorphism
$\phi ':X'\to \Sigma $
are equivalent if there is a fat graph homeomorphism
![]() $\sigma :X\to X'$
such that
$\sigma :X\to X'$
such that
![]() $\phi =\phi '\circ \sigma $
.
$\phi =\phi '\circ \sigma $
.
We stress something very important: The critical realization
![]() $\phi $
for
$\phi $
for
![]() $(X,\phi )\in {\mathbf {X}}_{g}$
is explicitly not assumed to respect the fat structure. On the other hand, the homeomorphism
$(X,\phi )\in {\mathbf {X}}_{g}$
is explicitly not assumed to respect the fat structure. On the other hand, the homeomorphism
![]() $\sigma $
in the definition of equivalence definitively has to preserve the fat structure.
$\sigma $
in the definition of equivalence definitively has to preserve the fat structure.
Note that if
![]() $(X,\phi )$
is a equivalent to
$(X,\phi )$
is a equivalent to
![]() $(X',\phi ')$
, then the curves
$(X',\phi ')$
, then the curves
![]() $\phi (\partial X)$
and
$\phi (\partial X)$
and
![]() $\phi '(\partial X')$
are freely homotopic to each other. In particular, we have a well-defined map
$\phi '(\partial X')$
are freely homotopic to each other. In particular, we have a well-defined map
where
![]() ${\mathbf {C}}$
is, as it was earlier, the collection of all oriented geodesics in
${\mathbf {C}}$
is, as it was earlier, the collection of all oriented geodesics in
![]() $\Sigma $
.
$\Sigma $
.
The basic idea of the proof of Theorem 1.1 is that the map (7.1) has the following informally stated properties:
-
1.
 $\Lambda $
is basically injective with image basically contained in
$\Lambda $
is basically injective with image basically contained in
 ${\mathbf {B}}_g$
,
${\mathbf {B}}_g$
, -
2.
 $\Lambda $
is basically surjective onto
$\Lambda $
is basically surjective onto
 ${\mathbf {B}}_g$
, and
${\mathbf {B}}_g$
, and -
3. generically, the geodesic
 $\Lambda (X,\phi )$
has length almost exactly equal to
$\Lambda (X,\phi )$
has length almost exactly equal to
 $2\cdot \ell (\phi )-C$
for some explicit constant C.
$2\cdot \ell (\phi )-C$
for some explicit constant C.
Let us start by clarifying the final point. Suppose that
![]() $(X,\phi )\in {\mathbf {X}}_g$
is such that
$(X,\phi )\in {\mathbf {X}}_g$
is such that
![]() $\phi $
is
$\phi $
is
![]() $\ell _0$
-long for some large
$\ell _0$
-long for some large
![]() $\ell _0$
. Since the curve
$\ell _0$
. Since the curve
![]() $\partial X$
runs exactly twice over each edge X, we get that it its image
$\partial X$
runs exactly twice over each edge X, we get that it its image
![]() $\phi (\partial X)$
consists of
$\phi (\partial X)$
consists of
![]() $2\operatorname {\mathrm {\mathbf {edge}}}(X)$
geodesic segments of length at least
$2\operatorname {\mathrm {\mathbf {edge}}}(X)$
geodesic segments of length at least
![]() $\ell _0$
and with
$\ell _0$
and with
![]() $3\cdot \operatorname {\mathrm {\mathbf {vert}}}(X)=-6\cdot \chi (X)$
corners where it makes an angle equal to
$3\cdot \operatorname {\mathrm {\mathbf {vert}}}(X)=-6\cdot \chi (X)$
corners where it makes an angle equal to
![]() $\frac {2\pi }3$
. We get now from a standard hyperbolic geometry computation (or, if you so wish, from a limiting argument) that when
$\frac {2\pi }3$
. We get now from a standard hyperbolic geometry computation (or, if you so wish, from a limiting argument) that when
![]() $\ell _0$
is large, then, up to an small error depending on
$\ell _0$
is large, then, up to an small error depending on
![]() $\ell _0$
, when we pull tight
$\ell _0$
, when we pull tight
![]() $\phi (\partial X)$
to get
$\phi (\partial X)$
to get
![]() $\Lambda (X,\phi )$
we save
$\Lambda (X,\phi )$
we save
![]() $\log \frac 43$
at each one of those corners. Taking into account that
$\log \frac 43$
at each one of those corners. Taking into account that
![]() $\chi (X)=1-2g$
when X has genus g, this is what we have proved:
$\chi (X)=1-2g$
when X has genus g, this is what we have proved:
Lemma 7.1. For every
![]() $\delta>0$
, there is
$\delta>0$
, there is
![]() $\ell _{\delta }$
with
$\ell _{\delta }$
with
 $$ \begin{align*}\left\vert\ell_{\Sigma}(\Lambda(X,\phi))-\left(2\ell_{\Sigma}(\phi)-6\cdot(2g-1)\cdot \log\frac 43\right)\right\vert\leqslant\delta\end{align*} $$
$$ \begin{align*}\left\vert\ell_{\Sigma}(\Lambda(X,\phi))-\left(2\ell_{\Sigma}(\phi)-6\cdot(2g-1)\cdot \log\frac 43\right)\right\vert\leqslant\delta\end{align*} $$
for every
![]() $(X,\phi )\in {\mathbf {X}}_{g}$
such that
$(X,\phi )\in {\mathbf {X}}_{g}$
such that
![]() $\phi $
is
$\phi $
is
![]() $\ell _{\delta }$
-long.
$\ell _{\delta }$
-long.
Remark. Where does
![]() $\log \frac 43$
come from? If
$\log \frac 43$
come from? If
![]() $\Delta \subset {\mathbb {H}}^2$
is an ideal triangle with vertices
$\Delta \subset {\mathbb {H}}^2$
is an ideal triangle with vertices
![]() $\theta _1,\theta _2$
and
$\theta _1,\theta _2$
and
![]() $\theta _3$
and center p and if
$\theta _3$
and center p and if
![]() $p'$
is the projection of p to the side say
$p'$
is the projection of p to the side say
![]() $(\theta _1,\theta _2)$
, then
$(\theta _1,\theta _2)$
, then
![]() $\log \frac 2{\sqrt 3}$
is the difference between the values at p and
$\log \frac 2{\sqrt 3}$
is the difference between the values at p and
![]() $p'$
of the Buseman function centered at
$p'$
of the Buseman function centered at
![]() $\theta _1$
, and every time we pass by a vertex we basically save twice that amount (see Figure 4).
$\theta _1$
, and every time we pass by a vertex we basically save twice that amount (see Figure 4).

Figure 4 The ideal triangle
![]() $\Delta $
with vertices
$\Delta $
with vertices
![]() $\theta _1, \theta _2, \theta _3=\infty $
and center p. Each one of the legs of the bold printed tripod has length
$\theta _1, \theta _2, \theta _3=\infty $
and center p. Each one of the legs of the bold printed tripod has length
![]() $\log \frac 2{\sqrt 3}$
.
$\log \frac 2{\sqrt 3}$
.
Our next goal is to prove that the map
![]() $\Lambda $
is basically bijective onto
$\Lambda $
is basically bijective onto
![]() ${\mathbf {B}}_g$
, but we should first formalize what we mean by ‘basically’. Suppose that we have a set Z consisting of either realizations, or curves, or of anything else consisting of elements
${\mathbf {B}}_g$
, but we should first formalize what we mean by ‘basically’. Suppose that we have a set Z consisting of either realizations, or curves, or of anything else consisting of elements
![]() $\alpha \in Z$
whose length
$\alpha \in Z$
whose length
![]() $\ell _{\Sigma }(\alpha )$
can be measured, and set
$\ell _{\Sigma }(\alpha )$
can be measured, and set
![]() $Z(L)=\{\alpha \in Z\text { with }\ell _{\Sigma }(\alpha )\leqslant L\}$
. We will say that a subset
$Z(L)=\{\alpha \in Z\text { with }\ell _{\Sigma }(\alpha )\leqslant L\}$
. We will say that a subset
If the ambient set Z is understood from the context, then we might just say that W is negligible. The complement of a negligible set is said to be generic and the elements of a generic set are themselves generic. For example, we get from Lemma 4.3 and Lemma 7.1 that for all
![]() $\delta $
we have that
$\delta $
we have that
 $$ \begin{align*}\left\vert\ell_{\Sigma}(\Lambda(X,\phi))-\left(2\ell_{\Sigma}(\phi)-2\cdot(6g-3)\cdot \log\frac 43\right)\right\vert\leqslant\delta\end{align*} $$
$$ \begin{align*}\left\vert\ell_{\Sigma}(\Lambda(X,\phi))-\left(2\ell_{\Sigma}(\phi)-2\cdot(6g-3)\cdot \log\frac 43\right)\right\vert\leqslant\delta\end{align*} $$
for
![]() $(X,\phi )\in {\mathbf {X}}_{g}$
generic.
$(X,\phi )\in {\mathbf {X}}_{g}$
generic.
Basic bijectivity of
 $\Lambda $
$\Lambda $
Above we used the word ‘basically’ as meaning that something was true up to negligible sets. Let us start by proving that the map
![]() $\Lambda $
is basically injective and that its image is contained in the set
$\Lambda $
is basically injective and that its image is contained in the set
![]() ${\mathbf {B}}_g$
of closed geodesics of genus g.
${\mathbf {B}}_g$
of closed geodesics of genus g.
Lemma 7.2. There is a generic subset
![]() $W\subset {\mathbf {X}}_{g}$
such that the restriction of
$W\subset {\mathbf {X}}_{g}$
such that the restriction of
![]() $\Lambda $
to W is injective and that its image is contained in
$\Lambda $
to W is injective and that its image is contained in
![]() ${\mathbf {B}}_g$
.
${\mathbf {B}}_g$
.
Proof. Let
![]() $\ell _0$
and C be such that for every
$\ell _0$
and C be such that for every
![]() $(X,\phi )\in {\mathbf {X}}_g$
so that
$(X,\phi )\in {\mathbf {X}}_g$
so that
![]() $\phi $
is
$\phi $
is
![]() $\ell _0$
-long we have
$\ell _0$
-long we have
and let
![]() ${\mathbf {X}}_{g,\ell _0}$
be the set of those pairs. We get from Lemma 4.3 that
${\mathbf {X}}_{g,\ell _0}$
be the set of those pairs. We get from Lemma 4.3 that
![]() ${\mathbf {X}}_{g,\ell _0}$
is generic in
${\mathbf {X}}_{g,\ell _0}$
is generic in
![]() ${\mathbf {X}}_g$
. It follows hence from Theorem 1.3 that
${\mathbf {X}}_g$
. It follows hence from Theorem 1.3 that
Note now that each element
![]() $(X,\phi )$
of
$(X,\phi )$
of
![]() ${\mathbf {X}}_g$
, and thus of
${\mathbf {X}}_g$
, and thus of
![]() ${\mathbf {X}}_{g,\ell _0}$
, determines not only the curve
${\mathbf {X}}_{g,\ell _0}$
, determines not only the curve
![]() $\Lambda (X,\phi )$
but also a homotopy class of fillings for this curve, namely
$\Lambda (X,\phi )$
but also a homotopy class of fillings for this curve, namely
![]() $\phi \circ \operatorname {\mathrm {spine}}:\operatorname {\mathrm {\mathbf {neigh}}}(X)\to \Sigma $
. Let now
$\phi \circ \operatorname {\mathrm {spine}}:\operatorname {\mathrm {\mathbf {neigh}}}(X)\to \Sigma $
. Let now
![]() $Z\subset {\mathbf {X}}_{g,\ell _0}$
be the set of pairs
$Z\subset {\mathbf {X}}_{g,\ell _0}$
be the set of pairs
![]() $(X,\phi )$
so that the filling
$(X,\phi )$
so that the filling
![]() $\phi \circ \operatorname {\mathrm {spine}}:\operatorname {\mathrm {\mathbf {neigh}}}(X)\to \Sigma $
is not unique in the sense that the curve
$\phi \circ \operatorname {\mathrm {spine}}:\operatorname {\mathrm {\mathbf {neigh}}}(X)\to \Sigma $
is not unique in the sense that the curve
![]() $\Lambda (X,\phi )$
admits another nonhomotopic genus g filling, and let
$\Lambda (X,\phi )$
admits another nonhomotopic genus g filling, and let
be its complement. From Theorem 1.4, we get that Z consists of at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
many elements and hence that W is generic.
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
many elements and hence that W is generic.
Claim. If
![]() $\ell _0$
is over some threshold, we have that
$\ell _0$
is over some threshold, we have that
![]() $\Lambda (W)\subset {\mathbf {B}}_g$
.
$\Lambda (W)\subset {\mathbf {B}}_g$
.
Proof. First, we have by construction that the curve
![]() $\Lambda (X,\phi )$
admits the genus g filling
$\Lambda (X,\phi )$
admits the genus g filling
![]() $\phi \circ \operatorname {\mathrm {spine}}_X:\operatorname {\mathrm {\mathbf {neigh}}}(X)\to \Sigma $
. Suppose that it admits a smaller genus filling. Then, adding handles and mapping them to points we get that
$\phi \circ \operatorname {\mathrm {spine}}_X:\operatorname {\mathrm {\mathbf {neigh}}}(X)\to \Sigma $
. Suppose that it admits a smaller genus filling. Then, adding handles and mapping them to points we get that
![]() $\Lambda (X,\phi )$
admits a non-
$\Lambda (X,\phi )$
admits a non-
![]() $\pi _1$
-injective genus g filling. Since on the other hand the filling
$\pi _1$
-injective genus g filling. Since on the other hand the filling
![]() $\phi \circ \operatorname {\mathrm {spine}}_X:\operatorname {\mathrm {\mathbf {neigh}}}(X)\to \Sigma $
is
$\phi \circ \operatorname {\mathrm {spine}}_X:\operatorname {\mathrm {\mathbf {neigh}}}(X)\to \Sigma $
is
![]() $\pi _1$
-injective as long as
$\pi _1$
-injective as long as
![]() $\ell _0$
is over some threshold, we get that
$\ell _0$
is over some threshold, we get that
![]() $\Lambda (X,\phi )$
admits two nonhomotopic genus g fillings, contradicting the assumption that
$\Lambda (X,\phi )$
admits two nonhomotopic genus g fillings, contradicting the assumption that
![]() $(X,\phi )\in W$
.
$(X,\phi )\in W$
.
It remains to prove that the restriction of
![]() $\Lambda $
to the generic set W is injective.
$\Lambda $
to the generic set W is injective.
Suppose that we have
![]() $(X,\phi ),(X',\phi ')\in W$
with
$(X,\phi ),(X',\phi ')\in W$
with
![]() $\Lambda (X,\phi )=\Lambda (X',\phi ')$
. Since
$\Lambda (X,\phi )=\Lambda (X',\phi ')$
. Since
![]() $(X,\phi )$
and
$(X,\phi )$
and
![]() $(X',\phi ')$
belong to W, we know that the two fillings
$(X',\phi ')$
belong to W, we know that the two fillings
are homotopic. Recall that this means that there is a homeomorphism
with
![]() $\phi '\circ \operatorname {\mathrm {spine}}_{X'}\circ \sigma $
homotopic to
$\phi '\circ \operatorname {\mathrm {spine}}_{X'}\circ \sigma $
homotopic to
![]() $\phi \circ \operatorname {\mathrm {spine}}_X$
. Since X and
$\phi \circ \operatorname {\mathrm {spine}}_X$
. Since X and
![]() $X'$
are spines of
$X'$
are spines of
![]() $\operatorname {\mathrm {\mathbf {neigh}}}(X)$
and
$\operatorname {\mathrm {\mathbf {neigh}}}(X)$
and
![]() $\operatorname {\mathrm {\mathbf {neigh}}}(X')$
, we deduce that there is a homotopy equivalence
$\operatorname {\mathrm {\mathbf {neigh}}}(X')$
, we deduce that there is a homotopy equivalence
![]() $\bar \sigma :X\to X'$
such that
$\bar \sigma :X\to X'$
such that
![]() $\phi '\circ \bar \sigma $
is homotopic to
$\phi '\circ \bar \sigma $
is homotopic to
![]() $\phi $
. Now, since the lengths of both
$\phi $
. Now, since the lengths of both
![]() $\phi (X)$
and
$\phi (X)$
and
![]() $\phi '(X')$
are, up to a constant, basically half the length of
$\phi '(X')$
are, up to a constant, basically half the length of
![]() $\Lambda (X,\phi )=\Lambda (X',\phi ')$
we see that
$\Lambda (X,\phi )=\Lambda (X',\phi ')$
we see that
![]() $\phi $
and
$\phi $
and
![]() $\phi '$
satisfy the conditions in Proposition 2.3. It thus follows that there is a homeomorphism
$\phi '$
satisfy the conditions in Proposition 2.3. It thus follows that there is a homeomorphism
![]() $F:X'\to X$
mapping edges at constant velocity, with
$F:X'\to X$
mapping edges at constant velocity, with
![]() $F\circ \bar \sigma $
homotopic to the identity, and with
$F\circ \bar \sigma $
homotopic to the identity, and with
![]() $\phi \circ F$
homotopic to
$\phi \circ F$
homotopic to
![]() $\phi '$
. Now, both
$\phi '$
. Now, both
are critical realizations and both are homotpic to each other. We get then from (1) in Lemma 2.2 that
![]() $\phi '=\phi \circ F$
. To conclude, note that since F is a homotopy inverse of
$\phi '=\phi \circ F$
. To conclude, note that since F is a homotopy inverse of
![]() $\bar \sigma $
and since
$\bar \sigma $
and since
![]() $\bar \sigma $
is induced by the homeomorphism
$\bar \sigma $
is induced by the homeomorphism
![]() $\sigma :\operatorname {\mathrm {\mathbf {neigh}}}(X')\to \operatorname {\mathrm {\mathbf {neigh}}}(X)$
we get that F is a fat graph homeomorphism. This proves that
$\sigma :\operatorname {\mathrm {\mathbf {neigh}}}(X')\to \operatorname {\mathrm {\mathbf {neigh}}}(X)$
we get that F is a fat graph homeomorphism. This proves that
![]() $(X,\phi )$
and
$(X,\phi )$
and
![]() $(X',\phi ')$
are equivalent and hence that the restriction of
$(X',\phi ')$
are equivalent and hence that the restriction of
![]() $\Lambda $
to W is injective. We are done with Lemma 7.2.
$\Lambda $
to W is injective. We are done with Lemma 7.2.
Remark. Note that Equation (7.3) and Lemma 7.2 imply that
for all L large enough.
Our next goal is to show that the image of
![]() $\Lambda $
contains a large subset of
$\Lambda $
contains a large subset of
![]() ${\mathbf {B}}_g$
.
${\mathbf {B}}_g$
.
Lemma 7.3. There is a generic subset of
![]() ${\mathbf {B}}_g$
which is contained in the image of
${\mathbf {B}}_g$
which is contained in the image of
![]() $\Lambda $
.
$\Lambda $
.
Proof. Let
![]() $Z\subset {\mathbf {B}}_g$
be the set of those geodesics which admits a hyperbolic genus g filling
$Z\subset {\mathbf {B}}_g$
be the set of those geodesics which admits a hyperbolic genus g filling
![]() $\beta :S\to \Sigma $
such that the
$\beta :S\to \Sigma $
such that the
![]() $\varepsilon _0$
-thin part of the double
$\varepsilon _0$
-thin part of the double
![]() $DS$
of S has at most
$DS$
of S has at most
![]() $6g-4$
connected components U through with
$6g-4$
connected components U through with
![]() $\iota (U,\partial S) = 2$
. It follows from Proposition 6.2 that Z has at most
$\iota (U,\partial S) = 2$
. It follows from Proposition 6.2 that Z has at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
elements with length
$\operatorname {\mathrm {\mathbf {const}}}\cdot L^{6g-5}\cdot e^{\frac L2}$
elements with length
![]() $\leqslant L$
. It follows from Equation (7.4) that Z is negligible and hence that its complement
$\leqslant L$
. It follows from Equation (7.4) that Z is negligible and hence that its complement
![]() $W={\mathbf {B}}_g\setminus Z$
is generic. We claim that W is contained in the image of
$W={\mathbf {B}}_g\setminus Z$
is generic. We claim that W is contained in the image of
![]() $\Lambda $
, at least if
$\Lambda $
, at least if
![]() $\varepsilon _0$
is chosen small enough.
$\varepsilon _0$
is chosen small enough.
Each
![]() $\gamma \in W$
admits a hyperbolic filling
$\gamma \in W$
admits a hyperbolic filling
![]() $\beta :S\to \Sigma $
such that the
$\beta :S\to \Sigma $
such that the
![]() $\varepsilon _0$
-thin part of the double
$\varepsilon _0$
-thin part of the double
![]() $DS$
has at least
$DS$
has at least
![]() $6g-3$
connected components U with
$6g-3$
connected components U with
![]() $\iota (\partial S,U)=2$
. Since
$\iota (\partial S,U)=2$
. Since
![]() $DS$
has genus
$DS$
has genus
![]() $2g$
, we have that
$2g$
, we have that
![]() $6g-3$
is actually the maximal number of connected components that its thin part can have. It follows that the double
$6g-3$
is actually the maximal number of connected components that its thin part can have. It follows that the double
![]() $DS$
of S admits a pants decomposition consisting of very short curves and that moreover
$DS$
of S admits a pants decomposition consisting of very short curves and that moreover
![]() $\partial S$
cuts each one of them exactly twice. It follows that S has
$\partial S$
cuts each one of them exactly twice. It follows that S has
![]() $6g-3$
orthogeodesics cutting S into a union of
$6g-3$
orthogeodesics cutting S into a union of
![]() $4g-2$
right-angle hexagons. These hexagons have three alternating sides which are extremely short. It follows that each one of the hexagons contains a pretty large compact set which is almost isometric to a large neighborhood of the center of an ideal triangle in
$4g-2$
right-angle hexagons. These hexagons have three alternating sides which are extremely short. It follows that each one of the hexagons contains a pretty large compact set which is almost isometric to a large neighborhood of the center of an ideal triangle in
![]() ${\mathbb {H}}^2$
. Declare the center of the hexagon to be the image of the center of the ideal triangle by this almost isometric map. Now, we can represent the dual graph of the decomposition of S by our short orthogeodesic segments as a geodesic subgraph X of S with vertices in the centers of the hexagons; see Figure 5.
${\mathbb {H}}^2$
. Declare the center of the hexagon to be the image of the center of the ideal triangle by this almost isometric map. Now, we can represent the dual graph of the decomposition of S by our short orthogeodesic segments as a geodesic subgraph X of S with vertices in the centers of the hexagons; see Figure 5.

Figure 5 Getting an almost critical realization out of a filling whose domain can be cut into hexagons by very short orthogeodesics.
The graph X is a spine of S, and hence it inherits from S a fat graph structure with S as its neighborhood. Let now
![]() $\psi :X\to \Sigma $
be the realization obtained from the restriction of
$\psi :X\to \Sigma $
be the realization obtained from the restriction of
![]() $\beta $
to X by pulling the edges tight.
$\beta $
to X by pulling the edges tight.
Claim. For all
![]() $\delta $
, there is
$\delta $
, there is
![]() $\varepsilon $
such that if
$\varepsilon $
such that if
![]() $\varepsilon _0<\varepsilon $
, then the realization
$\varepsilon _0<\varepsilon $
, then the realization
![]() $\psi :X\to \Sigma $
is
$\psi :X\to \Sigma $
is
![]() $\delta $
-critical.
$\delta $
-critical.
Proof. Suppose that the claim fails to be true. This means that for some
![]() $\delta $
there are a sequence of counter examples with
$\delta $
there are a sequence of counter examples with
![]() $\varepsilon _0\to 0$
. Since
$\varepsilon _0\to 0$
. Since
![]() $\varepsilon _0\to 0$
, we get that the images of the hexagons converge to a 1-Lipschitz map of a geodesic triangle into
$\varepsilon _0\to 0$
, we get that the images of the hexagons converge to a 1-Lipschitz map of a geodesic triangle into
![]() $\Sigma $
which, however, maps the boundary geodesics to geodesics. Such a map is an isometric embedding of the triangle in question. Now, in a geodesic triangle, the geodesic rays starting in the center and pointing into the cusps make angle
$\Sigma $
which, however, maps the boundary geodesics to geodesics. Such a map is an isometric embedding of the triangle in question. Now, in a geodesic triangle, the geodesic rays starting in the center and pointing into the cusps make angle
![]() $\frac {2\pi }3$
. This means that the angles in the approximates converge to
$\frac {2\pi }3$
. This means that the angles in the approximates converge to
![]() $\frac {2\pi }3$
contradicting our assumption that some of them were at least
$\frac {2\pi }3$
contradicting our assumption that some of them were at least
![]() $\delta $
off
$\delta $
off
![]() $\frac {2\pi }3$
. We have proved the claim.
$\frac {2\pi }3$
. We have proved the claim.
It follows thus from the claim and Corollary 2.4 that, as long as
![]() $\varepsilon _0$
is under some threshold, the realization
$\varepsilon _0$
is under some threshold, the realization
![]() $\psi :X\to \Sigma $
is homotopic to a critical realization
$\psi :X\to \Sigma $
is homotopic to a critical realization
![]() $\phi :X\to \Sigma $
. This implies
$\phi :X\to \Sigma $
. This implies
![]() $(X,\phi )$
belongs to the domain of
$(X,\phi )$
belongs to the domain of
![]() $\Lambda $
and that
$\Lambda $
and that
![]() $\gamma =\Lambda (X,\phi )$
. We have proved that the generic set
$\gamma =\Lambda (X,\phi )$
. We have proved that the generic set
![]() $W\subset {\mathbf {B}}_g$
is contained in the image of
$W\subset {\mathbf {B}}_g$
is contained in the image of
![]() $\Lambda $
.
$\Lambda $
.
We are now ready to wrap all of this up.
Proof of Theorem 1.1
Combining Lemma 7.1, Lemma 7.2 and Lemma 7.3, we get that for all
![]() $\delta>0$
there is a generic subset
$\delta>0$
there is a generic subset
![]() $W\subset {\mathbf {X}}_g$
which is mapped injectively under
$W\subset {\mathbf {X}}_g$
which is mapped injectively under
![]() $\Lambda $
to a generic subset of
$\Lambda $
to a generic subset of
![]() ${\mathbf {B}}_g$
in such a way that
${\mathbf {B}}_g$
in such a way that
where
 $$ \begin{align} \kappa=-3\chi(X)\cdot\log\frac 43=\log\left(\left(\frac 43\right)^{6g-3}\right). \end{align} $$
$$ \begin{align} \kappa=-3\chi(X)\cdot\log\frac 43=\log\left(\left(\frac 43\right)^{6g-3}\right). \end{align} $$
It follows that for all
![]() $\delta>0$
, our set
$\delta>0$
, our set
![]() ${\mathbf {B}}_g(L)$
has, for
${\mathbf {B}}_g(L)$
has, for
![]() $L\to \infty $
, at least as many elements as
$L\to \infty $
, at least as many elements as
![]() ${\mathbf {X}}_g(\frac L2+\kappa -\delta )$
and at most as many as
${\mathbf {X}}_g(\frac L2+\kappa -\delta )$
and at most as many as
![]() ${\mathbf {X}}_g(\frac L2+\kappa +\delta )$
. In symbols, this just means that
${\mathbf {X}}_g(\frac L2+\kappa +\delta )$
. In symbols, this just means that
 $$ \begin{align} \left\vert{\mathbf{X}}_g\middle(\frac L2+\kappa-\delta\middle)\right\vert\preceq\vert{\mathbf{B}}_g(L)\vert\preceq\left\vert{\mathbf{X}}_g\middle(\frac L2+\kappa+\delta\middle)\right\vert \end{align} $$
$$ \begin{align} \left\vert{\mathbf{X}}_g\middle(\frac L2+\kappa-\delta\middle)\right\vert\preceq\vert{\mathbf{B}}_g(L)\vert\preceq\left\vert{\mathbf{X}}_g\middle(\frac L2+\kappa+\delta\middle)\right\vert \end{align} $$
for large L. It thus remains to estimate the cardinality of
![]() ${\mathbf {X}}_g(L)$
.
${\mathbf {X}}_g(L)$
.
Lemma 7.4. We have
 $$ \begin{align*}\vert{\mathbf{X}}_g(L)\vert\sim \frac {1}{12^g}\cdot\left(\frac 32\right)^{6g-3}\cdot\frac{1}{g!\cdot(3g-2)!\cdot\operatorname{\mathrm{vol}}(T^1\Sigma)^{2g-1}}\cdot L^{6g-4}\cdot e^{L}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{X}}_g(L)\vert\sim \frac {1}{12^g}\cdot\left(\frac 32\right)^{6g-3}\cdot\frac{1}{g!\cdot(3g-2)!\cdot\operatorname{\mathrm{vol}}(T^1\Sigma)^{2g-1}}\cdot L^{6g-4}\cdot e^{L}\end{align*} $$
as
![]() $L\to \infty $
.
$L\to \infty $
.
Proof. From Theorem 1.3, we get that every trivalent graph X has
 $$ \begin{align*}\vert{\mathbf{G}}^X(L)\vert\sim \left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}^X(L)\vert\sim \left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}\end{align*} $$
critical realizations of length at most L in
![]() $\Sigma $
. This implies that whenever X is fat graph of genus g then asymptotically there are
$\Sigma $
. This implies that whenever X is fat graph of genus g then asymptotically there are
 $$ \begin{align*}\frac 1{\vert\operatorname{\mathrm{Aut}}(X)\vert}\left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}\end{align*} $$
$$ \begin{align*}\frac 1{\vert\operatorname{\mathrm{Aut}}(X)\vert}\left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}\end{align*} $$
many elements in
![]() ${\mathbf {X}}_g(L)$
represented by
${\mathbf {X}}_g(L)$
represented by
![]() $(X,\phi )$
for some critical
$(X,\phi )$
for some critical
![]() $\phi :X\to \Sigma $
of length
$\phi :X\to \Sigma $
of length
![]() $\ell (\phi )\leqslant L$
. Adding over all possible types of genus g fat graphs, we get that
$\ell (\phi )\leqslant L$
. Adding over all possible types of genus g fat graphs, we get that
 $$ \begin{align*}\vert{\mathbf{X}}_g(L)\vert\sim\sum_X\frac 1{\vert\operatorname{\mathrm{Aut}}(X)\vert}\left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}.\end{align*} $$
$$ \begin{align*}\vert{\mathbf{X}}_g(L)\vert\sim\sum_X\frac 1{\vert\operatorname{\mathrm{Aut}}(X)\vert}\left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}.\end{align*} $$
From the Bacher–Vdovina [Reference Bacher and Vdovina1] result mentioned earlier and taking into consideration that
![]() $\chi (X)=1-2g$
, we get
$\chi (X)=1-2g$
, we get
 $$ \begin{align*}\vert{\mathbf{X}}_g(L)\vert\sim\frac 2{12^g}\cdot\frac{(6g-5)!}{g!\cdot(3g-3)!}\cdot\left(\frac 32\right)^{6g-3}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{1-2g}}{(6g-4)!}\cdot L^{6g-4}\cdot e^{L}.\end{align*} $$
$$ \begin{align*}\vert{\mathbf{X}}_g(L)\vert\sim\frac 2{12^g}\cdot\frac{(6g-5)!}{g!\cdot(3g-3)!}\cdot\left(\frac 32\right)^{6g-3}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{1-2g}}{(6g-4)!}\cdot L^{6g-4}\cdot e^{L}.\end{align*} $$
The claim follows now from elementary algebra.
Now, from Lemma 7.4 we get that
 $$ \begin{align*}\left\vert{\mathbf{X}}_g\left(\frac L2\right)\right\vert\sim \frac {1}{12^g}\cdot\left(\frac 32\right)^{6g-3}\cdot\frac{1}{g!\cdot(3g-2)!\cdot\operatorname{\mathrm{vol}}(T^1\Sigma)^{2g-1}}\cdot\frac{L^{6g-4}}{2^{6g-4}}\cdot e^{\frac L2}.\end{align*} $$
$$ \begin{align*}\left\vert{\mathbf{X}}_g\left(\frac L2\right)\right\vert\sim \frac {1}{12^g}\cdot\left(\frac 32\right)^{6g-3}\cdot\frac{1}{g!\cdot(3g-2)!\cdot\operatorname{\mathrm{vol}}(T^1\Sigma)^{2g-1}}\cdot\frac{L^{6g-4}}{2^{6g-4}}\cdot e^{\frac L2}.\end{align*} $$
Taking into account that
 $$ \begin{align*}\left\vert{\mathbf{X}}_g\left(\frac L2+\kappa\right)\right\vert\sim\left\vert{\mathbf{X}}_g\left(\frac L2\right)\right\vert\cdot e^{\kappa}=\left\vert{\mathbf{X}}_g\left(\frac L2\right)\right\vert\cdot \left(\frac 43\right)^{6g-3},\end{align*} $$
$$ \begin{align*}\left\vert{\mathbf{X}}_g\left(\frac L2+\kappa\right)\right\vert\sim\left\vert{\mathbf{X}}_g\left(\frac L2\right)\right\vert\cdot e^{\kappa}=\left\vert{\mathbf{X}}_g\left(\frac L2\right)\right\vert\cdot \left(\frac 43\right)^{6g-3},\end{align*} $$
we get that
 $$ \begin{align*}\left\vert{\mathbf{X}}_g\left(\frac L2+\kappa\right)\right\vert \sim\frac {2}{12^g\cdot g!\cdot(3g-2)!\cdot\operatorname{\mathrm{vol}}(T^1\Sigma)^{2g-1}}\cdot L^{6g-4}\cdot e^{\frac L2}.\end{align*} $$
$$ \begin{align*}\left\vert{\mathbf{X}}_g\left(\frac L2+\kappa\right)\right\vert \sim\frac {2}{12^g\cdot g!\cdot(3g-2)!\cdot\operatorname{\mathrm{vol}}(T^1\Sigma)^{2g-1}}\cdot L^{6g-4}\cdot e^{\frac L2}.\end{align*} $$
It follows thus from Equation (7.6) that
as we wanted to show. This concludes the proof of Theorem 1.1.
8 Curves bounding immersed surfaces
We now turn our attention to Theorem 1.2:
Theorem 1.2. Let
![]() $\Sigma $
be a closed, connected and oriented hyperbolic surface and for
$\Sigma $
be a closed, connected and oriented hyperbolic surface and for
![]() $g\geqslant 1$
and
$g\geqslant 1$
and
![]() $L>0$
let
$L>0$
let
![]() ${\mathbf {B}}_g(L)$
be as in Equation (1.3). We have
${\mathbf {B}}_g(L)$
be as in Equation (1.3). We have
as
![]() $L\to \infty $
.
$L\to \infty $
.
Denote by
the set we want to count. From the proof of Theorem 1.1, we get that
 $$ \begin{align*}\vert{\mathbf{B}}_g^{\operatorname{\mathrm{imm}}}(L)\vert\sim\left\vert{\mathbf{X}}_g^{\operatorname{\mathrm{imm}}}\left(\frac L2+\kappa\right)\right\vert,\end{align*} $$
$$ \begin{align*}\vert{\mathbf{B}}_g^{\operatorname{\mathrm{imm}}}(L)\vert\sim\left\vert{\mathbf{X}}_g^{\operatorname{\mathrm{imm}}}\left(\frac L2+\kappa\right)\right\vert,\end{align*} $$
where
![]() $\kappa $
is as in Equation (7.5) and where
$\kappa $
is as in Equation (7.5) and where
 $$ \begin{align*}{\mathbf{X}}_g^{\operatorname{\mathrm{imm}}}(L)\stackrel{\text{def}}=\left\{(X,\phi)\in{\mathbf{X}}_g(L)\,\middle\vert\begin{array}{c}\text{the realization }\phi:X\to\Sigma\text{ extends}\\ \text{to an immersion of the thickening}\\ \operatorname{\mathrm{\mathbf{neigh}}}(X)\text{ of }X\end{array}\right\}.\end{align*} $$
$$ \begin{align*}{\mathbf{X}}_g^{\operatorname{\mathrm{imm}}}(L)\stackrel{\text{def}}=\left\{(X,\phi)\in{\mathbf{X}}_g(L)\,\middle\vert\begin{array}{c}\text{the realization }\phi:X\to\Sigma\text{ extends}\\ \text{to an immersion of the thickening}\\ \operatorname{\mathrm{\mathbf{neigh}}}(X)\text{ of }X\end{array}\right\}.\end{align*} $$
Equivalently,
![]() $(X,\phi )\in {\mathbf {X}}_g$
belongs to
$(X,\phi )\in {\mathbf {X}}_g$
belongs to
![]() ${\mathbf {X}}_g^{\operatorname {\mathrm {imm}}}$
if the cyclic ordering at each vertex of X agrees with the one pulled back from
${\mathbf {X}}_g^{\operatorname {\mathrm {imm}}}$
if the cyclic ordering at each vertex of X agrees with the one pulled back from
![]() $\Sigma $
via
$\Sigma $
via
![]() $\phi $
, that is, the one coming from the orientation of
$\phi $
, that is, the one coming from the orientation of
![]() $\Sigma $
. We can refer to such realizations of a fat graph as fat realizations. With this language, we have that
$\Sigma $
. We can refer to such realizations of a fat graph as fat realizations. With this language, we have that
For a given trivalent fat graph X, let
be the set of fat critical realizations of X of total length at most L. Note that
 $$ \begin{align*}\vert{\mathbf{X}}_g^{\operatorname{\mathrm{imm}}}(L)\vert=\sum_X\frac 1{\vert\operatorname{\mathrm{Aut}}(X)\vert}\vert{\mathbf{G}}^X_{\operatorname{\mathrm{imm}}}(L)\vert.\end{align*} $$
$$ \begin{align*}\vert{\mathbf{X}}_g^{\operatorname{\mathrm{imm}}}(L)\vert=\sum_X\frac 1{\vert\operatorname{\mathrm{Aut}}(X)\vert}\vert{\mathbf{G}}^X_{\operatorname{\mathrm{imm}}}(L)\vert.\end{align*} $$
What is still missing to be able to run the proof as in that of Theorem 1.1 is a version of Theorem 1.3 for
![]() ${\mathbf {G}}^X_{\operatorname {\mathrm {imm}}}$
. Here it is:
${\mathbf {G}}^X_{\operatorname {\mathrm {imm}}}$
. Here it is:
Theorem 8.1. Let
![]() $\Sigma $
be a closed, connected and oriented hyperbolic surface. For every connected trivalent fat graph X, we have
$\Sigma $
be a closed, connected and oriented hyperbolic surface. For every connected trivalent fat graph X, we have
 $$ \begin{align*}\vert{\mathbf{G}}^X_{\operatorname{\mathrm{imm}}}(L)\vert\sim 2^{2\chi(X)}\cdot\left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}^X_{\operatorname{\mathrm{imm}}}(L)\vert\sim 2^{2\chi(X)}\cdot\left(\frac 23\right)^{3\chi(X)}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{\chi(X)}}{(-3\chi(X)-1)!}\cdot L^{-3\chi(X)-1}\cdot e^{L}\end{align*} $$
as
![]() $L\to \infty $
.
$L\to \infty $
.
Assuming Theorem 8.1 for the moment, we get from
![]() $\chi (X)=1-2g$
and from the Bacher–Vdovina theorem that
$\chi (X)=1-2g$
and from the Bacher–Vdovina theorem that
 $$ \begin{align*}\vert{\mathbf{X}}^{\operatorname{\mathrm{imm}}}_g(L)\vert\sim\frac 1{2^{4g-2}}\cdot\frac 2{12^g}\cdot\frac{(6g-5)!}{g!\cdot(3g-3)!}\cdot\left(\frac 32\right)^{6g-3}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{1-2g}}{(6g-4)!}\cdot L^{6g-4}\cdot e^{L}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{X}}^{\operatorname{\mathrm{imm}}}_g(L)\vert\sim\frac 1{2^{4g-2}}\cdot\frac 2{12^g}\cdot\frac{(6g-5)!}{g!\cdot(3g-3)!}\cdot\left(\frac 32\right)^{6g-3}\cdot\frac{\operatorname{\mathrm{vol}}(T^1\Sigma)^{1-2g}}{(6g-4)!}\cdot L^{6g-4}\cdot e^{L}\end{align*} $$
from where we get, as in the proof of Theorem 1.1, that
The claim of Theorem 1.2 follows now from this statement combined with Theorem 1.1.
All that is left to do is to prove Theorem 8.1. Since it is basically identical to the proof of Theorem 1.3, we just point out the differences. The key is to obtain a fat graph version of Proposition 4.2. In a nutshell, the idea of the proof of this proposition was that
-
1. we could compute the volume
 $\operatorname {\mathrm {vol}}(\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}^X(\vec L,h))$
of the set of
$\operatorname {\mathrm {vol}}(\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}^X(\vec L,h))$
of the set of
 $\varepsilon $
-critical realizations of X whose edge lengths were in a box, and
$\varepsilon $
-critical realizations of X whose edge lengths were in a box, and -
2. we knew that every connected component contributes the same amount, and how much.
Let thus
![]() $\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}-\operatorname {\mathrm {imm}}}^X(\vec L,h)\subset \mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}^X(\vec L,h)$
be those
$\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}-\operatorname {\mathrm {imm}}}^X(\vec L,h)\subset \mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}^X(\vec L,h)$
be those
![]() $\varepsilon $
-critical realizations in our box which preserve the fat structure. Recalling now that by Proposition 2.6 the connected components of
$\varepsilon $
-critical realizations in our box which preserve the fat structure. Recalling now that by Proposition 2.6 the connected components of
![]() $\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}^X(\vec L,h)$
have small diameter, we deduce that the induced fat structure is constant over each such connected component. It follows that
$\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}^X(\vec L,h)$
have small diameter, we deduce that the induced fat structure is constant over each such connected component. It follows that
![]() $\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}-\operatorname {\mathrm {imm}}}^X(\vec L,h)$
is a union of connected components of
$\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}-\operatorname {\mathrm {imm}}}^X(\vec L,h)$
is a union of connected components of
![]() $\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}^X(\vec L,h)$
. In particular, to be able to obtain a fat graph version of Proposition 4.2 we just need to be able to compute
$\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}^X(\vec L,h)$
. In particular, to be able to obtain a fat graph version of Proposition 4.2 we just need to be able to compute
![]() $\operatorname {\mathrm {vol}}(\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}-\operatorname {\mathrm {imm}}}^X(\vec L,h))$
.
$\operatorname {\mathrm {vol}}(\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}-\operatorname {\mathrm {imm}}}^X(\vec L,h))$
.
Now, in the proof of Proposition 4.2, the key ingredient of the computation of the volume of
![]() $\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(\vec L,h)$
was Corollary 3.3 – we remind the reader that the statement of the said corollary was that for any
$\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(\vec L,h)$
was Corollary 3.3 – we remind the reader that the statement of the said corollary was that for any
![]() $\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}} X}$
we have
$\vec x\in \Sigma ^{\operatorname {\mathrm {\mathbf {vert}}} X}$
we have
 $$ \begin{align*}\vert{\mathbf{G}}_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}^X(\vec L,h)\vert \sim \varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-3\chi(X)}}\end{align*} $$
$$ \begin{align*}\vert{\mathbf{G}}_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}^X(\vec L,h)\vert \sim \varepsilon^{4\vert\chi(X)\vert}\cdot\left(\frac{2}{3}\right)^{2\chi(X)}\cdot\pi^{\chi(X)}\cdot\frac{(e^h-1)^{-3\chi(X)}\cdot e^{\Vert\vec L\Vert}}{\operatorname{\mathrm{vol}}(\Sigma)^{-3\chi(X)}}\end{align*} $$
as
![]() $\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}L_e\to \infty $
, where
$\min _{e\in \operatorname {\mathrm {\mathbf {edge}}}(X)}L_e\to \infty $
, where
![]() ${\mathbf {G}}^X_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}(\vec L,h)$
is the set of
${\mathbf {G}}^X_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}(\vec L,h)$
is the set of
![]() $\varepsilon $
-critical realizations
$\varepsilon $
-critical realizations
![]() $\phi :X\to \Sigma $
mapping the vertex v to the point
$\phi :X\to \Sigma $
mapping the vertex v to the point
![]() $x_v=\phi (v)$
. As we see, if we want to just copy line-by-line the computation of the volume of
$x_v=\phi (v)$
. As we see, if we want to just copy line-by-line the computation of the volume of
![]() $\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(\vec L,h)$
to get the volume of
$\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}}(\vec L,h)$
to get the volume of
![]() $\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}-\operatorname {\mathrm {imm}}}(\vec L,h)$
what we need to know is the number of elements in the set
$\mathcal G_{\varepsilon -\operatorname {\mathrm {crit}}-\operatorname {\mathrm {imm}}}(\vec L,h)$
what we need to know is the number of elements in the set
![]() ${\mathbf {G}}^X_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}-\operatorname {\mathrm {imm}}}(\vec L,h)$
of
${\mathbf {G}}^X_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}-\operatorname {\mathrm {imm}}}(\vec L,h)$
of
![]() $\varepsilon $
-critical realizations
$\varepsilon $
-critical realizations
![]() $\phi :X\to \Sigma $
mapping the vertex v to the point
$\phi :X\to \Sigma $
mapping the vertex v to the point
![]() $x_v=\phi (v)$
and preserving the fat structure.
$x_v=\phi (v)$
and preserving the fat structure.
Now, to obtain the number of elements in
![]() ${\mathbf {G}}_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X(\vec L,h)$
we invoked Theorem 3.2 and computed the volume of the set
${\mathbf {G}}_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}}^X(\vec L,h)$
we invoked Theorem 3.2 and computed the volume of the set
 $$ \begin{align*}U_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}^X\subset\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\bigoplus_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} T^1_{x_v}\Sigma\right)\end{align*} $$
$$ \begin{align*}U_{\vec x,\varepsilon-\operatorname{\mathrm{crit}}}^X\subset\prod_{v\in\operatorname{\mathrm{\mathbf{vert}}}(X)}\left(\bigoplus_{\bar e\in\operatorname{\mathrm{\mathbf{half}}}_v(X)} T^1_{x_v}\Sigma\right)\end{align*} $$
of those tuples
![]() $(v_{\vec e})_{\vec e\in \operatorname {\mathrm {\mathbf {half}}}(X)}$
with
$(v_{\vec e})_{\vec e\in \operatorname {\mathrm {\mathbf {half}}}(X)}$
with
![]() $\angle (v_{\vec e_1},v_{\vec e_2})\in [\frac {2\pi }3-\varepsilon ,\frac {2\pi }3+\varepsilon ]$
for all distinct
$\angle (v_{\vec e_1},v_{\vec e_2})\in [\frac {2\pi }3-\varepsilon ,\frac {2\pi }3+\varepsilon ]$
for all distinct
![]() $\vec e_1,\vec e_2\in \operatorname {\mathrm {\mathbf {half}}}(X)$
incident to the same vertex. Accordingly, to compute the number of elements in
$\vec e_1,\vec e_2\in \operatorname {\mathrm {\mathbf {half}}}(X)$
incident to the same vertex. Accordingly, to compute the number of elements in
![]() ${\mathbf {G}}_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}\operatorname {\mathrm {imm}}}^X(\vec L,h)$
we need to compute the volume of the set
${\mathbf {G}}_{\vec x,\varepsilon -\operatorname {\mathrm {crit}}\operatorname {\mathrm {imm}}}^X(\vec L,h)$
we need to compute the volume of the set
consisting of tuples such that for any vertex
![]() $v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
the cyclic order of the half-edges incident to v agrees with the one of the corresponding unit tangent vectors. Following the computation of
$v\in \operatorname {\mathrm {\mathbf {vert}}}(X)$
the cyclic order of the half-edges incident to v agrees with the one of the corresponding unit tangent vectors. Following the computation of
![]() $\operatorname {\mathrm {vol}}(U_{\vec x,\varepsilon =\operatorname {\mathrm {crit}}})$
, we get that
$\operatorname {\mathrm {vol}}(U_{\vec x,\varepsilon =\operatorname {\mathrm {crit}}})$
, we get that
As we just discussed, this implies that
and hence that
and thus that
9 Comments
In this section, we discuss where and how much we use the assumption that
![]() $\Sigma $
is a closed orientable surface.
$\Sigma $
is a closed orientable surface.
First, do the results here apply if we replace
 $\Sigma $
by a compact two-dimensional orbifold
$\Sigma $
by a compact two-dimensional orbifold
 $\mathcal O=\Gamma \backslash {\mathbb {H}}^2$
?
$\mathcal O=\Gamma \backslash {\mathbb {H}}^2$
?
The answer is yes for Theorem 1.3, with exactly the same proof. One should just do everything equivariantly. For example, a realization in
![]() $\mathcal O$
of a graph X should be a map
$\mathcal O$
of a graph X should be a map
![]() $\tilde \phi :\tilde X\to {\mathbb {H}}^2$
from the universal cover of X to
$\tilde \phi :\tilde X\to {\mathbb {H}}^2$
from the universal cover of X to
![]() ${\mathbb {H}}^2$
which is equivariant under a homomorphism
${\mathbb {H}}^2$
which is equivariant under a homomorphism
![]() $\tilde \phi _*:\pi _1(X)\to \Gamma $
and where two such pairs
$\tilde \phi _*:\pi _1(X)\to \Gamma $
and where two such pairs
![]() $(\tilde \phi ,\tilde \phi _*)$
and
$(\tilde \phi ,\tilde \phi _*)$
and
![]() $(\tilde \psi ,\tilde \psi _*)$
are identified if they differ by an element of
$(\tilde \psi ,\tilde \psi _*)$
are identified if they differ by an element of
![]() $\Gamma $
. Once we rephrase the situation in those terms, everything extends in the obvious way. For example, the space
$\Gamma $
. Once we rephrase the situation in those terms, everything extends in the obvious way. For example, the space
![]() $\mathcal G^X$
of realizations of a graph in
$\mathcal G^X$
of realizations of a graph in
![]() $\mathcal O$
is now an orbifold: Tthe map
$\mathcal O$
is now an orbifold: Tthe map
![]() $\mathcal G^X\to \mathcal O^{\operatorname {\mathrm {\mathbf {vert}}} X}$
sending each realization to the images of the vertices is a covering in the category of orbifolds.
$\mathcal G^X\to \mathcal O^{\operatorname {\mathrm {\mathbf {vert}}} X}$
sending each realization to the images of the vertices is a covering in the category of orbifolds.
On the other hand, to prove Theorem 1.1 one needs to be a little bit careful because in Section 5 and Section 6 we used repeatedly that every sufficiently short curve in
![]() $\Sigma $
is homotopically trivial, and this is no longer true if we are working in
$\Sigma $
is homotopically trivial, and this is no longer true if we are working in
![]() $\mathcal O$
.
$\mathcal O$
.
What about allowing
 $\Sigma $
to have cusps?
$\Sigma $
to have cusps?
Here, we again have problems with the discussion in Section 5 and Section 6, but this time it is much worse. In some sense, the results of Section 5 and Section 6 are just generalizations of Lemma 4.1, and this lemma fails in the presence of cusps: Indeed, suppose that
![]() $\Sigma $
is a once punctured torus and X is a graph with two vertices x and
$\Sigma $
is a once punctured torus and X is a graph with two vertices x and
![]() $x'$
(if you wish, you can make X trivalent while essentially keeping the same reasoning as we will present, but doing so might obscure things slightly) and with six edges
$x'$
(if you wish, you can make X trivalent while essentially keeping the same reasoning as we will present, but doing so might obscure things slightly) and with six edges
![]() $f_1,f_2,e_1,e_2,e_3$
and h such that
$f_1,f_2,e_1,e_2,e_3$
and h such that
-
○ the edges
 $f_1,f_2$
are incident on both ends to x,
$f_1,f_2$
are incident on both ends to x, -
○ the edges
 $e_1,e_2,e_3$
are incidents on both ends to
$e_1,e_2,e_3$
are incidents on both ends to
 $x'$
and
$x'$
and -
○ the edge h runs from x to
 $x'$
.
$x'$
.
Fix now a horospherical neighborhood of the cusps in
![]() $\Sigma $
, fix a point
$\Sigma $
, fix a point
![]() $\mathbf {x}_0$
and let
$\mathbf {x}_0$
and let
![]() $\mathbf {x}_t$
be the point at distance t of
$\mathbf {x}_t$
be the point at distance t of
![]() $\mathbf {x}_0$
along the ray pointing directly into the cusp. Now, if we are given a vector
$\mathbf {x}_0$
along the ray pointing directly into the cusp. Now, if we are given a vector
![]() $\vec L=(F_1,F_2,E_1,E_3,E_3,H)$
with positive real coefficients consider realizations
$\vec L=(F_1,F_2,E_1,E_3,E_3,H)$
with positive real coefficients consider realizations
![]() $\phi :X\to \Sigma $
with
$\phi :X\to \Sigma $
with
![]() $\phi (x)=\mathbf {x}_0$
, with
$\phi (x)=\mathbf {x}_0$
, with
![]() $\phi (x')=\mathbf {x}_H$
, and with
$\phi (x')=\mathbf {x}_H$
, and with
![]() $\phi (h)$
equal to the segment of length H joining
$\phi (h)$
equal to the segment of length H joining
![]() $\mathbf {x}_0$
and
$\mathbf {x}_0$
and
![]() $\mathbf {x}_H$
. Now, we have
$\mathbf {x}_H$
. Now, we have
![]() $\operatorname {\mathrm {\mathbf {const}}} e^{F_1+F_2}$
choices for the images of
$\operatorname {\mathrm {\mathbf {const}}} e^{F_1+F_2}$
choices for the images of
![]() $f_1$
and
$f_1$
and
![]() $f_2$
subject to the restriction that
$f_2$
subject to the restriction that
![]() $\phi (f_i)$
is for
$\phi (f_i)$
is for
![]() $i=1,2$
a geodesic segment of length at most
$i=1,2$
a geodesic segment of length at most
![]() $F_i$
. Note also that the horospherical simple loop based at
$F_i$
. Note also that the horospherical simple loop based at
![]() $\mathbf {x}_H$
has length
$\mathbf {x}_H$
has length
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot e^{-H}$
and that geodesic loops in the cusp, based at
$\operatorname {\mathrm {\mathbf {const}}}\cdot e^{-H}$
and that geodesic loops in the cusp, based at
![]() $\mathbf {x}_H$
and with length
$\mathbf {x}_H$
and with length
![]() $\ell $
are homotopic to horospherical segments of length at most
$\ell $
are homotopic to horospherical segments of length at most
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\frac \ell 2}$
. This implies that, if we want to map
$\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\frac \ell 2}$
. This implies that, if we want to map
![]() $e_i$
to a loop in the cusp and of length at most
$e_i$
to a loop in the cusp and of length at most
![]() $E_i$
, then we have at least
$E_i$
, then we have at least
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\frac 12E_i}\cdot e^H$
choices. Altogether we have at least
$\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\frac 12E_i}\cdot e^H$
choices. Altogether we have at least
choices of (homotopy classes of) realizations of X into
![]() $\Sigma $
with
$\Sigma $
with
![]() $\ell (\phi (f_1))\leqslant F_1$
,
$\ell (\phi (f_1))\leqslant F_1$
,
![]() $\ell (\phi (f_2))\leqslant F_2$
,
$\ell (\phi (f_2))\leqslant F_2$
,
![]() $\ell (\phi (e_1))\leqslant E_1$
,
$\ell (\phi (e_1))\leqslant E_1$
,
![]() $\ell (\phi (e_2))\leqslant E_2$
$\ell (\phi (e_2))\leqslant E_2$
![]() $\ell (\phi (e_3))\leqslant E_3$
,
$\ell (\phi (e_3))\leqslant E_3$
,
![]() $\ell (\phi (H))\leqslant H$
. In particular, if we set
$\ell (\phi (H))\leqslant H$
. In particular, if we set
 $$ \begin{align*}\vec L=(F_1,F_2,E_1,E_2,E_3,H)=\left(n,n,\frac 12n,\frac 12n,\frac 12 n,\frac 52n\right)\end{align*} $$
$$ \begin{align*}\vec L=(F_1,F_2,E_1,E_2,E_3,H)=\left(n,n,\frac 12n,\frac 12n,\frac 12 n,\frac 52n\right)\end{align*} $$
we have at least
![]() $\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\frac {61}4n}$
such realizations, and this is a much larger number than
$\operatorname {\mathrm {\mathbf {const}}}\cdot e^{\frac {61}4n}$
such realizations, and this is a much larger number than
![]() $\operatorname {\mathrm {\mathbf {const}}} e^{6n}=\operatorname {\mathrm {\mathbf {const}}} e^{\Vert L\Vert }$
. This proves that the analogue of Lemma 4.1 fails if
$\operatorname {\mathrm {\mathbf {const}}} e^{6n}=\operatorname {\mathrm {\mathbf {const}}} e^{\Vert L\Vert }$
. This proves that the analogue of Lemma 4.1 fails if
![]() $\Sigma $
is not compact.
$\Sigma $
is not compact.
In summary, if
![]() $\Sigma $
has finite volume but is not compact, then we do not even know whether Theorem 1.3 holds. Although, we suspect that the answer is yes.
$\Sigma $
has finite volume but is not compact, then we do not even know whether Theorem 1.3 holds. Although, we suspect that the answer is yes.
Can
 $\Sigma $
be nonorientable?
$\Sigma $
be nonorientable?
If
![]() $\Sigma $
is a compact hyperbolic surface which, however, is nonorientable, then we know that both Theorem 1.3 and Theorem 1.1 hold true: We never used orientability during their proofs. We did, however, in the proof of Theorem 1.2: Unless
$\Sigma $
is a compact hyperbolic surface which, however, is nonorientable, then we know that both Theorem 1.3 and Theorem 1.1 hold true: We never used orientability during their proofs. We did, however, in the proof of Theorem 1.2: Unless
![]() $\Sigma $
is oriented, it makes little sense to speak about the induced fat graph structure. We do not know what happens with Theorem 1.2 when the ambient surface is not oriented.
$\Sigma $
is oriented, it makes little sense to speak about the induced fat graph structure. We do not know what happens with Theorem 1.2 when the ambient surface is not oriented.
And what about higher dimensions?
If we replace
![]() $\Sigma $
by a closed hyperbolic manifold of other dimension than
$\Sigma $
by a closed hyperbolic manifold of other dimension than
![]() $2$
, then Theorem 1.3 and Theorem 1.1 should still hold and with proofs which, if not identical, keep the same spirit. It is, however, less clear whether there should be an interesting analogue of Theorem 1.2: at least if
$2$
, then Theorem 1.3 and Theorem 1.1 should still hold and with proofs which, if not identical, keep the same spirit. It is, however, less clear whether there should be an interesting analogue of Theorem 1.2: at least if
![]() $\dim \geqslant 5$
, where every map of a surface can be deformed to an embedding.
$\dim \geqslant 5$
, where every map of a surface can be deformed to an embedding.
A The geometric prime number theorem
The argument we used to prove Theorem 1.3 can be used to recover Huber’s geometric primer number theorem, and this is what we do here. Besides giving a simple proof of this theorem, it might help the reader understand the logic of the proof of Theorem 1.3.
The geometric prime number theorem (Huber)
Let
![]() $\Sigma $
be a closed, connected, orientable, hyperbolic surface, and let
$\Sigma $
be a closed, connected, orientable, hyperbolic surface, and let
![]() ${\mathbf {C}}(L)$
be the set of closed nontrivial oriented geodesics in
${\mathbf {C}}(L)$
be the set of closed nontrivial oriented geodesics in
![]() $\Sigma $
of length at most L. We have
$\Sigma $
of length at most L. We have
as
![]() $L\to \infty $
.
$L\to \infty $
.
Remark. In Section 9, we discussed some of the difficulties one would face when extending the main results to the case that
![]() $\Sigma $
is a finite volume surface or an orbifold. None of these problems really arise when proving the geometric prime number theorem, and indeed the proof we present here works with only minimal changes if
$\Sigma $
is a finite volume surface or an orbifold. None of these problems really arise when proving the geometric prime number theorem, and indeed the proof we present here works with only minimal changes if
![]() $\Sigma $
is replaced by an arbitrary finite area orbifold
$\Sigma $
is replaced by an arbitrary finite area orbifold
![]() $\Gamma \backslash {\mathbb {H}}^2$
. We decided to just deal with the compact case to avoid hiding the structure of the argument.
$\Gamma \backslash {\mathbb {H}}^2$
. We decided to just deal with the compact case to avoid hiding the structure of the argument.
The proof of Huber’s theorem would be cleaner and nicer if all closed geodesics were primitive. Luckily, this is almost true. Indeed, it follows, for example, from the work of Coornaert and Knieper [Reference Coornaert and Knieper6] that there is some
![]() $C>0$
with
$C>0$
with
for all
![]() $L>0$
. We stress that the Coornaert–Knieper argument is pretty coarse: What they actually prove is a statement about groups acting isometrically, discretely and cocompactly on Gromov-hyperbolic spaces.
$L>0$
. We stress that the Coornaert–Knieper argument is pretty coarse: What they actually prove is a statement about groups acting isometrically, discretely and cocompactly on Gromov-hyperbolic spaces.
The point for us is that Equation (A.1) implies that most geodesics of length at most L are primitive. Indeed, every nonprimitive geodesic of length at most L is a multiple of a primitive geodesic of length at most
![]() $\frac 12 L$
. On the other hand, if
$\frac 12 L$
. On the other hand, if
![]() $s_0$
is the systole of
$s_0$
is the systole of
![]() $\Sigma $
, then at most
$\Sigma $
, then at most
![]() $\frac {L}{s_0}$
geodesics of length at most L arise as multiples of any given geodesic. These two observations, together with the right side of Equation (A.1), imply that there are at most
$\frac {L}{s_0}$
geodesics of length at most L arise as multiples of any given geodesic. These two observations, together with the right side of Equation (A.1), imply that there are at most
![]() $\frac L{s_0}{\mathbf {C}}(\frac 12L)\leqslant \frac C{s_0}\cdot L\cdot e^{L/2}$
nonprimitive geodesics of length at most L. Taking the left side of Equation (A.1) into consideration we deduce that, as we had claimed above, most geodesics are primitive.
$\frac L{s_0}{\mathbf {C}}(\frac 12L)\leqslant \frac C{s_0}\cdot L\cdot e^{L/2}$
nonprimitive geodesics of length at most L. Taking the left side of Equation (A.1) into consideration we deduce that, as we had claimed above, most geodesics are primitive.
Lemma A.1. Fix h, and let
![]() ${\mathbf {C}}(L,h)$
and
${\mathbf {C}}(L,h)$
and
![]() ${\mathbf {P}}(L,h)$
be, respectively, the sets of all geodesics and of all primitive geodesics of length in
${\mathbf {P}}(L,h)$
be, respectively, the sets of all geodesics and of all primitive geodesics of length in
![]() $[L,L+h]$
. Then we have
$[L,L+h]$
. Then we have
as
![]() $L\to \infty $
.
$L\to \infty $
.
After this preparatory comment, let us start the real business. Let
![]() ${\mathcal {L}}$
be the space of all geodesic loops in
${\mathcal {L}}$
be the space of all geodesic loops in
![]() $\Sigma $
, and consider the map
$\Sigma $
, and consider the map
![]() $\Pi :{\mathcal {L}}\to \Sigma $
mapping each loop to its base point. As was the case for more general graphs, the map
$\Pi :{\mathcal {L}}\to \Sigma $
mapping each loop to its base point. As was the case for more general graphs, the map
![]() $\Pi $
is a covering, meaning that when we pull back the hyperbolic metric using
$\Pi $
is a covering, meaning that when we pull back the hyperbolic metric using
![]() $\Pi $
we can think of
$\Pi $
we can think of
![]() ${\mathcal {L}}$
as being a hyperbolic surface. Note also that the set of connected components of
${\mathcal {L}}$
as being a hyperbolic surface. Note also that the set of connected components of
![]() ${\mathcal {L}}$
agrees with the set of free homotopy classes of loops. It follows that for every closed geodesic
${\mathcal {L}}$
agrees with the set of free homotopy classes of loops. It follows that for every closed geodesic
![]() $\gamma $
we have a connected component
$\gamma $
we have a connected component
![]() ${\mathcal {L}}^{\gamma }$
.
${\mathcal {L}}^{\gamma }$
.
Now, given
![]() $\varepsilon>0$
small let
$\varepsilon>0$
small let
![]() ${\mathcal {L}}_{\varepsilon }$
be the set of all geodesic loops with angle defect at most
${\mathcal {L}}_{\varepsilon }$
be the set of all geodesic loops with angle defect at most
![]() $\varepsilon $
, that is, the set of geodesic loops whose initial and terminal velocity vectors meet with unoriented angle in
$\varepsilon $
, that is, the set of geodesic loops whose initial and terminal velocity vectors meet with unoriented angle in
![]() $[0,\varepsilon ]$
. For
$[0,\varepsilon ]$
. For
![]() $L>0$
, let
$L>0$
, let
![]() ${\mathcal {L}}_{\varepsilon }(L,L+h)$
be the elements in
${\mathcal {L}}_{\varepsilon }(L,L+h)$
be the elements in
![]() ${\mathcal {L}}_{\varepsilon }$
with length between L and
${\mathcal {L}}_{\varepsilon }$
with length between L and
![]() $L+h$
. Accordingly, set
$L+h$
. Accordingly, set
![]() ${\mathcal {L}}^{\gamma }_{\varepsilon }(L,L+h)={\mathcal {L}}^{\gamma }\cap {\mathcal {L}}_{\varepsilon }(L,L+h)$
.
${\mathcal {L}}^{\gamma }_{\varepsilon }(L,L+h)={\mathcal {L}}^{\gamma }\cap {\mathcal {L}}_{\varepsilon }(L,L+h)$
.
Let us establish some basic properties of
![]() ${\mathcal {L}}_{\varepsilon }(L,L+h)$
and
${\mathcal {L}}_{\varepsilon }(L,L+h)$
and
![]() ${\mathcal {L}}_{\varepsilon }^{\gamma }(L,L+h)$
:
${\mathcal {L}}_{\varepsilon }^{\gamma }(L,L+h)$
:
Lemma A.2. Fix
![]() $h>0$
and
$h>0$
and
![]() $\varepsilon>0$
. We have that
$\varepsilon>0$
. We have that
Moreover, there is a function
![]() $C(\varepsilon )$
with
$C(\varepsilon )$
with
![]() $\lim _{\varepsilon \to 0}C(\varepsilon )=1$
such that for every sufficiently long closed geodesic
$\lim _{\varepsilon \to 0}C(\varepsilon )=1$
such that for every sufficiently long closed geodesic
![]() $\gamma $
we have that
$\gamma $
we have that
-
1.
 ${\mathcal {L}}_{\varepsilon }^{\gamma }(L,L+h)=\varnothing $
unless
${\mathcal {L}}_{\varepsilon }^{\gamma }(L,L+h)=\varnothing $
unless
 $\ell (\gamma )\in [L-\varepsilon ,L+h]$
,
$\ell (\gamma )\in [L-\varepsilon ,L+h]$
, -
2.
 $\operatorname {\mathrm {vol}}({\mathcal {L}}_{\varepsilon }^{\gamma }(L,L+h))\leqslant C(\varepsilon )\cdot \varepsilon \cdot L$
and
$\operatorname {\mathrm {vol}}({\mathcal {L}}_{\varepsilon }^{\gamma }(L,L+h))\leqslant C(\varepsilon )\cdot \varepsilon \cdot L$
and -
3.
 $C(\varepsilon )^{-1}\leqslant \frac 1{\varepsilon \cdot L}\operatorname {\mathrm {vol}}({\mathcal {L}}_{\gamma }^{\varepsilon }(L,L+h))\leqslant C(\varepsilon )$
if
$C(\varepsilon )^{-1}\leqslant \frac 1{\varepsilon \cdot L}\operatorname {\mathrm {vol}}({\mathcal {L}}_{\gamma }^{\varepsilon }(L,L+h))\leqslant C(\varepsilon )$
if
 $\gamma $
is primitive and
$\gamma $
is primitive and
 $\ell (\gamma )\in [L,L+h-\varepsilon ]$
.
$\ell (\gamma )\in [L,L+h-\varepsilon ]$
.
Proof. As in the proof of Proposition 4.2, we exploit the cover
![]() $\Pi :{\mathcal {L}}\to \Sigma $
to compute the volume of
$\Pi :{\mathcal {L}}\to \Sigma $
to compute the volume of
![]() ${\mathcal {L}}_{\varepsilon }(L,L+h)$
:
${\mathcal {L}}_{\varepsilon }(L,L+h)$
:
Now,
![]() $\Pi ^{-1}(x)\cap {\mathcal {L}}_{\varepsilon }(L,L+h)$
is nothing other than the number of geodesic arcs going from x to x with length within
$\Pi ^{-1}(x)\cap {\mathcal {L}}_{\varepsilon }(L,L+h)$
is nothing other than the number of geodesic arcs going from x to x with length within
![]() $[L,L+h]$
and such that the initial and terminal velocities make at most angle
$[L,L+h]$
and such that the initial and terminal velocities make at most angle
![]() $\varepsilon $
. Once we fix x, the set of admissive pairs of initial and terminal velocities is a subset
$\varepsilon $
. Once we fix x, the set of admissive pairs of initial and terminal velocities is a subset
![]() $T^1_x\Sigma \times T^1_x\Sigma $
with volume
$T^1_x\Sigma \times T^1_x\Sigma $
with volume
![]() $4\pi \varepsilon $
. We thus get from Theorem 3.2 that
$4\pi \varepsilon $
. We thus get from Theorem 3.2 that
 $$ \begin{align*}\vert\Pi^{-1}(x)\cap{\mathcal{L}}_{\varepsilon}(L,L+h)\vert\sim\varepsilon\cdot\frac{e^{L+h}-e^L}{\operatorname{\mathrm{vol}}(\Sigma)}.\end{align*} $$
$$ \begin{align*}\vert\Pi^{-1}(x)\cap{\mathcal{L}}_{\varepsilon}(L,L+h)\vert\sim\varepsilon\cdot\frac{e^{L+h}-e^L}{\operatorname{\mathrm{vol}}(\Sigma)}.\end{align*} $$
Since we are assuming that
![]() $\Sigma $
is closed, this is uniform in x, meaning that we get
$\Sigma $
is closed, this is uniform in x, meaning that we get
 $$ \begin{align*}\operatorname{\mathrm{vol}}({\mathcal{L}}_{\varepsilon}(L,L+h))\sim\int_{\Sigma}\varepsilon\cdot\frac{e^{L+h}-e^L}{\operatorname{\mathrm{vol}}(\Sigma)}=\varepsilon\cdot(e^{L+h}-e^L).\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{vol}}({\mathcal{L}}_{\varepsilon}(L,L+h))\sim\int_{\Sigma}\varepsilon\cdot\frac{e^{L+h}-e^L}{\operatorname{\mathrm{vol}}(\Sigma)}=\varepsilon\cdot(e^{L+h}-e^L).\end{align*} $$
We have proved the first claim.
To prove the rest, let us give a concrete description of
![]() ${\mathcal {L}}^{\gamma }$
. Writing
${\mathcal {L}}^{\gamma }$
. Writing
![]() $\gamma =\eta ^k$
for some
$\gamma =\eta ^k$
for some
![]() $\eta $
primitive and
$\eta $
primitive and
![]() $k\geqslant 1$
, consider the cover
$k\geqslant 1$
, consider the cover
of
![]() $\Sigma $
corresponding to
$\Sigma $
corresponding to
![]() $\eta $
. Now, for each
$\eta $
. Now, for each
![]() $x\in \langle \eta \rangle \backslash {\mathbb {H}}^2$
there is a unique hyperbolic loop
$x\in \langle \eta \rangle \backslash {\mathbb {H}}^2$
there is a unique hyperbolic loop
![]() $\gamma _x$
based at x and freely homotopic to running k times over
$\gamma _x$
based at x and freely homotopic to running k times over
![]() $\eta $
. The basic observation is that the map
$\eta $
. The basic observation is that the map
is an isometry between
![]() $\langle \eta \rangle \backslash {\mathbb {H}}^2$
and the connected component
$\langle \eta \rangle \backslash {\mathbb {H}}^2$
and the connected component
![]() ${\mathcal {L}}^{\gamma }$
.
${\mathcal {L}}^{\gamma }$
.

Figure 6 The cylinder
![]() $\langle \gamma \rangle \backslash {\mathbb {H}}^2$
. The marked angles each measures one half of the angle defect of
$\langle \gamma \rangle \backslash {\mathbb {H}}^2$
. The marked angles each measures one half of the angle defect of
![]() $\gamma _x$
.
$\gamma _x$
.
Now, if one denotes by d the distance in
![]() $\langle \eta \rangle \backslash {\mathbb {H}}^2$
between x and the central geodesic (see Figure 6) one gets from formula 2.3.1(vi) in the final page in [Reference Buser3] that
$\langle \eta \rangle \backslash {\mathbb {H}}^2$
between x and the central geodesic (see Figure 6) one gets from formula 2.3.1(vi) in the final page in [Reference Buser3] that
 $$ \begin{align*} \frac 12\cdot(\text{angle defect of }\gamma_x) &\sim\tan\left(\frac 12\cdot(\text{angle defect of }\gamma_x)\right)\\ &=\sinh(d)\cdot\tanh\left(\frac{\ell(\gamma)}2\right)\sim d, \end{align*} $$
$$ \begin{align*} \frac 12\cdot(\text{angle defect of }\gamma_x) &\sim\tan\left(\frac 12\cdot(\text{angle defect of }\gamma_x)\right)\\ &=\sinh(d)\cdot\tanh\left(\frac{\ell(\gamma)}2\right)\sim d, \end{align*} $$
where the asymptotics hold when
![]() $\ell (\gamma )$
is large and the angle defect is small. Now, claims (1), (2) and (3) follow from elementary considerations.
$\ell (\gamma )$
is large and the angle defect is small. Now, claims (1), (2) and (3) follow from elementary considerations.
Armed with these two lemmas, we are ready to conclude the proof of the geometric prime number theorem. Note that it suffices to prove that for h positive and fixed we have
as
![]() $L\to \infty $
. Here,
$L\to \infty $
. Here,
![]() ${\mathbf {C}}(L,h)$
is as in Lemma A.1.
${\mathbf {C}}(L,h)$
is as in Lemma A.1.
Nevertheless, with notation as in both lemmas we have for
![]() $\varepsilon $
positive and small and for L large that
$\varepsilon $
positive and small and for L large that
 $$ \begin{align*} \vert{\mathbf{P}}(L,h)\vert &\stackrel{\text{A.2(3)}}\preceq\frac{C(\varepsilon)}{\varepsilon\cdot L}\operatorname{\mathrm{vol}}\left(\cup_{\gamma\in{\mathbf{P}}(L,h)}{\mathcal{L}}_{\varepsilon}^{\gamma}(L,L+h+\varepsilon)\right)\\ &\leqslant\frac{C(\varepsilon)}{\varepsilon\cdot L}\operatorname{\mathrm{vol}}({\mathcal{L}}_{\varepsilon}(L,L+h+\varepsilon))\\ &\stackrel{\text{A.2}}\sim C(\varepsilon)\cdot\frac{e^{L+h+\varepsilon}-e^L}L. \end{align*} $$
$$ \begin{align*} \vert{\mathbf{P}}(L,h)\vert &\stackrel{\text{A.2(3)}}\preceq\frac{C(\varepsilon)}{\varepsilon\cdot L}\operatorname{\mathrm{vol}}\left(\cup_{\gamma\in{\mathbf{P}}(L,h)}{\mathcal{L}}_{\varepsilon}^{\gamma}(L,L+h+\varepsilon)\right)\\ &\leqslant\frac{C(\varepsilon)}{\varepsilon\cdot L}\operatorname{\mathrm{vol}}({\mathcal{L}}_{\varepsilon}(L,L+h+\varepsilon))\\ &\stackrel{\text{A.2}}\sim C(\varepsilon)\cdot\frac{e^{L+h+\varepsilon}-e^L}L. \end{align*} $$
On the other hand, we also have that
 $$ \begin{align*} \vert{\mathbf{C}}(L,h)\vert &\stackrel{\text{A.2(2)}}\geqslant\frac 1{C(\varepsilon)\cdot\varepsilon\cdot L}\operatorname{\mathrm{vol}}\left(\cup_{\gamma\in{\mathbf{C}}(L,h)}{\mathcal{L}}_{\varepsilon}(L,h)\right)\\ &=\frac 1{C(\varepsilon)\cdot\varepsilon\cdot L}\operatorname{\mathrm{vol}}({\mathcal{L}}_{\varepsilon}(L,h))\\ &\stackrel{\text{A.2}}\sim \frac 1{C(\varepsilon)}\frac{e^{L+h}-e^L}L. \end{align*} $$
$$ \begin{align*} \vert{\mathbf{C}}(L,h)\vert &\stackrel{\text{A.2(2)}}\geqslant\frac 1{C(\varepsilon)\cdot\varepsilon\cdot L}\operatorname{\mathrm{vol}}\left(\cup_{\gamma\in{\mathbf{C}}(L,h)}{\mathcal{L}}_{\varepsilon}(L,h)\right)\\ &=\frac 1{C(\varepsilon)\cdot\varepsilon\cdot L}\operatorname{\mathrm{vol}}({\mathcal{L}}_{\varepsilon}(L,h))\\ &\stackrel{\text{A.2}}\sim \frac 1{C(\varepsilon)}\frac{e^{L+h}-e^L}L. \end{align*} $$
Since this holds for all
![]() $\varepsilon $
, and since
$\varepsilon $
, and since
![]() $C(\varepsilon )$
tends to
$C(\varepsilon )$
tends to
![]() $1$
when
$1$
when
![]() $\varepsilon \to 0$
we have that
$\varepsilon \to 0$
we have that
Now, Lemma A.1 implies Equation (A.2), and Bob’s your uncle.
Acknowledgements
We thank Vincent Delecroix, Lars Louder, Michael Magee and Peter Sarnak for their very helpful comments. The second author is also very grateful for the patience shown by Sébastien Gouëzel, Vincent Guirardel and François Maucourant with all his questions – it is nice to have one’s office next to theirs.
Competing interests
The authors have no competing interest to declare.
Data availability statement
No data were used in this research.
Funding statement
The first author gratefully acknowledges support from EPSRC grant EP/T015926/1 and UiT Aurora Center for Mathematical Structures in Computations (MASCOT).