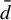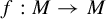Refine search
Actions for selected content:
147 results
The
 $\beta $-transformation with a hole at
$\beta $-transformation with a hole at  $0$: the general case
$0$: the general case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution of integers with digit restrictions via Markov chains
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SHORTEST DISTANCE BETWEEN ORBITS IN CONFORMAL ITERATED FUNCTION SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-11
-
- Article
- Export citation
KATSURA–EXEL–PARDO SELF-SIMILAR ACTIONS, PUTNAM’S BINARY FACTORS AND THEIR LIMIT SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 31 October 2025, pp. 382-417
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The group of reversible turing machines: subgroups, generators, and computability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 October 2025, e176
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy stability and Milnor–Thurston invariants for Bowen–Series-like maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\overline {d}$-continuity for countable state shifts
$\overline {d}$-continuity for countable state shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-24
-
- Article
- Export citation
Ergodic optimization for continuous functions on non-Markov shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 15 August 2025, pp. 263-290
- Print publication:
- January 2026
-
- Article
- Export citation
Topological structure of isolated points in the space of
 $\mathbb {Z}^d$-shifts
$\mathbb {Z}^d$-shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 18 June 2025, pp. 3344-3376
- Print publication:
- November 2025
-
- Article
- Export citation
Borel complexity of sets of points with prescribed Birkhoff averages in Polish dynamical systems with a specification property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 2695-2723
- Print publication:
- September 2025
-
- Article
- Export citation
On the algorithmic descriptive complexity of attractors in topological dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2533-2560
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On partial rigidity of
 $\mathcal {S}$-adic subshifts
$\mathcal {S}$-adic subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2724-2764
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds for equilibrium states on amenable group subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 2414-2438
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An embedding theorem for multidimensional subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 1870-1914
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decidability of the isomorphism problem between multidimensional substitutive subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2054-2094
- Print publication:
- July 2025
-
- Article
- Export citation
The socle of subshift algebras, with applications to subshift conjugacy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-26
-
- Article
- Export citation
Effective dynamical systems beyond dimension zero and factors of SFTs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1329-1369
- Print publication:
- May 2025
-
- Article
- Export citation
On transversal Hölder regularity for flat Wieler solenoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 294-320
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal and proximal examples of
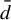 $\bar {d}$-stable and
$\bar {d}$-stable and 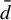 $\bar {d}$-approachable shift spaces
$\bar {d}$-approachable shift spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 396-426
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Symbolic dynamics for pointwise hyperbolic systems on open regions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 595-648
- Print publication:
- February 2025
-
- Article
- Export citation