No CrossRef data available.
Article contents
On a class of self-similar sets which contain finitely many common points
Published online by Cambridge University Press: 30 May 2024
Abstract
For $\lambda \in (0,\,1/2]$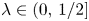 let $K_\lambda \subset \mathbb {R}$
let $K_\lambda \subset \mathbb {R}$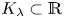 be a self-similar set generated by the iterated function system $\{\lambda x,\, \lambda x+1-\lambda \}$
be a self-similar set generated by the iterated function system $\{\lambda x,\, \lambda x+1-\lambda \}$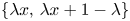 . Given $x\in (0,\,1/2)$
. Given $x\in (0,\,1/2)$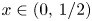 , let $\Lambda (x)$
, let $\Lambda (x)$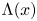 be the set of $\lambda \in (0,\,1/2]$
be the set of $\lambda \in (0,\,1/2]$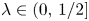 such that $x\in K_\lambda$
such that $x\in K_\lambda$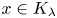 . In this paper we show that $\Lambda (x)$
. In this paper we show that $\Lambda (x)$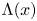 is a topological Cantor set having zero Lebesgue measure and full Hausdorff dimension. Furthermore, we show that for any $y_1,\,\ldots,\, y_p\in (0,\,1/2)$
is a topological Cantor set having zero Lebesgue measure and full Hausdorff dimension. Furthermore, we show that for any $y_1,\,\ldots,\, y_p\in (0,\,1/2)$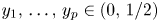 there exists a full Hausdorff dimensional set of $\lambda \in (0,\,1/2]$
there exists a full Hausdorff dimensional set of $\lambda \in (0,\,1/2]$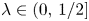 such that $y_1,\,\ldots,\, y_p \in K_\lambda$
such that $y_1,\,\ldots,\, y_p \in K_\lambda$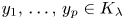 .
.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Astels, S.. Cantor sets and numbers with restricted partial quotients. Trans. Amer. Math. Soc. 352 (2000), 133–170.10.1090/S0002-9947-99-02272-2CrossRefGoogle Scholar
Biebler, S.. A complex gap lemma. Proc. Amer. Math. Soc. 148 (2020), 351–364.10.1090/proc/14716CrossRefGoogle Scholar
Bonanno, C., Carminati, C., Isola, S. and Tiozzo, G.. Dynamics of continued fractions and kneading sequences of unimodal maps. Discrete Contin. Dyn. Syst. 33 (2013), 1313–1332.10.3934/dcds.2013.33.1313CrossRefGoogle Scholar
Boes, D., Darst, R. and Erdős, P.. Fat, symmetric, irrational Cantor sets. Amer. Math. Monthly 88 (1981), 340–341.10.1080/00029890.1981.11995266CrossRefGoogle Scholar
Carminati, C. and Tiozzo, G.. The bifurcation locus for numbers of bounded type. Ergodic Theory Dynam. Syst. 42 (2022), 2239–2269.10.1017/etds.2021.28CrossRefGoogle Scholar
Douady, A., Topological entropy of unimodal maps: monotonicity for quadratic polynomials. Real and Complex Dynamical Systems (Hillerød, 1993) (NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, 464) (Kluwer, Dordrecht, 1995), pp. 65–87.Google Scholar
Falconer, K.. Fractal geometry: Mathematical foundations and applications, Third Edition (Chichester: John Wiley & Sons Ltd., 2014).Google Scholar
Falconer, K. and Yavicoli, A.. Intersections of thick compact sets in $\mathbb {R}^d$ . Math. Z. 301 (2022), 2291–2315.10.1007/s00209-022-02992-yCrossRefGoogle Scholar
. Math. Z. 301 (2022), 2291–2315.10.1007/s00209-022-02992-yCrossRefGoogle Scholar
Feng, D.-J. and Wu, Y.-F.. On arithmetic sums of fractal sets in $\mathbb {R}^d$ . J. Lond. Math. Soc. (2) 104 (2021), 35–65.10.1112/jlms.12422CrossRefGoogle Scholar
. J. Lond. Math. Soc. (2) 104 (2021), 35–65.10.1112/jlms.12422CrossRefGoogle Scholar
Fishman, L. and Simmons, D.. Intrinsic approximation for fractals defined by rational iterated function systems: Mahler's research suggestion. Proc. Lond. Math. Soc. (3) 109 (2014), 189–212.10.1112/plms/pdu002CrossRefGoogle Scholar
Fishman, L. and Simmons, D.. Extrinsic Diophantine approximation on manifolds and fractals. J. Math. Pures Appl. (9) 104 (2015), 83–101.10.1016/j.matpur.2015.02.002CrossRefGoogle Scholar
Hunt, B. R., Kan, I. and Yorke, J. A.. When Cantor sets intersect thickly. Trans. Amer. Math. Soc. 339 (1993), 869–888.10.1090/S0002-9947-1993-1117219-8CrossRefGoogle Scholar
Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J. 30 (1981), 713–747.10.1512/iumj.1981.30.30055CrossRefGoogle Scholar
Jiang, K., Kong, D. and Li, W.. How likely can a point be in different cantor sets. Nonlinearity 35 (2022), 1402–1430.10.1088/1361-6544/ac4b3cCrossRefGoogle Scholar
Kong, D., Li, W., Lü, F., Wang, Z. and Xu, J.. Univoque bases of real numbers: local dimension, Devil's staircase and isolated points. Adv. Appl. Math. 121 (2020), 102103.10.1016/j.aam.2020.102103CrossRefGoogle Scholar
Levesley, J., Salp, C. and Velani, S. L.. On a problem of K. Mahler: Diophantine approximation and Cantor sets. Math. Ann. 338 (2007), 97–118.10.1007/s00208-006-0069-8CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An introduction to symbolic dynamics and coding (Cambridge: Cambridge University Press, 1995).10.1017/CBO9780511626302CrossRefGoogle Scholar
Mahler, K.. Some suggestions for further research. Bull. Aust. Math. Soc. 29 (1984), 101–108.10.1017/S0004972700021316CrossRefGoogle Scholar
Newhouse, S. E., Nondensity of axiom ${\rm A}({\rm a})$ on $S^2$
on $S^2$ . In Global Analysis (Proc. Sympos. Pure Math., Vol. XIV, Berkeley, Calif, 1968) (Amer. Math. Soc., Providence, R.I., 1970), pp. 191–202.10.1090/pspum/014/0277005CrossRefGoogle Scholar
. In Global Analysis (Proc. Sympos. Pure Math., Vol. XIV, Berkeley, Calif, 1968) (Amer. Math. Soc., Providence, R.I., 1970), pp. 191–202.10.1090/pspum/014/0277005CrossRefGoogle Scholar
Newhouse, S. E.. The abundance of wild hyperbolic sets and non-smooth stable sets for diffeomorphisms. Inst. Hautes Etudes Sci. Publ. Math. 50 (1979), 101–151.10.1007/BF02684771CrossRefGoogle Scholar
Palis, J. and Takens, F., Hyperbolicity and sensitive chaotic dynamics at homoclinic bifurcations. Fractal dimensions and infinitely many attractors. Cambridge Studies in Advanced Mathematics, Vol. 35 (Cambridge University Press, Cambridge, 1993).Google Scholar
Schleischitz, J.. On intrinsic and extrinsic rational approximation to Cantor sets. Ergodic Theory Dyn. Syst. 41 (2021), 1560–1589.10.1017/etds.2020.7CrossRefGoogle Scholar
Shparlinski, I. E.. On the arithmetic structure of rational numbers in the Cantor set. Bull. Aust. Math. Soc. 103 (2021), 22–27.10.1017/S0004972720000386CrossRefGoogle Scholar
Tiozzo, G.. Topological entropy of quadratic polynomials and dimension of sections of the Mandelbrot set. Adv. Math. 273 (2015), 651–715.10.1016/j.aim.2014.12.033CrossRefGoogle Scholar
Urbanski, M.. On Hausdorff dimension of invariant sets for expanding maps of a circle. Ergodic Theory Dyn. Syst. 6 (1986), 295–309.10.1017/S0143385700003461CrossRefGoogle Scholar
Wall, C. R.. Terminating decimals in the Cantor ternary set. Fibonacci Quart. 28 (1990), 98–101.Google Scholar
Williams, R. F., How big is the intersection of two thick Cantor sets?. Continuum theory and dynamical systems, Contemp. Math. Vol. 117 (Amer. Math. Soc., Providence, RI, 1991), pp. 163–175.10.1090/conm/117/1112813CrossRefGoogle Scholar
Yavicoli, A.. Patterns in thick compact sets. Israel J. Math. 244 (2021), 95–126.10.1007/s11856-021-2173-6CrossRefGoogle Scholar
Yavicoli, A.. Thickness and a gap lemma in $\mathbb {R}^d$ . Int. Math. Res. Not. IMRN 19 (2023), 16453–16477.10.1093/imrn/rnac319CrossRefGoogle Scholar
. Int. Math. Res. Not. IMRN 19 (2023), 16453–16477.10.1093/imrn/rnac319CrossRefGoogle Scholar


