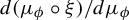1 Introduction
This paper is concerned with equilibrium states on subshifts over a countable amenable group. In particular, for an arbitrary subshift, given an equilibrium state
![]() $\mu $
for a potential with summable variation, we prove Gibbs-like bounds on the measures of finite configurations under a replicability condition. We use this result to prove a novel conformal Gibbs-like bound on the Lebesgue–Radon–Nikodym (LRN) derivative
$\mu $
for a potential with summable variation, we prove Gibbs-like bounds on the measures of finite configurations under a replicability condition. We use this result to prove a novel conformal Gibbs-like bound on the Lebesgue–Radon–Nikodym (LRN) derivative
![]() $d ( \mu \circ \xi ) / d\mu $
for a certain class of Borel isomorphisms
$d ( \mu \circ \xi ) / d\mu $
for a certain class of Borel isomorphisms
![]() $\xi $
. Our results generalize results of Meyerovitch [Reference Meyerovitch17] and García-Ramos and Pavlov [Reference García-Ramos and Pavlov11] and correct an error in the latter paper.
$\xi $
. Our results generalize results of Meyerovitch [Reference Meyerovitch17] and García-Ramos and Pavlov [Reference García-Ramos and Pavlov11] and correct an error in the latter paper.
Let
![]() $X \subset \mathcal {A}^G$
be a subshift (that is, a closed and shift-invariant subset) over a countable amenable group G with a finite alphabet
$X \subset \mathcal {A}^G$
be a subshift (that is, a closed and shift-invariant subset) over a countable amenable group G with a finite alphabet
![]() $\mathcal {A}$
. The dynamics of the system will be induced by the left-translation map
$\mathcal {A}$
. The dynamics of the system will be induced by the left-translation map
![]() $\{\sigma _g\}_{g \in G}$
where X is required to be compact and
$\{\sigma _g\}_{g \in G}$
where X is required to be compact and
![]() $\sigma $
-invariant. A potential is a continuous, real valued function
$\sigma $
-invariant. A potential is a continuous, real valued function
![]() $\phi : X \rightarrow \mathbb {R}$
. Equilibrium states are
$\phi : X \rightarrow \mathbb {R}$
. Equilibrium states are
![]() $\sigma $
-invariant Borel probability measures maximizing the pressure of
$\sigma $
-invariant Borel probability measures maximizing the pressure of
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $\phi $
:
$\phi $
:
![]() $P_\phi (\mu ) = h(\mu ) + \int \phi \,d\mu $
, where
$P_\phi (\mu ) = h(\mu ) + \int \phi \,d\mu $
, where
![]() $h(\mu )$
is the classical Kolmogorov–Sinai entropy of
$h(\mu )$
is the classical Kolmogorov–Sinai entropy of
![]() $\mu $
. Although we make no further assumptions on our subshift, we will require that the potential under consideration have summable variation, which will be defined in §3.2.
$\mu $
. Although we make no further assumptions on our subshift, we will require that the potential under consideration have summable variation, which will be defined in §3.2.
There is an extensive history in statistical physics and dynamical systems relating the global property of being an equilibrium state to local properties depending on the potential. Thermodynamic formalism, at its core, concerns itself with relating these global and local phenomena. Foundational results in this area were obtained by Dobrushin in [Reference Dobrushin9], and Lanford and Ruelle in [Reference Lanford and Ruelle15], who considered well-behaved
![]() $\mathbb {Z}^d$
-subshifts coupled with a sufficiently regular potential. In this setting, they were able to show that an invariant measure is an equilibrium state if and only if it can be locally characterized by the Gibbs property.
$\mathbb {Z}^d$
-subshifts coupled with a sufficiently regular potential. In this setting, they were able to show that an invariant measure is an equilibrium state if and only if it can be locally characterized by the Gibbs property.
We say a measure
![]() $\mu $
is Gibbs for
$\mu $
is Gibbs for
![]() $\phi $
if it satisfies a conditional probability condition. For a finite
$\phi $
if it satisfies a conditional probability condition. For a finite
![]() $F \Subset G$
, we define the F-language of X,
$F \Subset G$
, we define the F-language of X,
![]() $L_F(X) = \{ w \in \mathcal {A}^F : \text { there exists } x \in X : x_F = w \}$
, to be the set of all F-shape configurations that are legal in X. For
$L_F(X) = \{ w \in \mathcal {A}^F : \text { there exists } x \in X : x_F = w \}$
, to be the set of all F-shape configurations that are legal in X. For
![]() $w \in L_F(X)$
, we can define the extender set of w as in [Reference Kass and Madden14, Reference Ormes and Pavlov20],
$w \in L_F(X)$
, we can define the extender set of w as in [Reference Kass and Madden14, Reference Ormes and Pavlov20],
![]() $E_X(w) = \{ \eta \in \mathcal {A}^{F^c} : w \eta \in X \}$
, to be the collection of all background configurations for w such that
$E_X(w) = \{ \eta \in \mathcal {A}^{F^c} : w \eta \in X \}$
, to be the collection of all background configurations for w such that
![]() $w \eta \in X$
. We say that
$w \eta \in X$
. We say that
![]() $\mu $
is Gibbs for
$\mu $
is Gibbs for
![]() $\phi $
if for any configuration
$\phi $
if for any configuration
![]() $w \in L_F(X)$
, and almost every background configuration
$w \in L_F(X)$
, and almost every background configuration
![]() $\eta \in E_X(w)$
, we have
$\eta \in E_X(w)$
, we have
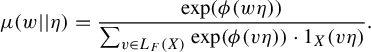 $$ \begin{align*}\mu(w || \eta) = \frac{\mathrm{exp }( \phi( w\eta))}{\sum_{v \in L_F(X)} \mathrm{exp }( \phi( v \eta)) \cdot 1_X(v \eta) } .\end{align*} $$
$$ \begin{align*}\mu(w || \eta) = \frac{\mathrm{exp }( \phi( w\eta))}{\sum_{v \in L_F(X)} \mathrm{exp }( \phi( v \eta)) \cdot 1_X(v \eta) } .\end{align*} $$
The Dobrušin theorem and Lanford–Ruelle theorem relating Gibbs measures and equilibrium states have been extended to the countable amenable group subshift setting in [Reference Ollagnier and Pinchon18, Reference Tempelman23], where it was shown that for sufficiently regular subshifts and potentials with summable variation, an invariant measure is an equilibrium state if and only if it is Gibbs for the potential.
In the case where
![]() $\phi = 0$
, equilibrium states correspond to measures of maximal entropy (MMEs). Parry showed in [Reference Parry22] that for
$\phi = 0$
, equilibrium states correspond to measures of maximal entropy (MMEs). Parry showed in [Reference Parry22] that for
![]() $\mathbb {Z}$
-subshifts of finite type, the MME is unique (and, in fact, by application of the Lanford–Ruelle theorem, it is Gibbs for
$\mathbb {Z}$
-subshifts of finite type, the MME is unique (and, in fact, by application of the Lanford–Ruelle theorem, it is Gibbs for
![]() $\phi = 0$
). In [Reference Bowen4], Bowen showed that for an expansive
$\phi = 0$
). In [Reference Bowen4], Bowen showed that for an expansive
![]() $\mathbb {Z}$
-action on a compact metric space satisfying the specification property and a potential with summable variation, there exists a unique equilibrium state. However, in the
$\mathbb {Z}$
-action on a compact metric space satisfying the specification property and a potential with summable variation, there exists a unique equilibrium state. However, in the
![]() $\mathbb {Z}^d$
setting with
$\mathbb {Z}^d$
setting with
![]() $d \geq 2$
, Burton and Steif in [Reference Burton and Steif6] were able to construct strongly irreducible subshifts of finite type with non-unique MMEs. Additionally, in the
$d \geq 2$
, Burton and Steif in [Reference Burton and Steif6] were able to construct strongly irreducible subshifts of finite type with non-unique MMEs. Additionally, in the
![]() $\mathbb {Z}$
setting, there are trivial examples of subshifts with positive entropy and a unique MME such that the MME is not Gibbs for
$\mathbb {Z}$
setting, there are trivial examples of subshifts with positive entropy and a unique MME such that the MME is not Gibbs for
![]() $\phi = 0$
. Take, for example, the product of a full shift with the orbit closure of the point
$\phi = 0$
. Take, for example, the product of a full shift with the orbit closure of the point
![]() $0^\infty 1 0^\infty $
, whose unique MME is the product of the unique MME on the full shift with
$0^\infty 1 0^\infty $
, whose unique MME is the product of the unique MME on the full shift with
![]() $\delta _{0^\infty }$
.
$\delta _{0^\infty }$
.
While neither uniqueness nor the Gibbs property may be attainable for MMEs for a general subshift, García-Ramos and Pavlov proved in [Reference García-Ramos and Pavlov11] that for arbitrary
![]() $\mathbb {Z}^d$
-subshifts, and any MME, one can obtain bounds on the measures of finite configurations under a replaceability condition. For a subshift
$\mathbb {Z}^d$
-subshifts, and any MME, one can obtain bounds on the measures of finite configurations under a replaceability condition. For a subshift
![]() $X \subset \mathcal {A}^{\mathbb {Z}^d}$
and
$X \subset \mathcal {A}^{\mathbb {Z}^d}$
and
![]() $w, v \in L_F(X)$
, we say v is replaceable by w if
$w, v \in L_F(X)$
, we say v is replaceable by w if
![]() $E_X(v) \subset E_X(w)$
. García-Ramos and Pavlov showed that for any MME
$E_X(v) \subset E_X(w)$
. García-Ramos and Pavlov showed that for any MME
![]() $\mu $
on a
$\mu $
on a
![]() $\mathbb {Z}^d$
-subshift, if v is replaceable by w, then
$\mathbb {Z}^d$
-subshift, if v is replaceable by w, then
![]() $\mu ([v]) \leq \mu ([w])$
.
$\mu ([v]) \leq \mu ([w])$
.
The context considered in this paper will combine that of Meyerovitch in [Reference Meyerovitch17] and of García-Ramos and Pavlov in [Reference García-Ramos and Pavlov11]. We make no assumptions on the subshift under consideration, and we require that the potential
![]() $\phi \in SV(X)$
has summable variation. Our results make use of a class of Borel isomorphisms: for finite configurations
$\phi \in SV(X)$
has summable variation. Our results make use of a class of Borel isomorphisms: for finite configurations
![]() $v, w \in L_F(X)$
, define
$v, w \in L_F(X)$
, define
![]() $\xi _{v, w}$
pointwise to swap v and w in the F location whenever legal in X. Note here that we do not require
$\xi _{v, w}$
pointwise to swap v and w in the F location whenever legal in X. Note here that we do not require
![]() $\xi _{v, w}$
to be continuous and, in general, it is not (see §2.2 for a precise definition and further discussion). Our first result can now be stated.
$\xi _{v, w}$
to be continuous and, in general, it is not (see §2.2 for a precise definition and further discussion). Our first result can now be stated.
Theorem 1.1. Let G be a countable amenable group and X be a G-subshift. Let
![]() $\phi \in SV(X)$
,
$\phi \in SV(X)$
,
![]() $\mu _\phi $
an equilibrium state for
$\mu _\phi $
an equilibrium state for
![]() $\phi $
,
$\phi $
,
![]() $F \Subset G$
and
$F \Subset G$
and
![]() $v, w \in L_F(X)$
. If
$v, w \in L_F(X)$
. If
![]() $E_X(v) \subset E_X(w)$
, then
$E_X(v) \subset E_X(w)$
, then
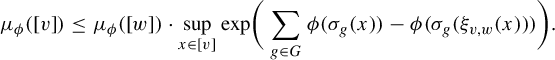 $$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \cdot \sup_{x \in [v]} \mathrm{exp }\bigg( \sum_{g \in G} \phi(\sigma_g(x)) - \phi(\sigma_g(\xi_{v, w}(x))) \bigg).\end{align*} $$
$$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \cdot \sup_{x \in [v]} \mathrm{exp }\bigg( \sum_{g \in G} \phi(\sigma_g(x)) - \phi(\sigma_g(\xi_{v, w}(x))) \bigg).\end{align*} $$
We note here that this inequality holds whenever the conclusion of the Lanford–Ruelle theorem also holds (Theorem 2.10 below), or even more generally when the conclusion of Theorem 1.3 holds (as noted in Observation 4.4). In particular, the equation immediately holds for all subshifts of finite type and potentials with summable variation, the novelty here is that we require no assumptions on the structure of the subshift X. It is in this general case where we must discuss extender sets, as in [Reference García-Ramos and Pavlov11].
In general, this supremum may be hard to compute. However, an immediate corollary in the locally constant case allows us to easily compute this bound when v and w agree on a sufficient boundary. First, for finite
![]() $H \Subset G$
, we call
$H \Subset G$
, we call
![]() $\phi $
an H-potential when if
$\phi $
an H-potential when if
![]() $x_H = y_H$
, then
$x_H = y_H$
, then
![]() $\phi (x) = \phi (y)$
. In particular, this means for any
$\phi (x) = \phi (y)$
. In particular, this means for any
![]() $v \in L_F(X)$
with
$v \in L_F(X)$
with
![]() $H \subset F$
, we can write
$H \subset F$
, we can write
![]() $\phi (v)$
unambiguously to mean
$\phi (v)$
unambiguously to mean
![]() $\phi (x)$
for any
$\phi (x)$
for any
![]() $x \in X$
such that
$x \in X$
such that
![]() $x_F = v$
since for all
$x_F = v$
since for all
![]() $x, y \in X$
with
$x, y \in X$
with
![]() $x_F = y_F = v$
,
$x_F = y_F = v$
,
![]() $\phi (x) = \phi (y)$
. We also denote
$\phi (x) = \phi (y)$
. We also denote
![]() $H^\pm = H \cup H^{-1}$
.
$H^\pm = H \cup H^{-1}$
.
Corollary 1.2. Let
![]() $H, F \Subset G$
,
$H, F \Subset G$
,
![]() $v, w \in L_F(X)$
, and
$v, w \in L_F(X)$
, and
![]() $\phi $
be an H-potential. Suppose that
$\phi $
be an H-potential. Suppose that
![]() $E_X(v) \subset E_X(w)$
and for all
$E_X(v) \subset E_X(w)$
and for all
![]() $g \in F^c H^\pm \cap F$
,
$g \in F^c H^\pm \cap F$
,
![]() $v_g = w_g$
. Then, for any equilibrium state
$v_g = w_g$
. Then, for any equilibrium state
![]() $\mu _\phi $
for
$\mu _\phi $
for
![]() $\phi $
,
$\phi $
,
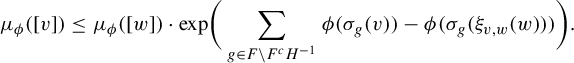 $$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \cdot \mathrm{exp }\bigg( \sum_{g \in F \backslash F^c H^{-1}} \phi ( \sigma_g (v)) - \phi ( \sigma_g(\xi_{v, w}(w))) \bigg).\end{align*} $$
$$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \cdot \mathrm{exp }\bigg( \sum_{g \in F \backslash F^c H^{-1}} \phi ( \sigma_g (v)) - \phi ( \sigma_g(\xi_{v, w}(w))) \bigg).\end{align*} $$
As another immediate corollary, by letting
![]() $\phi = 0$
, we extend [Reference García-Ramos and Pavlov11, Theorem 4.4] by García-Ramos and Pavlov to arbitrary countable amenable groups. Although the theorem in [Reference García-Ramos and Pavlov11] is stated for countable, finitely generated, torsion-free, amenable groups, due to an unfortunate error, their proof technique only applies immediately to the case where
$\phi = 0$
, we extend [Reference García-Ramos and Pavlov11, Theorem 4.4] by García-Ramos and Pavlov to arbitrary countable amenable groups. Although the theorem in [Reference García-Ramos and Pavlov11] is stated for countable, finitely generated, torsion-free, amenable groups, due to an unfortunate error, their proof technique only applies immediately to the case where
![]() $G = \mathbb {Z}^d$
. The error is the false assertion that for any torsion-free, finitely generated, countable amenable group
$G = \mathbb {Z}^d$
. The error is the false assertion that for any torsion-free, finitely generated, countable amenable group
![]() $G = \langle g_1, \ldots , g_k\rangle$
, the subgroup generated by
$G = \langle g_1, \ldots , g_k\rangle$
, the subgroup generated by
![]() $\langle g_1^n, \ldots , g_k^n\rangle$
has finite index in G. This is known to be false and can be shown not to hold in a variety of examples, including the Lamplighter group.
$\langle g_1^n, \ldots , g_k^n\rangle$
has finite index in G. This is known to be false and can be shown not to hold in a variety of examples, including the Lamplighter group.
In addition to the classical definition of Gibbs in the sense of Dobrušin, Lanford, and Ruelle, another fruitful approach has been to consider a measure that is conformal Gibbs for a potential. It was shown by Borsato and MacDonald in [Reference Borsato and MacDonald3] that for subshifts over a countable group and any potential
![]() $\phi $
, a measure is Gibbs for
$\phi $
, a measure is Gibbs for
![]() $\phi $
if and only if it is conformal Gibbs for
$\phi $
if and only if it is conformal Gibbs for
![]() $\phi $
(see §4 for a precise definition). As a consequence, this means that
$\phi $
(see §4 for a precise definition). As a consequence, this means that
![]() $\mu _\phi $
is Gibbs for
$\mu _\phi $
is Gibbs for
![]() $\phi $
if and only if, for every Borel isomorphism of the form
$\phi $
if and only if, for every Borel isomorphism of the form
![]() $\xi _{v, w}$
and for
$\xi _{v, w}$
and for
![]() $\mu _\phi $
-almost every (a.e.)
$\mu _\phi $
-almost every (a.e.)
![]() $x \in X$
,
$x \in X$
,
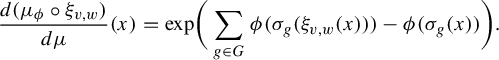 $$ \begin{align*}\frac{ d (\mu_\phi \circ \xi_{v, w} ) }{d \mu}(x) = \mathrm{exp }\bigg( \sum_{g \in G} \phi( \sigma_g(\xi_{v, w}(x))) - \phi( \sigma_g(x)) \bigg). \end{align*} $$
$$ \begin{align*}\frac{ d (\mu_\phi \circ \xi_{v, w} ) }{d \mu}(x) = \mathrm{exp }\bigg( \sum_{g \in G} \phi( \sigma_g(\xi_{v, w}(x))) - \phi( \sigma_g(x)) \bigg). \end{align*} $$
Since, in general, equilibrium states are not necessarily Gibbs, this equality cannot always hold. In the general subshift setting of this paper, little can be said of this LRN derivative.
In [Reference Meyerovitch17], Meyerovitch showed that for a general
![]() $\mathbb {Z}^d$
subshift X and potential
$\mathbb {Z}^d$
subshift X and potential
![]() $\phi $
with d-summable variation, if
$\phi $
with d-summable variation, if
![]() $\mu _\phi $
is an equilibrium state for
$\mu _\phi $
is an equilibrium state for
![]() $\phi $
and if
$\phi $
and if
![]() $E_X(v) = E_X(w)$
, then
$E_X(v) = E_X(w)$
, then
![]() ${ d (\mu _\phi \circ \xi _{v, w} ) }/{d \mu }$
satisfies the equation above. In the language of Meyerovitch,
${ d (\mu _\phi \circ \xi _{v, w} ) }/{d \mu }$
satisfies the equation above. In the language of Meyerovitch,
![]() $\mu _\phi $
must be
$\mu _\phi $
must be
![]() $(\mathfrak {T}_X^0, \psi _\phi )$
-conformal.
$(\mathfrak {T}_X^0, \psi _\phi )$
-conformal.
In §4, we will use Theorem 1.1 to obtain the following bound on this LRN, showing a conformal Gibbs-like result.
Theorem 1.3. Let
![]() $F \Subset G$
,
$F \Subset G$
,
![]() $v, w \in L_F(X)$
,
$v, w \in L_F(X)$
,
![]() $\phi \in SV(X)$
, and
$\phi \in SV(X)$
, and
![]() $\mu _\phi $
be an equilibrium state for
$\mu _\phi $
be an equilibrium state for
![]() $\phi $
. If
$\phi $
. If
![]() $E_X(v) \subset E_X(w)$
, then
$E_X(v) \subset E_X(w)$
, then
![]() $\mu _\phi \circ \xi _{v, w}$
is absolutely continuous with respect to
$\mu _\phi \circ \xi _{v, w}$
is absolutely continuous with respect to
![]() $\mu _\phi $
when restricted to
$\mu _\phi $
when restricted to
![]() $[w]$
and for
$[w]$
and for
![]() $\mu _\phi $
-a.e.
$\mu _\phi $
-a.e.
![]() $x \in [w]$
,
$x \in [w]$
,
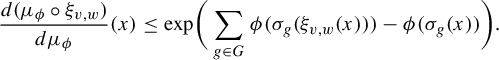 $$ \begin{align*}\frac{ d (\mu_\phi \circ \xi_{v, w} ) }{d \mu_\phi }(x) \leq \mathrm{exp }\bigg( \sum_{g \in G} \phi( \sigma_g(\xi_{v, w}(x))) - \phi( \sigma_g(x)) \bigg).\end{align*} $$
$$ \begin{align*}\frac{ d (\mu_\phi \circ \xi_{v, w} ) }{d \mu_\phi }(x) \leq \mathrm{exp }\bigg( \sum_{g \in G} \phi( \sigma_g(\xi_{v, w}(x))) - \phi( \sigma_g(x)) \bigg).\end{align*} $$
We have become aware that Corollary 1.4 has been proven in even greater generality in the sofic group setting in [Reference Barbieri and Meyerovitch2]. However, we recover the fact in the countable amenable group setting as an easy corollary of Theorem 1.3.
Corollary 1.4. Let
![]() $X \subset \mathcal {A}^G$
be a subshift over a countable amenable group G, let
$X \subset \mathcal {A}^G$
be a subshift over a countable amenable group G, let
![]() $\phi \in SV(X)$
be a potential with summable variation, and let
$\phi \in SV(X)$
be a potential with summable variation, and let
![]() $\mu _\phi $
be an equilibrium state for
$\mu _\phi $
be an equilibrium state for
![]() $\phi $
. Then,
$\phi $
. Then,
![]() $\mu _\phi $
is
$\mu _\phi $
is
![]() $(\mathfrak {T}_X^0, \psi _\phi )$
-conformal.
$(\mathfrak {T}_X^0, \psi _\phi )$
-conformal.
The structure of this paper is as follows. We begin with §2 on the relevant preliminaries, discussing countable amenable groups and their relevant properties. We then formally introduce subshifts over a countable amenable group, and discuss their thermodynamic formalism. Finally, we discuss equilibrium measures, the Gibbs property, and their relationship.
In §3, we prove Theorem 1.1, beginning with a lemma using Downarowicz, Huczek, and Zhang’s exact tiling result from [Reference Downarowicz, Huczek and Zhang10] to generate a sufficiently sparse almost partition of a given group G. After some preliminary lemmas in the subshift setting, we prove Theorem 1.1 and conclude Corollary 1.2 in the locally constant case.
Finally, §4 is concerned with the conformal Gibbs perspective where we formally introduce the concept and relevant definitions. We then prove Theorem 1.3, relate it to the results of Meyerovitch, and conclude by extending [Reference Meyerovitch17, Theorem 3.1 and Corollary 3.2] to the countable amenable subshift setting.
2 Preliminaries
2.1 Countable amenable groups
Let G be a countable group and denote the identity of G by e. We use the notation
![]() $K \Subset G$
to indicate that K is a finite subset of G. A Følner sequence for G is a collection of finite subsets
$K \Subset G$
to indicate that K is a finite subset of G. A Følner sequence for G is a collection of finite subsets
![]() $\{ F_n \}$
of G such that
$\{ F_n \}$
of G such that
![]() $G = \bigcup _{n \in \mathbb {N}} F_n$
and for all
$G = \bigcup _{n \in \mathbb {N}} F_n$
and for all
![]() $K \Subset G$
,
$K \Subset G$
,
![]() $\lim _{n \rightarrow \infty } |K F_n \triangle F_n| / |F_n| = 0$
. A countable group G is called amenable if there exists a Følner sequence in G.
$\lim _{n \rightarrow \infty } |K F_n \triangle F_n| / |F_n| = 0$
. A countable group G is called amenable if there exists a Følner sequence in G.
For a given Følner sequence
![]() $\{ F_n \}$
, we say the sequence is tempered if there exists some
$\{ F_n \}$
, we say the sequence is tempered if there exists some
![]() $C> 0$
such that for all
$C> 0$
such that for all
![]() $n> 0$
,
$n> 0$
,
![]() $| \bigcup _{k < n} F_k^{-1} F_n | \leq C |F_n |.$
For any Følner sequence, there exists a subsequence that is tempered, see [Reference Lindenstrauss16, Proposition 1.5] for a proof of this fact. A deeper discussion of Følner sequences and their relevant properties can be found in [Reference Ceccherini-Silberstein, Coornaert, Ceccherini-Silberstein and Coornaert8, Ch. 4], but for our purposes, we note that for any amenable group G, there exists a tempered Følner sequence that can be taken such that
$| \bigcup _{k < n} F_k^{-1} F_n | \leq C |F_n |.$
For any Følner sequence, there exists a subsequence that is tempered, see [Reference Lindenstrauss16, Proposition 1.5] for a proof of this fact. A deeper discussion of Følner sequences and their relevant properties can be found in [Reference Ceccherini-Silberstein, Coornaert, Ceccherini-Silberstein and Coornaert8, Ch. 4], but for our purposes, we note that for any amenable group G, there exists a tempered Følner sequence that can be taken such that
![]() $n!$
divides
$n!$
divides
![]() $|F_n|$
for every
$|F_n|$
for every
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Similar in spirit, we can define a relative almost-invariance: for any finite
![]() $F, T \Subset G$
and
$F, T \Subset G$
and
![]() $\epsilon> 0$
, we say T is right
$\epsilon> 0$
, we say T is right
![]() $(K, \epsilon )$
-invariant if
$(K, \epsilon )$
-invariant if
![]() $|TK \triangle T| / |T| < \epsilon $
. We can equivalently say G is amenable if for every finite
$|TK \triangle T| / |T| < \epsilon $
. We can equivalently say G is amenable if for every finite
![]() $K \Subset G$
and every
$K \Subset G$
and every
![]() $\epsilon> 0$
, there exists some finite
$\epsilon> 0$
, there exists some finite
![]() $T \Subset G$
that is right
$T \Subset G$
that is right
![]() $(K, \epsilon )$
-invariant.
$(K, \epsilon )$
-invariant.
In our setting, we will also be interested in a sense of sparseness of sets, for this, we define the following.
Definition 2.1. For any
![]() $S \subset G$
,
$S \subset G$
,
![]() $F \Subset G$
, we say S is left F-sparse if for all distinct
$F \Subset G$
, we say S is left F-sparse if for all distinct
![]() $s, s' \in S$
,
$s, s' \in S$
,
Note here, by a trivial application of the definition, we know for any
![]() $F \subset H \Subset G$
and
$F \subset H \Subset G$
and
![]() $S \subset G$
, if S is left H sparse, then S is left F sparse. We will now define the right (respectively left) H-interior and H-boundary of F for
$S \subset G$
, if S is left H sparse, then S is left F sparse. We will now define the right (respectively left) H-interior and H-boundary of F for
![]() $F, H \Subset G$
.
$F, H \Subset G$
.
Definition 2.2. The right H-interior of F, denoted by
![]() $\mathrm {Int}_H(F)$
, is defined by
$\mathrm {Int}_H(F)$
, is defined by
The right H-boundary of F, denoted
![]() $\partial _H(F)$
, is all elements of F not in the H-interior. Precisely,
$\partial _H(F)$
, is all elements of F not in the H-interior. Precisely,
The left H-interior/boundary of F is defined similarly.
The proof of our main theorem will also require taking advantage of a result by Downarowicz, Huczek, and Zhang regarding exact tilings of G from [Reference Downarowicz, Huczek and Zhang10]. For a countable amenable group G, a finite tiling
![]() $\mathcal {T} = \{ T_i : 1 \leq i \leq k \}$
is a collection of tiles such that
$\mathcal {T} = \{ T_i : 1 \leq i \leq k \}$
is a collection of tiles such that
![]() $\bigcup _{i \leq k} T_i = G$
and for each
$\bigcup _{i \leq k} T_i = G$
and for each
![]() $T_i \in \mathcal {T}$
, there exists a finite shape
$T_i \in \mathcal {T}$
, there exists a finite shape
![]() $S_i \Subset G$
, and a collection of centers
$S_i \Subset G$
, and a collection of centers
![]() $C(S_i) \subset G$
such that
$C(S_i) \subset G$
such that
![]() $T_i = S_i C(S_i)$
. In particular, a tiling
$T_i = S_i C(S_i)$
. In particular, a tiling
![]() $\mathcal {T}$
is called exact if for distinct
$\mathcal {T}$
is called exact if for distinct
![]() $c_1 , c_2 \in C(S_i)$
,
$c_1 , c_2 \in C(S_i)$
,
![]() $S_i c_1 \cap S_i c_2 = \emptyset $
. We also note it can be assumed that
$S_i c_1 \cap S_i c_2 = \emptyset $
. We also note it can be assumed that
![]() $e \in S$
for every shape. We can now state their result.
$e \in S$
for every shape. We can now state their result.
Theorem 2.3. [Reference Downarowicz, Huczek and Zhang10, Theorem 4.3]
Given any infinite, countable amenable group G, any
![]() $\epsilon> 0$
, and any finite
$\epsilon> 0$
, and any finite
![]() $K \Subset G$
, there exists an exact tiling
$K \Subset G$
, there exists an exact tiling
![]() $\mathcal {T}$
where each shape is right
$\mathcal {T}$
where each shape is right
![]() $(K, \epsilon )$
-invariant.
$(K, \epsilon )$
-invariant.
Their result in fact included statements regarding the entropy of the tiling space which we have omitted since they are not necessary for the purposes of this paper.
2.2 G-subshifts
Let G be a countable amenable group. Let
![]() $\mathcal {A}$
be a finite set, called the alphabet, endowed with the discrete topology. Our configuration space is the set of functions
$\mathcal {A}$
be a finite set, called the alphabet, endowed with the discrete topology. Our configuration space is the set of functions
![]() $x: G \rightarrow \mathcal {A}$
, which we denote
$x: G \rightarrow \mathcal {A}$
, which we denote
![]() $\mathcal {A}^G$
, endowed with the product topology. For any
$\mathcal {A}^G$
, endowed with the product topology. For any
![]() $H \subset G$
and
$H \subset G$
and
![]() $x \in \mathcal {A}^G$
, we denote the restriction of x to H by
$x \in \mathcal {A}^G$
, we denote the restriction of x to H by
![]() $x_H$
.
$x_H$
.
We define a G-action of homeomorphisms on
![]() $\mathcal {A}^G$
by the left-translation map: for all
$\mathcal {A}^G$
by the left-translation map: for all
![]() $g \in G$
and
$g \in G$
and
![]() $x \in \mathcal {A}^G$
, we define pointwise
$x \in \mathcal {A}^G$
, we define pointwise
![]() $\sigma _g(x)_h = x_{gh}$
. The set
$\sigma _g(x)_h = x_{gh}$
. The set
![]() $\mathcal {A}^G$
and the collection of left-translations
$\mathcal {A}^G$
and the collection of left-translations
![]() $(\sigma _g)_{g \in G}$
together form a topological dynamical system
$(\sigma _g)_{g \in G}$
together form a topological dynamical system
![]() $(\mathcal {A}^G, \sigma )$
which we call the full G-shift on
$(\mathcal {A}^G, \sigma )$
which we call the full G-shift on
![]() $\mathcal {A}$
. A G-subshift is a subset
$\mathcal {A}$
. A G-subshift is a subset
![]() $X \subset \mathcal {A}^G$
that is closed in the product topology and is
$X \subset \mathcal {A}^G$
that is closed in the product topology and is
![]() $\sigma $
-invariant (that is, for all
$\sigma $
-invariant (that is, for all
![]() $g \in G$
,
$g \in G$
,
![]() $\sigma _g(X) \subset X$
). When G is clear, we will refer to a G-subshift as just a subshift.
$\sigma _g(X) \subset X$
). When G is clear, we will refer to a G-subshift as just a subshift.
For any finite
![]() $F \Subset G$
and any
$F \Subset G$
and any
![]() $w \in \mathcal {A}^F$
, we call w a configuration of shape F. For a subshift X and a finite configuration w of shape
$w \in \mathcal {A}^F$
, we call w a configuration of shape F. For a subshift X and a finite configuration w of shape
![]() $F \Subset G$
, we say w is in the language of X (or w is legal in X) if there exists some
$F \Subset G$
, we say w is in the language of X (or w is legal in X) if there exists some
![]() $x \in X$
such that
$x \in X$
such that
![]() $x_F = w$
. We call
$x_F = w$
. We call
![]() $L_F(X) = \{ x_F : x \in X \}$
the F-language of X, and
$L_F(X) = \{ x_F : x \in X \}$
the F-language of X, and
![]() $L(X) = \bigcup _{F \Subset G} L_F(X)$
the language of X.
$L(X) = \bigcup _{F \Subset G} L_F(X)$
the language of X.
For any
![]() $F \Subset G$
and
$F \Subset G$
and
![]() $w \in \mathcal {A}^F$
, we define the cylinder set of w as follows:
$w \in \mathcal {A}^F$
, we define the cylinder set of w as follows:
In particular, the cylinder sets form a basis for the product topology on
![]() $\mathcal {A}^G$
. Cylinder sets are frequently taken intersected with a subshift, which will be clear by context.
$\mathcal {A}^G$
. Cylinder sets are frequently taken intersected with a subshift, which will be clear by context.
Finally, we note here that the product topology on
![]() $\mathcal {A}^G$
is metrizable, and for any Følner sequence
$\mathcal {A}^G$
is metrizable, and for any Følner sequence
![]() $\{ F_n \}$
, the metric
$\{ F_n \}$
, the metric
induces the product topology. This metric serves primarily to establish that G-subshifts are expansive.
For any disjoint
![]() $H, K \subset G$
and any
$H, K \subset G$
and any
![]() $x \in \mathcal {A}^H$
,
$x \in \mathcal {A}^H$
,
![]() $y \in \mathcal {A}^K$
, we define the concatenation of x and y by
$y \in \mathcal {A}^K$
, we define the concatenation of x and y by
![]() $xy \in \mathcal {A}^{H \cup K}$
such that
$xy \in \mathcal {A}^{H \cup K}$
such that
![]() $(xy)_H = x$
and
$(xy)_H = x$
and
![]() $(xy)_K = y$
. We also define for any
$(xy)_K = y$
. We also define for any
![]() $v \in L_F(X)$
, the extender set of v,
$v \in L_F(X)$
, the extender set of v,
![]() $E_X(v)$
, to be the collection of all background configurations for which v is legal. Specifically,
$E_X(v)$
, to be the collection of all background configurations for which v is legal. Specifically,
![]() $E_X(v) = \{ \eta \in \mathcal {A}^{G \backslash F} : v\eta \in X \}$
. For any
$E_X(v) = \{ \eta \in \mathcal {A}^{G \backslash F} : v\eta \in X \}$
. For any
![]() $v, w \in L_F(X)$
, we say v is replaceable by w if
$v, w \in L_F(X)$
, we say v is replaceable by w if
![]() $E_X(v) \subset E_X(w)$
.
$E_X(v) \subset E_X(w)$
.
We will now define the following functions that will be useful in the proof of our main results and essential to our discussion of the conformal Gibbs corollaries.
Definition 2.4. For any
![]() $F \Subset G$
,
$F \Subset G$
,
![]() $v, w \in L_F(X)$
, we define
$v, w \in L_F(X)$
, we define
![]() $\xi _{v, w} : X \rightarrow X$
through the following cases.
$\xi _{v, w} : X \rightarrow X$
through the following cases.
-
• For
 $x \in [v]$
, if the concatenation
$x \in [v]$
, if the concatenation
 $w x_{F^c} \in X$
, then
$w x_{F^c} \in X$
, then
 $\xi _{v, w}(x) = w x_{F^c}$
; otherwise,
$\xi _{v, w}(x) = w x_{F^c}$
; otherwise,
 $\xi _{v, w}(x) = x$
.
$\xi _{v, w}(x) = x$
. -
• For
 $x \in [w]$
, similarly define
$x \in [w]$
, similarly define
 $\xi _{v, w}(x)$
.
$\xi _{v, w}(x)$
. -
• Otherwise, let
 $\xi _{v, w}(x) = x$
.
$\xi _{v, w}(x) = x$
.
Note this is exactly switching v and w in the F-location whenever the resulting point is still in X. It will be noted in §4 that these functions are in fact Borel isomorphisms that generate the homoclinic (Gibbs) relation.
For a given subshift
![]() $X \subset \mathcal {A}^G$
, we will denote the collection of
$X \subset \mathcal {A}^G$
, we will denote the collection of
![]() $\sigma $
-invariant probability measures on X by
$\sigma $
-invariant probability measures on X by
![]() $\mathcal {M}_\sigma (X)$
. The existence of such measures is guaranteed by the fact that G is amenable. For a given
$\mathcal {M}_\sigma (X)$
. The existence of such measures is guaranteed by the fact that G is amenable. For a given
![]() $\mu \in \mathcal {M}_\sigma (X)$
, for any collection of legal finite configurations
$\mu \in \mathcal {M}_\sigma (X)$
, for any collection of legal finite configurations
![]() $W \subset L(X)$
, we will use
$W \subset L(X)$
, we will use
![]() $\mu (W) $
to mean
$\mu (W) $
to mean
![]() $\mu ( \bigcup _{w \in W} [w] )$
.
$\mu ( \bigcup _{w \in W} [w] )$
.
We say
![]() $\mu \in \mathcal {M}_\sigma (X)$
is ergodic if for all measurable
$\mu \in \mathcal {M}_\sigma (X)$
is ergodic if for all measurable
![]() $A \subset X$
, for all
$A \subset X$
, for all
![]() $g \in G$
, if
$g \in G$
, if
![]() $\mu ( A \triangle \sigma _g^{-1} A) = 0$
, then
$\mu ( A \triangle \sigma _g^{-1} A) = 0$
, then
![]() $\mu (A) \in \{ 0, 1\}$
. Here,
$\mu (A) \in \{ 0, 1\}$
. Here,
![]() $\mathcal {M}_\sigma (X)$
is convex and compact under the weak-
$\mathcal {M}_\sigma (X)$
is convex and compact under the weak-
![]() $*$
topology, in fact, it forms a Choquet simplex whose extreme points are exactly the ergodic measures.
$*$
topology, in fact, it forms a Choquet simplex whose extreme points are exactly the ergodic measures.
2.3 Thermodynamic formalism
The theory of thermodynamic formalism bridges the gap between microscopic and macroscopic descriptions of systems with many interacting particles, extending concepts of statistical mechanics to symbolic dynamics. Gibbs measures are central to this framework, enabling the analysis of global statistical properties derived from local interactions in a broad range of dynamical systems. This section delves into the thermodynamic formalism for countable amenable group actions on finite alphabet subshifts, examining topological pressure and its connection to statistical physics, the construction of partition functions, and the characterization of equilibrium states.
To begin, we must define topological pressure of a given potential over our subshift X. We first let
![]() $\phi : X \rightarrow \mathbb {R}$
be a real valued, continuous function which we will call a potential. We will denote the set of all potentials on a subshift X by
$\phi : X \rightarrow \mathbb {R}$
be a real valued, continuous function which we will call a potential. We will denote the set of all potentials on a subshift X by
![]() $C(X)$
. For any
$C(X)$
. For any
![]() $F \Subset G$
, we define the F-Birkhoff sum of
$F \Subset G$
, we define the F-Birkhoff sum of
![]() $\phi $
:
$\phi $
:
![]() $\phi _F = \sum _{g \in F} \phi \circ \sigma _g$
. Finally, for any open cover
$\phi _F = \sum _{g \in F} \phi \circ \sigma _g$
. Finally, for any open cover
![]() $\mathcal {U}$
of X, any
$\mathcal {U}$
of X, any
![]() $F \Subset G$
, we define the open cover
$F \Subset G$
, we define the open cover
![]() $\mathcal {U}^F = \bigvee _{f \in F} \sigma _f^{-1} \mathcal {U} = \{ \bigcap _{f \in F} \sigma _f^{-1}(U_f) : U_f \in \mathcal {U} \}$
. We use this notation to define the following partition function.
$\mathcal {U}^F = \bigvee _{f \in F} \sigma _f^{-1} \mathcal {U} = \{ \bigcap _{f \in F} \sigma _f^{-1}(U_f) : U_f \in \mathcal {U} \}$
. We use this notation to define the following partition function.
Definition 2.5. We define a partition function for any
![]() $F \Subset G$
and any open cover
$F \Subset G$
and any open cover
![]() $\mathcal {U}$
of X:
$\mathcal {U}$
of X:
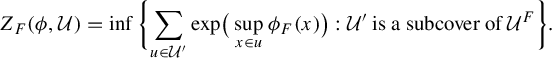 $$ \begin{align*}Z_F(\phi, \mathcal{U}) = \inf \bigg\{\! \sum_{u \in \mathcal{U}'} \mathrm{exp }\big( \sup_{x \in u} \phi_F(x) \big) : \mathcal{U}' \text{ is a subcover of } \mathcal{U}^F \bigg\} .\end{align*} $$
$$ \begin{align*}Z_F(\phi, \mathcal{U}) = \inf \bigg\{\! \sum_{u \in \mathcal{U}'} \mathrm{exp }\big( \sup_{x \in u} \phi_F(x) \big) : \mathcal{U}' \text{ is a subcover of } \mathcal{U}^F \bigg\} .\end{align*} $$
We can define the topological pressure of
![]() $\phi $
with respect to a given open cover
$\phi $
with respect to a given open cover
![]() $\mathcal {U}$
to be
$\mathcal {U}$
to be
for any Følner sequence
![]() $\{ F_n \}$
. This limit is guaranteed to exist and does not depend on the choice of Følner sequence, further discussion of which can be found in [Reference Bufetov5] and [Reference Gurevich and Tempelman12]. We can now define the following.
$\{ F_n \}$
. This limit is guaranteed to exist and does not depend on the choice of Følner sequence, further discussion of which can be found in [Reference Bufetov5] and [Reference Gurevich and Tempelman12]. We can now define the following.
Definition 2.6. The topological pressure of
![]() $\phi $
is then
$\phi $
is then
Since, in the subshift setting, the dynamical system
![]() $(X, \sigma )$
is expansive, the above supremum is attained at an open cover
$(X, \sigma )$
is expansive, the above supremum is attained at an open cover
![]() $\mathcal {U}$
of diameter less than or equal to the expansiveness constant. In particular, we can compute topological pressure by
$\mathcal {U}$
of diameter less than or equal to the expansiveness constant. In particular, we can compute topological pressure by
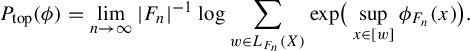 $$ \begin{align*} P_{\mathrm{top}}(\phi) = \lim_{n \rightarrow \infty} |F_n|^{-1} \log \sum_{w \in L_{F_n}(X)} \mathrm{exp }\big( \sup_{x \in [w]} \phi_{F_n}(x) \big). \end{align*} $$
$$ \begin{align*} P_{\mathrm{top}}(\phi) = \lim_{n \rightarrow \infty} |F_n|^{-1} \log \sum_{w \in L_{F_n}(X)} \mathrm{exp }\big( \sup_{x \in [w]} \phi_{F_n}(x) \big). \end{align*} $$
In addition to the topological pressure, for a given invariant measure
![]() $\mu \in \mathcal {M}_\sigma (X)$
, we can define the pressure of
$\mu \in \mathcal {M}_\sigma (X)$
, we can define the pressure of
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $\phi \in C(X)$
as follows:
$\phi \in C(X)$
as follows:
where
![]() $h(\mu )$
is the Kolmogorov–Sinai entropy of the invariant probability measure
$h(\mu )$
is the Kolmogorov–Sinai entropy of the invariant probability measure
![]() $\mu $
. As shown by Ollagnier and Pinchon [Reference Ollagnier and Pinchon19], in the countable amenable subshift setting, the variational principle holds. In particular, for all
$\mu $
. As shown by Ollagnier and Pinchon [Reference Ollagnier and Pinchon19], in the countable amenable subshift setting, the variational principle holds. In particular, for all
![]() $\phi \in C(X)$
,
$\phi \in C(X)$
,
In statistical physics, equilibrium states correspond with probability measures on the state space that minimize the Gibbs free energy of the system. Up to a multiplicative constant, the free energy of an invariant measure corresponds with the negative pressure, and so we similarly define an equilibrium state as follows.
Definition 2.7. We say
![]() $\mu \in M_\sigma $
is an equilibrium state for
$\mu \in M_\sigma $
is an equilibrium state for
![]() $\phi $
if it attains the variational principle supremum, that is,
$\phi $
if it attains the variational principle supremum, that is,
When h is upper semicontinuous (as in the case for expansive dynamical systems), we know the collection of equilibrium states for a given
![]() $\phi $
is non-empty, compact under the weak-
$\phi $
is non-empty, compact under the weak-
![]() $*$
topology, and convex, where the extreme points are exactly the ergodic equilibrium states.
$*$
topology, and convex, where the extreme points are exactly the ergodic equilibrium states.
2.4 Equilibrium measures and the Gibbs property
A rich theory has developed around relating equilibrium states and measures with the Gibbs property (for some definition of Gibbs property). In the classical results of Dobrušin, Lanford, and Ruelle, the Gibbs property can be defined in terms of conditional probabilities as follows.
Definition 2.8. For a subshift
![]() $X \subset \mathcal {A}^{\mathbb {Z}^d}$
and a potential
$X \subset \mathcal {A}^{\mathbb {Z}^d}$
and a potential
![]() $\phi \in C(X)$
, we say a measure
$\phi \in C(X)$
, we say a measure
![]() $\mu $
is Gibbs for
$\mu $
is Gibbs for
![]() $\phi $
if for all
$\phi $
if for all
![]() $F \Subset \mathbb {Z}^d$
, for all
$F \Subset \mathbb {Z}^d$
, for all
![]() $w \in L_F(X)$
, and for
$w \in L_F(X)$
, and for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $\eta \in \mathcal {A}^{\mathbb {Z}^d \backslash F}$
such that
$\eta \in \mathcal {A}^{\mathbb {Z}^d \backslash F}$
such that
![]() $w \eta \in X$
,
$w \eta \in X$
,
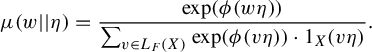 $$ \begin{align*}\mu( w || \eta ) = \frac{ \mathrm{exp }( \phi( w \eta )) }{\sum_{v \in L_F(X)} \mathrm{exp }( \phi( v \eta )) \cdot 1_X(v\eta)}.\end{align*} $$
$$ \begin{align*}\mu( w || \eta ) = \frac{ \mathrm{exp }( \phi( w \eta )) }{\sum_{v \in L_F(X)} \mathrm{exp }( \phi( v \eta )) \cdot 1_X(v\eta)}.\end{align*} $$
In other words, we say a measure is Gibbs for
![]() $\phi $
when the probability of a local configuration, w, given a background configuration,
$\phi $
when the probability of a local configuration, w, given a background configuration,
![]() $\eta $
, can be computed in the typical way one computes Gibbs measures in the finite case. The results of Dobrušin combined with those of Lanford and Ruelle show equivalence to the Gibbs property and being an equilibrium state under certain assumptions on subshift.
$\eta $
, can be computed in the typical way one computes Gibbs measures in the finite case. The results of Dobrušin combined with those of Lanford and Ruelle show equivalence to the Gibbs property and being an equilibrium state under certain assumptions on subshift.
The following theorem involves a technical condition called property (D), which is described in [Reference Dobrushin9].
Theorem 2.9. (Dobrushin [Reference Dobrushin9])
Let
![]() $X \subset \mathcal {A}^{\mathbb {Z}^d}$
be a subshift satisfying property (D) and
$X \subset \mathcal {A}^{\mathbb {Z}^d}$
be a subshift satisfying property (D) and
![]() $\phi \in C(X)$
be a potential with d-summable variation. If
$\phi \in C(X)$
be a potential with d-summable variation. If
![]() $\mu \in \mathcal {M}_\sigma (X)$
is an invariant probability measure that is Gibbs for
$\mu \in \mathcal {M}_\sigma (X)$
is an invariant probability measure that is Gibbs for
![]() $\phi $
, then
$\phi $
, then
![]() $\mu $
is an equilibrium state for
$\mu $
is an equilibrium state for
![]() $\phi $
.
$\phi $
.
Theorem 2.10. (Lanford and Ruelle [Reference Lanford and Ruelle15])
Let
![]() $X \subset \mathcal {A}^{\mathbb {Z}^d}$
be a subshift of finite type and
$X \subset \mathcal {A}^{\mathbb {Z}^d}$
be a subshift of finite type and
![]() $\phi \in C(X)$
be a potential with d-summable variation. If
$\phi \in C(X)$
be a potential with d-summable variation. If
![]() $\mu $
is an equilibrium state for
$\mu $
is an equilibrium state for
![]() $\phi $
, then
$\phi $
, then
![]() $\mu $
is Gibbs for
$\mu $
is Gibbs for
![]() $\phi $
.
$\phi $
.
Subshifts of finite type, SFTs, are an important and well-studied class of subshifts that are not defined here. Analogous results have since been shown in the countable amenable subshift setting [Reference Ollagnier and Pinchon18, Reference Tempelman23]. Note that these statements rely on relatively strong assumptions on both the subshift and the potential. When no assumptions are made of the potential, little can be said about the equilibrium state. In fact, by upper semicontinuity of the entropy map, it can be shown that for any subshift
![]() $X \subset \mathcal {A}^G$
and any ergodic state
$X \subset \mathcal {A}^G$
and any ergodic state
![]() $\mu \in \mathcal {M}_{\sigma }(X)$
, there exists a potential
$\mu \in \mathcal {M}_{\sigma }(X)$
, there exists a potential
![]() $\phi \in C(X)$
for which
$\phi \in C(X)$
for which
![]() $\mu $
is the unique equilibrium state [Reference Jenkinson13]. It is therefore quite natural to retain some regularity assumptions on the class of potentials under consideration.
$\mu $
is the unique equilibrium state [Reference Jenkinson13]. It is therefore quite natural to retain some regularity assumptions on the class of potentials under consideration.
3 Proof of Theorem 1.1
For our results, we will impose a natural regularity assumption on our potential
![]() $\phi $
, but impose no restriction on the subshift
$\phi $
, but impose no restriction on the subshift
![]() $X \subset \mathcal {A}^G$
. Our proof of Theorem 1.1 will be adapted from the proof technique of García-Ramos and Pavlov in [Reference García-Ramos and Pavlov11], which involves replacing v with w along a sufficiently sparse and regular grid in G. Lemma 3.1 allows us to construct a partition of G from which we may choose the appropriate grid. We will then prove a few technical lemmas, and finally we will show our main result and conclude with a few notable corollaries.
$X \subset \mathcal {A}^G$
. Our proof of Theorem 1.1 will be adapted from the proof technique of García-Ramos and Pavlov in [Reference García-Ramos and Pavlov11], which involves replacing v with w along a sufficiently sparse and regular grid in G. Lemma 3.1 allows us to construct a partition of G from which we may choose the appropriate grid. We will then prove a few technical lemmas, and finally we will show our main result and conclude with a few notable corollaries.
3.1 Sufficiently sparse almost partitions
The following lemma allows us to generate a finite
![]() $\epsilon $
-almost partition of G where each part is sufficiently sparse relative to some fixed
$\epsilon $
-almost partition of G where each part is sufficiently sparse relative to some fixed
![]() $F \Subset G$
.
$F \Subset G$
.
Lemma 3.1. For any
![]() $F \Subset G$
,
$F \Subset G$
,
![]() $\epsilon> 0$
, and Følner sequence
$\epsilon> 0$
, and Følner sequence
![]() $\{ F_n \}$
, there exists a finite collection
$\{ F_n \}$
, there exists a finite collection
![]() $\mathcal {P} = \{ P_i : 1 \leq i \leq N \}$
of pairwise disjoint, left F-sparse subsets of G and a subsequence
$\mathcal {P} = \{ P_i : 1 \leq i \leq N \}$
of pairwise disjoint, left F-sparse subsets of G and a subsequence
![]() $\{ F_{n_k} \}$
such that
$\{ F_{n_k} \}$
such that
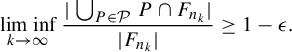 $$ \begin{align*}\liminf_{k \rightarrow \infty} \frac{| \bigcup_{P \in \mathcal{P}}P \cap F_{n_k}|}{|F_{n_k}|} \geq 1-\epsilon .\end{align*} $$
$$ \begin{align*}\liminf_{k \rightarrow \infty} \frac{| \bigcup_{P \in \mathcal{P}}P \cap F_{n_k}|}{|F_{n_k}|} \geq 1-\epsilon .\end{align*} $$
In lieu of a complete and technical proof, we provide an outline of how this result can be shown. The result can be viewed as a weakened reformulation of a quasitiling result of Ornstein and Weiss in [Reference Ornstein and Weiss21], or an application of the exact tiling results in [Reference Downarowicz, Huczek and Zhang10]. In essence, one can construct a quasitiling (or an exact tiling) of G using a finite collection of shapes that are sufficiently F-invariant. The F-invariance ensures that we can consider only the F-interiors of these shapes and maintain a
![]() $(1-\epsilon )$
-covering of G. We then let
$(1-\epsilon )$
-covering of G. We then let
![]() $P \in \mathcal {P}$
represent all the shifts of a particular location of an element in a specified shape. This allows us to ensure that
$P \in \mathcal {P}$
represent all the shifts of a particular location of an element in a specified shape. This allows us to ensure that
![]() $\mathcal {P}$
is left F-sparse since we have restricted to the F-interiors of the relevant shapes.
$\mathcal {P}$
is left F-sparse since we have restricted to the F-interiors of the relevant shapes.
3.2 Subshift lemmas
We begin by describing our regularity constraints imposed on the potential
![]() $\phi $
.
$\phi $
.
Definition 3.2. The F-variation of
![]() $\phi $
for any
$\phi $
for any
![]() $F \subset G$
is defined as
$F \subset G$
is defined as
Definition 3.3. We say
![]() $\{ E_n \}$
is an exhaustive sequence in G if
$\{ E_n \}$
is an exhaustive sequence in G if
![]() $E_1 \subset E_2 \subset \cdots $
and
$E_1 \subset E_2 \subset \cdots $
and
![]() $G = \bigcup _{n \in \mathbb {N}} E_n$
.
$G = \bigcup _{n \in \mathbb {N}} E_n$
.
Definition 3.4. We say
![]() $\phi $
has summable variation according to the exhaustive sequence
$\phi $
has summable variation according to the exhaustive sequence
![]() $\{ E_n \}$
if
$\{ E_n \}$
if
Additionally, we will say
![]() $\phi \in C(X)$
has summable variation if
$\phi \in C(X)$
has summable variation if
![]() $\phi $
has summable variation according to some exhaustive sequence.
$\phi $
has summable variation according to some exhaustive sequence.
For a fixed exhaustive sequence
![]() $\{ E_n \}$
, we define
$\{ E_n \}$
, we define
![]() $SV_{\{ E_n \}}(X)$
to be the collection of all potentials with summable variation according to
$SV_{\{ E_n \}}(X)$
to be the collection of all potentials with summable variation according to
![]() $\{ E_n \}$
. We also let
$\{ E_n \}$
. We also let
![]() $SV(X) = \bigcup _{\{ E_n \}} SV_{\{ E_n \}}(X)$
denote the collection of all potentials with summable variation according to some exhaustive sequence.
$SV(X) = \bigcup _{\{ E_n \}} SV_{\{ E_n \}}(X)$
denote the collection of all potentials with summable variation according to some exhaustive sequence.
It is worth noting here that when
![]() $G = \mathbb {Z}^d$
, we can take
$G = \mathbb {Z}^d$
, we can take
![]() $E_n = \{ k \in \mathbb {Z}^d : |k_i| \leq n \}$
and summable variation according to this sequence corresponds to d-summable variation in the typical sense.
$E_n = \{ k \in \mathbb {Z}^d : |k_i| \leq n \}$
and summable variation according to this sequence corresponds to d-summable variation in the typical sense.
Definition 3.5. For an exhaustive sequence
![]() $\{ E_n \}$
, we define the summable variation norm on
$\{ E_n \}$
, we define the summable variation norm on
![]() $SV_{\{ E_n \}}(X)$
by
$SV_{\{ E_n \}}(X)$
by
Observation 3.6. If
![]() $\phi $
has summable variation according to some exhaustive sequence
$\phi $
has summable variation according to some exhaustive sequence
![]() $\{ E_n \}$
, then for any
$\{ E_n \}$
, then for any
![]() $F \Subset G$
such that
$F \Subset G$
such that
![]() $e \in F$
,
$e \in F$
,
![]() $\phi $
has summable variation according to exhaustive sequence
$\phi $
has summable variation according to exhaustive sequence
![]() $\{ E_n F \}$
.
$\{ E_n F \}$
.
Proof. First, let
![]() $H \Subset G$
and note
$H \Subset G$
and note
![]() $ HF^{-1}$
is also a finite set. We therefore have some
$ HF^{-1}$
is also a finite set. We therefore have some
![]() $N \in \mathbb {N}$
such that for all
$N \in \mathbb {N}$
such that for all
![]() $n \geq N$
,
$n \geq N$
,
![]() $ H F^{-1} \subset E_n$
and so
$ H F^{-1} \subset E_n$
and so
![]() $H \subset E_n F$
. It immediately follows that
$H \subset E_n F$
. It immediately follows that
![]() $\{ E_n F \}$
is an exhaustive sequence.
$\{ E_n F \}$
is an exhaustive sequence.
Since
![]() $e \in F$
by assumption, we have
$e \in F$
by assumption, we have
![]() $E_n \subset E_n F$
. We now see that
$E_n \subset E_n F$
. We now see that
We now restate relevant definitions and lemmas from García-Ramos and Pavlov in [Reference García-Ramos and Pavlov11].
Definition 3.7. For
![]() $v, u \in L(X)$
, we define
$v, u \in L(X)$
, we define
![]() $O_v(u) = \{ g \in G : \sigma _g(u)_F = v \}$
.
$O_v(u) = \{ g \in G : \sigma _g(u)_F = v \}$
.
In particular,
![]() $O_v(u)$
represents the indices where v occurs in u and can be read as ‘occurrences of v in u’. We will now define a replacement function that for a given finite configuration u, replaces occurrences of v with w in specified locations.
$O_v(u)$
represents the indices where v occurs in u and can be read as ‘occurrences of v in u’. We will now define a replacement function that for a given finite configuration u, replaces occurrences of v with w in specified locations.
Definition 3.8. Let
![]() $F, H \Subset G$
and fix any
$F, H \Subset G$
and fix any
![]() $v, w \in L_F(X)$
and
$v, w \in L_F(X)$
and
![]() $u \in L_H(X)$
. Let
$u \in L_H(X)$
. Let
![]() $S \subset O_v(u)$
be an F-sparse set of occurrences of v in u. We now define
$S \subset O_v(u)$
be an F-sparse set of occurrences of v in u. We now define
![]() $R_u^{v \rightarrow w}(S) = u'$
as follows:
$R_u^{v \rightarrow w}(S) = u'$
as follows:
-
• for
 $s \in S$
,
$s \in S$
,
 $f \in F$
, let
$f \in F$
, let
 $u^{\prime }_{sf} = w_f$
; and
$u^{\prime }_{sf} = w_f$
; and -
• for all other
 $g \in H \backslash SF$
, let
$g \in H \backslash SF$
, let
 $u^{\prime }_g = u_g$
.
$u^{\prime }_g = u_g$
.
Since S is an F-sparse subset of
![]() $O_v(u)$
, we know
$O_v(u)$
, we know
![]() $u'$
is well defined and uniquely determined. Note here that
$u'$
is well defined and uniquely determined. Note here that
![]() $u'$
is exactly the configuration obtained by replacing v with w in the S-locations.
$u'$
is exactly the configuration obtained by replacing v with w in the S-locations.
We remind the reader that for any finite configuration
![]() $v \in L_F(X)$
, the extender set of v is defined as
$v \in L_F(X)$
, the extender set of v is defined as
![]() $E_X(v) = \{ \eta \in \mathcal {A}^{F^c} : v \eta \in X \}$
. Note here, whenever
$E_X(v) = \{ \eta \in \mathcal {A}^{F^c} : v \eta \in X \}$
. Note here, whenever
![]() $E_X(v) \subset E_X(w)$
, then
$E_X(v) \subset E_X(w)$
, then
![]() $R_u^{v \rightarrow w}(S) \in L(X)$
for any left F-sparse set
$R_u^{v \rightarrow w}(S) \in L(X)$
for any left F-sparse set
![]() $S \subset O_v(u)$
.
$S \subset O_v(u)$
.
Lemma 3.9. [Reference García-Ramos and Pavlov11, Lemma 4.2]
For any F,
![]() $v, w \in L_F(X)$
with
$v, w \in L_F(X)$
with
![]() $v \neq w$
, and left F-sparse set
$v \neq w$
, and left F-sparse set
![]() $T \subset O_v(u)$
,
$T \subset O_v(u)$
,
![]() $R_u^{v \rightarrow w}$
is injective on subsets of T.
$R_u^{v \rightarrow w}$
is injective on subsets of T.
Lemma 3.10. [Reference García-Ramos and Pavlov11, Lemma 4.3]
For any F and
![]() $v, w \in L_F(X)$
, any left F-sparse set
$v, w \in L_F(X)$
, any left F-sparse set
![]() $T \subset O_v(u)$
, any
$T \subset O_v(u)$
, any
![]() $u'$
, and any
$u'$
, and any
![]() $m \leq |T \cap O_w(u')|$
,
$m \leq |T \cap O_w(u')|$
,
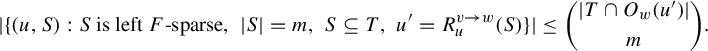 $$ \begin{align*}| \{ (u, S) : S \text{ is left } F\text{-sparse}, \; |S| = m, \; S \subseteq T, \; u' = R_u^{v\rightarrow w}(S) \} | \leq {|T \cap O_w(u')| \choose m}. \end{align*} $$
$$ \begin{align*}| \{ (u, S) : S \text{ is left } F\text{-sparse}, \; |S| = m, \; S \subseteq T, \; u' = R_u^{v\rightarrow w}(S) \} | \leq {|T \cap O_w(u')| \choose m}. \end{align*} $$
The following lemma will be useful for computing topological pressure.
Lemma 3.11. Let
![]() $\mu _\phi $
be an ergodic equilibrium measure for any
$\mu _\phi $
be an ergodic equilibrium measure for any
![]() $\phi \in C(X)$
. For any tempered Følner sequence
$\phi \in C(X)$
. For any tempered Følner sequence
![]() $ \{ F_n \}$
, if
$ \{ F_n \}$
, if
![]() $S_n \subset L_{F_n}(X)$
such that
$S_n \subset L_{F_n}(X)$
such that
![]() $\mu _\phi (S_n) \rightarrow 1$
, then
$\mu _\phi (S_n) \rightarrow 1$
, then
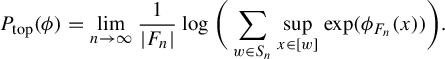 $$ \begin{align*}P_{\mathrm{top}}(\phi) = \lim_{n \rightarrow \infty} \frac{1}{|F_n|} \log \bigg( \sum_{w \in S_n} \sup_{x \in [w]} \mathrm{exp }(\phi_{F_n} (x) ) \bigg). \end{align*} $$
$$ \begin{align*}P_{\mathrm{top}}(\phi) = \lim_{n \rightarrow \infty} \frac{1}{|F_n|} \log \bigg( \sum_{w \in S_n} \sup_{x \in [w]} \mathrm{exp }(\phi_{F_n} (x) ) \bigg). \end{align*} $$
Proof. Let
![]() $\epsilon> 0$
and note by definition of topological pressure above, we have
$\epsilon> 0$
and note by definition of topological pressure above, we have
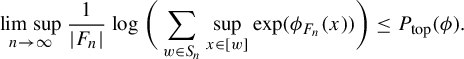 $$ \begin{align*} \limsup_{n \rightarrow \infty} \frac{1}{|F_n|} \log \bigg( \sum_{w \in S_n} \sup_{x \in [w]} \mathrm{exp }(\phi_{F_n} (x) ) \bigg) \leq P_{\mathrm{top}}(\phi). \end{align*} $$
$$ \begin{align*} \limsup_{n \rightarrow \infty} \frac{1}{|F_n|} \log \bigg( \sum_{w \in S_n} \sup_{x \in [w]} \mathrm{exp }(\phi_{F_n} (x) ) \bigg) \leq P_{\mathrm{top}}(\phi). \end{align*} $$
For every n, define
Note since
![]() $F_n$
is a tempered Følner sequence and
$F_n$
is a tempered Følner sequence and
![]() $\mu _\phi $
is ergodic, we can apply the pointwise ergodic theorem and the Shannon–Macmillan–Breiman theorem proven in [Reference Gurevich and Tempelman12, Reference Ornstein and Weiss21] to see for
$\mu _\phi $
is ergodic, we can apply the pointwise ergodic theorem and the Shannon–Macmillan–Breiman theorem proven in [Reference Gurevich and Tempelman12, Reference Ornstein and Weiss21] to see for
![]() $\mu _\phi $
-a.e.
$\mu _\phi $
-a.e.
![]() $x \in X$
,
$x \in X$
,
By the definition of
![]() $T_n$
, it therefore follows that
$T_n$
, it therefore follows that
![]() $\mu _\phi ( \bigcup _{N \in \mathbb {N}} \bigcap _{n \geq N} T_n) = 1$
, and so
$\mu _\phi ( \bigcup _{N \in \mathbb {N}} \bigcap _{n \geq N} T_n) = 1$
, and so
![]() $\mu _\phi (T_n) \rightarrow 1$
. Further,
$\mu _\phi (T_n) \rightarrow 1$
. Further,
![]() $\mu ( S_n \cap T_n) \rightarrow 1$
and by definition of
$\mu ( S_n \cap T_n) \rightarrow 1$
and by definition of
![]() $T_n$
,
$T_n$
,
By taking sufficiently large n, we therefore have
Since
![]() $\epsilon> 0$
was arbitrary, we are finished.
$\epsilon> 0$
was arbitrary, we are finished.
We remind the reader that for
![]() $v, w \in L_F(X)$
,
$v, w \in L_F(X)$
,
![]() $\xi _{v, w}: X \rightarrow X$
is the map that swaps v and w in the F location whenever legal.
$\xi _{v, w}: X \rightarrow X$
is the map that swaps v and w in the F location whenever legal.
Observation 3.12. If
![]() $\phi $
has summable variation according to the exhaustive sequence
$\phi $
has summable variation according to the exhaustive sequence
![]() $\{ E_n \}$
, then for any
$\{ E_n \}$
, then for any
![]() $F \Subset G$
,
$F \Subset G$
,
![]() $v, w \in L_F(X)$
, and any
$v, w \in L_F(X)$
, and any
![]() $x \in [v]$
,
$x \in [v]$
,
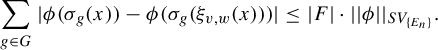 $$ \begin{align*} \sum_{g \in G} | \phi(\sigma_g(x)) - \phi(\sigma_g(\xi_{v, w}(x))) | \leq |F| \cdot ||\phi||_{SV_{\{ E_n\}}}. \end{align*} $$
$$ \begin{align*} \sum_{g \in G} | \phi(\sigma_g(x)) - \phi(\sigma_g(\xi_{v, w}(x))) | \leq |F| \cdot ||\phi||_{SV_{\{ E_n\}}}. \end{align*} $$
We note the proof of Observation 3.12 is standard and the statement appears nearly identically as [Reference Barbieri, Gómez, Marcus, Meyerovitch and Taati1, Proposition 3.1]. The final lemma in this section is a Stirling approximation that will be necessary to compute a lower bound on pressure in the proof of Theorem 1.1.
Lemma 3.13. For
![]() $b, a \in \mathbb {Q}_+$
, and any sequence
$b, a \in \mathbb {Q}_+$
, and any sequence
![]() $n_k \in \mathbb {N}$
such that for all k,
$n_k \in \mathbb {N}$
such that for all k,
![]() $k!$
divides
$k!$
divides
![]() $n_k$
, let
$n_k$
, let
![]() $D \in \mathbb {R}$
satisfying
$D \in \mathbb {R}$
satisfying
![]() $\log ({a}/{b})> D$
. Then, for sufficiently small
$\log ({a}/{b})> D$
. Then, for sufficiently small
![]() $c \in \mathbb {Q}_+$
, we have
$c \in \mathbb {Q}_+$
, we have
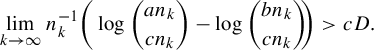 $$ \begin{align*} \lim_{k \rightarrow \infty} n_k^{-1} \bigg( \log { an_k \choose c n_k} - \log {b n_k \choose c n_k} \!\bigg)> cD .\end{align*} $$
$$ \begin{align*} \lim_{k \rightarrow \infty} n_k^{-1} \bigg( \log { an_k \choose c n_k} - \log {b n_k \choose c n_k} \!\bigg)> cD .\end{align*} $$
Proof. We define for all
![]() $c \in (0, \min \{ a, b\} ) \cap \mathbb {Q}$
,
$c \in (0, \min \{ a, b\} ) \cap \mathbb {Q}$
,
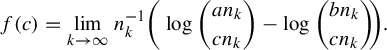 $$ \begin{align*}f(c) = \lim_{k \rightarrow \infty} n_k^{-1} \bigg( \log { an_k \choose c n_k} - \log {b n_k \choose c n_k} \!\bigg) .\end{align*} $$
$$ \begin{align*}f(c) = \lim_{k \rightarrow \infty} n_k^{-1} \bigg( \log { an_k \choose c n_k} - \log {b n_k \choose c n_k} \!\bigg) .\end{align*} $$
First note, we have for all
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
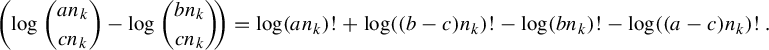 $$ \begin{align*}\bigg(\! \log { an_k \choose c n_k} - \log {b n_k \choose c n_k} \!\bigg) = \log (a n_k)! + \log ((b-c)n_k)! - \log (b n_k)! - \log ((a-c)n_k)!. \end{align*} $$
$$ \begin{align*}\bigg(\! \log { an_k \choose c n_k} - \log {b n_k \choose c n_k} \!\bigg) = \log (a n_k)! + \log ((b-c)n_k)! - \log (b n_k)! - \log ((a-c)n_k)!. \end{align*} $$
If we divide by
![]() $n_k$
and take the limit as k goes to infinity, Stirling’s approximation implies
$n_k$
and take the limit as k goes to infinity, Stirling’s approximation implies
We now examine
Note here
![]() $f'(0) = \log ({a}/{b})> D$
. Since
$f'(0) = \log ({a}/{b})> D$
. Since
![]() $f(0) = 0$
, it immediately follows that for sufficiently small
$f(0) = 0$
, it immediately follows that for sufficiently small
![]() $c \in \mathbb {Q}_+$
, we know
$c \in \mathbb {Q}_+$
, we know
![]() $f(c)> cD$
.
$f(c)> cD$
.
3.3 Proof of Theorem 1.1
Theorem 3.1. Let G be a countable amenable group and X be a G-subshift. Let
![]() $\phi \in SV(X)$
,
$\phi \in SV(X)$
,
![]() $\mu _\phi $
an equilibrium state for
$\mu _\phi $
an equilibrium state for
![]() $\phi $
,
$\phi $
,
![]() $F \Subset G$
and
$F \Subset G$
and
![]() $v, w \in L_F(X)$
. If
$v, w \in L_F(X)$
. If
![]() $E_X(v) \subset E_X(w)$
, then
$E_X(v) \subset E_X(w)$
, then
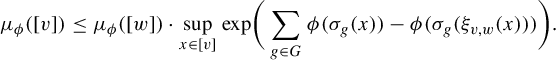 $$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \cdot \sup_{x \in [v]} \mathrm{exp }\bigg( \sum_{g \in G} \phi(\sigma_g(x)) - \phi(\sigma_g(\xi_{v, w}(x))) \bigg).\end{align*} $$
$$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \cdot \sup_{x \in [v]} \mathrm{exp }\bigg( \sum_{g \in G} \phi(\sigma_g(x)) - \phi(\sigma_g(\xi_{v, w}(x))) \bigg).\end{align*} $$
First, we let X,
![]() $\phi $
, F, v and w be as in the statement of the theorem. By ergodic decomposition, it is sufficient to show the desired result for ergodic equilibrium states, so we let
$\phi $
, F, v and w be as in the statement of the theorem. By ergodic decomposition, it is sufficient to show the desired result for ergodic equilibrium states, so we let
![]() $\mu _\phi $
be an ergodic equilibrium state for
$\mu _\phi $
be an ergodic equilibrium state for
![]() $\phi $
. Fix
$\phi $
. Fix
![]() $C = \sup _{x \in [v]} \sum _{g \in G} \phi (\sigma _g(x)) - \phi (\sigma _g(\xi _{v, w}(x)))$
and note by Observation 3.12, we know
$C = \sup _{x \in [v]} \sum _{g \in G} \phi (\sigma _g(x)) - \phi (\sigma _g(\xi _{v, w}(x)))$
and note by Observation 3.12, we know
![]() $-\infty < C < \infty $
. We now suppose for a contradiction that
$-\infty < C < \infty $
. We now suppose for a contradiction that
![]() $\mu _\phi ([v])> \mu _\phi ([w]) \cdot e^C$
.
$\mu _\phi ([v])> \mu _\phi ([w]) \cdot e^C$
.
We now take
![]() $\delta \in (0, \frac {4 }{5} \mu _\phi ([v])) $
satisfying
$\delta \in (0, \frac {4 }{5} \mu _\phi ([v])) $
satisfying
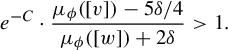 $$ \begin{align*}e^{-C} \cdot \frac{\mu_\phi([v]) - 5 \delta / 4}{\mu_\phi([w]) + 2 \delta}> 1 .\end{align*} $$
$$ \begin{align*}e^{-C} \cdot \frac{\mu_\phi([v]) - 5 \delta / 4}{\mu_\phi([w]) + 2 \delta}> 1 .\end{align*} $$
Note here, this is attainable for all sufficiently small
![]() $\delta $
since we know
$\delta $
since we know
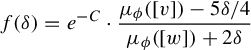 $$ \begin{align*}f(\delta ) = e^{-C} \cdot \frac{\mu_\phi([v]) - 5 \delta / 4}{\mu_\phi([w]) + 2 \delta} \end{align*} $$
$$ \begin{align*}f(\delta ) = e^{-C} \cdot \frac{\mu_\phi([v]) - 5 \delta / 4}{\mu_\phi([w]) + 2 \delta} \end{align*} $$
is continuous and, by assumption,
![]() $f(0)> 1$
.
$f(0)> 1$
.
Let
![]() $F_n$
be a Følner sequence such that for each n,
$F_n$
be a Følner sequence such that for each n,
![]() $n!$
divides
$n!$
divides
![]() $|F_n|$
and
$|F_n|$
and
![]() $F_n^{-1} = F_n$
. It is noted by Xu and Zheng in [Reference Xu and Zheng24] that we can assume
$F_n^{-1} = F_n$
. It is noted by Xu and Zheng in [Reference Xu and Zheng24] that we can assume
![]() $F_n$
is tempered by passing to a subsequence. Re-index this sequence by n, and thus since
$F_n$
is tempered by passing to a subsequence. Re-index this sequence by n, and thus since
![]() $F_n$
is tempered, we know it satisfies the requirements for the lemmas above.
$F_n$
is tempered, we know it satisfies the requirements for the lemmas above.
We now define
![]() $S_n \subset L_{F_n}(X)$
as follows:
$S_n \subset L_{F_n}(X)$
as follows:
We note here since
![]() $\mu _\phi $
is ergodic,
$\mu _\phi $
is ergodic,
![]() $\mu _\phi ( S_n) \rightarrow 1$
and we can therefore apply Lemma 3.11 to see
$\mu _\phi ( S_n) \rightarrow 1$
and we can therefore apply Lemma 3.11 to see
We now apply Lemma 3.1 with respect to F and
![]() $\epsilon = \delta / 8$
, re-index our Følner sequence according to the lemma, and let
$\epsilon = \delta / 8$
, re-index our Følner sequence according to the lemma, and let
![]() $\mathcal {P} = \{ P_i : 1 \leq i \leq N \}$
be our collection of pairwise disjoint, left F-sparse sets. We also pass to the tail of the sequence of Følner sets ensuring that for each n, we have
$\mathcal {P} = \{ P_i : 1 \leq i \leq N \}$
be our collection of pairwise disjoint, left F-sparse sets. We also pass to the tail of the sequence of Følner sets ensuring that for each n, we have
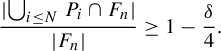 $$ \begin{align*} \frac{|\!\bigcup_{i \leq N} P_i \cap F_n|}{|F_n|} \geq 1 - \frac{\delta}{4}. \end{align*} $$
$$ \begin{align*} \frac{|\!\bigcup_{i \leq N} P_i \cap F_n|}{|F_n|} \geq 1 - \frac{\delta}{4}. \end{align*} $$
For each
![]() $1 \leq i \leq N$
, we now define
$1 \leq i \leq N$
, we now define
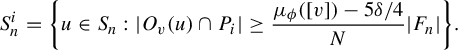 $$ \begin{align*}S_n^{i} = \bigg\{ u \in S_n : |O_v(u) \cap P_i| \geq \frac{\mu_\phi([v]) - 5 \delta / 4}{N} |F_n| \bigg\}. \end{align*} $$
$$ \begin{align*}S_n^{i} = \bigg\{ u \in S_n : |O_v(u) \cap P_i| \geq \frac{\mu_\phi([v]) - 5 \delta / 4}{N} |F_n| \bigg\}. \end{align*} $$
Lemma 3.2. For each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $S_n = \bigcup _{1 \leq i \leq N} S_n^i$
.
$S_n = \bigcup _{1 \leq i \leq N} S_n^i$
.
Proof. Suppose there exists some
![]() $u \in S_n \backslash \bigcup _{1 \leq i \leq N} S_n^{i}$
. We therefore know for all
$u \in S_n \backslash \bigcup _{1 \leq i \leq N} S_n^{i}$
. We therefore know for all
![]() $P \in \mathcal {P}$
,
$P \in \mathcal {P}$
,
![]() $|O_v(u) \cap P| < ({\mu _\phi ([v]) - 5 \delta / 4})/{N} |F_n| $
. Let
$|O_v(u) \cap P| < ({\mu _\phi ([v]) - 5 \delta / 4})/{N} |F_n| $
. Let
![]() $Q = F_n \backslash \bigcup _{i \leq N} P_i$
and note that
$Q = F_n \backslash \bigcup _{i \leq N} P_i$
and note that
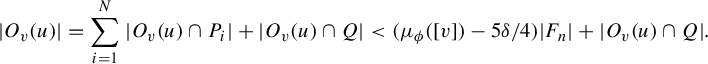 $$ \begin{align*}|O_v(u)| = \sum_{i=1}^N | O_v(u) \cap P_i| + |O_v(u) \cap Q| < (\mu_\phi([v]) - 5 \delta / 4) |F_n| + |O_v(u) \cap Q|. \end{align*} $$
$$ \begin{align*}|O_v(u)| = \sum_{i=1}^N | O_v(u) \cap P_i| + |O_v(u) \cap Q| < (\mu_\phi([v]) - 5 \delta / 4) |F_n| + |O_v(u) \cap Q|. \end{align*} $$
However, since
![]() $u \in S_n$
, we know
$u \in S_n$
, we know
![]() $(\mu _\phi ([v]) - \delta ) \cdot |F_n| < |O_v(u)|$
. It follows that
$(\mu _\phi ([v]) - \delta ) \cdot |F_n| < |O_v(u)|$
. It follows that
By our construction of
![]() $\mathcal {P}$
and since we took a sufficiently long tail for
$\mathcal {P}$
and since we took a sufficiently long tail for
![]() $F_n$
, we know that
$F_n$
, we know that
![]() $ |O_v(u) \cap Q| \leq |Q \cap F_n| \leq ({\delta }/{4})|F_n|$
. We therefore have
$ |O_v(u) \cap Q| \leq |Q \cap F_n| \leq ({\delta }/{4})|F_n|$
. We therefore have
![]() $\mu _\phi ([v]) - \delta < \mu _\phi ([v]) -\delta $
, arriving at a contradiction, and we can conclude that
$\mu _\phi ([v]) - \delta < \mu _\phi ([v]) -\delta $
, arriving at a contradiction, and we can conclude that
![]() $S_n = \bigcup _{1 \leq i \leq N} S_n^{i}$
.
$S_n = \bigcup _{1 \leq i \leq N} S_n^{i}$
.
Lemma 3.3. There exists some fixed
![]() $1 \leq i \leq N$
and a subsequence
$1 \leq i \leq N$
and a subsequence
![]() $(n_k)$
for which we have
$(n_k)$
for which we have
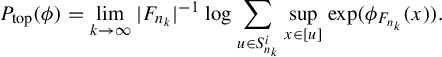 $$ \begin{align*}P_{\mathrm{top}}(\phi) = \lim_{k \rightarrow \infty} |F_{n_k}|^{-1} \log \sum_{u \in S_{n_k}^i} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_{n_k}}(x) ). \end{align*} $$
$$ \begin{align*}P_{\mathrm{top}}(\phi) = \lim_{k \rightarrow \infty} |F_{n_k}|^{-1} \log \sum_{u \in S_{n_k}^i} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_{n_k}}(x) ). \end{align*} $$
Proof. First notice, since
![]() $S_n = \bigcup _{i \leq N} S_n^i$
,
$S_n = \bigcup _{i \leq N} S_n^i$
,
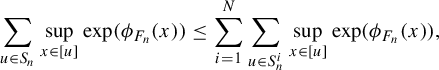 $$ \begin{align*}\sum_{ u \in S_n} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x)) \leq \sum_{i=1}^N \sum_{ u \in S_n^{i}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x)),\end{align*} $$
$$ \begin{align*}\sum_{ u \in S_n} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x)) \leq \sum_{i=1}^N \sum_{ u \in S_n^{i}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x)),\end{align*} $$
and we therefore have for each n, some
![]() $1 \leq i_n \leq N$
such that
$1 \leq i_n \leq N$
such that
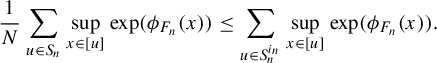 $$ \begin{align*}\frac{1}{N} \sum_{u \in S_n} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x)) \leq \sum_{ u \in S_n^{i_n}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x)). \end{align*} $$
$$ \begin{align*}\frac{1}{N} \sum_{u \in S_n} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x)) \leq \sum_{ u \in S_n^{i_n}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x)). \end{align*} $$
We now use the pigeonhole principle to find a subsequence
![]() $n_k$
such that
$n_k$
such that
![]() $i_{n_k} = i$
is constant. Note, by our construction, we have
$i_{n_k} = i$
is constant. Note, by our construction, we have
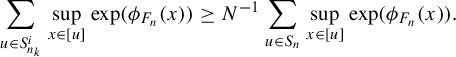 $$ \begin{align*}\sum_{u \in S_{n_k}^i} \sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x)) \geq N^{-1} \sum_{u \in S_n}\sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x)). \end{align*} $$
$$ \begin{align*}\sum_{u \in S_{n_k}^i} \sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x)) \geq N^{-1} \sum_{u \in S_n}\sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x)). \end{align*} $$
We now examine
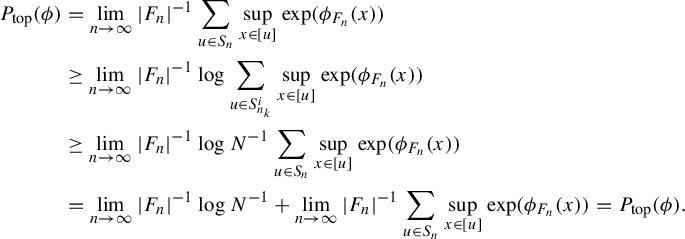 $$ \begin{align*}\kern-15pt P_{\mathrm{top}}(\phi) &= \lim_{n \rightarrow \infty} |F_n|^{-1} \sum_{u \in S_n} \sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x))\\ &\geq \lim_{n \rightarrow \infty} |F_n|^{-1} \log \sum_{u \in S_{n_k}^i} \sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x))\\ & \geq \lim_{n \rightarrow \infty} |F_n|^{-1} \log N^{-1} \sum_{u \in S_n}\sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x))\\ &= \lim_{n \rightarrow \infty} |F_n|^{-1} \log N^{-1} + \lim_{n \rightarrow \infty} |F_n|^{-1} \sum_{u \in S_n} \sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x)) = P_{\mathrm{top}}(\phi).\\[-47pt] \end{align*} $$
$$ \begin{align*}\kern-15pt P_{\mathrm{top}}(\phi) &= \lim_{n \rightarrow \infty} |F_n|^{-1} \sum_{u \in S_n} \sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x))\\ &\geq \lim_{n \rightarrow \infty} |F_n|^{-1} \log \sum_{u \in S_{n_k}^i} \sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x))\\ & \geq \lim_{n \rightarrow \infty} |F_n|^{-1} \log N^{-1} \sum_{u \in S_n}\sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x))\\ &= \lim_{n \rightarrow \infty} |F_n|^{-1} \log N^{-1} + \lim_{n \rightarrow \infty} |F_n|^{-1} \sum_{u \in S_n} \sup_{x \in [u]} \mathrm{exp }(\phi_{F_n}(x)) = P_{\mathrm{top}}(\phi).\\[-47pt] \end{align*} $$
We now apply Lemma 3.3 and fix the resulting
![]() $1 \leq i \leq N$
and re-index along the resulting subsequence
$1 \leq i \leq N$
and re-index along the resulting subsequence
![]() $(n_k)$
. Denote
$(n_k)$
. Denote
![]() $S_k' = S_{n_k}^i$
and fix
$S_k' = S_{n_k}^i$
and fix
![]() $P = P_i$
. We can therefore compute topological pressure by restricting to the sequence of collections of finite configurations
$P = P_i$
. We can therefore compute topological pressure by restricting to the sequence of collections of finite configurations
![]() $S_n^{\prime }$
. We will now make replacements of v with w in every
$S_n^{\prime }$
. We will now make replacements of v with w in every
![]() $u \in S_n^{\prime }$
at locations in P with a small frequency to increase the pressure of the dynamical system to arrive at our contradiction.
$u \in S_n^{\prime }$
at locations in P with a small frequency to increase the pressure of the dynamical system to arrive at our contradiction.
We let
![]() $a, b \in \mathbb {Q}_+$
such that
$a, b \in \mathbb {Q}_+$
such that
![]() $a \leq (\mu _\phi ([v]) - 5\delta / 4) /N$
,
$a \leq (\mu _\phi ([v]) - 5\delta / 4) /N$
,
![]() $b \geq (\mu _\phi ([w]) + 2\delta ) / N $
, and
$b \geq (\mu _\phi ([w]) + 2\delta ) / N $
, and
![]() $\log ({a}/{b})> C$
. Note, such
$\log ({a}/{b})> C$
. Note, such
![]() $a, b \in \mathbb {Q}_+$
must exist since
$a, b \in \mathbb {Q}_+$
must exist since
![]() $\log ({ \mu _\phi ([v]) - 5\delta / 4})/ (\mu _\phi ([w]) + 2\delta )> C$
by assumption. We now let
$\log ({ \mu _\phi ([v]) - 5\delta / 4})/ (\mu _\phi ([w]) + 2\delta )> C$
by assumption. We now let
![]() $\epsilon \in \mathbb {Q}_+$
be sufficiently small to satisfy Lemma 3.13 with respect to
$\epsilon \in \mathbb {Q}_+$
be sufficiently small to satisfy Lemma 3.13 with respect to
![]() $a, b$
and
$a, b$
and
![]() $D = C$
.
$D = C$
.
Define for each
![]() $u \in S_n^{\prime }$
,
$u \in S_n^{\prime }$
,
Since
![]() $\epsilon \in \mathbb {Q}$
and
$\epsilon \in \mathbb {Q}$
and
![]() $n!$
divides
$n!$
divides
![]() $|F_n|$
, for sufficiently large n,
$|F_n|$
, for sufficiently large n,
![]() $ \epsilon \cdot |F_n| \in \mathbb {N}$
and
$ \epsilon \cdot |F_n| \in \mathbb {N}$
and
![]() $A_u$
is well defined. We restrict our consideration for all n large enough that this definition makes sense. Additionally, since
$A_u$
is well defined. We restrict our consideration for all n large enough that this definition makes sense. Additionally, since
![]() $E_X(v) \subset E_X(w)$
, we have
$E_X(v) \subset E_X(w)$
, we have
![]() $A_u \subset L(X)$
.
$A_u \subset L(X)$
.
We can now define for each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $L_n = \bigcup _{u \in S_n^{\prime }} A_u$
.
$L_n = \bigcup _{u \in S_n^{\prime }} A_u$
.
Lemma 3.4. For each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\sum _{u \in L_n} \sup _{x \in [u]} \mathrm {exp }( \phi _{F_n}(x) )$
is bounded below by
$\sum _{u \in L_n} \sup _{x \in [u]} \mathrm {exp }( \phi _{F_n}(x) )$
is bounded below by
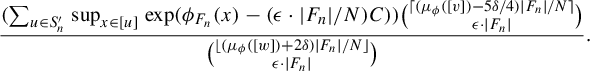 $$ \begin{align} \frac{( \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) - ({ \epsilon \cdot |F_n| }/{ N}) C ) ) { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| }}{ { \lfloor (\mu_\phi([w]) + 2\delta) |F_n|/ N \rfloor \choose \epsilon \cdot |F_n| }}. \end{align} $$
$$ \begin{align} \frac{( \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) - ({ \epsilon \cdot |F_n| }/{ N}) C ) ) { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| }}{ { \lfloor (\mu_\phi([w]) + 2\delta) |F_n|/ N \rfloor \choose \epsilon \cdot |F_n| }}. \end{align} $$
Proof. Note here, for each
![]() $u \in S_n^{\prime }$
,
$u \in S_n^{\prime }$
,
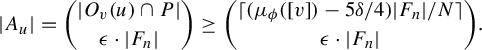 $$ \begin{align*}|A_u| = {|O_v(u) \cap P| \choose \epsilon \cdot |F_n| } \geq { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| }. \end{align*} $$
$$ \begin{align*}|A_u| = {|O_v(u) \cap P| \choose \epsilon \cdot |F_n| } \geq { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| }. \end{align*} $$
However, for every
![]() $u' \in \bigcup _{u \in S_n} A_u$
, we know
$u' \in \bigcup _{u \in S_n} A_u$
, we know
![]() $u'$
came from some
$u'$
came from some
![]() $u \in S_n$
by replacing the
$u \in S_n$
by replacing the
![]() $\epsilon \cdot |F_n| / N$
v terms with w. We can therefore get a bound on the following:
$\epsilon \cdot |F_n| / N$
v terms with w. We can therefore get a bound on the following:
Since
![]() $|FF^{-1}| \geq 1$
, we therefore have
$|FF^{-1}| \geq 1$
, we therefore have
We therefore know for any fixed
![]() $u' \in A_u$
, there are at most
$u' \in A_u$
, there are at most
 $$ \begin{align*}{ \lfloor (\mu_\phi([w]) + 2\delta) |F_n| /N \rfloor \choose \epsilon \cdot |F_n| }\end{align*} $$
$$ \begin{align*}{ \lfloor (\mu_\phi([w]) + 2\delta) |F_n| /N \rfloor \choose \epsilon \cdot |F_n| }\end{align*} $$
u terms for which
![]() $u' \in A_u$
.
$u' \in A_u$
.
It follows that
![]() $\sum _{u \in L_n} \sup _{x \in [u]} \mathrm {exp }( \phi _{F_n}(x) )$
is bounded below by
$\sum _{u \in L_n} \sup _{x \in [u]} \mathrm {exp }( \phi _{F_n}(x) )$
is bounded below by
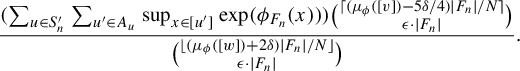 $$ \begin{align} \frac{( \sum_{u \in S_n^{\prime}} \sum_{u' \in A_u} \sup_{x \in [u']} \mathrm{exp }( \phi_{F_n}(x) ) ) { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| }}{ { \lfloor (\mu_\phi([w]) + 2\delta) |F_n|/ N \rfloor \choose \epsilon \cdot |F_n| }}. \end{align} $$
$$ \begin{align} \frac{( \sum_{u \in S_n^{\prime}} \sum_{u' \in A_u} \sup_{x \in [u']} \mathrm{exp }( \phi_{F_n}(x) ) ) { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| }}{ { \lfloor (\mu_\phi([w]) + 2\delta) |F_n|/ N \rfloor \choose \epsilon \cdot |F_n| }}. \end{align} $$
We now bound for any fixed
![]() $u \in S_n^{\prime }$
and each
$u \in S_n^{\prime }$
and each
![]() $u' \in A_u$
,
$u' \in A_u$
,
![]() $\sup _{x \in [u']} \phi _{F_n}(x)$
. First, note
$\sup _{x \in [u']} \phi _{F_n}(x)$
. First, note
![]() $u' = R_u^{v \rightarrow w}(S)$
for some
$u' = R_u^{v \rightarrow w}(S)$
for some
![]() $S \subset F_n$
. Since
$S \subset F_n$
. Since
![]() $E_X(v) \subset E_X(w)$
and by our choice of S, we know
$E_X(v) \subset E_X(w)$
and by our choice of S, we know
![]() $E_X(u) \subset E_X(u')$
. We therefore know
$E_X(u) \subset E_X(u')$
. We therefore know
![]() $\xi _{u, u'}$
(as defined above) is injective and non-identity on
$\xi _{u, u'}$
(as defined above) is injective and non-identity on
![]() $[u]$
. In particular, we are replacing our v terms located at S with w terms just as we did in the construction of
$[u]$
. In particular, we are replacing our v terms located at S with w terms just as we did in the construction of
![]() $u'$
. Note here,
$u'$
. Note here,
![]() $\xi _{u, u'}([u]) \subset [u']$
and thus, we have
$\xi _{u, u'}([u]) \subset [u']$
and thus, we have
We now fix any
![]() $x \in [u]$
. Note that since S is finite and left F-sparse, we may make the v to w replacements sequentially. Each of these replacements takes the form
$x \in [u]$
. Note that since S is finite and left F-sparse, we may make the v to w replacements sequentially. Each of these replacements takes the form
![]() $\sigma _{g^{-1}} ( \xi _{v, w}( \sigma _g (x)) $
for some
$\sigma _{g^{-1}} ( \xi _{v, w}( \sigma _g (x)) $
for some
![]() $g \in G$
. Note here, for each replacement of this kind, by definition of C, we have
$g \in G$
. Note here, for each replacement of this kind, by definition of C, we have
Since we will make
![]() $|S|$
of these replacements, it follows that
$|S|$
of these replacements, it follows that
We therefore know that
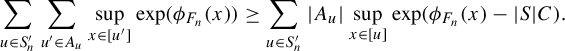 $$ \begin{align*}\sum_{u \in S_n^{\prime}} \sum_{u' \in A_u} \sup_{x \in [u']} \mathrm{exp }( \phi_{F_n}(x) ) \geq \sum_{u \in S_n^{\prime}} |A_u| \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) - |S| C). \end{align*} $$
$$ \begin{align*}\sum_{u \in S_n^{\prime}} \sum_{u' \in A_u} \sup_{x \in [u']} \mathrm{exp }( \phi_{F_n}(x) ) \geq \sum_{u \in S_n^{\prime}} |A_u| \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) - |S| C). \end{align*} $$
Since
![]() $|A_u| \geq 1$
, we therefore have
$|A_u| \geq 1$
, we therefore have
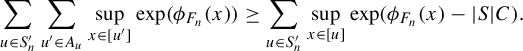 $$ \begin{align} \sum_{u \in S_n^{\prime}} \sum_{u' \in A_u} \sup_{x \in [u']} \mathrm{exp }( \phi_{F_n}(x) ) \geq \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) - |S| C). \end{align} $$
$$ \begin{align} \sum_{u \in S_n^{\prime}} \sum_{u' \in A_u} \sup_{x \in [u']} \mathrm{exp }( \phi_{F_n}(x) ) \geq \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) - |S| C). \end{align} $$
Combining equations (2) and (3), we arrive at our desired result that
![]() $\sum _{u \in L_n} \sup _{x \in [u]} \mathrm {exp }( \phi _{F_n}(x) )$
is bounded below by equation (1).
$\sum _{u \in L_n} \sup _{x \in [u]} \mathrm {exp }( \phi _{F_n}(x) )$
is bounded below by equation (1).
We will conclude the proof of Theorem 1.1 by computing a lower bound on topological pressure and arrive at a contradiction. Since
![]() $L_n \subset L_{F_n}(X)$
, it must be the case that
$L_n \subset L_{F_n}(X)$
, it must be the case that
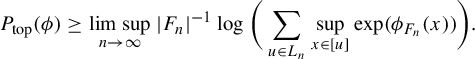 $$ \begin{align*} P_{\mathrm{top}}(\phi) \geq \limsup_{n \rightarrow \infty} |F_n|^{-1} \log \bigg( \sum_{u \in L_n} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) ) \bigg). \end{align*} $$
$$ \begin{align*} P_{\mathrm{top}}(\phi) \geq \limsup_{n \rightarrow \infty} |F_n|^{-1} \log \bigg( \sum_{u \in L_n} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) ) \bigg). \end{align*} $$
By application of Lemma 3.4, we can see that
![]() $P_{\mathrm {top}}(\phi )$
is bounded below by
$P_{\mathrm {top}}(\phi )$
is bounded below by
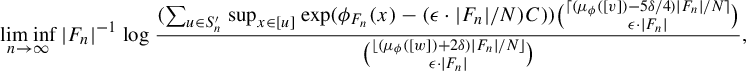 $$ \begin{align*}\liminf_{n \rightarrow \infty} |F_n|^{-1} \log \frac{( \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) - ({ \epsilon \cdot |F_n| }/{ N}) C ) ) { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| }}{ { \lfloor (\mu_\phi([w]) + 2\delta) |F_n|/ N \rfloor \choose \epsilon \cdot |F_n| }}, \end{align*} $$
$$ \begin{align*}\liminf_{n \rightarrow \infty} |F_n|^{-1} \log \frac{( \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) - ({ \epsilon \cdot |F_n| }/{ N}) C ) ) { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| }}{ { \lfloor (\mu_\phi([w]) + 2\delta) |F_n|/ N \rfloor \choose \epsilon \cdot |F_n| }}, \end{align*} $$
which is exactly equal to
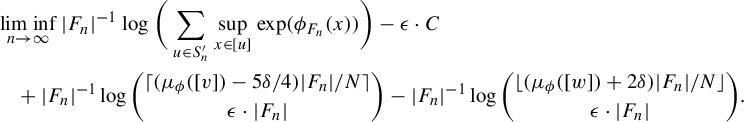 $$ \begin{align} &\liminf_{n \rightarrow \infty} |F_n|^{-1} \log \bigg( \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) ) \bigg) - \epsilon \cdot C\nonumber\\& \quad + |F_n|^{-1} {\kern-1pt}\log{\kern-1pt} { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| } - |F_n|^{-1} {\kern-1pt}\log{\kern-1pt} {\lfloor(\mu_\phi([w]) + 2\delta) |F_n|/ N \rfloor \choose\epsilon \cdot |F_n| }. \end{align} $$
$$ \begin{align} &\liminf_{n \rightarrow \infty} |F_n|^{-1} \log \bigg( \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) ) \bigg) - \epsilon \cdot C\nonumber\\& \quad + |F_n|^{-1} {\kern-1pt}\log{\kern-1pt} { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| } - |F_n|^{-1} {\kern-1pt}\log{\kern-1pt} {\lfloor(\mu_\phi([w]) + 2\delta) |F_n|/ N \rfloor \choose\epsilon \cdot |F_n| }. \end{align} $$
We now note by our choice of a, b, and
![]() $\epsilon $
,
$\epsilon $
,
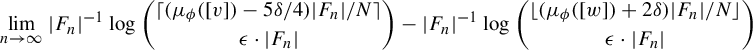 $$ \begin{align*}\lim_{n \rightarrow \infty} |F_n|^{-1} \log { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| } -|F_n|^{-1} \log { \lfloor (\mu_\phi([w]) + 2\delta) |F_n|/ N \rfloor \choose \epsilon \cdot |F_n| }\end{align*} $$
$$ \begin{align*}\lim_{n \rightarrow \infty} |F_n|^{-1} \log { \lceil (\mu_\phi([v]) - 5\delta / 4) |F_n| /N \rceil \choose \epsilon \cdot |F_n| } -|F_n|^{-1} \log { \lfloor (\mu_\phi([w]) + 2\delta) |F_n|/ N \rfloor \choose \epsilon \cdot |F_n| }\end{align*} $$
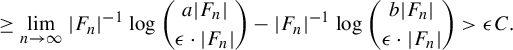 $$ \begin{align*}\geq \lim_{n \rightarrow \infty} |F_n|^{-1} \log { a |F_n| \choose \epsilon \cdot |F_n| } -|F_n|^{-1} \log { b |F_n| \choose \epsilon \cdot |F_n| }> \epsilon C .\end{align*} $$
$$ \begin{align*}\geq \lim_{n \rightarrow \infty} |F_n|^{-1} \log { a |F_n| \choose \epsilon \cdot |F_n| } -|F_n|^{-1} \log { b |F_n| \choose \epsilon \cdot |F_n| }> \epsilon C .\end{align*} $$
It therefore follows that equation (4) is strictly greater than
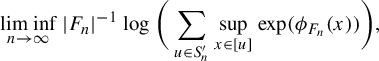 $$ \begin{align*}\liminf_{n \rightarrow \infty} |F_n|^{-1} \log \bigg( \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) ) \bigg) , \end{align*} $$
$$ \begin{align*}\liminf_{n \rightarrow \infty} |F_n|^{-1} \log \bigg( \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) ) \bigg) , \end{align*} $$
and since equation (4) is a lower bound for pressure, we therefore know
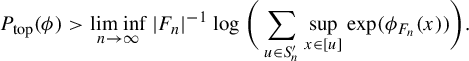 $$ \begin{align*}P_{\mathrm{top}}(\phi)> \liminf_{n \rightarrow \infty} |F_n|^{-1} \log \bigg( \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) ) \bigg). \end{align*} $$
$$ \begin{align*}P_{\mathrm{top}}(\phi)> \liminf_{n \rightarrow \infty} |F_n|^{-1} \log \bigg( \sum_{u \in S_n^{\prime}} \sup_{x \in [u]} \mathrm{exp }( \phi_{F_n}(x) ) \bigg). \end{align*} $$
This contradicts Lemma 3.3. In particular, this means our assumption that
![]() $\mu _\phi ([v])> \mu _\phi ([w]) \cdot e^C$
was incorrect, arriving at our desired result that if
$\mu _\phi ([v])> \mu _\phi ([w]) \cdot e^C$
was incorrect, arriving at our desired result that if
![]() $E_X(v) \subset E_X(w)$
, then
$E_X(v) \subset E_X(w)$
, then
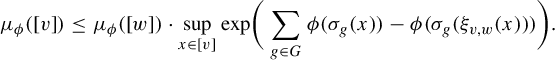 $$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \cdot \sup_{x \in [v]} \mathrm{exp }\bigg( \sum_{g \in G} \phi(\sigma_g(x)) - \phi(\sigma_g(\xi_{v, w}(x))) \bigg). \end{align*} $$
$$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \cdot \sup_{x \in [v]} \mathrm{exp }\bigg( \sum_{g \in G} \phi(\sigma_g(x)) - \phi(\sigma_g(\xi_{v, w}(x))) \bigg). \end{align*} $$
3.4 Locally constant corollaries
We will now explore the case where
![]() $\phi $
is locally constant.
$\phi $
is locally constant.
The following result shows that when the finite configurations v and w agree on a sufficiently chosen boundary, we may compute bounds for their relative measure using only information from the configurations themselves. Further, when they have equal extender sets, we have a closed form formula depending only on
![]() $\phi $
, v, and w to compute the ratio of their measures.
$\phi $
, v, and w to compute the ratio of their measures.
We will say that
![]() $\phi $
is an H-potential for some
$\phi $
is an H-potential for some
![]() $H \Subset G$
if for all
$H \Subset G$
if for all
![]() $x, y \in X$
such that
$x, y \in X$
such that
![]() $x_H = y_H$
, then
$x_H = y_H$
, then
![]() $\phi (x) = \phi (y)$
, that is,
$\phi (x) = \phi (y)$
, that is,
![]() $\mathrm {Var}_H(\phi ) = 0$
. Additionally, for any
$\mathrm {Var}_H(\phi ) = 0$
. Additionally, for any
![]() $H \subset G$
, we will denote
$H \subset G$
, we will denote
![]() $H^\pm = H \cup H^{-1}$
.
$H^\pm = H \cup H^{-1}$
.
Corollary 3.5. Let
![]() $H, F \Subset G$
,
$H, F \Subset G$
,
![]() $v, w \in L_F(X)$
, and
$v, w \in L_F(X)$
, and
![]() $\phi $
be an H-potential. Suppose that
$\phi $
be an H-potential. Suppose that
![]() $E_X(v) \subset E_X(w)$
and for all
$E_X(v) \subset E_X(w)$
and for all
![]() $g \in F^c H^\pm \cap F$
,
$g \in F^c H^\pm \cap F$
,
![]() $v_g = w_g$
(that is, v and w agree on their H-boundary). Then, for any equilibrium state
$v_g = w_g$
(that is, v and w agree on their H-boundary). Then, for any equilibrium state
![]() $\mu _\phi $
for
$\mu _\phi $
for
![]() $\phi $
,
$\phi $
,
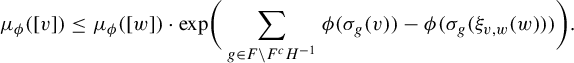 $$ \begin{align*} \mu_\phi([v]) \leq \mu_\phi([w]) \cdot \mathrm{exp }\bigg( \sum_{g \in F \backslash F^c H^{-1}} \phi ( \sigma_g (v)) - \phi ( \sigma_g(\xi_{v, w}(w))) \bigg). \end{align*} $$
$$ \begin{align*} \mu_\phi([v]) \leq \mu_\phi([w]) \cdot \mathrm{exp }\bigg( \sum_{g \in F \backslash F^c H^{-1}} \phi ( \sigma_g (v)) - \phi ( \sigma_g(\xi_{v, w}(w))) \bigg). \end{align*} $$
Proof. We first note, for all
![]() $x \in [v]$
and for any
$x \in [v]$
and for any
![]() $g \in F \cap F^c H^{-1}$
, by assumption, we have
$g \in F \cap F^c H^{-1}$
, by assumption, we have
![]() $x_{gH} = \xi _{v, w}(x)_{gH}$
. Since
$x_{gH} = \xi _{v, w}(x)_{gH}$
. Since
![]() $\phi $
is an H-potential, it immediately follows that for all
$\phi $
is an H-potential, it immediately follows that for all
![]() $g \in F \cap F^c H^{-1}$
,
$g \in F \cap F^c H^{-1}$
,
We now consider
![]() $g \in F^c$
. If
$g \in F^c$
. If
![]() $gH \cap F = \emptyset $
, then
$gH \cap F = \emptyset $
, then
![]() $x_{gH} = \xi _{v, w}(x)_{gH}$
by definition of
$x_{gH} = \xi _{v, w}(x)_{gH}$
by definition of
![]() $\xi _{v, w}$
. We now consider
$\xi _{v, w}$
. We now consider
![]() $gH \cap F \neq \emptyset $
. However, by assumption, since
$gH \cap F \neq \emptyset $
. However, by assumption, since
![]() $g \in F^c$
, we know for all
$g \in F^c$
, we know for all
![]() $f \in gH \cap F$
,
$f \in gH \cap F$
,
![]() $v_f = w_f$
and again we can conclude
$v_f = w_f$
and again we can conclude
![]() $x_{gH} = \xi _{v, w}(x)_{gH}$
. Thus, we know for all
$x_{gH} = \xi _{v, w}(x)_{gH}$
. Thus, we know for all
![]() $g \in F^c$
,
$g \in F^c$
,
Since
![]() $\phi $
is locally constant, it has summable variation, and we can apply Theorem 1.1 to see
$\phi $
is locally constant, it has summable variation, and we can apply Theorem 1.1 to see
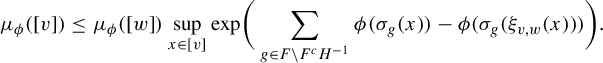 $$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \sup_{x \in [v]} \mathrm{exp }\bigg( \sum_{g \in F \backslash F^c H^{-1}} \phi ( \sigma_g (x)) - \phi ( \sigma_g(\xi_{v, w}(x))) \bigg). \end{align*} $$
$$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \sup_{x \in [v]} \mathrm{exp }\bigg( \sum_{g \in F \backslash F^c H^{-1}} \phi ( \sigma_g (x)) - \phi ( \sigma_g(\xi_{v, w}(x))) \bigg). \end{align*} $$
We let
![]() $x, y \in [v]$
,
$x, y \in [v]$
,
![]() $g\in F \backslash F^c H^\pm $
, and
$g\in F \backslash F^c H^\pm $
, and
![]() $h \in H$
. By construction, we know
$h \in H$
. By construction, we know
![]() $g \notin F^c H^{-1}$
and, thus,
$g \notin F^c H^{-1}$
and, thus,
![]() $gH \cap F^c = \emptyset $
. Since
$gH \cap F^c = \emptyset $
. Since
![]() $\phi $
is an H-potential, it follows that
$\phi $
is an H-potential, it follows that
![]() $\phi \circ \sigma _g (x) = \phi \circ \sigma _g (y)$
, and similarly for
$\phi \circ \sigma _g (x) = \phi \circ \sigma _g (y)$
, and similarly for
![]() $\xi _{v, w}(x)$
and
$\xi _{v, w}(x)$
and
![]() $\xi _{v, w}(y)$
. We can therefore conclude that
$\xi _{v, w}(y)$
. We can therefore conclude that
![]() $\sum _{g \in F \backslash F^c H^\pm } \phi ( \sigma _g (x)) - \phi ( \sigma _g(\xi _{v, w}(x)))$
does not depend on the choice of
$\sum _{g \in F \backslash F^c H^\pm } \phi ( \sigma _g (x)) - \phi ( \sigma _g(\xi _{v, w}(x)))$
does not depend on the choice of
![]() $x \in [v]$
and can be computed by only looking at the cylinder set, and we have arrived at our desired result.
$x \in [v]$
and can be computed by only looking at the cylinder set, and we have arrived at our desired result.
As an immediate corollary, we have the following.
Corollary 3.6. Let
![]() $H, F \Subset G$
,
$H, F \Subset G$
,
![]() $v, w \in L_F(X)$
, and
$v, w \in L_F(X)$
, and
![]() $\phi $
be an H potential. Suppose that
$\phi $
be an H potential. Suppose that
![]() $E_X(v) = E_X(w)$
and for all
$E_X(v) = E_X(w)$
and for all
![]() $g \in F^c H^\pm \cap F$
,
$g \in F^c H^\pm \cap F$
,
![]() $v_g = w_g$
(that is, v and w agree on their H-boundary). Then, for any equilibrium state
$v_g = w_g$
(that is, v and w agree on their H-boundary). Then, for any equilibrium state
![]() $\mu _\phi $
for
$\mu _\phi $
for
![]() $\phi $
,
$\phi $
,
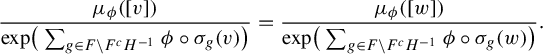 $$ \begin{align*}\frac{\mu_\phi([v])}{\mathrm{exp } \big( \sum_{g \in F \backslash F^c H^{-1}} \phi \circ \sigma_g (v) \big)} = \frac{\mu_\phi([w])}{\mathrm{ exp } \big( \sum_{g \in F \backslash F^c H^{-1}} \phi \circ \sigma_g (w) \big)}. \end{align*} $$
$$ \begin{align*}\frac{\mu_\phi([v])}{\mathrm{exp } \big( \sum_{g \in F \backslash F^c H^{-1}} \phi \circ \sigma_g (v) \big)} = \frac{\mu_\phi([w])}{\mathrm{ exp } \big( \sum_{g \in F \backslash F^c H^{-1}} \phi \circ \sigma_g (w) \big)}. \end{align*} $$
We remind the reader that in the case of
![]() $\phi = 0$
, equilibrium states correspond with measures of maximal entropy. In this case, as a corollary of Theorem 1.1, we extend the results of García-Ramos and Pavlov in [Reference García-Ramos and Pavlov11] to the countable amenable subshift setting.
$\phi = 0$
, equilibrium states correspond with measures of maximal entropy. In this case, as a corollary of Theorem 1.1, we extend the results of García-Ramos and Pavlov in [Reference García-Ramos and Pavlov11] to the countable amenable subshift setting.
Corollary 3.7. Let X be a G-subshift,
![]() $F \Subset G$
,
$F \Subset G$
,
![]() $v, w \in L_F(X)$
, and
$v, w \in L_F(X)$
, and
![]() $\mu $
a measure of maximal entropy. If
$\mu $
a measure of maximal entropy. If
![]() $E_X(v) \subset E_X(w)$
, then
$E_X(v) \subset E_X(w)$
, then
![]() $\mu ([v]) \leq \mu ([w])$
.
$\mu ([v]) \leq \mu ([w])$
.
4 Conformal Gibbs results
4.1 Homoclinic relation and conformal Gibbs
As previously mentioned, a measure
![]() $\mu $
is Gibbs for a potential
$\mu $
is Gibbs for a potential
![]() $\phi $
(in the sense of the theorem of Dobrušin and that of Lanford–Ruelle) if and only if it is conformal Gibbs for
$\phi $
(in the sense of the theorem of Dobrušin and that of Lanford–Ruelle) if and only if it is conformal Gibbs for
![]() $\phi $
. This section will explore our conformal Gibbs-like result, for which we will follow the definition found in [Reference Borsato and MacDonald3].
$\phi $
. This section will explore our conformal Gibbs-like result, for which we will follow the definition found in [Reference Borsato and MacDonald3].
First, we define the homoclinic relation, also known as the Gibbs relation, as
![]() $\mathfrak {T}_X \subset X \times X$
such that
$\mathfrak {T}_X \subset X \times X$
such that
![]() $(x, y) \in \mathfrak {T}_X$
if and only if
$(x, y) \in \mathfrak {T}_X$
if and only if
![]() $x_{F^c} = y_{F^c}$
for some
$x_{F^c} = y_{F^c}$
for some
![]() $F \Subset G$
. We now say a Borel isomorphism
$F \Subset G$
. We now say a Borel isomorphism
![]() $f: X \rightarrow X$
is a holonomy of
$f: X \rightarrow X$
is a holonomy of
![]() $\mathfrak {T}_X$
if for all
$\mathfrak {T}_X$
if for all
![]() $x \in X$
,
$x \in X$
,
![]() $(x, f(x)) \in \mathfrak {T}_X$
. It is known (see [Reference Borsato and MacDonald3]) that there exists a countable group
$(x, f(x)) \in \mathfrak {T}_X$
. It is known (see [Reference Borsato and MacDonald3]) that there exists a countable group
![]() $\Gamma $
of holonomies of X such that
$\Gamma $
of holonomies of X such that
![]() $\mathfrak {T}_X = \{ (x, \gamma (x)) : x \in X, \gamma \in \Gamma \}$
. In fact, by a trivial extension of [Reference Borsato and MacDonald3, Lemma 1], we can see immediately that
$\mathfrak {T}_X = \{ (x, \gamma (x)) : x \in X, \gamma \in \Gamma \}$
. In fact, by a trivial extension of [Reference Borsato and MacDonald3, Lemma 1], we can see immediately that
![]() $\Gamma = \langle \xi _{v, w} : v, w \in L_F(X), F \Subset G \rangle$
is a countable group of holonomies such that
$\Gamma = \langle \xi _{v, w} : v, w \in L_F(X), F \Subset G \rangle$
is a countable group of holonomies such that
![]() $\mathfrak {T}_X = \{ (x, \gamma (x)) : x \in X, \gamma \in \Gamma \}$
.
$\mathfrak {T}_X = \{ (x, \gamma (x)) : x \in X, \gamma \in \Gamma \}$
.
For any measurable
![]() $A \subset X$
, we define
$A \subset X$
, we define
![]() $\mathfrak {T}_X(A) = \bigcup _{x \in A} \{ y \in X : (x, y) \in \mathfrak {T}_X \}$
. For a Borel measure
$\mathfrak {T}_X(A) = \bigcup _{x \in A} \{ y \in X : (x, y) \in \mathfrak {T}_X \}$
. For a Borel measure
![]() $\mu $
on X, we say
$\mu $
on X, we say
![]() $\mu $
is
$\mu $
is
![]() $\mathfrak {T}_X$
-non-singular if for all null sets
$\mathfrak {T}_X$
-non-singular if for all null sets
![]() $A \subset X$
,
$A \subset X$
,
![]() $\mu (\mathfrak {T}_X(A)) = 0$
. Note for any holonomy
$\mu (\mathfrak {T}_X(A)) = 0$
. Note for any holonomy
![]() $f:X \rightarrow X$
, if
$f:X \rightarrow X$
, if
![]() $A \subset X$
is a null set and
$A \subset X$
is a null set and
![]() $\mu $
is
$\mu $
is
![]() $\mathfrak {T}_X$
-non-singular, then
$\mathfrak {T}_X$
-non-singular, then
![]() $\mu \circ f(A) \leq \mu (\mathfrak {T}_X(A)) = 0$
and therefore
$\mu \circ f(A) \leq \mu (\mathfrak {T}_X(A)) = 0$
and therefore
![]() $\mu \circ f << \mu $
.
$\mu \circ f << \mu $
.
We define a cocycle on
![]() $\mathfrak {T}_X$
to be any measurable
$\mathfrak {T}_X$
to be any measurable
![]() $\psi : \mathfrak {T}_X \rightarrow \mathbb {R}$
such that for all
$\psi : \mathfrak {T}_X \rightarrow \mathbb {R}$
such that for all
![]() $x, y, z \in X$
with
$x, y, z \in X$
with
![]() $(x,y), (y, z) \in \mathfrak {T}_X$
, we have
$(x,y), (y, z) \in \mathfrak {T}_X$
, we have
![]() $\psi (x, y) + \psi (y, z) = \psi (x, z)$
. We can now define conformality following [Reference Borsato and MacDonald3, Definition 1].
$\psi (x, y) + \psi (y, z) = \psi (x, z)$
. We can now define conformality following [Reference Borsato and MacDonald3, Definition 1].
Definition 4.1. Let
![]() $\mu $
be a
$\mu $
be a
![]() $\mathfrak {T}_X$
-non-singular Borel probability measure on X and let
$\mathfrak {T}_X$
-non-singular Borel probability measure on X and let
![]() $\psi : \mathfrak {T}_X \rightarrow \mathbb {R}$
be a cocycle. We say
$\psi : \mathfrak {T}_X \rightarrow \mathbb {R}$
be a cocycle. We say
![]() $\mu $
is
$\mu $
is
![]() $(\psi , \mathfrak {T}_X)$
-conformal if for any holonomy
$(\psi , \mathfrak {T}_X)$
-conformal if for any holonomy
![]() $f: X \rightarrow X$
, we have
$f: X \rightarrow X$
, we have
Since we are concerned with Gibbs measures, in general, for a potential
![]() $\phi \in SV(X)$
, we define the following cocycle:
$\phi \in SV(X)$
, we define the following cocycle:
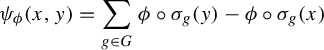 $$ \begin{align*}\psi_\phi (x, y) = \sum_{g \in G} \phi \circ \sigma_g (y) - \phi \circ \sigma_g(x)\end{align*} $$
$$ \begin{align*}\psi_\phi (x, y) = \sum_{g \in G} \phi \circ \sigma_g (y) - \phi \circ \sigma_g(x)\end{align*} $$
and we will say that a measure
![]() $\mu $
is conformal Gibbs for
$\mu $
is conformal Gibbs for
![]() $\phi $
if it is
$\phi $
if it is
![]() $(\psi _\phi , \mathfrak {T}_X)$
-conformal.
$(\psi _\phi , \mathfrak {T}_X)$
-conformal.
Connecting this concept further to the classical notion of Gibbs measures, it was shown in [Reference Borsato and MacDonald3] that a measure is conformal Gibbs for
![]() $\phi $
if and only if it is Gibbs for
$\phi $
if and only if it is Gibbs for
![]() $\phi $
in the sense of Definition 2.8.
$\phi $
in the sense of Definition 2.8.
In addition to the homoclinic relation, in [Reference Meyerovitch17], Meyerovitch defined a subrelation as follows. First, let
In particular,
![]() $\mathcal {F}(X)$
is the group of all background preserving homeomorphisms. We then define
$\mathcal {F}(X)$
is the group of all background preserving homeomorphisms. We then define
![]() $\mathfrak {T}_X^0 = \{ (x, f(x)) : x \in X, f \in \mathcal {F}(X) \}$
. Clearly,
$\mathfrak {T}_X^0 = \{ (x, f(x)) : x \in X, f \in \mathcal {F}(X) \}$
. Clearly,
![]() $\mathfrak {T}_X^0 \subset \mathfrak {T}_X$
; however, in general, these are not necessarily equal.
$\mathfrak {T}_X^0 \subset \mathfrak {T}_X$
; however, in general, these are not necessarily equal.
Notice that when X is an SFT, then each
![]() $\xi _{ v, w}$
is in fact a homeomorphism and thus
$\xi _{ v, w}$
is in fact a homeomorphism and thus
![]() $\xi _{v, w} \in \mathcal {F}(X)$
. In this case,
$\xi _{v, w} \in \mathcal {F}(X)$
. In this case,
![]() $\mathfrak {T}_X^0 = \mathfrak {T}_X$
. Additionally, even if X is not an SFT, if
$\mathfrak {T}_X^0 = \mathfrak {T}_X$
. Additionally, even if X is not an SFT, if
![]() $E_X(v) = E_X(w)$
,
$E_X(v) = E_X(w)$
,
![]() $\xi _{v, w}$
is again a homeomorphism. However, it need not be the case that
$\xi _{v, w}$
is again a homeomorphism. However, it need not be the case that
![]() $\xi _{ v, w}$
is continuous in general.
$\xi _{ v, w}$
is continuous in general.
Example 4.2. Take
![]() $X \subset \{ 0, 1\}^{\mathbb {Z}}$
to the orbit closure of
$X \subset \{ 0, 1\}^{\mathbb {Z}}$
to the orbit closure of
![]() $x = 0^\infty 1 0^\infty $
(which is sometimes referred to as the sunny-side-up subshift). We define
$x = 0^\infty 1 0^\infty $
(which is sometimes referred to as the sunny-side-up subshift). We define
![]() $\xi _{1, 0}$
to swap a
$\xi _{1, 0}$
to swap a
![]() $1$
and
$1$
and
![]() $0$
in the identity location, and note here that
$0$
in the identity location, and note here that
![]() $E_X(1) \subsetneq E_X(0)$
. For each
$E_X(1) \subsetneq E_X(0)$
. For each
![]() $n \geq 0$
, define
$n \geq 0$
, define
![]() $x_n \in X$
such that
$x_n \in X$
such that
![]() $(x_n)_n = 1$
. Then, for all
$(x_n)_n = 1$
. Then, for all
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $\xi _{1, 0}(x_n) = x_n$
. However, we have
$\xi _{1, 0}(x_n) = x_n$
. However, we have
![]() $x_n \rightarrow 0^\infty $
and
$x_n \rightarrow 0^\infty $
and
![]() $\xi _{1, 0}(0^\infty ) = x_0$
. It immediately follows that
$\xi _{1, 0}(0^\infty ) = x_0$
. It immediately follows that
and we can conclude
![]() $\xi _{1, 0}$
is not continuous.
$\xi _{1, 0}$
is not continuous.
In the case of
![]() $G = \mathbb {Z}^d$
and
$G = \mathbb {Z}^d$
and
![]() $\phi \in C(X)$
has d-summable variation, Meyerovitch proved the following result.
$\phi \in C(X)$
has d-summable variation, Meyerovitch proved the following result.
Theorem 4.3. (Meyerovitch [Reference Meyerovitch17])
Let
![]() $X \subset \mathcal {A}^{\mathbb {Z}^d}$
be a subshift,
$X \subset \mathcal {A}^{\mathbb {Z}^d}$
be a subshift,
![]() $\phi \in C(X)$
a potential with d-summable variation, and
$\phi \in C(X)$
a potential with d-summable variation, and
![]() $\mu _\phi $
be an equilibrium state for
$\mu _\phi $
be an equilibrium state for
![]() $\phi $
that is
$\phi $
that is
![]() $\mathfrak {T}_X$
-non-singular. Then,
$\mathfrak {T}_X$
-non-singular. Then,
![]() $\mu _\phi $
is
$\mu _\phi $
is
![]() $(\psi _\phi , \mathfrak {T}_X^0)$
-conformal.
$(\psi _\phi , \mathfrak {T}_X^0)$
-conformal.
In particular,
![]() $\mu _\phi $
is conformal Gibbs with respect to the sub-relation
$\mu _\phi $
is conformal Gibbs with respect to the sub-relation
![]() $\mathfrak {T}_X^0$
. What this means in the terminology of our paper is for
$\mathfrak {T}_X^0$
. What this means in the terminology of our paper is for
![]() $G = \mathbb {Z}^d$
and
$G = \mathbb {Z}^d$
and
![]() $\phi $
with d-summable variation, if
$\phi $
with d-summable variation, if
![]() $E_X(v) = E_X(w)$
, then for
$E_X(v) = E_X(w)$
, then for
![]() $\mu _\phi $
-a.e.
$\mu _\phi $
-a.e.
![]() $x \in X$
,
$x \in X$
,
![]() $({d (\mu \circ \xi _{v, w} ) }/{d\mu })(x) = \mathrm {exp }( \psi _\phi (x, \xi _{v, w}(x)) )$
. We will use Theorem 1.1 to extend this result both to the general amenable group setting as well as to provide an inequality on the derivative when
$({d (\mu \circ \xi _{v, w} ) }/{d\mu })(x) = \mathrm {exp }( \psi _\phi (x, \xi _{v, w}(x)) )$
. We will use Theorem 1.1 to extend this result both to the general amenable group setting as well as to provide an inequality on the derivative when
![]() $E_X(v) \subset E_X(w)$
.
$E_X(v) \subset E_X(w)$
.
4.2 Proof of conformal Gibbs result
In this section, we will prove the following theorem.
Theorem 4.4. Let
![]() $F \Subset G$
,
$F \Subset G$
,
![]() $v, w \in L_F(X)$
,
$v, w \in L_F(X)$
,
![]() $\phi \in SV(X)$
, and
$\phi \in SV(X)$
, and
![]() $\mu _\phi $
be an equilibrium state for
$\mu _\phi $
be an equilibrium state for
![]() $\phi $
. If
$\phi $
. If
![]() $E_X(v) \subset E_X(w)$
, then
$E_X(v) \subset E_X(w)$
, then
![]() $\mu _\phi \circ \xi _{v, w}$
is absolutely continuous with respect to
$\mu _\phi \circ \xi _{v, w}$
is absolutely continuous with respect to
![]() $\mu _\phi $
when restricted to
$\mu _\phi $
when restricted to
![]() $[w]$
and for
$[w]$
and for
![]() $\mu _\phi $
-a.e.
$\mu _\phi $
-a.e.
![]() $x \in [w]$
,
$x \in [w]$
,
For the remainder of this section, we fix some
![]() $F \Subset G$
,
$F \Subset G$
,
![]() $v, w \in L_F(X)$
,
$v, w \in L_F(X)$
,
![]() $\phi \in SV(X)$
, and
$\phi \in SV(X)$
, and
![]() $\mu _\phi $
an equilibrium state for
$\mu _\phi $
an equilibrium state for
![]() $\phi $
.
$\phi $
.
Observation 4.5. If
![]() $E_X(v) \subset E_X(w)$
, then
$E_X(v) \subset E_X(w)$
, then
![]() $\mu _\phi \circ \xi _{v, w} << \mu _\phi $
when restricted to
$\mu _\phi \circ \xi _{v, w} << \mu _\phi $
when restricted to
![]() $[w]$
.
$[w]$
.
Proof. Let
![]() $A \subset [w]$
be a null set. Note here
$A \subset [w]$
be a null set. Note here
Since
![]() $ \{ x \in A : \xi _{v, w}(x) = x\} \subset A$
, it must be a null set, and thus it is sufficient to assume without loss of generality that
$ \{ x \in A : \xi _{v, w}(x) = x\} \subset A$
, it must be a null set, and thus it is sufficient to assume without loss of generality that
![]() $\xi _{v, w}(A) \cap A = \emptyset $
.
$\xi _{v, w}(A) \cap A = \emptyset $
.
Since we know
![]() $\mu _\phi $
is outer regular, we can let
$\mu _\phi $
is outer regular, we can let
![]() $U_n =\bigcup _{ i \leq N_n} [w_{n, i}]$
be an outer approximation by cylinder sets such that
$U_n =\bigcup _{ i \leq N_n} [w_{n, i}]$
be an outer approximation by cylinder sets such that
![]() $\mu _\phi (A) = \lim _{n \rightarrow \infty } \mu _\phi (U_n)$
. By taking sufficiently large n, we can assume without loss of generality that
$\mu _\phi (A) = \lim _{n \rightarrow \infty } \mu _\phi (U_n)$
. By taking sufficiently large n, we can assume without loss of generality that
![]() $[w_{n, i}] \subset [w]$
for all
$[w_{n, i}] \subset [w]$
for all
![]() $n, i$
. Note for each
$n, i$
. Note for each
![]() $n, i$
, we have
$n, i$
, we have
![]() $E_X(\xi _{v, w}(w_{n, i})) \subset E_X(w_{n, i})$
. We now apply Theorem 1.1 with respect to
$E_X(\xi _{v, w}(w_{n, i})) \subset E_X(w_{n, i})$
. We now apply Theorem 1.1 with respect to
![]() $\phi $
,
$\phi $
,
![]() $\mu _\phi $
,
$\mu _\phi $
,
![]() $v_{n, i}$
, and
$v_{n, i}$
, and
![]() $w_{n, i}$
to see
$w_{n, i}$
to see
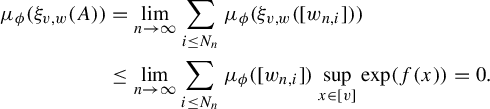 $$ \begin{align*}\mu_\phi(\xi_{v, w}(A)) &= \lim_{n \rightarrow \infty} \sum_{i \leq N_n} \mu_\phi ( \xi_{v, w}([w_{n, i}]) )\\ &\leq \lim_{n \rightarrow \infty} \sum_{i \leq N_n} \mu_\phi ([w_{n, i}]) \sup_{x \in [v]} \mathrm{exp } (f(x)) = 0.\\[-3.9pc] \end{align*} $$
$$ \begin{align*}\mu_\phi(\xi_{v, w}(A)) &= \lim_{n \rightarrow \infty} \sum_{i \leq N_n} \mu_\phi ( \xi_{v, w}([w_{n, i}]) )\\ &\leq \lim_{n \rightarrow \infty} \sum_{i \leq N_n} \mu_\phi ([w_{n, i}]) \sup_{x \in [v]} \mathrm{exp } (f(x)) = 0.\\[-3.9pc] \end{align*} $$
In particular, this means we can discuss the LRN derivative when restricted to
![]() $[w]$
. We now define for each
$[w]$
. We now define for each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\phi _n : X \rightarrow \mathbb {R}$
to be an
$\phi _n : X \rightarrow \mathbb {R}$
to be an
![]() $E_n$
potential approximating
$E_n$
potential approximating
![]() $\phi $
from above. In particular, for all
$\phi $
from above. In particular, for all
![]() $u \in L_{E_n}(X)$
, for any
$u \in L_{E_n}(X)$
, for any
![]() $x \in [u]$
, let
$x \in [u]$
, let
![]() $\phi _n(x) = \sup _{y \in [u]} \phi (y)$
.
$\phi _n(x) = \sup _{y \in [u]} \phi (y)$
.
Observation 4.6.
![]() $\phi _n$
converges to
$\phi _n$
converges to
![]() $\phi $
with respect to the summable variation norm induced by
$\phi $
with respect to the summable variation norm induced by
![]() $\{ E_n \}$
.
$\{ E_n \}$
.
Proof. First note, for any
![]() $k, n \in \mathbb {N}$
, we have
$k, n \in \mathbb {N}$
, we have
Let
![]() $\epsilon> 0$
and note since
$\epsilon> 0$
and note since
![]() $\phi $
has summable variation according to
$\phi $
has summable variation according to
![]() $\{ E_n \}$
, by definition, there exists some
$\{ E_n \}$
, by definition, there exists some
![]() $M \in \mathbb {N}$
such that
$M \in \mathbb {N}$
such that
![]() $\sum _{k=M+1}^\infty |E_{k+1} \backslash E_k| \mathrm {Var}_{E_k}( \phi ) < \epsilon $
. We fix this M. We now note by continuity of
$\sum _{k=M+1}^\infty |E_{k+1} \backslash E_k| \mathrm {Var}_{E_k}( \phi ) < \epsilon $
. We fix this M. We now note by continuity of
![]() $\phi $
and since
$\phi $
and since
![]() $\{ E_n\}$
is an exhaustive sequence, we know there exists some
$\{ E_n\}$
is an exhaustive sequence, we know there exists some
![]() $N \in \mathbb {N}$
such that for all
$N \in \mathbb {N}$
such that for all
![]() $n \geq N$
,
$n \geq N$
,
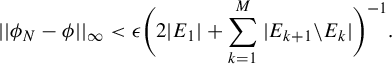 $$ \begin{align*} || \phi_N - \phi||_\infty < \epsilon \bigg( 2 |E_1| + \sum_{k=1}^M |E_{k+1} \backslash E_k| \bigg)^{-1}. \end{align*} $$
$$ \begin{align*} || \phi_N - \phi||_\infty < \epsilon \bigg( 2 |E_1| + \sum_{k=1}^M |E_{k+1} \backslash E_k| \bigg)^{-1}. \end{align*} $$
We now let
![]() $n \geq N$
and we examine
$n \geq N$
and we examine
 $$ \begin{align*}|| \phi_N - \phi||_{SV_{\{ E_n \}}} &= 2 |E_1| \cdot || \phi_n - \phi||_\infty + \sum_{k=1}^M |E_{k+1} \backslash E_k| \mathrm{Var}_{E_k}(\phi_n - \phi)\\&\quad + \sum_{k=M+1}^\infty |E_{k+1} \backslash E_k| \mathrm{Var}_{E_k}(\phi_n - \phi)\\&\leq || \phi_n - \phi||_\infty \bigg(\! 2 |E_1| + \sum_{k=1}^M |E_{k+1} \backslash E_k| \!\bigg) + 2 \sum_{k=M+1}^\infty\! |E_{k+1} \backslash E_k| \mathrm{ Var}_{E_k}( \phi).\end{align*} $$
$$ \begin{align*}|| \phi_N - \phi||_{SV_{\{ E_n \}}} &= 2 |E_1| \cdot || \phi_n - \phi||_\infty + \sum_{k=1}^M |E_{k+1} \backslash E_k| \mathrm{Var}_{E_k}(\phi_n - \phi)\\&\quad + \sum_{k=M+1}^\infty |E_{k+1} \backslash E_k| \mathrm{Var}_{E_k}(\phi_n - \phi)\\&\leq || \phi_n - \phi||_\infty \bigg(\! 2 |E_1| + \sum_{k=1}^M |E_{k+1} \backslash E_k| \!\bigg) + 2 \sum_{k=M+1}^\infty\! |E_{k+1} \backslash E_k| \mathrm{ Var}_{E_k}( \phi).\end{align*} $$
By our choice of N and M, we know for all
![]() $n \geq N$
,
$n \geq N$
,
![]() $||\phi _N - \phi ||_{SV_{\{ E_n \}}} < 3 \epsilon $
. Since
$||\phi _N - \phi ||_{SV_{\{ E_n \}}} < 3 \epsilon $
. Since
![]() $\epsilon $
was arbitrary, we can conclude the proof of the observation.
$\epsilon $
was arbitrary, we can conclude the proof of the observation.
Observation 4.7. If
![]() $E_X(v) \subset E_X(w)$
, then the function
$E_X(v) \subset E_X(w)$
, then the function
![]() $f(x) = \psi _\phi (x, \xi _{v, w}(x))$
is continuous on
$f(x) = \psi _\phi (x, \xi _{v, w}(x))$
is continuous on
![]() $[v]$
.
$[v]$
.
Proof. Using our locally constant approximations
![]() $\phi _n$
, we define for each
$\phi _n$
, we define for each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $$ \begin{align*}f_n(x) = \psi_{\phi_n}(x, \xi_{v, w}(x) ) = \sum_{g \in G} \phi_n(\sigma_g(\xi_{v, w}(x))) - \phi_n(\sigma_g(x)). \end{align*} $$
$$ \begin{align*}f_n(x) = \psi_{\phi_n}(x, \xi_{v, w}(x) ) = \sum_{g \in G} \phi_n(\sigma_g(\xi_{v, w}(x))) - \phi_n(\sigma_g(x)). \end{align*} $$
Since
![]() $\phi _n$
is locally constant, we know the infinite sum is in fact a finite sum and so
$\phi _n$
is locally constant, we know the infinite sum is in fact a finite sum and so
![]() $f_n$
is continuous on
$f_n$
is continuous on
![]() $[v]$
. We now claim that
$[v]$
. We now claim that
![]() $f_n \rightarrow f$
uniformly on
$f_n \rightarrow f$
uniformly on
![]() $[v]$
. By Observation 3.12, we know for all
$[v]$
. By Observation 3.12, we know for all
![]() $x \in [v]$
,
$x \in [v]$
,
Since
![]() $\phi _n \rightarrow \phi $
with respect to the summable variation norm by Observation 4.6, we can conclude that
$\phi _n \rightarrow \phi $
with respect to the summable variation norm by Observation 4.6, we can conclude that
![]() $f_n \rightarrow f$
uniformly on
$f_n \rightarrow f$
uniformly on
![]() $[v]$
. It immediately follows that f is continuous on
$[v]$
. It immediately follows that f is continuous on
![]() $[v]$
.
$[v]$
.
We can combine the above observations with Theorem 1.1 to prove the desired result.
Theorem 4.3. Let
![]() $F \Subset G$
,
$F \Subset G$
,
![]() $v, w \in L_F(X)$
,
$v, w \in L_F(X)$
,
![]() $\phi \in SV(X)$
, and
$\phi \in SV(X)$
, and
![]() $\mu _\phi $
be an equilibrium state for
$\mu _\phi $
be an equilibrium state for
![]() $\phi $
. If
$\phi $
. If
![]() $E_X(v) \subset E_X(w)$
, then for
$E_X(v) \subset E_X(w)$
, then for
![]() $\mu _\phi $
-a.e.
$\mu _\phi $
-a.e.
![]() $x \in [w]$
,
$x \in [w]$
,
Proof. First, we fix
![]() $F \Subset G$
,
$F \Subset G$
,
![]() $v, w \in L_F(X)$
,
$v, w \in L_F(X)$
,
![]() $\phi \in C(X)$
, and
$\phi \in C(X)$
, and
![]() $\mu _\phi $
as in the theorem. We again define for all
$\mu _\phi $
as in the theorem. We again define for all
![]() $x \in X$
,
$x \in X$
,
 $$ \begin{align*}f(x) = \psi_\phi(x, \xi_{v, w}(x)) = \sum_{g \in G} \phi(\sigma_g(\xi_{v,w}(x))) - \phi(\sigma_g(x)),\end{align*} $$
$$ \begin{align*}f(x) = \psi_\phi(x, \xi_{v, w}(x)) = \sum_{g \in G} \phi(\sigma_g(\xi_{v,w}(x))) - \phi(\sigma_g(x)),\end{align*} $$
which we know to be continuous on
![]() $[v]$
by Observation 4.7.
$[v]$
by Observation 4.7.
We fix any Følner sequence
![]() $\{ F_n \}$
and assume without loss of generality that
$\{ F_n \}$
and assume without loss of generality that
![]() $F \subset F_n$
for all n. Fix any
$F \subset F_n$
for all n. Fix any
![]() $x \in [w]$
. We define
$x \in [w]$
. We define
![]() $w_n = x_{F_n}$
and
$w_n = x_{F_n}$
and
![]() $v_n = \xi _{v, w}(x)_{F_n}$
. Note here
$v_n = \xi _{v, w}(x)_{F_n}$
. Note here
![]() $\bigcap _{n\in \mathbb {N}} [w_n] = x$
,
$\bigcap _{n\in \mathbb {N}} [w_n] = x$
,
![]() $\bigcap _{n \in \mathbb {N}} [v_n] = \xi _{v, w}(x)$
. Since
$\bigcap _{n \in \mathbb {N}} [v_n] = \xi _{v, w}(x)$
. Since
![]() $F \subset F_n$
, we know
$F \subset F_n$
, we know
![]() $E_X(v_n) \subset E_X(w_n)$
. We can directly apply Theorem 1.1 to see for each
$E_X(v_n) \subset E_X(w_n)$
. We can directly apply Theorem 1.1 to see for each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
Since by Observation 4.7, we know f is continuous on
![]() $[v]$
and thus there exists some
$[v]$
and thus there exists some
![]() $y_n \in [v_n]$
such that
$y_n \in [v_n]$
such that
![]() $\sup _{y \in [v_n]} \mathrm {exp }( - f(y) ) = \mathrm {exp }( - f(y_n) )$
. We therefore have
$\sup _{y \in [v_n]} \mathrm {exp }( - f(y) ) = \mathrm {exp }( - f(y_n) )$
. We therefore have
Since
![]() $y_n \in [v_n]$
and
$y_n \in [v_n]$
and
![]() $\bigcap _{n \in \mathbb {N}} [v_n] = \{ \xi _{v, w}(x) \}$
, we know
$\bigcap _{n \in \mathbb {N}} [v_n] = \{ \xi _{v, w}(x) \}$
, we know
![]() $y_n \rightarrow \xi _{v, w}(x)$
. We can now take limits to see
$y_n \rightarrow \xi _{v, w}(x)$
. We can now take limits to see
Finally, we note that whenever
![]() $\mu _\phi $
satisfies the equations in Theorem 1.3, it is trivial to show
$\mu _\phi $
satisfies the equations in Theorem 1.3, it is trivial to show
![]() $\mu _\phi $
must also satisfy the equations in Theorem 1.1.
$\mu _\phi $
must also satisfy the equations in Theorem 1.1.
Observation 4.4. Let X be a subshift and
![]() $u, v \in L_F(X)$
such that
$u, v \in L_F(X)$
such that
![]() $E_X(v) \subset E_X(w)$
. Let
$E_X(v) \subset E_X(w)$
. Let
![]() $\phi \in C(X)$
and
$\phi \in C(X)$
and
![]() $\mu _\phi $
satisfy for
$\mu _\phi $
satisfy for
![]() $\mu _\phi $
-a.e.
$\mu _\phi $
-a.e.
![]() $x \in [w]$
,
$x \in [w]$
,
Then,
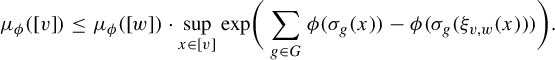 $$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \cdot \sup_{x \in [v]} \mathrm{exp }\bigg( \sum_{g \in G} \phi ( \sigma_g(x)) - \phi(\sigma_g(\xi_{v, w}(x))) \bigg). \end{align*} $$
$$ \begin{align*}\mu_\phi([v]) \leq \mu_\phi([w]) \cdot \sup_{x \in [v]} \mathrm{exp }\bigg( \sum_{g \in G} \phi ( \sigma_g(x)) - \phi(\sigma_g(\xi_{v, w}(x))) \bigg). \end{align*} $$
Proof. First, we notice that since
![]() $E_X(v) \subset E_X(w)$
, then
$E_X(v) \subset E_X(w)$
, then
![]() $[v] \subseteq \xi _{v,w}([w])$
. Further, since
$[v] \subseteq \xi _{v,w}([w])$
. Further, since
![]() $\xi _{v, w}$
is an involution, we know
$\xi _{v, w}$
is an involution, we know
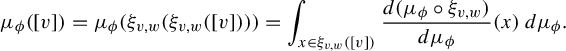 $$ \begin{align*}\mu_\phi([v]) = \mu_\phi( \xi_{v, w}( \xi_{v, w}([v]))) = \int_{x \in \xi_{v, w}([v])} \frac{d (\mu_\phi \circ \xi_{v, w} ) }{d \mu_\phi }(x)\, d\mu_\phi .\end{align*} $$
$$ \begin{align*}\mu_\phi([v]) = \mu_\phi( \xi_{v, w}( \xi_{v, w}([v]))) = \int_{x \in \xi_{v, w}([v])} \frac{d (\mu_\phi \circ \xi_{v, w} ) }{d \mu_\phi }(x)\, d\mu_\phi .\end{align*} $$
Since by assumption, for
![]() $\mu _\phi $
-a.e.
$\mu _\phi $
-a.e.
![]() $x \in [w]$
,
$x \in [w]$
,
we know that
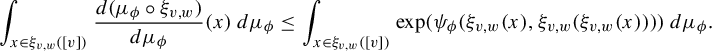 $$ \begin{align*}\int_{x \in \xi_{v, w}([v])} \frac{d (\mu_\phi \circ \xi_{v, w} ) }{d \mu_\phi }(x) \,d\mu_\phi \leq \int_{x \in \xi_{v, w}([v])} \mathrm{exp }( \psi_\phi( \xi_{v,w}(x), \xi_{v,w}(\xi_{v, w}(x))) )\, d\mu_\phi. \end{align*} $$
$$ \begin{align*}\int_{x \in \xi_{v, w}([v])} \frac{d (\mu_\phi \circ \xi_{v, w} ) }{d \mu_\phi }(x) \,d\mu_\phi \leq \int_{x \in \xi_{v, w}([v])} \mathrm{exp }( \psi_\phi( \xi_{v,w}(x), \xi_{v,w}(\xi_{v, w}(x))) )\, d\mu_\phi. \end{align*} $$
It follows immediately that
Since
![]() $\xi _{v, w}([v]) \subset [w]$
, we arrive at our desired conclusion.
$\xi _{v, w}([v]) \subset [w]$
, we arrive at our desired conclusion.
We will now note that as a corollary of Theorem 1.3, we can extend [Reference Meyerovitch17, Theorem 3.1 and Corollary 3.2] to the countable amenable group subshift setting. We have become aware that [Reference Barbieri and Meyerovitch2, Theorem B] extends this further to the countable sofic group subshift setting.
Corollary 4.5. Let
![]() $X \subset \mathcal {A}^G$
be a subshift over a countable amenable group G, let
$X \subset \mathcal {A}^G$
be a subshift over a countable amenable group G, let
![]() $\phi \in SV(X)$
be a potential with summable variation, and let
$\phi \in SV(X)$
be a potential with summable variation, and let
![]() $\mu _\phi $
be an equilibrium state for
$\mu _\phi $
be an equilibrium state for
![]() $\phi $
. Then,
$\phi $
. Then,
![]() $\mu _\phi $
is
$\mu _\phi $
is
![]() $(\mathfrak {T}_X^0, \psi _\phi )$
-conformal.
$(\mathfrak {T}_X^0, \psi _\phi )$
-conformal.
Proof. First note, as observed in [Reference Meyerovitch17], the collection
![]() $\{ \xi _{v, w} : E_X(v) = E_X(w) \}$
generates
$\{ \xi _{v, w} : E_X(v) = E_X(w) \}$
generates
![]() $\mathcal {F}(X)$
. By application of the results in [Reference Meyerovitch17], it is therefore sufficient to show that for any
$\mathcal {F}(X)$
. By application of the results in [Reference Meyerovitch17], it is therefore sufficient to show that for any
![]() $v, w \in L_F(X)$
with
$v, w \in L_F(X)$
with
![]() $E_X(v) = E_X(w)$
, we have for all
$E_X(v) = E_X(w)$
, we have for all
![]() $x \in X$
,
$x \in X$
,
Let
![]() $v, w \in L_F(X)$
such that
$v, w \in L_F(X)$
such that
![]() $E_X(v) = E_X(w)$
. Let
$E_X(v) = E_X(w)$
. Let
![]() $x \in [w]$
and for all
$x \in [w]$
and for all
![]() $n \in \mathbb {N}$
, define
$n \in \mathbb {N}$
, define
![]() $v_n, w_n \in L_{F_n}(X)$
as in the proof of Theorem 1.3. By application of Theorem 1.1, we can see that
$v_n, w_n \in L_{F_n}(X)$
as in the proof of Theorem 1.3. By application of Theorem 1.1, we can see that
 $$ \begin{align*}\inf_{y \in [v_n]} \mathrm{exp }( - f(y) ) \leq \frac{\mu_\phi([v_n])}{\mu_\phi([w_n])} \leq \sup_{y \in [v_n]} \mathrm{exp }( - f(y) ). \end{align*} $$
$$ \begin{align*}\inf_{y \in [v_n]} \mathrm{exp }( - f(y) ) \leq \frac{\mu_\phi([v_n])}{\mu_\phi([w_n])} \leq \sup_{y \in [v_n]} \mathrm{exp }( - f(y) ). \end{align*} $$
By taking limits, we can conclude that for all
![]() $x \in [w]$
,
$x \in [w]$
,
The proof is similar for
![]() $x \in [v]$
and for all
$x \in [v]$
and for all
![]() $x \in X \backslash ([v] \cup [w])$
, we know
$x \in X \backslash ([v] \cup [w])$
, we know
Again, by following the techniques in [Reference Meyerovitch17], it follows that
![]() $\mu _\phi $
is
$\mu _\phi $
is
![]() $(\mathfrak {T}_X^0, \psi _\phi )$
-conformal.
$(\mathfrak {T}_X^0, \psi _\phi )$
-conformal.
Acknowledgements
This work was conducted during the author’s PhD studies under the supervision of Dr Ronnie Pavlov. The author would like to thank Dr Pavlov for all of his assistance throughout the research and writing process. We would also like to thank the referee for their helpful report.