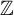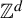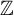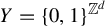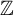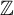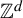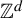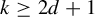1 Introduction and statement of the main results
Krieger ’s embedding theorem [Reference Krieger18] provides simple necessary and sufficient conditions for an arbitrary subshift to embed in a given topologically mixing
![]() $\mathbb {Z}$
-subshift of finite type.
$\mathbb {Z}$
-subshift of finite type.
Here is a formulation of Krieger’s embedding theorem [Reference Krieger18].
Theorem 1.1. (Krieger’s embedding theorem [Reference Krieger18])
Let X be an arbitrary
![]() $\mathbb {Z}$
-subshift and let Y be a topologically mixing
$\mathbb {Z}$
-subshift and let Y be a topologically mixing
![]() $\mathbb {Z}$
-shift of finite type. Then, X embeds in Y if and only if either X is topologically conjugate to Y or
$\mathbb {Z}$
-shift of finite type. Then, X embeds in Y if and only if either X is topologically conjugate to Y or
![]() $h(X) < h(Y)$
and for every
$h(X) < h(Y)$
and for every
![]() $n \in \mathbb {N}$
, the number of points in X that have least period n is less than or equal to the number of points in Y that have least period n.
$n \in \mathbb {N}$
, the number of points in X that have least period n is less than or equal to the number of points in Y that have least period n.
Because Krieger’s embedding theorem is a fundamental result in symbolic dynamics, it was quite natural to seek a multidimensional version. Lightwood carried out significant steps in this direction [Reference Lightwood19, Reference Lightwood20] approximately a quarter of a century ago. In particular, Lightwood characterized the aperiodic
![]() $\mathbb {Z}^d$
-subshifts that can embed in a certain class of
$\mathbb {Z}^d$
-subshifts that can embed in a certain class of
![]() $\mathbb {Z}^d$
-subshifts of finite type. A subshift X is aperiodic if the stabilizer of every point in X is trivial. Lightwood proved the following theorem.
$\mathbb {Z}^d$
-subshifts of finite type. A subshift X is aperiodic if the stabilizer of every point in X is trivial. Lightwood proved the following theorem.
Theorem 1.2. (Lightwood’s embedding theorem for square-filling mixing
 $\mathbb {Z}^2$
-SFTs [Reference Lightwood19, Reference Lightwood20])
$\mathbb {Z}^2$
-SFTs [Reference Lightwood19, Reference Lightwood20])
Let X be an aperiodic
![]() $\mathbb {Z}^2$
subshift and let Y be a square-filling mixing
$\mathbb {Z}^2$
subshift and let Y be a square-filling mixing
![]() $\mathbb {Z}^2$
-subshift of finite type (SFT). Then, X embeds in Y if and only if
$\mathbb {Z}^2$
-subshift of finite type (SFT). Then, X embeds in Y if and only if
![]() $h(X) < h(Y)$
.
$h(X) < h(Y)$
.
We refrain from defining ‘square-filling mixing’, as this notion does not play a role in the current paper. We mention however that a
![]() $\mathbb {Z}$
-SFT is square-filling mixing if and only if it is topologically mixing. For
$\mathbb {Z}$
-SFT is square-filling mixing if and only if it is topologically mixing. For
![]() $\mathbb {Z}^2$
-SFTs, ‘square-filling mixing’ is strictly stronger than topological mixing and strictly weaker than being strongly irreducible (see Definition 4.22).
$\mathbb {Z}^2$
-SFTs, ‘square-filling mixing’ is strictly stronger than topological mixing and strictly weaker than being strongly irreducible (see Definition 4.22).
The central missing ingredient in Lightwood’s work is a method of handling points with non-trivial stabilizers in the domain X. In his paper [Reference Lightwood20], Lightwood announced: ‘The techniques developed here play a central role in the proof of an embedding theorem for general
![]() $\mathbb {Z}^2$
subshifts into square-filling mixing SFTs which will be carried out in a subsequent paper’. To the best of our knowledge, no such result has been published so far. In this paper, building on previous work, including those of Krieger and Lightwood, we obtain a complete characterization of the subsystems for a natural class of
$\mathbb {Z}^2$
subshifts into square-filling mixing SFTs which will be carried out in a subsequent paper’. To the best of our knowledge, no such result has been published so far. In this paper, building on previous work, including those of Krieger and Lightwood, we obtain a complete characterization of the subsystems for a natural class of
![]() $\mathbb {Z}^d$
-SFTs.
$\mathbb {Z}^d$
-SFTs.
To defer some definitions, we first state a particular case of our main result. Given a
![]() $\mathbb {Z}^2$
subshift X and
$\mathbb {Z}^2$
subshift X and
![]() $v \in \mathbb {Z}^2$
, let
$v \in \mathbb {Z}^2$
, let
Similarly, for a pair of linearly independent vectors
![]() $v,w \in \mathbb {Z}^2$
, let
$v,w \in \mathbb {Z}^2$
, let
![]() $X_{v,w}$
denote the set of points in x whose stabilizer is equal to the integer linear combinations of v and w. It is easily verified that for any
$X_{v,w}$
denote the set of points in x whose stabilizer is equal to the integer linear combinations of v and w. It is easily verified that for any
![]() $\mathbb {Z}^2$
subshift X and any pair of linearly independent vectors
$\mathbb {Z}^2$
subshift X and any pair of linearly independent vectors
![]() $v,w \in \mathbb {Z}^2$
, the space
$v,w \in \mathbb {Z}^2$
, the space
![]() $X_{v,w}$
is a finite set.
$X_{v,w}$
is a finite set.
Recall that a vector
![]() $v \in \mathbb {Z}^2$
is primitive if it is not a multiple of some other vector in
$v \in \mathbb {Z}^2$
is primitive if it is not a multiple of some other vector in
![]() $w \in \mathbb {Z}^2$
. If
$w \in \mathbb {Z}^2$
. If
![]() $v \in \mathbb {Z}^2$
is a primitive vector and
$v \in \mathbb {Z}^2$
is a primitive vector and
![]() $n \in \mathbb {N}$
, then the group
$n \in \mathbb {N}$
, then the group
![]() $\mathbb {Z}^2/\langle n v \rangle $
is isomorphic to
$\mathbb {Z}^2/\langle n v \rangle $
is isomorphic to
![]() $\mathbb {Z} \times ( \mathbb {Z} / n \mathbb {Z})$
, and so
$\mathbb {Z} \times ( \mathbb {Z} / n \mathbb {Z})$
, and so
![]() $X_v$
can naturally be viewed as a
$X_v$
can naturally be viewed as a
![]() $\mathbb {Z} \times (\mathbb {Z}/n\mathbb {Z})$
-subshift.
$\mathbb {Z} \times (\mathbb {Z}/n\mathbb {Z})$
-subshift.
Theorem 1.3. A
![]() $\mathbb {Z}^2$
-subshift X embeds in
$\mathbb {Z}^2$
-subshift X embeds in
![]() $A^{\mathbb {Z}^2}$
if and only if either X is topologically conjugate to
$A^{\mathbb {Z}^2}$
if and only if either X is topologically conjugate to
![]() $A^{\mathbb {Z}^2}$
or
$A^{\mathbb {Z}^2}$
or
![]() $h(X) < \log |A|$
and both of the following conditions hold.
$h(X) < \log |A|$
and both of the following conditions hold.
-
(1) For every primitive vector
 $v \in \mathbb {Z}^2$
and every
$v \in \mathbb {Z}^2$
and every
 $n \in \mathbb {N}$
, either
$n \in \mathbb {N}$
, either
 $X_{nv}$
is topologically conjugate to the full-shift
$X_{nv}$
is topologically conjugate to the full-shift
 $A^{\mathbb {Z} \times (\mathbb {Z} / n \mathbb {Z})}$
or the topological entropy of the
$A^{\mathbb {Z} \times (\mathbb {Z} / n \mathbb {Z})}$
or the topological entropy of the
 $\mathbb {Z} \times (\mathbb {Z}/n\mathbb {Z})$
-action on
$\mathbb {Z} \times (\mathbb {Z}/n\mathbb {Z})$
-action on
 $X_{nv}$
is strictly less than
$X_{nv}$
is strictly less than
 $\log (A)$
.
$\log (A)$
. -
(2) For every pair of independent vectors
 $v,w \in \mathbb {Z}^2$
, the number of points in
$v,w \in \mathbb {Z}^2$
, the number of points in
 $X_{v,w}$
does not exceed the number of points in
$X_{v,w}$
does not exceed the number of points in
 $A^{\mathbb {Z}^2}$
whose stabilizer is equal to the integer linear combinations of v and w.
$A^{\mathbb {Z}^2}$
whose stabilizer is equal to the integer linear combinations of v and w.
The statement of Theorem 1.3 suggests that subshifts over more general abelian groups must be considered even when one is initially only interested in the characterization of subsystems of
![]() $\mathbb {Z}^d$
-SFTs.
$\mathbb {Z}^d$
-SFTs.
In this paper, by a map between
![]() $\Gamma $
-subshifts X and Y, we mean a continuous,
$\Gamma $
-subshifts X and Y, we mean a continuous,
![]() $\Gamma $
-equivariant function from X into Y. An embedding of X into Y is an injective map from X into Y. An isomorphism of X and Y is a bijective map between X and Y. We use the notation
$\Gamma $
-equivariant function from X into Y. An embedding of X into Y is an injective map from X into Y. An isomorphism of X and Y is a bijective map between X and Y. We use the notation
![]() $X \hookrightarrow Y$
to indicate that X embeds continuously and
$X \hookrightarrow Y$
to indicate that X embeds continuously and
![]() $\Gamma $
-equivariantly into Y.
$\Gamma $
-equivariantly into Y.
The following is the main result of this paper.
Theorem 1.4. Let
![]() $\Gamma $
be a countable abelian group and let
$\Gamma $
be a countable abelian group and let
![]() $X,Y$
be
$X,Y$
be
![]() $\Gamma $
-subshifts. Suppose that Y has the map extension property. Let
$\Gamma $
-subshifts. Suppose that Y has the map extension property. Let
![]() $Z \subseteq X$
be a (possibly empty)
$Z \subseteq X$
be a (possibly empty)
![]() $\Gamma $
-subshift contained in X and let
$\Gamma $
-subshift contained in X and let
![]() $\hat \rho :Z \to Y$
be an embedding. Then,
$\hat \rho :Z \to Y$
be an embedding. Then,
![]() $\hat \rho $
extends to an embedding
$\hat \rho $
extends to an embedding
![]() $\rho :X \to Y$
if and only if for every subgroup
$\rho :X \to Y$
if and only if for every subgroup
![]() $\Gamma _0 \le \Gamma $
, one of the following conditions holds:
$\Gamma _0 \le \Gamma $
, one of the following conditions holds:
-
(1)
 $\hat \rho \vert _{Z_{\Gamma _0}}:Z_{\Gamma _0} \to Y_{\Gamma _0}$
extends to an isomorphism
$\hat \rho \vert _{Z_{\Gamma _0}}:Z_{\Gamma _0} \to Y_{\Gamma _0}$
extends to an isomorphism
 $\rho _{\Gamma _0}:X_{\Gamma _0} \to Y_{\Gamma _0}$
;
$\rho _{\Gamma _0}:X_{\Gamma _0} \to Y_{\Gamma _0}$
; -
(2)
 $h(\overline {X}_{\Gamma _0}) < h(\overline {Y}_{\Gamma _0})$
and
$h(\overline {X}_{\Gamma _0}) < h(\overline {Y}_{\Gamma _0})$
and
 $\mathrm {Ker}(Y_{\Gamma _0}) \le \mathrm {Ker}(X_{\Gamma _0})$
.
$\mathrm {Ker}(Y_{\Gamma _0}) \le \mathrm {Ker}(X_{\Gamma _0})$
.
The map extension property is defined and discussed in §4. A
![]() $\mathbb {Z}$
-subshift has the map extension property if and only if it is a mixing SFT (Proposition 4.27). All the other new notation that appears in the statement of Theorem 1.4 is defined in §2. Specifically, the notation
$\mathbb {Z}$
-subshift has the map extension property if and only if it is a mixing SFT (Proposition 4.27). All the other new notation that appears in the statement of Theorem 1.4 is defined in §2. Specifically, the notation
![]() $X_{\Gamma _0}$
is explained in Definition 2.11 and the notation
$X_{\Gamma _0}$
is explained in Definition 2.11 and the notation
![]() $\overline {X}_{\Gamma _0}$
is explained in Definition 2.12.
$\overline {X}_{\Gamma _0}$
is explained in Definition 2.12.
We emphasize the primary case
![]() $Z=\emptyset $
in the following corollary.
$Z=\emptyset $
in the following corollary.
Corollary 1.5. Let
![]() $\Gamma $
be a countable abelian group and let
$\Gamma $
be a countable abelian group and let
![]() $X,Y$
be
$X,Y$
be
![]() $\Gamma $
-subshifts. Suppose that Y has the map extension property. Then,
$\Gamma $
-subshifts. Suppose that Y has the map extension property. Then,
![]() $X \hookrightarrow Y$
if and only if for every subgroup
$X \hookrightarrow Y$
if and only if for every subgroup
![]() $\Gamma _0 \le \Gamma $
, one of the following conditions holds:
$\Gamma _0 \le \Gamma $
, one of the following conditions holds:
-
(1)
 $X_{\Gamma _0}$
is topologically conjugate to
$X_{\Gamma _0}$
is topologically conjugate to
 $Y_{\Gamma _0}$
;
$Y_{\Gamma _0}$
; -
(2)
 $h(\overline {X}_{\Gamma _0}) < h(\overline {Y}_{\Gamma _0})$
and
$h(\overline {X}_{\Gamma _0}) < h(\overline {Y}_{\Gamma _0})$
and
 $\mathrm {Ker}(Y_{\Gamma _0}) \le \mathrm {Ker}(X_{\Gamma _0})$
.
$\mathrm {Ker}(Y_{\Gamma _0}) \le \mathrm {Ker}(X_{\Gamma _0})$
.
In the particular case that
![]() $\Gamma =\mathbb {Z}$
, the statement of Corollary 1.5 coincides with the statement of Krieger’s embedding theorem, as stated in Theorem 1.1. In the case
$\Gamma =\mathbb {Z}$
, the statement of Corollary 1.5 coincides with the statement of Krieger’s embedding theorem, as stated in Theorem 1.1. In the case
![]() $\Gamma = \mathbb {Z}^2$
, the statement of Corollary 1.5 coincides with the statement of Theorem 1.3.
$\Gamma = \mathbb {Z}^2$
, the statement of Corollary 1.5 coincides with the statement of Theorem 1.3.
1.1 Structure of the paper
In §2, we review some basic definitions regrading countable abelian groups and subshifts, also introducing a few new ad hoc definitions needed for our work. In §3, we present and prove a specific version of Krieger’s fundamental marker lemma for actions of countable groups. In §4, the map extension property is introduced and studied, along with the notion of retracts, absolute retracts, and contractibility for subshifts. In §5, we briefly recall the notion of entropy minimality for subshifts and use it to prove the necessity of the conditions for embedding in our main result. In §6, we introduce truncated Voronoi diagrams of subsets in
![]() $\mathbb {R}^d$
and in finitely generated abelian groups, deriving results about the existence of ‘sufficiently invariant partial continuous equivariant tilings’ for subshifts. These are based on techniques developed by Lightwood as part of his embedding theorems, with suitable adaptations that are required by the presence of periodic points. Lightwood’s papers are not a prerequisite for this work. In §7, we derive a specific and somewhat technical statement regarding the existence of ‘good markers’, using the map extension property. In §8, we conclude the proof of Theorem 1.4 for the case where
$\mathbb {R}^d$
and in finitely generated abelian groups, deriving results about the existence of ‘sufficiently invariant partial continuous equivariant tilings’ for subshifts. These are based on techniques developed by Lightwood as part of his embedding theorems, with suitable adaptations that are required by the presence of periodic points. Lightwood’s papers are not a prerequisite for this work. In §7, we derive a specific and somewhat technical statement regarding the existence of ‘good markers’, using the map extension property. In §8, we conclude the proof of Theorem 1.4 for the case where
![]() $\Gamma $
is a finitely generated abelian group. In §9, we extend the proof to countable abelian groups (possibly not finitely generated). In §10, we prove a multidimensional version of Boyle’s theorem regarding lower entropy factors of subshifts that applies to subshifts with the map extension property.
$\Gamma $
is a finitely generated abelian group. In §9, we extend the proof to countable abelian groups (possibly not finitely generated). In §10, we prove a multidimensional version of Boyle’s theorem regarding lower entropy factors of subshifts that applies to subshifts with the map extension property.
1.2 A remark regarding the relation to Poirier and Salo’s work [Reference Poirier and Salo23]
The notion of ‘contractibility’ for subshifts, along with symbolic-dynamics analogs of other classical notions in topology such as homotopy, have been developed by Poirier and Salo concurrently with the writing of this paper. We have not been aware of each other’s work when I posted a preliminary version of this work in December 2023. Immediately after I made the first version of this work public, Ville Salo contacted me and informed me of his work with Leo Poirier. An initial version of [Reference Poirier and Salo23] was uploaded to Arxiv around the same time. It quickly became evident to us that Poirier and Salo’s notion of contractility is closely related to the map extension property that I introduced. My initial definition of the map extension property included an additional technical requirement. Ville Salo quickly realized that my initial definition of the map extension property can be streamlined to its current form. At least when abelian groups are concerned, for an arbitrary subshift, the map extension property coincides with being a contractible subshift of finite type. The overlap between the current work and [Reference Poirier and Salo23] is partly an historical artifact due to concurrency. There are, however, significant differences in the point of view and emphasis between the current paper and Poirier and Salo’s work [Reference Poirier and Salo23]. The current paper is aimed at proving the embedding theorem for subshifts over countable abelian groups (with
![]() $\mathbb {Z}^d$
-subshifts as the primary motivation). Poirier and Salo’s work deals with subshifts over arbitrary countable groups (possibly non-commutative). In an attempt to keep the current papers self-contained and readable, there is some overlap between these papers. Some results, although not the main ones, also overlap. Reading [Reference Poirier and Salo23] concurrently with the current paper is encouraged for deeper understanding the notion of contractility and homotopy that will be used in this paper, although it is not a prerequisite for this reading.
$\mathbb {Z}^d$
-subshifts as the primary motivation). Poirier and Salo’s work deals with subshifts over arbitrary countable groups (possibly non-commutative). In an attempt to keep the current papers self-contained and readable, there is some overlap between these papers. Some results, although not the main ones, also overlap. Reading [Reference Poirier and Salo23] concurrently with the current paper is encouraged for deeper understanding the notion of contractility and homotopy that will be used in this paper, although it is not a prerequisite for this reading.
2 Notation and definitions
2.1 Countable abelian groups
Throughout this paper,
![]() $\Gamma $
will be a countable or finite abelian group. We will use additive notation for the group operation in
$\Gamma $
will be a countable or finite abelian group. We will use additive notation for the group operation in
![]() $\Gamma $
. We will denote the identity element of
$\Gamma $
. We will denote the identity element of
![]() $\Gamma $
by
$\Gamma $
by
![]() $0$
. We write
$0$
. We write
![]() $A \Subset \Gamma $
to indicate that A is a finite subset of
$A \Subset \Gamma $
to indicate that A is a finite subset of
![]() $\Gamma $
. For
$\Gamma $
. For
![]() $A,B \subseteq \Gamma $
and
$A,B \subseteq \Gamma $
and
![]() $\gamma \in \Gamma $
, the following standard notation will be used:
$\gamma \in \Gamma $
, the following standard notation will be used:
 $$ \begin{align*} \gamma + A &= \{ \gamma +a : a\in A\},\\ A+B &= \{ a+b : a\in A,~ b \in B\},\\ A-B &=\{ a-b : a\in A,~ b \in B\}, \\ -A &= \{ -a : a \in A \}. \end{align*} $$
$$ \begin{align*} \gamma + A &= \{ \gamma +a : a\in A\},\\ A+B &= \{ a+b : a\in A,~ b \in B\},\\ A-B &=\{ a-b : a\in A,~ b \in B\}, \\ -A &= \{ -a : a \in A \}. \end{align*} $$
For
![]() $A,B,C \subseteq \Gamma $
, we use the notation
$A,B,C \subseteq \Gamma $
, we use the notation
![]() $C=A \oplus B$
to indicate that for every
$C=A \oplus B$
to indicate that for every
![]() $c \in C$
, there exists a unique
$c \in C$
, there exists a unique
![]() $a \in A$
and a unique
$a \in A$
and a unique
![]() $b \in B$
such that
$b \in B$
such that
![]() $c=a+b$
.
$c=a+b$
.
Call a set
![]() $A \subseteq \Gamma $
symmetric if
$A \subseteq \Gamma $
symmetric if
![]() $A=-A$
.
$A=-A$
.
Definition 2.1. Given
![]() $K, F \subseteq \Gamma $
, let
$K, F \subseteq \Gamma $
, let
![]() $\partial _K F$
denote the set of
$\partial _K F$
denote the set of
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
![]() $(\gamma + K) \cap F \ne ~\emptyset $
and
$(\gamma + K) \cap F \ne ~\emptyset $
and
![]() $(\gamma +K) \setminus F \ne \emptyset $
. We refer to
$(\gamma +K) \setminus F \ne \emptyset $
. We refer to
![]() $\partial _K F$
as the K-boundary of F.
$\partial _K F$
as the K-boundary of F.
Definition 2.2. Given
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $K \Subset \Gamma $
, a set
$K \Subset \Gamma $
, a set
![]() $F \Subset \Gamma $
is called
$F \Subset \Gamma $
is called
![]() $(K,\epsilon )$
-invariant if
$(K,\epsilon )$
-invariant if
![]() $|\partial _K F| < \epsilon |F|$
.
$|\partial _K F| < \epsilon |F|$
.
Definition 2.3. A sequence
![]() $(F_n)_{n=1}^\infty $
of finite subsets
$(F_n)_{n=1}^\infty $
of finite subsets
![]() $F_n \Subset \Gamma $
is called a Følner sequence in
$F_n \Subset \Gamma $
is called a Følner sequence in
![]() $\Gamma $
if for every
$\Gamma $
if for every
![]() $\epsilon>0$
and any
$\epsilon>0$
and any
![]() $K \Subset \Gamma $
, there exists
$K \Subset \Gamma $
, there exists
![]() $n_0 \in \mathbb {N}$
such that
$n_0 \in \mathbb {N}$
such that
![]() $F_n$
is
$F_n$
is
![]() $(K,\epsilon )$
-invariant for every
$(K,\epsilon )$
-invariant for every
![]() $n \ge n_0$
.
$n \ge n_0$
.
It is well known that any countable abelian group admits a Følner sequence. A countable group
![]() $\Gamma $
is called amenable if it admits a Følner sequence.
$\Gamma $
is called amenable if it admits a Følner sequence.
Definition 2.4. Given a set
![]() $K \subseteq \Gamma $
, we say that a set
$K \subseteq \Gamma $
, we say that a set
![]() $F \subseteq \Gamma $
is K-separated if
$F \subseteq \Gamma $
is K-separated if
![]() $(v_1+K) \cap (v_2+K) = \emptyset $
whenever
$(v_1+K) \cap (v_2+K) = \emptyset $
whenever
![]() $v_1,v_2 \in F$
and
$v_1,v_2 \in F$
and
![]() $v_1 \ne v_2$
. We say that
$v_1 \ne v_2$
. We say that
![]() $F \subseteq \Gamma $
is a maximal K-separated set if F is K-separated and there is no K-separated set that properly contains F.
$F \subseteq \Gamma $
is a maximal K-separated set if F is K-separated and there is no K-separated set that properly contains F.
The following lemma collects some elementary, yet useful, statements related to the notion of an A-separated set.
Lemma 2.5. Let
![]() $A,B,C \subset \Gamma $
be subsets. Then:
$A,B,C \subset \Gamma $
be subsets. Then:
-
(1) A is B-separated if and only if
 $(A-A)\cap (B-B) = \{0\}$
;
$(A-A)\cap (B-B) = \{0\}$
; -
(2) A is B-separated if and only if B is A-separated;
-
(3) if A is B-separated and
 $(A+B)$
is C-separated, then A is
$(A+B)$
is C-separated, then A is
 $(B+C)$
-separated.
$(B+C)$
-separated.
Proof. (1) The statement that A is B-separated means that whenever
![]() $a_1,a_2 \in A$
,
$a_1,a_2 \in A$
,
![]() $b_1, b_2 \in B$
satisfy
$b_1, b_2 \in B$
satisfy
![]() $a_1+b_1 = a_2 +b_2$
, then
$a_1+b_1 = a_2 +b_2$
, then
![]() $a_1=a_2$
. Equivalently, whenever
$a_1=a_2$
. Equivalently, whenever
![]() $a_1,a_2 \in A$
,
$a_1,a_2 \in A$
,
![]() $b_1,b_2 \in B$
satisfy
$b_1,b_2 \in B$
satisfy
![]() $a_1-a_2 = b_2 -b_1$
, then
$a_1-a_2 = b_2 -b_1$
, then
![]() $a_1=a_2$
and
$a_1=a_2$
and
![]() $b_1=b_2$
. Rephrasing, A is B-separated if and only if whenever
$b_1=b_2$
. Rephrasing, A is B-separated if and only if whenever
![]() $\gamma \in (A-A) \cap (B-B)$
, then
$\gamma \in (A-A) \cap (B-B)$
, then
![]() $\gamma = 0$
.
$\gamma = 0$
.
(2) The previous formulation shows that the role of the sets A and B in the statement ‘A is B-separated’ are completely symmetric. So, A is B-separated if and only if B is A-separated.
(3) Suppose that A is B-separated and that
![]() $A+B$
is C-separated. Suppose
$A+B$
is C-separated. Suppose
![]() $a_1,a_2 \in A$
,
$a_1,a_2 \in A$
,
![]() $b_1,b_2 \in B$
, and
$b_1,b_2 \in B$
, and
![]() $c_1,c_2 \in C$
satisfy that
$c_1,c_2 \in C$
satisfy that
Because
![]() $A+B$
is C-separated, we have that
$A+B$
is C-separated, we have that
![]() $a_1+b_1=a_2+b_2$
and
$a_1+b_1=a_2+b_2$
and
![]() $c_1=c_2$
. Because A is B-separated, we have conclude that
$c_1=c_2$
. Because A is B-separated, we have conclude that
![]() $a_1=a_2$
and
$a_1=a_2$
and
![]() $b_1=b_2$
. We conclude that under the assumptions above, whenever
$b_1=b_2$
. We conclude that under the assumptions above, whenever
![]() $a_1,a_2 \in A$
,
$a_1,a_2 \in A$
,
![]() $b_1,b_2 \in B$
, and
$b_1,b_2 \in B$
, and
![]() $c_1,c_2 \in C$
satisfy that
$c_1,c_2 \in C$
satisfy that
then
![]() $a_1=a_2$
. Equivalently, we showed that A is
$a_1=a_2$
. Equivalently, we showed that A is
![]() $(B+C)$
-separated.
$(B+C)$
-separated.
It is easy to check that an increasing union of K-separated sets is again a K-separated set, so any K-separated set is contained in a maximal K-separated set. The following basic lemma regarding maximal K-separated sets will be useful.
Lemma 2.6. Let
![]() $K \subseteq \Gamma $
be a non-empty symmetric set and let
$K \subseteq \Gamma $
be a non-empty symmetric set and let
![]() $F \subseteq \Gamma $
be a maximal K-separated set. Then,
$F \subseteq \Gamma $
be a maximal K-separated set. Then,
![]() $F+K+K= \Gamma $
.
$F+K+K= \Gamma $
.
Proof. Since F is a maximal K-separated set, for any
![]() $v \in \Gamma $
, there exists
$v \in \Gamma $
, there exists
![]() $k,k_1 \in K$
and
$k,k_1 \in K$
and
![]() $v_1 \in F$
such that
$v_1 \in F$
such that
![]() $v+k = v_1 + k_1$
. It follows that
$v+k = v_1 + k_1$
. It follows that
![]() $v= v_1 + k_1 -k$
. Since K is symmetric,
$v= v_1 + k_1 -k$
. Since K is symmetric,
![]() $-k \in K$
, so
$-k \in K$
, so
![]() $v \in F + K +K$
, proving that
$v \in F + K +K$
, proving that
![]() $\Gamma = F+K+K$
.
$\Gamma = F+K+K$
.
Definition 2.7. A subset
![]() $D \subseteq \Gamma $
is a fundamental domain for
$D \subseteq \Gamma $
is a fundamental domain for
![]() $\Gamma _0 \le \Gamma $
if for each
$\Gamma _0 \le \Gamma $
if for each
![]() $v \in \Gamma $
, the coset
$v \in \Gamma $
, the coset
![]() $v+ \Gamma _0$
intersects D exactly once.
$v+ \Gamma _0$
intersects D exactly once.
Equivalently,
![]() $D \subseteq \Gamma $
is a fundamental domain for
$D \subseteq \Gamma $
is a fundamental domain for
![]() $\Gamma _0 \le \Gamma $
if and only if
$\Gamma _0 \le \Gamma $
if and only if
![]() $\Gamma = D \oplus \Gamma _0$
. It can be directly verified that a subset
$\Gamma = D \oplus \Gamma _0$
. It can be directly verified that a subset
![]() $D \subseteq \Gamma $
is a fundamental domain for
$D \subseteq \Gamma $
is a fundamental domain for
![]() $\Gamma _0 \le \Gamma $
if and only if D is a maximal
$\Gamma _0 \le \Gamma $
if and only if D is a maximal
![]() $\Gamma _0$
-separated set.
$\Gamma _0$
-separated set.
We denote the space of subgroups of
![]() $\Gamma $
by
$\Gamma $
by
![]() $\mathrm {Sub}(\Gamma )$
. The space
$\mathrm {Sub}(\Gamma )$
. The space
![]() $\mathrm {Sub}(\Gamma )$
admits a standard topology called the Chabauty topology.
$\mathrm {Sub}(\Gamma )$
admits a standard topology called the Chabauty topology.
For a countable discrete group
![]() $\Gamma $
, by viewing
$\Gamma $
, by viewing
![]() $\mathrm {Sub}(\Gamma )$
as a closed subset of
$\mathrm {Sub}(\Gamma )$
as a closed subset of
![]() $\{0,1\}^\Gamma $
, the Chabauty topology can be interpreted as the relative topology induced from the product topology on
$\{0,1\}^\Gamma $
, the Chabauty topology can be interpreted as the relative topology induced from the product topology on
![]() $\{0,1\}^\Gamma $
.
$\{0,1\}^\Gamma $
.
A basis for the Chabauty topology is given by sets of the form
Thus, the statement
![]() $\lim _{n\to \infty }\Gamma _n = \Gamma _0$
means that for any finite set
$\lim _{n\to \infty }\Gamma _n = \Gamma _0$
means that for any finite set
![]() $B \Subset \Gamma $
, there exists
$B \Subset \Gamma $
, there exists
![]() $n_0 \in \mathbb {N}$
such that for any
$n_0 \in \mathbb {N}$
such that for any
![]() $n \ge n_0$
, we have
$n \ge n_0$
, we have
![]() $\Gamma _n \cap B = \Gamma _0 \cap B$
.
$\Gamma _n \cap B = \Gamma _0 \cap B$
.
2.2 Subshifts
Definition 2.8. Let A be a finite set. For
![]() $x \in A^\Gamma $
and
$x \in A^\Gamma $
and
![]() $v \in \Gamma $
, we denote the value of x at v by
$v \in \Gamma $
, we denote the value of x at v by
![]() $x_v$
. Given
$x_v$
. Given
![]() $w \in \Gamma $
and
$w \in \Gamma $
and
![]() $x \in A^\Gamma $
, let
$x \in A^\Gamma $
, let
![]() $\sigma _w(x) \in A^\Gamma $
be given by
$\sigma _w(x) \in A^\Gamma $
be given by
![]() $\sigma _{w}(x)_v = x_{v+w}$
for every
$\sigma _{w}(x)_v = x_{v+w}$
for every
![]() $v \in \Gamma $
. This defines an action of
$v \in \Gamma $
. This defines an action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $A^\Gamma $
called the shift action. Since, in this paper, we restrict to commutative groups
$A^\Gamma $
called the shift action. Since, in this paper, we restrict to commutative groups
![]() $\Gamma $
, any left-action is also a right action, and the convention we chose is both standard and simple. In the case of non-commutative groups (in multiplcative notation), to get an action from the left, one uses
$\Gamma $
, any left-action is also a right action, and the convention we chose is both standard and simple. In the case of non-commutative groups (in multiplcative notation), to get an action from the left, one uses
![]() $(\sigma _g(x))_h=x_{g^{-1}h}$
. We equip
$(\sigma _g(x))_h=x_{g^{-1}h}$
. We equip
![]() $A^\Gamma $
with the product topology, where A is given the discrete topology. This makes
$A^\Gamma $
with the product topology, where A is given the discrete topology. This makes
![]() $A^\Gamma $
a compact metrizable topological space. A
$A^\Gamma $
a compact metrizable topological space. A
![]() $\Gamma $
-subshift is a closed shift-invariant subset of
$\Gamma $
-subshift is a closed shift-invariant subset of
![]() $A^\Gamma $
for some finite set A. In this context, we refer to
$A^\Gamma $
for some finite set A. In this context, we refer to
![]() $A^\Gamma $
as the
$A^\Gamma $
as the
![]() $\Gamma $
-full-shift (or simply the full-shift when
$\Gamma $
-full-shift (or simply the full-shift when
![]() $\Gamma $
is fixed) over the alphabet A. Given
$\Gamma $
is fixed) over the alphabet A. Given
![]() $F \subseteq \Gamma $
and
$F \subseteq \Gamma $
and
![]() $x \in A^\Gamma $
, we let
$x \in A^\Gamma $
, we let
![]() $x_F \in A^F$
denote the restriction of x to F.
$x_F \in A^F$
denote the restriction of x to F.
Definition 2.9. Let
![]() $X \subseteq A^\Gamma $
be a
$X \subseteq A^\Gamma $
be a
![]() $\Gamma $
-subshift and
$\Gamma $
-subshift and
![]() $F \Subset \Gamma $
a finite set. We denote
$F \Subset \Gamma $
a finite set. We denote
The elements of
![]() $\mathcal {L}_F(X)$
are called X-admissible F-patterns.
$\mathcal {L}_F(X)$
are called X-admissible F-patterns.
Definition 2.10. For
![]() $x \in A^\Gamma $
, the stabilizer of x is given by
$x \in A^\Gamma $
, the stabilizer of x is given by
Clearly,
![]() $\mathrm {stab}(x)$
is a subgroup of
$\mathrm {stab}(x)$
is a subgroup of
![]() $\Gamma $
.
$\Gamma $
.
Definition 2.11. Given a
![]() $\Gamma $
-subshift X and a subgroup
$\Gamma $
-subshift X and a subgroup
![]() $\Gamma _0 \le \Gamma $
, let
$\Gamma _0 \le \Gamma $
, let
and
 $$ \begin{align*} X_{\Gamma_0} = \begin{cases} X_{[\Gamma_0]} & \text{if } [\Gamma : \Gamma_0] = \infty,\\ \{x \in X: \mathrm{stab}(x) = \Gamma_0 \} & \text{if } [\Gamma:\Gamma_0]<\infty. \end{cases} \end{align*} $$
$$ \begin{align*} X_{\Gamma_0} = \begin{cases} X_{[\Gamma_0]} & \text{if } [\Gamma : \Gamma_0] = \infty,\\ \{x \in X: \mathrm{stab}(x) = \Gamma_0 \} & \text{if } [\Gamma:\Gamma_0]<\infty. \end{cases} \end{align*} $$
Definition 2.12. Given a
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $X \subseteq A^{\Gamma }$
and a subgroup
$X \subseteq A^{\Gamma }$
and a subgroup
![]() $\Gamma _0 < \Gamma $
, let
$\Gamma _0 < \Gamma $
, let
![]() $\overline {X}_{[\Gamma _0]},\overline {X}_{\Gamma _0} \subseteq A^{\Gamma / \Gamma _0}$
denote the natural images of
$\overline {X}_{[\Gamma _0]},\overline {X}_{\Gamma _0} \subseteq A^{\Gamma / \Gamma _0}$
denote the natural images of
![]() $X_{[\Gamma _0]}$
and
$X_{[\Gamma _0]}$
and
![]() $X_{\Gamma _0}$
, respectively. Namely,
$X_{\Gamma _0}$
, respectively. Namely,
and
It is clear that both
![]() $\overline {X}_{[\Gamma _0]}$
and
$\overline {X}_{[\Gamma _0]}$
and
![]() $\overline {X}_{\Gamma _0}$
are closed
$\overline {X}_{\Gamma _0}$
are closed
![]() $(\Gamma /\Gamma _0)$
-invariant sets, and that there are continuous bijections
$(\Gamma /\Gamma _0)$
-invariant sets, and that there are continuous bijections
![]() $\overline {X}_{\Gamma _0} \leftrightarrow X_{\Gamma _0}$
and
$\overline {X}_{\Gamma _0} \leftrightarrow X_{\Gamma _0}$
and
![]() $\overline {X}_{[\Gamma _0]} \leftrightarrow X_{[\Gamma _0]}$
. Thus,
$\overline {X}_{[\Gamma _0]} \leftrightarrow X_{[\Gamma _0]}$
. Thus,
![]() $\overline {X}_{\Gamma _0}$
and
$\overline {X}_{\Gamma _0}$
and
![]() $\overline {X}_{[\Gamma _0]}$
are (possibly empty)
$\overline {X}_{[\Gamma _0]}$
are (possibly empty)
![]() $(\Gamma /\Gamma _0)$
-subshifts.
$(\Gamma /\Gamma _0)$
-subshifts.
Definition 2.13. Given a
![]() $\Gamma $
-subshift X, let
$\Gamma $
-subshift X, let
Equivalently,
The action of
![]() $\Gamma $
on X is called faithful if
$\Gamma $
on X is called faithful if
![]() $\mathrm {Ker}(X)$
is equal to the trivial subgroup.
$\mathrm {Ker}(X)$
is equal to the trivial subgroup.
Definition 2.14. Let
![]() $W \Subset \Gamma $
be a finite set and let
$W \Subset \Gamma $
be a finite set and let
![]() $\mathcal {F} \subset A^W$
be a set of W-patterns. We say that a pattern
$\mathcal {F} \subset A^W$
be a set of W-patterns. We say that a pattern
![]() $w \in A^W$
occurs in
$w \in A^W$
occurs in
![]() $x \in A^\Gamma $
at
$x \in A^\Gamma $
at
![]() $v \in \Gamma $
if
$v \in \Gamma $
if
![]() $\sigma _v(x)_{W} = w$
.
$\sigma _v(x)_{W} = w$
.
Definition 2.15. A
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $Y \subseteq A^\Gamma $
is called an SFT if there exists a finite set
$Y \subseteq A^\Gamma $
is called an SFT if there exists a finite set
![]() $W\Subset \Gamma $
and a set of patterns
$W\Subset \Gamma $
and a set of patterns
![]() $\mathcal {F} \subset A^W$
such that
$\mathcal {F} \subset A^W$
such that
In this case, we say that
![]() $\mathcal {F} \subset A^W$
is a defining set of forbidden patterns for Y.
$\mathcal {F} \subset A^W$
is a defining set of forbidden patterns for Y.
For a given shift of finite type
![]() $Y \subseteq A^\Gamma $
, it is possible to find many different sets
$Y \subseteq A^\Gamma $
, it is possible to find many different sets
![]() $W_1 \Subset \Gamma $
and
$W_1 \Subset \Gamma $
and
![]() $\mathcal {F}_1 \subseteq A^{W_1}$
such that
$\mathcal {F}_1 \subseteq A^{W_1}$
such that
![]() $\mathcal {F}_1$
is a defining set of forbidden patterns for Y.
$\mathcal {F}_1$
is a defining set of forbidden patterns for Y.
Definition 2.16. Given a finite set
![]() $W_0 \Subset \Gamma $
, a function
$W_0 \Subset \Gamma $
, a function
![]() $\Phi :A^{W_0} \to B$
, and another set
$\Phi :A^{W_0} \to B$
, and another set
![]() $E \subseteq \Gamma $
, let
$E \subseteq \Gamma $
, let
![]() $\Phi ^E:A^{W_0+E} \to B^{E}$
be given by
$\Phi ^E:A^{W_0+E} \to B^{E}$
be given by
Definition 2.17. Let
![]() $\rho :X \to Y$
be a map between
$\rho :X \to Y$
be a map between
![]() $\Gamma $
-subshifts
$\Gamma $
-subshifts
![]() $X \subseteq A^\Gamma $
,
$X \subseteq A^\Gamma $
,
![]() $Y \subseteq B^\Gamma $
. A finite set
$Y \subseteq B^\Gamma $
. A finite set
![]() $W \Subset \Gamma $
is a coding window for
$W \Subset \Gamma $
is a coding window for
![]() $\rho $
if there exists a function
$\rho $
if there exists a function
![]() $\Phi :A^{W} \to B$
such that
$\Phi :A^{W} \to B$
such that
![]() $\rho (x)_0 = \Phi (x_W)$
for all
$\rho (x)_0 = \Phi (x_W)$
for all
![]() $x \in X$
. In this case, we say that
$x \in X$
. In this case, we say that
![]() $\Phi $
is a sliding block code for
$\Phi $
is a sliding block code for
![]() $\rho $
.
$\rho $
.
From the definition of the product topology, any map
![]() $\rho :X \to Y$
admits a coding window and a sliding block code. This basic fact is known as the Curtis–Hedlund–Lyndon theorem. As in the case of a defining set of forbidden patterns for a subshift of finite type, there is no uniqueness: a map
$\rho :X \to Y$
admits a coding window and a sliding block code. This basic fact is known as the Curtis–Hedlund–Lyndon theorem. As in the case of a defining set of forbidden patterns for a subshift of finite type, there is no uniqueness: a map
![]() $\rho :X\to Y$
can admit many different coding windows and many different sliding block codes.
$\rho :X\to Y$
can admit many different coding windows and many different sliding block codes.
Definition 2.18. Let
![]() $\rho :X\to Y$
be a map between subshifts
$\rho :X\to Y$
be a map between subshifts
![]() $X\subseteq A^\Gamma $
and
$X\subseteq A^\Gamma $
and
![]() $Y\subseteq B^\Gamma $
, and let
$Y\subseteq B^\Gamma $
, and let
![]() $\Phi :A^W \to B$
be a sliding block code for
$\Phi :A^W \to B$
be a sliding block code for
![]() $\rho $
. We say that a finite set
$\rho $
. We say that a finite set
![]() $W_0 \Subset \Gamma $
is an injectivity window for
$W_0 \Subset \Gamma $
is an injectivity window for
![]() $\rho $
if for any
$\rho $
if for any
![]() $w^{(1)},w^{(2)} \in \mathcal {L}_{W+W_0}(X)$
such that
$w^{(1)},w^{(2)} \in \mathcal {L}_{W+W_0}(X)$
such that
![]() $w{(1)}_0 \ne w^{(2)}_0$
, we have
$w{(1)}_0 \ne w^{(2)}_0$
, we have
![]() $\Phi ^{W_0}(w^{(1)}) \ne \Phi ^{W_0}(w^{(2)})$
.
$\Phi ^{W_0}(w^{(1)}) \ne \Phi ^{W_0}(w^{(2)})$
.
By a standard compactness argument, a map
![]() $\rho :X \to Y$
is injective if and only if it admits a finite injectivity coding window.
$\rho :X \to Y$
is injective if and only if it admits a finite injectivity coding window.
Definition 2.19. Given a countable group
![]() $\Gamma $
, a subgroup
$\Gamma $
, a subgroup
![]() $\Delta < \Gamma $
, and a
$\Delta < \Gamma $
, and a
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $X \subseteq A^\Gamma $
, the
$X \subseteq A^\Gamma $
, the
![]() $\Delta $
-projection of X is defined to be the
$\Delta $
-projection of X is defined to be the
![]() $\Delta $
-subshift
$\Delta $
-subshift
![]() $X^{(\Delta )} \subseteq A^{\Delta }$
given by
$X^{(\Delta )} \subseteq A^{\Delta }$
given by
Let
![]() $X^{[\Delta ]} \subseteq A^{\Gamma }$
denote the
$X^{[\Delta ]} \subseteq A^{\Gamma }$
denote the
![]() $\Gamma $
-subshift given by
$\Gamma $
-subshift given by
It is straightforward to check that
![]() $X^{(\Delta )}$
is indeed a
$X^{(\Delta )}$
is indeed a
![]() $\Delta $
-subshift. It is also clear that
$\Delta $
-subshift. It is also clear that
![]() $X^{[\Delta ]}$
is a
$X^{[\Delta ]}$
is a
![]() $\Gamma $
subshift.
$\Gamma $
subshift.
It follows directly from the definitions that
![]() $X= X^{(\Gamma )}= X^{[\Gamma ]}$
.
$X= X^{(\Gamma )}= X^{[\Gamma ]}$
.
Clearly,
![]() $X \subseteq X^{[\Delta ]}$
and, more generally, if
$X \subseteq X^{[\Delta ]}$
and, more generally, if
![]() $\Delta \le \tilde \Delta \le \Gamma $
, then
$\Delta \le \tilde \Delta \le \Gamma $
, then
![]() $X^{[\tilde \Delta ]} \subseteq X^{[\Delta ]}$
. Moreover, we have the following lemma.
$X^{[\tilde \Delta ]} \subseteq X^{[\Delta ]}$
. Moreover, we have the following lemma.
Lemma 2.20. Let X be a
![]() $\Gamma $
-subshift of finite type, then there exists a finitely generated subgroup
$\Gamma $
-subshift of finite type, then there exists a finitely generated subgroup
![]() $\Delta \le \Gamma $
such that
$\Delta \le \Gamma $
such that
![]() $X= X^{[\Delta ]}$
.
$X= X^{[\Delta ]}$
.
Proof. Let X be a
![]() $\Gamma $
-subshift of finite type. So, there exists a finite set
$\Gamma $
-subshift of finite type. So, there exists a finite set
![]() $W \Subset \Gamma $
and
$W \Subset \Gamma $
and
![]() $\mathcal {F} \subseteq A^W$
such that
$\mathcal {F} \subseteq A^W$
such that
![]() $\mathcal {F}$
is a defining set of forbidden patterns for X. It follows that
$\mathcal {F}$
is a defining set of forbidden patterns for X. It follows that
![]() $X= X^{[\Delta ]}$
, where
$X= X^{[\Delta ]}$
, where
![]() $\Delta $
is the group generated by W.
$\Delta $
is the group generated by W.
Definition 2.21. (Topological entropy for subshifts)
Let X be a
![]() $\Gamma $
-subshift. The topological entropy of X, denoted by
$\Gamma $
-subshift. The topological entropy of X, denoted by
![]() $h(X)$
, is given by
$h(X)$
, is given by
where
![]() $(F_n)_{n=1}^\infty $
is any Følner sequence in
$(F_n)_{n=1}^\infty $
is any Følner sequence in
![]() $\Gamma $
. For convenience, we denote
$\Gamma $
. For convenience, we denote
The existence of the limit (which is actually an infimum) and the fact that it does not depend on the choice of Følner sequence are well known. See, for instance, [Reference Downarowicz, Frej and Romagnoli12].
A simpler, equivalent definition is the following:
where the infimum is over all finite subsets of
![]() $\Gamma $
.
$\Gamma $
.
The equivalence of these definitions can be obtained from the following lemma, which we will use subsequently.
Lemma 2.22. For any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\delta>0$
and a finite set
$\delta>0$
and a finite set
![]() $W \Subset \Gamma $
such that for any
$W \Subset \Gamma $
such that for any
![]() $(W,\delta )$
-invariant set
$(W,\delta )$
-invariant set
![]() $F \Subset \Gamma $
, the following inequality holds:
$F \Subset \Gamma $
, the following inequality holds:
A short proof of Lemma 2.22 can be obtained using Shearer’s inequality [Reference Downarowicz, Frej and Romagnoli12].
The topological entropy of a subshift is invariant under isomorphism. Furthermore, if
![]() $\rho :X \to Y$
is a map, then
$\rho :X \to Y$
is a map, then
![]() $h(\rho (X)) \le h(X)$
.
$h(\rho (X)) \le h(X)$
.
It can be easily verified that for any
![]() $\Gamma _0 \le \Gamma $
and any
$\Gamma _0 \le \Gamma $
and any
![]() $\Gamma $
-subshift X, we have
$\Gamma $
-subshift X, we have
 $$ \begin{align*} h(\overline{X}_{\Gamma_0}) = \inf \bigg\{ \frac{1}{|K|}\log | \mathcal{L}_K(X_{\Gamma_0}) | : K \Subset \Gamma, \Gamma_0 \text{ is } K \text{-separated}\bigg\} \end{align*} $$
$$ \begin{align*} h(\overline{X}_{\Gamma_0}) = \inf \bigg\{ \frac{1}{|K|}\log | \mathcal{L}_K(X_{\Gamma_0}) | : K \Subset \Gamma, \Gamma_0 \text{ is } K \text{-separated}\bigg\} \end{align*} $$
and
 $$ \begin{align*} h(\overline{X}_{[\Gamma_0]}) = \inf \bigg\{ \frac{1}{|K|}\log | \mathcal{L}_K(X_{[\Gamma_0]}) | : K \Subset \Gamma, \Gamma_0 \text{ is } K \text{-separated}\bigg\}. \end{align*} $$
$$ \begin{align*} h(\overline{X}_{[\Gamma_0]}) = \inf \bigg\{ \frac{1}{|K|}\log | \mathcal{L}_K(X_{[\Gamma_0]}) | : K \Subset \Gamma, \Gamma_0 \text{ is } K \text{-separated}\bigg\}. \end{align*} $$
Note that when
![]() $\Gamma $
is a finite group and X is a
$\Gamma $
is a finite group and X is a
![]() $\Gamma $
-subshift, we have
$\Gamma $
-subshift, we have
The following result is probably folklore, we include it for completeness.
Proposition 2.23. Let X be a
![]() $\Gamma $
-subshift. Then,
$\Gamma $
-subshift. Then,
Proof. We need to prove that for every
![]() $\epsilon>0$
, there exists a finite set
$\epsilon>0$
, there exists a finite set
![]() $K \Subset \Gamma $
such that for any K-separated subgroup
$K \Subset \Gamma $
such that for any K-separated subgroup
![]() $\Gamma _0 < \Gamma $
, it holds that
$\Gamma _0 < \Gamma $
, it holds that
![]() $ h(\overline {X}_{\Gamma _0}) \le h(X)+ \epsilon $
. Fix
$ h(\overline {X}_{\Gamma _0}) \le h(X)+ \epsilon $
. Fix
![]() $\epsilon>0$
. Since
$\epsilon>0$
. Since
![]() $h(X) = \inf _{K \Subset \Gamma }({1}/{|K|})\log |\mathcal {L}_K(X)|$
, there exists
$h(X) = \inf _{K \Subset \Gamma }({1}/{|K|})\log |\mathcal {L}_K(X)|$
, there exists
![]() $K \Subset \Gamma $
such that
$K \Subset \Gamma $
such that
Let
![]() $\Gamma _0 \le \Gamma $
be any K-separated subgroup. Then,
$\Gamma _0 \le \Gamma $
be any K-separated subgroup. Then,
Since
![]() $\mathcal {L}(X_{[\Gamma _0]}) \subseteq \mathcal {L}(X)$
, we have that
$\mathcal {L}(X_{[\Gamma _0]}) \subseteq \mathcal {L}(X)$
, we have that
so
In the classical case
![]() $\Gamma = \mathbb {Z}$
, Proposition 2.23 coincides with the well-known fact that for any
$\Gamma = \mathbb {Z}$
, Proposition 2.23 coincides with the well-known fact that for any
![]() $\mathbb {Z}$
-subshift X, the number of points with period at most n is bounded above by
$\mathbb {Z}$
-subshift X, the number of points with period at most n is bounded above by
![]() $e^{nh(X)+o(n)}$
as
$e^{nh(X)+o(n)}$
as
![]() $n \to \infty $
.
$n \to \infty $
.
We introduce some specific notation to avoid repetition of the conditions that appear in the statement of Theorem 1.4.
Definition 2.24. Given
![]() $\Gamma $
-subshifts
$\Gamma $
-subshifts
![]() $X,Y$
, a
$X,Y$
, a
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $Z \subseteq X$
, an injective map
$Z \subseteq X$
, an injective map
![]() $\hat \rho :Z \to Y$
, and
$\hat \rho :Z \to Y$
, and
![]() $\Gamma _0 \le \Gamma $
, we use the notation
$\Gamma _0 \le \Gamma $
, we use the notation
![]() $X \hookrightarrow _{\hat \rho } Y$
to indicate that
$X \hookrightarrow _{\hat \rho } Y$
to indicate that
![]() $\hat \rho $
extends to an embedding of X into Y, and use the notation
$\hat \rho $
extends to an embedding of X into Y, and use the notation
![]() $X \cong _{\hat \rho } Y$
to indicate that
$X \cong _{\hat \rho } Y$
to indicate that
![]() $\hat \rho $
extends to an isomorphism of X and Y. We write
$\hat \rho $
extends to an isomorphism of X and Y. We write
![]() $E(X,Y,\hat \rho ,\Gamma _0)$
to indicate that either
$E(X,Y,\hat \rho ,\Gamma _0)$
to indicate that either
![]() $h(\overline {X}_{\Gamma _0}) < h(\overline {Y}_{\Gamma _0})$
and
$h(\overline {X}_{\Gamma _0}) < h(\overline {Y}_{\Gamma _0})$
and
![]() $\mathrm {Ker}(Y_{\Gamma _0}) \le \mathrm {Ker}(X_{\Gamma _0})$
or
$\mathrm {Ker}(Y_{\Gamma _0}) \le \mathrm {Ker}(X_{\Gamma _0})$
or
![]() $X_{\Gamma _0} \cong _{\hat \rho } Y_{\Gamma _0}$
.
$X_{\Gamma _0} \cong _{\hat \rho } Y_{\Gamma _0}$
.
Note that when
![]() $Z= \emptyset $
and
$Z= \emptyset $
and
![]() $\hat \rho :Z \to Y$
is the ‘empty map’, then
$\hat \rho :Z \to Y$
is the ‘empty map’, then
![]() $X \hookrightarrow _{\hat \rho } Y$
simply means that X embeds in Y and
$X \hookrightarrow _{\hat \rho } Y$
simply means that X embeds in Y and
![]() $X \cong _{\hat \rho } Y$
simply means that X is topologically conjugate to Y.
$X \cong _{\hat \rho } Y$
simply means that X is topologically conjugate to Y.
3 Markers in the domain: Krieger’s marker lemma
In this section, we state and prove a version of Krieger’s marker lemma that applies to
![]() $\Gamma $
-subshifts, where
$\Gamma $
-subshifts, where
![]() $\Gamma $
is a countable abelian group (Lemma 3.3). Krieger’s original lemma is stated for
$\Gamma $
is a countable abelian group (Lemma 3.3). Krieger’s original lemma is stated for
![]() $\mathbb {Z}$
-subshifts [Reference Krieger18, Lemma 2]. Several variants of this lemma can be found in the literature, for instance, [Reference Gutman, Lindenstrauss and Tsukamoto15, Lemma
$\mathbb {Z}$
-subshifts [Reference Krieger18, Lemma 2]. Several variants of this lemma can be found in the literature, for instance, [Reference Gutman, Lindenstrauss and Tsukamoto15, Lemma
![]() $3.4$
], [Reference Gao and Jackson14, Lemma 2.1], and [Reference McGoff and Pavlov22, Lemma 3.2], all with very similar proofs. The main reason that we reprove the lemma here is that our formulation of Lemma 3.3 involves a detailed treatment of non-free actions (a slightly different treatment of non-free actions appears in [Reference McGoff and Pavlov22, Lemma 3.2]). We only deal here with abelian groups purely for simplicity of notation, to maintain consistency of notation with the rest of the paper: using suitable (multiplicative) notion, Krieger’s marker lemma is valid for any action of a countable group on a compact zero dimensional space, essentially with the same proof as our proof of Lemma 3.3 below.
$3.4$
], [Reference Gao and Jackson14, Lemma 2.1], and [Reference McGoff and Pavlov22, Lemma 3.2], all with very similar proofs. The main reason that we reprove the lemma here is that our formulation of Lemma 3.3 involves a detailed treatment of non-free actions (a slightly different treatment of non-free actions appears in [Reference McGoff and Pavlov22, Lemma 3.2]). We only deal here with abelian groups purely for simplicity of notation, to maintain consistency of notation with the rest of the paper: using suitable (multiplicative) notion, Krieger’s marker lemma is valid for any action of a countable group on a compact zero dimensional space, essentially with the same proof as our proof of Lemma 3.3 below.
Definition 3.1. Let X be a
![]() $\Gamma $
-subshift and let
$\Gamma $
-subshift and let
![]() $P \subset \Gamma \setminus \{0\}$
be a finite set. We say that
$P \subset \Gamma \setminus \{0\}$
be a finite set. We say that
![]() $A \subset X$
is a P-marker if
$A \subset X$
is a P-marker if
The following basic lemma says that markers can be effectively merged.
Lemma 3.2. Suppose that X is a
![]() $\Gamma $
-subshift, and that
$\Gamma $
-subshift, and that
![]() $P \subset \Gamma \setminus \{0\}$
is finite and symmetric. Suppose
$P \subset \Gamma \setminus \{0\}$
is finite and symmetric. Suppose
![]() $A,B \subseteq X$
are clopen P-markers. Then, there exists a clopen P-marker
$A,B \subseteq X$
are clopen P-markers. Then, there exists a clopen P-marker
![]() $C \subseteq X$
such that
$C \subseteq X$
such that
![]() $A \subseteq C$
,
$A \subseteq C$
,
![]() $B \subseteq C \cup \bigcup _{\gamma \in P}\sigma _{\gamma }C$
, and
$B \subseteq C \cup \bigcup _{\gamma \in P}\sigma _{\gamma }C$
, and
![]() $C \subseteq (A\cup B)$
.
$C \subseteq (A\cup B)$
.
Proof. Let
 $$ \begin{align*} C := A \cup \bigg( B \setminus \bigcup_{\gamma \in P} \sigma_{\gamma}(A)\bigg). \end{align*} $$
$$ \begin{align*} C := A \cup \bigg( B \setminus \bigcup_{\gamma \in P} \sigma_{\gamma}(A)\bigg). \end{align*} $$
Clearly,
![]() $C \subseteq (A \cup B)$
. The set C is clopen because it is contained in the Boolean algebra spanned by
$C \subseteq (A \cup B)$
. The set C is clopen because it is contained in the Boolean algebra spanned by
![]() $\{A,B\}\cup \{\sigma _\gamma (A) : \gamma \in P\}$
. It is clear that
$\{A,B\}\cup \{\sigma _\gamma (A) : \gamma \in P\}$
. It is clear that
![]() $A \subseteq C$
.
$A \subseteq C$
.
Next, we check that
![]() $B \subseteq C \cup \bigcup _{\gamma \in P}\sigma _{\gamma }C$
: Otherwise, suppose that
$B \subseteq C \cup \bigcup _{\gamma \in P}\sigma _{\gamma }C$
: Otherwise, suppose that
![]() $x \in B \setminus (C \cup \bigcup _{\gamma \in P} \sigma _\gamma (C))$
, then, in particular,
$x \in B \setminus (C \cup \bigcup _{\gamma \in P} \sigma _\gamma (C))$
, then, in particular,
![]() $x \not \in C$
so
$x \not \in C$
so
![]() $x \not \in A$
because
$x \not \in A$
because
![]() $A \subseteq C$
. Also, because
$A \subseteq C$
. Also, because
![]() $x \not \in B \setminus C$
, we have that
$x \not \in B \setminus C$
, we have that
![]() $x \in \sigma _\gamma (A)$
for some
$x \in \sigma _\gamma (A)$
for some
![]() $\gamma \in P$
. However, since
$\gamma \in P$
. However, since
![]() $A \subseteq C$
, it follows that
$A \subseteq C$
, it follows that
![]() $\sigma _\gamma (A) \subseteq \sigma _\gamma (C)$
, so
$\sigma _\gamma (A) \subseteq \sigma _\gamma (C)$
, so
![]() $x \in \sigma _\gamma C$
for this
$x \in \sigma _\gamma C$
for this
![]() $\gamma \in P$
, which contradicts the assumption that
$\gamma \in P$
, which contradicts the assumption that
![]() $x \in B \setminus (C \cup \bigcup _{\gamma \in P} \sigma _\gamma (C))$
. This shows that
$x \in B \setminus (C \cup \bigcup _{\gamma \in P} \sigma _\gamma (C))$
. This shows that
![]() $B \subseteq C \cup \bigcup _{\gamma \in P} \sigma _\gamma (C)$
.
$B \subseteq C \cup \bigcup _{\gamma \in P} \sigma _\gamma (C)$
.
It remains to check that C is a P-marker. For any
![]() $\gamma \in P$
, we have
$\gamma \in P$
, we have
Because P is symmetric, also
![]() $-\gamma \in P$
, so
$-\gamma \in P$
, so
Applying
![]() $\sigma _\gamma $
to both sides, we get
$\sigma _\gamma $
to both sides, we get
It follows that
![]() $C \cap \sigma _\gamma C$
is contained in the union of the following four sets:
$C \cap \sigma _\gamma C$
is contained in the union of the following four sets:
-
(1)
 $E_1 := A \cap \sigma _\gamma A$
;
$E_1 := A \cap \sigma _\gamma A$
; -
(2)
 $E_2:= A \cap ( \sigma _\gamma B \cap A^c )$
;
$E_2:= A \cap ( \sigma _\gamma B \cap A^c )$
; -
(3)
 $E_3 := ( B \cap \sigma _\gamma A^c ) \cap \sigma _\gamma A$
;
$E_3 := ( B \cap \sigma _\gamma A^c ) \cap \sigma _\gamma A$
; -
(4)
 $E_4:= ( B \cap \sigma _\gamma A^c ) \cap ( \sigma _\gamma B \cap A^c )$
.
$E_4:= ( B \cap \sigma _\gamma A^c ) \cap ( \sigma _\gamma B \cap A^c )$
.
By assumption, A is a P-marker, so
![]() $E_1 \ = \emptyset $
. Clearly,
$E_1 \ = \emptyset $
. Clearly,
![]() $E_2 \subseteq A \cap (A^c) = \emptyset $
and
$E_2 \subseteq A \cap (A^c) = \emptyset $
and
![]() ${E_3 \subseteq \sigma _\gamma (A^c) \cap \sigma _{\gamma }(A) = \emptyset} $
. Also,
${E_3 \subseteq \sigma _\gamma (A^c) \cap \sigma _{\gamma }(A) = \emptyset} $
. Also,
![]() $E_4 \subseteq B \cap \sigma _\gamma (B) = \emptyset $
by assumption that B is a P-marker. This shows that
$E_4 \subseteq B \cap \sigma _\gamma (B) = \emptyset $
by assumption that B is a P-marker. This shows that
![]() $C\cap \sigma _\gamma C =\emptyset $
for all
$C\cap \sigma _\gamma C =\emptyset $
for all
![]() $\gamma \in P$
.
$\gamma \in P$
.
Lemma 3.3. (Krieger’s marker lemma for
 $\Gamma $
-subshifts)
$\Gamma $
-subshifts)
Let X be a
![]() $\Gamma $
-subshift. Let
$\Gamma $
-subshift. Let
![]() ${P \Subset \Gamma \setminus \{0\}}$
be a finite symmetric set, and let
${P \Subset \Gamma \setminus \{0\}}$
be a finite symmetric set, and let
![]() $V \subseteq X$
be a clopen set such that
$V \subseteq X$
be a clopen set such that
![]() $\sigma _\gamma (x) \ne x$
for every
$\sigma _\gamma (x) \ne x$
for every
![]() $\gamma \in P$
and every
$\gamma \in P$
and every
![]() $x \in V$
. Then, there exists a clopen set
$x \in V$
. Then, there exists a clopen set
![]() $C \subseteq V$
so that
$C \subseteq V$
so that
 $$ \begin{align} C \cap \sigma_\gamma (C) = \emptyset \quad\text{for every } \gamma \in P \text { and } V \subseteq C \cup \bigcup_{\gamma \in P} \sigma_\gamma (C). \end{align} $$
$$ \begin{align} C \cap \sigma_\gamma (C) = \emptyset \quad\text{for every } \gamma \in P \text { and } V \subseteq C \cup \bigcup_{\gamma \in P} \sigma_\gamma (C). \end{align} $$
Proof. For every
![]() $x \in V$
and
$x \in V$
and
![]() $\gamma \in P$
, we have that
$\gamma \in P$
, we have that
![]() $x \ne \sigma _{\gamma }(x)$
. We can thus find for every
$x \ne \sigma _{\gamma }(x)$
. We can thus find for every
![]() $x \in V$
, a clopen set
$x \in V$
, a clopen set
![]() $E_x \subseteq V$
such that
$E_x \subseteq V$
such that
![]() $x \in E_x$
and
$x \in E_x$
and
![]() $E_x \cap \sigma _{\gamma }(E_x) = \emptyset $
for every
$E_x \cap \sigma _{\gamma }(E_x) = \emptyset $
for every
![]() $\gamma \in P$
(that is,
$\gamma \in P$
(that is,
![]() $E_x$
is a P-marker).
$E_x$
is a P-marker).
Since V is compact, we can find a finite subcover
![]() $\mathcal {U} = \{D_1,\ldots ,D_n\}$
of
$\mathcal {U} = \{D_1,\ldots ,D_n\}$
of
![]() $\{E_x : x \in V\}$
. Thus, each
$\{E_x : x \in V\}$
. Thus, each
![]() $D_j \subseteq V$
is a clopen P-marker and
$D_j \subseteq V$
is a clopen P-marker and
![]() $V \subseteq \bigcup _{j=1}^n D_j$
. We sequentially construct clopen P-markers
$V \subseteq \bigcup _{j=1}^n D_j$
. We sequentially construct clopen P-markers
![]() $C_1,\ldots ,C_n \subseteq V$
such that
$C_1,\ldots ,C_n \subseteq V$
such that
![]() $\bigcup _{k=1}^j D_k \subseteq C_j \cup \bigcup _{\gamma \in P} \sigma _{\gamma }(C_j)$
. We start by setting
$\bigcup _{k=1}^j D_k \subseteq C_j \cup \bigcup _{\gamma \in P} \sigma _{\gamma }(C_j)$
. We start by setting
![]() $C_1 = D_1$
. After
$C_1 = D_1$
. After
![]() $C_1,\ldots ,C_{j-1}$
have been constructed, apply Lemma 3.2 with
$C_1,\ldots ,C_{j-1}$
have been constructed, apply Lemma 3.2 with
![]() $A := C_{j-1}$
and
$A := C_{j-1}$
and
![]() $B:=D_j$
to obtain a clopen P-marker
$B:=D_j$
to obtain a clopen P-marker
![]() $C_j$
such that
$C_j$
such that
![]() $A \subseteq C_j$
and
$A \subseteq C_j$
and
![]() ${B \subseteq C_j \bigcup _{\gamma \in P}\sigma _\gamma (C_j)}$
. Then,
${B \subseteq C_j \bigcup _{\gamma \in P}\sigma _\gamma (C_j)}$
. Then,
![]() $C= C_n$
is a clopen set that satisfies the conclusion of the lemma.
$C= C_n$
is a clopen set that satisfies the conclusion of the lemma.
As mentioned in the beginning of this section, an inspection of the proof of Lemmas 3.2 and 3.3 reveals that commutativity of the group
![]() $\Gamma $
is not used in the proof, except for notational purposes. Also, the fact that X is a
$\Gamma $
is not used in the proof, except for notational purposes. Also, the fact that X is a
![]() $\Gamma $
-subshift rather than a general compact
$\Gamma $
-subshift rather than a general compact
![]() $\Gamma $
-space is only used to produce a clopen basis. In other words, expansiveness of the action is never used. Thus, the proof of Lemma 3.3 directly extends to the following (mentioned for future reference, the generality will not be used in the current paper).
$\Gamma $
-space is only used to produce a clopen basis. In other words, expansiveness of the action is never used. Thus, the proof of Lemma 3.3 directly extends to the following (mentioned for future reference, the generality will not be used in the current paper).
Lemma 3.4. (Krieger’s marker lemma for countable groups)
Let
![]() $\Gamma \curvearrowright X$
be an action of a countable group
$\Gamma \curvearrowright X$
be an action of a countable group
![]() $\Gamma $
on a totally disconnected compact metric space. Let
$\Gamma $
on a totally disconnected compact metric space. Let
![]() $P \Subset \Gamma $
be a finite symmetric set with
$P \Subset \Gamma $
be a finite symmetric set with
![]() $1_\Gamma \not \in P$
, and let
$1_\Gamma \not \in P$
, and let
![]() $V \subseteq X$
be a clopen set such that
$V \subseteq X$
be a clopen set such that
![]() $g(x) \ne x$
for every
$g(x) \ne x$
for every
![]() $g \in P$
and every
$g \in P$
and every
![]() $x \in V$
. Then, there exists a clopen set
$x \in V$
. Then, there exists a clopen set
![]() $C \subseteq V$
so that
$C \subseteq V$
so that
 $$ \begin{align} C \cap g(C) = \emptyset \quad\text{for every } g \in P \text { and } V \subseteq C \cup \bigcup_{g \in P} g (C). \end{align} $$
$$ \begin{align} C \cap g(C) = \emptyset \quad\text{for every } g \in P \text { and } V \subseteq C \cup \bigcup_{g \in P} g (C). \end{align} $$
As mentioned earlier, closely related statements have already appeared in the literature.
4 Retractions and the map extension property for subshifts
In this section, we introduce the map extension property for
![]() $\Gamma $
-subshifts and the notion of an absolute retract. Both of these properties make sense in the category of general topological dynamical systems and also in other categories. In topology, the notion of an absolute retract was introduced by Borsuk in the 1930s, see [Reference Mardešić21]. We show that a
$\Gamma $
-subshifts and the notion of an absolute retract. Both of these properties make sense in the category of general topological dynamical systems and also in other categories. In topology, the notion of an absolute retract was introduced by Borsuk in the 1930s, see [Reference Mardešić21]. We show that a
![]() $\Gamma $
-subshift has the map extension property if and only if it is an absolute retract for a certain class of subshifts. A
$\Gamma $
-subshift has the map extension property if and only if it is an absolute retract for a certain class of subshifts. A
![]() $\mathbb {Z}$
-subshift has the map extension property if and only if it is a topologically mixing subshift of finite type. As we will shortly explain, in the context of subshifts of finite type over countable abelian groups, the map extension property turns out to be equivalent to the notion of contractability [Reference Poirier and Salo23].
$\mathbb {Z}$
-subshift has the map extension property if and only if it is a topologically mixing subshift of finite type. As we will shortly explain, in the context of subshifts of finite type over countable abelian groups, the map extension property turns out to be equivalent to the notion of contractability [Reference Poirier and Salo23].
Definition 4.1. Let
![]() $X,Y$
be
$X,Y$
be
![]() $\Gamma $
-subshifts. We write
$\Gamma $
-subshifts. We write
![]() $X \rightsquigarrow Y$
if the following holds: for every
$X \rightsquigarrow Y$
if the following holds: for every
![]() $x \in X$
, there exists
$x \in X$
, there exists
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $\mathrm {stab}(x) \le \mathrm {stab}(y)$
.
$\mathrm {stab}(x) \le \mathrm {stab}(y)$
.
The condition
![]() $X \rightsquigarrow Y$
is a obviously a necessary condition for the existence of a map from X into Y. Indeed, if there exists a map
$X \rightsquigarrow Y$
is a obviously a necessary condition for the existence of a map from X into Y. Indeed, if there exists a map
![]() $\pi :X \to Y$
, then
$\pi :X \to Y$
, then
![]() $X \rightsquigarrow Y$
because for any
$X \rightsquigarrow Y$
because for any
![]() $x \in X$
, we have
$x \in X$
, we have
![]() $\mathrm {stab}(x) \le \mathrm {stab}(\pi (x))$
.
$\mathrm {stab}(x) \le \mathrm {stab}(\pi (x))$
.
Definition 4.2. A
![]() $\Gamma $
-subshift Y has the map extension property if the following holds. For every
$\Gamma $
-subshift Y has the map extension property if the following holds. For every
![]() $\Gamma $
-subshift X such that
$\Gamma $
-subshift X such that
![]() $X \rightsquigarrow Y$
and any map
$X \rightsquigarrow Y$
and any map
![]() $\tilde \pi : \tilde X \to Y$
from a (possibly empty)
$\tilde \pi : \tilde X \to Y$
from a (possibly empty)
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $\tilde X \subseteq X$
, there exists a map
$\tilde X \subseteq X$
, there exists a map
![]() $\pi :X \to Y$
that extends
$\pi :X \to Y$
that extends
![]() $\tilde \pi $
.
$\tilde \pi $
.
When
![]() $\Gamma $
is a finitely generated abelian group, the map extension property for a
$\Gamma $
is a finitely generated abelian group, the map extension property for a
![]() $\Gamma $
subshift already implies that the subshift is of finite type. For subshifts of finite type over a countable abelian group, the map extension property is equivalent to the notion of (strong) contractibility introduced recently by Poirier and Salo [Reference Poirier and Salo23].
$\Gamma $
subshift already implies that the subshift is of finite type. For subshifts of finite type over a countable abelian group, the map extension property is equivalent to the notion of (strong) contractibility introduced recently by Poirier and Salo [Reference Poirier and Salo23].
Definition 4.3. (Poirier and Salo [Reference Poirier and Salo23])
A
![]() $\Gamma $
-subshift Y is contractible if there exists a map
$\Gamma $
-subshift Y is contractible if there exists a map
![]() $\psi :\{0,1\}^\Gamma \times Y \times Y \to Y$
satisfying
$\psi :\{0,1\}^\Gamma \times Y \times Y \to Y$
satisfying
for every
![]() $y^{(0)},y^{(1)} \in Y$
, where
$y^{(0)},y^{(1)} \in Y$
, where
![]() $\overline {0},\overline {1} \in \{0,1\}^\Gamma $
are the two fixed points.
$\overline {0},\overline {1} \in \{0,1\}^\Gamma $
are the two fixed points.
A map
![]() $\psi :\{0,1\}^{\Gamma } \times Y \times Y \to Y$
that satisfies equation (3) is called a contraction homotopy.
$\psi :\{0,1\}^{\Gamma } \times Y \times Y \to Y$
that satisfies equation (3) is called a contraction homotopy.
Definition 4.4. A contraction homotopy
![]() $\psi :\{0,1\}^{\Gamma } \times Y \times Y \to Y$
that further satisfies
$\psi :\{0,1\}^{\Gamma } \times Y \times Y \to Y$
that further satisfies
![]() $\phi (z,y,y) = y$
for every
$\phi (z,y,y) = y$
for every
![]() $z \in \{0,1\}^{\mathbb {Z}}$
and every
$z \in \{0,1\}^{\mathbb {Z}}$
and every
![]() $y \in Y$
is called a strong contraction homotopy. If a
$y \in Y$
is called a strong contraction homotopy. If a
![]() $\Gamma $
-subshift Y admits a strong contraction homotopy, we say that Y is strongly contractable.
$\Gamma $
-subshift Y admits a strong contraction homotopy, we say that Y is strongly contractable.
The term ‘contractible’ comes from the observation that a topological space Y is contractible in the usual sense if and only there exists a continuous function
![]() $\psi :[0,1] \times Y \times Y \to Y$
satisfying equation (3) for every
$\psi :[0,1] \times Y \times Y \to Y$
satisfying equation (3) for every
![]() $y^{(0)},y^{(1)} \in Y$
, where this time,
$y^{(0)},y^{(1)} \in Y$
, where this time,
![]() $\overline {0}$
and
$\overline {0}$
and
![]() $\overline {1}$
are the two endpoints of the interval
$\overline {1}$
are the two endpoints of the interval
![]() $[0,1]$
. Poirier and Salo [Reference Poirier and Salo23] used the term ‘equiconnected’ instead of ‘strongly contractable’ because it is a direct analog of the corresponding notion of equiconnectedness in topology, with
$[0,1]$
. Poirier and Salo [Reference Poirier and Salo23] used the term ‘equiconnected’ instead of ‘strongly contractable’ because it is a direct analog of the corresponding notion of equiconnectedness in topology, with
![]() $\{0,1\}^\Gamma $
taking the role of the interval
$\{0,1\}^\Gamma $
taking the role of the interval
![]() $[0,1]$
. Poirier and Salo proved that a
$[0,1]$
. Poirier and Salo proved that a
![]() $\mathbb {Z}^d$
-subshift is a (strongly) contractible SFT if and only if it satisfies the map extension property [Reference Poirier and Salo23]. Their proof directly extends to
$\mathbb {Z}^d$
-subshift is a (strongly) contractible SFT if and only if it satisfies the map extension property [Reference Poirier and Salo23]. Their proof directly extends to
![]() $\Gamma $
-subshifts, where
$\Gamma $
-subshifts, where
![]() $\Gamma $
is a finitely generated abelian group.
$\Gamma $
is a finitely generated abelian group.
For the reader’s convenience, we recall the elegant argument for the easy implication, which assumes nothing about the countable group
![]() $\Gamma $
. The proof of the converse implication in [Reference Poirier and Salo23] uses a version of Krieger’s marker lemma very similar to Lemma 3.3. We will not use the converse implication in this paper.
$\Gamma $
. The proof of the converse implication in [Reference Poirier and Salo23] uses a version of Krieger’s marker lemma very similar to Lemma 3.3. We will not use the converse implication in this paper.
Proposition 4.5. (Poirier and Salo [Reference Poirier and Salo23])
Any
![]() $\Gamma $
-subshift with the map extension property is strongly contractible.
$\Gamma $
-subshift with the map extension property is strongly contractible.
Proof. Suppose that Y has the map extension property. Consider the subshift
![]() $X = \{0,1\}^\Gamma \times Y \times Y$
. Clearly, Y is a factor of X and so, in particular,
$X = \{0,1\}^\Gamma \times Y \times Y$
. Clearly, Y is a factor of X and so, in particular,
![]() $X \rightsquigarrow Y$
.
$X \rightsquigarrow Y$
.
Consider the subshifts
and
and the map
![]() $\tilde \pi : \tilde X \to Y$
given by
$\tilde \pi : \tilde X \to Y$
given by
for every
![]() $y^{(0)},y^{(1)} \in Y$
. By the map extension property,
$y^{(0)},y^{(1)} \in Y$
. By the map extension property,
![]() $\tilde \pi $
extends to a map
$\tilde \pi $
extends to a map
![]() $\psi :\{0,1\}^\Gamma \times Y \times Y \to Y$
. It is easily verified that the map
$\psi :\{0,1\}^\Gamma \times Y \times Y \to Y$
. It is easily verified that the map
![]() $\psi $
is a strong contraction homotopy. Hence, Y is indeed strongly contractible.
$\psi $
is a strong contraction homotopy. Hence, Y is indeed strongly contractible.
Under certain assumptions on the group
![]() $\Gamma $
, Poirier and Salo have proved that contractible
$\Gamma $
, Poirier and Salo have proved that contractible
![]() $\Gamma $
-subshifts have dense periodic points [Reference Poirier and Salo23, Theorem
$\Gamma $
-subshifts have dense periodic points [Reference Poirier and Salo23, Theorem
![]() $1.4$
]. These assumptions hold whenever
$1.4$
]. These assumptions hold whenever
![]() $\Gamma $
is a finitely generated abelian group.
$\Gamma $
is a finitely generated abelian group.
We need a statement that gives us more control over the collection of subgroups that occur as stabilizers of points of a subshift with the map extension property. The following lemma is an intermediate step.
Lemma 4.6. Let Y be a contractible
![]() $\Gamma $
-subshift and let
$\Gamma $
-subshift and let
![]() $\psi :\{0,1\}^\Gamma \times Y \times Y \to Y$
be a strong contraction homotopy with coding window
$\psi :\{0,1\}^\Gamma \times Y \times Y \to Y$
be a strong contraction homotopy with coding window
![]() $W \Subset \Gamma $
. For any surjective homomorphism
$W \Subset \Gamma $
. For any surjective homomorphism
![]() $\phi :\Gamma \to \mathbb {Z}$
and any
$\phi :\Gamma \to \mathbb {Z}$
and any
![]() $v \in \Gamma $
such that
$v \in \Gamma $
such that
![]() $\phi (v)> 4 \max |\phi (W)|$
and any
$\phi (v)> 4 \max |\phi (W)|$
and any
![]() $y^{(0)} \in Y$
, there exists
$y^{(0)} \in Y$
, there exists
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $\sigma _v(y)=y$
, and furthermore,
$\sigma _v(y)=y$
, and furthermore,
![]() $\mathrm {stab}(y^{(0)}) \cap \mathrm {Ker}(\phi ) \subseteq \mathrm {stab}(y)$
.
$\mathrm {stab}(y^{(0)}) \cap \mathrm {Ker}(\phi ) \subseteq \mathrm {stab}(y)$
.
Proof. Let
![]() $\phi :\Gamma \to \mathbb {Z}$
be a surjective homomorphism. Denote
$\phi :\Gamma \to \mathbb {Z}$
be a surjective homomorphism. Denote
![]() $N_0= \max |\phi (W)|$
. Choose
$N_0= \max |\phi (W)|$
. Choose
![]() $v_0 \in \Gamma $
such that
$v_0 \in \Gamma $
such that
![]() $\phi (v_0)=N_0$
. Let
$\phi (v_0)=N_0$
. Let
![]() $v \in \Gamma $
satisfy
$v \in \Gamma $
satisfy
![]() $\phi (v)> 4 N_0$
.
$\phi (v)> 4 N_0$
.
Denote
and choose
![]() $v_1 \in \Gamma $
such that
$v_1 \in \Gamma $
such that
![]() $\phi (v_1)= N_1$
.
$\phi (v_1)= N_1$
.
Let
![]() $z \in \{0,1\}^\Gamma $
be given by
$z \in \{0,1\}^\Gamma $
be given by
 $$ \begin{align*} z_w = \begin{cases} 0, & \phi(w) \le 0,\\ 1, & \phi(w)> 0. \end{cases} \end{align*} $$
$$ \begin{align*} z_w = \begin{cases} 0, & \phi(w) \le 0,\\ 1, & \phi(w)> 0. \end{cases} \end{align*} $$
We record a few simple observations that follow from the fact that
![]() $\psi $
is a strong contraction homotopy with coding window W.
$\psi $
is a strong contraction homotopy with coding window W.
-
(1) For any
 $\tilde y \in Y$
, the point (4)satisfies
$\tilde y \in Y$
, the point (4)satisfies $$ \begin{align} \hat y:= \psi(z,\tilde y,\sigma_{-v}(\tilde y)) \end{align} $$
$$ \begin{align} \hat y:= \psi(z,\tilde y,\sigma_{-v}(\tilde y)) \end{align} $$
 $\hat y_w = \hat y_{w+v}$
for every
$\hat y_w = \hat y_{w+v}$
for every
 $w \in \Gamma $
such that
$w \in \Gamma $
such that
 $ -N+N_0 < \phi (w) < -N_0$
and
$ -N+N_0 < \phi (w) < -N_0$
and
 $\hat y_w =\tilde y_w$
for every
$\hat y_w =\tilde y_w$
for every
 $w \in \Gamma $
such that
$w \in \Gamma $
such that
 $\phi (w) < -N_0$
.
$\phi (w) < -N_0$
.
-
(2) If
 $\tilde y \in Y$
satisfies
$\tilde y \in Y$
satisfies
 $\tilde y_w = \tilde y_{w+v}$
for every
$\tilde y_w = \tilde y_{w+v}$
for every
 $w \in \Gamma $
such that
$w \in \Gamma $
such that
 $|\phi (w)| < N_0$
, then the point
$|\phi (w)| < N_0$
, then the point
 $\hat y \in Y$
given by equation (4) satisfies
$\hat y \in Y$
given by equation (4) satisfies
 $\hat y_w = \tilde y_{w+v}$
whenever
$\hat y_w = \tilde y_{w+v}$
whenever
 $-\phi (v) < \phi (w) <0$
and also
$-\phi (v) < \phi (w) <0$
and also
 $\hat y_w= \tilde y_w$
for all
$\hat y_w= \tilde y_w$
for all
 $w \in \Gamma $
such that
$w \in \Gamma $
such that
 $\phi (w) < 0$
.
$\phi (w) < 0$
. -
(3) Suppose
 $\tilde y \in Y$
satisfies
$\tilde y \in Y$
satisfies
 $\tilde y_w =\tilde y_{w+v}$
for every
$\tilde y_w =\tilde y_{w+v}$
for every
 $w \in \Gamma $
such that
$w \in \Gamma $
such that
 $|\phi (w)| < kN_1+N_0$
for some
$|\phi (w)| < kN_1+N_0$
for some
 $k \in \mathbb {N}$
. Then, satisfies
$k \in \mathbb {N}$
. Then, satisfies $$ \begin{align*} \hat y = \sigma_{-kv_1}\phi(z,\sigma_{kv_1}(\tilde y),\sigma_{kv_1-v}(\tilde y)) \end{align*} $$
$$ \begin{align*} \hat y = \sigma_{-kv_1}\phi(z,\sigma_{kv_1}(\tilde y),\sigma_{kv_1-v}(\tilde y)) \end{align*} $$
 $\hat y_w =\tilde y_{w+v}$
for every
$\hat y_w =\tilde y_{w+v}$
for every
 $w \in \Gamma $
such that
$w \in \Gamma $
such that
 $|\phi (w)| < (k+1)N_1+N_0$
and also
$|\phi (w)| < (k+1)N_1+N_0$
and also
 $\hat y_w= \tilde y_w$
for all
$\hat y_w= \tilde y_w$
for all
 $w \in \Gamma $
such that
$w \in \Gamma $
such that
 $\phi (w) < kv_1$
.
$\phi (w) < kv_1$
.
Using the above observations, starting with any
![]() $y^{(0)} \in Y$
, we can construct by induction a sequence of points
$y^{(0)} \in Y$
, we can construct by induction a sequence of points
![]() $y^{(1)},\ldots , y^{(n)},\ldots \in Y$
such that
$y^{(1)},\ldots , y^{(n)},\ldots \in Y$
such that
![]() $y^{(n)}_w = y^{(n)}_{w+v}$
for any
$y^{(n)}_w = y^{(n)}_{w+v}$
for any
![]() $w \in \Gamma $
satisfying
$w \in \Gamma $
satisfying
![]() $|\phi (w)| < nN_1 +N_0$
, and also
$|\phi (w)| < nN_1 +N_0$
, and also
![]() $y^{(n+1)}_w = y^{(n)}_{w}$
for any
$y^{(n+1)}_w = y^{(n)}_{w}$
for any
![]() $w \in \Gamma $
satisfying
$w \in \Gamma $
satisfying
![]() $|\phi (w)| < n N_1$
. Thus, the limit
$|\phi (w)| < n N_1$
. Thus, the limit
![]() $y = \lim _{n \to \infty } y^{(n)}$
exists and satisfies
$y = \lim _{n \to \infty } y^{(n)}$
exists and satisfies
![]() $\sigma _v(y)=y$
. It also satisfies
$\sigma _v(y)=y$
. It also satisfies
![]() $\mathrm {stab}(y^{(0)}) \cap \mathrm {Ker}(\phi ) \subseteq \mathrm {stab}(y)$
.
$\mathrm {stab}(y^{(0)}) \cap \mathrm {Ker}(\phi ) \subseteq \mathrm {stab}(y)$
.
We remark that the statement of Lemma 4.6 remains valid with essentially the same proof for any countable group
![]() $\Gamma $
, without assuming commutativity.
$\Gamma $
, without assuming commutativity.
Recall the definition of
![]() $Y^{[\Delta ]}$
as defined in Definition 2.19.
$Y^{[\Delta ]}$
as defined in Definition 2.19.
Lemma 4.7. Let Y be a contractible
![]() $\Gamma $
-subshift. Then, there exists a finitely generated subgroup
$\Gamma $
-subshift. Then, there exists a finitely generated subgroup
![]() $\Delta < \Gamma $
so that
$\Delta < \Gamma $
so that
![]() $Y = Y^{[\Delta ]}$
.
$Y = Y^{[\Delta ]}$
.
Proof. Let
![]() $\psi : \{0,1\}^\Gamma \times Y \times Y \to Y$
be a contraction homotopy with coding window
$\psi : \{0,1\}^\Gamma \times Y \times Y \to Y$
be a contraction homotopy with coding window
![]() $W \Subset \Gamma $
and let
$W \Subset \Gamma $
and let
![]() $\Delta $
be the subgroup of
$\Delta $
be the subgroup of
![]() $\Gamma $
generated by W. In this case, we claim that
$\Gamma $
generated by W. In this case, we claim that
![]() $Y = Y^{[\Delta ]}$
. Indeed, for any
$Y = Y^{[\Delta ]}$
. Indeed, for any
![]() $y^{(1)},y^{(2)} \in Y$
and any
$y^{(1)},y^{(2)} \in Y$
and any
![]() $A \subseteq \Gamma /\Delta $
, we can find a point
$A \subseteq \Gamma /\Delta $
, we can find a point
![]() $y \in Y$
that agrees with
$y \in Y$
that agrees with
![]() $y^{(1)}$
on the cosets of
$y^{(1)}$
on the cosets of
![]() $\Delta $
that belong to A and agrees with
$\Delta $
that belong to A and agrees with
![]() $y^{(2)}$
on the cosets of
$y^{(2)}$
on the cosets of
![]() $\Delta $
that do not belong to A. Let
$\Delta $
that do not belong to A. Let
![]() $z \in \{0,1\}^\Gamma $
be the point satisfying that
$z \in \{0,1\}^\Gamma $
be the point satisfying that
![]() $z_w=1$
if the
$z_w=1$
if the
![]() $\Delta $
-coset of w is in A and
$\Delta $
-coset of w is in A and
![]() $0$
otherwise. Then, the point
$0$
otherwise. Then, the point
![]() $y= \psi (z,y^{(1)},y^{(2)})$
agrees with
$y= \psi (z,y^{(1)},y^{(2)})$
agrees with
![]() $y^{(1)}$
on the
$y^{(1)}$
on the
![]() $\Delta $
-cosets that belong to A and agrees with
$\Delta $
-cosets that belong to A and agrees with
![]() $y^{(2)}$
on the cosets of
$y^{(2)}$
on the cosets of
![]() $\Delta $
that do not belong to A. By repeated applications, for any tuple of distinct
$\Delta $
that do not belong to A. By repeated applications, for any tuple of distinct
![]() $\Delta $
-cosets
$\Delta $
-cosets
![]() $(v_1+\Delta ,\ldots ,v_k +\Delta )$
with
$(v_1+\Delta ,\ldots ,v_k +\Delta )$
with
![]() $v_1,\ldots , v_k \in \Gamma $
and any points
$v_1,\ldots , v_k \in \Gamma $
and any points
![]() $y^{(1)},\ldots , y^{(k)}$
, we can find
$y^{(1)},\ldots , y^{(k)}$
, we can find
![]() $y \in Y$
that agrees with
$y \in Y$
that agrees with
![]() $y^{(i)}$
on
$y^{(i)}$
on
![]() $v_i + \Delta $
. This proves that
$v_i + \Delta $
. This proves that
![]() $Y = Y^{[\Delta ]}$
.
$Y = Y^{[\Delta ]}$
.
Proposition 4.8. Let
![]() $\Gamma $
be a countable abelian group and let Y be a strongly contractible
$\Gamma $
be a countable abelian group and let Y be a strongly contractible
![]() $\Gamma $
-subshift. Then, there exists a finite set
$\Gamma $
-subshift. Then, there exists a finite set
![]() $F \Subset \Gamma \setminus \{0\}$
such that for any subgroup
$F \Subset \Gamma \setminus \{0\}$
such that for any subgroup
![]() $\Gamma _0 < \Gamma $
, with
$\Gamma _0 < \Gamma $
, with
![]() $\Gamma _0 \cap F =\emptyset $
, there exists
$\Gamma _0 \cap F =\emptyset $
, there exists
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $\Gamma _0 \le \mathrm {stab}(y)$
.
$\Gamma _0 \le \mathrm {stab}(y)$
.
Proof. By Lemma 4.7, we can assume without loss of generality that
![]() $\Gamma $
is a finitely generated abelian group. In this case, by the structure theorem for finitely generated abelian groups, we can assume that
$\Gamma $
is a finitely generated abelian group. In this case, by the structure theorem for finitely generated abelian groups, we can assume that
![]() $\Gamma = \mathbb {Z}^d \times G$
, where G is a finite abelian group. Let Y be a contractible
$\Gamma = \mathbb {Z}^d \times G$
, where G is a finite abelian group. Let Y be a contractible
![]() $\Gamma $
-subshift and let
$\Gamma $
-subshift and let
![]() $\psi :\{0,1\}^\Gamma \times Y \times Y \to Y$
be a strong contraction homotopy with coding window
$\psi :\{0,1\}^\Gamma \times Y \times Y \to Y$
be a strong contraction homotopy with coding window
![]() $W \Subset \Gamma $
.
$W \Subset \Gamma $
.
We first prove the following auxiliary statement. There exists a finite set
![]() $F \Subset \Gamma $
(that depends on the set W) such that for any subgroup
$F \Subset \Gamma $
(that depends on the set W) such that for any subgroup
![]() $\Gamma _0 \le \Gamma $
such that
$\Gamma _0 \le \Gamma $
such that
![]() $F \cap \Gamma _0 = \emptyset $
, there exists an integer
$F \cap \Gamma _0 = \emptyset $
, there exists an integer
![]() $0 \le n \le d$
, surjective homomorphisms
$0 \le n \le d$
, surjective homomorphisms
![]() $\phi _1,\ldots ,\phi _n : \Gamma \to \mathbb {Z}$
and
$\phi _1,\ldots ,\phi _n : \Gamma \to \mathbb {Z}$
and
![]() $v_1,\ldots ,v_n \in \Gamma _0$
such that
$v_1,\ldots ,v_n \in \Gamma _0$
such that
![]() $v_1,\ldots ,v_n$
is a generating set for
$v_1,\ldots ,v_n$
is a generating set for
![]() $\Gamma _0$
and so that:
$\Gamma _0$
and so that:
-
•
 $\phi _i(v_j)=0$
for all
$\phi _i(v_j)=0$
for all
 $0 \le i < j \le n$
;
$0 \le i < j \le n$
; -
•
 $\phi _i(v_i)> 2(\max \phi _i(W))$
for every
$\phi _i(v_i)> 2(\max \phi _i(W))$
for every
 $1\le i \le n$
.
$1\le i \le n$
.
Indeed, by taking F to be a set that contains the non-identity elements of the torsion subgroup of
![]() $\Gamma $
, we get that any subgroup
$\Gamma $
, we get that any subgroup
![]() $\Gamma _0 < \Gamma $
that does not intersect F is torsion free, and hence the projection of
$\Gamma _0 < \Gamma $
that does not intersect F is torsion free, and hence the projection of
![]() $\Gamma _0$
onto
$\Gamma _0$
onto
![]() $\mathbb {Z}^d$
is injective. So, without loss of generality, we can prove the statement under the assumption that
$\mathbb {Z}^d$
is injective. So, without loss of generality, we can prove the statement under the assumption that
![]() $\Gamma = \mathbb {Z}^d$
. We choose
$\Gamma = \mathbb {Z}^d$
. We choose
![]() $R>0$
large enough, in a manner that depends on the set W and the integer d (the precise conditions of R will be clarified soon). Let F denote the intersection of the Euclidean ball of radius R approximately
$R>0$
large enough, in a manner that depends on the set W and the integer d (the precise conditions of R will be clarified soon). Let F denote the intersection of the Euclidean ball of radius R approximately
![]() $0$
with
$0$
with
![]() $\mathbb {Z}^d \setminus \{0\}$
and let
$\mathbb {Z}^d \setminus \{0\}$
and let
![]() $\Gamma _0 < \Gamma = \mathbb {Z}^d$
be a subgroup that does not intersect F. We can assume without loss of generality that
$\Gamma _0 < \Gamma = \mathbb {Z}^d$
be a subgroup that does not intersect F. We can assume without loss of generality that
![]() $\Gamma _0$
is a finite index subgroup of
$\Gamma _0$
is a finite index subgroup of
![]() $\mathbb {Z}^d$
. In other words,
$\mathbb {Z}^d$
. In other words,
![]() $\Gamma _0$
is a lattice whose shortest non-zero element has length at least R. Let
$\Gamma _0$
is a lattice whose shortest non-zero element has length at least R. Let
![]() $v_1,\ldots ,v_d \in \Gamma _0$
be a Korkine–Zolotarev reduced basis of
$v_1,\ldots ,v_d \in \Gamma _0$
be a Korkine–Zolotarev reduced basis of
![]() $\Gamma _0$
as in [Reference Korkine17]. Then, there exists a constant
$\Gamma _0$
as in [Reference Korkine17]. Then, there exists a constant
![]() $c_1>0$
depending only on d such that for any
$c_1>0$
depending only on d such that for any
![]() $1\le i \le d$
, the orthogonal projection of
$1\le i \le d$
, the orthogonal projection of
![]() $v_i$
onto the orthogonal complement of the span of
$v_i$
onto the orthogonal complement of the span of
![]() $v_1,\ldots ,v_{i-1}$
has length at least
$v_1,\ldots ,v_{i-1}$
has length at least
![]() $c_1 R$
. Thus, there exists another constant
$c_1 R$
. Thus, there exists another constant
![]() $c_2>0$
that depends only on d, and primitive vectors
$c_2>0$
that depends only on d, and primitive vectors
![]() $w_1,\ldots ,w_d \in \mathbb {Z}^d$
such that
$w_1,\ldots ,w_d \in \mathbb {Z}^d$
such that
![]() $w_i$
belongs to the orthogonal complement of the span of
$w_i$
belongs to the orthogonal complement of the span of
![]() $v_1,\ldots ,v_{i-1}$
and
$v_1,\ldots ,v_{i-1}$
and
![]() $\langle v_i,w_i \rangle> c_2 R \|w_i \|$
. Define
$\langle v_i,w_i \rangle> c_2 R \|w_i \|$
. Define
![]() $\phi _i:\mathbb {Z}^d \to \mathbb {Z}$
by
$\phi _i:\mathbb {Z}^d \to \mathbb {Z}$
by
![]() $\phi _i(v)=\langle v,w_i \rangle $
. Then, for every
$\phi _i(v)=\langle v,w_i \rangle $
. Then, for every
![]() $i=1,\ldots ,d$
, we have that
$i=1,\ldots ,d$
, we have that
![]() $\phi _i$
is a surjective homomorphism that satisfies
$\phi _i$
is a surjective homomorphism that satisfies
![]() $\phi _i(v_i) \ge c_2 R \|w_i\|$
. Since
$\phi _i(v_i) \ge c_2 R \|w_i\|$
. Since
![]() $\max \phi _i(W) \le \| w_i \| \max _{w \in W}\| w\|$
, if
$\max \phi _i(W) \le \| w_i \| \max _{w \in W}\| w\|$
, if
![]() $R> 2 c_2^{-1} \max _{w \in W}\| w\|$
, we have that
$R> 2 c_2^{-1} \max _{w \in W}\| w\|$
, we have that
![]() $\phi _i(v_i)> 2(\max \phi _i(W)$
. This proves the auxiliary statement.
$\phi _i(v_i)> 2(\max \phi _i(W)$
. This proves the auxiliary statement.
Now, repeatedly apply Lemma 4.6 to produce a sequence of points
![]() $y^{(1)},\ldots ,y^{(d)} \in~Y$
such that
$y^{(1)},\ldots ,y^{(d)} \in~Y$
such that
![]() $v_1,\ldots ,v_i \in \mathrm {stab}(y^{(i)})$
. In particular,
$v_1,\ldots ,v_i \in \mathrm {stab}(y^{(i)})$
. In particular,
![]() $\Gamma _0$
is contained in
$\Gamma _0$
is contained in
![]() $\mathrm {stab}(y^{(d)})$
. This completes the proof.
$\mathrm {stab}(y^{(d)})$
. This completes the proof.
Next, we consider the notion of retractions, retracts, and absolute retracts in the context of symbolic dynamics. Recall that a subspace Y of a topological space X is called a retract if there is a continuous function
![]() $r:X \to Y$
such that the restriction of r to Y is the identity. Such a continuous function
$r:X \to Y$
such that the restriction of r to Y is the identity. Such a continuous function
![]() $r:X \to Y$
is called a retraction. Let
$r:X \to Y$
is called a retraction. Let
![]() $\mathcal {C}$
be a class of topological spaces, closed under homeomorphisms and passage to closed subsets. Following Borsuk [Reference Borsuk5], a topological space Y is called an absolute retract for the class
$\mathcal {C}$
be a class of topological spaces, closed under homeomorphisms and passage to closed subsets. Following Borsuk [Reference Borsuk5], a topological space Y is called an absolute retract for the class
![]() $\mathcal {C}$
if
$\mathcal {C}$
if
![]() $Y\in \mathcal {C}$
and whenever Y is a closed subspace of
$Y\in \mathcal {C}$
and whenever Y is a closed subspace of
![]() $X \in \mathcal {C}$
, then Y is a retract of X.
$X \in \mathcal {C}$
, then Y is a retract of X.
The notions of a retract and universal retract naturally adapt to the category of dynamical systems, in particular, to
![]() $\Gamma $
-subshifts.
$\Gamma $
-subshifts.
Definition 4.9. Let
![]() $Y \subseteq X$
be
$Y \subseteq X$
be
![]() $\Gamma $
-subshifts. We say that Y is a retract of X if there exists a map
$\Gamma $
-subshifts. We say that Y is a retract of X if there exists a map
![]() $r:X \to Y$
such that the restriction of r to Y is the identity. A map r as above is called a retraction.
$r:X \to Y$
such that the restriction of r to Y is the identity. A map r as above is called a retraction.
As shown by the following proposition, various important properties of subshifts are preserved under retractions.
Proposition 4.10. The following families of subshifts are closed under taking retracts:
-
(1) sofic shifts;
-
(2) topologically mixing subshifts;
-
(3) strongly irreducbile subshifts;
-
(4) subshifts with the map extension property;
-
(5) shifts of finite type.
Proof. The classes of sofic shifts, topological mixing subshifts, and strongly irreducible subshifts are each closed under taking (subshift) factors. In particular, they are closed under taking retracts.
Let us show that a retract of a subshift with the map extension property also has the map extension property. Suppose that
![]() $\hat Y$
is a subshift with the map extension property, that
$\hat Y$
is a subshift with the map extension property, that
![]() $Y \subseteq \hat Y$
, and that
$Y \subseteq \hat Y$
, and that
![]() $r:\hat Y \to Y$
is a retraction map. Let
$r:\hat Y \to Y$
is a retraction map. Let
![]() $\tilde X \subseteq X$
be subshifts so that
$\tilde X \subseteq X$
be subshifts so that
![]() $X \rightsquigarrow Y$
and
$X \rightsquigarrow Y$
and
![]() $\tilde \pi :\tilde X \to Y$
be a map. Since
$\tilde \pi :\tilde X \to Y$
be a map. Since
![]() $Y \subseteq \hat Y$
, it follows that
$Y \subseteq \hat Y$
, it follows that
![]() $X \rightsquigarrow \hat Y$
. Since
$X \rightsquigarrow \hat Y$
. Since
![]() $\hat Y$
has the map extension property,
$\hat Y$
has the map extension property,
![]() $\tilde \pi $
extends to a map
$\tilde \pi $
extends to a map
![]() $\hat \pi :X \to \hat Y$
. Then,
$\hat \pi :X \to \hat Y$
. Then,
![]() $\pi = r \circ \hat \pi : X \to Y$
is a map that extends
$\pi = r \circ \hat \pi : X \to Y$
is a map that extends
![]() $\tilde \pi $
.
$\tilde \pi $
.
It remains to show that a retract of any retract of a shift of finite type is also a shift of finite type. Let
![]() $X \subseteq A^\Gamma $
be a shift of finite type with a defining set of forbidden patterns
$X \subseteq A^\Gamma $
be a shift of finite type with a defining set of forbidden patterns
![]() $\mathcal {F}_1 \Subset A^{W_1}$
. Suppose that
$\mathcal {F}_1 \Subset A^{W_1}$
. Suppose that
![]() $Y \subseteq X$
is a retract, with
$Y \subseteq X$
is a retract, with
![]() $r:X \to Y$
a retraction. Let
$r:X \to Y$
a retraction. Let
![]() $W_0 \Subset \Gamma $
be a coding window for r such that
$W_0 \Subset \Gamma $
be a coding window for r such that
![]() $0 \in W_0$
and let
$0 \in W_0$
and let
![]() $\Phi :A^{W_0} \to A$
be a sliding block code for r. Let
$\Phi :A^{W_0} \to A$
be a sliding block code for r. Let
Now suppose that
![]() $x \in X$
satisfies that
$x \in X$
satisfies that
![]() $\sigma _v(x)_{W_0} \not \in \mathcal {F}_0$
for all
$\sigma _v(x)_{W_0} \not \in \mathcal {F}_0$
for all
![]() $v \in \Gamma $
. It follows that
$v \in \Gamma $
. It follows that
![]() $r(x)=x$
, so
$r(x)=x$
, so
![]() $x \in Y$
. This means that
$x \in Y$
. This means that
Denote
![]() $W = W_0 \cup W_1$
and let
$W = W_0 \cup W_1$
and let
Then,
![]() $\mathcal {F}$
is a defining set of forbidden patterns for Y. This proves that Y is a shift of finite type.
$\mathcal {F}$
is a defining set of forbidden patterns for Y. This proves that Y is a shift of finite type.
Definition 4.11. A
![]() $\Gamma $
-subshift Y is called an absolute retract if whenever Y embeds in a
$\Gamma $
-subshift Y is called an absolute retract if whenever Y embeds in a
![]() $\Gamma $
-subshift X, then Y is a retract of X.
$\Gamma $
-subshift X, then Y is a retract of X.
An absolute retract always has a fixed point for the following simple reason. Any subshift Y embeds in a subshift with a fixed point, and any retract of a subshift with a fixed point must admit a fixed point.
Definition 4.12. Let
![]() $\mathcal {C}$
be a class of
$\mathcal {C}$
be a class of
![]() $\Gamma $
-subshifts, closed under isomorphism and passing to subshifts. A
$\Gamma $
-subshifts, closed under isomorphism and passing to subshifts. A
![]() $\Gamma $
-subshift Y is called an absolute retract for the class
$\Gamma $
-subshift Y is called an absolute retract for the class
![]() $\mathcal {C}$
if
$\mathcal {C}$
if
![]() $Y \in \mathcal {C}$
and whenever Y embeds in a
$Y \in \mathcal {C}$
and whenever Y embeds in a
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $X \in \mathcal {C}$
, then Y is a retract of X.
$X \in \mathcal {C}$
, then Y is a retract of X.
Definition 4.13. Given a finite set
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
, we say that a
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
, we say that a
![]() $\Gamma $
-subshift X is
$\Gamma $
-subshift X is
![]() $\mathcal {G}$
-free if for every
$\mathcal {G}$
-free if for every
![]() $x \in X$
and
$x \in X$
and
![]() $\Gamma _0 \in \mathcal {G}$
, we have that
$\Gamma _0 \in \mathcal {G}$
, we have that
![]() $\Gamma _0 \not \subseteq \mathrm {stab}(x)$
.
$\Gamma _0 \not \subseteq \mathrm {stab}(x)$
.
Definition 4.14. Let Y be a
![]() $\Gamma $
-subshift and let
$\Gamma $
-subshift and let
![]() $\mathcal {G}$
be a finite set of finitely generated subgroups of
$\mathcal {G}$
be a finite set of finitely generated subgroups of
![]() $\Gamma $
. We say that a finite set
$\Gamma $
. We say that a finite set
![]() $K \Subset \Gamma $
witnesses that Y is
$K \Subset \Gamma $
witnesses that Y is
![]() $\mathcal {G}$
-free if each
$\mathcal {G}$
-free if each
![]() $\Gamma _0 \in \mathcal {G}$
admits a finite generating set
$\Gamma _0 \in \mathcal {G}$
admits a finite generating set
![]() $F_{\Gamma _0} \Subset \Gamma $
so that for every
$F_{\Gamma _0} \Subset \Gamma $
so that for every
![]() $w \in \mathcal {L}_{K}(Y)$
and every
$w \in \mathcal {L}_{K}(Y)$
and every
![]() $\Gamma _0 \in \mathcal {G}$
, there exists
$\Gamma _0 \in \mathcal {G}$
, there exists
![]() $\gamma \in F_{\Gamma _0}$
and
$\gamma \in F_{\Gamma _0}$
and
![]() $v \in K$
such that
$v \in K$
such that
![]() $v+ \gamma \in K$
and
$v+ \gamma \in K$
and
![]() $w_{v} \ne w_{v+\gamma }$
.
$w_{v} \ne w_{v+\gamma }$
.
Lemma 4.15. Let
![]() $\mathcal {G}\Subset \mathrm {Sub}(\Gamma )$
be a finite set of finitely generated subgroups of
$\mathcal {G}\Subset \mathrm {Sub}(\Gamma )$
be a finite set of finitely generated subgroups of
![]() $\Gamma $
and let Y be a
$\Gamma $
and let Y be a
![]() $\Gamma $
-subshift. Then, Y is
$\Gamma $
-subshift. Then, Y is
![]() $\mathcal {G}$
-free if and only if there exists a finite set
$\mathcal {G}$
-free if and only if there exists a finite set
![]() $K \Subset \Gamma $
with
$K \Subset \Gamma $
with
![]() $0 \in K$
that witnesses that Y is
$0 \in K$
that witnesses that Y is
![]() $\mathcal {G}$
-free.
$\mathcal {G}$
-free.
Proof. If
![]() $K \Subset \Gamma $
witnesses that Y is
$K \Subset \Gamma $
witnesses that Y is
![]() $\mathcal {G}$
-free, then each
$\mathcal {G}$
-free, then each
![]() $\Gamma _0 \in \mathcal {G}$
admits a finite generating set
$\Gamma _0 \in \mathcal {G}$
admits a finite generating set
![]() $F_{\Gamma _0} \Subset \Gamma $
so that for every
$F_{\Gamma _0} \Subset \Gamma $
so that for every
![]() $y \in Y$
and every
$y \in Y$
and every
![]() $\Gamma _0 \in \mathcal {G}$
, there exists
$\Gamma _0 \in \mathcal {G}$
, there exists
![]() $v \in K$
and
$v \in K$
and
![]() $\gamma \in F_{\Gamma _0}$
such that
$\gamma \in F_{\Gamma _0}$
such that
![]() $y_v \ne y_{v + \gamma }$
, and so
$y_v \ne y_{v + \gamma }$
, and so
![]() $\Gamma _0 \not \subseteq \mathrm {stab}(y)$
. This proves that Y is
$\Gamma _0 \not \subseteq \mathrm {stab}(y)$
. This proves that Y is
![]() $\mathcal {G}$
-free.
$\mathcal {G}$
-free.
For the converse direction, for each
![]() $\Gamma _0 \in \mathcal {G}$
, fix a finite generating set
$\Gamma _0 \in \mathcal {G}$
, fix a finite generating set
![]() $F_{\Gamma _0} \Subset \Gamma $
. Given
$F_{\Gamma _0} \Subset \Gamma $
. Given
![]() $K \Subset \Gamma $
, say that
$K \Subset \Gamma $
, say that
![]() $w \in \mathcal {L}_K(Y)$
is
$w \in \mathcal {L}_K(Y)$
is
![]() $F_{\Gamma _0}$
-periodic if
$F_{\Gamma _0}$
-periodic if
![]() $w_v = w_{v + \gamma }$
whenever
$w_v = w_{v + \gamma }$
whenever
![]() $\gamma \in F_{\Gamma _0}$
, and
$\gamma \in F_{\Gamma _0}$
, and
![]() $v,v + \gamma \in K$
. Suppose that Y is
$v,v + \gamma \in K$
. Suppose that Y is
![]() $\mathcal {G}$
-free. Then, for any
$\mathcal {G}$
-free. Then, for any
![]() $y \in Y$
and every
$y \in Y$
and every
![]() $\Gamma _0 \in \mathcal {G}$
, there exists a finite set
$\Gamma _0 \in \mathcal {G}$
, there exists a finite set
![]() $K_{y,\Gamma _0} \Subset \Gamma $
such that the restriction of y to
$K_{y,\Gamma _0} \Subset \Gamma $
such that the restriction of y to
![]() $K_{y,\Gamma _0}$
is not
$K_{y,\Gamma _0}$
is not
![]() $F_{\Gamma _0}$
periodic. Take
$F_{\Gamma _0}$
periodic. Take
![]() $K_y = \bigcup _{\Gamma _0 \in \mathcal {G}}K_{y,\Gamma _0}$
, then the restriction of y to
$K_y = \bigcup _{\Gamma _0 \in \mathcal {G}}K_{y,\Gamma _0}$
, then the restriction of y to
![]() $K_{y}$
is not
$K_{y}$
is not
![]() $F_{\Gamma _0}$
periodic for all
$F_{\Gamma _0}$
periodic for all
![]() $\Gamma _0 \in \mathcal {G}$
. For each
$\Gamma _0 \in \mathcal {G}$
. For each
![]() $y \in Y$
, let
$y \in Y$
, let
Then,
![]() $U_y \subseteq Y$
is an open neighborhood of y. By compactness of Y, the open cover
$U_y \subseteq Y$
is an open neighborhood of y. By compactness of Y, the open cover
![]() $\{U_y\}_{y \in Y}$
admits a finite subcover
$\{U_y\}_{y \in Y}$
admits a finite subcover
![]() $U_{y_1},\ldots ,U_{y_N}$
. Let
$U_{y_1},\ldots ,U_{y_N}$
. Let
![]() $K =\bigcup _{j=1}^N K_{y_j}$
, then for every
$K =\bigcup _{j=1}^N K_{y_j}$
, then for every
![]() $y \in Y$
, we have that
$y \in Y$
, we have that
![]() $y_K$
is not
$y_K$
is not
![]() $F_{\Gamma _0}$
periodic for all
$F_{\Gamma _0}$
periodic for all
![]() $\Gamma _0 \in \mathcal {G}$
. This proves that K witnesses that Y is
$\Gamma _0 \in \mathcal {G}$
. This proves that K witnesses that Y is
![]() $\mathcal {G}$
-free.
$\mathcal {G}$
-free.
Definition 4.16. Given a
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $Y \subseteq A^\Gamma $
and finite non-empty sets
$Y \subseteq A^\Gamma $
and finite non-empty sets
![]() $K,D \Subset \Gamma $
, let
$K,D \Subset \Gamma $
, let
In words, given a
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $Y \subseteq A^\Gamma $
, the subshift
$Y \subseteq A^\Gamma $
, the subshift
![]() $Y^{(K,D)} \subseteq A^{\Gamma }$
consists of elements of
$Y^{(K,D)} \subseteq A^{\Gamma }$
consists of elements of
![]() $A^\Gamma $
in which every
$A^\Gamma $
in which every
![]() $K+D$
pattern contains a Y-admissible K-pattern.
$K+D$
pattern contains a Y-admissible K-pattern.
Lemma 4.17. Let
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
be a finite set of finitely generated subgroups, let
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
be a finite set of finitely generated subgroups, let
![]() $Y \subseteq A^\Gamma $
be
$Y \subseteq A^\Gamma $
be
![]() $\mathcal {G}$
-free subshift, and let
$\mathcal {G}$
-free subshift, and let
![]() $K \Subset \Gamma $
be a finite set that witnesses that Y is
$K \Subset \Gamma $
be a finite set that witnesses that Y is
![]() $\mathcal {G}$
-free. For any non-empty finite set
$\mathcal {G}$
-free. For any non-empty finite set
![]() $D \Subset \Gamma $
, the subshift
$D \Subset \Gamma $
, the subshift
![]() $Y^{(K,D)}$
is a
$Y^{(K,D)}$
is a
![]() $\mathcal {G}$
-free subshift such that
$\mathcal {G}$
-free subshift such that
![]() $Y \subseteq Y^{(K,D)}$
.
$Y \subseteq Y^{(K,D)}$
.
Proof. It is clear that
![]() $Y \subseteq Y^{(K,D)}$
, because for any
$Y \subseteq Y^{(K,D)}$
, because for any
![]() $y \in Y$
, any
$y \in Y$
, any
![]() $v \in \Gamma $
, and
$v \in \Gamma $
, and
![]() $w \in D$
, we have that
$w \in D$
, we have that
![]() $\sigma _{v+w}(y)_K \in \mathcal {L}_K(Y)$
. Because K witness that Y is
$\sigma _{v+w}(y)_K \in \mathcal {L}_K(Y)$
. Because K witness that Y is
![]() $\mathcal {G}$
-free, it follows that
$\mathcal {G}$
-free, it follows that
![]() $D+K$
witnesses that
$D+K$
witnesses that
![]() $Y^{(K,D)}$
is
$Y^{(K,D)}$
is
![]() $\mathcal {G}$
-free.
$\mathcal {G}$
-free.
We proceed with some technical lemmas that will eventually be used to establish significant properties for subshifts with the map extension property. These properties will be exploited in our proof of the main theorem.
Lemma 4.18. Let
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
be a finite set of finitely generated subgroups. Then:
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
be a finite set of finitely generated subgroups. Then:
-
(i) any
 $\mathcal {G}$
-free
$\mathcal {G}$
-free
 $\Gamma $
-subshift Y is contained in a
$\Gamma $
-subshift Y is contained in a
 $\mathcal {G}$
-free
$\mathcal {G}$
-free
 $\Gamma $
-subshift of finite type
$\Gamma $
-subshift of finite type
 $\hat Y$
with the map extension property (possibly over a bigger alphabet);
$\hat Y$
with the map extension property (possibly over a bigger alphabet); -
(ii) if Y is an absolute retract for the class of
 $\mathcal {G}$
-free
$\mathcal {G}$
-free
 $\Gamma $
-subshifts, then there exists a finite set
$\Gamma $
-subshifts, then there exists a finite set
 $F \Subset \Gamma $
so that for any
$F \Subset \Gamma $
so that for any
 $\mathcal {G}$
-free
$\mathcal {G}$
-free
 $\Gamma $
-subshift X with
$\Gamma $
-subshift X with
 $Y \subseteq X$
, there exists a retraction map
$Y \subseteq X$
, there exists a retraction map
 $r: X \to Y$
such that whenever
$r: X \to Y$
such that whenever
 $y_F \in \mathcal {L}(Y)$
, then
$y_F \in \mathcal {L}(Y)$
, then
 $r(y)_0=y_0$
.
$r(y)_0=y_0$
.
Proof. Let
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
be a finite set and let Y be a
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
be a finite set and let Y be a
![]() $\mathcal {G}$
-free
$\mathcal {G}$
-free
![]() $\Gamma $
-subshift.
$\Gamma $
-subshift.
Choose a finite symmetric generating set
![]() $F_{\Gamma _0} \Subset \Gamma $
for each
$F_{\Gamma _0} \Subset \Gamma $
for each
![]() $\Gamma _0 \in \mathcal {G}$
. By Lemma 4.15, there exists a finite set
$\Gamma _0 \in \mathcal {G}$
. By Lemma 4.15, there exists a finite set
![]() $K_0 \Subset \Gamma $
with
$K_0 \Subset \Gamma $
with
![]() $0 \in K_0$
that witnesses that Y is
$0 \in K_0$
that witnesses that Y is
![]() $\mathcal {G}$
-free. Let
$\mathcal {G}$
-free. Let
 $$ \begin{align*}P= \bigcup_{\Gamma_0 \in \mathcal{G}}F_{\Gamma_0}\end{align*} $$
$$ \begin{align*}P= \bigcup_{\Gamma_0 \in \mathcal{G}}F_{\Gamma_0}\end{align*} $$
and let
![]() $\mathcal {Q}$
denote the collection of symmetric subsets
$\mathcal {Q}$
denote the collection of symmetric subsets
![]() $Q \subseteq P$
that satisfy
$Q \subseteq P$
that satisfy
![]() $Q \cap (\Gamma _0 \setminus \{0\}) \ne~\emptyset $
for all
$Q \cap (\Gamma _0 \setminus \{0\}) \ne~\emptyset $
for all
![]() $\Gamma _0 \in \mathcal {G}$
.
$\Gamma _0 \in \mathcal {G}$
.
We first prove part (i). We are about to define a
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $\hat Y \subseteq \hat A^{\Gamma }$
and show that
$\hat Y \subseteq \hat A^{\Gamma }$
and show that
![]() $\hat Y$
is
$\hat Y$
is
![]() $\mathcal {G}$
-free, contains Y, and has the map extension property. Let us first define the ‘alphabet’
$\mathcal {G}$
-free, contains Y, and has the map extension property. Let us first define the ‘alphabet’
![]() $\hat A$
:
$\hat A$
:
where
![]() $Y \subseteq A^\Gamma $
.
$Y \subseteq A^\Gamma $
.
We regard the finite set
![]() $\mathcal {Q}$
as another alphabet disjoint for A, and
$\mathcal {Q}$
as another alphabet disjoint for A, and
![]() $\hat a$
as a new ‘symbol’ not contained in A or in
$\hat a$
as a new ‘symbol’ not contained in A or in
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
Let
![]() $\hat Y \subseteq \hat A^{\Gamma }$
be the
$\hat Y \subseteq \hat A^{\Gamma }$
be the
![]() $\Gamma $
-subshift of finite type defined by the following constraints. For every
$\Gamma $
-subshift of finite type defined by the following constraints. For every
![]() $y \in \tilde Y$
and any
$y \in \tilde Y$
and any
![]() $v \in \Gamma $
:
$v \in \Gamma $
:
-
(1) there exists
 $u \in K_0$
such that either
$u \in K_0$
such that either
 $\sigma _{v-u}(y)_{K_0} \in \mathcal {L}_{K_0}(Y)$
or there exists
$\sigma _{v-u}(y)_{K_0} \in \mathcal {L}_{K_0}(Y)$
or there exists
 $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
 $\gamma \in Q \cup \{0\}$
such that
$\gamma \in Q \cup \{0\}$
such that
 $\sigma _{v-u+ \gamma }(y)=Q$
;
$\sigma _{v-u+ \gamma }(y)=Q$
; -
(2) if there exists
 $Q \in \mathcal {Q}$
such that
$Q \in \mathcal {Q}$
such that
 $y_v = Q$
, then for every
$y_v = Q$
, then for every
 $\gamma \in Q$
, we have that
$\gamma \in Q$
, we have that
 $y_{v+\gamma } \ne~Q$
.
$y_{v+\gamma } \ne~Q$
.
It is clear that
![]() $Y \subseteq \hat Y$
. If
$Y \subseteq \hat Y$
. If
![]() $y \in Y$
, then for every
$y \in Y$
, then for every
![]() $v \in \Gamma $
and every
$v \in \Gamma $
and every
![]() $u \in K_0$
, we have that
$u \in K_0$
, we have that
![]() $\sigma _{v-u}(y)_{K_0} \in \mathcal {L}_{K_0}(Y)$
and
$\sigma _{v-u}(y)_{K_0} \in \mathcal {L}_{K_0}(Y)$
and
![]() $y_v \not \in Q$
, so
$y_v \not \in Q$
, so
![]() $y \in \hat Y$
. This shows that
$y \in \hat Y$
. This shows that
![]() $Y \subseteq \hat Y$
. Let us prove that
$Y \subseteq \hat Y$
. Let us prove that
![]() $\hat Y$
is
$\hat Y$
is
![]() $\mathcal {G}$
-free. Given
$\mathcal {G}$
-free. Given
![]() $y \in \hat Y$
and
$y \in \hat Y$
and
![]() $\Gamma _0 \in \mathcal {G}$
, we need to show that
$\Gamma _0 \in \mathcal {G}$
, we need to show that
![]() $\Gamma _0 \not \le \mathrm {stab}(y)$
. Consider an arbitrary point
$\Gamma _0 \not \le \mathrm {stab}(y)$
. Consider an arbitrary point
![]() $y \in \hat Y$
. If there exists
$y \in \hat Y$
. If there exists
![]() $v \in \Gamma $
such that
$v \in \Gamma $
such that
![]() $\sigma _v(y)_{K_0} \in \mathcal {L}_{K_0}(Y)$
, then
$\sigma _v(y)_{K_0} \in \mathcal {L}_{K_0}(Y)$
, then
![]() $\Gamma _0 \not \le \mathrm {stab}(y)$
for any
$\Gamma _0 \not \le \mathrm {stab}(y)$
for any
![]() $\Gamma _0 \in \mathcal {G}$
, because
$\Gamma _0 \in \mathcal {G}$
, because
![]() $K_0$
witnesses that Y is
$K_0$
witnesses that Y is
![]() $\mathcal {G}$
-free. Otherwise, there exists
$\mathcal {G}$
-free. Otherwise, there exists
![]() $v \in \Gamma $
and
$v \in \Gamma $
and
![]() $Q \in \mathcal {Q}$
such that
$Q \in \mathcal {Q}$
such that
![]() $\sigma _v(y)=Q$
. In this case, for every
$\sigma _v(y)=Q$
. In this case, for every
![]() $\gamma \in Q$
, we have
$\gamma \in Q$
, we have
![]() $y_{v+\gamma } \ne y_v$
, so
$y_{v+\gamma } \ne y_v$
, so
![]() $\mathrm {stab}(y) \cap Q =~\emptyset $
. Since
$\mathrm {stab}(y) \cap Q =~\emptyset $
. Since
![]() $(\Gamma _0 \setminus \{0\}) \cap Q \ne \emptyset $
this shows that
$(\Gamma _0 \setminus \{0\}) \cap Q \ne \emptyset $
this shows that
![]() $\Gamma _0 \not \le \mathrm {stab}(y)$
.
$\Gamma _0 \not \le \mathrm {stab}(y)$
.
Let us show that
![]() $\hat Y$
has the map extension property. Suppose that X is a
$\hat Y$
has the map extension property. Suppose that X is a
![]() $\Gamma $
-subshift such that
$\Gamma $
-subshift such that
![]() $X \rightsquigarrow \hat Y$
. In particular,
$X \rightsquigarrow \hat Y$
. In particular,
![]() $X \subseteq B^\Gamma $
is a
$X \subseteq B^\Gamma $
is a
![]() $\mathcal {G}$
-free subshift and suppose that
$\mathcal {G}$
-free subshift and suppose that
![]() $\tilde \pi : \tilde X \to \hat Y$
is a map from a
$\tilde \pi : \tilde X \to \hat Y$
is a map from a
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $\tilde X \subseteq X$
. Let
$\tilde X \subseteq X$
. Let
![]() $W \Subset \Gamma $
be a coding window for
$W \Subset \Gamma $
be a coding window for
![]() $\tilde \pi $
and let
$\tilde \pi $
and let
![]() $K = K_0 + W$
. We will now describe a map
$K = K_0 + W$
. We will now describe a map
![]() $\pi :X \to \hat Y$
that extends
$\pi :X \to \hat Y$
that extends
![]() $\tilde \pi $
. As before, since X is compact and
$\tilde \pi $
. As before, since X is compact and
![]() $\mathcal {G}$
-free, there exists a finite set
$\mathcal {G}$
-free, there exists a finite set
![]() $K_2 \Subset \Gamma $
that witnesses that X is
$K_2 \Subset \Gamma $
that witnesses that X is
![]() $\mathcal {G}$
-free. For every
$\mathcal {G}$
-free. For every
![]() $Q \in \mathcal {Q}$
, let
$Q \in \mathcal {Q}$
, let
![]() $L_Q \subseteq B^{K_2}$
be the set of patterns
$L_Q \subseteq B^{K_2}$
be the set of patterns
![]() $w \in \mathcal {L}_{K_2}(X)$
such that:
$w \in \mathcal {L}_{K_2}(X)$
such that:
-
• for every
 $\gamma \in Q$
, there exists
$\gamma \in Q$
, there exists
 $v \in K_2$
such that
$v \in K_2$
such that
 $v+\gamma \in K_2$
and
$v+\gamma \in K_2$
and
 $w_v \ne v_{v+\gamma }$
;
$w_v \ne v_{v+\gamma }$
; -
• for every
 $\gamma \in P\setminus Q$
and every
$\gamma \in P\setminus Q$
and every
 $v \in K_2$
such that
$v \in K_2$
such that
 $v+\gamma \in K_2$
, we have
$v+\gamma \in K_2$
, we have
 $w_v = v_{v+\gamma }$
.
$w_v = v_{v+\gamma }$
.
The sets
![]() $\{L_Q\}_{Q \in \mathcal {Q}}$
are mutually disjoint and
$\{L_Q\}_{Q \in \mathcal {Q}}$
are mutually disjoint and
![]() $\mathcal {L}_{K_2}(X)) \subseteq \biguplus _{Q \in \mathcal {Q}}L_Q$
. For every
$\mathcal {L}_{K_2}(X)) \subseteq \biguplus _{Q \in \mathcal {Q}}L_Q$
. For every
![]() $Q \in \mathcal {Q}$
, let
$Q \in \mathcal {Q}$
, let
![]() $V_Q =\{ x \in X: x_{K_2} \in L_Q\}$
. Then,
$V_Q =\{ x \in X: x_{K_2} \in L_Q\}$
. Then,
![]() $V_Q$
is a clopen set in X. Furthermore, for every
$V_Q$
is a clopen set in X. Furthermore, for every
![]() $x \in V_Q$
and every
$x \in V_Q$
and every
![]() $\gamma \in Q$
, we have
$\gamma \in Q$
, we have
![]() $\sigma _\gamma (x) \ne x$
. By Lemma 3.3, there exists a clopen set
$\sigma _\gamma (x) \ne x$
. By Lemma 3.3, there exists a clopen set
![]() $C_Q \subseteq V_Q$
such that
$C_Q \subseteq V_Q$
such that
 $$ \begin{align*} C_Q \cap \sigma_\gamma(C_Q) = \emptyset \quad\text{for every } \gamma \in Q \text{ and } V_Q \subseteq C_Q \cup \bigcup_{\gamma \in Q}\sigma_\gamma(C_Q). \end{align*} $$
$$ \begin{align*} C_Q \cap \sigma_\gamma(C_Q) = \emptyset \quad\text{for every } \gamma \in Q \text{ and } V_Q \subseteq C_Q \cup \bigcup_{\gamma \in Q}\sigma_\gamma(C_Q). \end{align*} $$
Define a map
![]() $\pi :X\to \hat Y$
as follows:
$\pi :X\to \hat Y$
as follows:
 $$ \begin{align*} \pi(x)_v = \begin{cases} \tilde \pi(\sigma_v(x))_0 & \text{if } \text{ there exists } u \in K_0 \text{ such that } \sigma_{v-u}(x)_{K_0+W} \in \mathcal{L}_{W}(\tilde X),\\ Q & \text{if } \sigma_v(x)\in\!C_Q \text{ for some } Q \in\! \mathcal{Q} \text{ and we are not in the previous case},\\ \hat{a} & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \pi(x)_v = \begin{cases} \tilde \pi(\sigma_v(x))_0 & \text{if } \text{ there exists } u \in K_0 \text{ such that } \sigma_{v-u}(x)_{K_0+W} \in \mathcal{L}_{W}(\tilde X),\\ Q & \text{if } \sigma_v(x)\in\!C_Q \text{ for some } Q \in\! \mathcal{Q} \text{ and we are not in the previous case},\\ \hat{a} & \text{otherwise.} \end{cases} \end{align*} $$
Notice that if there exists
![]() $u \in K_0$
such that
$u \in K_0$
such that
![]() $\sigma _{v-u}(x)_{K_0+W} \in \mathcal {L}_{K_0+W}(\tilde X)$
, then it follows that
$\sigma _{v-u}(x)_{K_0+W} \in \mathcal {L}_{K_0+W}(\tilde X)$
, then it follows that
![]() $\sigma _v(x)_{W} \in \mathcal {L}_W(\tilde X)$
and so
$\sigma _v(x)_{W} \in \mathcal {L}_W(\tilde X)$
and so
![]() $\tilde \pi (\sigma _v(x))_0$
is well defined, because W is a coding window for
$\tilde \pi (\sigma _v(x))_0$
is well defined, because W is a coding window for
![]() $\tilde \pi $
. Moreover, if
$\tilde \pi $
. Moreover, if
![]() $\sigma _v(x)_K \in \mathcal {L}_{K_0+W}(\tilde X)$
, then there exists
$\sigma _v(x)_K \in \mathcal {L}_{K_0+W}(\tilde X)$
, then there exists
![]() $\tilde x \in \tilde X$
such that
$\tilde x \in \tilde X$
such that
![]() $\pi (x)_{K_0}= \tilde \pi (\tilde x)_{K_0}$
and, in particular,
$\pi (x)_{K_0}= \tilde \pi (\tilde x)_{K_0}$
and, in particular,
![]() $\pi (x)_0 = \tilde \pi (x)_0$
. Since
$\pi (x)_0 = \tilde \pi (x)_0$
. Since
![]() $X \subseteq \bigcup _{Q \in \mathcal {Q}} V_Q$
and
$X \subseteq \bigcup _{Q \in \mathcal {Q}} V_Q$
and
![]() $V_Q \subseteq C_Q \cup \bigcup _{\gamma \in Q}\sigma _\gamma (C_Q)$
for every
$V_Q \subseteq C_Q \cup \bigcup _{\gamma \in Q}\sigma _\gamma (C_Q)$
for every
![]() $Q \in \mathcal {Q}$
, it follows that for every
$Q \in \mathcal {Q}$
, it follows that for every
![]() $x \in X$
and
$x \in X$
and
![]() $v \in \Gamma $
, either there exists
$v \in \Gamma $
, either there exists
![]() $u \in K_0$
such that
$u \in K_0$
such that
![]() $\sigma _{v-u}(x)_{K} \in \mathcal {L}_{K_0+W}(X)$
, in which case
$\sigma _{v-u}(x)_{K} \in \mathcal {L}_{K_0+W}(X)$
, in which case
![]() $\sigma _{v-u}(\pi (x)) \in \mathcal {L}_{K_0}(Y)$
, or there exists
$\sigma _{v-u}(\pi (x)) \in \mathcal {L}_{K_0}(Y)$
, or there exists
![]() $Q \in \mathcal {Q}$
and
$Q \in \mathcal {Q}$
and
![]() $\gamma \in Q \cup \{0\}$
such that
$\gamma \in Q \cup \{0\}$
such that
![]() $\sigma _{v+\gamma }(\hat \pi (y))=Q$
. We have thus shown that
$\sigma _{v+\gamma }(\hat \pi (y))=Q$
. We have thus shown that
![]() $\pi (x) \in \hat Y$
for every
$\pi (x) \in \hat Y$
for every
![]() $x \in X$
, completing the proof of part (i).
$x \in X$
, completing the proof of part (i).
We now prove part (ii). Let Y be an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts and let
$\mathcal {G}$
-free subshifts and let
![]() $\hat Y$
be the subshift defined in the first part of the proof. Since
$\hat Y$
be the subshift defined in the first part of the proof. Since
![]() $Y \subseteq \hat Y$
and
$Y \subseteq \hat Y$
and
![]() $\hat Y$
is
$\hat Y$
is
![]() $\mathcal {G}$
-free, there exists a retraction map
$\mathcal {G}$
-free, there exists a retraction map
![]() $\hat r:\hat Y \to Y$
. Let
$\hat r:\hat Y \to Y$
. Let
![]() $W \Subset \Gamma $
be a coding window for
$W \Subset \Gamma $
be a coding window for
![]() $\hat r$
. Let X be a
$\hat r$
. Let X be a
![]() $\mathcal {G}$
-free subshift that contains Y. Again, choose a finite set
$\mathcal {G}$
-free subshift that contains Y. Again, choose a finite set
![]() $K_2 \Subset \Gamma $
that witnesses that X is
$K_2 \Subset \Gamma $
that witnesses that X is
![]() $\mathcal {G}$
-free. For every
$\mathcal {G}$
-free. For every
![]() $Q \in \mathcal {Q}$
, let
$Q \in \mathcal {Q}$
, let
![]() $L_Q$
,
$L_Q$
,
![]() $V_Q \subset X$
, and
$V_Q \subset X$
, and
![]() $C_Q$
be as in the previous part of the proof. Define a map
$C_Q$
be as in the previous part of the proof. Define a map
![]() $\tilde r:X\to \hat Y$
as follows:
$\tilde r:X\to \hat Y$
as follows:
 $$ \begin{align*}\tilde r(x)_v = \begin{cases} \sigma_v(x)_0 & \text{if } \text{ there exists } u \in K_0 \text{ such that } \sigma_{v-u}(x)_{K_0} \in \mathcal{L}_{K_0}(Y),\\ Q & \text{if } \sigma_v(x) \in C_Q \text{ for some } Q \in \mathcal{Q} \text{ and we are not in the previous case},\\ \hat{a} & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}\tilde r(x)_v = \begin{cases} \sigma_v(x)_0 & \text{if } \text{ there exists } u \in K_0 \text{ such that } \sigma_{v-u}(x)_{K_0} \in \mathcal{L}_{K_0}(Y),\\ Q & \text{if } \sigma_v(x) \in C_Q \text{ for some } Q \in \mathcal{Q} \text{ and we are not in the previous case},\\ \hat{a} & \text{otherwise.} \end{cases} \end{align*} $$
As in the previous part, it follows that indeed
![]() $\hat r(x) \in \hat Y$
for every
$\hat r(x) \in \hat Y$
for every
![]() $x \in X$
, so
$x \in X$
, so
![]() $\tilde r:X\to \hat Y$
is well defined. Clearly,
$\tilde r:X\to \hat Y$
is well defined. Clearly,
![]() $\tilde r(x)_0 = x_0$
whenever
$\tilde r(x)_0 = x_0$
whenever
![]() $x_{K_0} \in \mathcal {L}_{K_0}(Y)$
. Let
$x_{K_0} \in \mathcal {L}_{K_0}(Y)$
. Let
![]() $K = K_0 +W$
. Let
$K = K_0 +W$
. Let
![]() $r = \hat r \circ \tilde r$
. Then,
$r = \hat r \circ \tilde r$
. Then,
![]() $r: X \to Y$
is a retraction map, and
$r: X \to Y$
is a retraction map, and
![]() $r(y)_0= y_0$
whenever
$r(y)_0= y_0$
whenever
![]() $x \in X$
and
$x \in X$
and
![]() $x_{K} \in \mathcal {L}_K(Y)$
. This completes the proof of part (ii).
$x_{K} \in \mathcal {L}_K(Y)$
. This completes the proof of part (ii).
Proposition 4.19. A
![]() $\Gamma $
-subshift Y has the map extension property if and only if there exists a finite set
$\Gamma $
-subshift Y has the map extension property if and only if there exists a finite set
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
such that Y is an absolute retract for the class of
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
such that Y is an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts.
$\mathcal {G}$
-free subshifts.
Proof. Suppose that Y has the map extension property. By Proposition 4.8, there exists a finite set
![]() $F \Subset \Gamma \setminus \{0\}$
such that for every
$F \Subset \Gamma \setminus \{0\}$
such that for every
![]() $\Gamma _0 \le \Gamma $
with
$\Gamma _0 \le \Gamma $
with
![]() $\Gamma _0 \cap F = \emptyset $
, there exists
$\Gamma _0 \cap F = \emptyset $
, there exists
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $\Gamma _0 \le \mathrm {stab}(y)$
. Let
$\Gamma _0 \le \mathrm {stab}(y)$
. Let
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
denote the collection of subgroups
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
denote the collection of subgroups
![]() $\Gamma _0 \le \Gamma $
that are generated by a subset of F and so that
$\Gamma _0 \le \Gamma $
that are generated by a subset of F and so that
![]() $\Gamma _0 \not \le \mathrm {stab}(y)$
for every
$\Gamma _0 \not \le \mathrm {stab}(y)$
for every
![]() $y \in Y$
. It follows that Y is
$y \in Y$
. It follows that Y is
![]() $\mathcal {G}$
-free and that
$\mathcal {G}$
-free and that
![]() $X \rightsquigarrow Y$
for any
$X \rightsquigarrow Y$
for any
![]() $\mathcal {G}$
-free
$\mathcal {G}$
-free
![]() $\Gamma $
-subshift X. Let X be a
$\Gamma $
-subshift X. Let X be a
![]() $\mathcal {G}$
-free subshift that contains Y. Since Y has the map extension property and
$\mathcal {G}$
-free subshift that contains Y. Since Y has the map extension property and
![]() $Y \subseteq X$
, it follows that then the identity map on Y extends to a retraction from X to Y. This shows that Y is an absolute retract for the class of
$Y \subseteq X$
, it follows that then the identity map on Y extends to a retraction from X to Y. This shows that Y is an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts.
$\mathcal {G}$
-free subshifts.
For the converse direction, suppose that there exists a finite set
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
such that Y is an absolute retract for the class of
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
such that Y is an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts. Let X be a
$\mathcal {G}$
-free subshifts. Let X be a
![]() $\Gamma $
-subshift such that
$\Gamma $
-subshift such that
![]() $X \rightsquigarrow Y$
and let
$X \rightsquigarrow Y$
and let
![]() $\pi :\tilde X \to Y$
be a map from a closed,
$\pi :\tilde X \to Y$
be a map from a closed,
![]() $\Gamma $
-invariant subset
$\Gamma $
-invariant subset
![]() $\tilde X \subseteq X$
. Our goal is to show that
$\tilde X \subseteq X$
. Our goal is to show that
![]() $\tilde \pi $
extends to a map
$\tilde \pi $
extends to a map
![]() $\pi :X \to Y$
. By Lemma 4.18, since X is
$\pi :X \to Y$
. By Lemma 4.18, since X is
![]() $\mathcal {G}$
-free, there exists a
$\mathcal {G}$
-free, there exists a
![]() $\mathcal {G}$
-free subshift
$\mathcal {G}$
-free subshift
![]() $\hat Y$
that contains Y and has the map extension property. Since
$\hat Y$
that contains Y and has the map extension property. Since
![]() $Y \subseteq \hat Y$
, it follows that
$Y \subseteq \hat Y$
, it follows that
![]() $\tilde \pi $
extends to a map
$\tilde \pi $
extends to a map
![]() $\hat \pi :X \to \hat Y$
. Since Y is an absolute retract for the class of
$\hat \pi :X \to \hat Y$
. Since Y is an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts, there exists a retraction map
$\mathcal {G}$
-free subshifts, there exists a retraction map
![]() $r:\hat Y \to Y$
. Setting
$r:\hat Y \to Y$
. Setting
![]() $\pi = r \circ \hat \pi $
, we see that
$\pi = r \circ \hat \pi $
, we see that
![]() $\pi :X \to Y$
extends
$\pi :X \to Y$
extends
![]() $\tilde \pi $
.
$\tilde \pi $
.
Proposition 4.20. Let
![]() $\Gamma $
be a countable abelian group and let Y be a
$\Gamma $
be a countable abelian group and let Y be a
![]() $\Gamma $
-subshift with the map extension property. Then,
$\Gamma $
-subshift with the map extension property. Then,
If furthermore
![]() $\mathrm {Ker}(Y)=\{0\}$
, then
$\mathrm {Ker}(Y)=\{0\}$
, then
Proof. Suppose that
![]() $Y \subseteq A^{\Gamma }$
is a
$Y \subseteq A^{\Gamma }$
is a
![]() $\Gamma $
-subshift with the map extension property. The inequality
$\Gamma $
-subshift with the map extension property. The inequality
holds by Proposition 2.23 for any subshift, regardless of the map extension property. So, to conclude the first part of the statement, we only need to prove the inequality
By Lemma 4.7, it suffices to prove this under the additional assumption that
![]() $\Gamma $
is a finitely generated abelian group. Furthermore, using Proposition 2.23, it suffices to prove that for any
$\Gamma $
is a finitely generated abelian group. Furthermore, using Proposition 2.23, it suffices to prove that for any
![]() $\epsilon>0$
, there exists a finite set
$\epsilon>0$
, there exists a finite set
![]() $K \Subset \Gamma $
such that for any K-separated subgroup
$K \Subset \Gamma $
such that for any K-separated subgroup
![]() $\Gamma _0 < \Gamma $
of finite index, we have
$\Gamma _0 < \Gamma $
of finite index, we have
![]() $h(\overline {Y}_{[\Gamma _0]}) \ge h(Y) - \epsilon $
. By Proposition 4.19, there exists a finite set
$h(\overline {Y}_{[\Gamma _0]}) \ge h(Y) - \epsilon $
. By Proposition 4.19, there exists a finite set
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
such that Y is an absolute retract for the class of
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
such that Y is an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts. In particular, Y is
$\mathcal {G}$
-free subshifts. In particular, Y is
![]() $\mathcal {G}$
-free and so by Lemma 4.15, there exists a finite set
$\mathcal {G}$
-free and so by Lemma 4.15, there exists a finite set
![]() $K_0 \Subset \Gamma $
that witnesses that Y is
$K_0 \Subset \Gamma $
that witnesses that Y is
![]() $\mathcal {G}$
-free. By part (ii) of Lemma 4.18, there exists another finite set
$\mathcal {G}$
-free. By part (ii) of Lemma 4.18, there exists another finite set
![]() $K_1 \Subset \Gamma $
such that for any
$K_1 \Subset \Gamma $
such that for any
![]() $\mathcal {G}$
-free subshift
$\mathcal {G}$
-free subshift
![]() $\hat Y$
that contains Y, there exists a retraction map
$\hat Y$
that contains Y, there exists a retraction map
![]() $r:\hat Y \to Y$
so that
$r:\hat Y \to Y$
so that
![]() $r(y)_0=r_0$
for any
$r(y)_0=r_0$
for any
![]() $y \in \hat Y$
with
$y \in \hat Y$
with
![]() $y_{K_1} \in \mathcal {L}_{K_1}(Y)$
.
$y_{K_1} \in \mathcal {L}_{K_1}(Y)$
.
For a finitely generated abelian group
![]() $\Gamma $
, it is not difficult to show that for any
$\Gamma $
, it is not difficult to show that for any
![]() $\delta>0$
and any finite set
$\delta>0$
and any finite set
![]() $F \subset \Gamma $
, there exists a finite set
$F \subset \Gamma $
, there exists a finite set
![]() $K \Subset \Gamma $
so that any K-separated subgroup finite-index subgroup
$K \Subset \Gamma $
so that any K-separated subgroup finite-index subgroup
![]() $\Gamma _0$
admits a fundamental domain D which is
$\Gamma _0$
admits a fundamental domain D which is
![]() $(F,\delta )$
-invariant. This can be deduced from Lemma 6.14 in §6, by taking D to be the disjointified Voronoi cell of
$(F,\delta )$
-invariant. This can be deduced from Lemma 6.14 in §6, by taking D to be the disjointified Voronoi cell of
![]() $0$
with respect to
$0$
with respect to
![]() $\Gamma _0$
(see Definition 6.7). By Lemma 2.22, for any
$\Gamma _0$
(see Definition 6.7). By Lemma 2.22, for any
![]() $\epsilon>0$
, by choosing F and
$\epsilon>0$
, by choosing F and
![]() $\delta $
appropriately as functions of
$\delta $
appropriately as functions of
![]() $K_1$
and
$K_1$
and
![]() $\delta $
, for any
$\delta $
, for any
![]() $(F,\delta )$
-invariant, we have
$(F,\delta )$
-invariant, we have
So we can complete the proof by showing that for any finite index subgroup
![]() $\Gamma _0 < \Gamma $
that admits a fundamental domain
$\Gamma _0 < \Gamma $
that admits a fundamental domain
![]() $D \Subset \Gamma $
with
$D \Subset \Gamma $
with
![]() $K_0 \subseteq D$
and
$K_0 \subseteq D$
and
![]() $D \setminus \partial _{K_1} D \ne \emptyset $
, we have
$D \setminus \partial _{K_1} D \ne \emptyset $
, we have
We assume that
![]() $Y \subseteq A^\Gamma $
. Given a finite index subgroup
$Y \subseteq A^\Gamma $
. Given a finite index subgroup
![]() $\Gamma _0 < \Gamma $
that admits a fundamental domain
$\Gamma _0 < \Gamma $
that admits a fundamental domain
![]() $D \Subset \Gamma $
such that
$D \Subset \Gamma $
such that
![]() $K_0 \subseteq D$
and
$K_0 \subseteq D$
and
![]() $D \setminus \partial _{K_1} D \ne \emptyset $
, consider the subshift
$D \setminus \partial _{K_1} D \ne \emptyset $
, consider the subshift
Because
![]() $K_0 \subseteq D$
and
$K_0 \subseteq D$
and
![]() $K_0$
witnesses that Y is
$K_0$
witnesses that Y is
![]() $\mathcal {G}$
-free, it follows that
$\mathcal {G}$
-free, it follows that
![]() $\hat Y$
is also
$\hat Y$
is also
![]() $\mathcal {G}$
-free. Clearly,
$\mathcal {G}$
-free. Clearly,
![]() $Y \subseteq \hat Y$
. Thus, there exists a retraction map
$Y \subseteq \hat Y$
. Thus, there exists a retraction map
![]() $r:\hat Y \to Y$
so that
$r:\hat Y \to Y$
so that
![]() $r(y)_0=r_0$
for any
$r(y)_0=r_0$
for any
![]() $y \in \hat Y$
with
$y \in \hat Y$
with
![]() $y_{K_1} \in \mathcal {L}_{K_1}(Y)$
. For any
$y_{K_1} \in \mathcal {L}_{K_1}(Y)$
. For any
![]() $p \in \mathcal {L}_D(Y)$
, we can define a point
$p \in \mathcal {L}_D(Y)$
, we can define a point
![]() $y \in \hat Y_{[\Gamma _0]}$
such that
$y \in \hat Y_{[\Gamma _0]}$
such that
![]() $\sigma _w(y)_D = p$
for every
$\sigma _w(y)_D = p$
for every
![]() $w \in \Gamma _0$
. It follows that
$w \in \Gamma _0$
. It follows that
![]() $r(y)_{D \setminus \partial _{K_1} D} = y_{D \setminus \partial _{K_1} D}$
. Since
$r(y)_{D \setminus \partial _{K_1} D} = y_{D \setminus \partial _{K_1} D}$
. Since
![]() $r(y) \in Y_{[\Gamma _0]}$
, it follows that
$r(y) \in Y_{[\Gamma _0]}$
, it follows that
Since
![]() $h(Y_{[\Gamma _0]}) = {1}/{|D|} \log |\mathcal {L}_{D}(Y_{[\Gamma _0]})|$
, we have proven equation (5).
$h(Y_{[\Gamma _0]}) = {1}/{|D|} \log |\mathcal {L}_{D}(Y_{[\Gamma _0]})|$
, we have proven equation (5).
The proof that
under the assumption that
![]() $\mathrm {Ker}(Y) = \{0\}$
is similar, so we omit the details.
$\mathrm {Ker}(Y) = \{0\}$
is similar, so we omit the details.
Definition 4.21. Let
![]() $F_1,F_2,K \subsetneq \Gamma $
be subsets of
$F_1,F_2,K \subsetneq \Gamma $
be subsets of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\emptyset \ne K \Subset \Gamma $
. We say that
$\emptyset \ne K \Subset \Gamma $
. We say that
![]() $F_1,F_2$
are K-disjoint if
$F_1,F_2$
are K-disjoint if
![]() $(K+F_1) \cap (K+F_2) = \emptyset $
.
$(K+F_1) \cap (K+F_2) = \emptyset $
.
Definition 4.22. A subshift
![]() $X \Subset A^\Gamma $
is called strongly irreducible if there exists
$X \Subset A^\Gamma $
is called strongly irreducible if there exists
![]() $K \Subset \Gamma $
such that for any pair of K-disjoint sets
$K \Subset \Gamma $
such that for any pair of K-disjoint sets
![]() $F_1,F_2 \subseteq \Gamma $
and any
$F_1,F_2 \subseteq \Gamma $
and any
![]() $x^{(1)},x^{(2)} \in X$
, there exists
$x^{(1)},x^{(2)} \in X$
, there exists
![]() $x \in X$
such that
$x \in X$
such that
![]() $x_{F_1} = x^{(1)}_{F_1}$
and
$x_{F_1} = x^{(1)}_{F_1}$
and
![]() $x_{F_2} = x^{(2)}_{F_2}$
. We say that
$x_{F_2} = x^{(2)}_{F_2}$
. We say that
![]() $K \Subset \Gamma $
as above is an irreducibility window for X.
$K \Subset \Gamma $
as above is an irreducibility window for X.
Lemma 4.23. Let
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
be a finite set and let
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
be a finite set and let
![]() $Y \subseteq A^\Gamma $
be a
$Y \subseteq A^\Gamma $
be a
![]() $\mathcal {G}$
-free subshift. Then, there exists a finite set
$\mathcal {G}$
-free subshift. Then, there exists a finite set
![]() $\hat A$
with
$\hat A$
with
![]() $A \subset \hat A$
and a
$A \subset \hat A$
and a
![]() $\mathcal {G}$
-free subshift
$\mathcal {G}$
-free subshift
![]() $\hat Y \subseteq \hat A^\Gamma $
such that
$\hat Y \subseteq \hat A^\Gamma $
such that
![]() $Y \subseteq \hat Y$
and so that
$Y \subseteq \hat Y$
and so that
![]() $\hat Y$
is a strongly irreducible shift of finite type.
$\hat Y$
is a strongly irreducible shift of finite type.
Proof. Let
![]() $Y \subseteq A^\Gamma $
be a
$Y \subseteq A^\Gamma $
be a
![]() $\mathcal {G}$
-free subshift. By Lemma 4.15, there exists a finite set
$\mathcal {G}$
-free subshift. By Lemma 4.15, there exists a finite set
![]() $W \Subset \Gamma $
that witnesses that Y is
$W \Subset \Gamma $
that witnesses that Y is
![]() $\mathcal {G}$
-free. Replacing W by
$\mathcal {G}$
-free. Replacing W by
![]() $W \cup (-W) \cup \{0\}$
, we can assume that
$W \cup (-W) \cup \{0\}$
, we can assume that
![]() $0 \in W$
and that W is symmetric. Let
$0 \in W$
and that W is symmetric. Let
![]() $\hat A$
be a finite set with
$\hat A$
be a finite set with
![]() $|\hat A| \ge |W|$
such that
$|\hat A| \ge |W|$
such that
![]() $A \subseteq \hat A$
and let
$A \subseteq \hat A$
and let
![]() $\mathcal {F} \subset \hat A^W$
denote the set of patterns that are not
$\mathcal {F} \subset \hat A^W$
denote the set of patterns that are not
![]() $\mathcal {G}$
-free in the sense that there exists
$\mathcal {G}$
-free in the sense that there exists
![]() $\Gamma _0 \in~\mathcal {G}$
such that for every
$\Gamma _0 \in~\mathcal {G}$
such that for every
![]() $v \in \Gamma _0$
, if
$v \in \Gamma _0$
, if
![]() $u \in W$
and
$u \in W$
and
![]() $u+v \in W$
, then
$u+v \in W$
, then
![]() $w_u=w_{u+v}$
. Let
$w_u=w_{u+v}$
. Let
![]() $\hat Y \subseteq \hat A^\Gamma $
be the subshift of finite type defined by the set of forbidden words
$\hat Y \subseteq \hat A^\Gamma $
be the subshift of finite type defined by the set of forbidden words
![]() $\mathcal {F}$
. Then,
$\mathcal {F}$
. Then,
![]() $\hat Y$
is
$\hat Y$
is
![]() $\mathcal {G}$
-free, as witnessed by the set W. Clearly,
$\mathcal {G}$
-free, as witnessed by the set W. Clearly,
![]() $Y \subseteq \hat Y$
. We claim that
$Y \subseteq \hat Y$
. We claim that
![]() $\hat Y$
is strongly irreducible. To see this, it suffices to show that for any
$\hat Y$
is strongly irreducible. To see this, it suffices to show that for any
![]() $F \subseteq \Gamma \setminus \{0\}$
, any pattern
$F \subseteq \Gamma \setminus \{0\}$
, any pattern
![]() $w \in \hat A^F$
which is
$w \in \hat A^F$
which is
![]() $\mathcal {F}$
-free (in the sense that sub-patterns from
$\mathcal {F}$
-free (in the sense that sub-patterns from
![]() $\mathcal {F}$
do not occur in it) can be extended to a
$\mathcal {F}$
do not occur in it) can be extended to a
![]() $\mathcal {F}$
-free pattern
$\mathcal {F}$
-free pattern
![]() $\tilde w \in \hat A^{F \cup \{0\}}$
.
$\tilde w \in \hat A^{F \cup \{0\}}$
.
Let
![]() $F \subseteq \Gamma \setminus \{0\}$
and we have an
$F \subseteq \Gamma \setminus \{0\}$
and we have an
![]() $\mathcal {F}$
-free pattern
$\mathcal {F}$
-free pattern
![]() $w \in A^F$
. Since
$w \in A^F$
. Since
![]() $|W \setminus \{0\}| < |\hat A|$
, there exists
$|W \setminus \{0\}| < |\hat A|$
, there exists
![]() $\hat a \in \hat A$
such that
$\hat a \in \hat A$
such that
![]() $w_{v} \ne \hat a$
for any
$w_{v} \ne \hat a$
for any
![]() $v \in (W \cap F) \setminus \{0\}$
. Let
$v \in (W \cap F) \setminus \{0\}$
. Let
![]() $\tilde w \in \hat A^{F \cup \{0\}}$
be defined by
$\tilde w \in \hat A^{F \cup \{0\}}$
be defined by
 $$ \begin{align*} \tilde w_v = \begin{cases} \hat a & \text{if } v= 0,\\ w_v & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \tilde w_v = \begin{cases} \hat a & \text{if } v= 0,\\ w_v & \text{otherwise.} \end{cases} \end{align*} $$
Then,
![]() $\tilde W$
is also
$\tilde W$
is also
![]() $\mathcal {F}$
-free
$\mathcal {F}$
-free
![]() $\tilde w_F =w$
.
$\tilde w_F =w$
.
Proposition 4.24. Let
![]() $\Gamma $
be an infinite countable abelian group and let Y be a
$\Gamma $
be an infinite countable abelian group and let Y be a
![]() $\Gamma $
-subshift with the map extension property. Then, Y is a strongly irreducible shift of finite type.
$\Gamma $
-subshift with the map extension property. Then, Y is a strongly irreducible shift of finite type.
Proof. Suppose that Y has the map extension property. Then, by Proposition 4.19, there exists a finite set
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
such that Y is an absolute retract for the class of
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
such that Y is an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts.
$\mathcal {G}$
-free subshifts.
Then by Lemma 4.23, Y embeds in a
![]() $\mathcal {G}$
-free strongly irreducible SFT
$\mathcal {G}$
-free strongly irreducible SFT
![]() $\hat Y$
. By Proposition 4.10, it follows that Y is also a strongly irreducible subshift of finite type.
$\hat Y$
. By Proposition 4.10, it follows that Y is also a strongly irreducible subshift of finite type.
We remark that alternative proofs of Proposition 4.24 (as well as stronger statements) can be found in [Reference Poirier and Salo23].
Lemma 4.25. Let Y be a
![]() $\Gamma $
-subshift with the map extension property. Then,
$\Gamma $
-subshift with the map extension property. Then,
![]() $\overline {Y}_{[\Gamma _0]}$
has the map extension property for any subgroup
$\overline {Y}_{[\Gamma _0]}$
has the map extension property for any subgroup
![]() $\Gamma _0 \le \Gamma $
.
$\Gamma _0 \le \Gamma $
.
Proof. Let
![]() $\Gamma $
be a countable abelian group. Suppose that Y is a
$\Gamma $
be a countable abelian group. Suppose that Y is a
![]() $\Gamma $
-subshift with the map extension property and
$\Gamma $
-subshift with the map extension property and
![]() $\Gamma _0 < \Gamma $
. We want to prove that
$\Gamma _0 < \Gamma $
. We want to prove that
![]() $\overline {Y}_{[\Gamma _0]}$
also has the map extension property. Suppose that
$\overline {Y}_{[\Gamma _0]}$
also has the map extension property. Suppose that
![]() $\tilde X \subseteq X$
are
$\tilde X \subseteq X$
are
![]() $\Gamma /\Gamma _0$
subshifts with
$\Gamma /\Gamma _0$
subshifts with
![]() $X \rightsquigarrow \overline {Y}_{[\Gamma _0]}$
and that
$X \rightsquigarrow \overline {Y}_{[\Gamma _0]}$
and that
![]() $\tilde \pi :\tilde X \to \overline {Y}_{[\Gamma _0]}$
is a map of
$\tilde \pi :\tilde X \to \overline {Y}_{[\Gamma _0]}$
is a map of
![]() $\Gamma /\Gamma _0$
-subshifts. For any set finite set A, there is a natural continuous injective map
$\Gamma /\Gamma _0$
-subshifts. For any set finite set A, there is a natural continuous injective map
![]() $\psi _{\Gamma _0}: A^{\Gamma /\Gamma _0} \to A^{\Gamma _0}$
given by
$\psi _{\Gamma _0}: A^{\Gamma /\Gamma _0} \to A^{\Gamma _0}$
given by
![]() $\psi _{\Gamma _0}(x)_v = x_{v +\Gamma _0}$
for any
$\psi _{\Gamma _0}(x)_v = x_{v +\Gamma _0}$
for any
![]() $x \in A^{\Gamma /\Gamma _0}$
,
$x \in A^{\Gamma /\Gamma _0}$
,
![]() $v \in \Gamma $
, and
$v \in \Gamma $
, and
![]() $x \in A^{\Gamma /\Gamma _0}$
. Then,
$x \in A^{\Gamma /\Gamma _0}$
. Then,
![]() $\psi _{\Gamma _0}^{-1}(\tilde X) \subseteq \psi _{\Gamma _0}^{-1}(X)$
are
$\psi _{\Gamma _0}^{-1}(\tilde X) \subseteq \psi _{\Gamma _0}^{-1}(X)$
are
![]() $\Gamma $
-subshifts with
$\Gamma $
-subshifts with
![]() $\Gamma _0 < \ker (\psi _{\Gamma _0}^{-1}(X))$
and
$\Gamma _0 < \ker (\psi _{\Gamma _0}^{-1}(X))$
and
![]() $\psi _{\Gamma _0}^{-1}(X) \rightsquigarrow Y$
because
$\psi _{\Gamma _0}^{-1}(X) \rightsquigarrow Y$
because
![]() $X \rightsquigarrow \overline {Y}_{[\Gamma _0]}$
. The map
$X \rightsquigarrow \overline {Y}_{[\Gamma _0]}$
. The map
![]() $\tilde \pi $
naturally lifts to a map
$\tilde \pi $
naturally lifts to a map
![]() $\overline {\pi }:\psi _{\Gamma _0}(\tilde X) \to Y$
. By the map extension property, the map
$\overline {\pi }:\psi _{\Gamma _0}(\tilde X) \to Y$
. By the map extension property, the map
![]() $\overline {\pi }$
extends to a map
$\overline {\pi }$
extends to a map
![]() $\hat \pi :\psi _{\Gamma _0}(X) \to Y$
. Since
$\hat \pi :\psi _{\Gamma _0}(X) \to Y$
. Since
![]() $\Gamma _0 < \ker (\psi _{\Gamma _0}^{-1}(X))$
, it follows that the image of
$\Gamma _0 < \ker (\psi _{\Gamma _0}^{-1}(X))$
, it follows that the image of
![]() $\psi _{\Gamma _0}(X))$
under
$\psi _{\Gamma _0}(X))$
under
![]() $\hat \pi $
is contained in
$\hat \pi $
is contained in
![]() $Y_{[\Gamma _0]}$
. Hence,
$Y_{[\Gamma _0]}$
. Hence,
![]() $\hat \pi $
induces a well-defined map
$\hat \pi $
induces a well-defined map
![]() $\pi :X \to \overline {Y}_{[\Gamma _0]}$
that extends
$\pi :X \to \overline {Y}_{[\Gamma _0]}$
that extends
![]() $\tilde \pi $
.
$\tilde \pi $
.
In preparation for the next result, we recall Boyle’s extension lemma [Reference Boyle6, Lemma 2.2].
Lemma 4.26. (Boyle’s extension lemma [Reference Boyle6])
Let X be a
![]() $\mathbb {Z}$
-subshift, let
$\mathbb {Z}$
-subshift, let
![]() $\tilde X \subseteq X$
be a closed shift-invariant set, and let
$\tilde X \subseteq X$
be a closed shift-invariant set, and let
![]() $Y \subseteq B^{\mathbb {Z}}$
be a mixing subshift of finite type such that
$Y \subseteq B^{\mathbb {Z}}$
be a mixing subshift of finite type such that
![]() $X \rightsquigarrow Y$
. Let
$X \rightsquigarrow Y$
. Let
![]() $\tilde \pi :\tilde X \to Y$
be a map. Then,
$\tilde \pi :\tilde X \to Y$
be a map. Then,
![]() $\tilde \pi $
extends to a map
$\tilde \pi $
extends to a map
![]() $\pi :X \to Y$
.
$\pi :X \to Y$
.
Boyle’s extension lemma implies an alternative characterization of topologically mixing
![]() $\mathbb {Z}$
-subshifts of finite type.
$\mathbb {Z}$
-subshifts of finite type.
Proposition 4.27. A
![]() $\mathbb {Z}$
-subshift has the map extension property if and only if it is a topologically mixing subshift of finite type.
$\mathbb {Z}$
-subshift has the map extension property if and only if it is a topologically mixing subshift of finite type.
Proof. From Proposition 4.24, it follows that any
![]() $\Gamma $
-subshift which has the map extension property is a strongly irreducible SFT. In particular, any
$\Gamma $
-subshift which has the map extension property is a strongly irreducible SFT. In particular, any
![]() $\mathbb {Z}$
-subshift which is a restricted absolute retract is a mixing shift of finite type. Now suppose
$\mathbb {Z}$
-subshift which is a restricted absolute retract is a mixing shift of finite type. Now suppose
![]() $Y \subset A^{\mathbb {Z}}$
is a mixing SFT. Let
$Y \subset A^{\mathbb {Z}}$
is a mixing SFT. Let
![]() $\mathcal {G} \subset \mathrm {Sub}(\mathbb {Z})$
denote the collection of subgroups
$\mathcal {G} \subset \mathrm {Sub}(\mathbb {Z})$
denote the collection of subgroups
![]() $\Gamma _0 \le \mathbb {Z}$
such that for every
$\Gamma _0 \le \mathbb {Z}$
such that for every
![]() $y \in Y$
, the subgroup
$y \in Y$
, the subgroup
![]() $\Gamma _0$
is not contained in
$\Gamma _0$
is not contained in
![]() $\mathrm {stab}(x)$
. We claim that
$\mathrm {stab}(x)$
. We claim that
![]() $\mathcal {G}$
is a finite set. Indeed, since Y is a mixing
$\mathcal {G}$
is a finite set. Indeed, since Y is a mixing
![]() $\mathbb {Z}$
-SFT, there exists
$\mathbb {Z}$
-SFT, there exists
![]() $n_0 \in \mathbb {N}$
such that for every
$n_0 \in \mathbb {N}$
such that for every
![]() $n \ge n_0$
, there exists
$n \ge n_0$
, there exists
![]() $y \in Y$
with
$y \in Y$
with
![]() $\sigma ^n(y)=y$
. Thus, every subgroup
$\sigma ^n(y)=y$
. Thus, every subgroup
![]() $\Gamma _0 \in \mathcal {G}$
must be of the form
$\Gamma _0 \in \mathcal {G}$
must be of the form
![]() $n \mathbb {Z}$
with
$n \mathbb {Z}$
with
![]() $n < n_0$
. It follows from Boyle’s extension lemma (Lemma 4.26) that Y has the map extension property.
$n < n_0$
. It follows from Boyle’s extension lemma (Lemma 4.26) that Y has the map extension property.
Although the map extension property is a rather strong property for
![]() $\mathbb {Z}^d$
-subshifts, it is satisfied by many ‘naturally occurring’ subshifts of finite type.
$\mathbb {Z}^d$
-subshifts, it is satisfied by many ‘naturally occurring’ subshifts of finite type.
Definition 4.28. Let
![]() $X \subseteq A^\Gamma $
be a subshift. We say that
$X \subseteq A^\Gamma $
be a subshift. We say that
![]() $a \in A$
is a safe symbol or X if for any
$a \in A$
is a safe symbol or X if for any
![]() $F \Subset \Gamma $
, any
$F \Subset \Gamma $
, any
![]() $w \in \mathcal {L}_F(X)$
, and any
$w \in \mathcal {L}_F(X)$
, and any
![]() $\tilde w \in A^F$
, any pattern
$\tilde w \in A^F$
, any pattern
![]() $\tilde w \in A^F$
that satisfies
$\tilde w \in A^F$
that satisfies
![]() $\tilde w_v \in \{ a, w_v\}$
for all
$\tilde w_v \in \{ a, w_v\}$
for all
![]() $v \in F$
is in
$v \in F$
is in
![]() $\mathcal {L}_F(X)$
. Equivalently,
$\mathcal {L}_F(X)$
. Equivalently,
![]() $a \in A$
is a safe symbol for X if for any
$a \in A$
is a safe symbol for X if for any
![]() $x \in X$
, changing the value of x at any
$x \in X$
, changing the value of x at any
![]() $v \in \Gamma $
to the ‘symbol’ a results in a point of X.
$v \in \Gamma $
to the ‘symbol’ a results in a point of X.
Proposition 4.29. Any
![]() $\Gamma $
-SFT with a safe symbol is an absolute retract for the class of subshifts and, in particular, has the map extension property.
$\Gamma $
-SFT with a safe symbol is an absolute retract for the class of subshifts and, in particular, has the map extension property.
Proof. Let
![]() $X \subseteq A^\Gamma $
be a
$X \subseteq A^\Gamma $
be a
![]() $\Gamma $
-SFT with a safe symbol
$\Gamma $
-SFT with a safe symbol
![]() $a \in A$
and suppose that
$a \in A$
and suppose that
![]() $Y \subseteq \tilde A^\Gamma $
is another subshift such that
$Y \subseteq \tilde A^\Gamma $
is another subshift such that
![]() $X \subseteq Y$
. Let
$X \subseteq Y$
. Let
![]() $\mathcal {F} \subset A^W$
be a defining set of forbidden patterns for X. We can define a retraction
$\mathcal {F} \subset A^W$
be a defining set of forbidden patterns for X. We can define a retraction
![]() $r:Y \to X$
as follows:
$r:Y \to X$
as follows:
 $$ \begin{align*}r(y)_v = \begin{cases} y_v & \text{if }(\sigma_{-v-w}(y))_W \not \in \mathcal{F} \text{ for all } w \in W,\\ a & \text{otherwise}. \end{cases}\\[-37pt]\end{align*} $$
$$ \begin{align*}r(y)_v = \begin{cases} y_v & \text{if }(\sigma_{-v-w}(y))_W \not \in \mathcal{F} \text{ for all } w \in W,\\ a & \text{otherwise}. \end{cases}\\[-37pt]\end{align*} $$
The following proposition shows that the subshift of proper k-colorings of the Cayley graph of
![]() $\Gamma $
corresponding to a symmetric generating set with less than k generators has the map extension property. Another proof of the same result appears in [Reference Poirier and Salo23].
$\Gamma $
corresponding to a symmetric generating set with less than k generators has the map extension property. Another proof of the same result appears in [Reference Poirier and Salo23].
Proposition 4.30. For any finite symmetric set
![]() $F \Subset \Gamma \setminus \{0\}$
and any
$F \Subset \Gamma \setminus \{0\}$
and any
![]() $k \in \mathbb {N}$
, consider the subshift
$k \in \mathbb {N}$
, consider the subshift
![]() $X_{k,F}$
given by
$X_{k,F}$
given by
If
![]() $k> |F|$
, then
$k> |F|$
, then
![]() $X_{k,F}$
has the map extension property.
$X_{k,F}$
has the map extension property.
Proof. Let
![]() $F \Subset \Gamma \setminus \{0\}$
be a finite symmetric set and
$F \Subset \Gamma \setminus \{0\}$
be a finite symmetric set and
![]() $k>|F|$
. Let
$k>|F|$
. Let
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
denote the set of cyclic subgroups generated by elements of F:
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
denote the set of cyclic subgroups generated by elements of F:
We will prove that
![]() $X_{k,F}$
is an absolute retract for the class of
$X_{k,F}$
is an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts. Since
$\mathcal {G}$
-free subshifts. Since
![]() $x_{0} \ne x_{v}$
for any
$x_{0} \ne x_{v}$
for any
![]() $x \in X_{k,F}$
and
$x \in X_{k,F}$
and
![]() $v \in F$
, it is clear that
$v \in F$
, it is clear that
![]() $v \not \in \mathrm {stab}(x)$
for any
$v \not \in \mathrm {stab}(x)$
for any
![]() $x \in X_{k,F}$
, so
$x \in X_{k,F}$
, so
![]() $X_{k,F}$
is
$X_{k,F}$
is
![]() $\mathcal {G}$
-free. Let X be any
$\mathcal {G}$
-free. Let X be any
![]() $\mathcal {G}$
-free subshift such that
$\mathcal {G}$
-free subshift such that
![]() $X_{k,F} \subseteq X$
. By Lemma 3.3, there exists a clopen set
$X_{k,F} \subseteq X$
. By Lemma 3.3, there exists a clopen set
![]() $C \subset X$
such that
$C \subset X$
such that
![]() $C \cap \sigma _v(C) = \emptyset $
for every
$C \cap \sigma _v(C) = \emptyset $
for every
![]() $v \in F$
and
$v \in F$
and
![]() $X= C \bigcup _{v \in V} \sigma _v(C)$
. Define a map
$X= C \bigcup _{v \in V} \sigma _v(C)$
. Define a map
![]() $\alpha :X \to \{0,1\}^\Gamma $
by declaring for
$\alpha :X \to \{0,1\}^\Gamma $
by declaring for
![]() $x \in X$
and
$x \in X$
and
![]() $v \in \Gamma $
,
$v \in \Gamma $
,
 $$ \begin{align*}\alpha(x)_v= \begin{cases} 1 & \text{if }\sigma_v(x) \in C,\\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*}\alpha(x)_v= \begin{cases} 1 & \text{if }\sigma_v(x) \in C,\\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
For
![]() $x \in X$
, let
$x \in X$
, let
Let
![]() $F= \{ v_0,v_1,\ldots ,v_{|F|}\}$
be some enumeration of the elements of
$F= \{ v_0,v_1,\ldots ,v_{|F|}\}$
be some enumeration of the elements of
![]() $F \cup \{0\}$
. For every
$F \cup \{0\}$
. For every
![]() $x \in X$
, let
$x \in X$
, let
For every
![]() $0 \le j \le |F|$
, define a map
$0 \le j \le |F|$
, define a map
![]() $r^{(j)}:X \to X$
as follows by declaring for
$r^{(j)}:X \to X$
as follows by declaring for
![]() $x \in X$
and
$x \in X$
and
![]() $v \in \Gamma $
:
$v \in \Gamma $
:
 $$ \begin{align*} r^{(j)}(x)_v = \begin{cases} x_v & \text{if } t(X) \ne j \text{ or } x_v \in \{1,\ldots,k\} \setminus B(\sigma_{v}(x)),\\ \min( \{1,\ldots,k\} \setminus B(\sigma_{v}(x)) ) & \text{otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*} r^{(j)}(x)_v = \begin{cases} x_v & \text{if } t(X) \ne j \text{ or } x_v \in \{1,\ldots,k\} \setminus B(\sigma_{v}(x)),\\ \min( \{1,\ldots,k\} \setminus B(\sigma_{v}(x)) ) & \text{otherwise. } \end{cases} \end{align*} $$
Note that for every
![]() $v \in F \cap \{0\}$
, we have that since
$v \in F \cap \{0\}$
, we have that since
![]() $|B(\sigma _{v}(x)| \le |F| < k$
, it follows that
$|B(\sigma _{v}(x)| \le |F| < k$
, it follows that
![]() $ \{1,\ldots ,k\} \setminus B(\sigma _{v}(x)) \ne \emptyset $
, so
$ \{1,\ldots ,k\} \setminus B(\sigma _{v}(x)) \ne \emptyset $
, so
![]() $r^{(j)}$
is well defined.
$r^{(j)}$
is well defined.
Define
![]() $\tilde r^{(0)} = r^{(0)}$
and
$\tilde r^{(0)} = r^{(0)}$
and
![]() $\tilde r^{(j)}= r^{(j)} \circ \tilde r^{(j-1)}$
for every
$\tilde r^{(j)}= r^{(j)} \circ \tilde r^{(j-1)}$
for every
![]() $ 1\le j \le |F|$
. Let
$ 1\le j \le |F|$
. Let
![]() $r =\tilde r^{(|F|)}:X \to X$
. We claim that
$r =\tilde r^{(|F|)}:X \to X$
. We claim that
![]() $r:X \to X_{k,F}$
is a retraction. By induction, it follows that if
$r:X \to X_{k,F}$
is a retraction. By induction, it follows that if
![]() $x \in C \cup \bigcup _{\ell =1}^j \sigma _{v_\ell }^{-1}(C)$
, then
$x \in C \cup \bigcup _{\ell =1}^j \sigma _{v_\ell }^{-1}(C)$
, then
![]() $x_0 \in \{1\ldots ,k\} \setminus B(x)$
. In particular, since
$x_0 \in \{1\ldots ,k\} \setminus B(x)$
. In particular, since
![]() $X= \bigcup _{\ell =1}^{|F|} \sigma _{v_\ell }^{-1}(C)$
, it follows that
$X= \bigcup _{\ell =1}^{|F|} \sigma _{v_\ell }^{-1}(C)$
, it follows that
![]() $r(x)_0 \in \{1\ldots ,k\} \setminus B(x)$
for every
$r(x)_0 \in \{1\ldots ,k\} \setminus B(x)$
for every
![]() $x \in X$
. So for every
$x \in X$
. So for every
![]() $x \in X$
,
$x \in X$
,
![]() $r(x) \in \{1,\ldots ,l\}^\Gamma $
and
$r(x) \in \{1,\ldots ,l\}^\Gamma $
and
![]() $r(x)_v \ne r(x)_{v+W}$
for every
$r(x)_v \ne r(x)_{v+W}$
for every
![]() $v \in \Gamma $
and
$v \in \Gamma $
and
![]() $w \in F$
. This proves that
$w \in F$
. This proves that
![]() $r(x) \in X_{k,F}$
for every
$r(x) \in X_{k,F}$
for every
![]() $x \in X$
. It is easy to check that
$x \in X$
. It is easy to check that
![]() $r^{(j)}(x) = x$
for every
$r^{(j)}(x) = x$
for every
![]() $ 0 \le j \le |F|$
and
$ 0 \le j \le |F|$
and
![]() $x \in X_{k,F}$
, so
$x \in X_{k,F}$
, so
![]() $r(x)=x$
for every
$r(x)=x$
for every
![]() $x \in X_{k,F}$
. This proves that
$x \in X_{k,F}$
. This proves that
![]() $r:X \to X_{k,F}$
is indeed a retraction.
$r:X \to X_{k,F}$
is indeed a retraction.
As a particular case, when
![]() $\Gamma =Z^2$
and
$\Gamma =Z^2$
and
![]() $F = \{(\pm 1,0),(0,\pm 1)\}$
is the standard generating set, the subshift
$F = \{(\pm 1,0),(0,\pm 1)\}$
is the standard generating set, the subshift
![]() $X_{k,F}$
appearing in the statement of Proposition 4.30 is the subshift of k-colorings of the standard Cayley graph of
$X_{k,F}$
appearing in the statement of Proposition 4.30 is the subshift of k-colorings of the standard Cayley graph of
![]() $\mathbb {Z}^d$
. It is known that for any
$\mathbb {Z}^d$
. It is known that for any
![]() $d>1$
, the subshift
$d>1$
, the subshift
![]() $X_{F_3}$
of proper
$X_{F_3}$
of proper
![]() $3$
-colorings of the standard Cayley graph does not contain any strongly irreducible subshift [Reference Chandgotia and Meyerovitch10, Proposition 12.2], so certainly an analog of Theorem 1.4 does not hold with
$3$
-colorings of the standard Cayley graph does not contain any strongly irreducible subshift [Reference Chandgotia and Meyerovitch10, Proposition 12.2], so certainly an analog of Theorem 1.4 does not hold with
![]() $Y=X_{3,F}$
. The subshift of k-colorings of the
$Y=X_{3,F}$
. The subshift of k-colorings of the
![]() $\mathbb {Z}^2$
-lattice was shown to be strongly irreducible if and only if
$\mathbb {Z}^2$
-lattice was shown to be strongly irreducible if and only if
![]() $k \ge 4$
[Reference Alon, Briceño, Chandgotia, Magazinov and Spinka1].
$k \ge 4$
[Reference Alon, Briceño, Chandgotia, Magazinov and Spinka1].
5 Entropy minimal subshifts and necessity of the conditions for embedding
In this section, we recall the notion of entropy minimality for subshifts, and prove that for an entropy minimal
![]() $\Gamma $
-subshift Y, the conditions in the statement of Theorem 1.4 are necessary for the existence of an embedding
$\Gamma $
-subshift Y, the conditions in the statement of Theorem 1.4 are necessary for the existence of an embedding
![]() $\rho :X \to Y$
that extends
$\rho :X \to Y$
that extends
![]() $\hat \rho $
.
$\hat \rho $
.
A
![]() $\Gamma $
-subshift Y is called entropy minimal if the only
$\Gamma $
-subshift Y is called entropy minimal if the only
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $X \subseteq Y$
that satisfies
$X \subseteq Y$
that satisfies
![]() $h(X)=h(Y)$
is
$h(X)=h(Y)$
is
![]() $X=Y$
. Equivalently, any proper subshift of Y has strictly lower topological entropy.
$X=Y$
. Equivalently, any proper subshift of Y has strictly lower topological entropy.
The following easy result is a consequence of the fact that isomorphic subshifts have equal topological entropy and that a topological entropy of a subsystem of Y never exceeds the topological entropy of Y. Recall the definition of condition
![]() $E(X,Y,\hat \rho ,\Gamma _0)$
as defined in Definition 2.24.
$E(X,Y,\hat \rho ,\Gamma _0)$
as defined in Definition 2.24.
Proposition 5.1. Let
![]() $\Gamma $
be a countable abelian group and let
$\Gamma $
be a countable abelian group and let
![]() $X,Y$
be
$X,Y$
be
![]() $\Gamma $
-subshifts, let
$\Gamma $
-subshifts, let
![]() $Z \subseteq X$
be a closed
$Z \subseteq X$
be a closed
![]() $\Gamma $
-invariant set, and let
$\Gamma $
-invariant set, and let
![]() $\hat \rho :Z \to Y$
be an embedding. If
$\hat \rho :Z \to Y$
be an embedding. If
![]() $X \hookrightarrow _{\hat \rho } Y$
, then for any subgroup
$X \hookrightarrow _{\hat \rho } Y$
, then for any subgroup
![]() $\Gamma _0 \le \Gamma $
, we have that
$\Gamma _0 \le \Gamma $
, we have that
![]() $h(\overline {X}_{\Gamma _0})\le h(\overline {Y}_{\Gamma _0})$
. Furthermore, if for some subgroup
$h(\overline {X}_{\Gamma _0})\le h(\overline {Y}_{\Gamma _0})$
. Furthermore, if for some subgroup
![]() $\Gamma _0 \le \Gamma $
the subshift
$\Gamma _0 \le \Gamma $
the subshift
![]() $\overline {Y}_\Gamma $
is entropy minimal, then the condition
$\overline {Y}_\Gamma $
is entropy minimal, then the condition
![]() $E(X,Y,\hat \rho ,\Gamma _0)$
holds.
$E(X,Y,\hat \rho ,\Gamma _0)$
holds.
It is well known that any strongly irreducible
![]() $\Gamma $
-subshift is entropy minimal, see for instance [Reference Boyle, Pavlov and Schraudner7, Reference Quas and Trow24]. In particular, if Y is a
$\Gamma $
-subshift is entropy minimal, see for instance [Reference Boyle, Pavlov and Schraudner7, Reference Quas and Trow24]. In particular, if Y is a
![]() $\Gamma $
-subshift with the map extension property, then by Lemma 4.25 and Proposition 4.24, we have that
$\Gamma $
-subshift with the map extension property, then by Lemma 4.25 and Proposition 4.24, we have that
![]() $\overline {Y}_{\Gamma _0}$
is strongly irreducible for any
$\overline {Y}_{\Gamma _0}$
is strongly irreducible for any
![]() $\Gamma _0 \le \Gamma $
.
$\Gamma _0 \le \Gamma $
.
It follows that the conditions in the statement of Theorem 1.4 for extending an embedding of a subsystem to an embedding are necessary when the target Y has the following map extension property.
Corollary 5.2. Let
![]() $\Gamma $
be a countable abelian group, let
$\Gamma $
be a countable abelian group, let
![]() $X,Y$
be
$X,Y$
be
![]() $\Gamma $
-subshifts, where Y has the map extension property, let
$\Gamma $
-subshifts, where Y has the map extension property, let
![]() $Z \subseteq X$
be a closed
$Z \subseteq X$
be a closed
![]() $\Gamma $
-invariant set, and let
$\Gamma $
-invariant set, and let
![]() $\hat \rho :Z \to Y$
be an embedding. If
$\hat \rho :Z \to Y$
be an embedding. If
![]() $X \hookrightarrow _{\hat \rho } Y$
, then for any subgroup
$X \hookrightarrow _{\hat \rho } Y$
, then for any subgroup
![]() $\Gamma _0 \le \Gamma $
, the condition
$\Gamma _0 \le \Gamma $
, the condition
![]() $E(X,Y,\hat \rho ,\Gamma _0)$
holds.
$E(X,Y,\hat \rho ,\Gamma _0)$
holds.
6 Truncated Voronoi diagrams and partial tilings
Throughout this section,
![]() $\Gamma $
will be a finitely generated abelian group of the form
$\Gamma $
will be a finitely generated abelian group of the form
![]() $\Gamma = \mathbb {Z}^d \times G$
, where G is a finite abelian group.
$\Gamma = \mathbb {Z}^d \times G$
, where G is a finite abelian group.
Definition 6.1. A partial tiling of
![]() $\Gamma $
is a collection of pairwise disjoint finite subsets of
$\Gamma $
is a collection of pairwise disjoint finite subsets of
![]() $\Gamma $
. We denote the set of partial tilings of
$\Gamma $
. We denote the set of partial tilings of
![]() $\Gamma $
by
$\Gamma $
by
![]() $\mathit {PTilings}(\Gamma )$
. A tiling of
$\mathit {PTilings}(\Gamma )$
. A tiling of
![]() $\Gamma $
is a partition of
$\Gamma $
is a partition of
![]() $\Gamma $
into pairwise disjoint finite subsets. For a partial tiling
$\Gamma $
into pairwise disjoint finite subsets. For a partial tiling
![]() $\tau \in \mathit {PTilings}(\Gamma )$
, we refer to the elements of
$\tau \in \mathit {PTilings}(\Gamma )$
, we refer to the elements of
![]() $\tau $
as tiles.
$\tau $
as tiles.
The space
![]() $\mathit {PTilings}(\Gamma )$
admits a natural Polish topology, which we now describe. We describe a basis for this topology. For
$\mathit {PTilings}(\Gamma )$
admits a natural Polish topology, which we now describe. We describe a basis for this topology. For
![]() $F \Subset \Gamma $
and
$F \Subset \Gamma $
and
![]() $\tau \in \mathit {PTilings}(\Gamma )$
, let
$\tau \in \mathit {PTilings}(\Gamma )$
, let
![]() $N(F,\tau ) \subseteq \mathit {PTilings}(\Gamma )$
denote the collection of partial tilings
$N(F,\tau ) \subseteq \mathit {PTilings}(\Gamma )$
denote the collection of partial tilings
![]() $\tilde \tau \in \mathit {PTilings}(\Gamma )$
that satisfy the property that for
$\tilde \tau \in \mathit {PTilings}(\Gamma )$
that satisfy the property that for
![]() $T \subseteq F$
, we have that
$T \subseteq F$
, we have that
![]() $T \in \tilde \tau $
if and only if
$T \in \tilde \tau $
if and only if
![]() $T \in \tau $
. A closed subset
$T \in \tau $
. A closed subset
![]() $P \subseteq \mathit {PTilings}(\Gamma )$
is compact if and only if every
$P \subseteq \mathit {PTilings}(\Gamma )$
is compact if and only if every
![]() $\gamma \in \Gamma $
is covered by one of finitely many tiles (among all possibilities of tilings in
$\gamma \in \Gamma $
is covered by one of finitely many tiles (among all possibilities of tilings in
![]() $\Gamma $
). The group
$\Gamma $
). The group
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() $\mathit {PTilings}(\Gamma )$
by translations. Although we will not use this fact, we mention that any compact
$\mathit {PTilings}(\Gamma )$
by translations. Although we will not use this fact, we mention that any compact
![]() $\Gamma $
-invariant subsystem of
$\Gamma $
-invariant subsystem of
![]() $\mathit {PTilings}(\Gamma )$
is isomorphic to a
$\mathit {PTilings}(\Gamma )$
is isomorphic to a
![]() $\Gamma $
-subshift.
$\Gamma $
-subshift.
Definition 6.2. Let
![]() $\tau \in \mathit {PTilings}(\Gamma )$
be a partial tiling. Denote
$\tau \in \mathit {PTilings}(\Gamma )$
be a partial tiling. Denote
![]() $\bigcup \tau \subseteq \Gamma $
as the union of tiles in
$\bigcup \tau \subseteq \Gamma $
as the union of tiles in
![]() $\tau $
. We say that
$\tau $
. We say that
![]() $\tau \in \mathit {PTilings}(\Gamma )$
is
$\tau \in \mathit {PTilings}(\Gamma )$
is
![]() $(K,\epsilon )$
-invariant for
$(K,\epsilon )$
-invariant for
![]() $K \Subset \Gamma $
and
$K \Subset \Gamma $
and
![]() $\epsilon>0$
if each
$\epsilon>0$
if each
![]() $T \in \tau $
is
$T \in \tau $
is
![]() $(K,\epsilon )$
-invariant. Given a partial tiling
$(K,\epsilon )$
-invariant. Given a partial tiling
![]() $\tau \in \mathit {PTilings}(\Gamma )$
,
$\tau \in \mathit {PTilings}(\Gamma )$
,
![]() $T \in \tau $
, and
$T \in \tau $
, and
![]() $K \Subset \Gamma $
, we let
$K \Subset \Gamma $
, we let
 $$ \begin{align*}\partial_K^\tau T = \bigg\{ v \in \Gamma: (v+K) \cap T \ne \emptyset \text{ and } (v+K) \not \subseteq \bigcup \tau\bigg\}.\end{align*} $$
$$ \begin{align*}\partial_K^\tau T = \bigg\{ v \in \Gamma: (v+K) \cap T \ne \emptyset \text{ and } (v+K) \not \subseteq \bigcup \tau\bigg\}.\end{align*} $$
We refer to the set
![]() $\partial _K^\tau T$
as the exterior K-boundary of T with respect to
$\partial _K^\tau T$
as the exterior K-boundary of T with respect to
![]() $\tau $
. We say that a partial tiling
$\tau $
. We say that a partial tiling
![]() $\tau $
has
$\tau $
has
![]() $(K,\epsilon )$
-small exterior boundary if every
$(K,\epsilon )$
-small exterior boundary if every
![]() $T \in \tau $
satisfies
$T \in \tau $
satisfies
Definition 6.3. We identify the space
![]() $\{0,1\}^\Gamma $
with the space of subsets of
$\{0,1\}^\Gamma $
with the space of subsets of
![]() $\Gamma $
via the obvious bijection
$\Gamma $
via the obvious bijection
Given
![]() $F\Subset \Gamma $
, we say that a
$F\Subset \Gamma $
, we say that a
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $Z \subseteq \{0,1\}^\Gamma $
is F-separated if every
$Z \subseteq \{0,1\}^\Gamma $
is F-separated if every
![]() $z \in Z$
is F-separated (when viewed as a subset of
$z \in Z$
is F-separated (when viewed as a subset of
![]() $\Gamma $
). Given a
$\Gamma $
). Given a
![]() $\Gamma $
-subshift Z,
$\Gamma $
-subshift Z,
![]() $K \Subset \Gamma $
, and
$K \Subset \Gamma $
, and
![]() $\epsilon>0$
, we say that a map
$\epsilon>0$
, we say that a map
![]() $\tau :Z \to \mathit {PTilings}(\Gamma )$
is a
$\tau :Z \to \mathit {PTilings}(\Gamma )$
is a
![]() $(K,\epsilon )$
-invariant tiling of Z if for every
$(K,\epsilon )$
-invariant tiling of Z if for every
![]() $z \in Z$
, the partial tiling
$z \in Z$
, the partial tiling
![]() $\tau (z) \in \mathit {PTilings}(\Gamma )$
is
$\tau (z) \in \mathit {PTilings}(\Gamma )$
is
![]() $(K,\epsilon )$
-invariant. If
$(K,\epsilon )$
-invariant. If
![]() $Z \subseteq \{0,1\}^\Gamma $
is a
$Z \subseteq \{0,1\}^\Gamma $
is a
![]() $\Gamma $
-subshift, we say that a map
$\Gamma $
-subshift, we say that a map
![]() $\tau :Z \to \mathit {PTilings}(\Gamma )$
is a pointed partial tiling if for every
$\tau :Z \to \mathit {PTilings}(\Gamma )$
is a pointed partial tiling if for every
![]() $z \in Z$
and for every tile
$z \in Z$
and for every tile
![]() $T \in \tau (z)$
, there exists a unique
$T \in \tau (z)$
, there exists a unique
![]() $v \in T$
such that
$v \in T$
such that
![]() $z_v =1$
. In that case, we say that v is the center of the tile z.
$z_v =1$
. In that case, we say that v is the center of the tile z.
Our main goal is to prove that any
![]() $\Gamma $
-subshift X admits a ‘well-behaved’ continuous, equivariant map into the space of
$\Gamma $
-subshift X admits a ‘well-behaved’ continuous, equivariant map into the space of
![]() $(K,\epsilon )$
-invariant partial tilings, for arbitrary
$(K,\epsilon )$
-invariant partial tilings, for arbitrary
![]() $K \Subset \Gamma $
and
$K \Subset \Gamma $
and
![]() $\epsilon>0$
.
$\epsilon>0$
.
Proposition 6.4. Let
![]() $\Gamma $
be a finitely generated abelian group and let X be a
$\Gamma $
be a finitely generated abelian group and let X be a
![]() $\Gamma $
-subshift. For every
$\Gamma $
-subshift. For every
![]() $K \Subset \Gamma $
and
$K \Subset \Gamma $
and
![]() $\epsilon>0$
, there exists a finite set
$\epsilon>0$
, there exists a finite set
![]() $P \Subset \Gamma \setminus \{0\}$
so that given:
$P \Subset \Gamma \setminus \{0\}$
so that given:
-
• a finite subset
 $W\Subset \Gamma $
;
$W\Subset \Gamma $
; -
•
 $\epsilon _1>0$
;
$\epsilon _1>0$
; -
• a set of patterns
 $\mathcal {F} \subseteq \mathcal {L}_{W}(X)$
so that
$\mathcal {F} \subseteq \mathcal {L}_{W}(X)$
so that
 $x_W \not \in \mathcal {F}$
for any
$x_W \not \in \mathcal {F}$
for any
 $x \in X$
such that
$x \in X$
such that
 $\mathrm {stab}(x) \cap P =~\emptyset $
,
$\mathrm {stab}(x) \cap P =~\emptyset $
,
there exists a map
![]() $\alpha :X \to \{0,1\}^\Gamma $
and a pointed
$\alpha :X \to \{0,1\}^\Gamma $
and a pointed
![]() $(K,\epsilon )$
-invariant tiling
$(K,\epsilon )$
-invariant tiling
![]() $\tau : \alpha (X) \to \mathit {PTilings}(\Gamma )$
such that for every
$\tau : \alpha (X) \to \mathit {PTilings}(\Gamma )$
such that for every
![]() $x \in X$
:
$x \in X$
:
-
(1) if
 $v \not \in \bigcup \tau (\alpha (x))$
, then
$v \not \in \bigcup \tau (\alpha (x))$
, then
 $\sigma _{v}(x)_{W} \in \mathcal {F}$
;
$\sigma _{v}(x)_{W} \in \mathcal {F}$
; -
(2) if
 $v \in \Gamma $
satisfies
$v \in \Gamma $
satisfies
 $\alpha (x)_v=1$
, then
$\alpha (x)_v=1$
, then
 $\sigma (x)_{W} \not \in \mathcal {F}$
and there exist
$\sigma (x)_{W} \not \in \mathcal {F}$
and there exist
 $T \in \tau (\alpha (x))$
such that
$T \in \tau (\alpha (x))$
such that
 $v +K \subseteq T$
;
$v +K \subseteq T$
; -
(3) the partial tiling
 $\tau (\alpha (x)) \in \mathit {PTilings}(\Gamma )$
has
$\tau (\alpha (x)) \in \mathit {PTilings}(\Gamma )$
has
 $(W, \epsilon _1)$
-small exterior boundary.
$(W, \epsilon _1)$
-small exterior boundary.
The statement of Proposition 6.4 above is slightly involved because, in our application, it will be essential that the set
![]() $P \Subset \Gamma \setminus \{0\}$
can be chosen depending only on
$P \Subset \Gamma \setminus \{0\}$
can be chosen depending only on
![]() $K \Subset \Gamma $
and
$K \Subset \Gamma $
and
![]() $\epsilon>0$
, and independently from
$\epsilon>0$
, and independently from
![]() $\epsilon _1>0$
,
$\epsilon _1>0$
,
![]() $W\Subset \Gamma $
, and
$W\Subset \Gamma $
, and
![]() $\mathcal {F} \subseteq \mathcal {L}_{W}(Y)$
. In our application, the parameters
$\mathcal {F} \subseteq \mathcal {L}_{W}(Y)$
. In our application, the parameters
![]() $\epsilon _1>0$
,
$\epsilon _1>0$
,
![]() $W\Subset \Gamma $
, and
$W\Subset \Gamma $
, and
![]() $\mathcal {F} \subseteq \mathcal {L}_{W}(Y)$
will actually depend on the set
$\mathcal {F} \subseteq \mathcal {L}_{W}(Y)$
will actually depend on the set
![]() $P \Subset \Gamma \setminus \{0\}$
and the previously chosen parameters.
$P \Subset \Gamma \setminus \{0\}$
and the previously chosen parameters.
In the case where X is an aperiodic subshift, we actually get a map into the space of
![]() $(K,\epsilon )$
-invariant partial tiling.
$(K,\epsilon )$
-invariant partial tiling.
Corollary 6.5. (Lightwood [Reference Lightwood19])
Let
![]() $\Gamma $
be a finitely generated abelian group and let X be an aperiodic
$\Gamma $
be a finitely generated abelian group and let X be an aperiodic
![]() $\Gamma $
-subshift. Then, for any
$\Gamma $
-subshift. Then, for any
![]() $K \Subset \Gamma $
and
$K \Subset \Gamma $
and
![]() $\epsilon $
, there exists a map from
$\epsilon $
, there exists a map from
![]() $\tau :X \to \mathit {PTilings}(\Gamma )$
such that for every
$\tau :X \to \mathit {PTilings}(\Gamma )$
such that for every
![]() $x \in X$
,
$x \in X$
,
![]() $\tau (x)$
is a
$\tau (x)$
is a
![]() $(K,\epsilon )$
-invariant tiling.
$(K,\epsilon )$
-invariant tiling.
For context, we explain why Corollary 6.5 is a direct consequence of Proposition 6.4.
Proof. Let X be an aperiodic
![]() $\Gamma $
-subshift, and let
$\Gamma $
-subshift, and let
![]() $K\Subset \Gamma $
and
$K\Subset \Gamma $
and
![]() $\epsilon>0$
be given. Apply Proposition 6.4 on X with the given K and
$\epsilon>0$
be given. Apply Proposition 6.4 on X with the given K and
![]() $\epsilon $
. We obtain a corresponding set
$\epsilon $
. We obtain a corresponding set
![]() $P \Subset \Gamma \setminus \{0\}$
(and a map
$P \Subset \Gamma \setminus \{0\}$
(and a map
![]() $\alpha :X \to \{0,1\}^\Gamma $
). Choose any
$\alpha :X \to \{0,1\}^\Gamma $
). Choose any
![]() $W,\tilde W \Subset \Gamma $
and any
$W,\tilde W \Subset \Gamma $
and any
![]() $\epsilon _1>0$
. Take
$\epsilon _1>0$
. Take
![]() $\mathcal {F}= \emptyset $
, then
$\mathcal {F}= \emptyset $
, then
![]() $\mathcal {F}\subseteq \mathcal {L}_W(X)$
and since
$\mathcal {F}\subseteq \mathcal {L}_W(X)$
and since
![]() $\mathrm {stab}(x) \cap P = \emptyset $
for any
$\mathrm {stab}(x) \cap P = \emptyset $
for any
![]() $x \in X$
, in particular,
$x \in X$
, in particular,
![]() $x_W \not \in \mathcal {F}$
for any
$x_W \not \in \mathcal {F}$
for any
![]() $x \in X$
, then there exists a map
$x \in X$
, then there exists a map
![]() $\tau :X \to \mathit {PTilings}(X)$
such that
$\tau :X \to \mathit {PTilings}(X)$
such that
![]() $\tau (x)$
is
$\tau (x)$
is
![]() $(K\epsilon )$
-invariant and such that each
$(K\epsilon )$
-invariant and such that each
![]() $\tau (x)$
is a tiling.
$\tau (x)$
is a tiling.
We remark that the assumption that
![]() $\Gamma $
is finitely generated can be removed without much difficulty both in Corollary 6.5 and in Proposition 6.4. We also remark that the conclusion of Corollary 6.5 holds for various non-abelian amenable groups. See [Reference Downarowicz and Zhang13] and also [Reference Bland4], although in the more general setting, the proof proceeds via different methods.
$\Gamma $
is finitely generated can be removed without much difficulty both in Corollary 6.5 and in Proposition 6.4. We also remark that the conclusion of Corollary 6.5 holds for various non-abelian amenable groups. See [Reference Downarowicz and Zhang13] and also [Reference Bland4], although in the more general setting, the proof proceeds via different methods.
However, in the presence of points with non-trivial stabilizer, one can easily see that it is impossible to get a map into the space of
![]() $(K,\epsilon )$
-invariant partial tilings for arbitrary
$(K,\epsilon )$
-invariant partial tilings for arbitrary
![]() $K \Subset \Gamma $
and
$K \Subset \Gamma $
and
![]() $\epsilon>0$
.
$\epsilon>0$
.
The proof below of Proposition 6.4 proceeds via the notion of Voronoi diagrams (that still makes sense in any metric space, in particular, for finitely generated groups). The arguments involve some elementary convex analysis in Euclidean spaces. Similar results, proven using similar methods, can be found in the literature [Reference Balister, Bollobás and Quas2, Reference Gutman, Lindenstrauss and Tsukamoto15, Reference Lightwood19]. We present self-contained proofs here for the sake of completeness and also due to certain less standard variations that we seem to require for our specific application.
Recall that
![]() $\Gamma $
is a finitely generated abelain group of the form
$\Gamma $
is a finitely generated abelain group of the form
![]() $\Gamma =\mathbb {Z}^d \times G$
, where G is a finite abelian group. Let
$\Gamma =\mathbb {Z}^d \times G$
, where G is a finite abelian group. Let
![]() $P_{\Gamma ,\mathbb {Z}^d}:\Gamma \to \mathbb {Z}^d$
and
$P_{\Gamma ,\mathbb {Z}^d}:\Gamma \to \mathbb {Z}^d$
and
![]() $P_{\Gamma , G}: \Gamma \to G$
denote the obvious projection maps given by
$P_{\Gamma , G}: \Gamma \to G$
denote the obvious projection maps given by
and
On the group
![]() $\Gamma = \mathbb {Z}^d \times G$
, we consider the metric
$\Gamma = \mathbb {Z}^d \times G$
, we consider the metric
![]() $\mathrm {dist}_\Gamma :\Gamma \times \Gamma \to [0,+\infty )$
given by
$\mathrm {dist}_\Gamma :\Gamma \times \Gamma \to [0,+\infty )$
given by
where
![]() $\mathrm {dist}_{\mathbb {R}^d}:\mathbb {R}^d \times \mathbb {R}^d \to [0,+\infty )$
is the Euclidean distance in
$\mathrm {dist}_{\mathbb {R}^d}:\mathbb {R}^d \times \mathbb {R}^d \to [0,+\infty )$
is the Euclidean distance in
![]() $\mathbb {R}^d$
and
$\mathbb {R}^d$
and
 $$ \begin{align*} \delta(\gamma_1,\gamma_2) = \begin{cases} 0 & \text{if }\gamma_1=\gamma_2,\\ 1 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \delta(\gamma_1,\gamma_2) = \begin{cases} 0 & \text{if }\gamma_1=\gamma_2,\\ 1 & \text{otherwise.} \end{cases} \end{align*} $$
Definition 6.6. Let
![]() $C \subseteq \Gamma $
be a subset of
$C \subseteq \Gamma $
be a subset of
![]() $\Gamma $
. The Voronoi cell of
$\Gamma $
. The Voronoi cell of
![]() $c \in C$
with respect to C, denoted by
$c \in C$
with respect to C, denoted by
![]() $V(c,C)$
, is defined by the set of points in
$V(c,C)$
, is defined by the set of points in
![]() $v \in \Gamma $
such that the
$v \in \Gamma $
such that the
![]() $\mathrm {dist}_\Gamma $
distance between c and v is smaller than the distance to any other point in C:
$\mathrm {dist}_\Gamma $
distance between c and v is smaller than the distance to any other point in C:
The Voroni diagram of C is the collection of Voronoi cells.
Given
![]() $R>0$
, the R-truncated Voronoi cell of
$R>0$
, the R-truncated Voronoi cell of
![]() $c \in C$
with respect to C, denoted by
$c \in C$
with respect to C, denoted by
![]() $V_R(c,C)$
, is the intersection of the Voronoi cell of c with the ball of
$V_R(c,C)$
, is the intersection of the Voronoi cell of c with the ball of
![]() $\mathrm {dist}_\Gamma $
radius R around C:
$\mathrm {dist}_\Gamma $
radius R around C:
The R-truncated Voronoi diagram of C is the collection of R-truncated Voronoi cells.
In general, the R-truncated Voronoi cells corresponding to a subset C are not necessarily pairwise disjoint because it could happen that for some
![]() $v \in \Gamma $
, there exist
$v \in \Gamma $
, there exist
![]() $c_1,c_2 \in C$
with
$c_1,c_2 \in C$
with
![]() $c_1, \ne c_2$
such that
$c_1, \ne c_2$
such that
For our application, we would like to extract a partial tiling from the R-truncated Voronoi diagram. For this purpose, we need to ‘disjointify’ the cells.
Definition 6.7. Fix an arbitrary total order
![]() $\prec _\Gamma $
on the group
$\prec _\Gamma $
on the group
![]() $\Gamma $
, with the property that whenever
$\Gamma $
, with the property that whenever
![]() $\gamma _1,\tilde \gamma _1,\gamma _2,\tilde \gamma _2 \in \Gamma $
satisfy that
$\gamma _1,\tilde \gamma _1,\gamma _2,\tilde \gamma _2 \in \Gamma $
satisfy that
![]() $P_{\Gamma ,\mathbb {Z}^d}(\gamma _1)=P_{\Gamma ,\mathbb {Z}^d}(\tilde \gamma _1) \ne P_{\Gamma ,\mathbb {Z}^d}(\gamma _2)=P_{\Gamma ,\mathbb {Z}^d}(\tilde \gamma _2)$
and
$P_{\Gamma ,\mathbb {Z}^d}(\gamma _1)=P_{\Gamma ,\mathbb {Z}^d}(\tilde \gamma _1) \ne P_{\Gamma ,\mathbb {Z}^d}(\gamma _2)=P_{\Gamma ,\mathbb {Z}^d}(\tilde \gamma _2)$
and
![]() $\gamma _1 \prec _{\Gamma } \gamma _2$
, then
$\gamma _1 \prec _{\Gamma } \gamma _2$
, then
![]() $\tilde \gamma _1 \prec \tilde \gamma _2$
. We do not require that the total order
$\tilde \gamma _1 \prec \tilde \gamma _2$
. We do not require that the total order
![]() $\prec _\Gamma $
is invariant, as this can only be done in the case where G is the trivial group, otherwise
$\prec _\Gamma $
is invariant, as this can only be done in the case where G is the trivial group, otherwise
![]() $\Gamma $
has non-trivial torsion, and hence is not orderable.
$\Gamma $
has non-trivial torsion, and hence is not orderable.
The disjointified R-truncated Voronoi cell of
![]() $c \in C$
, denoted by
$c \in C$
, denoted by
![]() $\overline {V}_R(c,C)$
, is the subset of
$\overline {V}_R(c,C)$
, is the subset of
![]() $V_R(c,C)$
obtained by ‘breaking ties according to
$V_R(c,C)$
obtained by ‘breaking ties according to
![]() $\prec _{\Gamma }$
’:
$\prec _{\Gamma }$
’:
where
![]() $M(\gamma ,C) \subseteq C$
is the set of minimizers of
$M(\gamma ,C) \subseteq C$
is the set of minimizers of
![]() $\mathrm {dist}_{\Gamma }(\gamma ,\cdot )$
in C:
$\mathrm {dist}_{\Gamma }(\gamma ,\cdot )$
in C:
The disjointified R-truncated Voronoi digaram of
![]() $C \subset \Gamma $
, denoted
$C \subset \Gamma $
, denoted
![]() $\overline {V}(C)$
, is the collection
$\overline {V}(C)$
, is the collection
of disjointified R-truncated Voronoi cells.
Definition 6.8. Call a finite set
![]() $F \Subset \Gamma $
convex if there exists a compact convex subset
$F \Subset \Gamma $
convex if there exists a compact convex subset
![]() $\tilde F \subset \mathbb {R}^d$
such that
$\tilde F \subset \mathbb {R}^d$
such that
![]() $F= (\tilde F \cap \mathbb {Z}^d) \times G$
.
$F= (\tilde F \cap \mathbb {Z}^d) \times G$
.
Lemma 6.9. For any
![]() $C \subseteq \Gamma $
and
$C \subseteq \Gamma $
and
![]() $R>0$
, we have:
$R>0$
, we have:
-
(1) the disjointified R-truncated Voronoi diagram of C is a partial tiling of
 $\Gamma $
;
$\Gamma $
; -
(2)
 $ (C+B_R^\Gamma )\subseteq \biguplus _{c \in C}\overline {V}_R(c,C)= \bigcup _{c \in C} V_R(c,C)$
, where
$ (C+B_R^\Gamma )\subseteq \biguplus _{c \in C}\overline {V}_R(c,C)= \bigcup _{c \in C} V_R(c,C)$
, where  $$ \begin{align*}B_R^\Gamma = \{ \gamma \in \Gamma : \mathrm{dist}_{\mathbb{R}^d}(0,P_{\Gamma,\mathbb{Z}^d}(\gamma)) \le R\};\end{align*} $$
$$ \begin{align*}B_R^\Gamma = \{ \gamma \in \Gamma : \mathrm{dist}_{\mathbb{R}^d}(0,P_{\Gamma,\mathbb{Z}^d}(\gamma)) \le R\};\end{align*} $$
-
(3) if
 $C \subset \Gamma $
is a
$C \subset \Gamma $
is a
 $(\{0\}\times G)$
-separated set, then for every
$(\{0\}\times G)$
-separated set, then for every
 $c \in C$
, the R-truncated Voronoi cell
$c \in C$
, the R-truncated Voronoi cell
 $V_R(c,C) \Subset \Gamma $
is convex.
$V_R(c,C) \Subset \Gamma $
is convex.
Proof. (1) Fix
![]() $C \subseteq \Gamma $
and
$C \subseteq \Gamma $
and
![]() $R>0$
. For every
$R>0$
. For every
![]() $c \in c$
, the disjointified R-truncated Voronoi cell
$c \in c$
, the disjointified R-truncated Voronoi cell
![]() $\overline {V}_R(c,C)$
is finite, because the number of elements in
$\overline {V}_R(c,C)$
is finite, because the number of elements in
![]() $\Gamma $
whose distance from c is bounded by R is finite. We need to prove that
$\Gamma $
whose distance from c is bounded by R is finite. We need to prove that
![]() $\overline {V}_R(c_1,C) \cap \overline {V}_R(c_2,C)$
whenever
$\overline {V}_R(c_1,C) \cap \overline {V}_R(c_2,C)$
whenever
![]() $c_1, c_2 \in C$
and
$c_1, c_2 \in C$
and
![]() $c_1 \ne c_2$
. Choose any district elements
$c_1 \ne c_2$
. Choose any district elements
![]() $c_1,c_2 \in C$
. Suppose that
$c_1,c_2 \in C$
. Suppose that
![]() $v \in \overline {V}_R(c_1,C) \cap \overline {V}_R(c_1,C)$
. In particular,
$v \in \overline {V}_R(c_1,C) \cap \overline {V}_R(c_1,C)$
. In particular,
![]() $c_1,c_2 \in M(\gamma ,C)$
. Since
$c_1,c_2 \in M(\gamma ,C)$
. Since
![]() $c_1 \ne c_2$
, it follows that
$c_1 \ne c_2$
, it follows that
![]() $v- c_1 \ne v- c_2$
, so either
$v- c_1 \ne v- c_2$
, so either
![]() $v-c_1 \prec _{\Gamma } v- c_2$
or
$v-c_1 \prec _{\Gamma } v- c_2$
or
![]() $v-c_2 \prec _{\Gamma } v- c_1$
. In the first case, we have that
$v-c_2 \prec _{\Gamma } v- c_1$
. In the first case, we have that
![]() $v \not \in \overline {V}_R(c_2,C)$
and in the second case, we have that
$v \not \in \overline {V}_R(c_2,C)$
and in the second case, we have that
![]() $v \not \in \overline {V}_R(c_1,C)$
, either way we have a contradiction.
$v \not \in \overline {V}_R(c_1,C)$
, either way we have a contradiction.
(2) If
![]() $v \in C+ B_R^\Gamma $
, then there exists
$v \in C+ B_R^\Gamma $
, then there exists
![]() $c \in C$
such that
$c \in C$
such that
![]() $\mathrm {dist}_{\mathbb {R}^d}(P_{\Gamma ,\mathbb {Z}^d}(v)) \le R$
. It follows that
$\mathrm {dist}_{\mathbb {R}^d}(P_{\Gamma ,\mathbb {Z}^d}(v)) \le R$
. It follows that
![]() $v \in \overline {V}_R(\tilde c,C)$
, where
$v \in \overline {V}_R(\tilde c,C)$
, where
![]() $\tilde c \in M(v,C)$
is the element of
$\tilde c \in M(v,C)$
is the element of
![]() $M(v,c)$
such that
$M(v,c)$
such that
![]() $(v-\tilde c)$
is maximal with respect to
$(v-\tilde c)$
is maximal with respect to
![]() $\prec _{\Gamma }$
.
$\prec _{\Gamma }$
.
(3) The fact that every cell of the disjointified R-truncated Voronoi cell
![]() $\overline {V}_R(c,C) \Subset \Gamma $
is convex follows from the classical and well-known fact that every cell of a Voronoi diagram of a discrete subset of
$\overline {V}_R(c,C) \Subset \Gamma $
is convex follows from the classical and well-known fact that every cell of a Voronoi diagram of a discrete subset of
![]() $\mathbb {R}^d$
is a convex polygon.
$\mathbb {R}^d$
is a convex polygon.
The following simple lemma is closely related to [Reference Lightwood19, Lemma 3.5], except that in [Reference Lightwood19], the Voronoi diagram of syndetic sets was considered, rather than the disjointified R-truncated Voronoi diagram of an arbitrary subset of
![]() $\Gamma $
(also in [Reference Lightwood19], only the case
$\Gamma $
(also in [Reference Lightwood19], only the case
![]() $\Gamma = \mathbb {Z}^d$
was considered, though this is a trivial modification to consider the case
$\Gamma = \mathbb {Z}^d$
was considered, though this is a trivial modification to consider the case
![]() $\Gamma = \mathbb {Z}^d \times G$
, with G finite).
$\Gamma = \mathbb {Z}^d \times G$
, with G finite).
Lemma 6.10. For any
![]() $R>0$
, the function
$R>0$
, the function
![]() $V_R:\{0,1\}^\Gamma \to \mathit {PTilings}(\Gamma )$
that sends V to the disjointified R-truncated Voronoi diagram of (the set corresponding to) z is continuous and equivariant.
$V_R:\{0,1\}^\Gamma \to \mathit {PTilings}(\Gamma )$
that sends V to the disjointified R-truncated Voronoi diagram of (the set corresponding to) z is continuous and equivariant.
Proof. By Lemma 6.9,
![]() $\overline {V}_R(z) \in \mathit {PTilings}(\Gamma )$
for every
$\overline {V}_R(z) \in \mathit {PTilings}(\Gamma )$
for every
![]() $z \in Z$
. Equivariance follows directly from the fact that Euclidean distances are invariant under translations in
$z \in Z$
. Equivariance follows directly from the fact that Euclidean distances are invariant under translations in
![]() $\mathbb {R}^d$
.
$\mathbb {R}^d$
.
The following result is implicitly contained in [Reference Lightwood19], and also in [Reference Balister, Bollobás and Quas2], where it was shown that for any
![]() $\mathbb {Z}^d$
subshift X, we have
$\mathbb {Z}^d$
subshift X, we have
![]() $h(X) = \lim _{n \to \infty }({1}/{|C_n|})\log |\mathcal {L}_{C_n}(X)|$
for any sequence
$h(X) = \lim _{n \to \infty }({1}/{|C_n|})\log |\mathcal {L}_{C_n}(X)|$
for any sequence
![]() $(C_n)_{n=1}^\infty $
of bounded convex subsets in
$(C_n)_{n=1}^\infty $
of bounded convex subsets in
![]() $\mathbb {Z}^d$
such that for every
$\mathbb {Z}^d$
such that for every
![]() $r>0$
, there exist
$r>0$
, there exist
![]() $n_0 \in \mathbb {N}$
so that
$n_0 \in \mathbb {N}$
so that
![]() $C_n$
contains a ball of radius r for all
$C_n$
contains a ball of radius r for all
![]() $n \ge n_0$
. A similar statement (with a similar proof) can also be found in [Reference Gutman, Lindenstrauss and Tsukamoto15, Lemma 3.5]. Again, we include a proof for completeness.
$n \ge n_0$
. A similar statement (with a similar proof) can also be found in [Reference Gutman, Lindenstrauss and Tsukamoto15, Lemma 3.5]. Again, we include a proof for completeness.
Lemma 6.11. For any
![]() $K \Subset \Gamma $
and any
$K \Subset \Gamma $
and any
![]() $\epsilon>0$
, there exists a finite set
$\epsilon>0$
, there exists a finite set
![]() $F_0 \Subset \Gamma $
such that any convex set
$F_0 \Subset \Gamma $
such that any convex set
![]() $F \Subset \Gamma $
with
$F \Subset \Gamma $
with
![]() $F_0\subseteq F$
is
$F_0\subseteq F$
is
![]() $(K,\epsilon )$
-invariant.
$(K,\epsilon )$
-invariant.
For a subset
![]() $A \Subset \mathbb {R}^d$
and
$A \Subset \mathbb {R}^d$
and
![]() $t \in (0,\infty )$
, we use the notation
$t \in (0,\infty )$
, we use the notation
![]() $t A =\{ tv: v \in A\}$
. Also, for
$t A =\{ tv: v \in A\}$
. Also, for
![]() $t>0$
, let
$t>0$
, let
![]() $B^d_{t} \subseteq \mathbb {R}$
denote the Euclidean ball of radius t approximately
$B^d_{t} \subseteq \mathbb {R}$
denote the Euclidean ball of radius t approximately
![]() $0$
. We denote the Lebesgue measure of a measurable set
$0$
. We denote the Lebesgue measure of a measurable set
![]() $A \subseteq \mathbb {R}^d$
by
$A \subseteq \mathbb {R}^d$
by
![]() $m_d(A)$
. For a set
$m_d(A)$
. For a set
![]() $\tilde F \subseteq \mathbb {R}^d$
,
$\tilde F \subseteq \mathbb {R}^d$
,
![]() $\partial \tilde F$
denotes the boundary of
$\partial \tilde F$
denotes the boundary of
![]() $\tilde F$
with respect to the usual topology on
$\tilde F$
with respect to the usual topology on
![]() $\mathbb {R}^d$
. Given
$\mathbb {R}^d$
. Given
![]() $r_0>0$
, we denote
$r_0>0$
, we denote
The proof of Lemma 6.11 is based on the following lemma about convex sets in
![]() $\mathbb {R}^d$
.
$\mathbb {R}^d$
.
Lemma 6.12. For any convex compact set
![]() $\tilde F \subseteq \mathbb {R}^d$
that contains
$\tilde F \subseteq \mathbb {R}^d$
that contains
![]() $B^d_r$
, the Euclidean ball of radius r approximately
$B^d_r$
, the Euclidean ball of radius r approximately
![]() $0$
and any
$0$
and any
![]() $0< r_0 < r$
, the following inclusion holds:
$0< r_0 < r$
, the following inclusion holds:
 $$ \begin{align} \partial_{r_0} \tilde F \subseteq \overline{\bigg(1+ \frac{r_0}{r}\bigg)\tilde F \setminus \bigg( 1- \frac{r_0}{r}\bigg)\tilde F}. \end{align} $$
$$ \begin{align} \partial_{r_0} \tilde F \subseteq \overline{\bigg(1+ \frac{r_0}{r}\bigg)\tilde F \setminus \bigg( 1- \frac{r_0}{r}\bigg)\tilde F}. \end{align} $$
Thus,
 $$ \begin{align*} m_d( \partial_{r_0} \tilde F) \le \bigg( \bigg( 1+\frac{r_0}{r}\bigg)^d -\bigg( 1-\frac{r_0}{r}\bigg)^d \bigg) m_d(\tilde F). \end{align*} $$
$$ \begin{align*} m_d( \partial_{r_0} \tilde F) \le \bigg( \bigg( 1+\frac{r_0}{r}\bigg)^d -\bigg( 1-\frac{r_0}{r}\bigg)^d \bigg) m_d(\tilde F). \end{align*} $$
Proof. By assumption,
![]() $B^d_{r} \subseteq \tilde F$
, so
$B^d_{r} \subseteq \tilde F$
, so
![]() $B^d_{r_0} \subseteq ({r_0}/{r}) \tilde F$
. It follows that
$B^d_{r_0} \subseteq ({r_0}/{r}) \tilde F$
. It follows that
 $$ \begin{align*}\partial_{r_0} \tilde F = \partial \tilde F+ B^d_{r_0} \subseteq \partial \tilde F + \frac{r_0}{r} \tilde F \subseteq \tilde F + \frac{r_0}{r} \tilde F = \bigg( 1+ \frac{r_0}{r}\bigg) \tilde F.\end{align*} $$
$$ \begin{align*}\partial_{r_0} \tilde F = \partial \tilde F+ B^d_{r_0} \subseteq \partial \tilde F + \frac{r_0}{r} \tilde F \subseteq \tilde F + \frac{r_0}{r} \tilde F = \bigg( 1+ \frac{r_0}{r}\bigg) \tilde F.\end{align*} $$
In the last equality, we use the fact that for a convex set
![]() $A \subseteq \mathbb {R}^d$
and
$A \subseteq \mathbb {R}^d$
and
![]() $t_1,t_2>0$
, it holds that
$t_1,t_2>0$
, it holds that
![]() $t_1 A+ t_2A = (t_1+t_2)A$
.
$t_1 A+ t_2A = (t_1+t_2)A$
.
Also, by similar considerations for any
![]() $t < (1-{r_0}/{r})$
, we have that
$t < (1-{r_0}/{r})$
, we have that
It follows that
![]() $\partial _{r_0}\tilde F \subseteq \overline {\mathbb {R}^d \setminus ( 1- {r_0}/{r})\tilde F}$
. This proves that
$\partial _{r_0}\tilde F \subseteq \overline {\mathbb {R}^d \setminus ( 1- {r_0}/{r})\tilde F}$
. This proves that
 $$ \begin{align*} \partial_{r_0} \tilde F \subseteq \overline{\bigg(1+ \frac{r_0}{r}\bigg)\tilde F \setminus \bigg( 1- \frac{r_0}{r}\bigg)\tilde F}. \end{align*} $$
$$ \begin{align*} \partial_{r_0} \tilde F \subseteq \overline{\bigg(1+ \frac{r_0}{r}\bigg)\tilde F \setminus \bigg( 1- \frac{r_0}{r}\bigg)\tilde F}. \end{align*} $$
Thus (because the boundary of convex sets has zero Lebesgue measure),
 $$ \begin{align*} m_d(\partial_{r_0} \tilde F ) \le m_d\bigg(\bigg(1+ \frac{r_0}{r}\bigg)\tilde F \bigg)- m_d\bigg(\bigg(1- \frac{r_0}{r}\bigg)\tilde F \bigg). \end{align*} $$
$$ \begin{align*} m_d(\partial_{r_0} \tilde F ) \le m_d\bigg(\bigg(1+ \frac{r_0}{r}\bigg)\tilde F \bigg)- m_d\bigg(\bigg(1- \frac{r_0}{r}\bigg)\tilde F \bigg). \end{align*} $$
From this, it follows that
 $$ \begin{align*} m_d( \partial_{r_0} \tilde F) \le \bigg( \bigg( 1+\frac{r_0}{r}\bigg)^d -\bigg( 1-\frac{r_0}{r}\bigg)^d \bigg) m_d(\tilde F). \end{align*} $$
$$ \begin{align*} m_d( \partial_{r_0} \tilde F) \le \bigg( \bigg( 1+\frac{r_0}{r}\bigg)^d -\bigg( 1-\frac{r_0}{r}\bigg)^d \bigg) m_d(\tilde F). \end{align*} $$
For
![]() $k \in \mathbb {N}$
, we denote
$k \in \mathbb {N}$
, we denote
Proof of Lemma 6.11
For any finite subset
![]() $K \Subset \Gamma $
, we can find
$K \Subset \Gamma $
, we can find
![]() $r_0>0$
such that
$r_0>0$
such that
![]() $K \subseteq (B_{r_0}^d \cap \mathbb {Z}^d) \times G$
. For such
$K \subseteq (B_{r_0}^d \cap \mathbb {Z}^d) \times G$
. For such
![]() $r_0>0$
and any convex set
$r_0>0$
and any convex set
![]() $\tilde F\subseteq \mathbb {R}^d$
, it holds
$\tilde F\subseteq \mathbb {R}^d$
, it holds
Also, for any convex set
![]() $\tilde F \subseteq \mathbb {R}^d$
,
$\tilde F \subseteq \mathbb {R}^d$
,
Let
![]() $F \subset \Gamma $
be a convex set that contains
$F \subset \Gamma $
be a convex set that contains
![]() $B_j$
. By our definition of a convex set in
$B_j$
. By our definition of a convex set in
![]() $\Gamma $
, there exists a convex set
$\Gamma $
, there exists a convex set
![]() $\tilde F \subset \mathbb {Z}^d$
so that
$\tilde F \subset \mathbb {Z}^d$
so that
![]() $ F = (\tilde F \cap \mathbb {Z}^d) \times G$
. Since
$ F = (\tilde F \cap \mathbb {Z}^d) \times G$
. Since
![]() $B_j \subset F$
, i j is sufficiently big, it follows that
$B_j \subset F$
, i j is sufficiently big, it follows that
![]() $B_{r}^d \subseteq \tilde F$
.
$B_{r}^d \subseteq \tilde F$
.
It thus suffices to prove that for any
![]() $r_0>0$
and any
$r_0>0$
and any
![]() $\delta>0$
, there exists
$\delta>0$
, there exists
![]() $r>0$
such that for any compact convex subset
$r>0$
such that for any compact convex subset
![]() $\tilde F \subseteq \mathbb {R}^d$
that contains the Euclidean ball of radius r approximately
$\tilde F \subseteq \mathbb {R}^d$
that contains the Euclidean ball of radius r approximately
![]() $0$
, the following inequality holds:
$0$
, the following inequality holds:
Fix
![]() $r_0>0 $
and
$r_0>0 $
and
![]() $\delta>0$
. Since
$\delta>0$
. Since
 $$ \begin{align*} \lim_{r \to \infty} \bigg( 1+\frac{r_0}{r}\bigg)^d -\bigg( 1-\frac{r_0}{r}\bigg)^d =0,\end{align*} $$
$$ \begin{align*} \lim_{r \to \infty} \bigg( 1+\frac{r_0}{r}\bigg)^d -\bigg( 1-\frac{r_0}{r}\bigg)^d =0,\end{align*} $$
we can choose
![]() $r>0$
sufficiently big so that
$r>0$
sufficiently big so that
 $$ \begin{align*} \bigg( 1+\frac{r_0}{r}\bigg)^d -\bigg( 1-\frac{r_0}{r}\bigg)^d < \delta. \end{align*} $$
$$ \begin{align*} \bigg( 1+\frac{r_0}{r}\bigg)^d -\bigg( 1-\frac{r_0}{r}\bigg)^d < \delta. \end{align*} $$
Then, by Lemma 6.12, it follows that
![]() $m_d(\partial _{r_0} \tilde F) \le \delta \cdot m_d(\tilde F)$
for any convex set
$m_d(\partial _{r_0} \tilde F) \le \delta \cdot m_d(\tilde F)$
for any convex set
![]() $\tilde F$
that contains
$\tilde F$
that contains
![]() $B_{r}^d$
.
$B_{r}^d$
.
We now proceed to state and prove results needed to ensure that the cells of the disjointified R-truncated Voronoi diagram have ‘sufficiently small external boundary’, provided that R is sufficiently big.
Lemma 6.13. For any convex set
![]() $A \subseteq \mathbb {R}^d$
and any
$A \subseteq \mathbb {R}^d$
and any
![]() $0 < r_0 <R$
such that
$0 < r_0 <R$
such that
![]() $0 \in A$
, the following inequality holds:
$0 \in A$
, the following inequality holds:
 $$ \begin{align} m_d( A \cap B_{R+r_0} \setminus B_{R-{r_0}} ) \le \bigg( \frac{(R+r_0)^d-(R-r_0)^d}{(R-r_0)^d}\bigg)m_d(A). \end{align} $$
$$ \begin{align} m_d( A \cap B_{R+r_0} \setminus B_{R-{r_0}} ) \le \bigg( \frac{(R+r_0)^d-(R-r_0)^d}{(R-r_0)^d}\bigg)m_d(A). \end{align} $$
Proof. For
![]() $t>0$
, let
$t>0$
, let
![]() $S^{d-1} \subset \mathbb {R}^d$
denote the unit sphere in
$S^{d-1} \subset \mathbb {R}^d$
denote the unit sphere in
![]() $\mathbb {R}^d$
, namely,
$\mathbb {R}^d$
, namely,
![]() $S^{d-1} = \partial B_1^d$
. Let
$S^{d-1} = \partial B_1^d$
. Let
![]() $A \subseteq \mathbb {R}^d$
be a convex set such that
$A \subseteq \mathbb {R}^d$
be a convex set such that
![]() $0 \in A$
and
$0 \in A$
and
![]() $0 < r_0 <R$
. For
$0 < r_0 <R$
. For
![]() $t>0$
, consider the set
$t>0$
, consider the set
![]() $A_t \subseteq S^{d-1}$
given by
$A_t \subseteq S^{d-1}$
given by
Given a Borel subset
![]() $B \subseteq S^{d-1}$
, let
$B \subseteq S^{d-1}$
, let
![]() $H_{d-1}(B)$
denote the
$H_{d-1}(B)$
denote the
![]() $d-1$
-dimensional Hausdorff measure of B. Then, there exists a constant
$d-1$
-dimensional Hausdorff measure of B. Then, there exists a constant
![]() $c>0$
(that depends on the normalization of
$c>0$
(that depends on the normalization of
![]() $H_{d-1}$
) so that
$H_{d-1}$
) so that
 $$ \begin{align*}m_d(A) = c\int_0^\infty t^{d-1} H_{d-1}(A_t)\,dt\end{align*} $$
$$ \begin{align*}m_d(A) = c\int_0^\infty t^{d-1} H_{d-1}(A_t)\,dt\end{align*} $$
and so
 $$ \begin{align*}m_d( A \cap B_{R+r_0} \setminus B_{R-{r_0}} ) = c \int_{R-r_0}^{R+r_0} t^{d-1} H_{d-1}(A_t)\,dt.\end{align*} $$
$$ \begin{align*}m_d( A \cap B_{R+r_0} \setminus B_{R-{r_0}} ) = c \int_{R-r_0}^{R+r_0} t^{d-1} H_{d-1}(A_t)\,dt.\end{align*} $$
Because
![]() $0 \in A$
and A is convex, it follows that for every
$0 \in A$
and A is convex, it follows that for every
![]() $0 <t_1 <t_2$
, we have
$0 <t_1 <t_2$
, we have
![]() $A_{t_2} \subseteq A_{t_1}$
. Thus,
$A_{t_2} \subseteq A_{t_1}$
. Thus,
 $$ \begin{align*}m_d(A) \ge c \int_0^{R-r_0} t^{d-1} H_{d-1}(A_{R-r_0})\,dt = \frac{c H_{d-1}(A_{R-r_0}) }{d} \cdot (R-r_0)^d\end{align*} $$
$$ \begin{align*}m_d(A) \ge c \int_0^{R-r_0} t^{d-1} H_{d-1}(A_{R-r_0})\,dt = \frac{c H_{d-1}(A_{R-r_0}) }{d} \cdot (R-r_0)^d\end{align*} $$
and
 $$ \begin{align*}m_d( A \cap B_{R+r_0} \setminus B_{R-{r_0}} ) &\le c \int_{R-r_0}^{R+r_0} t^{d-1} H_{d-1}(A_{R-r_0})\,dt\\ &=\frac{c H_{d-1}(A_{R-r_0}) }{d} \cdot ((R+r_0)^d-(R-r_0)^d).\end{align*} $$
$$ \begin{align*}m_d( A \cap B_{R+r_0} \setminus B_{R-{r_0}} ) &\le c \int_{R-r_0}^{R+r_0} t^{d-1} H_{d-1}(A_{R-r_0})\,dt\\ &=\frac{c H_{d-1}(A_{R-r_0}) }{d} \cdot ((R+r_0)^d-(R-r_0)^d).\end{align*} $$
The proof of the lemma follows directly by combining these inequalities.
Lemma 6.14. For any
![]() $K \Subset \Gamma $
and
$K \Subset \Gamma $
and
![]() $\epsilon>0$
, there exists a finite set
$\epsilon>0$
, there exists a finite set
![]() $F \Subset \Gamma $
and
$F \Subset \Gamma $
and
![]() $R_0>0$
such that for any F-separated set
$R_0>0$
such that for any F-separated set
![]() $C \subseteq \Gamma $
and any
$C \subseteq \Gamma $
and any
![]() $R>R_0$
, the disjointified R-truncated Voronoi diagram of C is
$R>R_0$
, the disjointified R-truncated Voronoi diagram of C is
![]() $(K,\epsilon )$
-invariant.
$(K,\epsilon )$
-invariant.
Proof. Fix
![]() $K \Subset \Gamma $
and
$K \Subset \Gamma $
and
![]() $\epsilon>0$
. By Lemma 6.11, there exists
$\epsilon>0$
. By Lemma 6.11, there exists
![]() $F_0 \Subset \Gamma $
so that any convex set that contains
$F_0 \Subset \Gamma $
so that any convex set that contains
![]() $F_0$
is
$F_0$
is
![]() $(K,\epsilon )$
-invariant. Since the property of being
$(K,\epsilon )$
-invariant. Since the property of being
![]() $(K,\epsilon )$
-invariant remains unchanged under translations, it is clear that any convex set that contains
$(K,\epsilon )$
-invariant remains unchanged under translations, it is clear that any convex set that contains
![]() $v+ F_0$
for some
$v+ F_0$
for some
![]() $v \in \Gamma $
is also
$v \in \Gamma $
is also
![]() $(K,\epsilon )$
-invariant. Choose
$(K,\epsilon )$
-invariant. Choose
![]() $R_1> \max \{ \mathrm {dist}_{\mathbb {R}^d}(0,P_{\Gamma ,\mathbb {Z}^d}(v)) : v \in F_0\}$
. Let
$R_1> \max \{ \mathrm {dist}_{\mathbb {R}^d}(0,P_{\Gamma ,\mathbb {Z}^d}(v)) : v \in F_0\}$
. Let
![]() $F \Subset \Gamma $
be a finite set such that
$F \Subset \Gamma $
be a finite set such that
![]() $(\{0\} \times G )\subseteq F$
and also so that F contains the set
$(\{0\} \times G )\subseteq F$
and also so that F contains the set
![]() $B_{R_1}^\Gamma = \{ \gamma \in \Gamma : \mathrm {dist}_{\mathbb {R}^d}(0,P_{\Gamma ,\mathbb {Z}^d}(v)) \le R_1\}$
. Note that since
$B_{R_1}^\Gamma = \{ \gamma \in \Gamma : \mathrm {dist}_{\mathbb {R}^d}(0,P_{\Gamma ,\mathbb {Z}^d}(v)) \le R_1\}$
. Note that since
![]() $F \Subset \Gamma $
such that
$F \Subset \Gamma $
such that
![]() $(\{0\} \times G )\subseteq F$
, it follows that any F-separated set
$(\{0\} \times G )\subseteq F$
, it follows that any F-separated set
![]() $C \subseteq \Gamma $
is also
$C \subseteq \Gamma $
is also
![]() $(\{0\}\times G)$
-separated. Choose
$(\{0\}\times G)$
-separated. Choose
![]() $R_0> 2R_1$
. By Lemma 6.9, every cell
$R_0> 2R_1$
. By Lemma 6.9, every cell
![]() $\overline {V}_R(c,C)$
is convex and
$\overline {V}_R(c,C)$
is convex and
![]() $c+F \subseteq \overline {V}_R(c,C)$
, so
$c+F \subseteq \overline {V}_R(c,C)$
, so
![]() $\overline {V}_R(c,C)$
is
$\overline {V}_R(c,C)$
is
![]() $(K,\epsilon )$
-invariant.
$(K,\epsilon )$
-invariant.
Lemma 6.15. There exists
![]() $F_0 \Subset \Gamma $
so that for any
$F_0 \Subset \Gamma $
so that for any
![]() $K \Subset \Gamma $
and any
$K \Subset \Gamma $
and any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $R_0>0$
such that for any
$R_0>0$
such that for any
![]() $R>R_0$
and any
$R>R_0$
and any
![]() $F_0$
-separated
$F_0$
-separated
![]() $C \subseteq \Gamma $
, the disjointified R-truncated Voronoi diagram of C has
$C \subseteq \Gamma $
, the disjointified R-truncated Voronoi diagram of C has
![]() $(K,\epsilon )$
-small exterior boundary.
$(K,\epsilon )$
-small exterior boundary.
Proof. Using Lemma 6.14, we choose
![]() $F_0 \Subset \Gamma $
and
$F_0 \Subset \Gamma $
and
![]() $R_1$
so that for any
$R_1$
so that for any
![]() $F_0$
-separated set
$F_0$
-separated set
![]() $C \subseteq~\Gamma $
and any
$C \subseteq~\Gamma $
and any
![]() $R> R_1$
, the size of any cell in the disjointified R-truncated Voronoi diagram of C is at least half the size of the (non-disjointified) R-truncated Voronoi cell. Given
$R> R_1$
, the size of any cell in the disjointified R-truncated Voronoi diagram of C is at least half the size of the (non-disjointified) R-truncated Voronoi cell. Given
![]() $K \Subset \Gamma $
, we can find
$K \Subset \Gamma $
, we can find
![]() $r_0>0$
such that
$r_0>0$
such that
![]() $K \subseteq (B_{r_0}^d \cap \mathbb {Z}^d) \times G$
. Thus, if
$K \subseteq (B_{r_0}^d \cap \mathbb {Z}^d) \times G$
. Thus, if
![]() $F \Subset \Gamma $
is a cell of the R-truncated Voronoi diagram of C, there exists a compact convex set
$F \Subset \Gamma $
is a cell of the R-truncated Voronoi diagram of C, there exists a compact convex set
![]() $\tilde F \subseteq \mathbb {R}^d$
such that
$\tilde F \subseteq \mathbb {R}^d$
such that
![]() $F= (\tilde F \cap \mathbb {Z}^d) \times G$
. The exterior K-boundary of F is contained in
$F= (\tilde F \cap \mathbb {Z}^d) \times G$
. The exterior K-boundary of F is contained in
As in the proof of Lemma 6.11, it thus suffices to prove that for any
![]() $\delta>0$
, provided that R is sufficiently big, we have
$\delta>0$
, provided that R is sufficiently big, we have
This follows from Lemma 6.13, provided that R is big enough so that
 $$ \begin{align*} \frac{(R+r_0)^d-(R-r_0)^d}{(R-r_0)^d} < \delta.\\[-46pt] \end{align*} $$
$$ \begin{align*} \frac{(R+r_0)^d-(R-r_0)^d}{(R-r_0)^d} < \delta.\\[-46pt] \end{align*} $$
Proof of Proposition 6.4
Let
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $K \Subset \Gamma $
be given. By Lemma 6.14, there exists
$K \Subset \Gamma $
be given. By Lemma 6.14, there exists
![]() $F \Subset \Gamma $
and
$F \Subset \Gamma $
and
![]() $R_0>0$
such that for any F-separated set
$R_0>0$
such that for any F-separated set
![]() $C \subseteq \Gamma $
and any
$C \subseteq \Gamma $
and any
![]() $R>R_0$
, the disjointified R-truncated Voronoi diagram of C is
$R>R_0$
, the disjointified R-truncated Voronoi diagram of C is
![]() $(K,\epsilon )$
-invariant. By further enlarging F, we can assume that
$(K,\epsilon )$
-invariant. By further enlarging F, we can assume that
![]() $F_0 \subseteq F$
, where
$F_0 \subseteq F$
, where
![]() $F_0 \Subset \Gamma $
is as in Lemma 6.15, and that F is symmetric and so that
$F_0 \Subset \Gamma $
is as in Lemma 6.15, and that F is symmetric and so that
![]() $B_{R_1} \subseteq F$
, where
$B_{R_1} \subseteq F$
, where
![]() $R_1= 2\max \{ \mathrm {dist}_{\mathbb {R^d}}(0,v): v\in K\}$
and
$R_1= 2\max \{ \mathrm {dist}_{\mathbb {R^d}}(0,v): v\in K\}$
and
![]() $B_{R_1}= \{ v \in \Gamma : \mathrm {dist}_{\mathbb {R}^d}(0,P_{\Gamma ,\mathbb {Z}^d}(v)) \le R_1\}$
.
$B_{R_1}= \{ v \in \Gamma : \mathrm {dist}_{\mathbb {R}^d}(0,P_{\Gamma ,\mathbb {Z}^d}(v)) \le R_1\}$
.
Let
![]() $P = (F+F) \setminus \{0\}$
. Now let X be a
$P = (F+F) \setminus \{0\}$
. Now let X be a
![]() $\Gamma $
-subshift,
$\Gamma $
-subshift,
![]() $W \Subset \Gamma $
, and let
$W \Subset \Gamma $
, and let
![]() $\mathcal {F} \subseteq \mathcal {L}_W(X)$
be a set of patterns so that
$\mathcal {F} \subseteq \mathcal {L}_W(X)$
be a set of patterns so that
![]() $x_W \not \in \mathcal {F}$
for any
$x_W \not \in \mathcal {F}$
for any
![]() $x \in X$
such that
$x \in X$
such that
![]() $\mathrm {stab}(x) \cap P = \emptyset $
. By Lemma 3.3, there exists a clopen set
$\mathrm {stab}(x) \cap P = \emptyset $
. By Lemma 3.3, there exists a clopen set
![]() $C \subset X$
such that
$C \subset X$
such that
![]() $C \cap \sigma _v(C) = \emptyset $
for every
$C \cap \sigma _v(C) = \emptyset $
for every
![]() $v \in P$
and so that for every
$v \in P$
and so that for every
![]() $x \in X$
, either there exists
$x \in X$
, either there exists
![]() $v \in P \cup \{0\} = B_k$
such that
$v \in P \cup \{0\} = B_k$
such that
![]() $\sigma _v(x) \in C$
or
$\sigma _v(x) \in C$
or
![]() $x_W \in \mathcal {F}$
.
$x_W \in \mathcal {F}$
.
Define
![]() $\alpha :X \to \{0,1\}^\Gamma $
by
$\alpha :X \to \{0,1\}^\Gamma $
by
 $$ \begin{align*}\alpha(x)_v = \begin{cases} 1 & \text{if }\sigma_v(x) \in C,\\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*}\alpha(x)_v = \begin{cases} 1 & \text{if }\sigma_v(x) \in C,\\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
It is clear that
![]() $\alpha :X \to \{0,1\}^\Gamma $
is equivariant. Continuity of
$\alpha :X \to \{0,1\}^\Gamma $
is equivariant. Continuity of
![]() $\alpha $
follows from the fact that C is a clopen set.
$\alpha $
follows from the fact that C is a clopen set.
Because
![]() $C \cap \sigma _v(C) = \emptyset $
for every
$C \cap \sigma _v(C) = \emptyset $
for every
![]() $v \in P$
, it follows that for every
$v \in P$
, it follows that for every
![]() $x \in X$
,
$x \in X$
,
![]() $\alpha (x)$
corresponds to an F-separated set.
$\alpha (x)$
corresponds to an F-separated set.
Using Lemma 6.15, we can find
![]() $R>\max \{R_0,R_1\}$
so that for any F-separated
$R>\max \{R_0,R_1\}$
so that for any F-separated
![]() $C \subseteq \Gamma $
, the disjointified R-truncated diagram of C has
$C \subseteq \Gamma $
, the disjointified R-truncated diagram of C has
![]() $( W,\epsilon _1)$
-small exterior boundary.
$( W,\epsilon _1)$
-small exterior boundary.
Let
![]() $\tau :\{0,1\}^\Gamma \to \mathit {PTilings}(\Gamma )$
be the map given by
$\tau :\{0,1\}^\Gamma \to \mathit {PTilings}(\Gamma )$
be the map given by
![]() $\tau (z)= \overline {V}_R(z)$
that assigns to every
$\tau (z)= \overline {V}_R(z)$
that assigns to every
![]() $z \in \{0,1\}^\Gamma $
the disjointified R-truncated diagram of
$z \in \{0,1\}^\Gamma $
the disjointified R-truncated diagram of
![]() $\alpha (x) \in \{0,1\}^\Gamma $
(interpreted as a subset of
$\alpha (x) \in \{0,1\}^\Gamma $
(interpreted as a subset of
![]() $\Gamma $
). By Lemma 6.10,
$\Gamma $
). By Lemma 6.10,
![]() $\tau :\{0,1\}^\Gamma \to \mathit {PTilings}(\Gamma )$
is continuous and equivariant. For every
$\tau :\{0,1\}^\Gamma \to \mathit {PTilings}(\Gamma )$
is continuous and equivariant. For every
![]() $x \in X$
, since every
$x \in X$
, since every
![]() $\alpha (x)$
corresponds to an F-separated set, by the choice of F, it follows that
$\alpha (x)$
corresponds to an F-separated set, by the choice of F, it follows that
![]() $\tau (\alpha (x))$
is a pointed
$\tau (\alpha (x))$
is a pointed
![]() $(K,\epsilon )$
-invariant tiling. If
$(K,\epsilon )$
-invariant tiling. If
![]() $v \not \in \bigcup \tau (\alpha (x))$
, then
$v \not \in \bigcup \tau (\alpha (x))$
, then
![]() $\mathrm {dist}_{\mathbb {R}^d}(v,w) \ge R$
for every
$\mathrm {dist}_{\mathbb {R}^d}(v,w) \ge R$
for every
![]() $w \in \Gamma $
such that
$w \in \Gamma $
such that
![]() $\alpha (x)_w=1$
. This means that
$\alpha (x)_w=1$
. This means that
![]() $\sigma _{v}(x) \not \in \bigcup _{u \in P \cup \{0\}}\sigma _u(C)$
, so
$\sigma _{v}(x) \not \in \bigcup _{u \in P \cup \{0\}}\sigma _u(C)$
, so
![]() $\sigma _{-v}(x)_W \in \mathcal {F}$
. This proves that property
$\sigma _{-v}(x)_W \in \mathcal {F}$
. This proves that property
![]() $1$
is satisfied. Because
$1$
is satisfied. Because
![]() $B_{R_1} \subseteq F$
and
$B_{R_1} \subseteq F$
and
![]() $\alpha (x)$
is F-separated, it follows that whenever
$\alpha (x)$
is F-separated, it follows that whenever
![]() $\alpha (x)_v=1$
, then the unique
$\alpha (x)_v=1$
, then the unique
![]() $T \in \tau (\alpha (x))$
corresponding to the disjointified R-truncated Voronoi cell of v contains
$T \in \tau (\alpha (x))$
corresponding to the disjointified R-truncated Voronoi cell of v contains
![]() $v+K$
. This proves that property
$v+K$
. This proves that property
![]() $2$
is satisfied. By the choice of R using Lemma 6.15, the disjointified R-truncated diagram of the set corresponding to
$2$
is satisfied. By the choice of R using Lemma 6.15, the disjointified R-truncated diagram of the set corresponding to
![]() $\alpha (x)$
has
$\alpha (x)$
has
![]() $( W,\epsilon _1)$
-small exterior boundary for every
$( W,\epsilon _1)$
-small exterior boundary for every
![]() $x \in X$
. This proves that property
$x \in X$
. This proves that property
![]() $3$
is satisfied.
$3$
is satisfied.
7 Good marker patterns via the map extension property
One of the key ideas in Krieger’s proof of his embedding theorem is to designate a special pattern in the range of the embedding to mark the occurrences of some clopen set in the domain. These ‘marker patterns’ need to satisfy several conditions. In particular, they need to be ‘locally identifyable’, which, in particular, requires them to have no self-overlaps. Also, the subshift obtained from Y by forbidding this marker pattern needs to have entropy‘big enough to embed X’. The purpose of this section is to formulate and prove a lemma that guarantees suitable marker patterns in the domain. The slightly involved formulation is given in Lemma 7.3.
We first state a basic result about the existence of patterns without self-overlaps.
Definition 7.1. Given
![]() $F \Subset \Gamma $
,
$F \Subset \Gamma $
,
![]() $v \in \Gamma $
, and a pattern
$v \in \Gamma $
, and a pattern
![]() $w \in A^F$
, we say that w has a self-overlap v if
$w \in A^F$
, we say that w has a self-overlap v if
We say that
![]() $w^{(1)},w^{(2)} \in A^F$
have an overlap at
$w^{(1)},w^{(2)} \in A^F$
have an overlap at
![]() $v\in \Gamma $
if
$v\in \Gamma $
if
Lemma 7.2. Let G be a finite abelian group,
![]() $ d\ge 1$
, and
$ d\ge 1$
, and
![]() $\Gamma = \mathbb {Z}^d \times G$
, and for
$\Gamma = \mathbb {Z}^d \times G$
, and for
![]() $k \in \mathbb {N}$
, let
$k \in \mathbb {N}$
, let
and
and let Y be a non-trivial strongly irreducible
![]() $\Gamma $
-subshift of finite type. Then, there exists
$\Gamma $
-subshift of finite type. Then, there exists
![]() $n_0$
such that for every
$n_0$
such that for every
![]() $n \ge n_0$
, there exist
$n \ge n_0$
, there exist
![]() $w \in \mathcal {L}_{Q_n}(Y)$
that have no self-overlaps in
$w \in \mathcal {L}_{Q_n}(Y)$
that have no self-overlaps in
![]() $B_n \setminus \mathrm {Ker}(Y)$
.
$B_n \setminus \mathrm {Ker}(Y)$
.
Similar results have appeared in the literature. For instance, in [Reference Ward25], patterns without self-overlaps have been constructed for strongly irreducible
![]() $\mathbb {Z}^2$
-subshifts. Also see [Reference Hochman16], where the existence of a non-overlapping pattern is established using a non-constructive argument using only positive positive entropy. We briefly sketch a proof below.
$\mathbb {Z}^2$
-subshifts. Also see [Reference Hochman16], where the existence of a non-overlapping pattern is established using a non-constructive argument using only positive positive entropy. We briefly sketch a proof below.
Proof. Let Y be a non-trivial strongly irreducible
![]() $\Gamma $
-subshift of finite type. In particular, Y is topologically mixing and non-trivial so
$\Gamma $
-subshift of finite type. In particular, Y is topologically mixing and non-trivial so
![]() $\mathrm {Ker}(Y)$
is a finite subgroup of
$\mathrm {Ker}(Y)$
is a finite subgroup of
![]() $\Gamma $
. Since Y is a strongly irreducible subshift of finite type, there exists
$\Gamma $
. Since Y is a strongly irreducible subshift of finite type, there exists
![]() $N \in \mathbb {N}$
so that for any
$N \in \mathbb {N}$
so that for any
![]() $m \in \mathbb {N}$
, any set
$m \in \mathbb {N}$
, any set
![]() $F \Subset \Gamma $
, and any
$F \Subset \Gamma $
, and any
![]() $B_{n+N}$
-separated set K and any
$B_{n+N}$
-separated set K and any
![]() $f:K \to \mathcal {L}_{B_m}(Y)$
, there exists
$f:K \to \mathcal {L}_{B_m}(Y)$
, there exists
![]() $x \in X$
with
$x \in X$
with
![]() $\sigma _v(x)_{B_m} = f(v)$
for all
$\sigma _v(x)_{B_m} = f(v)$
for all
![]() $v \in K$
. Choose
$v \in K$
. Choose
![]() $m \in \mathbb {N}$
sufficiently big, and then choose
$m \in \mathbb {N}$
sufficiently big, and then choose
![]() $n \in \mathbb {N}$
much bigger. Since pairwise disjoint translates of
$n \in \mathbb {N}$
much bigger. Since pairwise disjoint translates of
![]() $B_m$
tile the group
$B_m$
tile the group
![]() $\Gamma $
, there is a
$\Gamma $
, there is a
![]() $B_{n+N}$
separated subset
$B_{n+N}$
separated subset
![]() $K_{n,m}$
of
$K_{n,m}$
of
![]() $Q_n$
of size at least
$Q_n$
of size at least
![]() $({|Q_n|- |\partial _{B_m}Q_n|})/{|B_m|}$
. Choose
$({|Q_n|- |\partial _{B_m}Q_n|})/{|B_m|}$
. Choose
![]() $f \in \mathcal {L}_{B_m}(Y)^{K_{n,m}}$
uniformly at random. In other words, for every
$f \in \mathcal {L}_{B_m}(Y)^{K_{n,m}}$
uniformly at random. In other words, for every
![]() $v \in K_{n,m}$
, choose
$v \in K_{n,m}$
, choose
![]() $f(v) \in \mathcal {L}_{B_m}(Y)$
uniformly at random so that the random variables
$f(v) \in \mathcal {L}_{B_m}(Y)$
uniformly at random so that the random variables
![]() $(f(v))_{v \in K_{n,m}}$
are jointly independent. Let
$(f(v))_{v \in K_{n,m}}$
are jointly independent. Let
![]() $w \in \mathcal {L}_{B_m}(Y)$
be such that
$w \in \mathcal {L}_{B_m}(Y)$
be such that
![]() $\sigma _v(w)_{B_m}= f(v)$
for every
$\sigma _v(w)_{B_m}= f(v)$
for every
![]() $v \in K_{n,m}$
. If m is sufficiently big, there exists
$v \in K_{n,m}$
. If m is sufficiently big, there exists
![]() $p <1$
such that the probability that a uniformly chosen
$p <1$
such that the probability that a uniformly chosen
![]() $w \in \mathcal {L}_{B_m}(Y)$
has a self-overlap in
$w \in \mathcal {L}_{B_m}(Y)$
has a self-overlap in
![]() $B_{2N} \setminus \mathrm {Ker}(Y)$
is at most p. Also, if m is sufficiently big, the probability that independently chosen
$B_{2N} \setminus \mathrm {Ker}(Y)$
is at most p. Also, if m is sufficiently big, the probability that independently chosen
![]() $w^{(1)},w^{(2)} \in \mathcal {L}_{B_m}(Y)$
have an overlap in
$w^{(1)},w^{(2)} \in \mathcal {L}_{B_m}(Y)$
have an overlap in
![]() $B_{\lfloor m/w \rfloor -N}$
is at most p. It follows that for any
$B_{\lfloor m/w \rfloor -N}$
is at most p. It follows that for any
![]() $v \in B_n \setminus \mathrm {Ker}(Y)$
, the probability that the randomly chosen w has a self-overlap v is at most
$v \in B_n \setminus \mathrm {Ker}(Y)$
, the probability that the randomly chosen w has a self-overlap v is at most
![]() $p^{{|Q_{n-m} \cap (v+Q_{n-m})|}/{|B_m|}}$
. Since
$p^{{|Q_{n-m} \cap (v+Q_{n-m})|}/{|B_m|}}$
. Since
![]() $Q_{n-m} \cap (v+Q_{n-m})$
contains a translate of
$Q_{n-m} \cap (v+Q_{n-m})$
contains a translate of
![]() $B_{\lfloor n/3 \rfloor }$
for every
$B_{\lfloor n/3 \rfloor }$
for every
![]() $v \in B_m$
, it follows that the probability that w has an overlap at
$v \in B_m$
, it follows that the probability that w has an overlap at
![]() $v \in B_m \setminus \mathrm {Ker}(Y)$
is at most
$v \in B_m \setminus \mathrm {Ker}(Y)$
is at most
![]() $p^{(n-m)/3m}$
. By a union-bound, the probability that w has a self-overlap in
$p^{(n-m)/3m}$
. By a union-bound, the probability that w has a self-overlap in
![]() $B_n \setminus \mathrm {Ker}(Y)$
is bounded from above by
$B_n \setminus \mathrm {Ker}(Y)$
is bounded from above by
![]() $(2n+1)^d p^{(n-m)/3m}$
, which tends to
$(2n+1)^d p^{(n-m)/3m}$
, which tends to
![]() $0$
as
$0$
as
![]() $n\to \infty $
, for fixed m.
$n\to \infty $
, for fixed m.
Lemma 7.3. Let
![]() $\Gamma $
be an infinite finitely generated abelian group, let Y be a non-trivial
$\Gamma $
be an infinite finitely generated abelian group, let Y be a non-trivial
![]() $\Gamma $
-subshift with the map extension property, and let
$\Gamma $
-subshift with the map extension property, and let
![]() $\hat Y \subset Y$
be a (possibly empty)
$\hat Y \subset Y$
be a (possibly empty)
![]() $\Gamma $
-subshift strictly contained in Y. For any given
$\Gamma $
-subshift strictly contained in Y. For any given
![]() $\epsilon>0$
and any finite set
$\epsilon>0$
and any finite set
![]() $F_0 \Subset \Gamma $
, there exist:
$F_0 \Subset \Gamma $
, there exist:
-
• a subshift
 $S \subset Y$
with
$S \subset Y$
with
 $\hat Y \subseteq S$
;
$\hat Y \subseteq S$
; -
• a retraction map
 $\tilde r:Y \to S$
;
$\tilde r:Y \to S$
; -
• a map
 $\kappa :S \times \{0,1\}^\Gamma \to Y$
;
$\kappa :S \times \{0,1\}^\Gamma \to Y$
; -
• a finite symmetric set
 $F \Subset \Gamma $
such that
$F \Subset \Gamma $
such that
 $F_0 \Subset F$
;
$F_0 \Subset F$
; -
• patterns
 $w^{(0)},w^{(1)} \in \mathcal {L}_{F}(Y)$
such that
$w^{(0)},w^{(1)} \in \mathcal {L}_{F}(Y)$
such that
 $w^{(0)} \not \in \mathcal {L}_{F}(S)$
,
$w^{(0)} \not \in \mathcal {L}_{F}(S)$
,
so that the following hold.
-
(1) For any
 $y \in Y$
, if
$y \in Y$
, if
 $\tilde r(y)_0 \ne y_0$
, then there exists
$\tilde r(y)_0 \ne y_0$
, then there exists
 $w \in F$
such that
$w \in F$
such that
 $\sigma _w(y)_F = w^{(0)}$
. In particular, if
$\sigma _w(y)_F = w^{(0)}$
. In particular, if
 $y \in Y$
and
$y \in Y$
and
 $y_{F+F} \in \mathcal {L}_{F+F}(S)$
, then
$y_{F+F} \in \mathcal {L}_{F+F}(S)$
, then
 $\tilde r(y)_0=y_0$
.
$\tilde r(y)_0=y_0$
. -
(2) For every
 $y \in S$
and
$y \in S$
and
 $z \in \{0,1\}^\Gamma $
, if
$z \in \{0,1\}^\Gamma $
, if
 $\tilde y = \kappa (y,z)$
, then
$\tilde y = \kappa (y,z)$
, then
 $\tilde y_{F}= w^{(0)}$
if and only if
$\tilde y_{F}= w^{(0)}$
if and only if
 $y_F=~w^{(1)}$
and
$y_F=~w^{(1)}$
and
 $z_0 =1$
.
$z_0 =1$
. -
(3) For every
 $y \in S$
and
$y \in S$
and
 $z \in \{0,1\}^\Gamma $
, if
$z \in \{0,1\}^\Gamma $
, if
 $\tilde y = \kappa (y,z)$
and
$\tilde y = \kappa (y,z)$
and
 $z_v \ne 1$
for all
$z_v \ne 1$
for all
 $v \in F$
, then
$v \in F$
, then
 $\tilde y_0 =~y_0$
.
$\tilde y_0 =~y_0$
. -
(4) For any
 $\Gamma _0 \le \Gamma $
, if
$\Gamma _0 \le \Gamma $
, if
 $Y_{\Gamma _0} \ne \emptyset $
, then
$Y_{\Gamma _0} \ne \emptyset $
, then
 $S_{\Gamma _0} \ne \emptyset $
.
$S_{\Gamma _0} \ne \emptyset $
. -
(5) For any
 $\Gamma _0 \le \Gamma $
, it holds that
$\Gamma _0 \le \Gamma $
, it holds that
 $\mathrm {Ker}( Y_{\Gamma _0})= \mathrm {Ker}(S_{\Gamma _0})$
and
$\mathrm {Ker}( Y_{\Gamma _0})= \mathrm {Ker}(S_{\Gamma _0})$
and
 $h(\overline {S}_{\Gamma _0}) \ge h(\overline {Y}_{\Gamma _0})-\epsilon $
.
$h(\overline {S}_{\Gamma _0}) \ge h(\overline {Y}_{\Gamma _0})-\epsilon $
.
Proof. By the structure of finitely generated abelian groups, we can assume that
![]() $\Gamma = \mathbb {Z}^d \times G$
, where G is a finite abelian group and
$\Gamma = \mathbb {Z}^d \times G$
, where G is a finite abelian group and
![]() $d \ge 1$
. Let Y be a non-trivial
$d \ge 1$
. Let Y be a non-trivial
![]() $\Gamma $
-subshift with the map extension property and let
$\Gamma $
-subshift with the map extension property and let
![]() $\hat Y \subset Y$
be a (possibly empty) closed,
$\hat Y \subset Y$
be a (possibly empty) closed,
![]() $\Gamma $
-invariant set such that
$\Gamma $
-invariant set such that
![]() $\hat Y \ne Y$
. Note that since Y is a non-trivial subshift with the map extension property, it is topologically mixing and, in particular,
$\hat Y \ne Y$
. Note that since Y is a non-trivial subshift with the map extension property, it is topologically mixing and, in particular,
![]() $\mathrm {Ker}((Y)$
is finite and hence contained in
$\mathrm {Ker}((Y)$
is finite and hence contained in
![]() $\{0\} \times G \le \Gamma $
. Replacing
$\{0\} \times G \le \Gamma $
. Replacing
![]() $\Gamma $
with
$\Gamma $
with
![]() $\Gamma / \mathrm {Ker}(Y)$
, we can conveniently assume that
$\Gamma / \mathrm {Ker}(Y)$
, we can conveniently assume that
![]() $\mathrm {Ker}(Y)= \{0\}$
. Fix any
$\mathrm {Ker}(Y)= \{0\}$
. Fix any
![]() $\epsilon>0$
and any finite set
$\epsilon>0$
and any finite set
![]() $F_0 \Subset \Gamma $
. For any
$F_0 \Subset \Gamma $
. For any
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $B_n, Q_n \Subset \Gamma $
be defined as in Lemma 7.2 and let
$B_n, Q_n \Subset \Gamma $
be defined as in Lemma 7.2 and let
Since Y has the map extension property, by Proposition 4.24, Y is strongly irreducible. By Lemma 7.2, for sufficiently big
![]() $n \in \mathbb {N}$
, we can find a pattern
$n \in \mathbb {N}$
, we can find a pattern
![]() $w^{(1)} \in \mathcal {L}_{B_n}(Y)$
such that
$w^{(1)} \in \mathcal {L}_{B_n}(Y)$
such that
![]() $w^{(1)}_{Q_n}$
has no self-overlaps in
$w^{(1)}_{Q_n}$
has no self-overlaps in
![]() $B_n$
. Because Y is strongly irreducible, we can choose
$B_n$
. Because Y is strongly irreducible, we can choose
![]() $n \in \mathbb {N}$
sufficiently big and
$n \in \mathbb {N}$
sufficiently big and
![]() $({1}/{20}) n < k < ({1}/{11}) n$
so that the following are also satisfied.
$({1}/{20}) n < k < ({1}/{11}) n$
so that the following are also satisfied.
-
• For every
 $\hat w \in \mathcal {L}_{Q_n}(Y)$
and
$\hat w \in \mathcal {L}_{Q_n}(Y)$
and
 $\tilde w \in \mathcal {L}_{B_k}(Y)$
, there exists
$\tilde w \in \mathcal {L}_{B_k}(Y)$
, there exists
 $w \in \mathcal {L}_{B_n}(Y)$
so that
$w \in \mathcal {L}_{B_n}(Y)$
so that
 $w_{Q_n} = \hat w$
and
$w_{Q_n} = \hat w$
and
 $w_{B_k}= \tilde w$
.
$w_{B_k}= \tilde w$
. -
•
 $F_0 \subseteq B_{\lfloor n/11 \rfloor }$
.
$F_0 \subseteq B_{\lfloor n/11 \rfloor }$
. -
•
 $|\mathcal {L}_{B_k}(Y)\setminus \mathcal {L}_{B_k}(\hat Y)| \ge |B_n|+2$
.
$|\mathcal {L}_{B_k}(Y)\setminus \mathcal {L}_{B_k}(\hat Y)| \ge |B_n|+2$
. -
•
 $$ \begin{align*} \log \bigg(\frac{ |W_{n,k}| }{|W_{n,k}|-1} \bigg) \le \epsilon. \end{align*} $$
$$ \begin{align*} \log \bigg(\frac{ |W_{n,k}| }{|W_{n,k}|-1} \bigg) \le \epsilon. \end{align*} $$
The properties above guarantees that there exist two distinct words
![]() $\tilde w^{(0)},\tilde w^{(2)} \in \mathcal {L}_{B_{k}}(Y)\setminus \mathcal {L}_{B_{k}}(\tilde Y)$
that do not occur in
$\tilde w^{(0)},\tilde w^{(2)} \in \mathcal {L}_{B_{k}}(Y)\setminus \mathcal {L}_{B_{k}}(\tilde Y)$
that do not occur in
![]() $w^{(1)}$
, and also (under our assumption that
$w^{(1)}$
, and also (under our assumption that
![]() $\mathrm {Ker}(Y)= \{0\}$
) so that
$\mathrm {Ker}(Y)= \{0\}$
) so that
![]() $\sigma _v(\tilde w^{(i)}) \ne \tilde w^{(i)}$
for every
$\sigma _v(\tilde w^{(i)}) \ne \tilde w^{(i)}$
for every
![]() $v \in \{0\} \times G$
and
$v \in \{0\} \times G$
and
![]() $i \in \{0,2\}$
. Also, there exists
$i \in \{0,2\}$
. Also, there exists
![]() $w^{(0)},w^{(2)} \in \mathcal {L}_{B_n}(Y)$
such that
$w^{(0)},w^{(2)} \in \mathcal {L}_{B_n}(Y)$
such that
![]() $w^{(0)}_{Q_n} = w^{(1)}_{Q_n}= w^{(2)}_{Q_n}$
and
$w^{(0)}_{Q_n} = w^{(1)}_{Q_n}= w^{(2)}_{Q_n}$
and
![]() $w^{(i)}_{B_k} = \tilde w^{(i)}$
for
$w^{(i)}_{B_k} = \tilde w^{(i)}$
for
![]() $i \in \{0,2\}$
.
$i \in \{0,2\}$
.
Let
![]() $F= B_n$
and let
$F= B_n$
and let
Since
![]() $\tilde w \not \in \mathcal {L}_{B_k}(\hat Y)$
, it follows that
$\tilde w \not \in \mathcal {L}_{B_k}(\hat Y)$
, it follows that
![]() $w^{(0)} \not \in \mathcal {L}_{B_n}(\hat Y)$
, so
$w^{(0)} \not \in \mathcal {L}_{B_n}(\hat Y)$
, so
![]() $\hat Y \subseteq S$
.
$\hat Y \subseteq S$
.
Let
![]() $\tilde r:Y \to S$
be the map that replaces every occurrence of
$\tilde r:Y \to S$
be the map that replaces every occurrence of
![]() $w^{(0)}$
with an occurrence of
$w^{(0)}$
with an occurrence of
![]() $w^{(1)}$
. The map r is well defined because the occurrences of
$w^{(1)}$
. The map r is well defined because the occurrences of
![]() $w^{(0)}$
in any
$w^{(0)}$
in any
![]() $y \in Y$
are
$y \in Y$
are
![]() $B_n$
-separated and also
$B_n$
-separated and also
![]() $B_{n-k}$
-disjoint from the occurrences of
$B_{n-k}$
-disjoint from the occurrences of
![]() $w^{(1)}$
. The map
$w^{(1)}$
. The map
![]() $\tilde r$
is a retraction map from Y to S. It is clear that condition
$\tilde r$
is a retraction map from Y to S. It is clear that condition
![]() $(1)$
in the statement of the lemma holds.
$(1)$
in the statement of the lemma holds.
Let
![]() $\kappa : S \times \{0,1\}^\Gamma \to Y$
be the map defined as follows. For
$\kappa : S \times \{0,1\}^\Gamma \to Y$
be the map defined as follows. For
![]() $y \in S$
and
$y \in S$
and
![]() $z \in \{0,1\}^\Gamma $
, the point
$z \in \{0,1\}^\Gamma $
, the point
![]() $\tilde y \in Y$
is obtained by replacing the occurrences of
$\tilde y \in Y$
is obtained by replacing the occurrences of
![]() $w^{(1)}$
in the set
$w^{(1)}$
in the set
![]() $\{ v \in \Gamma : z_v=1\}$
by occurrences of
$\{ v \in \Gamma : z_v=1\}$
by occurrences of
![]() $w^{(0)}$
. Because the occurrences of
$w^{(0)}$
. Because the occurrences of
![]() $w^{(1)}$
are
$w^{(1)}$
are
![]() $B_n$
-separated, this is well defined. From the definition, it follows that conditions
$B_n$
-separated, this is well defined. From the definition, it follows that conditions
![]() $(2)$
and
$(2)$
and
![]() $(3)$
in the statement of the lemma are satisfied.
$(3)$
in the statement of the lemma are satisfied.
We will now show that for any
![]() $y \in Y$
, there exists
$y \in Y$
, there exists
![]() $\hat y \in S$
with
$\hat y \in S$
with
![]() $\mathrm {stab}(y) = \mathrm {stab}(\hat y)$
. Take any
$\mathrm {stab}(y) = \mathrm {stab}(\hat y)$
. Take any
![]() $y \in Y$
. If
$y \in Y$
. If
![]() $w^{(0)}$
does not occur in y, then
$w^{(0)}$
does not occur in y, then
![]() $y \in S$
and we can take
$y \in S$
and we can take
![]() $\hat y= y$
. Otherwise, there exists
$\hat y= y$
. Otherwise, there exists
![]() $v \in \Gamma $
such that
$v \in \Gamma $
such that
![]() $w^{(0)}$
occurs in y at
$w^{(0)}$
occurs in y at
![]() $v+w$
for every
$v+w$
for every
![]() $w \in \mathrm {stab}(y)$
. Replacing y by
$w \in \mathrm {stab}(y)$
. Replacing y by
![]() $\sigma _{-v}(y)$
, we can assume that
$\sigma _{-v}(y)$
, we can assume that
![]() $w^{(0)}$
occurs in y at every
$w^{(0)}$
occurs in y at every
![]() $w \in \mathrm {stab}(y)$
. Let
$w \in \mathrm {stab}(y)$
. Let
![]() $\hat y \in Y$
be the point obtained from y by replacing each occurrence of
$\hat y \in Y$
be the point obtained from y by replacing each occurrence of
![]() $w^{(0)}$
in
$w^{(0)}$
in
![]() $\mathrm {stab}(y)$
by an occurrence of
$\mathrm {stab}(y)$
by an occurrence of
![]() $w^{(2)}$
, and replacing every other occurrence of
$w^{(2)}$
, and replacing every other occurrence of
![]() $w^{(0)}$
or
$w^{(0)}$
or
![]() $w^{(2)}$
in y by an occurrence of
$w^{(2)}$
in y by an occurrence of
![]() $w^{(1)}$
. It is clear that
$w^{(1)}$
. It is clear that
![]() $\mathrm {stab}(y) \le \mathrm {stab}(\hat y)$
. However, since
$\mathrm {stab}(y) \le \mathrm {stab}(\hat y)$
. However, since
![]() $w^{(2)}$
only occurs in y at
$w^{(2)}$
only occurs in y at
![]() $\mathrm {stab}(y)$
, it follows that
$\mathrm {stab}(y)$
, it follows that
![]() $\mathrm {stab}(\hat y) \le \mathrm {stab}(y)$
.
$\mathrm {stab}(\hat y) \le \mathrm {stab}(y)$
.
From this, it follows that if
![]() $Y_{\Gamma _0} \ne \emptyset $
, then
$Y_{\Gamma _0} \ne \emptyset $
, then
![]() $S_{\Gamma _0} \ne \emptyset $
, and also that for every
$S_{\Gamma _0} \ne \emptyset $
, and also that for every
![]() $\Gamma _0 \le \Gamma $
, we have
$\Gamma _0 \le \Gamma $
, we have
![]() $\mathrm {Ker}(S_{\Gamma _0})=\mathrm {Ker}(Y_{\Gamma _0})$
. In particular, condition
$\mathrm {Ker}(S_{\Gamma _0})=\mathrm {Ker}(Y_{\Gamma _0})$
. In particular, condition
![]() $(4)$
in the statement of the lemma is satisfied.
$(4)$
in the statement of the lemma is satisfied.
Let
![]() $\Gamma _0 \le \Gamma $
be a subgroup which is not
$\Gamma _0 \le \Gamma $
be a subgroup which is not
![]() $B_n$
-separated, then
$B_n$
-separated, then
![]() $w^{(0)}$
does not occur in
$w^{(0)}$
does not occur in
![]() $Y_{\Gamma _0}$
, and so
$Y_{\Gamma _0}$
, and so
![]() $S_{\Gamma _0}= Y_{\Gamma _0}$
and, in particular, if
$S_{\Gamma _0}= Y_{\Gamma _0}$
and, in particular, if
![]() $Y_{\Gamma _0} \ne \emptyset $
, then
$Y_{\Gamma _0} \ne \emptyset $
, then
![]() $S_{\Gamma _0} \ne \emptyset $
, and in that case,
$S_{\Gamma _0} \ne \emptyset $
, and in that case,
![]() $\mathrm {Ker}(S_{\Gamma _0})=\mathrm {Ker}(Y_{\Gamma _0})$
and
$\mathrm {Ker}(S_{\Gamma _0})=\mathrm {Ker}(Y_{\Gamma _0})$
and
![]() $h(S_{\Gamma _0})=h(Y_{\Gamma _0})$
. Take any
$h(S_{\Gamma _0})=h(Y_{\Gamma _0})$
. Take any
![]() $B_n$
-separated subgroup
$B_n$
-separated subgroup
![]() $\Gamma _0 \le \Gamma $
and let
$\Gamma _0 \le \Gamma $
and let
![]() $D_{\Gamma _0}$
be a fundamental domain for
$D_{\Gamma _0}$
be a fundamental domain for
![]() $\Gamma _0$
.
$\Gamma _0$
.
Then,
 $$ \begin{align*} \frac{|\mathcal{L}_{B_m}(Y_{\Gamma_0})|}{|\mathcal{L}_{B_n}(S_{\Gamma_0})|} \le \bigg(\frac{ |W_{n,k}| }{|W_{n,k}|-1}\bigg)^{|B_m \cap D_{\Gamma_0}|}. \end{align*} $$
$$ \begin{align*} \frac{|\mathcal{L}_{B_m}(Y_{\Gamma_0})|}{|\mathcal{L}_{B_n}(S_{\Gamma_0})|} \le \bigg(\frac{ |W_{n,k}| }{|W_{n,k}|-1}\bigg)^{|B_m \cap D_{\Gamma_0}|}. \end{align*} $$
It follows that
 $$ \begin{align*} \frac{1}{|B_m \cap D_{\Gamma}|}\log| \mathcal{L}_{B_m}(Y_{\Gamma_0})| -\frac{1}{|B_m \cap D_{\Gamma}|}\log| \mathcal{L}_{B_m}(S_{\Gamma_0}) | \le \log \bigg(\frac{ |W_{n,k}| }{|W_{n,k}|-1} \bigg). \end{align*} $$
$$ \begin{align*} \frac{1}{|B_m \cap D_{\Gamma}|}\log| \mathcal{L}_{B_m}(Y_{\Gamma_0})| -\frac{1}{|B_m \cap D_{\Gamma}|}\log| \mathcal{L}_{B_m}(S_{\Gamma_0}) | \le \log \bigg(\frac{ |W_{n,k}| }{|W_{n,k}|-1} \bigg). \end{align*} $$
So taking
![]() $m \to \infty $
, we have that
$m \to \infty $
, we have that
This shows that condition
![]() $(5)$
is satisfied and completes the proof of the lemma.
$(5)$
is satisfied and completes the proof of the lemma.
8 Proof of the embedding theorem for subshifts over a finitely generated abelian group
In this section, we complete the proof of the more difficult direction of our main theorem for the case that
![]() $\Gamma $
is a finitely generated abelian group. Namely, we prove that in the case where
$\Gamma $
is a finitely generated abelian group. Namely, we prove that in the case where
![]() $\Gamma $
is a finitely generated abelain group, the conditions
$\Gamma $
is a finitely generated abelain group, the conditions
![]() $E(X,Y,\hat \rho ,\Gamma _0)$
from Definition 2.24 are sufficient to assure that
$E(X,Y,\hat \rho ,\Gamma _0)$
from Definition 2.24 are sufficient to assure that
![]() $X_{\tilde \Gamma } \hookrightarrow _{\hat \rho } Y_{\tilde \Gamma }$
. We phrase a slightly more involved statement for the purpose of the internal inductive nature of our proof.
$X_{\tilde \Gamma } \hookrightarrow _{\hat \rho } Y_{\tilde \Gamma }$
. We phrase a slightly more involved statement for the purpose of the internal inductive nature of our proof.
Proposition 8.1. Let
![]() $\Gamma $
be a finitely generated abelian group and let
$\Gamma $
be a finitely generated abelian group and let
![]() $X,Y$
be
$X,Y$
be
![]() $\Gamma $
-subshifts. Suppose that Y has the map extension property. Let
$\Gamma $
-subshifts. Suppose that Y has the map extension property. Let
![]() $Z \subseteq X$
be a closed
$Z \subseteq X$
be a closed
![]() $\Gamma $
-invariant set and let
$\Gamma $
-invariant set and let
![]() $\hat \rho :Z \to Y$
be an embedding. Suppose that
$\hat \rho :Z \to Y$
be an embedding. Suppose that
![]() $E(X,Y,\hat \rho ,\Gamma _0)$
holds for any subgroup
$E(X,Y,\hat \rho ,\Gamma _0)$
holds for any subgroup
![]() $\Gamma _0 \le \Gamma $
. Then,
$\Gamma _0 \le \Gamma $
. Then,
![]() $X_{\tilde \Gamma } \hookrightarrow _{\hat \rho } Y_{\tilde \Gamma }$
.
$X_{\tilde \Gamma } \hookrightarrow _{\hat \rho } Y_{\tilde \Gamma }$
.
Proof. We will prove the statement by a double induction: the external induction on the rank of the group
![]() $\Gamma $
and the internal induction over the size of the torsion subgroup of
$\Gamma $
and the internal induction over the size of the torsion subgroup of
![]() $\Gamma $
.
$\Gamma $
.
Let
![]() $X \subseteq B^\Gamma $
,
$X \subseteq B^\Gamma $
,
![]() $Y \subseteq A^\Gamma $
,
$Y \subseteq A^\Gamma $
,
![]() $Z\subseteq X$
, and
$Z\subseteq X$
, and
![]() $\hat \rho :Z \to Y$
be as in the statement of the lemma.
$\hat \rho :Z \to Y$
be as in the statement of the lemma.
By Proposition 4.19, there exists a finite set
![]() $\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
such that Y is an absolute retract for the class of
$\mathcal {G} \Subset \mathrm {Sub}(\Gamma )$
such that Y is an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts. In particular, by Lemma 4.15, there exists a finite set
$\mathcal {G}$
-free subshifts. In particular, by Lemma 4.15, there exists a finite set
![]() $W_0 \Subset \Gamma $
that witnesses that Y is
$W_0 \Subset \Gamma $
that witnesses that Y is
![]() $\mathcal {G}$
-free. By part (ii) of Lemma 4.18, there exists a finite set
$\mathcal {G}$
-free. By part (ii) of Lemma 4.18, there exists a finite set
![]() $F \Subset \Gamma $
so that for any
$F \Subset \Gamma $
so that for any
![]() $\mathcal {G}$
-free subshift
$\mathcal {G}$
-free subshift
![]() $\hat Y$
, there exists a retraction map
$\hat Y$
, there exists a retraction map
![]() $\hat r:\hat Y \to Y$
such that if
$\hat r:\hat Y \to Y$
such that if
![]() $y \in \hat Y$
and
$y \in \hat Y$
and
![]() $y_F \in \mathcal {L}_F(Y)$
, then
$y_F \in \mathcal {L}_F(Y)$
, then
![]() $\hat r(y)_0=y_0$
.
$\hat r(y)_0=y_0$
.
Since
![]() $E(X,Y,\hat \rho ,\{0\})$
holds, either
$E(X,Y,\hat \rho ,\{0\})$
holds, either
![]() $h(X) < h(Y)$
or
$h(X) < h(Y)$
or
![]() $X \cong _{\hat \rho } Y$
. In the second case, there is nothing to prove. So we can assume that
$X \cong _{\hat \rho } Y$
. In the second case, there is nothing to prove. So we can assume that
![]() $h(X) < h(Y)$
. Let
$h(X) < h(Y)$
. Let
![]() $\eta = \tfrac 13(h(Y)- h(X))$
. Choose
$\eta = \tfrac 13(h(Y)- h(X))$
. Choose
![]() $n \in \mathbb {N}$
sufficiently big so that
$n \in \mathbb {N}$
sufficiently big so that
![]() $F \subseteq B_n$
, and also so that for any pattern
$F \subseteq B_n$
, and also so that for any pattern
![]() $w \in \mathcal {L}_{B_{5n}(Y)}$
and any
$w \in \mathcal {L}_{B_{5n}(Y)}$
and any
![]() $y \in Y$
, there exists
$y \in Y$
, there exists
![]() $\tilde y \in Y$
so that
$\tilde y \in Y$
so that
![]() $\tilde y_{B_{5n}}=w$
and
$\tilde y_{B_{5n}}=w$
and
![]() $\tilde y_{\Gamma \setminus B_{6n}}=y_{\Gamma \setminus B_{6n}}$
.
$\tilde y_{\Gamma \setminus B_{6n}}=y_{\Gamma \setminus B_{6n}}$
.
By Proposition 4.20, there exists a finite set
![]() $F_1 \Subset \Gamma \setminus \{0\}$
such that for any
$F_1 \Subset \Gamma \setminus \{0\}$
such that for any
![]() $\Gamma _0 < \Gamma $
with
$\Gamma _0 < \Gamma $
with
![]() $\Gamma _0 \cap F_1 \ne \emptyset $
, we have that
$\Gamma _0 \cap F_1 \ne \emptyset $
, we have that
![]() $h_{\Gamma _0}(Y)> h(Y) - \eta $
. By Proposition 2.23, there exists a finite set
$h_{\Gamma _0}(Y)> h(Y) - \eta $
. By Proposition 2.23, there exists a finite set
![]() $F_2 \Subset \Gamma \setminus \{0\}$
such that for any
$F_2 \Subset \Gamma \setminus \{0\}$
such that for any
![]() $\Gamma _0 < \Gamma $
with
$\Gamma _0 < \Gamma $
with
![]() $\Gamma _0 \cap F_2 \ne \emptyset $
, we have that
$\Gamma _0 \cap F_2 \ne \emptyset $
, we have that
![]() $h_{\Gamma _0}(X) < h(X) + \eta $
. Let
$h_{\Gamma _0}(X) < h(X) + \eta $
. Let
![]() $F_0= F_1 \cup F_2$
. It follows that
$F_0= F_1 \cup F_2$
. It follows that
![]() $h_{\Gamma _0}(X) < h_{\Gamma _0}(Y) -\eta $
whenever
$h_{\Gamma _0}(X) < h_{\Gamma _0}(Y) -\eta $
whenever
![]() $\Gamma _0 < \Gamma $
satisfies that
$\Gamma _0 < \Gamma $
satisfies that
![]() $F \cap \Gamma _0 \ne \emptyset $
.
$F \cap \Gamma _0 \ne \emptyset $
.
Let
![]() $\mathcal {G}_0$
denote the family of non-trivial subgroups of
$\mathcal {G}_0$
denote the family of non-trivial subgroups of
![]() $\Gamma $
generated by a subset of the elements of
$\Gamma $
generated by a subset of the elements of
![]() $F_0$
. Let
$F_0$
. Let
![]() $\hat Y= \hat \rho (Z) \cup \bigcup _{\Gamma _0 \in \mathcal {G}_0} Y_{\Gamma _0}$
.
$\hat Y= \hat \rho (Z) \cup \bigcup _{\Gamma _0 \in \mathcal {G}_0} Y_{\Gamma _0}$
.
Applying Lemma 7.3 with
![]() $X,Y, \hat Y$
,
$X,Y, \hat Y$
,
![]() $F_0$
as above, and
$F_0$
as above, and
![]() $\epsilon = \eta $
, we can find a finite symmetric set
$\epsilon = \eta $
, we can find a finite symmetric set
![]() $F \subset \Gamma $
, subshift
$F \subset \Gamma $
, subshift
![]() $S \subset Y$
, a retraction map
$S \subset Y$
, a retraction map
![]() $\tilde r:Y \to S$
, a map
$\tilde r:Y \to S$
, a map
![]() $\kappa :S \times \{0,1\}^\Gamma \to Y$
, and patterns
$\kappa :S \times \{0,1\}^\Gamma \to Y$
, and patterns
![]() $w^{(0)},w^{(1)} \in \mathcal {L}_F(Y)$
such that
$w^{(0)},w^{(1)} \in \mathcal {L}_F(Y)$
such that
![]() $w^{(0)} \not \in \mathcal {L}_F(S)$
so that conditions (1)–(5) in the statement of Lemma 7.3 hold.
$w^{(0)} \not \in \mathcal {L}_F(S)$
so that conditions (1)–(5) in the statement of Lemma 7.3 hold.
Observe that the subshift S also has the map extension property, since it is a retract of Y. Furthermore,
![]() $h(S)> h(X)$
and for any
$h(S)> h(X)$
and for any
![]() $\Gamma _0 \le \Gamma $
, the condition
$\Gamma _0 \le \Gamma $
, the condition
![]() $E(X,S,\hat \rho , \Gamma _0)$
holds. Since
$E(X,S,\hat \rho , \Gamma _0)$
holds. Since
![]() $h(X) < h(S)$
, by Lemma 2.22, we can find
$h(X) < h(S)$
, by Lemma 2.22, we can find
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $K \Subset \Gamma $
so that for any
$K \Subset \Gamma $
so that for any
![]() $(K,\epsilon )$
-invariant set
$(K,\epsilon )$
-invariant set
![]() $T \Subset \Gamma $
, we have
$T \Subset \Gamma $
, we have
Applying Proposition 6.4 with X,
![]() $K \subset \Gamma $
, and
$K \subset \Gamma $
, and
![]() $\epsilon>0$
, we obtain a suitable set
$\epsilon>0$
, we obtain a suitable set
![]() $P \Subset \Gamma \setminus \{0\}$
.
$P \Subset \Gamma \setminus \{0\}$
.
Let
![]() $\mathcal {G}_1 \Subset \mathrm {Sub}(\Gamma )$
denote the union of
$\mathcal {G}_1 \Subset \mathrm {Sub}(\Gamma )$
denote the union of
![]() $\mathcal {G}_0$
with the family of non-trivial subgroups of
$\mathcal {G}_0$
with the family of non-trivial subgroups of
![]() $\Gamma $
generated by a subset of the elements of P.
$\Gamma $
generated by a subset of the elements of P.
Order the elements of
![]() $\mathcal {G}_1$
as
$\mathcal {G}_1$
as
![]() $\mathcal {G}_1 = \{\Gamma _1,\ldots ,\Gamma _m\}$
. We will prove that for every
$\mathcal {G}_1 = \{\Gamma _1,\ldots ,\Gamma _m\}$
. We will prove that for every
![]() $1\le j \le m$
, there exists an embedding
$1\le j \le m$
, there exists an embedding
![]() $\rho _j: (Z \cup \bigcup _{\ell =1}^j X_{\Gamma _\ell }) \to \tilde Y$
that extends
$\rho _j: (Z \cup \bigcup _{\ell =1}^j X_{\Gamma _\ell }) \to \tilde Y$
that extends
![]() $\tilde \rho $
. The construction proceeds in m steps, where in step j, we extend
$\tilde \rho $
. The construction proceeds in m steps, where in step j, we extend
![]() $\rho _j$
to
$\rho _j$
to
![]() $\rho _{j+1}$
using the main induction hypothesis with
$\rho _{j+1}$
using the main induction hypothesis with
![]() $\Gamma $
replaced by
$\Gamma $
replaced by
![]() $\Gamma /\Gamma _{j+1}$
(noting that
$\Gamma /\Gamma _{j+1}$
(noting that
![]() $\Gamma /\Gamma _{j+1}$
either has lower rank than
$\Gamma /\Gamma _{j+1}$
either has lower rank than
![]() $\Gamma $
or smaller torsion).
$\Gamma $
or smaller torsion).
So now we can conveniently replace Z with
![]() $Z \cup \bigcup _{j=1}^m X_{\Gamma _j}$
and replace
$Z \cup \bigcup _{j=1}^m X_{\Gamma _j}$
and replace
![]() $\hat \rho $
with
$\hat \rho $
with
![]() $\rho _m$
, and thus assume that
$\rho _m$
, and thus assume that
![]() $X_{\Gamma _j} \subseteq Z$
for every
$X_{\Gamma _j} \subseteq Z$
for every
![]() $1\le j \le m$
.
$1\le j \le m$
.
Let
![]() $W_1 \Subset \Gamma $
be a coding window for
$W_1 \Subset \Gamma $
be a coding window for
![]() $\hat \rho $
and let
$\hat \rho $
and let
![]() $\hat \Phi :B^{W_1} \to A$
be a sliding block code for
$\hat \Phi :B^{W_1} \to A$
be a sliding block code for
![]() $\hat \rho $
. By possibly enlarging
$\hat \rho $
. By possibly enlarging
![]() $W_1 \Subset \Gamma $
, we can also assume that
$W_1 \Subset \Gamma $
, we can also assume that
![]() $F\subseteq W_1$
(and in particular that
$F\subseteq W_1$
(and in particular that
![]() $0 \in W_1$
), and also that
$0 \in W_1$
), and also that
![]() $W_1$
is symmetric. Since Z is relatively of finite type on X, we can further enlarge
$W_1$
is symmetric. Since Z is relatively of finite type on X, we can further enlarge
![]() $W_1$
so that if
$W_1$
so that if
![]() $x \in X$
, then
$x \in X$
, then
![]() $x \in Z$
if and only if
$x \in Z$
if and only if
![]() $\sigma _v(x)_W \in \mathcal {F}$
for all
$\sigma _v(x)_W \in \mathcal {F}$
for all
![]() $v \in \Gamma $
. In particular, if
$v \in \Gamma $
. In particular, if
![]() $x \in X$
and
$x \in X$
and
![]() $x_W \not \in \mathcal {F}$
, then
$x_W \not \in \mathcal {F}$
, then
![]() $x \not \in Z$
, and in particular
$x \not \in Z$
, and in particular
![]() $\mathrm {stab}(x) \cap P = \emptyset $
. Let
$\mathrm {stab}(x) \cap P = \emptyset $
. Let
![]() $\mathcal {F} = \mathcal {L}_{W_1}(Z)$
. Then, indeed if
$\mathcal {F} = \mathcal {L}_{W_1}(Z)$
. Then, indeed if
![]() $x \in X$
and
$x \in X$
and
![]() $x_W \not \in \mathcal {F}$
, then
$x_W \not \in \mathcal {F}$
, then
![]() $\mathrm {stab}(x) \cap P = \emptyset $
. Let
$\mathrm {stab}(x) \cap P = \emptyset $
. Let
![]() $W_2$
be a symmetric injectivity window for
$W_2$
be a symmetric injectivity window for
![]() $\hat \rho $
(with respect to the sliding block
$\hat \rho $
(with respect to the sliding block
![]() $\hat \Phi $
), with
$\hat \Phi $
), with
![]() $0 \in W_2$
. Let
$0 \in W_2$
. Let
![]() $\tilde W = W_1 +W_2$
. Then,
$\tilde W = W_1 +W_2$
. Then,
![]() $\hat \rho $
extends to an embedding of the subshift of finite type
$\hat \rho $
extends to an embedding of the subshift of finite type
![]() $\tilde Z$
given by
$\tilde Z$
given by
Since
![]() $Z \subseteq \tilde Z$
, we can conveniently replace Z by
$Z \subseteq \tilde Z$
, we can conveniently replace Z by
![]() $\tilde Z$
.
$\tilde Z$
.
Given a map
![]() $\alpha :X \to \{0,1\}^\Gamma $
, a pointed partial tiling
$\alpha :X \to \{0,1\}^\Gamma $
, a pointed partial tiling
![]() $\tau :\alpha (X) \to \mathit {PTilings}(\Gamma )$
,
$\tau :\alpha (X) \to \mathit {PTilings}(\Gamma )$
,
![]() $x \in X$
, and
$x \in X$
, and
![]() $v \in \Gamma $
such that
$v \in \Gamma $
such that
![]() $\alpha (x)_v=1$
, let
$\alpha (x)_v=1$
, let
![]() $T_v(x) \Subset \Gamma $
denote the tile in
$T_v(x) \Subset \Gamma $
denote the tile in
![]() $\tau (\alpha (x))$
that contains v, and let
$\tau (\alpha (x))$
that contains v, and let
and
Applying Proposition 6.4 with the previously obtained set
![]() $P \Subset \Gamma \setminus \{0\}$
,
$P \Subset \Gamma \setminus \{0\}$
,
![]() $W= W_1$
, and
$W= W_1$
, and
![]() $\tilde W = W_1 +W_2$
and
$\tilde W = W_1 +W_2$
and
![]() $\epsilon _1>0$
sufficiently small, we obtain the existence of a map
$\epsilon _1>0$
sufficiently small, we obtain the existence of a map
![]() $\alpha :X \to \{0,1\}$
and a pointed
$\alpha :X \to \{0,1\}$
and a pointed
![]() $(K,\epsilon )$
-invariant tiling
$(K,\epsilon )$
-invariant tiling
![]() $\tau : \alpha (X) \to \mathit {PTilings}(\Gamma )$
such that for every
$\tau : \alpha (X) \to \mathit {PTilings}(\Gamma )$
such that for every
![]() $x \in X$
:
$x \in X$
:
-
(1) for every
 $v \in \Gamma $
such that
$v \in \Gamma $
such that
 $\alpha (x)_v=1$
, letting
$\alpha (x)_v=1$
, letting
 $T^- = T^-_v(x)$
and
$T^- = T^-_v(x)$
and
 $T^+=T^+_v(x)$
, it holds that
$T^+=T^+_v(x)$
, it holds that
 $| \mathcal {L}_{T^+}(X)| \le |\mathcal {L}_{T^-}(Y) |$
;
$| \mathcal {L}_{T^+}(X)| \le |\mathcal {L}_{T^-}(Y) |$
; -
(2) if
 $v \in \Gamma $
is not contained in some tile
$v \in \Gamma $
is not contained in some tile
 $T \in \tau (\alpha (x))$
, then
$T \in \tau (\alpha (x))$
, then
 $\sigma _v(x)_{W_1+W_2} \in \mathcal {L}(Z)$
.
$\sigma _v(x)_{W_1+W_2} \in \mathcal {L}(Z)$
.
Given
![]() $x \in X$
, let
$x \in X$
, let
For every
![]() $T,T^-,T^+ \Subset \Gamma $
that occur as
$T,T^-,T^+ \Subset \Gamma $
that occur as
![]() $T_0(x),T_0^-(x),T_0^+(x)$
for some
$T_0(x),T_0^-(x),T_0^+(x)$
for some
![]() $x \in X$
with
$x \in X$
with
![]() $\alpha (x)_0 =1$
, choose an injective function
$\alpha (x)_0 =1$
, choose an injective function
Now, choose a function
so that
![]() $\Phi ^+_{T,T^+}(w)_{T^-} = \Phi _{T^-,T^+}(w)$
for every
$\Phi ^+_{T,T^+}(w)_{T^-} = \Phi _{T^-,T^+}(w)$
for every
![]() $w \in \mathcal {L}_{T^+}(X)$
, and so that
$w \in \mathcal {L}_{T^+}(X)$
, and so that
![]() $\Phi ^+_{T,T^+}(w)_{F}=w^{(1)}$
. The existence of an injective function from
$\Phi ^+_{T,T^+}(w)_{F}=w^{(1)}$
. The existence of an injective function from
![]() $\mathcal {L}_{T^+}(X)$
to
$\mathcal {L}_{T^+}(X)$
to
![]() $\mathcal {L}_{T^-}(Y)$
for every pair of sets
$\mathcal {L}_{T^-}(Y)$
for every pair of sets
![]() $T^-,T^+ \Subset \Gamma $
that occur as
$T^-,T^+ \Subset \Gamma $
that occur as
![]() $T_0^-(x),T_-^+(x)$
for some
$T_0^-(x),T_-^+(x)$
for some
![]() $x \in X$
and
$x \in X$
and
![]() $v \in \Gamma $
such that
$v \in \Gamma $
such that
![]() $\alpha (x)_v=1$
follows from the inequality
$\alpha (x)_v=1$
follows from the inequality
![]() $| \mathcal {L}_{T^+}(X)| \le |\mathcal {L}_{T^-}(Y) |$
.
$| \mathcal {L}_{T^+}(X)| \le |\mathcal {L}_{T^-}(Y) |$
.
We now define a map
![]() $\tilde \rho :X \to A^\Gamma $
. For
$\tilde \rho :X \to A^\Gamma $
. For
![]() $x \in X$
, let
$x \in X$
, let
![]() $\tilde \rho (x) \in A^\Gamma $
be the unique point
$\tilde \rho (x) \in A^\Gamma $
be the unique point
![]() $y \in A^\Gamma $
satisfying:
$y \in A^\Gamma $
satisfying:
-
• for every
 $v \in \Gamma $
such that
$v \in \Gamma $
such that
 $\alpha (x)_v=1$
,
$\alpha (x)_v=1$
,
 $y_{T_v(x)}:= \sigma _{-v}( \Phi ^+_{T_v,T_v^+}(P_0^+(\sigma _{v}(x))) )$
;
$y_{T_v(x)}:= \sigma _{-v}( \Phi ^+_{T_v,T_v^+}(P_0^+(\sigma _{v}(x))) )$
; -
• for every
 $v \in \Gamma \setminus \bigcup \tau (\alpha (x))$
,
$v \in \Gamma \setminus \bigcup \tau (\alpha (x))$
,
 $y_v:= \tilde \Phi (\sigma _{v}(x)_{W})$
.
$y_v:= \tilde \Phi (\sigma _{v}(x)_{W})$
.
Let
![]() $\tilde Y= \tilde \rho (X)$
. We will now check that
$\tilde Y= \tilde \rho (X)$
. We will now check that
![]() $\tilde Y$
is
$\tilde Y$
is
![]() $\mathcal {G}$
-free. It suffices to show that for any
$\mathcal {G}$
-free. It suffices to show that for any
![]() $x \in X$
, the group
$x \in X$
, the group
![]() $\Gamma _x = \mathrm {stab}(\hat \rho (x))$
does not contain any subgroup from
$\Gamma _x = \mathrm {stab}(\hat \rho (x))$
does not contain any subgroup from
![]() $\mathcal {G}$
. If
$\mathcal {G}$
. If
![]() $x\not \in Z$
, then there exists
$x\not \in Z$
, then there exists
![]() $v \in \Gamma $
such that
$v \in \Gamma $
such that
![]() $\sigma _v(x)_{W_1} \not \in \mathcal {F}$
and so there exists
$\sigma _v(x)_{W_1} \not \in \mathcal {F}$
and so there exists
![]() $v' \in \Gamma $
such that
$v' \in \Gamma $
such that
![]() $\alpha (x)_{v'}=1$
. Then,
$\alpha (x)_{v'}=1$
. Then,
![]() $\sigma _v(\tilde \rho (x))_{B_{5n}} = w^{(1)}$
and this witnesses that
$\sigma _v(\tilde \rho (x))_{B_{5n}} = w^{(1)}$
and this witnesses that
![]() $\mathrm {stab}(x)$
does not contain a subgroup from
$\mathrm {stab}(x)$
does not contain a subgroup from
![]() $\mathcal {G}$
. If
$\mathcal {G}$
. If
![]() $x \in Z$
, then
$x \in Z$
, then
![]() $\tilde \rho(x)= \hat \rho(x)$
, and because the map
$\tilde \rho(x)= \hat \rho(x)$
, and because the map
![]() $\hat\rho$
is injective, it follows that in this case
$\hat\rho$
is injective, it follows that in this case
![]() $\mathrm{stab}(\tilde \rho(x)) = \mathrm{stab}(x)$
. Because
$\mathrm{stab}(\tilde \rho(x)) = \mathrm{stab}(x)$
. Because
![]() $X$
is
$X$
is
![]() $\mathcal{G}$
-free, it follows that also in this case
$\mathcal{G}$
-free, it follows that also in this case
![]() $\mathrm{stab}(\tilde \rho(x))$
does not contain any subgroup from
$\mathrm{stab}(\tilde \rho(x))$
does not contain any subgroup from
![]() $\mathcal{G}$
. It follows that there exists a retraction map
$\mathcal{G}$
. It follows that there exists a retraction map
![]() $\hat r:\tilde Y \to Y$
so that
$\hat r:\tilde Y \to Y$
so that
![]() $\tilde r(y)_v= y_v$
whenever
$\tilde r(y)_v= y_v$
whenever
![]() $\sigma _v(y)_{B_{n}} \in \mathcal {L}_{B_n}(Y)$
. Let
$\sigma _v(y)_{B_{n}} \in \mathcal {L}_{B_n}(Y)$
. Let
![]() $\check \rho :X \to S$
be defined by
$\check \rho :X \to S$
be defined by
![]() $\check \rho = \tilde r \circ \hat r \circ \hat \rho $
and let
$\check \rho = \tilde r \circ \hat r \circ \hat \rho $
and let
![]() $\rho :X \to Y$
be defined by
$\rho :X \to Y$
be defined by
To finish the proof, it remains to show that the map
![]() $\rho $
is injective. If
$\rho $
is injective. If
![]() $x \in X$
,
$x \in X$
,
![]() $v \in \Gamma $
,
$v \in \Gamma $
,
![]() $\check y = \check \rho (x)$
, then
$\check y = \check \rho (x)$
, then
![]() $\sigma _v(\check \rho (y))_{F} = w^{(1)}$
whenever
$\sigma _v(\check \rho (y))_{F} = w^{(1)}$
whenever
![]() $\alpha (x)_v=1$
. Thus, if
$\alpha (x)_v=1$
. Thus, if
![]() $y= \rho (x)$
, we have that
$y= \rho (x)$
, we have that
![]() $\sigma _v(y)_{F}=w^{(0)}$
if and only if
$\sigma _v(y)_{F}=w^{(0)}$
if and only if
![]() $\alpha (x)_v=1$
. Now suppose that
$\alpha (x)_v=1$
. Now suppose that
![]() $x^{(1)},x^{(2)} \in X$
are two distinct points. Let
$x^{(1)},x^{(2)} \in X$
are two distinct points. Let
![]() $y^{(1)}=\rho (x^{(1)})$
and
$y^{(1)}=\rho (x^{(1)})$
and
![]() $y^{(2)}=\rho (x^{(2)})$
. If
$y^{(2)}=\rho (x^{(2)})$
. If
![]() $\alpha (x^{(1)}) \ne \alpha (x^{(2)})$
, then there exists
$\alpha (x^{(1)}) \ne \alpha (x^{(2)})$
, then there exists
![]() $v \in \Gamma $
such that only one of the patterns
$v \in \Gamma $
such that only one of the patterns
![]() $\sigma _v(y^{(1)})_{F},\sigma _v(y^{(2)})_{F}$
is equal to
$\sigma _v(y^{(1)})_{F},\sigma _v(y^{(2)})_{F}$
is equal to
![]() $w^{(0)}$
, and in particular in this case,
$w^{(0)}$
, and in particular in this case,
![]() $y^{(1)} \ne y^{(2)}$
. So consider the case that
$y^{(1)} \ne y^{(2)}$
. So consider the case that
![]() $\alpha (x^{(1)})=\alpha (x^{(2)})$
. In this case,
$\alpha (x^{(1)})=\alpha (x^{(2)})$
. In this case,
![]() $\tau (\alpha (x^{(1)}))=\tau (\alpha (x^{(2)}))$
. Let
$\tau (\alpha (x^{(1)}))=\tau (\alpha (x^{(2)}))$
. Let
![]() $\mathcal {T}= \tau (\alpha (x^{(1)}))$
. By the assumption that
$\mathcal {T}= \tau (\alpha (x^{(1)}))$
. By the assumption that
![]() $x^{(1)} \ne x^{(2)}$
, there exists
$x^{(1)} \ne x^{(2)}$
, there exists
![]() $v \in V$
such that
$v \in V$
such that
![]() $x^{(1)}_v \ne x^{(2)}_v$
. If there exists
$x^{(1)}_v \ne x^{(2)}_v$
. If there exists
![]() $T \in \mathcal {T}$
such that
$T \in \mathcal {T}$
such that
![]() $v \in T^+$
, then
$v \in T^+$
, then
![]() $x^{(1)}_{T^+} \ne x^{(2)}_{T^+}$
and, by injectivity of
$x^{(1)}_{T^+} \ne x^{(2)}_{T^+}$
and, by injectivity of
![]() $\Phi _{T,T^+}$
, we have that
$\Phi _{T,T^+}$
, we have that
![]() $\hat \rho (x^{(1)})_{T^-} \ne \hat \rho (x^{(2)})_{T^-}$
. Since
$\hat \rho (x^{(1)})_{T^-} \ne \hat \rho (x^{(2)})_{T^-}$
. Since
![]() $\hat \rho (x^{(1)})_T, \hat \rho (x^{(1)})_T \in \mathcal {L}_T(\tilde Y)$
, it follows that
$\hat \rho (x^{(1)})_T, \hat \rho (x^{(1)})_T \in \mathcal {L}_T(\tilde Y)$
, it follows that
![]() $\rho (x^{(1)})_{T^-}= \hat \rho (x^{(1)})_{T^-}$
and
$\rho (x^{(1)})_{T^-}= \hat \rho (x^{(1)})_{T^-}$
and
![]() $\rho (x^{(2)})_{T^-} =\hat \rho (x^{(2)})_{T^-}$
, so
$\rho (x^{(2)})_{T^-} =\hat \rho (x^{(2)})_{T^-}$
, so
![]() $\rho (x^{(1)})_{T^-} \ne \rho (x^{(2)})_{T^-}$
. If
$\rho (x^{(1)})_{T^-} \ne \rho (x^{(2)})_{T^-}$
. If
![]() $v \in \Gamma \setminus \bigcup _{T \in \mathcal {T}}T$
, then
$v \in \Gamma \setminus \bigcup _{T \in \mathcal {T}}T$
, then
![]() $x^{(1)}_{W}, x^{(2)}_{W} \in \mathcal {L}_{W}(Z)$
, and so
$x^{(1)}_{W}, x^{(2)}_{W} \in \mathcal {L}_{W}(Z)$
, and so
![]() $\hat \rho (x^{(i)})_u = \tilde \Phi (\sigma _u(x^{(i)})_{W_1})$
for every
$\hat \rho (x^{(i)})_u = \tilde \Phi (\sigma _u(x^{(i)})_{W_1})$
for every
![]() $u \in W_2$
and
$u \in W_2$
and
![]() $i=1,2$
. Since
$i=1,2$
. Since
![]() $W_2$
is an injectivity window for
$W_2$
is an injectivity window for
![]() $\hat \rho $
, there exists
$\hat \rho $
, there exists
![]() $u \in W_2$
such that
$u \in W_2$
such that
![]() $\rho (x^{(1)})_{v+u} \ne \rho (x^{(2)})_{v+u}$
. Thus,
$\rho (x^{(1)})_{v+u} \ne \rho (x^{(2)})_{v+u}$
. Thus,
![]() $\rho :X \to Y$
is indeed an injective map.
$\rho :X \to Y$
is indeed an injective map.
9 Reduction to the finitely generated abelian case
We have already established our main result for the case where
![]() $\Gamma $
is a finitely generated abelian group. Various results about subshifts of finite type over countable groups can be reduced to the finitely generated case. Sometimes, the reduction is not completely trivial. For example, in [Reference Barbieri3], the problem of classification of countable groups that admit an aperiodic subshift has been reduced (in a non-trivial manner) to the finitely generated case. In this last section, we complete the proof of the embedding theorem for subshifts over general countable abelian groups by reducing it to the case where the acting group
$\Gamma $
is a finitely generated abelian group. Various results about subshifts of finite type over countable groups can be reduced to the finitely generated case. Sometimes, the reduction is not completely trivial. For example, in [Reference Barbieri3], the problem of classification of countable groups that admit an aperiodic subshift has been reduced (in a non-trivial manner) to the finitely generated case. In this last section, we complete the proof of the embedding theorem for subshifts over general countable abelian groups by reducing it to the case where the acting group
![]() $\Gamma $
is a finitely generated abelian group.
$\Gamma $
is a finitely generated abelian group.
In the following, we will say that a sentence
![]() $P(\Delta )$
‘holds’ for all sufficiently large
$P(\Delta )$
‘holds’ for all sufficiently large
![]() $\Delta \le \Gamma $
if there exists a finite set
$\Delta \le \Gamma $
if there exists a finite set
![]() $F\Subset \Gamma $
such that
$F\Subset \Gamma $
such that
![]() $P(\Delta )$
holds for any subgroup
$P(\Delta )$
holds for any subgroup
![]() $\Delta \le \Gamma $
such that
$\Delta \le \Gamma $
such that
![]() $F \Subset \Delta $
.
$F \Subset \Delta $
.
If
![]() $\rho :X \to Y$
is a map between
$\rho :X \to Y$
is a map between
![]() $\Gamma $
-subshifts and
$\Gamma $
-subshifts and
![]() $W_0 \Subset \Gamma $
is a coding window for
$W_0 \Subset \Gamma $
is a coding window for
![]() $\rho $
, then the map
$\rho $
, then the map
![]() $\rho $
naturally extends to a map
$\rho $
naturally extends to a map
![]() $\rho ^{[\Delta ]}:X^{[\Delta ]} \to Y^{[\Delta ]}$
for any
$\rho ^{[\Delta ]}:X^{[\Delta ]} \to Y^{[\Delta ]}$
for any
![]() $\Delta \le \Gamma $
such that
$\Delta \le \Gamma $
such that
![]() $W_0 \Subset \Delta $
. Furthermore, if
$W_0 \Subset \Delta $
. Furthermore, if
![]() $\rho :X\to Y$
is injective and
$\rho :X\to Y$
is injective and
![]() $W_1 \Subset \Gamma $
is an injectivity window for
$W_1 \Subset \Gamma $
is an injectivity window for
![]() $\rho $
, then
$\rho $
, then
![]() $\rho ^{[\Delta ]}:X^{[\Delta ]} \to Y^{[\Delta ]}$
is injective for any
$\rho ^{[\Delta ]}:X^{[\Delta ]} \to Y^{[\Delta ]}$
is injective for any
![]() $\Delta \le \Gamma $
that contains
$\Delta \le \Gamma $
that contains
![]() $W_0\cup W_1$
. It follows that whenever
$W_0\cup W_1$
. It follows that whenever
![]() $Z \subseteq Y$
is a closed,
$Z \subseteq Y$
is a closed,
![]() $\Gamma $
-invariant set and
$\Gamma $
-invariant set and
![]() $\hat \rho :Z \to Y$
is an injective map, then
$\hat \rho :Z \to Y$
is an injective map, then
![]() $X \hookrightarrow _{\hat \rho } Y$
implies that
$X \hookrightarrow _{\hat \rho } Y$
implies that
![]() $X^{[\Delta ]} \hookrightarrow _{\hat \rho } Y^{[\Delta ]}$
for all sufficiently large
$X^{[\Delta ]} \hookrightarrow _{\hat \rho } Y^{[\Delta ]}$
for all sufficiently large
![]() $\Delta \le \Gamma $
, and
$\Delta \le \Gamma $
, and
![]() $X \cong _{\hat \rho } Y$
implies that
$X \cong _{\hat \rho } Y$
implies that
![]() $X^{[\Delta ]} \cong _{\hat \rho } Y^{[\Delta ]}$
for all sufficiently large
$X^{[\Delta ]} \cong _{\hat \rho } Y^{[\Delta ]}$
for all sufficiently large
![]() $\Delta \le \Gamma $
.
$\Delta \le \Gamma $
.
A word of caution: if
![]() $X,Y$
are
$X,Y$
are
![]() $\Gamma $
subshifts such that
$\Gamma $
subshifts such that
![]() $X \cong Y$
, it is not necessarily true that
$X \cong Y$
, it is not necessarily true that
![]() $X^{[\Delta ]} \cong Y^{[\Delta ]}$
for all finitely generated subgroups
$X^{[\Delta ]} \cong Y^{[\Delta ]}$
for all finitely generated subgroups
![]() $\Delta \le \Gamma $
. Moreover, if
$\Delta \le \Gamma $
. Moreover, if
![]() $Y= Y^{[\Delta ]}$
for some finitely generated subgroup
$Y= Y^{[\Delta ]}$
for some finitely generated subgroup
![]() $\Delta \le \Gamma $
and
$\Delta \le \Gamma $
and
![]() $X \cong Y$
, then it does not follow that
$X \cong Y$
, then it does not follow that
![]() $X = X^{[\Delta ]}$
. However, by the argument above, in this case, it is still true that
$X = X^{[\Delta ]}$
. However, by the argument above, in this case, it is still true that
![]() $X^{[\tilde \Delta ]} \cong Y^{[\tilde \Delta ]}$
and that
$X^{[\tilde \Delta ]} \cong Y^{[\tilde \Delta ]}$
and that
![]() $X= X^{[\tilde \Delta ]}$
for all sufficiently large
$X= X^{[\tilde \Delta ]}$
for all sufficiently large
![]() $\tilde \Delta \le \Gamma $
.
$\tilde \Delta \le \Gamma $
.
Lemma 9.1. Suppose
![]() $X,Y$
are
$X,Y$
are
![]() $\Gamma $
-subshifts, that Y has the map extension property, and that
$\Gamma $
-subshifts, that Y has the map extension property, and that
![]() $\hat \rho :Z \to Y$
is an injective map. If
$\hat \rho :Z \to Y$
is an injective map. If
![]() $E(X,Y,\hat \rho ,\Gamma _0)$
holds for every
$E(X,Y,\hat \rho ,\Gamma _0)$
holds for every
![]() $\Gamma _0 \le \Gamma $
, then for every sufficiently large
$\Gamma _0 \le \Gamma $
, then for every sufficiently large
![]() $\Delta \le \Gamma $
, we have
$\Delta \le \Gamma $
, we have
![]() $Y=Y^{[\Delta ]}$
and
$Y=Y^{[\Delta ]}$
and
![]() $E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _0)$
holds for every subgroup
$E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _0)$
holds for every subgroup
![]() $\Gamma _0 \le \Gamma $
.
$\Gamma _0 \le \Gamma $
.
Proof. Let
![]() $X,Y,Z$
, and
$X,Y,Z$
, and
![]() $\hat \rho :Z \to Y$
be as in the statement. Because Y is has the map extension property, by Proposition 4.5, it follows that Y is contractible, so by Lemma 4.7,
$\hat \rho :Z \to Y$
be as in the statement. Because Y is has the map extension property, by Proposition 4.5, it follows that Y is contractible, so by Lemma 4.7,
![]() $\Delta _0 < \Gamma $
such that
$\Delta _0 < \Gamma $
such that
![]() $Y= Y^{[\Delta _0]}$
, and thus
$Y= Y^{[\Delta _0]}$
, and thus
![]() $Y= Y^{[\Delta ]}$
for every sufficiently large
$Y= Y^{[\Delta ]}$
for every sufficiently large
![]() $\Delta \le \Gamma $
.
$\Delta \le \Gamma $
.
We will prove that for any
![]() $\Gamma _0 \in \mathrm {Sub}(\Gamma )$
, there exists an open neighborhood
$\Gamma _0 \in \mathrm {Sub}(\Gamma )$
, there exists an open neighborhood
![]() $\mathcal {U}_{\Gamma _0} \subseteq \mathrm {Sub}(\Gamma )$
with
$\mathcal {U}_{\Gamma _0} \subseteq \mathrm {Sub}(\Gamma )$
with
![]() $\Gamma _0 \in \mathcal {U}_{\Gamma _0}$
such that for all sufficiently large
$\Gamma _0 \in \mathcal {U}_{\Gamma _0}$
such that for all sufficiently large
![]() $\Delta \le \Gamma $
, the condition
$\Delta \le \Gamma $
, the condition
![]() $E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _1)$
holds for any
$E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _1)$
holds for any
![]() $\Gamma _1 \in \mathcal {U}_{\Gamma _0}$
. By compactness of
$\Gamma _1 \in \mathcal {U}_{\Gamma _0}$
. By compactness of
![]() $\mathrm {Sub}(\Gamma )$
, it will follow that there exist a finite number of finitely generated subgroups
$\mathrm {Sub}(\Gamma )$
, it will follow that there exist a finite number of finitely generated subgroups
![]() $\Delta _1,\ldots , \Delta _N \le \Gamma $
such that for any
$\Delta _1,\ldots , \Delta _N \le \Gamma $
such that for any
![]() $\Gamma _0 \le \Gamma $
, there exists
$\Gamma _0 \le \Gamma $
, there exists
![]() $1\le j \le N$
so that
$1\le j \le N$
so that
![]() $E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _0)$
holds for any finitely generated subgroup
$E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _0)$
holds for any finitely generated subgroup
![]() $\Delta \le \Gamma $
satisfying
$\Delta \le \Gamma $
satisfying
![]() $\Delta _j \le \Delta $
. The proof will be completed by taking
$\Delta _j \le \Delta $
. The proof will be completed by taking
![]() $\Delta _0$
to be the group generated by
$\Delta _0$
to be the group generated by
![]() $\{ \Delta _1,\ldots , \Delta _N\}$
.
$\{ \Delta _1,\ldots , \Delta _N\}$
.
Let
![]() $\Gamma _0 \le \Gamma $
be an arbitrary subgroup.
$\Gamma _0 \le \Gamma $
be an arbitrary subgroup.
We first show that there exists an open neighborhood
![]() $\mathcal {W}_{\Gamma _0} \subseteq \mathrm {Sub}(\Gamma )$
of
$\mathcal {W}_{\Gamma _0} \subseteq \mathrm {Sub}(\Gamma )$
of
![]() $\Gamma _0$
such that
$\Gamma _0$
such that
![]() $\mathrm {Ker}(Y^{[\Delta ]}_{\Gamma _0}) \le \mathrm {Ker}(X^{[\Delta ]}_{\Gamma _0})$
for any
$\mathrm {Ker}(Y^{[\Delta ]}_{\Gamma _0}) \le \mathrm {Ker}(X^{[\Delta ]}_{\Gamma _0})$
for any
![]() $\Gamma _1 \in \mathcal {W}_{\Gamma _0}$
and any sufficiently large subgroup
$\Gamma _1 \in \mathcal {W}_{\Gamma _0}$
and any sufficiently large subgroup
![]() $\Delta \le \Gamma $
. If
$\Delta \le \Gamma $
. If
![]() $Y^{[\Gamma _0]}$
consists of a unique fixed point, then
$Y^{[\Gamma _0]}$
consists of a unique fixed point, then
![]() $X^{[\Gamma _0]}$
must also consist of at most a single fixed point. In this case, the set of subgroups
$X^{[\Gamma _0]}$
must also consist of at most a single fixed point. In this case, the set of subgroups
![]() $\mathcal {W} = \{ \Gamma _1 \in \mathrm {Sub}(\Gamma ): | \mathcal {L}_{\{0\}}(X_{\Gamma _1}) | = 1 \}$
is an open neighborhood of
$\mathcal {W} = \{ \Gamma _1 \in \mathrm {Sub}(\Gamma ): | \mathcal {L}_{\{0\}}(X_{\Gamma _1}) | = 1 \}$
is an open neighborhood of
![]() $\Gamma _0$
that satisfies the requirement.
$\Gamma _0$
that satisfies the requirement.
Otherwise, since
![]() $Y=Y^{[\Delta _0]}$
, it follows that the group
$Y=Y^{[\Delta _0]}$
, it follows that the group
![]() $\mathrm {Ker}(\overline {Y}_{\Gamma _0})$
is contained in
$\mathrm {Ker}(\overline {Y}_{\Gamma _0})$
is contained in
![]() $\Delta _0/(\Gamma _0 \cap \Delta _0)$
, and hence
$\Delta _0/(\Gamma _0 \cap \Delta _0)$
, and hence
![]() $\mathrm {Ker}(\overline {Y}_{\Gamma _0})$
is finitely generated. It follows that for every
$\mathrm {Ker}(\overline {Y}_{\Gamma _0})$
is finitely generated. It follows that for every
![]() $\Gamma _0$
, there exist finite subsets
$\Gamma _0$
, there exist finite subsets
![]() $F,K \Subset \Gamma $
with
$F,K \Subset \Gamma $
with
![]() $F\cup \{0\} \subset K$
such that the condition that
$F\cup \{0\} \subset K$
such that the condition that
![]() $\mathrm {Ker}(Y_{\Gamma _0}) \le \mathrm {Ker}(X_{\Gamma _0})$
is equivalent to the condition that for any
$\mathrm {Ker}(Y_{\Gamma _0}) \le \mathrm {Ker}(X_{\Gamma _0})$
is equivalent to the condition that for any
![]() $w \in \mathcal {L}_{K}(X_{\Gamma _0})$
and any
$w \in \mathcal {L}_{K}(X_{\Gamma _0})$
and any
![]() $v \in F$
, we have
$v \in F$
, we have
![]() $w_0 =w_v$
. Let
$w_0 =w_v$
. Let
Then,
![]() $\mathcal {W}_{\Gamma _0} \subseteq \mathrm {Sub}(\Gamma )$
is an open neighborhood of
$\mathcal {W}_{\Gamma _0} \subseteq \mathrm {Sub}(\Gamma )$
is an open neighborhood of
![]() $\Gamma _0$
, and
$\Gamma _0$
, and
![]() $\mathrm {Ker}(Y^{[\Delta ]}_{\Gamma _0}) \le \mathrm {Ker}(X^{[\Delta ]}_{\Gamma _0})$
for any
$\mathrm {Ker}(Y^{[\Delta ]}_{\Gamma _0}) \le \mathrm {Ker}(X^{[\Delta ]}_{\Gamma _0})$
for any
![]() $\Gamma _1 \in \mathcal {W}_{\Gamma _0}$
and any finitely generated subgroup
$\Gamma _1 \in \mathcal {W}_{\Gamma _0}$
and any finitely generated subgroup
![]() $\Delta $
such that
$\Delta $
such that
![]() $\Delta _0 \le \Delta $
and
$\Delta _0 \le \Delta $
and
![]() $K \subseteq \Delta $
.
$K \subseteq \Delta $
.
If
![]() $h(\overline {X}_{\Gamma _0}) < h(\overline {Y}_{\Gamma _0})$
, then there exists a finite
$h(\overline {X}_{\Gamma _0}) < h(\overline {Y}_{\Gamma _0})$
, then there exists a finite
![]() $\Gamma _0$
-separated set
$\Gamma _0$
-separated set
![]() $K \Subset \Gamma $
such that
$K \Subset \Gamma $
such that
![]() $({1}/{|K|})\log | \mathcal {L}_{K}(X_{\Gamma _0}) |< h(\overline {Y}_{\Gamma _0})$
.
$({1}/{|K|})\log | \mathcal {L}_{K}(X_{\Gamma _0}) |< h(\overline {Y}_{\Gamma _0})$
.
Since
![]() $Y = Y^{[\Delta _0]}$
, it follows that
$Y = Y^{[\Delta _0]}$
, it follows that
![]() $h(\overline {Y}_{\Gamma _1})=h(\overline {Y}_{\Gamma _0})$
whenever
$h(\overline {Y}_{\Gamma _1})=h(\overline {Y}_{\Gamma _0})$
whenever
![]() $\Gamma _1 \cap \Delta _0 = \Gamma _0 \cap \Delta _0$
. Note that for any
$\Gamma _1 \cap \Delta _0 = \Gamma _0 \cap \Delta _0$
. Note that for any
![]() $\Gamma _1 \le \Gamma _0$
such that
$\Gamma _1 \le \Gamma _0$
such that
![]() $[\Gamma :\Gamma _1]= +\infty $
, we have that
$[\Gamma :\Gamma _1]= +\infty $
, we have that
![]() $\mathcal {L}(X_{\Gamma _0}) \subseteq \mathcal {L}_K(X_{\Gamma _1})$
. By a compactness argument (using that
$\mathcal {L}(X_{\Gamma _0}) \subseteq \mathcal {L}_K(X_{\Gamma _1})$
. By a compactness argument (using that
![]() $\mathcal {L}_K(X_{\Gamma _0})$
is a finite set), we can thus find a finitely generated subgroup
$\mathcal {L}_K(X_{\Gamma _0})$
is a finite set), we can thus find a finitely generated subgroup
![]() $\Delta _1 \le \Gamma $
such that for any
$\Delta _1 \le \Gamma $
such that for any
![]() $\Gamma _1 \le \Gamma $
with
$\Gamma _1 \le \Gamma $
with
![]() $\Gamma _1 \cap \Delta _1 = \Gamma _0 \cap \Delta _0$
, we have
$\Gamma _1 \cap \Delta _1 = \Gamma _0 \cap \Delta _0$
, we have
![]() $\mathcal {L}(X_{\Gamma _0}) \subseteq \mathcal {L}_{K}(X_{\Gamma _1})$
. Let
$\mathcal {L}(X_{\Gamma _0}) \subseteq \mathcal {L}_{K}(X_{\Gamma _1})$
. Let
![]() $\mathcal {U}_{\Gamma _0}$
denote the collection of subgroups
$\mathcal {U}_{\Gamma _0}$
denote the collection of subgroups
![]() $\Gamma _1 \in \mathcal {W}_{\Gamma _0}$
so that
$\Gamma _1 \in \mathcal {W}_{\Gamma _0}$
so that
![]() $\Gamma _1 \cap \Delta _0 = \Gamma _0 \cap \Delta _0$
and
$\Gamma _1 \cap \Delta _0 = \Gamma _0 \cap \Delta _0$
and
![]() $\Gamma _1 \cap \Delta _1 = \Gamma _0 \cap \Delta _0$
.
$\Gamma _1 \cap \Delta _1 = \Gamma _0 \cap \Delta _0$
.
Then,
![]() $\mathcal {U}_{\Gamma _0} \subseteq \mathrm {Sub}(\Gamma )$
is an open neighborhood of
$\mathcal {U}_{\Gamma _0} \subseteq \mathrm {Sub}(\Gamma )$
is an open neighborhood of
![]() $\Gamma _0$
and for any finitely generated subgroup
$\Gamma _0$
and for any finitely generated subgroup
![]() $\Delta \le \Gamma $
that contains
$\Delta \le \Gamma $
that contains
![]() $\Delta _0,\Delta _1$
, and
$\Delta _0,\Delta _1$
, and
![]() $K-K$
, we have
$K-K$
, we have
![]() $E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _1)$
for any
$E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _1)$
for any
![]() $\Gamma _1 \in \mathcal {U}_{\Gamma _0}$
and any subgroup
$\Gamma _1 \in \mathcal {U}_{\Gamma _0}$
and any subgroup
![]() $\Delta <\Gamma $
such that
$\Delta <\Gamma $
such that
![]() $\Delta _0 \le \Delta $
satisfies
$\Delta _0 \le \Delta $
satisfies
![]() $(K-K) \le \Delta $
.
$(K-K) \le \Delta $
.
It remains to consider the case where
![]() $h(X_{\Gamma _0})$
is not strictly smaller than
$h(X_{\Gamma _0})$
is not strictly smaller than
![]() $h(Y_{\Gamma _0})$
. In this case, since
$h(Y_{\Gamma _0})$
. In this case, since
![]() $E(X,Y,\hat \rho ,\Gamma _0)$
holds, we have that
$E(X,Y,\hat \rho ,\Gamma _0)$
holds, we have that
![]() $X_{\Gamma _0} \cong _{\hat \rho } Y_{\Gamma _0}$
. In other words, there exists an isomorphism
$X_{\Gamma _0} \cong _{\hat \rho } Y_{\Gamma _0}$
. In other words, there exists an isomorphism
![]() $\rho _{\Gamma _0}:X_{\Gamma _0} \to Y_{\Gamma _0}$
that extends
$\rho _{\Gamma _0}:X_{\Gamma _0} \to Y_{\Gamma _0}$
that extends
![]() $\hat \rho $
. Let
$\hat \rho $
. Let
![]() $W_1 \Subset \Gamma $
be a coding window for
$W_1 \Subset \Gamma $
be a coding window for
![]() $\rho _{\Gamma _0}$
and let
$\rho _{\Gamma _0}$
and let
![]() $W_2 \Subset \Gamma $
be an injectivity window for
$W_2 \Subset \Gamma $
be an injectivity window for
![]() $\rho _{\Gamma _0}$
. Let
$\rho _{\Gamma _0}$
. Let
![]() $W = W_1 +W_2$
. It follows that for any subgroup
$W = W_1 +W_2$
. It follows that for any subgroup
![]() $\Gamma _1$
such that
$\Gamma _1$
such that
![]() $\Gamma _1 \cap (W -W) = \Gamma _0 \cap (W -W)$
and any finitely generated subgroup
$\Gamma _1 \cap (W -W) = \Gamma _0 \cap (W -W)$
and any finitely generated subgroup
![]() $\tilde \Delta \le \Gamma $
such that
$\tilde \Delta \le \Gamma $
such that
![]() $(W-W) \subseteq \Delta $
, the same sliding block code defines an embedding
$(W-W) \subseteq \Delta $
, the same sliding block code defines an embedding
![]() $X^{[\tilde \Delta ]}_{\Gamma _1} \hookrightarrow _{\hat \rho } Y^{[\tilde \Delta \}]}_{\Gamma _1}$
. The set
$X^{[\tilde \Delta ]}_{\Gamma _1} \hookrightarrow _{\hat \rho } Y^{[\tilde \Delta \}]}_{\Gamma _1}$
. The set
![]() $\mathcal {U}_{\Gamma _0}$
of all such subgroups is an open neighborhood of
$\mathcal {U}_{\Gamma _0}$
of all such subgroups is an open neighborhood of
![]() $\Gamma _0$
, and
$\Gamma _0$
, and
![]() $E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _1)$
holds for any
$E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _1)$
holds for any
![]() $\Gamma _1 \in \mathcal {U}_{\Gamma _0}$
and any finite generated subgroup
$\Gamma _1 \in \mathcal {U}_{\Gamma _0}$
and any finite generated subgroup
![]() $\Delta \le \Gamma $
with
$\Delta \le \Gamma $
with
![]() $(W-W) \subseteq \Delta $
.
$(W-W) \subseteq \Delta $
.
To complete the proof of Theorem 1.4 in the case where
![]() $\Gamma $
is a countable abelian group, not necessarily finitely generated, we use Lemma 9.1 as follows. Let
$\Gamma $
is a countable abelian group, not necessarily finitely generated, we use Lemma 9.1 as follows. Let
![]() $\Gamma $
be a countable abelian group and let
$\Gamma $
be a countable abelian group and let
![]() $X,Y$
be
$X,Y$
be
![]() $\Gamma $
-subshifts. Assume that Y has the map extension property, that
$\Gamma $
-subshifts. Assume that Y has the map extension property, that
![]() $Z \subseteq X$
is a closed
$Z \subseteq X$
is a closed
![]() $\Gamma $
-invariant set which is either empty or relatively of finite type, and let
$\Gamma $
-invariant set which is either empty or relatively of finite type, and let
![]() $\hat \rho :Z \to Y$
be an injective map. Suppose that
$\hat \rho :Z \to Y$
be an injective map. Suppose that
![]() $E(X,Y,\hat \rho ,\Gamma _0)$
holds for any
$E(X,Y,\hat \rho ,\Gamma _0)$
holds for any
![]() $\Gamma _0 \le~\Gamma $
. Then, by Lemma 9.1, we have
$\Gamma _0 \le~\Gamma $
. Then, by Lemma 9.1, we have
![]() $Y=Y^{[\Delta ]}$
, and
$Y=Y^{[\Delta ]}$
, and
![]() $E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _0)$
holds for every subgroup
$E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _0)$
holds for every subgroup
![]() $\Gamma _0 \le \Gamma $
and every sufficiently large finitely generated subgroup
$\Gamma _0 \le \Gamma $
and every sufficiently large finitely generated subgroup
![]() $\Delta \le \Gamma $
. Also observe that for any sufficiently large finitely generated subgroup
$\Delta \le \Gamma $
. Also observe that for any sufficiently large finitely generated subgroup
![]() $\Delta \le \Gamma $
, we have that
$\Delta \le \Gamma $
, we have that
![]() $E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _0)$
holds for every
$E(X^{[\Delta ]},Y^{[\Delta ]},\hat \rho ,\Gamma _0)$
holds for every
![]() $\Gamma _0 \le \Gamma $
if and only if
$\Gamma _0 \le \Gamma $
if and only if
![]() $E(X^{(\Delta )},Y^{(\Delta )},\hat \rho ,\Gamma _0)$
holds for every
$E(X^{(\Delta )},Y^{(\Delta )},\hat \rho ,\Gamma _0)$
holds for every
![]() $\Gamma _0 \le \Delta $
. Thus, by Proposition 8.1,
$\Gamma _0 \le \Delta $
. Thus, by Proposition 8.1,
![]() $X^{(\Delta )} \hookrightarrow _{\hat \rho } Y^{(\Delta )}$
for any sufficiently large finitely generated subgroup
$X^{(\Delta )} \hookrightarrow _{\hat \rho } Y^{(\Delta )}$
for any sufficiently large finitely generated subgroup
![]() $\Delta \le \Gamma $
. This implies that
$\Delta \le \Gamma $
. This implies that
![]() $X^{[\Delta ]} \hookrightarrow _{\hat \rho } Y^{[\Delta ]}$
for any sufficiently large finitely generated subgroup
$X^{[\Delta ]} \hookrightarrow _{\hat \rho } Y^{[\Delta ]}$
for any sufficiently large finitely generated subgroup
![]() $\Delta \le \Gamma $
. Since
$\Delta \le \Gamma $
. Since
![]() $X \subseteq X^{[\Delta ]}$
for any
$X \subseteq X^{[\Delta ]}$
for any
![]() $\Delta \le \Gamma $
and
$\Delta \le \Gamma $
and
![]() $Y=Y^{[\Delta ]}$
for all sufficiently large
$Y=Y^{[\Delta ]}$
for all sufficiently large
![]() $\Delta $
, it follows that
$\Delta $
, it follows that
![]() $X \hookrightarrow _{\hat \rho } Y$
.
$X \hookrightarrow _{\hat \rho } Y$
.
10 Lower entropy factors and the map extension property
Recall that the condition
![]() $X\rightsquigarrow Y$
defined in Definition 4.1 is necessary for the existence of a map from X into Y. Boyle’s lower entropy factor theorem says it is a necessary and sufficient condition for the existence of a factor map between irreducible
$X\rightsquigarrow Y$
defined in Definition 4.1 is necessary for the existence of a map from X into Y. Boyle’s lower entropy factor theorem says it is a necessary and sufficient condition for the existence of a factor map between irreducible
![]() $\mathbb {Z}$
-subshifts of finite type [Reference Boyle6].
$\mathbb {Z}$
-subshifts of finite type [Reference Boyle6].
Theorem 10.1. (Boyle’s lower entropy factor theorem [Reference Boyle6])
Let
![]() $X,Y$
be irreducible
$X,Y$
be irreducible
![]() $\mathbb {Z}$
-subshifts of finite type with
$\mathbb {Z}$
-subshifts of finite type with
![]() $h(X)>h(Y)$
. Then, there exists a factor map from X to Y if and only if
$h(X)>h(Y)$
. Then, there exists a factor map from X to Y if and only if
![]() $X \rightsquigarrow Y$
.
$X \rightsquigarrow Y$
.
In contrast, there exist topologically mixing
![]() $\mathbb {Z}^2$
-subshifts with arbitrarily high entropy which do not factor onto any non-trivial full-shift [Reference Boyle, Pavlov and Schraudner7]. However, various multidimensional analogs of Boyle’s lower entropy factor theorem have been obtained for certain classes of
$\mathbb {Z}^2$
-subshifts with arbitrarily high entropy which do not factor onto any non-trivial full-shift [Reference Boyle, Pavlov and Schraudner7]. However, various multidimensional analogs of Boyle’s lower entropy factor theorem have been obtained for certain classes of
![]() $\mathbb {Z}^2$
-subshifts [Reference Boyle, Pavlov and Schraudner7, Reference Briceño, McGoff and Pavlov9, Reference Desai11].
$\mathbb {Z}^2$
-subshifts [Reference Boyle, Pavlov and Schraudner7, Reference Briceño, McGoff and Pavlov9, Reference Desai11].
To provide the context of previously known results about factors of subshifts of finite type, we now recall more properties of subshifts. The block gluing property was introduced in [Reference Boyle, Pavlov and Schraudner7].
Definition 10.2. A
![]() $\mathbb {Z}^d$
-subshift X is block gluing if there exists a finite set
$\mathbb {Z}^d$
-subshift X is block gluing if there exists a finite set
![]() $K \Subset \mathbb {Z}^d$
such that for any pair of K-disjoint hyperrecatangles
$K \Subset \mathbb {Z}^d$
such that for any pair of K-disjoint hyperrecatangles
![]() $F_1,F_2 \Subset \Gamma $
and any
$F_1,F_2 \Subset \Gamma $
and any
![]() $x^{(1)},x^{(2)} \in X$
, there exists
$x^{(1)},x^{(2)} \in X$
, there exists
![]() $x \in X$
such that
$x \in X$
such that
![]() $x_{F_1} = x^{(1)}_{F_1}$
and
$x_{F_1} = x^{(1)}_{F_1}$
and
![]() $x_{F_2} = x^{(2)}_{F_2}$
.
$x_{F_2} = x^{(2)}_{F_2}$
.
The finite extension property was introduced in [Reference Briceño, McGoff and Pavlov9].
Definition 10.3. A
![]() $\Gamma $
-subshift
$\Gamma $
-subshift
![]() $Y \subseteq B^\Gamma $
has the finite extension property if there exists finite sets
$Y \subseteq B^\Gamma $
has the finite extension property if there exists finite sets
![]() $W,F \Subset \Gamma $
so that for any
$W,F \Subset \Gamma $
so that for any
![]() $K \subseteq \Gamma $
, if
$K \subseteq \Gamma $
, if
![]() $x \in B^\Gamma $
satisfies that
$x \in B^\Gamma $
satisfies that
![]() $\sigma _v(y)_W \in \mathcal {L}_W(Y)$
for every
$\sigma _v(y)_W \in \mathcal {L}_W(Y)$
for every
![]() $v \in K+F$
, then there exists
$v \in K+F$
, then there exists
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $y\vert _K= x\vert _K$
.
$y\vert _K= x\vert _K$
.
The above definition of the finite extension property slightly differs from the original formulation in [Reference Briceño, McGoff and Pavlov9].
The current state-of-the-art regarding lower entropy factors of
![]() $\mathbb {Z}^d$
-subshifts of finite type is the following theorem.
$\mathbb {Z}^d$
-subshifts of finite type is the following theorem.
Theorem 10.4. (Briceño, Mcgoff, and Pavlov [Reference Briceño, McGoff and Pavlov9])
Let X be a block gluing
![]() $\mathbb {Z}^d$
-subshift and let Y be a
$\mathbb {Z}^d$
-subshift and let Y be a
![]() $\mathbb {Z}^d$
-subshift of finite type with a fixed point and the finite extension property such that
$\mathbb {Z}^d$
-subshift of finite type with a fixed point and the finite extension property such that
![]() $h(X)>h(Y)$
. Then, there exists a factor map from X to Y.
$h(X)>h(Y)$
. Then, there exists a factor map from X to Y.
We now prove the following variant.
Theorem 10.5. Let X be a block gluing
![]() $\mathbb {Z}^d$
-subshift and let Y be a
$\mathbb {Z}^d$
-subshift and let Y be a
![]() $\mathbb {Z}^d$
-subshift with the map extension property such that
$\mathbb {Z}^d$
-subshift with the map extension property such that
![]() $h(X)>h(Y)$
. Then, there exists a factor map from X to Y if and only if
$h(X)>h(Y)$
. Then, there exists a factor map from X to Y if and only if
![]() $X \rightsquigarrow Y$
.
$X \rightsquigarrow Y$
.
Proof. As we have already explained, in general, if there exists a factor map from X to Y, then
![]() $X \rightsquigarrow Y$
. Let X be a block gluing
$X \rightsquigarrow Y$
. Let X be a block gluing
![]() $\mathbb {Z}^d$
-subshift and let
$\mathbb {Z}^d$
-subshift and let
![]() $Y \subseteq B^{\mathbb {Z}^d}$
be a
$Y \subseteq B^{\mathbb {Z}^d}$
be a
![]() $\mathbb {Z}^d$
-subshift of finite type with the map extension property such that
$\mathbb {Z}^d$
-subshift of finite type with the map extension property such that
![]() $h(X)>h(Y)$
.
$h(X)>h(Y)$
.
Now suppose that
![]() $X \rightsquigarrow Y$
. Let
$X \rightsquigarrow Y$
. Let
![]() $B_n= \{-n,\ldots ,n\}^d \Subset \mathbb {Z}^d$
. Because Y has the map extension property, there exists a finite set of subgroups
$B_n= \{-n,\ldots ,n\}^d \Subset \mathbb {Z}^d$
. Because Y has the map extension property, there exists a finite set of subgroups
![]() $\mathcal {G} \Subset \mathrm {Sub}(\mathbb {Z}^d)$
such that Y is an absolute retract for the class of
$\mathcal {G} \Subset \mathrm {Sub}(\mathbb {Z}^d)$
such that Y is an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts. In particular, Y is
$\mathcal {G}$
-free subshifts. In particular, Y is
![]() $\mathcal {G}$
-free, and so there exists
$\mathcal {G}$
-free, and so there exists
![]() $M \in \mathbb {N}$
so that
$M \in \mathbb {N}$
so that
![]() $B_M$
witnesses that Y is
$B_M$
witnesses that Y is
![]() $\mathcal {G}$
-free. Because X is block gluing, there exists
$\mathcal {G}$
-free. Because X is block gluing, there exists
![]() $N \in \mathbb {N}$
so that for every
$N \in \mathbb {N}$
so that for every
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $f:(2n+2N)\mathbb {Z}^d \to \mathcal {L}_{B_n}(X)$
, there exists
$f:(2n+2N)\mathbb {Z}^d \to \mathcal {L}_{B_n}(X)$
, there exists
![]() $x \in X$
such that
$x \in X$
such that
![]() $\sigma _v(x)_{B_n} = f(v)$
for all
$\sigma _v(x)_{B_n} = f(v)$
for all
![]() $v \in (2n+2N)\mathbb {Z}^d$
. Given
$v \in (2n+2N)\mathbb {Z}^d$
. Given
![]() $w \in \mathcal {L}_{B_{3N}}(X)$
and
$w \in \mathcal {L}_{B_{3N}}(X)$
and
![]() $n> 3N$
, let
$n> 3N$
, let
![]() $W_{w,n}$
denote the set of patterns
$W_{w,n}$
denote the set of patterns
![]() $\tilde w \in \mathcal {L}_{B_n}(X)$
such that
$\tilde w \in \mathcal {L}_{B_n}(X)$
such that
![]() $w_{B_{3N}}=w$
and so that the only overlap of w with
$w_{B_{3N}}=w$
and so that the only overlap of w with
![]() $\tilde w$
in
$\tilde w$
in
![]() $B_{n+N}$
occurs at
$B_{n+N}$
occurs at
![]() $0$
. Similarly to the proof Lemma 7.2, one can show using
$0$
. Similarly to the proof Lemma 7.2, one can show using
![]() $h(X)> h(Y)$
and the fact that X is block gluing that for sufficiently large n, there exists
$h(X)> h(Y)$
and the fact that X is block gluing that for sufficiently large n, there exists
![]() $w \in \mathcal {L}_{B_{3N}}$
such that
$w \in \mathcal {L}_{B_{3N}}$
such that
![]() $|W_{w,n}|> |\mathcal {L}_{B_{n+N}}(Y)|$
. Choose
$|W_{w,n}|> |\mathcal {L}_{B_{n+N}}(Y)|$
. Choose
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $w \in \mathcal {L}_{B_{3N}}$
satisfying the above, with
$w \in \mathcal {L}_{B_{3N}}$
satisfying the above, with
![]() $n \ge 3M$
. Let
$n \ge 3M$
. Let
![]() $\Phi :W_{w,n} \to \mathcal {L}_{B_{n+N}}(Y)$
be a surjective function and let
$\Phi :W_{w,n} \to \mathcal {L}_{B_{n+N}}(Y)$
be a surjective function and let
It follows that for any
![]() $x \in \tilde X$
, there exists a unique coset of
$x \in \tilde X$
, there exists a unique coset of
![]() $(2n+2N)\mathbb {Z}^d$
, where the pattern w occurs. Define a map
$(2n+2N)\mathbb {Z}^d$
, where the pattern w occurs. Define a map
![]() $\tilde \rho :\tilde X \to B^{\mathbb {Z}^d}$
by declaring
$\tilde \rho :\tilde X \to B^{\mathbb {Z}^d}$
by declaring
![]() $\sigma _v(\tilde \rho (x))_{B_{n+N}} = \Phi (\sigma _v(x)_{B_n})$
whenever
$\sigma _v(\tilde \rho (x))_{B_{n+N}} = \Phi (\sigma _v(x)_{B_n})$
whenever
![]() $\sigma _v(x)_{B_N}=w$
. Since the occurrences of w in any
$\sigma _v(x)_{B_N}=w$
. Since the occurrences of w in any
![]() $x\in \tilde X$
coincide with a coset of
$x\in \tilde X$
coincide with a coset of
![]() $(2n+2N)\mathbb {Z}^d$
, the map
$(2n+2N)\mathbb {Z}^d$
, the map
![]() $\sigma _v$
is well defined. Let
$\sigma _v$
is well defined. Let
![]() $\hat Y= \tilde \rho (\tilde X)$
. Because
$\hat Y= \tilde \rho (\tilde X)$
. Because
![]() $B_M$
witnesses that Y is
$B_M$
witnesses that Y is
![]() $\mathcal {G}$
-free and
$\mathcal {G}$
-free and
![]() $M < 3N$
, it follows that
$M < 3N$
, it follows that
![]() $\hat Y$
is
$\hat Y$
is
![]() $\mathcal {G}$
-free. We claim that
$\mathcal {G}$
-free. We claim that
![]() $Y \subseteq \hat Y$
. Indeed, given any
$Y \subseteq \hat Y$
. Indeed, given any
![]() $y \in Y$
, choose
$y \in Y$
, choose
![]() $f:(2n+2N)\mathbb {Z}^d \to W_{w,n}$
so that
$f:(2n+2N)\mathbb {Z}^d \to W_{w,n}$
so that
![]() $\Phi (f(v))= \sigma _v(y)_{B_{n+N}}$
for every
$\Phi (f(v))= \sigma _v(y)_{B_{n+N}}$
for every
![]() $v \in (2n+2N)\mathbb {Z}^d$
. Now find
$v \in (2n+2N)\mathbb {Z}^d$
. Now find
![]() $x \in X$
such that
$x \in X$
such that
![]() $\sigma _v(x)_{B_n}= f(v)$
for every
$\sigma _v(x)_{B_n}= f(v)$
for every
![]() $v \in (2n+2N)\mathbb {Z}^d$
. Then,
$v \in (2n+2N)\mathbb {Z}^d$
. Then,
![]() $x \in \tilde X$
and
$x \in \tilde X$
and
![]() $\hat \rho (x) =y$
. Because Y is an absolute retract for the class of
$\hat \rho (x) =y$
. Because Y is an absolute retract for the class of
![]() $\mathcal {G}$
-free subshifts, there exists a retraction map
$\mathcal {G}$
-free subshifts, there exists a retraction map
![]() $r:\hat Y \to Y$
. Let
$r:\hat Y \to Y$
. Let
![]() $\tilde \pi :\tilde X \to Y$
be defined by
$\tilde \pi :\tilde X \to Y$
be defined by
![]() $\tilde \pi = r \circ \hat \rho $
. Since r is a retraction and
$\tilde \pi = r \circ \hat \rho $
. Since r is a retraction and
![]() $Y \subseteq \hat \rho (\tilde X)$
, it follows that
$Y \subseteq \hat \rho (\tilde X)$
, it follows that
![]() $\tilde \pi (\tilde X)=Y$
. By the map extension property of Y, since
$\tilde \pi (\tilde X)=Y$
. By the map extension property of Y, since
![]() $X \rightsquigarrow Y$
, the map
$X \rightsquigarrow Y$
, the map
![]() $\tilde \pi $
extends to a map
$\tilde \pi $
extends to a map
![]() $\pi :X \to Y$
. Since
$\pi :X \to Y$
. Since
![]() $\tilde \pi (\tilde X)=Y$
, it follows that
$\tilde \pi (\tilde X)=Y$
, it follows that
![]() $\pi (X)=Y$
, so Y is a factor map.
$\pi (X)=Y$
, so Y is a factor map.
Poirier and Salo showed that the map extension property implies the finite extension property [Reference Poirier and Salo23]. This fact is a strengthening of Proposition 4.24, because the finite extension property implies strong irreducibility and finite type. However, the finite extension property does not imply the map extension property, so Theorem 10.5 does not completely recover Theorem 10.4. Furthermore, for
![]() $\mathbb {Z}^2$
-subsfhits, the map extension property does not follow from a stronger property called topological strong spatial mixing, introduced in [Reference Briceño8].
$\mathbb {Z}^2$
-subsfhits, the map extension property does not follow from a stronger property called topological strong spatial mixing, introduced in [Reference Briceño8].
Definition 10.6. A subshift
![]() $X \Subset A^\Gamma $
is topologically strong spacial mixing [Reference Briceño8] (abbreviated by TSSM) if there exists a finite set
$X \Subset A^\Gamma $
is topologically strong spacial mixing [Reference Briceño8] (abbreviated by TSSM) if there exists a finite set
![]() $K \Subset \Gamma $
so that for any subsets
$K \Subset \Gamma $
so that for any subsets
![]() $F,F_1,F_2 \Subset \Gamma $
such that
$F,F_1,F_2 \Subset \Gamma $
such that
![]() $F_1,F_2 \Subset \Gamma $
are K-disjoint and any
$F_1,F_2 \Subset \Gamma $
are K-disjoint and any
![]() $x^{(1)},x^{(2)} \in X$
such that
$x^{(1)},x^{(2)} \in X$
such that
![]() $x^{(1)}_F = x^{(2)}_F$
, there exists
$x^{(1)}_F = x^{(2)}_F$
, there exists
![]() $x \in X$
such that
$x \in X$
such that
![]() $x_F= x^{(1)}_F = x^{(2)}_F$
,
$x_F= x^{(1)}_F = x^{(2)}_F$
,
![]() $x_{F_1} = x^{(1)}_{F_1}$
and
$x_{F_1} = x^{(1)}_{F_1}$
and
![]() $x_{F_2} = x^{(2)}_{F_2}$
.
$x_{F_2} = x^{(2)}_{F_2}$
.
It was shown in [Reference Briceño, McGoff and Pavlov9] that topologically strong spacial mixing subshifts have the finite extension property.
In personal communication, Raimundo Briceno and Alvaro Bustos have constructed a simple example of a topologically strong spacial mixing
![]() $\mathbb {Z}^2$
-subshift X such that
$\mathbb {Z}^2$
-subshift X such that
![]() $\overline {X}_{\Gamma _0}$
is not strongly irreducible, where
$\overline {X}_{\Gamma _0}$
is not strongly irreducible, where
![]() $\Gamma _0 = \mathbb {Z} \times \{0\} < \mathbb {Z}^2$
. In particular, this example demonstrates that X, the finite extension property, does not imply the map extension property. Here is a version of the construction with
$\Gamma _0 = \mathbb {Z} \times \{0\} < \mathbb {Z}^2$
. In particular, this example demonstrates that X, the finite extension property, does not imply the map extension property. Here is a version of the construction with
![]() $\mathbb {Z}^2$
replaced by
$\mathbb {Z}^2$
replaced by
![]() $\Gamma = \mathbb {Z} \times (\mathbb {Z}/2\mathbb {Z})$
. Let
$\Gamma = \mathbb {Z} \times (\mathbb {Z}/2\mathbb {Z})$
. Let
![]() $\Gamma _0 = \{0\} \times (\mathbb {Z} /2\mathbb {Z})~<~\Gamma $
. Let
$\Gamma _0 = \{0\} \times (\mathbb {Z} /2\mathbb {Z})~<~\Gamma $
. Let
![]() $X \subseteq \{0,1\}^\Gamma $
be the subshift of finite type defined by the following rule: for every
$X \subseteq \{0,1\}^\Gamma $
be the subshift of finite type defined by the following rule: for every
![]() $v \in \Gamma $
, if
$v \in \Gamma $
, if
![]() $x_v=x_{v+(0,1)}$
and
$x_v=x_{v+(0,1)}$
and
![]() $x_{v+(1,0)}=x_{v+(1,1)}$
, then
$x_{v+(1,0)}=x_{v+(1,1)}$
, then
![]() $x_{v}=x_{v+(1,0)}$
. Then, it is not difficult to check that X is topologically strong spacial mixing, but
$x_{v}=x_{v+(1,0)}$
. Then, it is not difficult to check that X is topologically strong spacial mixing, but
![]() $X_{\Gamma _0}$
consists of two fixed points.
$X_{\Gamma _0}$
consists of two fixed points.
In view of the above discussion, Theorem 10.5 does not completely recover Theorem 10.4 of Briceno, Mcgoff, and Pavlov. However, Theorem 10.5 does address some new cases where the target subshift Y does not have a fixed point. For instance, Theorem 10.5 characterizes the (greater entropy) block-gluing subshifts that factor onto the
![]() $5$
-colorings of
$5$
-colorings of
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
Acknowledgments
I am grateful to Leo Poirier and Ville Salo for insightful discussions, in particular, regarding homotopy and contractability in symbolic dynamics. I thank Barak Weiss for providing background about Korkine–Zolotarev reduced bases of lattices in
![]() $\mathbb {R}^d$
and the anonymous reviewer for a thorough review. This research was supported by the Israel Science Foundation grant No. 985/23.
$\mathbb {R}^d$
and the anonymous reviewer for a thorough review. This research was supported by the Israel Science Foundation grant No. 985/23.