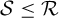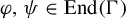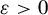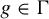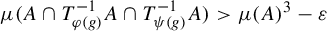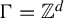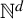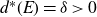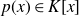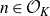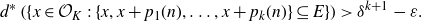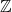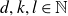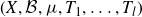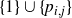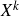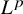Refine search
Actions for selected content:
64 results
On ergodicity and transience for a class of level-dependent GI/M/1-type Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 21 November 2025, pp. 1301-1317
- Print publication:
- December 2025
-
- Article
- Export citation
Some ergodic theorems involving Omega function and their applications
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
 $\overline {d}$-continuity for countable state shifts
$\overline {d}$-continuity for countable state shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-24
-
- Article
- Export citation
Pointwise convergence of bilinear polynomial averages over the primes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 01 September 2025, pp. 3760-3799
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-leading eigenvalues of the Perron–Frobenius operators for beta-maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 29 August 2025, pp. 291-319
- Print publication:
- January 2026
-
- Article
- Export citation
A Kakutani–Rokhlin decomposition for conditionally ergodic process in the measure-free setting of vector lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 05 August 2025, pp. 3600-3618
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hereditarily frequently hypercyclic operators and disjoint frequent hypercyclicity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 3021-3072
- Print publication:
- October 2025
-
- Article
- Export citation
Two dynamical approaches to the notion of exponential separation for random systems of delay differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joining properties of automorphisms disjoint with all ergodic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 1998-2022
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simplices in large sets and directional expansion in ergodic actions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUASI-ERGODICITY OF COMPACT STRONG FELLER SEMIGROUPS ON
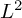 $L^2$
$L^2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 541-584
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the speed of convergence in the ergodic theorem for shift operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 04 November 2024, pp. 1919-1937
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform syndeticity in multiple recurrence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 28 May 2024, pp. 504-525
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Co-spectral radius for countable equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 3385-3427
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Khintchine-type double recurrence in abelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 April 2024, pp. 1-33
- Print publication:
- January 2025
-
- Article
- Export citation
Bohr chaoticity of principal algebraic actions and Riesz product measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 2933-2959
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiple recurrence and popular differences for polynomial patterns in rings of integers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 239-278
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a multi-parameter variant of the Bellow–Furstenberg problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 September 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral cocycle for substitution tilings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 1629-1672
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adaptation of a population to a changing environment in the light of quasi-stationarity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 235-286
- Print publication:
- March 2024
-
- Article
- Export citation










































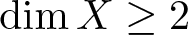
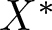
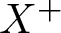
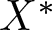
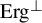
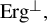
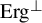
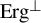

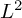








 . We discuss several applications and illustrate our results with examples. This includes a complete description of quasi-ergodicity for a large class of semigroups corresponding to non-local Schrödinger operators with confining potentials.
. We discuss several applications and illustrate our results with examples. This includes a complete description of quasi-ergodicity for a large class of semigroups corresponding to non-local Schrödinger operators with confining potentials.