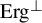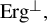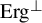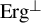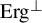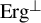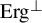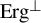1 Introduction
The study of disjointness which expresses the extreme degree of non-isomorphism (in particular, the absence of non-trivial common factors) of two measure-preserving automorphisms originated in the seminal work of Furstenberg [Reference Furstenberg7] in 1967. It is an important direction of research until today and determining whether two automorphisms are disjoint still remains a challenging problem. In particular, given a class
![]() $\mathcal A$
of automorphisms, a full description of the class
$\mathcal A$
of automorphisms, a full description of the class
![]() $\mathcal A^{\perp }$
of automorphisms disjoint with every element of
$\mathcal A^{\perp }$
of automorphisms disjoint with every element of
![]() $\mathcal A$
is often a hard task. Let us recall some classical results:
$\mathcal A$
is often a hard task. Let us recall some classical results:
-
(i) the class
 $\operatorname {ID} ^\perp $
of automorphisms disjoint with all identities equals the class
$\operatorname {ID} ^\perp $
of automorphisms disjoint with all identities equals the class
 $\operatorname {Erg}$
of all ergodic transformations (by
$\operatorname {Erg}$
of all ergodic transformations (by
 $\operatorname {ID} $
we denote the class of all identities), see [Reference Furstenberg7];
$\operatorname {ID} $
we denote the class of all identities), see [Reference Furstenberg7]; -
(ii) the class
 $\operatorname {ZE}^\perp $
of maps disjoint with the zero entropy automorphisms is equal to the family of K-automorphisms ([Reference Furstenberg7], together with [Reference Lemańczyk, Parreau and Thouvenot20, Reference Sinai24]).
$\operatorname {ZE}^\perp $
of maps disjoint with the zero entropy automorphisms is equal to the family of K-automorphisms ([Reference Furstenberg7], together with [Reference Lemańczyk, Parreau and Thouvenot20, Reference Sinai24]).
For some other classical classes, only weaker relations are known: the class
![]() $\operatorname {Dist}$
of distal automorphisms is disjoint from the class
$\operatorname {Dist}$
of distal automorphisms is disjoint from the class
![]() $\operatorname {WM}$
of weakly mixing automorphisms [Reference Furstenberg7] or the class
$\operatorname {WM}$
of weakly mixing automorphisms [Reference Furstenberg7] or the class
![]() $\operatorname {Rig}$
of rigid automorphisms is disjoint from the class
$\operatorname {Rig}$
of rigid automorphisms is disjoint from the class
![]() $\operatorname {MM}$
of mildly mixing automorphisms [Reference Furstenberg and Weiss8]. Usually, the problem of deciding about the disjointness of two automorphisms slightly simplifies when we consider them both ergodic as it is reduced to study ergodic joinings. However, if two automorphisms are disjoint, then one of them has to be ergodic (otherwise, they both have non-trivial identities as factors and these are not disjoint). In connection with item (i), it is natural to ask whether
$\operatorname {MM}$
of mildly mixing automorphisms [Reference Furstenberg and Weiss8]. Usually, the problem of deciding about the disjointness of two automorphisms slightly simplifies when we consider them both ergodic as it is reduced to study ergodic joinings. However, if two automorphisms are disjoint, then one of them has to be ergodic (otherwise, they both have non-trivial identities as factors and these are not disjoint). In connection with item (i), it is natural to ask whether
![]() $\operatorname {Erg}^\perp $
goes beyond identities. It indeed does (this observation was a folklore), however, a satisfactory characterization of elements of the class
$\operatorname {Erg}^\perp $
goes beyond identities. It indeed does (this observation was a folklore), however, a satisfactory characterization of elements of the class
![]() $\operatorname {Erg}^\perp $
was only given very recently in [Reference Górska, Lemańczyk and de la Rue13], see Theorem 2 below. One of the recent reasons to study the non-ergodic case (the elements of
$\operatorname {Erg}^\perp $
was only given very recently in [Reference Górska, Lemańczyk and de la Rue13], see Theorem 2 below. One of the recent reasons to study the non-ergodic case (the elements of
![]() $\operatorname {Erg}^\perp $
, other than the one-point system, are obviously non-ergodic) came recently from Frantzikinakis and Host [Reference Frantzikinakis and Host6], who studied so-called (logarithmic) Furstenberg systems of the classical Liouville function and discovered that the celebrated Sarnak conjecture may fail because some (hypothetic) of its Furstenberg systems might be elements of
$\operatorname {Erg}^\perp $
, other than the one-point system, are obviously non-ergodic) came recently from Frantzikinakis and Host [Reference Frantzikinakis and Host6], who studied so-called (logarithmic) Furstenberg systems of the classical Liouville function and discovered that the celebrated Sarnak conjecture may fail because some (hypothetic) of its Furstenberg systems might be elements of
![]() $\operatorname {Erg}^\perp $
. (See also the still open Problem 3.1 of a workshop [1] where Frantzikinakis’ question whether an automorphism considered in Example 1 below can be realized as a Furstenberg system of the Liouville function.)
$\operatorname {Erg}^\perp $
. (See also the still open Problem 3.1 of a workshop [1] where Frantzikinakis’ question whether an automorphism considered in Example 1 below can be realized as a Furstenberg system of the Liouville function.)
Another natural problem when studying classes of the form
![]() $\mathcal A^\perp $
is to describe the class
$\mathcal A^\perp $
is to describe the class
![]() $\mathcal M(\mathcal A^\perp )\subseteq \mathcal A^\perp $
of its multipliers, that is, of automorphisms
$\mathcal M(\mathcal A^\perp )\subseteq \mathcal A^\perp $
of its multipliers, that is, of automorphisms
![]() $S\in \mathcal A^\perp $
such that every joining of S with every element of
$S\in \mathcal A^\perp $
such that every joining of S with every element of
![]() $\mathcal A^\perp $
also belongs to
$\mathcal A^\perp $
also belongs to
![]() $\mathcal A^\perp $
. The study of this class is, in general, very difficult and leads often to many surprising results. In 1989, Glasner and Weiss [Reference Glasner and Weiss12] pioneered the study of the class
$\mathcal A^\perp $
. The study of this class is, in general, very difficult and leads often to many surprising results. In 1989, Glasner and Weiss [Reference Glasner and Weiss12] pioneered the study of the class
![]() $\operatorname {WM}^\perp $
, and they proved that
$\operatorname {WM}^\perp $
, and they proved that
![]() $\operatorname {Dist}\subsetneq \operatorname {WM}^\perp $
. Continuing on their result, in two papers [Reference Glasner10, Reference Lemańczyk and Parreau19], it was proved that
$\operatorname {Dist}\subsetneq \operatorname {WM}^\perp $
. Continuing on their result, in two papers [Reference Glasner10, Reference Lemańczyk and Parreau19], it was proved that
Returning to the
![]() $\operatorname {Erg}$
class, we clearly have
$\operatorname {Erg}$
class, we clearly have
where it is easy to see that
![]() $\mathcal {M}(\operatorname {Erg}^\perp )\subsetneq \operatorname {Erg}^\perp $
. In fact, in §4 (see Example 1), we consider a standard twist on the torus
$\mathcal {M}(\operatorname {Erg}^\perp )\subsetneq \operatorname {Erg}^\perp $
. In fact, in §4 (see Example 1), we consider a standard twist on the torus
![]() $(x,y)\mapsto (x,x+y)$
as an example of an element in
$(x,y)\mapsto (x,x+y)$
as an example of an element in
![]() $\operatorname {Erg}^\perp $
and directly show that it is not an element of
$\operatorname {Erg}^\perp $
and directly show that it is not an element of
![]() $\mathcal M(\operatorname {Erg}^\perp )$
. The latter assertion follows also from our main, somewhat surprising, result. (It was formulated as a conjecture by M. Lemańczyk in 2018 (private communication).)
$\mathcal M(\operatorname {Erg}^\perp )$
. The latter assertion follows also from our main, somewhat surprising, result. (It was formulated as a conjecture by M. Lemańczyk in 2018 (private communication).)
Theorem 1. We have
![]() $\operatorname {ID} =\mathcal {M}(\operatorname {Erg}^\perp )$
.
$\operatorname {ID} =\mathcal {M}(\operatorname {Erg}^\perp )$
.
While the class
![]() $\operatorname {Erg}^\perp $
is not closed under taking joinings, in §5, we prove that it is closed under Cartesian products.
$\operatorname {Erg}^\perp $
is not closed under taking joinings, in §5, we prove that it is closed under Cartesian products.
To show that an ergodic automorphism T is a multiplier of a class
![]() $\mathcal {A}^\perp $
, it is enough to show that the automorphisms determined by all self-joinings of T are disjoint from the elements of
$\mathcal {A}^\perp $
, it is enough to show that the automorphisms determined by all self-joinings of T are disjoint from the elements of
![]() $\mathcal {A}$
, see for example, [Reference Lemańczyk and Parreau19, §5] (see also Proposition 33). We show in §6 however that this approach fails when we study the class
$\mathcal {A}$
, see for example, [Reference Lemańczyk and Parreau19, §5] (see also Proposition 33). We show in §6 however that this approach fails when we study the class
![]() $\operatorname {Erg}^\perp $
by exhibiting a non-identity automorphism T whose all self-joinings yield elements of
$\operatorname {Erg}^\perp $
by exhibiting a non-identity automorphism T whose all self-joinings yield elements of
![]() $\operatorname {Erg}^\perp $
and which cannot be in
$\operatorname {Erg}^\perp $
and which cannot be in
![]() $\mathcal {M}(\operatorname {Erg}^\perp )$
by Theorem 1. Moreover, the example constructed in §6 serves to create a non-trivial characteristic class (see §2.4), which does not contain a non-trivial ergodic automorphism, yet it is not formed only of identities. This answers a question posed by Adam Kanigowski and Mariusz Lemańczyk in a private correspondence.
$\mathcal {M}(\operatorname {Erg}^\perp )$
by Theorem 1. Moreover, the example constructed in §6 serves to create a non-trivial characteristic class (see §2.4), which does not contain a non-trivial ergodic automorphism, yet it is not formed only of identities. This answers a question posed by Adam Kanigowski and Mariusz Lemańczyk in a private correspondence.
2 Preliminaries
2.1 Measure-preserving automorphism and ergodic decomposition
We consider invertible, bi-measurable and measure-preserving transformations T of standard Borel probability spaces
![]() $(X,\mathcal {B},\mu )$
. Recall that T is
$(X,\mathcal {B},\mu )$
. Recall that T is
![]() $\mu $
-preserving means that
$\mu $
-preserving means that
![]() $T_*\mu =\mu $
, where
$T_*\mu =\mu $
, where
![]() $T_*(\cdot )$
denotes the push-forward of a measure by the transformation T. Then, the quadruple
$T_*(\cdot )$
denotes the push-forward of a measure by the transformation T. Then, the quadruple
![]() $(X,\mathcal {B},\mu ,T)$
is called a dynamical system.
$(X,\mathcal {B},\mu ,T)$
is called a dynamical system.
Without loss of generality, we can assume up to isomorphism that X is a compact metric space and T is a homeomorphism. Each Borel probability measure
![]() $\mu $
of a compact metric space X yields a standard Borel probability space. We denote by
$\mu $
of a compact metric space X yields a standard Borel probability space. We denote by
![]() $\mathscr {M}(X)$
the space of such measures (it is compact in the weak
$\mathscr {M}(X)$
the space of such measures (it is compact in the weak
![]() $^\ast $
-topology). If
$^\ast $
-topology). If
![]() $T:X\to X$
is a homeomorphism, then we denote by
$T:X\to X$
is a homeomorphism, then we denote by
![]() $\mathscr {M}(X,T)$
the subspace of
$\mathscr {M}(X,T)$
the subspace of
![]() $\mathscr {M}(X)$
consisting of T-invariant measures (it is a non-empty closed subset of
$\mathscr {M}(X)$
consisting of T-invariant measures (it is a non-empty closed subset of
![]() $\mathscr {M}(X)$
).
$\mathscr {M}(X)$
).
Two transformations T and S on a standard Borel probability space
![]() $(X,\mathcal {B},\mu )$
are identified if
$(X,\mathcal {B},\mu )$
are identified if
![]() $T(x)=S(x)$
for
$T(x)=S(x)$
for
![]() $\mu $
-almost every (a.e.)
$\mu $
-almost every (a.e.)
![]() $x\in X$
, and we call an automorphism of
$x\in X$
, and we call an automorphism of
![]() $(X,\mathcal {B},\mu )$
an equivalence class of transformations modulo this identification. The group of automorphisms of
$(X,\mathcal {B},\mu )$
an equivalence class of transformations modulo this identification. The group of automorphisms of
![]() $(X,\mathcal {B},\mu )$
is denoted by
$(X,\mathcal {B},\mu )$
is denoted by
![]() $\operatorname {Aut}(X,\mathcal {B},\mu )$
. It is a classical fact that
$\operatorname {Aut}(X,\mathcal {B},\mu )$
. It is a classical fact that
![]() $\operatorname {Aut}(X,\mathcal {B},\mu )$
with the so-called weak topology is a Polish group (see e.g. [Reference Kechris17]).
$\operatorname {Aut}(X,\mathcal {B},\mu )$
with the so-called weak topology is a Polish group (see e.g. [Reference Kechris17]).
Each automorphism T of
![]() $(X,\mathcal {B},\mu )$
defines a unitary operator
$(X,\mathcal {B},\mu )$
defines a unitary operator
![]() $U_T$
on
$U_T$
on
![]() $L^2(X,\mathcal {B},\mu )$
, called a Koopman operator, defined by
$L^2(X,\mathcal {B},\mu )$
, called a Koopman operator, defined by
![]() $U_Tf := f\circ T$
. We recall that T is said to be ergodic if the only
$U_Tf := f\circ T$
. We recall that T is said to be ergodic if the only
![]() $U_T$
-invariant functions are constant. If, additionally,
$U_T$
-invariant functions are constant. If, additionally,
![]() $U_T$
has no other eigenfunctions, then T is said to be weakly mixing.
$U_T$
has no other eigenfunctions, then T is said to be weakly mixing.
We denote by
![]() $\operatorname {Aut}$
the class of all automorphisms on all standard Borel probability spaces, considered up to isomorphism. By
$\operatorname {Aut}$
the class of all automorphisms on all standard Borel probability spaces, considered up to isomorphism. By
![]() $\operatorname {Erg}\subset \operatorname {Aut}$
, we denote the class of all ergodic automorphisms and by
$\operatorname {Erg}\subset \operatorname {Aut}$
, we denote the class of all ergodic automorphisms and by
![]() $\operatorname {WM}\subset \operatorname {Erg}$
, the class of all weakly mixing automorphisms. Recall also that
$\operatorname {WM}\subset \operatorname {Erg}$
, the class of all weakly mixing automorphisms. Recall also that
![]() $\operatorname {ID} \subset \operatorname {Aut}$
stands for the class of identities on all standard Borel probability spaces. Since we allow the measures under consideration to have atoms, the class
$\operatorname {ID} \subset \operatorname {Aut}$
stands for the class of identities on all standard Borel probability spaces. Since we allow the measures under consideration to have atoms, the class
![]() $\operatorname {ID} $
is uncountable.
$\operatorname {ID} $
is uncountable.
Of course, in general,
![]() $T\in \operatorname {Aut}(X,\mathcal {B},\mu )$
need not be ergodic. Let us recall the classical concept of ergodic decomposition (see [Reference Rokhlin21]). Denote by
$T\in \operatorname {Aut}(X,\mathcal {B},\mu )$
need not be ergodic. Let us recall the classical concept of ergodic decomposition (see [Reference Rokhlin21]). Denote by
![]() $\mathrm {Inv}(T)$
the
$\mathrm {Inv}(T)$
the
![]() $\sigma $
-algebra of invariant sets. Let also
$\sigma $
-algebra of invariant sets. Let also
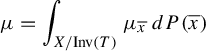 $$ \begin{align} \mu=\int_{X/\mathrm{Inv}(T)}\mu_{\overline{x}}\,dP(\overline{x}) \end{align} $$
$$ \begin{align} \mu=\int_{X/\mathrm{Inv}(T)}\mu_{\overline{x}}\,dP(\overline{x}) \end{align} $$
be the disintegration of
![]() $\mu $
over
$\mu $
over
![]() $P:=\mu |_{\mathrm {{Inv}(T)}}$
. Then, there exists a measurable partition of
$P:=\mu |_{\mathrm {{Inv}(T)}}$
. Then, there exists a measurable partition of
![]() $\overline {X}:=X/\mathrm {Inv}(T)$
:
$\overline {X}:=X/\mathrm {Inv}(T)$
:
and a standard Borel probability space
![]() $(Z,\mathcal {D},\kappa )$
, with
$(Z,\mathcal {D},\kappa )$
, with
![]() $\kappa $
non-atomic, such that the space
$\kappa $
non-atomic, such that the space
![]() $(X,\mathcal {B},\mu )$
can be identified with the disjoint union of the corresponding product spaces (on
$(X,\mathcal {B},\mu )$
can be identified with the disjoint union of the corresponding product spaces (on
![]() $\mathbb Z_n:=\mathbb {Z}/n\mathbb {Z}$
, we consider the uniform measure)
$\mathbb Z_n:=\mathbb {Z}/n\mathbb {Z}$
, we consider the uniform measure)
and the action of T in these new ‘coordinates’ is given by
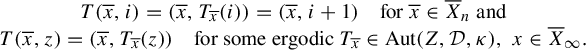 $$ \begin{align} \begin{array}{c} T(\overline{x},i)=(\overline{x},T_{\overline{x}}(i))=(\overline{x},i+1)\quad \text{for }\overline{x}\in\overline{X}_n\text{ and}\\ T(\overline{x},z)=(\overline{x},T_{\overline{x}}(z))\quad\text{for some ergodic }T_{\overline{x}}\in\operatorname{Aut}(Z,\mathcal{D},\kappa), {\ x\in \overline X_\infty}.\end{array}\end{align} $$
$$ \begin{align} \begin{array}{c} T(\overline{x},i)=(\overline{x},T_{\overline{x}}(i))=(\overline{x},i+1)\quad \text{for }\overline{x}\in\overline{X}_n\text{ and}\\ T(\overline{x},z)=(\overline{x},T_{\overline{x}}(z))\quad\text{for some ergodic }T_{\overline{x}}\in\operatorname{Aut}(Z,\mathcal{D},\kappa), {\ x\in \overline X_\infty}.\end{array}\end{align} $$
The map
![]() $\overline {x}\mapsto T_{\overline {x}}$
is measurable in the relevant Borel structures. The space
$\overline {x}\mapsto T_{\overline {x}}$
is measurable in the relevant Borel structures. The space
![]() $(\overline {X},P)$
is called the space of ergodic components, and the representation of
$(\overline {X},P)$
is called the space of ergodic components, and the representation of
![]() $(X,\mathcal {B},\mu ,T)$
given in equation (4) is called the ergodic decomposition of T. The ergodic decomposition is given up to a P-null subset. For example, if
$(X,\mathcal {B},\mu ,T)$
given in equation (4) is called the ergodic decomposition of T. The ergodic decomposition is given up to a P-null subset. For example, if
![]() $X=\mathbb {T}^2$
(considered with Lebesgue measure
$X=\mathbb {T}^2$
(considered with Lebesgue measure
![]() $\operatorname {Leb}_{\mathbb {T}^2}$
) and
$\operatorname {Leb}_{\mathbb {T}^2}$
) and
![]() $T:(x,y)\mapsto (x,y+x)$
, then it is already the ergodic decomposition of T since
$T:(x,y)\mapsto (x,y+x)$
, then it is already the ergodic decomposition of T since
![]() $\mathbb {T}\times \{0\}$
is the space of ergodic components (with
$\mathbb {T}\times \{0\}$
is the space of ergodic components (with
![]() $P=\operatorname {Leb}_{\mathbb {T}}$
) and for P-a.e.
$P=\operatorname {Leb}_{\mathbb {T}}$
) and for P-a.e.
![]() $x\in \mathbb {T}$
,
$x\in \mathbb {T}$
,
![]() $T_x(y)=x+y$
is an (ergodic) irrational rotation.
$T_x(y)=x+y$
is an (ergodic) irrational rotation.
2.2 Joinings
Let
![]() $(X,\mathcal B,\mu , T)$
and
$(X,\mathcal B,\mu , T)$
and
![]() $(Y,\mathcal C,\nu ,S)$
be two dynamical systems. We say that a probability measure
$(Y,\mathcal C,\nu ,S)$
be two dynamical systems. We say that a probability measure
![]() $\unicode{x3bb} $
on
$\unicode{x3bb} $
on
![]() $(X\times Y, \mathcal B\otimes \mathcal C)$
is a joining of T and S if:
$(X\times Y, \mathcal B\otimes \mathcal C)$
is a joining of T and S if:
-
(1)
 $\unicode{x3bb} $
is
$\unicode{x3bb} $
is
 $T\times S$
- invariant;
$T\times S$
- invariant; -
(2) the marginals of
 $\unicode{x3bb} $
on X- and Y-coordinates are
$\unicode{x3bb} $
on X- and Y-coordinates are
 $\mu $
and
$\mu $
and
 $\nu $
, respectively.
$\nu $
, respectively.
We note that
![]() $(X\times Y, \mathcal {B}\otimes \mathcal {C}, \unicode{x3bb} , T\times S)$
is a dynamical system (sometimes, we denote such a system simply by
$(X\times Y, \mathcal {B}\otimes \mathcal {C}, \unicode{x3bb} , T\times S)$
is a dynamical system (sometimes, we denote such a system simply by
![]() $T\vee S$
). We denote the set of all joinings of T and S by
$T\vee S$
). We denote the set of all joinings of T and S by
![]() $J(T,S)$
. Note that
$J(T,S)$
. Note that
![]() $\mu \otimes \nu $
is always an element of
$\mu \otimes \nu $
is always an element of
![]() $J(T,S)$
. Following [Reference Furstenberg7], we say that T and S are disjoint if
$J(T,S)$
. Following [Reference Furstenberg7], we say that T and S are disjoint if
![]() $J(T,S)=\{\mu \otimes \nu \}$
and write
$J(T,S)=\{\mu \otimes \nu \}$
and write
![]() $T\perp S$
. Note that if T and S are ergodic and
$T\perp S$
. Note that if T and S are ergodic and
![]() $\unicode{x3bb} \in J(T,S)$
, then the ergodic components of
$\unicode{x3bb} \in J(T,S)$
, then the ergodic components of
![]() $\unicode{x3bb} $
are also elements of
$\unicode{x3bb} $
are also elements of
![]() $J(T,S)$
. In particular, we have
$J(T,S)$
. In particular, we have
In the case where
![]() $T=S$
, we set
$T=S$
, we set
![]() $J_2(T):=J(T,T)$
and refer to the elements of
$J_2(T):=J(T,T)$
and refer to the elements of
![]() $J_2(T)$
as 2-self-joinings. Unless T is the
$J_2(T)$
as 2-self-joinings. Unless T is the
![]() $1$
-point dynamical system, it is never disjoint with itself. Indeed, the diagonal measure is a
$1$
-point dynamical system, it is never disjoint with itself. Indeed, the diagonal measure is a
![]() $2$
-self-joining:
$2$
-self-joining:
![]() $\mu _{\mathrm {Id}}:=(\mathrm {Id},\mathrm {Id})_*\mu $
and
$\mu _{\mathrm {Id}}:=(\mathrm {Id},\mathrm {Id})_*\mu $
and
![]() $\mu _{\mathrm {Id}}= \mu \otimes \mu $
if and only if T is a
$\mu _{\mathrm {Id}}= \mu \otimes \mu $
if and only if T is a
![]() $1$
-point dynamical system. (Here and thereafter, we denote
$1$
-point dynamical system. (Here and thereafter, we denote
![]() $(f,g)(x)=(f(x),g(x))$
.) More generally, if
$(f,g)(x)=(f(x),g(x))$
.) More generally, if
![]() $R\in C(T)$
is an element of the centralizer of T (that is,
$R\in C(T)$
is an element of the centralizer of T (that is,
![]() $R\in \operatorname {Aut}(X,\mathcal {B},\mu )$
and
$R\in \operatorname {Aut}(X,\mathcal {B},\mu )$
and
![]() $R\circ T=T\circ R$
), then the graph measure
$R\circ T=T\circ R$
), then the graph measure
![]() $\mu _R:=(\mathrm {Id},R)_*\mu $
is a member of
$\mu _R:=(\mathrm {Id},R)_*\mu $
is a member of
![]() $J_2(T)$
. In particular, the off-diagonal self-joinings
$J_2(T)$
. In particular, the off-diagonal self-joinings
![]() $\mu _{T^n}$
,
$\mu _{T^n}$
,
![]() $n\in \mathbb {Z}$
, belong to
$n\in \mathbb {Z}$
, belong to
![]() $J_2(T)$
. In addition, note that
$J_2(T)$
. In addition, note that
![]() $C(T)$
is a closed subgroup of
$C(T)$
is a closed subgroup of
![]() $\operatorname {Aut}(X,\mathcal {B},\mu )$
.
$\operatorname {Aut}(X,\mathcal {B},\mu )$
.
It is a classical fact that in the weak-
![]() $\ast $
topology,
$\ast $
topology,
![]() $J_2(T)$
is a compact set, see [Reference Glasner11]. Moreover, if T is additionally ergodic, then
$J_2(T)$
is a compact set, see [Reference Glasner11]. Moreover, if T is additionally ergodic, then
![]() $J_2(T)$
is a simplex and the set of extremal points of
$J_2(T)$
is a simplex and the set of extremal points of
![]() $J_2(T)$
consists of ergodic 2-self-joinings. In particular, the set of ergodic self-joinings is non-empty and we denote it by
$J_2(T)$
consists of ergodic 2-self-joinings. In particular, the set of ergodic self-joinings is non-empty and we denote it by
![]() $J_2^e(T)$
. Note that the graph joinings
$J_2^e(T)$
. Note that the graph joinings
![]() $\mu _R$
are always ergodic as long as T is ergodic. In fact, the corresponding automorphisms are isomorphic to T, where an isomorphism is given by the map
$\mu _R$
are always ergodic as long as T is ergodic. In fact, the corresponding automorphisms are isomorphic to T, where an isomorphism is given by the map
![]() $x\mapsto (x,Rx)$
.
$x\mapsto (x,Rx)$
.
Given
![]() $(X_i,\mathcal {B}_i,\mu _i, T_i) $
,
$(X_i,\mathcal {B}_i,\mu _i, T_i) $
,
![]() $i\geq 1$
, we also consider infinite joinings
$i\geq 1$
, we also consider infinite joinings
![]() $\unicode{x3bb} \in J(T_1,T_2,\ldots )$
(invariant measures on
$\unicode{x3bb} \in J(T_1,T_2,\ldots )$
(invariant measures on
![]() $X_1\times X_2\times \cdots $
whose marginals are
$X_1\times X_2\times \cdots $
whose marginals are
![]() $\mu _i$
,
$\mu _i$
,
![]() $i\geq 1$
). If
$i\geq 1$
). If
![]() $T_i$
are ergodic, then
$T_i$
are ergodic, then
![]() $J^e(T_1,T_2,\ldots )\neq \emptyset $
. Note that if
$J^e(T_1,T_2,\ldots )\neq \emptyset $
. Note that if
![]() $A\subset \mathbb {N}$
, then we can speak about
$A\subset \mathbb {N}$
, then we can speak about
![]() $J(T_{i_1},T_{i_2}, \ldots )$
, where
$J(T_{i_1},T_{i_2}, \ldots )$
, where
![]() $A=\{i_1,i_2,\ldots \}$
(A can be finite here). Whenever
$A=\{i_1,i_2,\ldots \}$
(A can be finite here). Whenever
![]() $T_1=T_2=\cdots =T$
, we speak about
$T_1=T_2=\cdots =T$
, we speak about
![]() $J_{\infty }(T)$
the set of (infinite) self-joinings. Now, if
$J_{\infty }(T)$
the set of (infinite) self-joinings. Now, if
![]() $A\subset \mathbb {N}$
and
$A\subset \mathbb {N}$
and
![]() $R_{i_k}\in C(T)$
,
$R_{i_k}\in C(T)$
,
![]() $k\geq 2$
, then we can consider the corresponding graph self-joining
$k\geq 2$
, then we can consider the corresponding graph self-joining
![]() $\mu _{R_{i_2},R_{i_3},\ldots }:=(\mathrm {Id},R_{i_2}, R_{i_3},\ldots )_\ast \mu $
. If
$\mu _{R_{i_2},R_{i_3},\ldots }:=(\mathrm {Id},R_{i_2}, R_{i_3},\ldots )_\ast \mu $
. If
![]() $R_{i_k}$
are powers of T, then we speak about off-diagonal self-joinings. If each
$R_{i_k}$
are powers of T, then we speak about off-diagonal self-joinings. If each
![]() $\unicode{x3bb} \in J_{\infty }^e(T)$
is a product of off-diagonal self-joinings, then we say that the automorphism T has the minimal self-joining property (or MSJ), see [Reference Rudolph22].
$\unicode{x3bb} \in J_{\infty }^e(T)$
is a product of off-diagonal self-joinings, then we say that the automorphism T has the minimal self-joining property (or MSJ), see [Reference Rudolph22].
Following [Reference Halmos15], we say that
![]() $(X,\mathcal B, \mu , T)$
has the PID property if for every
$(X,\mathcal B, \mu , T)$
has the PID property if for every
![]() $\unicode{x3bb} \in J_{\infty }(X,\mathcal B,\mu , T)$
, if
$\unicode{x3bb} \in J_{\infty }(X,\mathcal B,\mu , T)$
, if
![]() $\unicode{x3bb} $
projects on every pair of coordinates as
$\unicode{x3bb} $
projects on every pair of coordinates as
![]() $\mu \otimes \mu $
, then
$\mu \otimes \mu $
, then
![]() $\unicode{x3bb} $
is the product measure. Note that each
$\unicode{x3bb} $
is the product measure. Note that each
![]() $MSJ$
automorphism has the PID property.
$MSJ$
automorphism has the PID property.
Let
![]() $(X_i,\mathcal B_i,\mu _i,T_i)$
for
$(X_i,\mathcal B_i,\mu _i,T_i)$
for
![]() $i=1,2$
be a pair of dynamical systems. Let also
$i=1,2$
be a pair of dynamical systems. Let also
![]() $\mathcal A_i\subset \mathcal B_i$
be factors of those systems, that is, invariant sub-
$\mathcal A_i\subset \mathcal B_i$
be factors of those systems, that is, invariant sub-
![]() $\sigma $
-algebras. Let
$\sigma $
-algebras. Let
![]() $\mu _i =\int _{X_i/\mathcal A_i}\mu _{i,\bar x_i}\, d\mu _i|_{\mathcal A_i}$
be the disintegration of
$\mu _i =\int _{X_i/\mathcal A_i}\mu _{i,\bar x_i}\, d\mu _i|_{\mathcal A_i}$
be the disintegration of
![]() $\mu _i$
over the respective factor. Assume that
$\mu _i$
over the respective factor. Assume that
![]() $\unicode{x3bb} \in J(T_1|_{\mathcal A_1}, T_2|_{\mathcal A_2})$
. Then, the formula
$\unicode{x3bb} \in J(T_1|_{\mathcal A_1}, T_2|_{\mathcal A_2})$
. Then, the formula
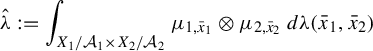 $$ \begin{align*} \hat{\unicode{x3bb}}:=\int_{X_1/\mathcal A_1\times X_2/\mathcal A_2}\mu_{1,\bar x_1}\otimes\mu_{2,\bar x_2}\,d\unicode{x3bb}(\bar x_1,\bar x_2) \end{align*} $$
$$ \begin{align*} \hat{\unicode{x3bb}}:=\int_{X_1/\mathcal A_1\times X_2/\mathcal A_2}\mu_{1,\bar x_1}\otimes\mu_{2,\bar x_2}\,d\unicode{x3bb}(\bar x_1,\bar x_2) \end{align*} $$
defines an element in
![]() $J(T_1,T_2)$
called the relatively independent extension of
$J(T_1,T_2)$
called the relatively independent extension of
![]() $\unicode{x3bb} $
. We proceed similarly for finite and countable families of automorphisms (cf. proof of Lemma 8). If additionally
$\unicode{x3bb} $
. We proceed similarly for finite and countable families of automorphisms (cf. proof of Lemma 8). If additionally
![]() $T_1|_{\mathcal A_1}$
and
$T_1|_{\mathcal A_1}$
and
![]() $T_2|_{\mathcal A_2}$
are both isomorphic to some
$T_2|_{\mathcal A_2}$
are both isomorphic to some
![]() $(Y,\mathcal C,\nu , S)$
, then we may consider the relatively independent extension over
$(Y,\mathcal C,\nu , S)$
, then we may consider the relatively independent extension over
![]() $\mathcal C$
given by
$\mathcal C$
given by
This corresponds to taking a diagonal joining as
![]() $\unicode{x3bb} $
in the definition of the relatively independent extension.
$\unicode{x3bb} $
in the definition of the relatively independent extension.
We are interested in properties of the class of dynamical systems disjoint with all ergodic systems, that is, with
In the following subsection, we give some facts describing the structure of
![]() $\operatorname {Erg}^{\perp }$
as well as some basic examples of elements from this class.
$\operatorname {Erg}^{\perp }$
as well as some basic examples of elements from this class.
2.3 Elements of
 $\kern1pt\operatorname {Erg}^{\perp }$
$\kern1pt\operatorname {Erg}^{\perp }$
Let us first recall some well-known examples of automorphisms from
![]() $\operatorname {Erg}^\perp $
. It is a classical fact that
$\operatorname {Erg}^\perp $
. It is a classical fact that
![]() $\mathrm {Id}\in \operatorname {Erg}^{\perp }$
. Also, every system of the form
$\mathrm {Id}\in \operatorname {Erg}^{\perp }$
. Also, every system of the form
![]() $(x,y)\mapsto (x,x+y)$
on
$(x,y)\mapsto (x,x+y)$
on
![]() $\mathbb T^2$
with invariant measure
$\mathbb T^2$
with invariant measure
![]() $\mu \otimes \operatorname {Leb}_{\mathbb {T}}$
is an element of
$\mu \otimes \operatorname {Leb}_{\mathbb {T}}$
is an element of
![]() $\operatorname {Erg}^{\perp }$
, as long as
$\operatorname {Erg}^{\perp }$
, as long as
![]() $\mu $
is a continuous measure on
$\mu $
is a continuous measure on
![]() $\mathbb {T}$
(see e.g. Theorem 2). In fact, a recent result from [Reference Górska, Lemańczyk and de la Rue13] gives the full characterization of elements of
$\mathbb {T}$
(see e.g. Theorem 2). In fact, a recent result from [Reference Górska, Lemańczyk and de la Rue13] gives the full characterization of elements of
![]() $\operatorname {Erg}^\perp $
in the form of the following result.
$\operatorname {Erg}^\perp $
in the form of the following result.
Theorem 2. [Reference Górska, Lemańczyk and de la Rue13, Theorem 3.1]
An automorphism T belongs to
![]() $\operatorname {Erg}^{\perp }$
if and only if (see (2)) for
$\operatorname {Erg}^{\perp }$
if and only if (see (2)) for
![]() $P\otimes P$
-almost every
$P\otimes P$
-almost every
![]() $(\bar x,\bar y)\in \overline {X}^2$
, the automorphisms
$(\bar x,\bar y)\in \overline {X}^2$
, the automorphisms
![]() $T_{\bar x}$
and
$T_{\bar x}$
and
![]() $T_{\bar y}$
are disjoint.
$T_{\bar y}$
are disjoint.
The only ergodic element of
![]() $\operatorname {Erg}^{\perp }$
is the 1-point system. Indeed, a system
$\operatorname {Erg}^{\perp }$
is the 1-point system. Indeed, a system
![]() $(T,\mu )$
is disjoint from itself if and only if the diagonal self-joining is the product measure and this holds if and only if
$(T,\mu )$
is disjoint from itself if and only if the diagonal self-joining is the product measure and this holds if and only if
![]() $\mu $
is a Dirac measure. Hence, the elements of the class
$\mu $
is a Dirac measure. Hence, the elements of the class
![]() $\operatorname {Erg}^{\perp }$
in
$\operatorname {Erg}^{\perp }$
in
![]() $\operatorname {Aut}(X,\mathcal {B},\mu )$
form a meagre set (as the ergodic systems form a generic subset of
$\operatorname {Aut}(X,\mathcal {B},\mu )$
form a meagre set (as the ergodic systems form a generic subset of
![]() $\operatorname {Aut}(X,\mathcal {B},\mu )$
[Reference Halmos15]). Now, in view of Theorem 2 and the disjointness of time automorphisms result in [Reference Danilenko and Ryzhikov3], the automorphism on
$\operatorname {Aut}(X,\mathcal {B},\mu )$
[Reference Halmos15]). Now, in view of Theorem 2 and the disjointness of time automorphisms result in [Reference Danilenko and Ryzhikov3], the automorphism on
![]() $\mathbb T\times X$
given by
$\mathbb T\times X$
given by
![]() $(t,x)\mapsto (t,T_t(x))$
, where
$(t,x)\mapsto (t,T_t(x))$
, where
![]() $(T_t)_{t\in \mathbb {R}}$
is a generic flow, is an element of
$(T_t)_{t\in \mathbb {R}}$
is a generic flow, is an element of
![]() $\operatorname {Erg}^\perp $
.
$\operatorname {Erg}^\perp $
.
The following fact is also useful when trying to describe the class
![]() $\operatorname {Erg}^{\perp }$
.
$\operatorname {Erg}^{\perp }$
.
Proposition 3. Let
![]() $T \in \operatorname {Erg}^\perp $
and let R be an ergodic automorphism. Then, R is disjoint from P-a.e. fibre automorphism
$T \in \operatorname {Erg}^\perp $
and let R be an ergodic automorphism. Then, R is disjoint from P-a.e. fibre automorphism
![]() $T_{\bar x}$
.
$T_{\bar x}$
.
Indeed, in view of Theorem 2, the measure P is continuous if T is non-trivial. Then, Proposition 3 follows from the following result (note that the measure
![]() $P|_{\overline {X}_\infty }$
has no atoms, since otherwise,
$P|_{\overline {X}_\infty }$
has no atoms, since otherwise,
![]() $P\otimes P$
would have an atom in some point of the form
$P\otimes P$
would have an atom in some point of the form
![]() $(\bar x, \bar x)$
, with
$(\bar x, \bar x)$
, with
![]() $T_{\bar x}$
not being a one-point system, which contradicts Theorem 2).
$T_{\bar x}$
not being a one-point system, which contradicts Theorem 2).
Proposition 4. [Reference Górska, Lemańczyk and de la Rue13, Lemma 2.10]
Let R be an ergodic automorphism. Then, for every set
![]() $B\subset \operatorname {Aut}(X,\mathcal {B},\mu )$
of pairwise disjoint automorphisms, R is disjoint with all but at most countably many elements of B.
$B\subset \operatorname {Aut}(X,\mathcal {B},\mu )$
of pairwise disjoint automorphisms, R is disjoint with all but at most countably many elements of B.
In Lemma 12, we prove that
![]() $\alpha \in \mathbb {S}^1$
is an eigenvalue of T if and only if
$\alpha \in \mathbb {S}^1$
is an eigenvalue of T if and only if
![]() $\alpha $
is an eigenvalue for a positive P-measure set of fibre automorphisms
$\alpha $
is an eigenvalue for a positive P-measure set of fibre automorphisms
![]() $T_{\bar x}$
. In particular, if there exists
$T_{\bar x}$
. In particular, if there exists
![]() $\alpha \in \mathbb S^1\setminus \{1\}$
such that
$\alpha \in \mathbb S^1\setminus \{1\}$
such that
![]() $\alpha $
is an eigenvalue for a set of positive P-measure fibre automorphisms, then
$\alpha $
is an eigenvalue for a set of positive P-measure fibre automorphisms, then
2.4 Characteristic classes
Recall that a class
![]() $\mathcal F\subset \operatorname {Aut}$
of measure-preserving dynamical systems is characteristic if it is closed under countable joinings and taking factors. In [Reference Kanigowski, Kułaga-Przymus, Lemańczyk and de la Rue16], the authors give a list of many examples of such classes. In particular, they proved that
$\mathcal F\subset \operatorname {Aut}$
of measure-preserving dynamical systems is characteristic if it is closed under countable joinings and taking factors. In [Reference Kanigowski, Kułaga-Przymus, Lemańczyk and de la Rue16], the authors give a list of many examples of such classes. In particular, they proved that
![]() $\operatorname {ID}$
—the class consisting of all identities of standard probability Borel spaces—is a characteristic class and is contained in every non-trivial characteristic class. A natural question arises, whether
$\operatorname {ID}$
—the class consisting of all identities of standard probability Borel spaces—is a characteristic class and is contained in every non-trivial characteristic class. A natural question arises, whether
![]() $\operatorname {ID} $
is the only characteristic class that does not contain a non-trivial ergodic automorphism. One of our goals is to answer positively to this question, by constructing such a class inside
$\operatorname {ID} $
is the only characteristic class that does not contain a non-trivial ergodic automorphism. One of our goals is to answer positively to this question, by constructing such a class inside
![]() $\operatorname {Erg}^{\perp }$
.
$\operatorname {Erg}^{\perp }$
.
First, we show that for every class
![]() $\mathcal A\subset \operatorname {Aut}$
, the set of all multipliers
$\mathcal A\subset \operatorname {Aut}$
, the set of all multipliers
![]() $\mathcal M(\mathcal A^{\perp })$
is a characteristic class. We prove the following general result.
$\mathcal M(\mathcal A^{\perp })$
is a characteristic class. We prove the following general result.
Lemma 5. Let
![]() $\mathcal A\subset {\operatorname {Aut}}$
. Then,
$\mathcal A\subset {\operatorname {Aut}}$
. Then,
![]() $(X,\mathcal B,\mu , T)$
is a multiplier of
$(X,\mathcal B,\mu , T)$
is a multiplier of
![]() $\mathcal A^{\perp }$
if and only if
$\mathcal A^{\perp }$
if and only if
![]() $(X^{\times \infty },\mathcal B^{\otimes \infty },\eta , T^{\times \infty })$
is a multiplier of
$(X^{\times \infty },\mathcal B^{\otimes \infty },\eta , T^{\times \infty })$
is a multiplier of
![]() $\mathcal A^{\perp }$
for every
$\mathcal A^{\perp }$
for every
![]() $\eta \in J_\infty (T)$
.
$\eta \in J_\infty (T)$
.
Proof.
![]() $\Longleftarrow $
: It is enough to notice that T is isomorphic to the diagonal joining
$\Longleftarrow $
: It is enough to notice that T is isomorphic to the diagonal joining
![]() $(\mathrm {Id}\times \mathrm {Id}\times \cdots )_*\mu $
.
$(\mathrm {Id}\times \mathrm {Id}\times \cdots )_*\mu $
.
![]() $\Longrightarrow $
: Assume now that
$\Longrightarrow $
: Assume now that
![]() $(X,\mathcal B,\mu ,T)\in \mathcal A^\perp $
is a multiplier of
$(X,\mathcal B,\mu ,T)\in \mathcal A^\perp $
is a multiplier of
![]() $\mathcal A^\perp $
. Notice first that for every
$\mathcal A^\perp $
. Notice first that for every
![]() $n\ge 2$
and every
$n\ge 2$
and every
![]() $\tilde{\unicode{x3bb}} \in J_n(T)$
, the automorphism
$\tilde{\unicode{x3bb}} \in J_n(T)$
, the automorphism
![]() $(X^{\times n},\mathcal B^{\otimes n},\tilde{\unicode{x3bb}} , T^{\times n})$
is an element of
$(X^{\times n},\mathcal B^{\otimes n},\tilde{\unicode{x3bb}} , T^{\times n})$
is an element of
![]() $\mathcal A^{\perp }$
and is a multiplier of this class. Indeed, since T is a multiplier of
$\mathcal A^{\perp }$
and is a multiplier of this class. Indeed, since T is a multiplier of
![]() $\mathcal A^{\perp }$
, then for
$\mathcal A^{\perp }$
, then for
![]() $n=1$
and
$n=1$
and
![]() $(Y,\mathcal {C},\nu , S)\in \mathcal {A}^\perp $
, we have that
$(Y,\mathcal {C},\nu , S)\in \mathcal {A}^\perp $
, we have that
![]() $T\vee S\in \mathcal A^{\perp }$
. Again, using the fact that T is a multiplier of
$T\vee S\in \mathcal A^{\perp }$
. Again, using the fact that T is a multiplier of
![]() $\mathcal A^{\perp }$
,
$\mathcal A^{\perp }$
,
![]() $T\vee (T\vee S)\in \mathcal A^{\perp }$
, which settles the case
$T\vee (T\vee S)\in \mathcal A^{\perp }$
, which settles the case
![]() $n=2$
. The argument follows by induction.
$n=2$
. The argument follows by induction.
Let now
![]() $(Y,\mathcal C,\nu , S)\in \mathcal A^{\perp }$
and let
$(Y,\mathcal C,\nu , S)\in \mathcal A^{\perp }$
and let
![]() $(Z,\mathcal D,\rho , R)\in \mathcal {A}$
. Consider also
$(Z,\mathcal D,\rho , R)\in \mathcal {A}$
. Consider also
![]() $\eta \in J(T^{\times \infty })$
and
$\eta \in J(T^{\times \infty })$
and
![]() $\zeta \in J(T^{\times \infty }\vee S, R)$
. Let
$\zeta \in J(T^{\times \infty }\vee S, R)$
. Let
![]() $\zeta _n:=\pi ^{n,Y,Z}_*{\zeta }$
be the projection on the first n X-coordinates, Y-coordinate and Z-coordinate of
$\zeta _n:=\pi ^{n,Y,Z}_*{\zeta }$
be the projection on the first n X-coordinates, Y-coordinate and Z-coordinate of
![]() $\zeta $
. In particular,
$\zeta $
. In particular,
![]() $\zeta _n\in J(T^{\times n}\vee S,R)$
. By the finite case,
$\zeta _n\in J(T^{\times n}\vee S,R)$
. By the finite case,
![]() $\zeta _n=\zeta _n|_{X^n\times Y}\otimes \rho $
. Since finite cylinders generate the whole product
$\zeta _n=\zeta _n|_{X^n\times Y}\otimes \rho $
. Since finite cylinders generate the whole product
![]() $\sigma $
-algebra, by passing with n to infinity, we obtain that
$\sigma $
-algebra, by passing with n to infinity, we obtain that
![]() $\zeta =\eta \otimes \rho $
.
$\zeta =\eta \otimes \rho $
.
Corollary 6. Let
![]() $\mathcal A\subseteq \operatorname {Aut}$
. Then,
$\mathcal A\subseteq \operatorname {Aut}$
. Then,
![]() $\mathcal M(\mathcal A^\perp )$
is a characteristic class.
$\mathcal M(\mathcal A^\perp )$
is a characteristic class.
Proof. In view of Lemma 5, the class
![]() $\mathcal M(\mathcal A^\perp )$
is closed under taking countable joinings. It remains to see that it is closed under taking factors. Let
$\mathcal M(\mathcal A^\perp )$
is closed under taking countable joinings. It remains to see that it is closed under taking factors. Let
![]() $(X,\mathcal B,\mu , T)\in \mathcal M(\mathcal A^\perp )$
and let
$(X,\mathcal B,\mu , T)\in \mathcal M(\mathcal A^\perp )$
and let
![]() $(Y,\mathcal C,\nu , S)$
be a factor of T. If S has a non-trivial joining with
$(Y,\mathcal C,\nu , S)$
be a factor of T. If S has a non-trivial joining with
![]() $R\in \mathcal A$
, then so does T, via the relatively independent extension. Hence,
$R\in \mathcal A$
, then so does T, via the relatively independent extension. Hence,
![]() $\mathcal M(\mathcal A^\perp )$
is also closed under taking factors.
$\mathcal M(\mathcal A^\perp )$
is also closed under taking factors.
In view of the above corollary, a natural candidate for an example of a class that does not contain a non-trivial ergodic element and is larger than
![]() $\operatorname {ID} $
would be the set
$\operatorname {ID} $
would be the set
![]() $\mathcal M(\operatorname {Erg}^\perp )$
. However, in §4, we show that this class contains only identities. To show that nonetheless such a class exists, we present the following construction.
$\mathcal M(\operatorname {Erg}^\perp )$
. However, in §4, we show that this class contains only identities. To show that nonetheless such a class exists, we present the following construction.
Let
![]() $T\in \operatorname {Aut}(X,\mathcal B,\mu )$
. Let
$T\in \operatorname {Aut}(X,\mathcal B,\mu )$
. Let
![]() $\mathcal F(T)$
be the class of measure-preserving dynamical systems, which consists of all countable self-joinings of T, as well as all factors of those joinings.
$\mathcal F(T)$
be the class of measure-preserving dynamical systems, which consists of all countable self-joinings of T, as well as all factors of those joinings.
Lemma 7. The class
![]() $\mathcal {F}(T)$
is characteristic.
$\mathcal {F}(T)$
is characteristic.
This result follows from the fact that a factor of a factor of a fixed automorphism R is still a factor of R and from the following classical lemma, whose proof we provide below for the sake of completeness.
Lemma 8. Let
![]() $\{(X_i,\mathcal B_i,\mu _i,T_i)\}_{i=1}^{\infty }$
be a family of measure-preserving automorphisms. For every
$\{(X_i,\mathcal B_i,\mu _i,T_i)\}_{i=1}^{\infty }$
be a family of measure-preserving automorphisms. For every
![]() $i\in \mathbb {N}$
, let
$i\in \mathbb {N}$
, let
![]() $(Y_i,\mathcal C_i,\nu _i,S_i)$
be a factor of
$(Y_i,\mathcal C_i,\nu _i,S_i)$
be a factor of
![]() $T_i$
and let
$T_i$
and let
![]() $F_i:X_i\to Y_i$
be the factorizing map. Then, for any
$F_i:X_i\to Y_i$
be the factorizing map. Then, for any
![]() $\unicode{x3bb} \in J(S_1,S_2,\ldots )$
, there exists a joining
$\unicode{x3bb} \in J(S_1,S_2,\ldots )$
, there exists a joining
![]() $\eta \in J(T_1,T_2,\ldots )$
such that
$\eta \in J(T_1,T_2,\ldots )$
such that
![]() $(S_1\times S_2\times \cdots ,\unicode{x3bb} )$
is a factor of
$(S_1\times S_2\times \cdots ,\unicode{x3bb} )$
is a factor of
![]() $(T_1\times T_2\times \cdots ,\eta )$
.
$(T_1\times T_2\times \cdots ,\eta )$
.
Proof. For every
![]() $i\in \mathbb {N}$
, consider the disintegration of
$i\in \mathbb {N}$
, consider the disintegration of
![]() $\mu _i$
with respect to the factor
$\mu _i$
with respect to the factor
![]() $S_i$
:
$S_i$
:
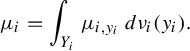 $$ \begin{align*} \mu_i=\int_{Y_i}\mu_{i,y_i}\, d\nu_i(y_i). \end{align*} $$
$$ \begin{align*} \mu_i=\int_{Y_i}\mu_{i,y_i}\, d\nu_i(y_i). \end{align*} $$
Then, consider the measure
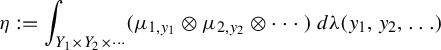 $$ \begin{align*} \eta:=\int_{Y_1\times Y_2\times\cdots} (\mu_{1,y_1}\otimes \mu_{2,y_2}\otimes \cdots)\,d\unicode{x3bb}(y_1,y_2,\ldots) \end{align*} $$
$$ \begin{align*} \eta:=\int_{Y_1\times Y_2\times\cdots} (\mu_{1,y_1}\otimes \mu_{2,y_2}\otimes \cdots)\,d\unicode{x3bb}(y_1,y_2,\ldots) \end{align*} $$
on
![]() $X_1\times X_2\times \cdots $
. It is a non-trivial element of
$X_1\times X_2\times \cdots $
. It is a non-trivial element of
![]() $J(T_1,T_2,\ldots )$
. Then,
$J(T_1,T_2,\ldots )$
. Then,
![]() $(S_1\times S_2\times \cdots , \unicode{x3bb} )$
is a factor of
$(S_1\times S_2\times \cdots , \unicode{x3bb} )$
is a factor of
![]() $(T_1\times T_2\times \cdots ,\eta )$
through the following factorizing map:
$(T_1\times T_2\times \cdots ,\eta )$
through the following factorizing map:
In §6, we provide an example of a non-identity automorphism
![]() $T\in \operatorname {Erg}^\perp $
such that
$T\in \operatorname {Erg}^\perp $
such that
![]() $\mathcal F(T)$
does not contain a non-trivial ergodic element, see Corollary 30.
$\mathcal F(T)$
does not contain a non-trivial ergodic element, see Corollary 30.
2.5 Elements of spectral theory
Let us recall here some notions and facts concerning the spectral theory of dynamical systems. Let
![]() $(X,\mathcal B,\mu ,T)$
be a dynamical system. For any
$(X,\mathcal B,\mu ,T)$
be a dynamical system. For any
![]() $f\in L^2(X,\mathcal B,\mu )$
, we define the spectral measure
$f\in L^2(X,\mathcal B,\mu )$
, we define the spectral measure
![]() $\sigma _{f,\mu }$
(a finite positive measure defined on
$\sigma _{f,\mu }$
(a finite positive measure defined on
![]() $\mathbb {S}^1$
) which, via the Herglotz theorem, is given by its Fourier transform:
$\mathbb {S}^1$
) which, via the Herglotz theorem, is given by its Fourier transform:
for
![]() $n\in \mathbb Z$
. Among spectral measures of functions in
$n\in \mathbb Z$
. Among spectral measures of functions in
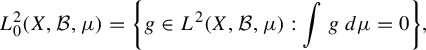 $$ \begin{align*}L^2_0(X,\mathcal B,\mu)=\bigg\{g\in L^2(X,\mathcal B,\mu): \int g\,d\mu=0\bigg\},\end{align*} $$
$$ \begin{align*}L^2_0(X,\mathcal B,\mu)=\bigg\{g\in L^2(X,\mathcal B,\mu): \int g\,d\mu=0\bigg\},\end{align*} $$
there are dominating ones (in the absolute continuity sense). All such must be equivalent, and their equivalence class is called the maximal spectral type of
![]() $U_T$
. If
$U_T$
. If
![]() $\mu $
is understood, we write
$\mu $
is understood, we write
![]() $\hat \sigma _{f}$
instead of
$\hat \sigma _{f}$
instead of
![]() $\hat \sigma _{f,\mu }$
. Note that
$\hat \sigma _{f,\mu }$
. Note that
![]() $\sigma _f(\mathbb {S}^1)=\|f\|_{L^2(\mu )}^2$
. Moreover, f of norm 1 is an eigenfunction of
$\sigma _f(\mathbb {S}^1)=\|f\|_{L^2(\mu )}^2$
. Moreover, f of norm 1 is an eigenfunction of
![]() $U_T$
if and only if
$U_T$
if and only if
![]() $\sigma _{f,\mu }$
is the Dirac measure at the corresponding eigenvalue.
$\sigma _{f,\mu }$
is the Dirac measure at the corresponding eigenvalue.
We now show some measurability results concerning spectral measures.
Lemma 9. Let X be a compact metric space and
![]() $T:X\to X$
be a homeomorphism. Let
$T:X\to X$
be a homeomorphism. Let
![]() $f\in C(X)$
be a complex-valued continuous function such that
$f\in C(X)$
be a complex-valued continuous function such that
![]() $|f|=1$
. Then, the map
$|f|=1$
. Then, the map
![]() $F:\mathscr M(X,T)\mapsto \mathscr M(\mathbb {S}^1)$
defined as
$F:\mathscr M(X,T)\mapsto \mathscr M(\mathbb {S}^1)$
defined as
is continuous.
Proof. Recall that by the definition of weak
![]() $^\ast $
-convergence in
$^\ast $
-convergence in
![]() $\mathscr {M}(X)$
, for every
$\mathscr {M}(X)$
, for every
![]() $g\in C(X)$
, the map
$g\in C(X)$
, the map
![]() $\eta \mapsto \int _{X}g\,d\eta $
is continuous. Thus, the function
$\eta \mapsto \int _{X}g\,d\eta $
is continuous. Thus, the function
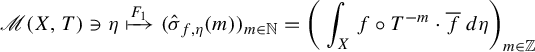
is continuous. It follows that the map
![]() $F_1:\mathscr M(X,T)\to \mathbb {D}^{\mathbb Z}$
(recall that
$F_1:\mathscr M(X,T)\to \mathbb {D}^{\mathbb Z}$
(recall that
![]() $\mathbb {D}=\{z\in \mathbb C:{|z|\leq 1}\}$
and on
$\mathbb {D}=\{z\in \mathbb C:{|z|\leq 1}\}$
and on
![]() $\mathbb {D}^{\mathbb {Z}}$
, we consider the usual product metric d) given by
$\mathbb {D}^{\mathbb {Z}}$
, we consider the usual product metric d) given by
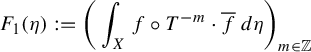 $$ \begin{align*} F_1(\eta):= \bigg(\int_{X}f\circ T^{-m}\cdot \overline f\, d\eta\bigg)_{m\in \mathbb Z} \end{align*} $$
$$ \begin{align*} F_1(\eta):= \bigg(\int_{X}f\circ T^{-m}\cdot \overline f\, d\eta\bigg)_{m\in \mathbb Z} \end{align*} $$
is continuous. Since
![]() $\mathscr M(X,T)$
is compact, the image
$\mathscr M(X,T)$
is compact, the image
![]() $\Upsilon :=F_1(\mathscr M(X,T))$
is also compact in
$\Upsilon :=F_1(\mathscr M(X,T))$
is also compact in
![]() $\mathbb D^{\mathbb Z}$
.
$\mathbb D^{\mathbb Z}$
.
Now, we define a function
![]() $F_2:\Upsilon \to \mathscr M(\mathbb S ^1)$
in the following way:
$F_2:\Upsilon \to \mathscr M(\mathbb S ^1)$
in the following way:
It is well defined via the Herglotz theorem. Note that since the family
![]() $\{z^m\}_{m\in \mathbb Z}$
is linearly dense in
$\{z^m\}_{m\in \mathbb Z}$
is linearly dense in
![]() $C(\mathbb S^1)$
, the map
$C(\mathbb S^1)$
, the map
![]() $F_2$
is also continuous. Indeed, let
$F_2$
is also continuous. Indeed, let
![]() $(a_m^n)_{m\in \mathbb Z},(b_m)_{m\in \mathbb Z}\in \Upsilon $
and
$(a_m^n)_{m\in \mathbb Z},(b_m)_{m\in \mathbb Z}\in \Upsilon $
and
![]() $\sigma _n:=F_2((a_m^n)_{m\in \mathbb Z})$
,
$\sigma _n:=F_2((a_m^n)_{m\in \mathbb Z})$
,
![]() $\sigma :=F_2((b_m)_{m\in \mathbb Z})$
and assume that
$\sigma :=F_2((b_m)_{m\in \mathbb Z})$
and assume that
![]() $d((a_m^n)_{m\in \mathbb Z},(b_m)_{m\in \mathbb Z})\to 0$
as
$d((a_m^n)_{m\in \mathbb Z},(b_m)_{m\in \mathbb Z})\to 0$
as
![]() $n\to \infty $
in
$n\to \infty $
in
![]() $\Upsilon $
. Then, for every
$\Upsilon $
. Then, for every
![]() $m\in \mathbb Z$
, we have
$m\in \mathbb Z$
, we have
![]() $\int _{\mathbb T}z^m\,d\sigma _n\to \int _{\mathbb T}z^m\, d\sigma $
. Since the functions
$\int _{\mathbb T}z^m\,d\sigma _n\to \int _{\mathbb T}z^m\, d\sigma $
. Since the functions
![]() $z^m$
are linearly dense, this yields the continuity of
$z^m$
are linearly dense, this yields the continuity of
![]() $F_2$
. Since
$F_2$
. Since
![]() $F=F_2\circ F_1$
, this finishes the proof.
$F=F_2\circ F_1$
, this finishes the proof.
Lemma 10. Let X be a compact metric space. Let
![]() $T:X\to X$
be a homeomorphism and let
$T:X\to X$
be a homeomorphism and let
![]() $f\in C(X)$
,
$f\in C(X)$
,
![]() $|f|=1$
. Then, for every
$|f|=1$
. Then, for every
![]() $\alpha \in \mathbb S ^1$
, the map
$\alpha \in \mathbb S ^1$
, the map
![]() $G:\mathscr M(X,T)\mapsto [0,1]$
defined as
$G:\mathscr M(X,T)\mapsto [0,1]$
defined as
is measurable.
Proof. Fix
![]() $\alpha \in \mathbb S ^1$
. In view of Lemma 9, the map
$\alpha \in \mathbb S ^1$
. In view of Lemma 9, the map
![]() $F:\mathscr M(X,T)\mapsto \mathscr M(\mathbb S^1)$
given by the formula
$F:\mathscr M(X,T)\mapsto \mathscr M(\mathbb S^1)$
given by the formula
![]() $F(\eta )=\sigma _{f,\eta }$
is continuous. In particular, the set
$F(\eta )=\sigma _{f,\eta }$
is continuous. In particular, the set
![]() $\Omega =F(\mathscr M(X,T))$
is compact in the weak
$\Omega =F(\mathscr M(X,T))$
is compact in the weak
![]() $^\ast $
-topology. It is thus enough to show that the map
$^\ast $
-topology. It is thus enough to show that the map
![]() $G':\mathscr M (\mathbb S^1)\mapsto [0,1]$
defined as
$G':\mathscr M (\mathbb S^1)\mapsto [0,1]$
defined as
![]() $G'(\sigma ):=\sigma (\{\alpha \})$
is measurable.
$G'(\sigma ):=\sigma (\{\alpha \})$
is measurable.
Let
![]() $(g_n)_{n\in \mathbb {N}}\subset C(\mathbb S^1)$
be a sequence of (bounded by
$(g_n)_{n\in \mathbb {N}}\subset C(\mathbb S^1)$
be a sequence of (bounded by
![]() $1$
) real continuous functions converging pointwise to the indicator function
$1$
) real continuous functions converging pointwise to the indicator function
![]() $\chi _{\{\alpha \}}$
. Define, for every
$\chi _{\{\alpha \}}$
. Define, for every
![]() $n\in \mathbb {N}$
, the map
$n\in \mathbb {N}$
, the map
![]() $G_n':\mathscr M(\mathbb S ^1)\to \mathbb {R}$
as
$G_n':\mathscr M(\mathbb S ^1)\to \mathbb {R}$
as
![]() $G_n'(\sigma )=\int _{\mathbb T}g_n\,d\sigma $
which is continuous. Then,
$G_n'(\sigma )=\int _{\mathbb T}g_n\,d\sigma $
which is continuous. Then,
![]() $\lim _{n\to \infty }G_n'=G'$
pointwise. As a point limit of continuous functions,
$\lim _{n\to \infty }G_n'=G'$
pointwise. As a point limit of continuous functions,
![]() $G'$
is measurable. Since
$G'$
is measurable. Since
![]() $G=G'\circ F$
, this finishes the proof.
$G=G'\circ F$
, this finishes the proof.
Remark 11. Notice that if F and G are defined as
![]() $F(\eta ):=\sigma _{f-\int f\, d \eta ,\eta }$
and
$F(\eta ):=\sigma _{f-\int f\, d \eta ,\eta }$
and
![]() $G(\eta ):=\sigma _{f-\int f\, d\eta ,\eta }(\{\alpha \})$
, then, by repeating proofs of Lemmas 9 and 10, we get that F is continuous and G is measurable.
$G(\eta ):=\sigma _{f-\int f\, d\eta ,\eta }(\{\alpha \})$
, then, by repeating proofs of Lemmas 9 and 10, we get that F is continuous and G is measurable.
We will also make use of the following fact based on spectral theory that provides a tool to detect eigenvalues of non-ergodic dynamical systems.
Lemma 12. Let X be a compact metric space. Let
![]() $\mu \in \mathscr M(X,T)$
, where T is a homeomorphism of T. Let also
$\mu \in \mathscr M(X,T)$
, where T is a homeomorphism of T. Let also
be the ergodic decomposition of T and let
![]() $ T_{\bar x}$
denote the fibre automorphism, corresponding to
$ T_{\bar x}$
denote the fibre automorphism, corresponding to
![]() $\bar x\in \overline X$
. Then,
$\bar x\in \overline X$
. Then,
![]() $\alpha \in \mathbb S^1$
is an eigenvalue of
$\alpha \in \mathbb S^1$
is an eigenvalue of
![]() $(T,\mu _{\bar x})$
for a P-positive measure set of
$(T,\mu _{\bar x})$
for a P-positive measure set of
![]() $\bar x$
if and only if
$\bar x$
if and only if
![]() $\alpha $
is an eigenvalue of
$\alpha $
is an eigenvalue of
![]() $(T,\mu )$
.
$(T,\mu )$
.
Proof. Let
![]() $\alpha \in \mathbb {S}^1$
be as in the assumption. Consider a sequence
$\alpha \in \mathbb {S}^1$
be as in the assumption. Consider a sequence
![]() $\{f_n\}_{n\in \mathbb {N}}$
of functions which are dense in the space of complex continuous functions on X. Note that
$\{f_n\}_{n\in \mathbb {N}}$
of functions which are dense in the space of complex continuous functions on X. Note that
![]() $\sigma _{f_n,\mu }=\int _{\overline {X}}\sigma _{f_n,\mu _{\bar x}}\,dP(\bar x)$
. Indeed, the mth coefficient of the Fourier transform of the right-hand side measure equals
$\sigma _{f_n,\mu }=\int _{\overline {X}}\sigma _{f_n,\mu _{\bar x}}\,dP(\bar x)$
. Indeed, the mth coefficient of the Fourier transform of the right-hand side measure equals
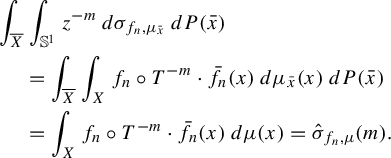 $$ \begin{align*} \begin{aligned} \int_{\overline{X}}&\int_{\mathbb S^1} z^{-m}\, d\sigma_{f_n,\mu_{\bar x}}\,dP(\bar x)\\&=\int_{\overline{X}}\int_{X}f_n\circ T^{-m}\cdot \bar f_n(x)\,d\mu_{\bar x}(x)\,dP(\bar x)\\ &=\int_{X}f_n\circ T^{-m}\cdot \bar f_n(x)\,d\mu(x)=\hat\sigma_{f_n,\mu}(m). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \int_{\overline{X}}&\int_{\mathbb S^1} z^{-m}\, d\sigma_{f_n,\mu_{\bar x}}\,dP(\bar x)\\&=\int_{\overline{X}}\int_{X}f_n\circ T^{-m}\cdot \bar f_n(x)\,d\mu_{\bar x}(x)\,dP(\bar x)\\ &=\int_{X}f_n\circ T^{-m}\cdot \bar f_n(x)\,d\mu(x)=\hat\sigma_{f_n,\mu}(m). \end{aligned} \end{align*} $$
Then, the following conditions are equivalent:
-
•
 $\alpha $
is an eigenvalue of
$\alpha $
is an eigenvalue of
 $(T,\mu )$
;
$(T,\mu )$
; -
• there exists
 $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
 $\sigma _{f_n,\mu }(\{\alpha \})>0$
;
$\sigma _{f_n,\mu }(\{\alpha \})>0$
; -
• there exists
 $n\in \mathbb {N}$
and a P-positive measure set of
$n\in \mathbb {N}$
and a P-positive measure set of
 $\bar x$
such that
$\bar x$
such that
 $\sigma _{f_n,\mu _{\bar x}}(\{\alpha \})>0$
;
$\sigma _{f_n,\mu _{\bar x}}(\{\alpha \})>0$
; -
• there exists a P-positive measure set of
 $\bar x$
such that
$\bar x$
such that
 $\alpha $
is an eigenvalue.
$\alpha $
is an eigenvalue.
Corollary 13. Let
![]() $T\in \operatorname {Erg}^\perp $
. For any
$T\in \operatorname {Erg}^\perp $
. For any
![]() $\alpha \in \mathbb S^1\setminus \{1\}$
, the set of ergodic components of T which have
$\alpha \in \mathbb S^1\setminus \{1\}$
, the set of ergodic components of T which have
![]() $\alpha $
as an eigenvalue has
$\alpha $
as an eigenvalue has
![]() $0$
measure with respect to P. In particular,
$0$
measure with respect to P. In particular,
![]() $P(\overline X_n)=0$
for every
$P(\overline X_n)=0$
for every
![]() $n\ge 2$
.
$n\ge 2$
.
The following fact is folklore, but for the sake of completeness of the presentation, we recall its proof.
Lemma 14. Let X be a compact metric space. Let
![]() $\mu \in \mathscr M(X,T)$
, where T is a homeomorphism of T. Let also
$\mu \in \mathscr M(X,T)$
, where T is a homeomorphism of T. Let also
be the ergodic decomposition of T and let
![]() $T_{\bar x}$
denote the fibre automorphism, corresponding to
$T_{\bar x}$
denote the fibre automorphism, corresponding to
![]() $\bar x\in \overline X$
. Then, the set
$\bar x\in \overline X$
. Then, the set
is measurable.
Proof. Let
![]() $\{f_n\}_{n\in \mathbb {N}}$
be a dense family in
$\{f_n\}_{n\in \mathbb {N}}$
be a dense family in
![]() $C(X)$
and fix
$C(X)$
and fix
![]() $f=f_n$
. Recall that an automorphism is weakly mixing if and only if it has no non-trivial eigenvalues or, in other words, all spectral measures on
$f=f_n$
. Recall that an automorphism is weakly mixing if and only if it has no non-trivial eigenvalues or, in other words, all spectral measures on
![]() $L_0^2$
are continuous. Let us recall that for any measure
$L_0^2$
are continuous. Let us recall that for any measure
![]() $\sigma \in \mathscr M(\mathbb S^1)$
, by Wiener’s lemma, we have
$\sigma \in \mathscr M(\mathbb S^1)$
, by Wiener’s lemma, we have
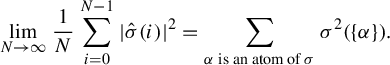 $$ \begin{align*} \lim_{N\to\infty}\frac{1}{N}\sum_{i=0}^{N-1}|\hat\sigma(i)|^2={\sum_{\alpha \,\text{is an atom of }\sigma} \sigma^2(\{\alpha\})}. \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty}\frac{1}{N}\sum_{i=0}^{N-1}|\hat\sigma(i)|^2={\sum_{\alpha \,\text{is an atom of }\sigma} \sigma^2(\{\alpha\})}. \end{align*} $$
It is enough to show that the above equality holds for
![]() $\sigma =\sigma _{f-\int f\, d \mu ,\mu }$
. Note that the function
$\sigma =\sigma _{f-\int f\, d \mu ,\mu }$
. Note that the function
![]() $H_N:\mathscr M(\mathbb S^1)\to \mathbb R_{\ge 0}$
given by
$H_N:\mathscr M(\mathbb S^1)\to \mathbb R_{\ge 0}$
given by
![]() $H_N(\sigma ):=({1}/{N})\sum _{i=0}^{N-1}|\hat \sigma (i)|^2$
, by the definition of weak*-convergence, is continuous. Thus, the function
$H_N(\sigma ):=({1}/{N})\sum _{i=0}^{N-1}|\hat \sigma (i)|^2$
, by the definition of weak*-convergence, is continuous. Thus, the function
![]() $H:\mathscr M(\mathbb S^1)\to \mathbb R_{\ge 0}$
given by
$H:\mathscr M(\mathbb S^1)\to \mathbb R_{\ge 0}$
given by
![]() $H(\sigma ):=\lim _{N\to \infty }H_N(\sigma )$
, as a pointwise limit of continuous functions, is measurable.
$H(\sigma ):=\lim _{N\to \infty }H_N(\sigma )$
, as a pointwise limit of continuous functions, is measurable.
By Remark 11, the map
![]() $F:\mathscr M(X,T)\mapsto \mathscr M(\mathbb S^1)$
is continuous. Moreover, by the properties of disintegration of measures, the assignment
$F:\mathscr M(X,T)\mapsto \mathscr M(\mathbb S^1)$
is continuous. Moreover, by the properties of disintegration of measures, the assignment
![]() $E:\overline X\to \mathscr M(X,T)$
given by
$E:\overline X\to \mathscr M(X,T)$
given by
![]() $E(\bar x)=\mu _{\bar x}$
is also measurable. Thus, the map
$E(\bar x)=\mu _{\bar x}$
is also measurable. Thus, the map
![]() $H\circ F\circ E$
is measurable. It remains to notice that, since f is arbitrary,
$H\circ F\circ E$
is measurable. It remains to notice that, since f is arbitrary,
![]() $\mathcal {WM}=(H\circ F\circ E)^{-1}(\{0\}).$
$\mathcal {WM}=(H\circ F\circ E)^{-1}(\{0\}).$
We also recall that if
![]() $T\in \operatorname {Aut}(X,\mathcal {B},\mu )$
and
$T\in \operatorname {Aut}(X,\mathcal {B},\mu )$
and
![]() $f,g\in L^2_0(X,\mathcal {B},\mu )$
, then
$f,g\in L^2_0(X,\mathcal {B},\mu )$
, then
![]() $f\perp g$
whenever
$f\perp g$
whenever
![]() $\sigma _f\perp \sigma _g$
, that is, when the spectral measures are mutually singular. It follows that two automorphisms are disjoint whenever the maximal spectral types on the relevant
$\sigma _f\perp \sigma _g$
, that is, when the spectral measures are mutually singular. It follows that two automorphisms are disjoint whenever the maximal spectral types on the relevant
![]() $L^2_0$
spaces are mutually singular [Reference Hahn and Parry14].
$L^2_0$
spaces are mutually singular [Reference Hahn and Parry14].
3 Identities are multipliers of
 $\kern1pt\operatorname{Erg}^\perp $
$\kern1pt\operatorname{Erg}^\perp $
The following fact is classical (and follows from the spectral disjointness of ergodic automorphism with the identity maps), we recall the classical proof for completeness.
Proposition 15. Any identity map is disjoint with all ergodic systems.
Proof. Assume that
![]() $(Z,\mathcal {D},\rho ,R)$
is ergodic and consider the identity on
$(Z,\mathcal {D},\rho ,R)$
is ergodic and consider the identity on
![]() $(Y,\mathcal {C},\nu )$
. Let
$(Y,\mathcal {C},\nu )$
. Let
![]() $\eta \in J(R,\mathrm {Id})$
. Take
$\eta \in J(R,\mathrm {Id})$
. Take
![]() $h\in L^2(Z,\rho )$
of zero mean and let
$h\in L^2(Z,\rho )$
of zero mean and let
![]() $g\in L^2(Y,\nu )$
. By the von Neumann theorem (and ergodicity),
$g\in L^2(Y,\nu )$
. By the von Neumann theorem (and ergodicity),
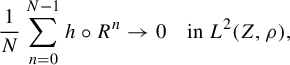 $$ \begin{align*} \frac1N\sum_{n=0}^{N-1}h\circ R^n\to 0\quad\text{in } L^2(Z,\rho), \end{align*} $$
$$ \begin{align*} \frac1N\sum_{n=0}^{N-1}h\circ R^n\to 0\quad\text{in } L^2(Z,\rho), \end{align*} $$
so the same convergence takes place also in
![]() $L^2(Z\times Y,\eta )$
. Since the strong convergence implies the weak convergence,
$L^2(Z\times Y,\eta )$
. Since the strong convergence implies the weak convergence,
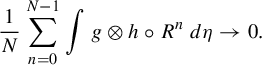 $$ \begin{align*} \frac1N\sum_{n=0}^{N-1}\int g\otimes h\circ R^n\,d\eta\to0.\end{align*} $$
$$ \begin{align*} \frac1N\sum_{n=0}^{N-1}\int g\otimes h\circ R^n\,d\eta\to0.\end{align*} $$
However, for each
![]() $N\geq 1$
,
$N\geq 1$
,
![]() $\int (1/N)\sum _{n=0}^{N-1} (g\otimes h\circ (\mathrm {Id}\times R)^n)\,d\eta =\int g\otimes h\,d\eta $
, whence
$\int (1/N)\sum _{n=0}^{N-1} (g\otimes h\circ (\mathrm {Id}\times R)^n)\,d\eta =\int g\otimes h\,d\eta $
, whence
![]() $\int g\otimes h\,d\eta =0$
.
$\int g\otimes h\,d\eta =0$
.
Now, our main goal in this section is to show that any identity is actually also a multiplier of
![]() $\operatorname {Erg}^\perp $
.
$\operatorname {Erg}^\perp $
.
Proposition 16. Let
![]() $(Z,\mathcal {D},\rho ,R)\in \operatorname {Erg}$
and let
$(Z,\mathcal {D},\rho ,R)\in \operatorname {Erg}$
and let
![]() $(X,\mathcal B,\mu ,T)$
be such that
$(X,\mathcal B,\mu ,T)$
be such that
![]() $T\perp R$
. Consider also an identity map
$T\perp R$
. Consider also an identity map
![]() $(Y,\mathcal C,\nu , \mathrm {Id})$
and let
$(Y,\mathcal C,\nu , \mathrm {Id})$
and let
![]() $\unicode{x3bb} \in J(T,\mathrm {Id})$
. Then,
$\unicode{x3bb} \in J(T,\mathrm {Id})$
. Then,
Proof. Let
![]() $\eta \in J(T,\mathrm {Id},R)$
be such that
$\eta \in J(T,\mathrm {Id},R)$
be such that
![]() $\eta |_{X\times Y}=\unicode{x3bb} $
. Note that, by Proposition 15, it holds that
$\eta |_{X\times Y}=\unicode{x3bb} $
. Note that, by Proposition 15, it holds that
![]() $\eta |_{Y\times Z}=\nu \otimes \rho $
and (by assumption)
$\eta |_{Y\times Z}=\nu \otimes \rho $
and (by assumption)
Fix bounded, real functions
![]() $f\in L^2(X,\mu )$
,
$f\in L^2(X,\mu )$
,
![]() $g\in L^2(Y,\nu )$
and
$g\in L^2(Y,\nu )$
and
![]() $h\in L^2_0(Z,\rho )$
. All we need to show is that
$h\in L^2_0(Z,\rho )$
. All we need to show is that
Let
![]() $f=f_1+f_2$
, where
$f=f_1+f_2$
, where
![]() $f_1\circ T=f_1$
and
$f_1\circ T=f_1$
and
![]() $f_2\perp L^2(\mathrm {Inv}(T))$
. Then,
$f_2\perp L^2(\mathrm {Inv}(T))$
. Then,
Now, the spectral measure (all the spectral measures are computed in
![]() $L^2(X\times Y\times Z,\eta )$
) of the function
$L^2(X\times Y\times Z,\eta )$
) of the function
![]() $f_1\otimes g$
is equivalent to
$f_1\otimes g$
is equivalent to
![]() $\delta _{1}$
, while the spectral measure of h has no atom at 1 since R is ergodic. Hence, these spectral measures are mutually singular and, therefore,
$\delta _{1}$
, while the spectral measure of h has no atom at 1 since R is ergodic. Hence, these spectral measures are mutually singular and, therefore,
![]() $f_1\otimes g$
and h are orthogonal in
$f_1\otimes g$
and h are orthogonal in
![]() $L^2(X\times Y\times Z,\eta )$
, so the first term on the right-hand side of equation (11) disappears. In view of equation (9), we have
$L^2(X\times Y\times Z,\eta )$
, so the first term on the right-hand side of equation (11) disappears. In view of equation (9), we have
Suppose that this measure has an atom at 1. Then, both spectral measures
![]() $\sigma _{f_2}$
and
$\sigma _{f_2}$
and
![]() $\sigma _h$
must have an atom at
$\sigma _h$
must have an atom at
![]() $c\in \mathbb {S}^1$
and
$c\in \mathbb {S}^1$
and
![]() $\bar c\in \mathbb {S}^1$
, respectively, where
$\bar c\in \mathbb {S}^1$
, respectively, where
![]() $c\neq 1$
(as R is ergodic). However, since h is real, c is also an atom of
$c\neq 1$
(as R is ergodic). However, since h is real, c is also an atom of
![]() $\sigma _h$
. Then,
$\sigma _h$
. Then, ![]() , which is a contradiction. Hence, the spectral measures of
, which is a contradiction. Hence, the spectral measures of
![]() $f_2\otimes h$
and g are mutually singular, and thus these functions are orthogonal in
$f_2\otimes h$
and g are mutually singular, and thus these functions are orthogonal in
![]() $L^2(X\times Y\times Z,\eta )$
and equation (10) holds.
$L^2(X\times Y\times Z,\eta )$
and equation (10) holds.
Corollary 17. Let
![]() $(X,\mathcal B,\mu ,T)\in \operatorname {Erg}^{\perp }$
and let
$(X,\mathcal B,\mu ,T)\in \operatorname {Erg}^{\perp }$
and let
![]() $(Y,\mathcal C,\nu , \mathrm {Id})$
be an identity map. Consider
$(Y,\mathcal C,\nu , \mathrm {Id})$
be an identity map. Consider
![]() $\unicode{x3bb} \in J(T,\mathrm {Id})$
. Then,
$\unicode{x3bb} \in J(T,\mathrm {Id})$
. Then,
In other words, any identity is a multiplier of
![]() $\kern1pt\operatorname {Erg}^{\perp }$
.
$\kern1pt\operatorname {Erg}^{\perp }$
.
Proof. The result follows directly from Proposition 16, by applying it to T and every
![]() $R\in \operatorname {Erg}$
.
$R\in \operatorname {Erg}$
.
4 Identities are the only multipliers of
 $\kern1pt\operatorname {Erg}^\perp $
$\kern1pt\operatorname {Erg}^\perp $
In this section, we prove that there is no non-identity element of
![]() $\operatorname {Erg}^\perp $
which is a multiplier of this class. First, we show that the twist transformation on the torus is not a multiplier of
$\operatorname {Erg}^\perp $
which is a multiplier of this class. First, we show that the twist transformation on the torus is not a multiplier of
![]() $\operatorname {Erg}^\perp $
.
$\operatorname {Erg}^\perp $
.
Example 1. Let
![]() $T:X\times \mathbb T\to X\times \mathbb T$
be given by
$T:X\times \mathbb T\to X\times \mathbb T$
be given by
![]() $T(x,y)=(x,y+\beta (x))$
, where
$T(x,y)=(x,y+\beta (x))$
, where
![]() ${\beta :X\to \mathbb T}$
is measurable. Assume that
${\beta :X\to \mathbb T}$
is measurable. Assume that
![]() $\rho \in \mathscr {M}(X)$
is a measure on X such that for every
$\rho \in \mathscr {M}(X)$
is a measure on X such that for every
![]() $z\in \mathbb T$
, we have
$z\in \mathbb T$
, we have
![]() $\rho \{x\in X,\ \beta (x)=z\}=0$
. In particular,
$\rho \{x\in X,\ \beta (x)=z\}=0$
. In particular,
![]() $\rho $
is continuous. Note that since for every
$\rho $
is continuous. Note that since for every
![]() $\alpha \in \mathbb T$
, there is only countably many non-disjoint rotations, the assumptions of Theorem 2 are satisfied and, therefore,
$\alpha \in \mathbb T$
, there is only countably many non-disjoint rotations, the assumptions of Theorem 2 are satisfied and, therefore,
![]() $T\in \operatorname {Erg}^\perp $
. (Another, more elementary, proof follows by the fact that almost every ergodic component of T is disjoint (even spectrally disjoint) with a fixed ergodic automorphism R and, by the ergodicity of R, any joining between R and T is a convex combination of joinings between R and ergodic components of T.) We will show that the system
$T\in \operatorname {Erg}^\perp $
. (Another, more elementary, proof follows by the fact that almost every ergodic component of T is disjoint (even spectrally disjoint) with a fixed ergodic automorphism R and, by the ergodicity of R, any joining between R and T is a convex combination of joinings between R and ergodic components of T.) We will show that the system
![]() $(T,\rho \otimes \mathrm {Leb}_{\mathbb {T}})$
is not a multiplier of
$(T,\rho \otimes \mathrm {Leb}_{\mathbb {T}})$
is not a multiplier of
![]() $\operatorname {Erg}^{\perp }$
.
$\operatorname {Erg}^{\perp }$
.
Let
![]() $\alpha \in \mathbb {R}\setminus \mathbb {Q}$
and consider the automorphism
$\alpha \in \mathbb {R}\setminus \mathbb {Q}$
and consider the automorphism
on
![]() $\mathbb {T}^2$
, which preserves the measure
$\mathbb {T}^2$
, which preserves the measure
![]() $\rho \otimes \mathrm {Leb}_{\mathbb T}$
. One can check that R also satisfies the assumptions of Theorem 2, and hence
$\rho \otimes \mathrm {Leb}_{\mathbb T}$
. One can check that R also satisfies the assumptions of Theorem 2, and hence
![]() $R\in \operatorname {Erg}^\perp $
. Now, consider the transformation P on
$R\in \operatorname {Erg}^\perp $
. Now, consider the transformation P on
![]() $X\times \mathbb {T}^2$
given by
$X\times \mathbb {T}^2$
given by
![]() $P(x,y,z)=(x,y+\beta (x),z+\beta (x)+\alpha )$
. It is easy to see that P is an automorphism of
$P(x,y,z)=(x,y+\beta (x),z+\beta (x)+\alpha )$
. It is easy to see that P is an automorphism of
![]() $(X\times \mathbb {T}^2,\rho \otimes \mathrm {Leb}_{\mathbb {T}} \otimes \mathrm {Leb}_{\mathbb {T}})$
. Moreover, we can treat
$(X\times \mathbb {T}^2,\rho \otimes \mathrm {Leb}_{\mathbb {T}} \otimes \mathrm {Leb}_{\mathbb {T}})$
. Moreover, we can treat
![]() $\rho \otimes \mathrm {Leb}_{\mathbb {T}} \otimes \mathrm {Leb}_{\mathbb {T}}$
as a measure on
$\rho \otimes \mathrm {Leb}_{\mathbb {T}} \otimes \mathrm {Leb}_{\mathbb {T}}$
as a measure on
![]() $X^2\times \mathbb {T}^2$
(up to a permutation of coordinates):
$X^2\times \mathbb {T}^2$
(up to a permutation of coordinates):
where
![]() $A_i\in \mathcal {B}(\mathbb {T})$
for
$A_i\in \mathcal {B}(\mathbb {T})$
for
![]() $i=1,2,3,4$
. In other words, we consider the relatively independent extension over the common factor on the first coordinate, which is the identity map on X. Notice that then, we have
$i=1,2,3,4$
. In other words, we consider the relatively independent extension over the common factor on the first coordinate, which is the identity map on X. Notice that then, we have
and the measure we consider is
![]() $T\times R$
-invariant, so it is easy to see that it is a joining of automorphisms T and R. Now, notice that
$T\times R$
-invariant, so it is easy to see that it is a joining of automorphisms T and R. Now, notice that
![]() $( T\times R,\rho \otimes \mathrm {Leb}_{\mathbb {T}}\otimes \mathrm {Leb}_{\mathbb {T}})$
has the rotation by
$( T\times R,\rho \otimes \mathrm {Leb}_{\mathbb {T}}\otimes \mathrm {Leb}_{\mathbb {T}})$
has the rotation by
![]() $\alpha $
as a factor. Indeed, consider the map
$\alpha $
as a factor. Indeed, consider the map
![]() $\Pi :(X\times \mathbb {T}^2,\rho \otimes \mathrm {Leb}_{\mathbb {T}} \otimes \mathrm {Leb}_{\mathbb {T}})\to (\mathbb {T},\mathrm {Leb}_{\mathbb {T}} )$
given by
$\Pi :(X\times \mathbb {T}^2,\rho \otimes \mathrm {Leb}_{\mathbb {T}} \otimes \mathrm {Leb}_{\mathbb {T}})\to (\mathbb {T},\mathrm {Leb}_{\mathbb {T}} )$
given by
![]() $\Pi (x,y,z)=z-y$
. Then, we have
$\Pi (x,y,z)=z-y$
. Then, we have
and
where
![]() $R_\alpha $
denotes the ergodic rotation by
$R_\alpha $
denotes the ergodic rotation by
![]() $\alpha $
on
$\alpha $
on
![]() $\mathbb {T}$
. In particular, in view of equation (6), the automorphism
$\mathbb {T}$
. In particular, in view of equation (6), the automorphism
![]() $(T\times R,\rho \otimes \mathrm {Leb}_{\mathbb {T}}\otimes \mathrm {Leb}_{\mathbb {T}})$
is not an element of
$(T\times R,\rho \otimes \mathrm {Leb}_{\mathbb {T}}\otimes \mathrm {Leb}_{\mathbb {T}})$
is not an element of
![]() $\operatorname {Erg}^\perp $
.
$\operatorname {Erg}^\perp $
.
As one of the crucial steps to prove the main result of this section, we show first an important special case, when all ergodic components of the considered system are weakly mixing.
For every Borel space
![]() $(X,\mathcal B,\mu )$
, we consider the flip map
$(X,\mathcal B,\mu )$
, we consider the flip map
![]() $R=R_X:X\times X\to X\times X$
given by
$R=R_X:X\times X\to X\times X$
given by
Note that R preserves
![]() $\mu \otimes \mu $
and for every
$\mu \otimes \mu $
and for every
![]() $T\in \operatorname {Aut}(X,\mathcal B,\mu )$
, we have
$T\in \operatorname {Aut}(X,\mathcal B,\mu )$
, we have
This map will serve as a tool to produce ergodic factors of appropriately constructed self-joinings of considered systems. Hence, we first prove some auxiliary lemmas concerning the flip map.
Lemma 18. Let
![]() $(X,\mathcal B,\mu ,T)$
be a weakly mixing system. Then,
$(X,\mathcal B,\mu ,T)$
be a weakly mixing system. Then,
![]() $(X\times X,(T\times T)\circ R_X, \mu \otimes \mu )$
is also weakly mixing.
$(X\times X,(T\times T)\circ R_X, \mu \otimes \mu )$
is also weakly mixing.
Proof. Since
![]() $(T,\mu )$
is weakly mixing, then so is
$(T,\mu )$
is weakly mixing, then so is
![]() $(T^2,\mu )$
and hence
$(T^2,\mu )$
and hence
![]() $(X\times X,T^2\times T^2, \mu \otimes \mu )$
is also weakly mixing. The result now follows from the fact that, by equation (12), we have
$(X\times X,T^2\times T^2, \mu \otimes \mu )$
is also weakly mixing. The result now follows from the fact that, by equation (12), we have
Lemma 19. Let
![]() $(X,\mathcal B,\mu ,T)$
and
$(X,\mathcal B,\mu ,T)$
and
![]() $(Y,\mathcal C,\nu ,S)$
be two weakly mixing systems such that
$(Y,\mathcal C,\nu ,S)$
be two weakly mixing systems such that
Then,
Proof. Let
![]() $\rho {\kern-1pt}\in{\kern-1pt} J((T{\kern-1pt}\times{\kern-1pt} T)\circ R_X,(S{\kern-1pt}\times{\kern-1pt} S)\circ R_Y)$
. We will show that
$\rho {\kern-1pt}\in{\kern-1pt} J((T{\kern-1pt}\times{\kern-1pt} T)\circ R_X,(S{\kern-1pt}\times{\kern-1pt} S)\circ R_Y)$
. We will show that
![]() $\rho {\kern-1pt}={\kern-1pt}(\mu {\kern-1pt}\otimes{\kern-1pt} \mu ){\kern-1pt}\otimes{\kern-1pt} (\nu {\kern-1pt}\otimes{\kern-1pt} \nu )$
.
$\rho {\kern-1pt}={\kern-1pt}(\mu {\kern-1pt}\otimes{\kern-1pt} \mu ){\kern-1pt}\otimes{\kern-1pt} (\nu {\kern-1pt}\otimes{\kern-1pt} \nu )$
.
Note that
Thus,
![]() $\tfrac 12\rho +\tfrac 12(R_X\times R_Y)_*\rho =(\mu \otimes \mu )\otimes (\nu \otimes \nu )$
, since
$\tfrac 12\rho +\tfrac 12(R_X\times R_Y)_*\rho =(\mu \otimes \mu )\otimes (\nu \otimes \nu )$
, since
![]() $(T\times T)$
and
$(T\times T)$
and
![]() $(S\times S)$
are disjoint. However, by Lemma 18, we have that
$(S\times S)$
are disjoint. However, by Lemma 18, we have that
Since an ergodic measure cannot be a non-trivial convex combination of other invariant measures, we obtain
![]() $\rho =(\mu \otimes \mu )\, \otimes \, (\nu \otimes \nu )$
, which finishes the proof.
$\rho =(\mu \otimes \mu )\, \otimes \, (\nu \otimes \nu )$
, which finishes the proof.
We may now proceed to the proof of the special case of the main result of this section.
Lemma 20. Let
![]() $T\in \operatorname {Erg}^{\perp }$
be such that almost every ergodic component is weakly mixing and not a one-point system. Then, T is not a multiplier of
$T\in \operatorname {Erg}^{\perp }$
be such that almost every ergodic component is weakly mixing and not a one-point system. Then, T is not a multiplier of
![]() $\operatorname {Erg}^{\perp }$
.
$\operatorname {Erg}^{\perp }$
.
Proof. Let
![]() $T\in \operatorname {Erg}^\perp $
be such that almost every ergodic component is weakly mixing and not a one-point system. Assume that
$T\in \operatorname {Erg}^\perp $
be such that almost every ergodic component is weakly mixing and not a one-point system. Assume that
![]() $T\in \mathcal {M}(\operatorname {Erg}^\perp )$
. Let
$T\in \mathcal {M}(\operatorname {Erg}^\perp )$
. Let
be the ergodic decomposition of
![]() $(T,\mu )$
. Let
$(T,\mu )$
. Let
![]() $\tilde {\mu }\in J_2(T,\mu )$
be given by
$\tilde {\mu }\in J_2(T,\mu )$
be given by
Since P-a.e ergodic component of T is weakly mixing, then equation (13) actually gives the ergodic decomposition of
![]() $\tilde \mu $
.
$\tilde \mu $
.
Note that, since for P-a.e.
![]() $\bar x\in \overline {X}$
, the map
$\bar x\in \overline {X}$
, the map
![]() $(T,\mu _{\bar x})$
is weakly mixing and not a one-point system, it follows that
$(T,\mu _{\bar x})$
is weakly mixing and not a one-point system, it follows that
![]() $\mu _{\bar {x}}$
is non-atomic and we have that
$\mu _{\bar {x}}$
is non-atomic and we have that
Consider
![]() $R=R_X$
, the flip map on
$R=R_X$
, the flip map on
![]() $X\times X$
. Since R preserves
$X\times X$
. Since R preserves
![]() $\mu _{\bar {x}} \otimes \mu _{\bar {x}}$
for all
$\mu _{\bar {x}} \otimes \mu _{\bar {x}}$
for all
![]() $\bar x\in \overline X$
, we have that
$\bar x\in \overline X$
, we have that
![]() $\tilde \mu $
is
$\tilde \mu $
is
![]() $(T\times T)\circ R$
-invariant. Moreover, by Lemma 18, the systems
$(T\times T)\circ R$
-invariant. Moreover, by Lemma 18, the systems
![]() $\big ((T\times T)\circ R,\mu _{\bar x}\otimes \mu _{\bar x}\big )$
,
$\big ((T\times T)\circ R,\mu _{\bar x}\otimes \mu _{\bar x}\big )$
,
![]() $\bar x \in \overline {X}$
, are ergodic and thus equation (13) also yields an ergodic decomposition of
$\bar x \in \overline {X}$
, are ergodic and thus equation (13) also yields an ergodic decomposition of
![]() $\tilde \mu $
with respect to
$\tilde \mu $
with respect to
![]() $(T\times T)\circ R$
.
$(T\times T)\circ R$
.
As a consequence of Lemma 5, we get that
In particular, by Theorem 2, for
![]() $P\otimes P$
-a.e.
$P\otimes P$
-a.e.
![]() $(\bar {x},\bar {y})\in \overline {X}^2$
, we have
$(\bar {x},\bar {y})\in \overline {X}^2$
, we have
Hence, by Lemma 19, we obtain that for
![]() $P\otimes P$
-a.e.
$P\otimes P$
-a.e.
![]() $(\bar {x},\bar {y})\in \overline {X}^2$
,
$(\bar {x},\bar {y})\in \overline {X}^2$
,
This, again by Theorem 2, gives that
![]() $((T\times T)\circ R,\tilde \mu )\in \operatorname {Erg}^\perp $
.
$((T\times T)\circ R,\tilde \mu )\in \operatorname {Erg}^\perp $
.
Denote by
![]() $\mathcal {R}$
the
$\mathcal {R}$
the
![]() $\sigma $
-algebra of R-invariant sets. Note that
$\sigma $
-algebra of R-invariant sets. Note that
![]() $\mathcal {R}$
is a factor
$\mathcal {R}$
is a factor
![]() $\sigma $
-algebra for both
$\sigma $
-algebra for both
![]() $T\times T$
and
$T\times T$
and
![]() $(T\times T)\circ R$
. Hence, we may consider the associated relatively independent extension
$(T\times T)\circ R$
. Hence, we may consider the associated relatively independent extension
![]() $\tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu } \in J\big ((T\times T, \tilde {\mu }), ((T\times T)\circ R, \tilde {\mu })\big )$
. Note that for
$\tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu } \in J\big ((T\times T, \tilde {\mu }), ((T\times T)\circ R, \tilde {\mu })\big )$
. Note that for
![]() $\tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu }$
-a.e.
$\tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu }$
-a.e.
![]() $(x_1,x_2,y_1,y_2)$
, the following hold:
$(x_1,x_2,y_1,y_2)$
, the following hold:
-
•
 $(x_1,x_2)=(y_1,y_2)$
or
$(x_1,x_2)=(y_1,y_2)$
or
 $(x_1,x_2)=(y_2,y_1)$
(because the restriction of
$(x_1,x_2)=(y_2,y_1)$
(because the restriction of
 $\tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu }$
to
$\tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu }$
to
 $\mathcal {R}\otimes \mathcal {R}$
is the diagonal joining);
$\mathcal {R}\otimes \mathcal {R}$
is the diagonal joining); -
•
 $x_1\neq x_2$
and
$x_1\neq x_2$
and
 $y_1\neq y_2$
by equation (14).
$y_1\neq y_2$
by equation (14).
Therefore, we can consider the map
![]() $\varphi :(X\times X)^2 \to \mathbb {Z}_2$
, defined
$\varphi :(X\times X)^2 \to \mathbb {Z}_2$
, defined
![]() $\tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu }$
-almost everywhere, by
$\tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu }$
-almost everywhere, by
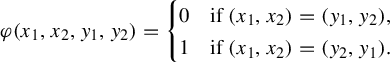 $$ \begin{align*} \varphi(x_1,x_2,y_1,y_2)=\begin{cases} 0 &\text{if } (x_1,x_2)=(y_1,y_2),\\ 1 &\text{if } (x_1,x_2)=(y_2,y_1). \end{cases} \end{align*} $$
$$ \begin{align*} \varphi(x_1,x_2,y_1,y_2)=\begin{cases} 0 &\text{if } (x_1,x_2)=(y_1,y_2),\\ 1 &\text{if } (x_1,x_2)=(y_2,y_1). \end{cases} \end{align*} $$
Let A be the addition of
![]() $1$
on
$1$
on
![]() $\mathbb {Z}_2$
. Then,
$\mathbb {Z}_2$
. Then,
![]() $\varphi $
is a factor map between
$\varphi $
is a factor map between
![]() $((T{\kern-1pt}\times{\kern-1pt} T) {\kern-1pt}\times{\kern-1pt} (T{\kern-1pt}\times{\kern-1pt} T) \circ R, \tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu } )$
and the ergodic rotation
$((T{\kern-1pt}\times{\kern-1pt} T) {\kern-1pt}\times{\kern-1pt} (T{\kern-1pt}\times{\kern-1pt} T) \circ R, \tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu } )$
and the ergodic rotation
![]() $(\mathbb {Z}_2, \tfrac 12(\delta _0 + \delta _1), A)$
. Indeed, for
$(\mathbb {Z}_2, \tfrac 12(\delta _0 + \delta _1), A)$
. Indeed, for
![]() $\tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu }$
-a.e.
$\tilde {\mu } \otimes _{\mathcal {R}} \tilde {\mu }$
-a.e.
![]() $(x_1,x_2, y_1,y_2)$
, it holds that
$(x_1,x_2, y_1,y_2)$
, it holds that
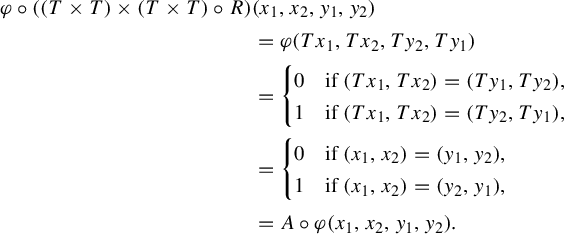 $$ \begin{align*} \begin{aligned} \varphi \circ ((T\times T) \times (T\times T)\circ R)&(x_1,x_2,y_1,y_2)\\&= \varphi (Tx_1,Tx_2,Ty_2,Ty_1)\\ &=\begin{cases} 0 &\text{if } (Tx_1,Tx_2)=(Ty_1,Ty_2),\\ 1 &\text{if } (Tx_1,Tx_2)=(Ty_2,Ty_1), \end{cases}\\ &=\begin{cases} 0 &\text{if } (x_1,x_2)=(y_1,y_2),\\ 1 &\text{if } (x_1,x_2)=(y_2,y_1), \end{cases}\\ &=A\circ \varphi (x_1,x_2,y_1,y_2). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \varphi \circ ((T\times T) \times (T\times T)\circ R)&(x_1,x_2,y_1,y_2)\\&= \varphi (Tx_1,Tx_2,Ty_2,Ty_1)\\ &=\begin{cases} 0 &\text{if } (Tx_1,Tx_2)=(Ty_1,Ty_2),\\ 1 &\text{if } (Tx_1,Tx_2)=(Ty_2,Ty_1), \end{cases}\\ &=\begin{cases} 0 &\text{if } (x_1,x_2)=(y_1,y_2),\\ 1 &\text{if } (x_1,x_2)=(y_2,y_1), \end{cases}\\ &=A\circ \varphi (x_1,x_2,y_1,y_2). \end{aligned} \end{align*} $$
Hence, we found a joining of
![]() $(T\times T,\tilde \mu )\in \mathcal M(\operatorname {Erg}^{\perp })$
(see equation (15)) and
$(T\times T,\tilde \mu )\in \mathcal M(\operatorname {Erg}^{\perp })$
(see equation (15)) and
![]() $((T\times T)\circ R,\tilde \mu )\in \operatorname {Erg}^{\perp }$
, which has an ergodic rotation as a factor. This contradiction proves that
$((T\times T)\circ R,\tilde \mu )\in \operatorname {Erg}^{\perp }$
, which has an ergodic rotation as a factor. This contradiction proves that
![]() $T\notin \mathcal {M}(\operatorname {Erg}^\perp )$
.
$T\notin \mathcal {M}(\operatorname {Erg}^\perp )$
.
Before passing to prove the main result of this section, let us deal with the measurability issues concerning the choice of a discrete factor. For this purpose, let us recall the classical Kuratowski–Ryll-Nardzewski theorem.
Theorem 21. (Kuratowski and Ryll-Nardzewski [Reference Kuratowski and Ryll-Nardzewski18])
Let
![]() $(X,\mathcal B)$
be a Polish space with the Borel
$(X,\mathcal B)$
be a Polish space with the Borel
![]() $\sigma $
-algebra and let
$\sigma $
-algebra and let
![]() $(\Omega ,\mathcal C)$
be a measurable space. Let f be a multifunction on
$(\Omega ,\mathcal C)$
be a measurable space. Let f be a multifunction on
![]() $\Omega $
which takes values in closed subsets of X. Assume moreover that f is weakly measurable, that is, for every open
$\Omega $
which takes values in closed subsets of X. Assume moreover that f is weakly measurable, that is, for every open
![]() $A\subset X$
, the set
$A\subset X$
, the set
![]() $\{\omega \in \Omega ;\,f(\omega )\cap A\neq \emptyset \}$
is measurable. Then, there exists a measurable selector
$\{\omega \in \Omega ;\,f(\omega )\cap A\neq \emptyset \}$
is measurable. Then, there exists a measurable selector
![]() $F:\Omega \to X$
of f, that is,
$F:\Omega \to X$
of f, that is,
![]() $F(\omega )\in f(\omega )$
for every
$F(\omega )\in f(\omega )$
for every
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
We use the above result to show that we can measurably assign an eigenvalue to any element of ergodic decomposition. Recall the notions of space of ergodic components
![]() $\overline {X}$
and its subsets
$\overline {X}$
and its subsets
![]() $\overline {X}_n$
and
$\overline {X}_n$
and
![]() $\overline {X}_{\infty }$
from equation (3).
$\overline {X}_{\infty }$
from equation (3).
Lemma 22. Let
![]() $T\in \operatorname {Aut} (X,\mathcal B, \mu )$
and let
$T\in \operatorname {Aut} (X,\mathcal B, \mu )$
and let
be the ergodic decomposition. Assume that P-a.e. fibre automorphism is non-weakly mixing (that is, possesses a non-trivial eigenvalue). Then, there exists a measurable map
![]() $F:\overline {X}_{\infty }\to L^2(Z,\mathcal D, \kappa )$
, where
$F:\overline {X}_{\infty }\to L^2(Z,\mathcal D, \kappa )$
, where
![]() $(Z,\mathcal D, \kappa )$
is defined in equation (4), such that
$(Z,\mathcal D, \kappa )$
is defined in equation (4), such that
![]() $F(\bar x)$
is an eigenfunction of modulus 1 of
$F(\bar x)$
is an eigenfunction of modulus 1 of
![]() $T_{\bar x}$
in
$T_{\bar x}$
in
![]() $L^2_0(Z,\kappa )$
(identified with
$L^2_0(Z,\kappa )$
(identified with
![]() $L^2_0(X,\mu _{\bar x})$
).
$L^2_0(X,\mu _{\bar x})$
).
Proof. We will define F on the set
![]() $\overline {X}_{\infty }$
by considering a multifunction H defined below and taking F as a measurable selector given by Theorem 21. Therefore, the remainder of the proof is devoted to picking a proper multifunction and checking that the assumptions of Theorem 21 are satisfied.
$\overline {X}_{\infty }$
by considering a multifunction H defined below and taking F as a measurable selector given by Theorem 21. Therefore, the remainder of the proof is devoted to picking a proper multifunction and checking that the assumptions of Theorem 21 are satisfied.
Let
![]() $W\subset L^2_0(Z,\mathcal D, \kappa )$
be the subset of function of integral 0 and modulus 1 (note that W is a Polish space in
$W\subset L^2_0(Z,\mathcal D, \kappa )$
be the subset of function of integral 0 and modulus 1 (note that W is a Polish space in
![]() $L^2$
-topology). Let H be a multifunction which assigns to each element
$L^2$
-topology). Let H be a multifunction which assigns to each element
![]() $T_{\bar x}:=(T,\mu _{\bar x})$
the set
$T_{\bar x}:=(T,\mu _{\bar x})$
the set
![]() $H(T_{\bar x})\subset W$
of its eigenfunctions. Note that this is a closed set. Indeed, assume that
$H(T_{\bar x})\subset W$
of its eigenfunctions. Note that this is a closed set. Indeed, assume that
![]() $f_n\to f\in L^2_0(Z,\mathcal D, \kappa )$
, where
$f_n\to f\in L^2_0(Z,\mathcal D, \kappa )$
, where
![]() $(f_n)_{n\in \mathbb {N}}$
is a sequence of functions in
$(f_n)_{n\in \mathbb {N}}$
is a sequence of functions in
![]() $H(T_{\bar x})$
. Then, f is also of modulus 1. Moreover, by using the compactness of the circle and passing to a subsequence if necessary, we also have that the sequence
$H(T_{\bar x})$
. Then, f is also of modulus 1. Moreover, by using the compactness of the circle and passing to a subsequence if necessary, we also have that the sequence
![]() $(\unicode{x3bb} _n)_{n\in \mathbb {N}}$
of the corresponding eigenvalues converges to some number
$(\unicode{x3bb} _n)_{n\in \mathbb {N}}$
of the corresponding eigenvalues converges to some number
![]() $\unicode{x3bb} \in \mathbb S^1$
. It is now easy to check that f is an eigenfunction corresponding to the eigenvalue
$\unicode{x3bb} \in \mathbb S^1$
. It is now easy to check that f is an eigenfunction corresponding to the eigenvalue
![]() $\unicode{x3bb} $
.
$\unicode{x3bb} $
.
We now prove that H is weakly measurable so that we can apply Theorem 21. Let
![]() $A\subset W$
be open. Without loss of generality, we can assume that
$A\subset W$
be open. Without loss of generality, we can assume that
![]() $\overline X_{\infty }$
is a metric compact space. Consider the map
$\overline X_{\infty }$
is a metric compact space. Consider the map
![]() $\varphi _A:\overline {X}_{\infty }\times \mathbb S^1\times A\to L^2(Z,\mathcal D, \kappa )$
, given by
$\varphi _A:\overline {X}_{\infty }\times \mathbb S^1\times A\to L^2(Z,\mathcal D, \kappa )$
, given by
By equation (4),
![]() $T_{\bar x}\in \operatorname {Aut}(Z,\mathcal D, \kappa )$
. Hence, the right-hand side of the above formula is an element of
$T_{\bar x}\in \operatorname {Aut}(Z,\mathcal D, \kappa )$
. Hence, the right-hand side of the above formula is an element of
![]() $L^2(Z,\mathcal D, \kappa )$
. Let
$L^2(Z,\mathcal D, \kappa )$
. Let
be the projection on the first coordinate. To prove the weak measurability of H, we need to show that the set
is measurable. Since the map
![]() $\bar x\mapsto T_{\bar x}$
is Borel measurable, then so is
$\bar x\mapsto T_{\bar x}$
is Borel measurable, then so is
![]() $\varphi _A$
. Thus,
$\varphi _A$
. Thus,
![]() $\pi _{\overline X}(\varphi ^{-1}_A({0})) $
is analytic, and hence measurable with respect to
$\pi _{\overline X}(\varphi ^{-1}_A({0})) $
is analytic, and hence measurable with respect to
![]() $\mathcal C$
being the
$\mathcal C$
being the
![]() $\sigma $
-algebra of P-measurable sets. It remains to use Theorem 21 for
$\sigma $
-algebra of P-measurable sets. It remains to use Theorem 21 for
![]() $\Omega =\overline X_{\infty }$
and
$\Omega =\overline X_{\infty }$
and
![]() $\mathcal C$
.
$\mathcal C$
.
Remark 23. The following result follows immediately from the fact that the class of automorphisms whose almost all ergodic components have discrete spectra is a characteristic class as proved in [Reference Kanigowski, Kułaga-Przymus, Lemańczyk and de la Rue16]. Hence, for T, there exists the largest factor of T belonging to this characteristic class, and this factor considered on each fibre
![]() $T_{\bar x}$
is the Kronecker factor of
$T_{\bar x}$
is the Kronecker factor of
![]() $T_{\bar x}$
, see [Reference Kanigowski, Kułaga-Przymus, Lemańczyk and de la Rue16, §2.3.1]. However, we need a special form of this factor, and hence we give the complete proof below.
$T_{\bar x}$
, see [Reference Kanigowski, Kułaga-Przymus, Lemańczyk and de la Rue16, §2.3.1]. However, we need a special form of this factor, and hence we give the complete proof below.
Lemma 24. Let T satisfy the assumptions of Lemma 22. Then, there exists a non-trivial factor of T whose ergodic decomposition consists of ergodic rotations.
Proof. Let F be given by Lemma 22. Note that for every
![]() $\bar x\in \overline {X}_{\infty }$
, the corresponding eigenvalue
$\bar x\in \overline {X}_{\infty }$
, the corresponding eigenvalue
![]() $\varphi (\bar x)$
is equal to
$\varphi (\bar x)$
is equal to
![]() ${F(\bar x)\circ T_{\bar x}}/{F(\bar x)}$
, and hence it depends measurably on
${F(\bar x)\circ T_{\bar x}}/{F(\bar x)}$
, and hence it depends measurably on
![]() $\bar x$
. Thus, in view of the fact that the map
$\bar x$
. Thus, in view of the fact that the map
![]() $\mathbb S^1\ni \alpha \mapsto R_\alpha \in {\operatorname {Aut}(\mathbb S^1, \mathrm {Leb}_{\mathbb S^1})}$
is continuous, the automorphism
$\mathbb S^1\ni \alpha \mapsto R_\alpha \in {\operatorname {Aut}(\mathbb S^1, \mathrm {Leb}_{\mathbb S^1})}$
is continuous, the automorphism
![]() $S\in \operatorname {Aut}(\overline X\times \mathbb S^1,P\otimes \mathrm {Leb}_{\mathbb S^1})$
,
$S\in \operatorname {Aut}(\overline X\times \mathbb S^1,P\otimes \mathrm {Leb}_{\mathbb S^1})$
,
is the desired factor and factorizing map
![]() $J:\overline X\times Z\to \overline X\times \mathbb S^1$
is given by
$J:\overline X\times Z\to \overline X\times \mathbb S^1$
is given by
Proof of Theorem 1
Let
![]() $(X,\mathcal B,\mu , T)\in \mathcal M(\operatorname {Erg}^{\perp })$
and let
$(X,\mathcal B,\mu , T)\in \mathcal M(\operatorname {Erg}^{\perp })$
and let
![]() $\mu =\int _{\overline {X}}\mu _{\bar x}\,dP(\bar x)$
be its ergodic decomposition. In view of Corollary 13, we have
$\mu =\int _{\overline {X}}\mu _{\bar x}\,dP(\bar x)$
be its ergodic decomposition. In view of Corollary 13, we have
![]() $P(\overline X_1\cup \overline X_{\infty })=1$
. We will show that
$P(\overline X_1\cup \overline X_{\infty })=1$
. We will show that
![]() $P(\overline X_1)=1$
. Assume by contradiction that
$P(\overline X_1)=1$
. Assume by contradiction that
![]() $P(\overline X_\infty )>0$
.
$P(\overline X_\infty )>0$
.
Consider first the case when
![]() $P(\mathcal {WM})>0$
, where
$P(\mathcal {WM})>0$
, where
![]() $\mathcal {WM}:=\{\bar x\in \overline {X}_{\infty }: T_{\bar x}\text { is weakly} \text {mixing}\}$
(it is measurable via Lemma 14). Then, T can be decomposed into a disjoint action of two automorphisms
$\mathcal {WM}:=\{\bar x\in \overline {X}_{\infty }: T_{\bar x}\text { is weakly} \text {mixing}\}$
(it is measurable via Lemma 14). Then, T can be decomposed into a disjoint action of two automorphisms
![]() $\tilde T$
and
$\tilde T$
and
![]() $\tilde {T}^\ast $
. Here,
$\tilde {T}^\ast $
. Here,
![]() $\tilde {T}$
stands for the restriction of T to the union of fibres corresponding to
$\tilde {T}$
stands for the restriction of T to the union of fibres corresponding to
![]() $\mathcal {WM}$
, that is, it is measure
$\mathcal {WM}$
, that is, it is measure
![]() $\tilde \mu $
-preserving, where the ergodic decomposition of
$\tilde \mu $
-preserving, where the ergodic decomposition of
![]() $\tilde {T}$
is of the form
$\tilde {T}$
is of the form
and the automorphism
![]() $\tilde T^*$
is the restriction of T to the union of the fibres corresponding to
$\tilde T^*$
is the restriction of T to the union of the fibres corresponding to
![]() $\overline X\setminus \mathcal {WM}$
. Then,
$\overline X\setminus \mathcal {WM}$
. Then,
![]() $(\tilde {T},\tilde {\mu })$
satisfies the assumption of Lemma 20 and thus, it is not a multiplier of
$(\tilde {T},\tilde {\mu })$
satisfies the assumption of Lemma 20 and thus, it is not a multiplier of
![]() $\operatorname {Erg}^{\perp }$
, that is, there exists
$\operatorname {Erg}^{\perp }$
, that is, there exists
![]() $S\in \operatorname {Erg}^\perp $
and a joining
$S\in \operatorname {Erg}^\perp $
and a joining
![]() $\tilde \eta \in J(\tilde T,S)$
such that
$\tilde \eta \in J(\tilde T,S)$
such that
![]() $(\tilde T\times S,\tilde \eta )\notin \operatorname {Erg}^\perp $
. It is now enough to join
$(\tilde T\times S,\tilde \eta )\notin \operatorname {Erg}^\perp $
. It is now enough to join
![]() $\tilde T^*$
and S independently to get a non-trivial joining
$\tilde T^*$
and S independently to get a non-trivial joining
![]() $\eta \in J(T,S)$
such that
$\eta \in J(T,S)$
such that
![]() $(T\times S,\eta )\notin \operatorname {Erg}^\perp $
, which is a contradiction with the fact that
$(T\times S,\eta )\notin \operatorname {Erg}^\perp $
, which is a contradiction with the fact that
![]() $T\in \operatorname {Erg}^{\perp }$
.
$T\in \operatorname {Erg}^{\perp }$
.
Thus, we can assume that for P-a.e.
![]() $\bar x\in \overline X_{\infty }$
, the automorphism
$\bar x\in \overline X_{\infty }$
, the automorphism
![]() $T_{\bar x}$
has a non-trivial eigenvalue. Let
$T_{\bar x}$
has a non-trivial eigenvalue. Let
![]() $\mu _{\infty }=({1}/{P(\overline X_{\infty })})\int _{\overline X_{\infty }} \mu _{\bar x}\, dP(x)$
. Then, by Lemma 24, there exists a factor
$\mu _{\infty }=({1}/{P(\overline X_{\infty })})\int _{\overline X_{\infty }} \mu _{\bar x}\, dP(x)$
. Then, by Lemma 24, there exists a factor
![]() $\hat T$
of
$\hat T$
of
![]() $(T,\mu _{\infty })$
such that all ergodic components
$(T,\mu _{\infty })$
such that all ergodic components
![]() $\hat T_{\bar x}$
of
$\hat T_{\bar x}$
of
![]() $\hat T$
are rotations on the circle. Note that for a.e. pair of
$\hat T$
are rotations on the circle. Note that for a.e. pair of
![]() $(\bar x,\bar y)\in \overline {X}_{\infty }\times \overline {X}_{\infty }$
, the associated rotations are disjoint in view of Theorem 2. Then,
$(\bar x,\bar y)\in \overline {X}_{\infty }\times \overline {X}_{\infty }$
, the associated rotations are disjoint in view of Theorem 2. Then,
![]() $\hat T$
has exactly the form of Example 1, which is not in
$\hat T$
has exactly the form of Example 1, which is not in
![]() $\mathcal M(\operatorname {Erg}^{\perp })$
. Since, by Corollary 6,
$\mathcal M(\operatorname {Erg}^{\perp })$
. Since, by Corollary 6,
![]() $\mathcal M(\operatorname {Erg}^{\perp })$
is a characteristic class, we get that
$\mathcal M(\operatorname {Erg}^{\perp })$
is a characteristic class, we get that
![]() $(T,\mu _{\infty })\notin \mathcal M(\operatorname {Erg}^{\perp })$
. Thus, again by joining the restriction of T to the fibres in
$(T,\mu _{\infty })\notin \mathcal M(\operatorname {Erg}^{\perp })$
. Thus, again by joining the restriction of T to the fibres in
![]() $\overline X_1$
independently, we get that
$\overline X_1$
independently, we get that
![]() $(T,\mu )\notin \mathcal {M}(\operatorname {Erg}^\perp )$
.
$(T,\mu )\notin \mathcal {M}(\operatorname {Erg}^\perp )$
.
Hence,
![]() $P(\overline X_1)=1$
, which means that T is an identity. This proves that
$P(\overline X_1)=1$
, which means that T is an identity. This proves that
![]() $\mathcal {M}(\operatorname {Erg}^\perp )\subset \operatorname {ID} $
. The opposite inclusion follows directly from Corollary 17. This finishes the proof.
$\mathcal {M}(\operatorname {Erg}^\perp )\subset \operatorname {ID} $
. The opposite inclusion follows directly from Corollary 17. This finishes the proof.
5
 $\operatorname {Erg}^{\perp }$
is closed under taking products
$\operatorname {Erg}^{\perp }$
is closed under taking products
As Theorem 1 shows, the class
![]() $\operatorname {Erg}^{\perp }$
is not closed under taking joinings due to an interplay between fibre automorphisms over the ‘common’ part of ergodic components. It turns out that this phenomenon can not happen if the spaces of ergodic components are independent—in this section, we show the class
$\operatorname {Erg}^{\perp }$
is not closed under taking joinings due to an interplay between fibre automorphisms over the ‘common’ part of ergodic components. It turns out that this phenomenon can not happen if the spaces of ergodic components are independent—in this section, we show the class
![]() $\operatorname {Erg}^\perp $
is actually closed under taking the Cartesian products.
$\operatorname {Erg}^\perp $
is actually closed under taking the Cartesian products.
Theorem 25. Assume that
![]() $(X,\mathcal B,\mu , T), (Y,\mathcal C,\nu , S)\in \operatorname {Erg}^\perp $
. Then,
$(X,\mathcal B,\mu , T), (Y,\mathcal C,\nu , S)\in \operatorname {Erg}^\perp $
. Then,
Proof. Let
![]() $(Z,\mathcal D,\rho , R)$
be an arbitrary ergodic system. Recall first that all systems under consideration may be viewed as measure-preserving homeomorphisms of compact metric spaces. The above observation allows one to use Lemma 10 later in the proof.
$(Z,\mathcal D,\rho , R)$
be an arbitrary ergodic system. Recall first that all systems under consideration may be viewed as measure-preserving homeomorphisms of compact metric spaces. The above observation allows one to use Lemma 10 later in the proof.
On the space
![]() $X\times Y\times Z$
, for every
$X\times Y\times Z$
, for every
![]() $A\in \{X,Y,Z,X\times Y,X\times Z,Y\times Z\}$
, denote by
$A\in \{X,Y,Z,X\times Y,X\times Z,Y\times Z\}$
, denote by
![]() $\pi ^{A}:X\times Y\times Z\to A$
the standard projection on the corresponding coordinates. Consider any joining
$\pi ^{A}:X\times Y\times Z\to A$
the standard projection on the corresponding coordinates. Consider any joining
![]() $\unicode{x3bb} \in J((T\times S,\mu \otimes \nu ),(R,\rho ))$
. We aim at showing that
$\unicode{x3bb} \in J((T\times S,\mu \otimes \nu ),(R,\rho ))$
. We aim at showing that
![]() $\unicode{x3bb} =\mu \otimes \nu \otimes \rho $
.
$\unicode{x3bb} =\mu \otimes \nu \otimes \rho $
.
First, note that
![]() $(\pi ^{{ X\times Z}})_*\unicode{x3bb} =\mu \otimes \rho $
and
$(\pi ^{{ X\times Z}})_*\unicode{x3bb} =\mu \otimes \rho $
and
![]() $(\pi ^{ Y\times Z})_*\unicode{x3bb} =\nu \otimes \rho $
as
$(\pi ^{ Y\times Z})_*\unicode{x3bb} =\nu \otimes \rho $
as
![]() $T,S\in \operatorname {Erg}^\perp $
. Let
$T,S\in \operatorname {Erg}^\perp $
. Let
be the ergodic decomposition of
![]() $\mu $
(with
$\mu $
(with
![]() $P=\mu |_{\mathrm {{Inv}(T)}}$
). Since
$P=\mu |_{\mathrm {{Inv}(T)}}$
). Since
![]() $\mathrm {Inv}(T)$
is also a factor of
$\mathrm {Inv}(T)$
is also a factor of
![]() $(T\times S\times R,\unicode{x3bb} )$
and
$(T\times S\times R,\unicode{x3bb} )$
and
![]() $(\pi ^X)_\ast \unicode{x3bb} =\mu $
,
$(\pi ^X)_\ast \unicode{x3bb} =\mu $
,
and
![]() $(\pi ^X)_*\unicode{x3bb} _{\bar x}=\mu _{\bar x} P$
-almost everywhere, by the uniqueness of disintegrations. Moreover, note that
$(\pi ^X)_*\unicode{x3bb} _{\bar x}=\mu _{\bar x} P$
-almost everywhere, by the uniqueness of disintegrations. Moreover, note that
Since
![]() $(\pi ^{ X\times Z})_*\unicode{x3bb} =\mu \otimes \rho $
, again by using the uniqueness of disintegration, we get
$(\pi ^{ X\times Z})_*\unicode{x3bb} =\mu \otimes \rho $
, again by using the uniqueness of disintegration, we get
Analogously, since
![]() $(\pi ^{ X\times Y})_*\unicode{x3bb} =\mu \otimes \nu $
, we also have
$(\pi ^{ X\times Y})_*\unicode{x3bb} =\mu \otimes \nu $
, we also have
In particular,
![]() $(\pi ^{Y})_*\unicode{x3bb} _{\bar x}=\nu $
. Thus, by equation (18), we have
$(\pi ^{Y})_*\unicode{x3bb} _{\bar x}=\nu $
. Thus, by equation (18), we have
What remains to show is that
Indeed, if equation (20) holds, then since
![]() $S\in \operatorname {Erg}^\perp $
, we obtain that
$S\in \operatorname {Erg}^\perp $
, we obtain that
which together with equation (17) yields
![]() $\unicode{x3bb} =\mu \otimes \nu \otimes \rho $
.
$\unicode{x3bb} =\mu \otimes \nu \otimes \rho $
.
To show equation (20), recall first that R can have at most countably many eigenvalues. Moreover, the Cartesian product of two ergodic systems is not ergodic if and only if they have a non-trivial common eigenvalue. It is thus enough to show that for any fixed
![]() $\alpha \in \mathbb T\setminus \{0\}$
, we have
$\alpha \in \mathbb T\setminus \{0\}$
, we have
Assume that equation (21) does not hold, that is,
Then, by Lemma 12,
![]() $\alpha $
is an eigenvalue of T. This is a contradiction with equation (6). Hence, we proved equation (21) which in turn completes the proof of the theorem.
$\alpha $
is an eigenvalue of T. This is a contradiction with equation (6). Hence, we proved equation (21) which in turn completes the proof of the theorem.
By induction, we obtain from the above result the following corollary.
Corollary 26. If
![]() ${(X_i,\mathcal B_i,\mu _i, T_i)}_{i\in \mathbb {N}}$
is a sequence of elements of
${(X_i,\mathcal B_i,\mu _i, T_i)}_{i\in \mathbb {N}}$
is a sequence of elements of
![]() $\operatorname {Erg}^{\perp }$
, then
$\operatorname {Erg}^{\perp }$
, then
 $$ \begin{align*} \bigg(\prod_{i=0}^{\infty}X_i,\bigotimes_{i=0}^{\infty}\mathcal B_i,\bigotimes_{i=0}^{\infty}\mathcal \mu_i, \prod_{i=0}^{\infty}T_i\bigg)\ \in\ \operatorname{Erg}^{\perp}. \end{align*} $$
$$ \begin{align*} \bigg(\prod_{i=0}^{\infty}X_i,\bigotimes_{i=0}^{\infty}\mathcal B_i,\bigotimes_{i=0}^{\infty}\mathcal \mu_i, \prod_{i=0}^{\infty}T_i\bigg)\ \in\ \operatorname{Erg}^{\perp}. \end{align*} $$
6 An automorphism whose self-joinings are disjoint with ergodic automorphisms
We are going to construct an automorphism whose self-joinings are all elements of
![]() $\operatorname {Erg}^{\perp }$
. To do that, we will rely on the PID property. We need the following result.
$\operatorname {Erg}^{\perp }$
. To do that, we will rely on the PID property. We need the following result.
Theorem 27. (Ryzhikov [Reference Ryzhikov23])
Assume that
![]() $(X,\mathcal B,\mu , T)$
has the PID property and
$(X,\mathcal B,\mu , T)$
has the PID property and
![]() $(Y_i,\mathcal B_i,\nu _i,S_i)$
,
$(Y_i,\mathcal B_i,\nu _i,S_i)$
,
![]() $i=1,2$
, are measure-preserving automorphisms. If
$i=1,2$
, are measure-preserving automorphisms. If
![]() $\unicode{x3bb} \in J(T,S_1,S_2)$
projects as product measures on each pair of coordinates, then
$\unicode{x3bb} \in J(T,S_1,S_2)$
projects as product measures on each pair of coordinates, then
In the proof of Theorem 29, we will use several times the following corollary of the above result.
Corollary 28. Let
![]() $n\ge 2$
and let
$n\ge 2$
and let
![]() $(X_i,\mathcal B_i,\mu _i,T_i)$
,
$(X_i,\mathcal B_i,\mu _i,T_i)$
,
![]() $i=1,\ldots ,n$
, be measure-preserving automorphisms satisfying the PID property. Let
$i=1,\ldots ,n$
, be measure-preserving automorphisms satisfying the PID property. Let
![]() $(Y,\mathcal C,\nu ,S)$
be a measure-preserving automorphism. If
$(Y,\mathcal C,\nu ,S)$
be a measure-preserving automorphism. If
![]() $\unicode{x3bb} \in J(S,T_1,\ldots ,T_n)$
projects as product measures on each pair of coordinates, then
$\unicode{x3bb} \in J(S,T_1,\ldots ,T_n)$
projects as product measures on each pair of coordinates, then
Proof. We use induction. For
![]() $n=2$
, the result follows directly from Theorem 27. Assume that it is true for some
$n=2$
, the result follows directly from Theorem 27. Assume that it is true for some
![]() $n\ge 2$
, we will prove that it holds for
$n\ge 2$
, we will prove that it holds for
![]() $n+1$
. Let
$n+1$
. Let
![]() $\unicode{x3bb} \in J(S,T_1,\ldots ,T_{n+1})$
and let
$\unicode{x3bb} \in J(S,T_1,\ldots ,T_{n+1})$
and let
![]() $\tilde{\unicode{x3bb}} $
be the projection of
$\tilde{\unicode{x3bb}} $
be the projection of
![]() $\unicode{x3bb} $
on
$\unicode{x3bb} $
on
![]() $Y\times X_1\times \cdots \times X_n$
and let
$Y\times X_1\times \cdots \times X_n$
and let
![]() $\bar{\unicode{x3bb}} $
be the projection of
$\bar{\unicode{x3bb}} $
be the projection of
![]() $\unicode{x3bb} $
on
$\unicode{x3bb} $
on
![]() $X_1\times \cdots \times X_{n+1}$
. By the induction assumption, we get that
$X_1\times \cdots \times X_{n+1}$
. By the induction assumption, we get that
The result now follows from Theorem 27 by taking
![]() $T:=T_{n+1}$
,
$T:=T_{n+1}$
,
![]() $S_1:=S$
and
$S_1:=S$
and
![]() $S_2:= T_1\times \cdots \times ~T_n$
.
$S_2:= T_1\times \cdots \times ~T_n$
.
We are now ready to present and prove the main result of this section.
Theorem 29. Let
![]() $T:X\to X$
be a
$T:X\to X$
be a
![]() $\mu $
-preserving homeomorphism of a compact metric space X. Let
$\mu $
-preserving homeomorphism of a compact metric space X. Let
be the ergodic decomposition and let
![]() $T_{\bar x}$
denote the action of T on the fibre corresponding to
$T_{\bar x}$
denote the action of T on the fibre corresponding to
![]() $\bar x\in \overline {X}$
. Assume that P is a continuous probability measure. Assume moreover that:
$\bar x\in \overline {X}$
. Assume that P is a continuous probability measure. Assume moreover that:
-
• for every
 $\bar x\in \overline {X}$
, there exists a set of
$\bar x\in \overline {X}$
, there exists a set of
 $\bar y\in \overline {X}$
, whose complement is countable, such that for every
$\bar y\in \overline {X}$
, whose complement is countable, such that for every
 $\bar y$
from this set, we have
$\bar y$
from this set, we have
 $T_{\bar x}\perp T_{\bar y}$
;
$T_{\bar x}\perp T_{\bar y}$
; -
• for every
 $\bar x,\bar y\in \overline {X}$
, if
$\bar x,\bar y\in \overline {X}$
, if  , then
, then
 $T_{\bar x}$
and
$T_{\bar x}$
and
 $T_{\bar y}$
are isomorphic;
$T_{\bar y}$
are isomorphic; -
• for every
 $\bar x\in \overline {X}$
, the automorphism
$\bar x\in \overline {X}$
, the automorphism
 $(T_{\bar x},\mu _{\bar x})$
has the MSJ property (in particular, it has the PID property).
$(T_{\bar x},\mu _{\bar x})$
has the MSJ property (in particular, it has the PID property).
Then,
![]() $(T^{\times \infty },\eta )\in \operatorname {Erg}^{\perp }$
for every
$(T^{\times \infty },\eta )\in \operatorname {Erg}^{\perp }$
for every
![]() $\eta \in J_\infty (T,\mu )$
.
$\eta \in J_\infty (T,\mu )$
.
Proof. It is enough to prove that for every
![]() $n\ge 1$
and every
$n\ge 1$
and every
![]() $\eta \in J_n(T,\mu )$
,
$\eta \in J_n(T,\mu )$
,
![]() $(T^{\times n},\eta )\in \operatorname {Erg}^\perp $
. Note that since P is continuous, for
$(T^{\times n},\eta )\in \operatorname {Erg}^\perp $
. Note that since P is continuous, for
![]() $P\otimes P$
-a.e.
$P\otimes P$
-a.e.
![]() $(\bar x, \bar y)\in \overline X\times \overline X$
, we have
$(\bar x, \bar y)\in \overline X\times \overline X$
, we have
![]() $T_{\bar x}\perp T_{\bar y}$
. Then, by Theorem 2,
$T_{\bar x}\perp T_{\bar y}$
. Then, by Theorem 2,
![]() $T\in \operatorname {Erg}^\perp $
.
$T\in \operatorname {Erg}^\perp $
.
Let
![]() $2\le n<\infty $
, fix
$2\le n<\infty $
, fix
![]() $\eta \in J_n(T,\mu )$
and let
$\eta \in J_n(T,\mu )$
and let
![]() $(R,\rho )\in \operatorname {Erg}$
be arbitrary. Let
$(R,\rho )\in \operatorname {Erg}$
be arbitrary. Let
![]() $\psi \in J((T^{\times n},\eta ),(R,\rho ))$
. We want to show that
$\psi \in J((T^{\times n},\eta ),(R,\rho ))$
. We want to show that
![]() $\psi =\eta \otimes \rho $
. To distinguish between the n copies of X and
$\psi =\eta \otimes \rho $
. To distinguish between the n copies of X and
![]() $\overline {X}$
, we denote by
$\overline {X}$
, we denote by
![]() $X_k$
and
$X_k$
and
![]() $\overline X_k$
the domain and the space of ergodic components of T on the kth coordinate for every
$\overline X_k$
the domain and the space of ergodic components of T on the kth coordinate for every
![]() $k=1,\ldots n$
. We assign the coordinate
$k=1,\ldots n$
. We assign the coordinate
![]() $(n+1)$
to the automorphism R. Finally, we set
$(n+1)$
to the automorphism R. Finally, we set
![]() ${\mathbf X}=X_1\times \cdots \times X_n$
and by
${\mathbf X}=X_1\times \cdots \times X_n$
and by
![]() $\pi ^{k_1,\ldots ,k_m}:{\mathbf X}\to X_{k_1}\times \cdots \times X_{k_m}$
, we denote the projection on
$\pi ^{k_1,\ldots ,k_m}:{\mathbf X}\to X_{k_1}\times \cdots \times X_{k_m}$
, we denote the projection on
![]() $k_1,\ldots ,k_m$
coordinates.
$k_1,\ldots ,k_m$
coordinates.
Consider the ergodic decomposition of
![]() $(T^{\times n},\eta )$
:
$(T^{\times n},\eta )$
:
Thus, we also have the following disintegration of
![]() $\psi $
:
$\psi $
:
By uniqueness of ergodic decomposition, we have that
![]() $(\pi ^{\mathbf X})_*\psi _{\bar {\mathbf x}}=\eta _{\bar {\mathbf x}}$
and by ergodicity of R, we get
$(\pi ^{\mathbf X})_*\psi _{\bar {\mathbf x}}=\eta _{\bar {\mathbf x}}$
and by ergodicity of R, we get
![]() $(\pi ^{n+1})_*\psi _{\bar {\mathbf x}}=\rho $
. Thus,
$(\pi ^{n+1})_*\psi _{\bar {\mathbf x}}=\rho $
. Thus,
![]() $\psi _{\bar {\mathbf x}}\in J((T^{\times n},\eta _{\bar {\mathbf x}}), (R,\rho ))$
for Q-a.e.
$\psi _{\bar {\mathbf x}}\in J((T^{\times n},\eta _{\bar {\mathbf x}}), (R,\rho ))$
for Q-a.e.
![]() $\bar {\mathbf x}$
. To show that
$\bar {\mathbf x}$
. To show that
![]() $\psi =\eta \otimes \rho $
, we just have to show that
$\psi =\eta \otimes \rho $
, we just have to show that
Note that by uniqueness of ergodic decomposition, for Q-a.e.
![]() $\bar {\mathbf x}\in \overline {\mathbf X}$
and for every
$\bar {\mathbf x}\in \overline {\mathbf X}$
and for every
![]() $k=1,\ldots ,n$
, we have
$k=1,\ldots ,n$
, we have
Moreover, all marginals of Q are equal to P. Therefore, since P is continuous, we get that for every
![]() $\bar x\in \overline X$
, we have
$\bar x\in \overline X$
, we have
In particular, since there are only up to countably many ergodic components of T isomorphic to
![]() $\mu _{\bar x}$
, we get by equation (24) that for every
$\mu _{\bar x}$
, we get by equation (24) that for every
![]() $\bar x\in \overline {X}$
,
$\bar x\in \overline {X}$
,
Now, to show equation (23), we consider cases which depend on the form of
![]() $\eta _{\bar {\mathbf x}}$
. More precisely, we consider the number of coordinates on which the projection yields isomorphic maps (recall that by assumption, the ergodic components are either isomorphic or disjoint).
$\eta _{\bar {\mathbf x}}$
. More precisely, we consider the number of coordinates on which the projection yields isomorphic maps (recall that by assumption, the ergodic components are either isomorphic or disjoint).
Case 1: No isomorphic components. Let
![]() $\mathcal D_0\subset \overline {\mathbf X}$
be the set of elements satisfying the following:
$\mathcal D_0\subset \overline {\mathbf X}$
be the set of elements satisfying the following:
Then, by Corollary 28 and mutual disjointness assumption, for every
![]() $\bar {\mathbf x}\in \mathcal D_0$
, we get
$\bar {\mathbf x}\in \mathcal D_0$
, we get
Note also that for Q-a.e.
![]() $\bar {\mathbf x}\in \mathcal D_0$
, the automorphism
$\bar {\mathbf x}\in \mathcal D_0$
, the automorphism
![]() $(R,\rho )$
is disjoint with
$(R,\rho )$
is disjoint with
![]() $(T,\mu _{\bar x_k})$
for every
$(T,\mu _{\bar x_k})$
for every
![]() $k=1,\ldots , n$
. Indeed, otherwise for some
$k=1,\ldots , n$
. Indeed, otherwise for some
![]() $1\le k_0\le n$
, we would have that
$1\le k_0\le n$
, we would have that
 $$ \begin{align*}\begin{aligned} Q&(\{\bar{\mathbf x}\in \overline{\mathbf X};\ (T,\mu_{\bar x_{k_0}})\text{ and }(R,\rho) \text{ are not disjoint } \})\\&= P(\{\bar{x}\in \overline{X};\ (T,\mu_{\bar x})\text{ and }(R,\rho) \text{ are not disjoint } \})>0. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} Q&(\{\bar{\mathbf x}\in \overline{\mathbf X};\ (T,\mu_{\bar x_{k_0}})\text{ and }(R,\rho) \text{ are not disjoint } \})\\&= P(\{\bar{x}\in \overline{X};\ (T,\mu_{\bar x})\text{ and }(R,\rho) \text{ are not disjoint } \})>0. \end{aligned} \end{align*} $$
(The measurability of sets considered follows from [Reference Górska, Lemańczyk and de la Rue13, Corollary 3.8].)
By Proposition 4 and the assumptions of the theorem, the set considered above can be at most countable. This is a contradiction with the fact that P is continuous.
Thus, for Q-a.e.
![]() $\bar {\mathbf x}\in \mathcal D_0$
, the automorphism
$\bar {\mathbf x}\in \mathcal D_0$
, the automorphism
![]() $(R,\rho )$
is disjoint with
$(R,\rho )$
is disjoint with
![]() $(T,\mu _{\bar x_k})$
for every
$(T,\mu _{\bar x_k})$
for every
![]() $k=1,\ldots , n$
. In particular, by equation (27), for every such
$k=1,\ldots , n$
. In particular, by equation (27), for every such
![]() $\bar {\mathbf x}$
, the measure
$\bar {\mathbf x}$
, the measure
![]() $\psi _{\bar {\mathbf x}}$
projects on each pair of coordinates as a product measure. By Corollary 28, we get that
$\psi _{\bar {\mathbf x}}$
projects on each pair of coordinates as a product measure. By Corollary 28, we get that
for Q-a.e.
![]() $\bar {\mathbf x}\in \mathcal D_0$
. This finishes the proof of Case 1.
$\bar {\mathbf x}\in \mathcal D_0$
. This finishes the proof of Case 1.
Case 2: There exist isomorphic components. Consider now the elements
![]() $\bar {\mathbf x}\in \overline {\mathbf X}$
such that, up to a permutation of coordinates, there exist
$\bar {\mathbf x}\in \overline {\mathbf X}$
such that, up to a permutation of coordinates, there exist
![]() $m<n$
and indices
$m<n$
and indices
![]() $0=\ell _0< \ell _1<\cdots <\ell _{m-1}<\ell _m=n$
such that
$0=\ell _0< \ell _1<\cdots <\ell _{m-1}<\ell _m=n$
such that
![]() $(T,\mu _{\bar x_{\ell _{k-1}+1}}),\ldots , (T,\mu _{\bar x_{\ell _k}})$
are isomorphic for every
$(T,\mu _{\bar x_{\ell _{k-1}+1}}),\ldots , (T,\mu _{\bar x_{\ell _k}})$
are isomorphic for every
![]() $k=1,\ldots , m$
and m is minimal in this representation. For every
$k=1,\ldots , m$
and m is minimal in this representation. For every
![]() $m=1,\ldots ,n-1$
, denote by
$m=1,\ldots ,n-1$
, denote by
![]() $\mathcal D_m\subset \overline {\mathbf X}$
the set of elements for which there are exactly m groups of indices in the above decomposition. We will show that this case reduces to Case 1.
$\mathcal D_m\subset \overline {\mathbf X}$
the set of elements for which there are exactly m groups of indices in the above decomposition. We will show that this case reduces to Case 1.
Fix
![]() $m=1,\ldots ,n-1$
and let
$m=1,\ldots ,n-1$
and let
![]() $\bar {\mathbf x}\in \mathcal D_m$
. Let
$\bar {\mathbf x}\in \mathcal D_m$
. Let
![]() $\ell _0,\ldots ,\ell _m$
be as above. Since
$\ell _0,\ldots ,\ell _m$
be as above. Since
![]() $\eta _{\bar {\mathbf x}}$
is ergodic, for every
$\eta _{\bar {\mathbf x}}$
is ergodic, for every
![]() $k=1,\ldots ,m$
, the projection
$k=1,\ldots ,m$
, the projection
![]() $(\pi ^{\ell _{k-1}+1,\ldots ,\ell _{k}})_*\eta _{\bar {\mathbf x}}$
is an ergodic measure for the map
$(\pi ^{\ell _{k-1}+1,\ldots ,\ell _{k}})_*\eta _{\bar {\mathbf x}}$
is an ergodic measure for the map
![]() $T^{\times \ell _{k}-\ell _{k-1}}$
(up to an isomorphism, it is a self-joining of
$T^{\times \ell _{k}-\ell _{k-1}}$
(up to an isomorphism, it is a self-joining of
![]() $(T,\mu _{\bar x_{\ell _k}})$
). Moreover, recalling that
$(T,\mu _{\bar x_{\ell _k}})$
). Moreover, recalling that
![]() $(T,\mu _{\bar x})$
has the MSJ property for every
$(T,\mu _{\bar x})$
has the MSJ property for every
![]() $\bar x\in \overline X$
, we obtain that
$\bar x\in \overline X$
, we obtain that
Thus, the measure
![]() $\eta _{\bar {\mathbf x}}$
is actually a joining of
$\eta _{\bar {\mathbf x}}$
is actually a joining of
![]() $r_1+\cdots +r_m$
automorphisms such that any two of them are either disjoint or isomorphic, and in the latter case,
$r_1+\cdots +r_m$
automorphisms such that any two of them are either disjoint or isomorphic, and in the latter case,
![]() $\eta _{\bar {\mathbf x}}$
projects on the corresponding coordinates as the product measure. Hence, by using Corollary 28, we get that
$\eta _{\bar {\mathbf x}}$
projects on the corresponding coordinates as the product measure. Hence, by using Corollary 28, we get that
![]() $\eta _{\bar {\mathbf x}}$
is a product joining of
$\eta _{\bar {\mathbf x}}$
is a product joining of
![]() $r_1+\cdots +r_m$
ergodic components of T. In other words, we reduced the problem, where equation (27) is satisfied for a smaller number of indices. The remainder of the proof of Case 2 is analogous to the proof of Case 1 by taking
$r_1+\cdots +r_m$
ergodic components of T. In other words, we reduced the problem, where equation (27) is satisfied for a smaller number of indices. The remainder of the proof of Case 2 is analogous to the proof of Case 1 by taking
![]() $n:=r_1+\cdots +r_m$
.
$n:=r_1+\cdots +r_m$
.
Recalling the definition of a characteristic class and
![]() $\mathcal F(T)$
from §2.4, we get the following result.
$\mathcal F(T)$
from §2.4, we get the following result.
Corollary 30. If T satisfies the assumptions of Theorem 29, then
![]() $\mathcal F(T)$
is a characteristic class of elements from
$\mathcal F(T)$
is a characteristic class of elements from
![]() $\operatorname {Erg}^\perp $
.
$\operatorname {Erg}^\perp $
.
Proof. By Lemma 7, Theorem 29 and the fact that any factor of an element of
![]() $\operatorname {Erg}^\perp $
is also a member of this class.
$\operatorname {Erg}^\perp $
is also a member of this class.
We now construct an example to show that the set of automorphisms satisfying the assumptions of Theorem 29 is non-empty. We build it by using the classical cutting and stacking construction of systems of rank 1. We have the following fact, which is a special case of the results by Gao and Hill [Reference Gao and Hill9] and Danilenko [Reference Danilenko2].
Proposition 31. Let
![]() $\bar a=\{a_n\}_{n\in \mathbb {N}}\in \{0,1\}^{\mathbb N}$
be the binary expansion of
$\bar a=\{a_n\}_{n\in \mathbb {N}}\in \{0,1\}^{\mathbb N}$
be the binary expansion of
![]() $a\in [0,1]$
. Let
$a\in [0,1]$
. Let
![]() $T_{a}:[0,1]\to [0,1]$
be a rank 1 automorphism defined in the following way, via the cutting and stacking procedure:
$T_{a}:[0,1]\to [0,1]$
be a rank 1 automorphism defined in the following way, via the cutting and stacking procedure:
-
• on each step, the cutting parameter is equal to 3;
-
• on step n, we add a spacer over the first tower if
 $a_n=0$
and over the second if
$a_n=0$
and over the second if
 $a_n=1$
.
$a_n=1$
.
Assume that
![]() $|a-b|\neq {k}/{2^l}$
for any
$|a-b|\neq {k}/{2^l}$
for any
![]() $k,l\in \mathbb {N}$
. Then,
$k,l\in \mathbb {N}$
. Then,
![]() $T_a $
and
$T_a $
and
![]() $T_b$
are disjoint. Otherwise, they are isomorphic.
$T_b$
are disjoint. Otherwise, they are isomorphic.
By [Reference del Junco, Rahe and Swanson4], the systems considered in the above proposition are ergodic and satisfy the MSJ property. Note that the sequence heights of towers in the cutting and stacking construction described in the above theorem is universal for all
![]() $a\in [0,1]$
. We leave the proof of the following easy lemma to the reader.
$a\in [0,1]$
. We leave the proof of the following easy lemma to the reader.
Lemma 32. The map
![]() $[0,1]\ni a\mapsto T_a\in \operatorname {Aut}(X,\nu )$
is well defined and continuous in
$[0,1]\ni a\mapsto T_a\in \operatorname {Aut}(X,\nu )$
is well defined and continuous in
![]() $[0,1]\setminus \mathbb Q$
.
$[0,1]\setminus \mathbb Q$
.
Let us consider
![]() $S\in \operatorname {Aut}([0,1]\times X, \mathrm {Leb}_{[0,1]}\otimes \nu )$
defined in the following way:
$S\in \operatorname {Aut}([0,1]\times X, \mathrm {Leb}_{[0,1]}\otimes \nu )$
defined in the following way:
Then, in view of Proposition 31 and Lemma 32, by previous remarks, S satisfies the assumptions of Theorem 29. In particular, we have
![]() $S\in \operatorname {Erg}^{\perp }$
.
$S\in \operatorname {Erg}^{\perp }$
.
7 A remark on multipliers
We will now show some connections between the multipliers of a class
![]() $\mathcal {A}^\perp $
and the characteristic classes included in
$\mathcal {A}^\perp $
and the characteristic classes included in
![]() $\mathcal {A}^\perp $
. We recall that
$\mathcal {A}^\perp $
. We recall that
![]() $\mathcal M(\mathcal A^{\perp })$
is always a characteristic class (see Corollary 6).
$\mathcal M(\mathcal A^{\perp })$
is always a characteristic class (see Corollary 6).
Proposition 33. For any T and R, we have that
![]() $T\in \mathcal {M}(\{R\}^\perp )$
provided that for each
$T\in \mathcal {M}(\{R\}^\perp )$
provided that for each
![]() $\unicode{x3bb} \in J_2(T)$
, we have
$\unicode{x3bb} \in J_2(T)$
, we have
![]() $(T\times T,\unicode{x3bb} )\perp R\times R$
, where
$(T\times T,\unicode{x3bb} )\perp R\times R$
, where
![]() $R\times R$
is considered with product measure.
$R\times R$
is considered with product measure.
The proof of the proposition follows by word for word repetition (ignoring the ergodicity of T) of the proof of [Reference Lemańczyk and Parreau19, Proposition 5.1]. Notice moreover that this proposition applies (non- trivially) only if
![]() $R\in \operatorname {WM}$
(because we consider all self-joinings of T, and hence also non-ergodic; however,
$R\in \operatorname {WM}$
(because we consider all self-joinings of T, and hence also non-ergodic; however,
![]() $R \times R$
which is considered with product measure is not ergodic whenever R is not weakly mixing; finally use that two non-trivial non-ergodic automorphisms are not disjoint).
$R \times R$
which is considered with product measure is not ergodic whenever R is not weakly mixing; finally use that two non-trivial non-ergodic automorphisms are not disjoint).
Corollary 34. Assume that
![]() $\mathcal {A}$
is a class closed under taking Cartesian squares. Then,
$\mathcal {A}$
is a class closed under taking Cartesian squares. Then,
![]() $T\in \mathcal {M}(\mathcal {A}^\perp )$
if and only if for each
$T\in \mathcal {M}(\mathcal {A}^\perp )$
if and only if for each
![]() $\unicode{x3bb} \in J_2(T)$
, we have
$\unicode{x3bb} \in J_2(T)$
, we have
![]() $(T\times T,\unicode{x3bb} )\perp R$
for each
$(T\times T,\unicode{x3bb} )\perp R$
for each
![]() $R\in \mathcal {A}$
.
$R\in \mathcal {A}$
.
Note that the necessity in the corollary is obvious and the other direction follows from Proposition 33. Similarly to Proposition 33, the above corollary only applies when
![]() $\mathcal A\subset \operatorname {WM}$
. Corollary 34 implies also the following result.
$\mathcal A\subset \operatorname {WM}$
. Corollary 34 implies also the following result.
Corollary 35. Assume that
![]() $\mathcal {A}$
is a class closed under taking Cartesian squares. Then,
$\mathcal {A}$
is a class closed under taking Cartesian squares. Then,
![]() $\mathcal {M}(\mathcal {A}^\perp )$
is the largest characteristic class included in
$\mathcal {M}(\mathcal {A}^\perp )$
is the largest characteristic class included in
![]() $\mathcal {A}^\perp $
. In particular, the result holds when
$\mathcal {A}^\perp $
. In particular, the result holds when
![]() $\mathcal {A}=\operatorname {WM}$
.
$\mathcal {A}=\operatorname {WM}$
.
Note that
![]() $\operatorname {ID} $
satisfies the assumptions of Corollary 35. It would be interesting to know whether the assertion of Corollary 35 holds for any class
$\operatorname {ID} $
satisfies the assumptions of Corollary 35. It would be interesting to know whether the assertion of Corollary 35 holds for any class
![]() $\mathcal A$
. Notice that for
$\mathcal A$
. Notice that for
![]() $\mathcal {A}= \operatorname {Erg}$
, the assumption on the Cartesian squares is not satisfied as the Cartesian square of any (non-trivial) rotation is not ergodic. More than that, in
$\mathcal {A}= \operatorname {Erg}$
, the assumption on the Cartesian squares is not satisfied as the Cartesian square of any (non-trivial) rotation is not ergodic. More than that, in
![]() $\operatorname {Erg}^\perp $
, the class of multipliers is
$\operatorname {Erg}^\perp $
, the class of multipliers is
![]() $\operatorname {ID} $
, and it is the smallest characteristic class included in
$\operatorname {ID} $
, and it is the smallest characteristic class included in
![]() $\operatorname {Erg}^\perp $
(the existence of larger than
$\operatorname {Erg}^\perp $
(the existence of larger than
![]() $\operatorname {ID} $
characteristic classes follows from Corollary 30), so the assertion of Corollary 35 fails for
$\operatorname {ID} $
characteristic classes follows from Corollary 30), so the assertion of Corollary 35 fails for
![]() $\operatorname {Erg}^\perp $
.
$\operatorname {Erg}^\perp $
.
A general question arises, whether given a characteristic class
![]() $\mathcal {C}\subset \mathcal A^{\perp }$
, there exists a maximal characteristic class
$\mathcal {C}\subset \mathcal A^{\perp }$
, there exists a maximal characteristic class
![]() $\mathcal {C'}\subset \mathcal A^{\perp }$
such that
$\mathcal {C'}\subset \mathcal A^{\perp }$
such that
![]() $\mathcal {C}\subset \mathcal {C'}$
. To see that this holds, we apply the Kuratowski–Zorn lemma. Consider a chain
$\mathcal {C}\subset \mathcal {C'}$
. To see that this holds, we apply the Kuratowski–Zorn lemma. Consider a chain
![]() $(\mathcal {C}_i)_{i\in \mathbb {I}}$
of characteristic classes such that
$(\mathcal {C}_i)_{i\in \mathbb {I}}$
of characteristic classes such that
![]() $\mathcal {C}\subset \mathcal C_i\subset \mathcal A^{\perp }$
. Let
$\mathcal {C}\subset \mathcal C_i\subset \mathcal A^{\perp }$
. Let
![]() $\tilde {\mathcal C}$
be the smallest characteristic class containing
$\tilde {\mathcal C}$
be the smallest characteristic class containing
![]() $\bigcup _{i\in \mathbb {I}} \mathcal {C}_i$
. We need to show that
$\bigcup _{i\in \mathbb {I}} \mathcal {C}_i$
. We need to show that
![]() $\tilde {\mathcal C}\subset \mathcal A^{\perp }$
. It is enough to check that if
$\tilde {\mathcal C}\subset \mathcal A^{\perp }$
. It is enough to check that if
![]() $T_n\in \bigcup _{i\in \mathbb {I}} \mathcal {C}_i$
,
$T_n\in \bigcup _{i\in \mathbb {I}} \mathcal {C}_i$
,
![]() $n=1,2,\ldots,$
then for every
$n=1,2,\ldots,$
then for every
![]() $\eta \in J(T_1,T_2,\ldots )$
, we have
$\eta \in J(T_1,T_2,\ldots )$
, we have
![]() $(T_1\times T_2 \times \cdots , \eta )\in \mathcal {A}^\perp $
.
$(T_1\times T_2 \times \cdots , \eta )\in \mathcal {A}^\perp $
.
Let
![]() $T_k \in \mathcal {C}_{i_k}$
,
$T_k \in \mathcal {C}_{i_k}$
,
![]() $k=1,\ldots , n$
, then, since
$k=1,\ldots , n$
, then, since
![]() $(\mathcal C_i)_{i\in \mathbb I}$
is a chain, without loss of generality, we can assume that
$(\mathcal C_i)_{i\in \mathbb I}$
is a chain, without loss of generality, we can assume that
![]() $T_1, T_2,\ldots , T_n \in \mathcal {C}_{i_n}$
. Since
$T_1, T_2,\ldots , T_n \in \mathcal {C}_{i_n}$
. Since
![]() $\mathcal {C}_{i_n}\subset \mathcal A^{\perp }$
is a characteristic class, we receive that all joinings of
$\mathcal {C}_{i_n}\subset \mathcal A^{\perp }$
is a characteristic class, we receive that all joinings of
![]() $T_1, T_2,\ldots , T_n$
are in
$T_1, T_2,\ldots , T_n$
are in
![]() $\mathcal {C}_{i_n}\subset \mathcal A^{\perp }$
. To conclude, it remains to use the fact that every infinite joining is an inverse limit of finite joinings.
$\mathcal {C}_{i_n}\subset \mathcal A^{\perp }$
. To conclude, it remains to use the fact that every infinite joining is an inverse limit of finite joinings.
Corollary 36. For every T satisfying the assumptions of Theorem 29, there exists maximal characteristic class
![]() $\mathcal {C}\ni T$
such that
$\mathcal {C}\ni T$
such that
![]() $\mathcal {M}(\operatorname {Erg}^\perp )\subset \mathcal {C}\subsetneq \operatorname {Erg}^{\perp }$
.
$\mathcal {M}(\operatorname {Erg}^\perp )\subset \mathcal {C}\subsetneq \operatorname {Erg}^{\perp }$
.
We have not been able to describe the maximal characteristic classes in
![]() $\operatorname {Erg}^{\perp }$
, it is even not clear whether there is only one.
$\operatorname {Erg}^{\perp }$
, it is even not clear whether there is only one.
Acknowledgements
We thank Mariusz Lemańczyk for numerous comments and discussions, and the anonymous referee for improving the readability of the article and simplifying some arguments. The first author was supported by NCN Grant 2022/45/B/ST1/00179. This article is also a part of the project IZES-ANR-22-CE40-0011.