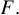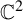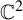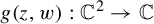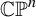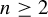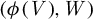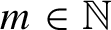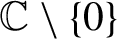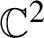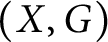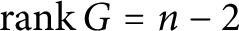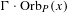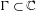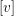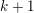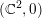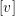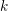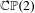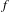Refine search
Actions for selected content:
27 results
Generic unfolding of an antiholomorphic parabolic point of codimension k
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of generic automorphisms of Stein manifolds with the density property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 09 June 2025, pp. 3305-3324
- Print publication:
- November 2025
-
- Article
- Export citation
A flower theorem in dimension two
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 08 May 2025, pp. 3223-3254
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Every complex Hénon map is exponentially mixing of all orders and satisfies the CLT
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A fixed-point curve theorem for finite-orbits local diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 4138-4165
- Print publication:
- December 2023
-
- Article
- Export citation
Invariant escaping Fatou components with two rank-one limit functions for automorphisms of
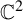 ${\mathbb C}^2$
${\mathbb C}^2$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 22 November 2021, pp. 401-416
- Print publication:
- February 2023
-
- Article
- Export citation
Analytic classification of germs of parabolic antiholomorphic diffeomorphisms of codimension k
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3619-3655
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic points of post-critically algebraic holomorphic endomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 2382-2414
- Print publication:
- July 2022
-
- Article
- Export citation
BOUNDNESS OF INTERSECTION NUMBERS FOR ACTIONS BY TWO-DIMENSIONAL BIHOLOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 1677-1700
- Print publication:
- September 2022
-
- Article
- Export citation
Value distribution of derivatives in polynomial dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 05 January 2021, pp. 3780-3806
- Print publication:
- December 2021
-
- Article
- Export citation
A local study near the Wolff point on the ball
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 17 June 2020, pp. 761-779
-
- Article
- Export citation
Free abelian group actions on normal projective varieties: submaximal dynamical rank case
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 14 May 2020, pp. 1057-1073
- Print publication:
- August 2021
-
- Article
- Export citation
Orbits of homogeneous polynomials on Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 1627-1655
- Print publication:
- June 2021
-
- Article
- Export citation
Characteristic directions of two-dimensional biholomorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 31 March 2020, pp. 869-880
- Print publication:
- May 2020
-
- Article
- Export citation
The numbers of periodic orbits hidden at fixed points of holomorphic maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 03 September 2019, pp. 578-592
- Print publication:
- February 2021
-
- Article
- Export citation
Dimension of ergodic measures and currents on
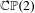 $\mathbb{C}\mathbb{P}(2)$
$\mathbb{C}\mathbb{P}(2)$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 04 January 2019, pp. 2131-2155
- Print publication:
- August 2020
-
- Article
- Export citation
Chaotic Vibration of a Two-dimensional Non-strictly Hyperbolic Equation
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 4 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 768-786
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
Renormalization in the golden-mean semi-Siegel Hénon family: universality and non-rigidity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 25 September 2018, pp. 1108-1152
- Print publication:
- April 2020
-
- Article
- Export citation
DEGENERATION OF ENDOMORPHISMS OF THE COMPLEX PROJECTIVE SPACE IN THE HYBRID SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 31 August 2018, pp. 1141-1183
- Print publication:
- July 2020
-
- Article
- Export citation
SUR L’ÉTUDE DE L’ENTROPIE DESAPPLICATIONS MÉROMORPHES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 02 November 2017, pp. 1-19
- Print publication:
- January 2020
-
- Article
- Export citation