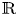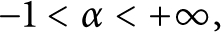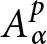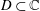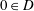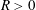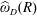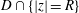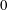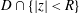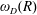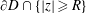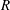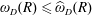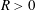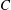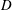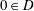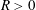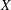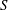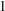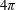Refine search
Actions for selected content:
21 results
VARIABILITY REGIONS FOR THE nth DERIVATIVE OF BOUNDED ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 14 February 2025, pp. 312-322
- Print publication:
- October 2025
-
- Article
- Export citation
Schwarz lemma for harmonic functions in the unit ball
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 616-633
-
- Article
- Export citation
Spectral theory of the invariant Laplacian on the disk and the sphere – a complex analysis approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 01 March 2024, pp. 940-974
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Liouville property and quasi-isometries on negatively curved Riemannian surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 131-153
- Print publication:
- February 2024
-
- Article
- Export citation
Hyperbolic metric and membership of conformal maps in the Bergman space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 06 May 2020, pp. 174-181
- Print publication:
- March 2021
-
- Article
- Export citation
SPHERICALIZATION AND FLATTENING PRESERVE UNIFORM DOMAINS IN NONLOCALLY COMPACT METRIC SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 February 2020, pp. 68-89
- Print publication:
- February 2022
-
- Article
- Export citation
Short closed geodesics with self-intersections
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 3 / November 2020
- Published online by Cambridge University Press:
- 24 January 2020, pp. 623-638
- Print publication:
- November 2020
-
- Article
- Export citation
On a Property of Harmonic Measure on Simply Connected Domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 22 November 2019, pp. 297-317
- Print publication:
- April 2021
-
- Article
- Export citation
Green Function and Self-adjoint Laplacians on Polyhedral Surfaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 02 July 2019, pp. 1324-1351
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Determinant of the Laplacian on Tori of Constant Positive Curvature with one Conical Point
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 341-347
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
MAPPING PROPERTIES OF A SCALE INVARIANT CASSINIAN METRIC AND A GROMOV HYPERBOLIC METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 18 August 2017, pp. 141-152
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Function-theoretic Properties for the Gauss Maps of Various Classes of Surfaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 6 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1411-1434
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
Versions of Schwarz's Lemma for Condenser Capacity and Inner Radius
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-250
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
Holomorphic mappings between compact Riemann surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 109-126
-
- Article
-
- You have access
- Export citation
THE ROLE OF FUNNELS AND PUNCTURES IN THE GROMOV HYPERBOLICITY OF RIEMANN SURFACES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 49 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 30 May 2006, pp. 399-425
-
- Article
-
- You have access
- Export citation
CONVEX REGIONS IN THE PLANE AND THEIR DOMES
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 92 / Issue 3 / May 2006
- Published online by Cambridge University Press:
- 18 April 2006, pp. 624-654
- Print publication:
- May 2006
-
- Article
- Export citation
QUASICONFORMAL DEFORMATIONS AND VOLUME GROWTH
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 92 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 19 December 2005, pp. 161-199
- Print publication:
- January 2006
-
- Article
- Export citation
STRUCTURE THEOREMS FOR RIEMANN AND TOPOLOGICAL SURFACES
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 28 January 2004, pp. 153-168
- Print publication:
- February 2004
-
- Article
- Export citation
Smale's mean value conjecture for odd polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 409-412
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
Uniformly perfect sets and distortion of holomorphic functions
-
- Journal:
- Nagoya Mathematical Journal / Volume 164 / December 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 17-33
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation













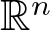
 of the “complexified unit circle”
of the “complexified unit circle”