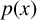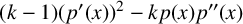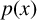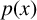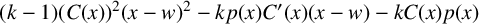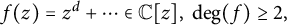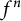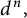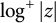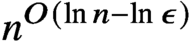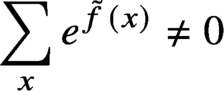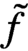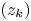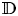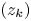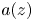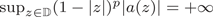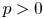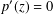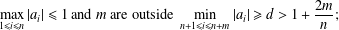Refine search
Actions for selected content:
30 results
UPPER BOUNDS ON POLYNOMIAL ROOT SEPARATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 274-289
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random analytic functions with a prescribed growth rate in the unit disk
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 April 2024, pp. 1546-1569
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE NUMBER OF REAL ZEROS OF POLYNOMIALS OF EVEN DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 89-93
- Print publication:
- February 2024
-
- Article
- Export citation
Mahler measure of polynomial iterates
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 881-885
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An algebraic approach to a quartic analogue of the Kontsevich model
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 20 September 2022, pp. 471-495
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero and uniqueness sets for Fock spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 532-543
- Print publication:
- June 2023
-
- Article
- Export citation
On the roots of polynomials with log-convex coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 470-493
- Print publication:
- April 2023
-
- Article
- Export citation
More on zeros and approximation of the Ising partition function
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e46
-
- Article
-
- You have access
- Open access
- Export citation
Une note sur la densité des zéros des sommes partielles de la fonction zeta de Dedekind sur un corps quadratique
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 409-415
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On non-separated zero sequences of solutions of a linear differential equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 247-261
-
- Article
- Export citation
A STABILITY VERSION OF THE GAUSS–LUCAS THEOREM AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 05 September 2019, pp. 262-269
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Division algebras of slice functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 15 March 2019, pp. 2055-2082
- Print publication:
- August 2020
-
- Article
- Export citation
On the Size of an Expression in the Nyman–Beurling-Báez–Duarte Criterion for the Riemann Hypothesis
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 3 / 01 September 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 622-627
- Print publication:
- 01 September 2018
-
- Article
-
- You have access
- Export citation
INVERSE BERNSTEIN INEQUALITIES AND MIN–MAX–MIN PROBLEMS ON THE UNIT CIRCLE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 581-590
- Print publication:
- September 2015
-
- Article
- Export citation
A Note on a Conjecture of S. Stahl
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 4 / 01 August 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 958-959
- Print publication:
- 01 August 2008
-
- Article
-
- You have access
- Export citation
Erratum: On the Zeros of Some Genus Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 4 / 01 August 2008
- Published online by Cambridge University Press:
- 20 November 2018, p. 960
- Print publication:
- 01 August 2008
-
- Article
-
- You have access
- Export citation
The zeros of random polynomials cluster uniformly near the unit circle
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 734-746
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Unimodular Roots of Special Littlewood Polynomials
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 3 / 01 September 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 438-447
- Print publication:
- 01 September 2006
-
- Article
-
- You have access
- Export citation
COUNTEREXAMPLES TO TISCHLER'S STRONG FORM OF SMALE'S MEAN VALUE CONJECTURE
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 08 February 2005, pp. 95-106
- Print publication:
- January 2005
-
- Article
- Export citation
Elementary Symmetric Polynomials in Numbers of Modulus 1
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 2 / 01 April 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 239-262
- Print publication:
- 01 April 2002
-
- Article
-
- You have access
- Export citation